Question 1. Electromagnetic field. EMF vectors. Graphic representation of fields Electromagnetic field- a fundamental physical field interacting with electrically charged bodies, as well as with bodies that have their own dipole and multipole electric and magnetic moments. It is a combination of electric and magnetic fields that can, under certain conditions, generate each other, but in fact they are one entity formalized through the electro tensor magnetic field.

Electromagnetic field vectors:

Electric field. One of the main vector characteristics of the electromagnetic field is tension electric field. Under the electric field strength is meant the force with which the electric field acts on a positive unit point charge introduced into the field.

(1)

In physics, this is specified: the charge q must be small enough so that the change in the distribution of electric charges that form this field can be neglected.

Let's consider this process in a simplified way within the classical theory:

Matter is made up of atoms. An atom consists of a positive nucleus and negative electrons. The combination of atoms form a molecule. There are substances with polar and non-polar molecules. In the case of non-polar atoms or molecules, the point of application of the resultant of all forces acting on negative charges coincides with the point of application of the resultant of all forces acting on positive charges. This is possible if the center of gravity of the molecule coincides with the center of gravity of the protons. In polar molecules, these centers do not coincide, and a polar molecule can be likened to an elementary dipole, i.e. a system consisting of two opposite charges separated in space by a distance l. Dipoles are characterized by a dipole moment:

The effect of substance polarization is characterized by the total dipole moment: in the considered volume dV:

(4) - dipole moment corresponding to individual atoms or molecules. Formula (4) the geometric summation is carried out in the volume V.

Along with the electric field strength, another vector quantity is also used: - electric induction vector, or electric displacement vector: (8); ;

Hence it follows that for the same arrangement and magnitude of electric charges, the vector field does not depend on the properties of the medium.

As you know, the force acting on a positive point electric charge moving in a magnetic field is determined by the Lorentz force: (1),

where (2) ; (3) ; .

The magnetic force is proportional to the speed of movement of the charge and is directed perpendicular to the direction of movement of the charge.

Physical meaning: the value is called the vector of magnetic induction and is equal to the force with which the magnetic field acts on a positive point charge moving at unit speed in a direction perpendicular to it.

Fields are depicted using lines of force. By "power" they mean lines, at each point of which the tangents depict the direction of the depicted field. The change in the amplitude of the field is indicated by the number of lines of force per unit area of ​​the surface perpendicular to the lines of force. Let there be a vector field BUT, which at each point in space can be expressed in the Cartesian system:

l- field line fields BUT, - unit vectors. We obtain the differential equation of the field line: dr can be written in terms of its projection: (1),

We assume that the function describing the field line is known:

From vector analysis it is known that two vectors are parallel if the ratios of the corresponding projections are equal:

This is the differential equation of the field line.

Question 2. Maxwell's first equation in integral and differential forms.

Maxwell's first equation is a generalization of the total current law (Ampère's law). In the pre-Maxwellian formulation, this equation could be formulated as follows: circulation of the intensity vector H magnetic field along a closed circuit Г is equal to the current / penetrating this circuit:

Before Maxwell, the current / understood only the conduction current. In the general case, the distribution of current / inside the circuit G can be non-uniform. Wherein

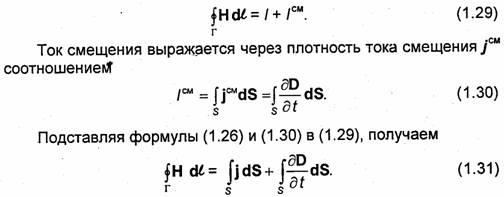
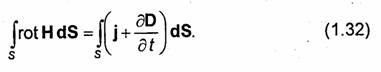
Question 3. Maxwell's second equation in integral and differential forms.

Maxwell's second equation is

generalization of Faraday's law of induction, which is formulated as follows: if a closed circuit Г is permeated with a variable magnetic fluxФ, then an EMF e appears in the circuit, equal to the rate of change of this flow:

The minus sign on the right side of formula (1.34) means that the emf that arises in the circuit always tends, as it were, to prevent a change in the flow penetrating this circuit. This provision is known as "Lenz's rule".

Relation (1.37) is formulated for a contour of finite dimensions and is called Maxwell's second equation in integral form. Maxwell also formulated this equation in differential form.

Question 4. Maxwell's third equation in integral and differential forms.

The third Maxwell equation is a generalization of the Gauss law for the case of variable processes. The Gauss law relates the flow of the electric displacement vector through an arbitrary closed surface S with the charge Q concentrated inside this surface:

where dS = n o dS ; n 0 - unit vector of the outer normal to the surface S.

Substituting (1.41) into (1.40), we obtain

Equation (1.43) is usually called Maxwell's third equation in integral form. To go to the differential form

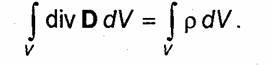
This equality must hold for an arbitrary volume V, which is only possible if

Question 5. Maxwell's fourth equation in integral and differential forms.

Maxwell's fourth equation in integral form coincides with the Gauss law for a magnetic field, which can be formulated as follows. Vector flow AT through any closed surface S is equal to zero, i.e.

This means that there are no vector lines AT, which only enter the closed surface S (or, conversely, only exit the surface S): they always penetrate it (Fig. 1.9).

Equation (1.46) is called Maxwell's fourth equation in integral form. One can pass to the differential form of equation (1.46) using the Ostrogradsky-Gauss theorem in the same way as it was done in the case of the third Maxwell equation. As a result, we get

divB = 0 (1.47)

Equation (1.47) is Maxwell's fourth equation. It shows that in nature there are no solitary magnetic charges of the same sign. It also follows from this equation that the lines of the vector AT(field lines of the magnetic field) are continuous.

Maxwell's system of equations includes four basic equations

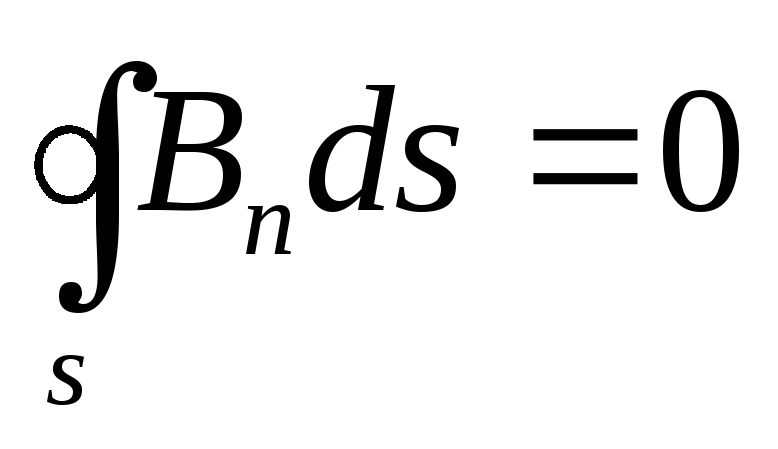, (3.2)

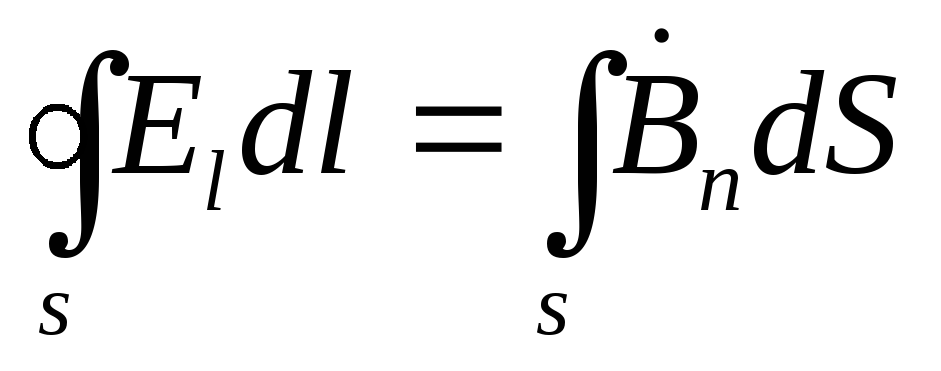, (3.3)

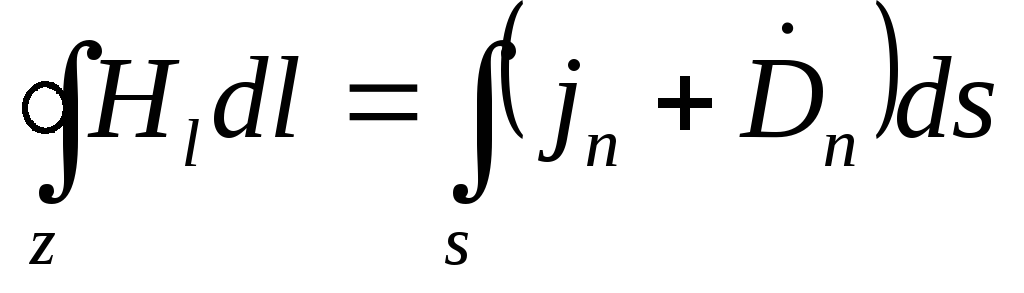. (3.4)

This system is complemented by three material equations, linking physical quantities included in the Maxwell equations:

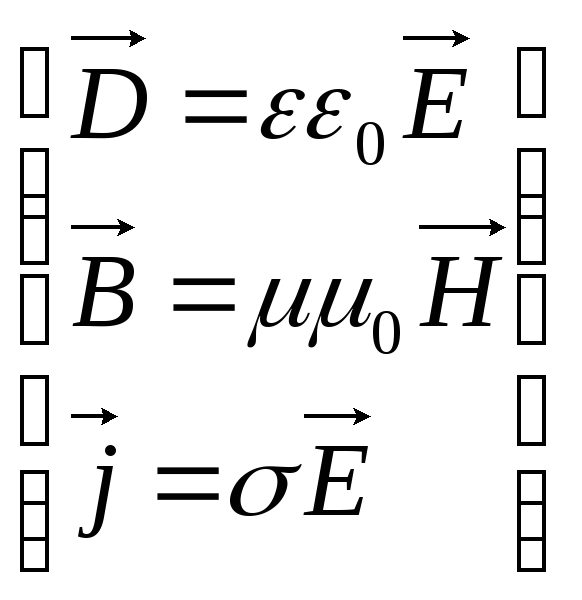(3.5)

Let's remember physical meaning these mathematical phrases.

The first equation (3.1) states that electrostatic the field can only be created by electric charges. In this equation 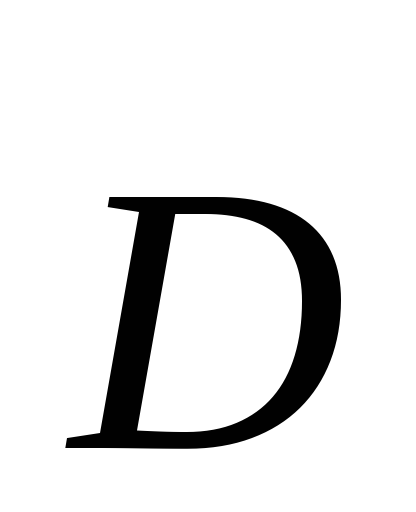is the electric displacement vector, ρ is the volume density of the electric charge.

The flow of the electric displacement vector through any closed surface is equal to the charge enclosed inside this surface.

As the experiment shows, the flux of the magnetic induction vector through a closed surface is always equal to zero (3.2)

Comparison of equations (3.2) and (3.1) allows us to conclude that there are no magnetic charges in nature.

Equations (3.3) and (3.4) are of great interest and importance. Here we consider the circulation of the vectors of electric strength ( ) and magnetic ( ) fields along a closed contour.

Equation (3.3) states that the alternating magnetic field ( 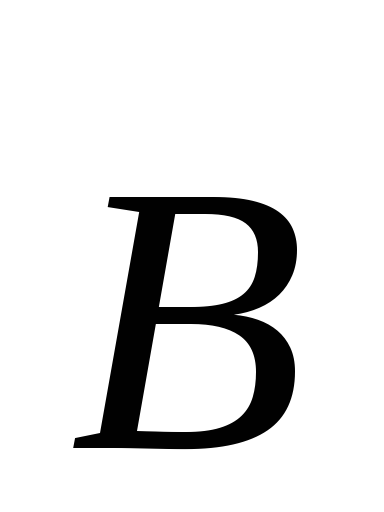) is the source of the vortex electric field ( ).This is nothing more than a mathematical record of the phenomenon of Faraday's electromagnetic induction.

Equation (3.4) establishes a connection between the magnetic field and the alternating electric field. According to this equation, the magnetic field can be created not only by the conduction current ( 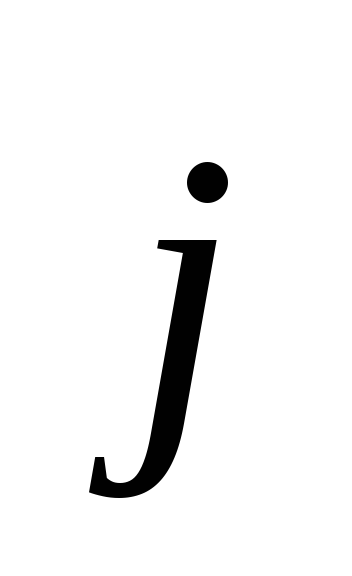), but also by an alternating electric field .

In these equations:

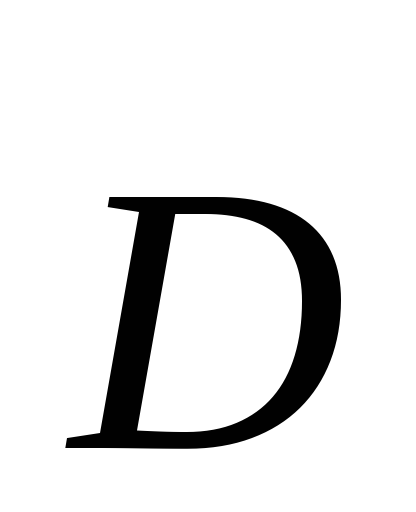is the electric displacement vector,

H- magnetic field strength,

E- electric field strength,

j is the conduction current density,

μ - magnetic permeability of the medium,

ε is the dielectric constant of the medium.

1. Electromagnetic waves. Properties of electromagnetic waves

Last semester, completing the consideration of the system of equations of classical Maxwell electrodynamics, we found that the joint solution of the last two equations (on the circulation of vectors and ) leads to a differential wave equation.

So we got the wave equation of the "Y" wave:

. (3.6)

The electrical component y - the wave propagates in the positive direction of the X axis with phase velocity

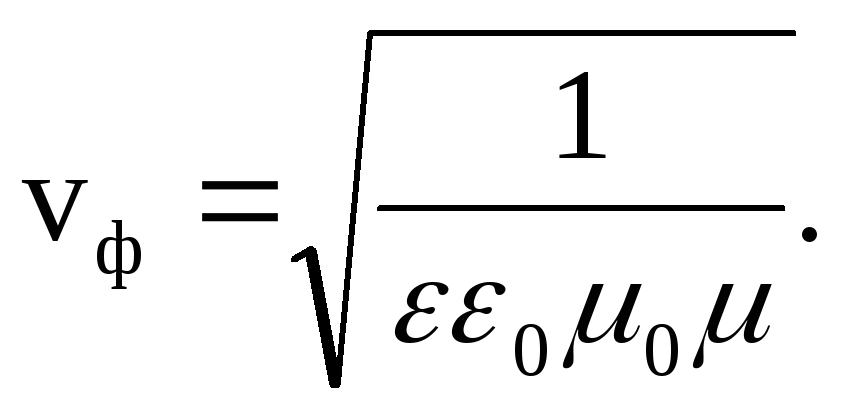(3.7)

A similar equation describes the change in space and time of the magnetic field y - waves:

. (3.8)

Analyzing the obtained results, it is possible to formulate a number of properties inherent in electromagnetic waves.

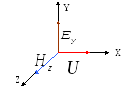
1. Plane "y" - the wave is a linearly polarized transverse wave. Electric strength vectors ( 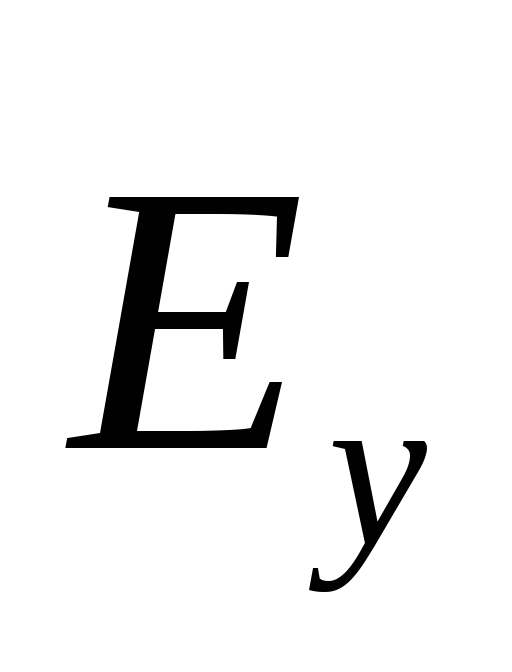), magnetic ( ) field and phase velocity of the wave ( 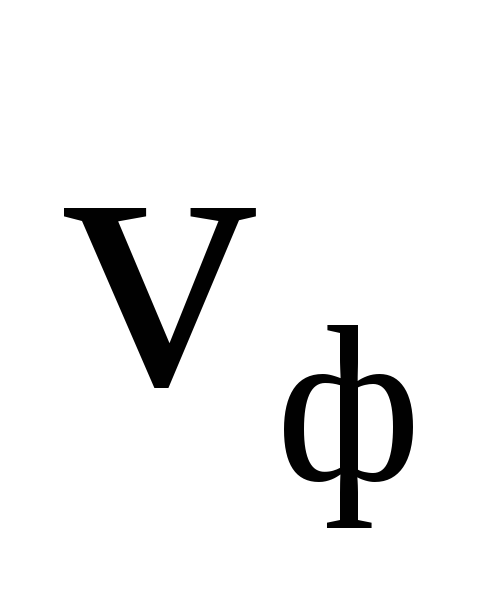) are mutually perpendicular and form a “right-handed” system (Fig. 3.1).

2. At each point in the space of the wave component H z is proportional to the electric field strength E y:

Here, the sign "+" corresponds to a wave propagating in the positive direction of the X axis. The sign "-" - in the negative direction.

3. An electromagnetic wave moves along the X axis with a phase velocity

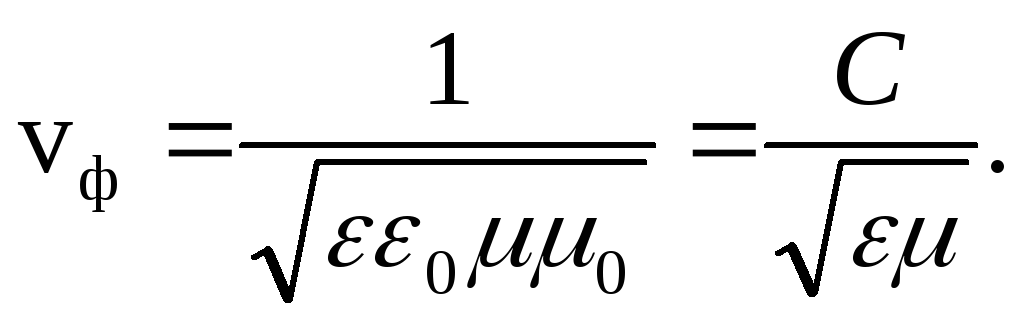
Here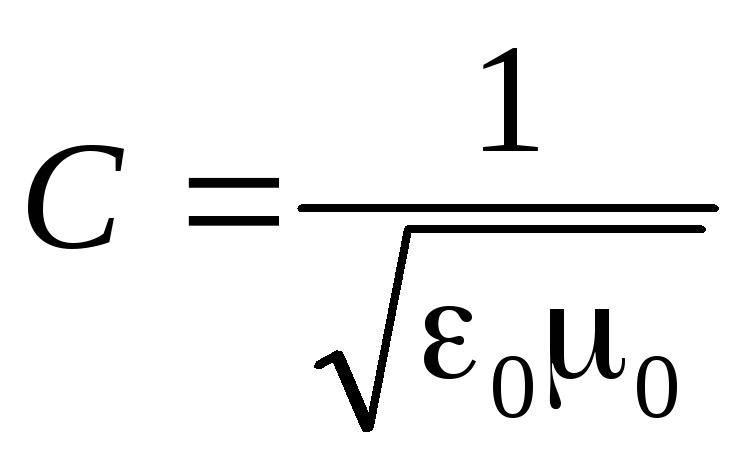

.

When an electromagnetic wave propagates in vacuum (ε = 1, μ = 1), the phase velocity

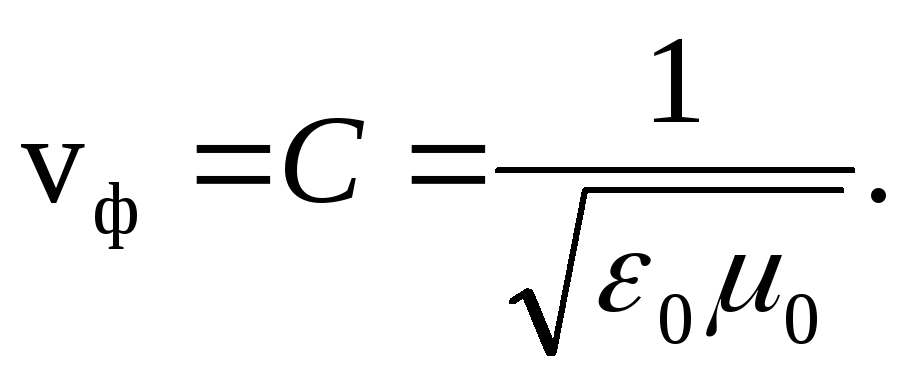
Here the electrical constant ε 0 = 8.85 10 -12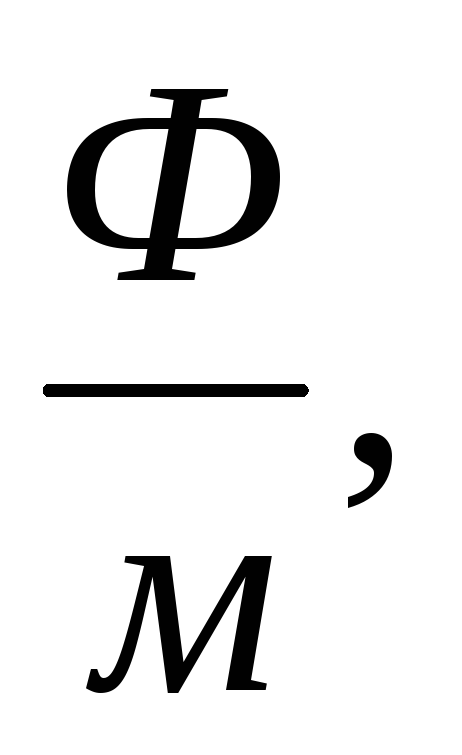

magnetic constant μ 0 = 4π 10 -7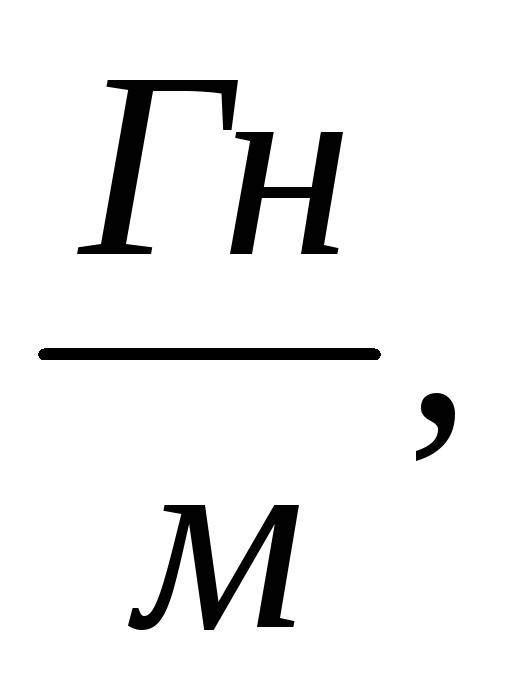

.

.

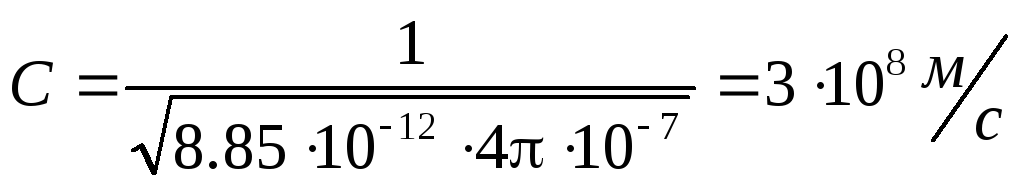The coincidence of the speed of an electromagnetic wave in vacuum with the speed of light was the first proof of the electromagnetic nature of light.

In a vacuum, the relationship between the strength of the magnetic and electric fields in the wave is simplified.

.

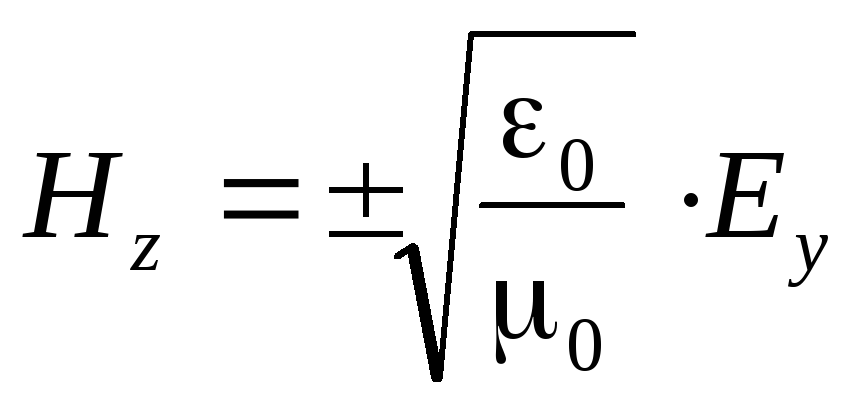When an electromagnetic wave propagates in a dielectric medium (μ = 1)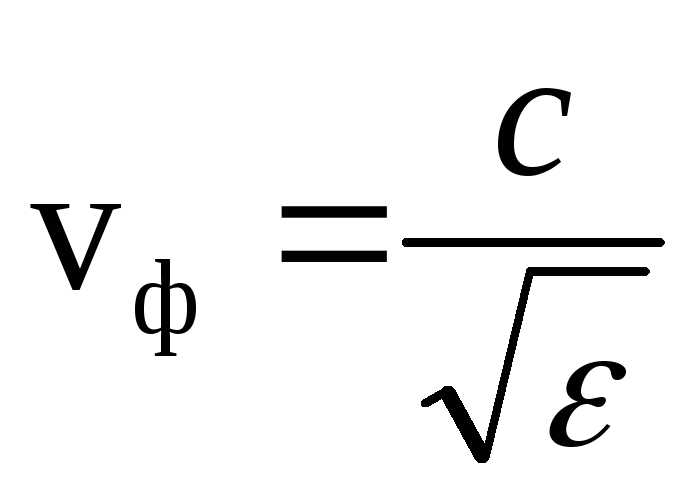

and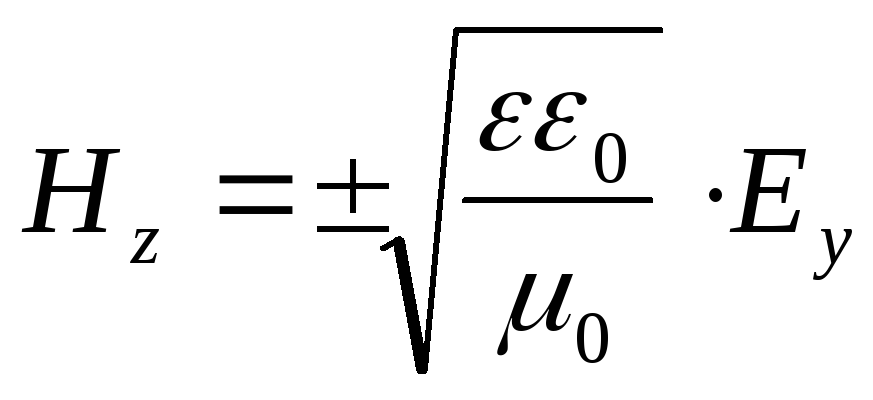

.

The introduction of the concept of displacement current by Maxwell led him to the completion of the unified macroscopic theory of the electromagnetic field he created, which made it possible from a unified point of view not only to explain electrical and magnetic phenomena, but also to predict new ones, the existence of which was subsequently confirmed.

Maxwell's theory is based on the four equations discussed above:

1. The electric field (see § 137) can be both potential ( e q) and vortex ( E B), so the strength of the total field E=E Q+ E b. Since the circulation of the vector e q is equal to zero (see (137.3)), and the circulation of the vector E B is determined by expression (137.2), then the circulation of the total field strength vector

This equation shows that the sources of the electric field can be not only electric charges, but also time-varying magnetic fields.

2. Generalized vector circulation theorem H(see (138.4)):

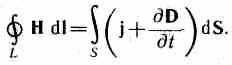
This equation shows that magnetic fields can be excited either by moving charges (electric currents) or by alternating electric fields.

3. Gauss's theorem for the field D(see (89.3)):

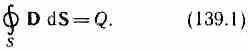
If the charge is distributed continuously inside a closed surface with a bulk density , then formula (139.1) will be written as

4. Gauss's theorem for the field B (see (120.3)):

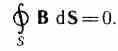
And 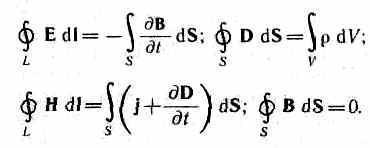So, complete system of Maxwell equations in integral form:

The quantities included in the Maxwell equations are not independent and there is the following relationship between them (isotropic non-ferroelectric and non-ferromagnetic media):

D= 0 E,

B= 0 H,

j=E,

where  0 and  0 are respectively electric and magnetic constants,  and  - respectively dielectric and magnetic permeability,  - specific conductivity of the substance.

It follows from Maxwell's equations that the sources of an electric field can be either electric charges or time-varying magnetic fields, and magnetic fields can be excited either by moving electric charges (electric currents) or by alternating electric fields. Maxwell's equations are not symmetrical with respect to electric and magnetic fields. This is due to the fact that in nature there are electric charges, but there are no magnetic charges.

D 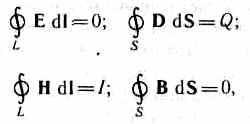for stationary fields (E= const and AT= const) Maxwell's equations take the form

i.e., the sources of the electric field in this case are only electric charges, the sources of the magnetic field are only conduction currents. In this case, the electric and magnetic fields are independent of each other, which makes it possible to study separately permanent electric and magnetic fields.

Using the Stokes and Gauss theorems known from vector analysis, m 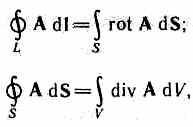one can imagine the complete system of Maxwell's equations in differential form(characterizing the field at each point in space):

If charges and currents are distributed in space continuously, then both forms of Maxwell's equations are integral

and 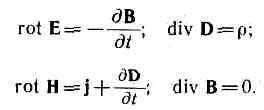differential - equivalent. However, when there are fracture surfaces- surfaces on which the properties of the medium or fields change abruptly, then the integral form of the equations is more general.

Maxwell's equations in differential form assume that all quantities in space and time change continuously. To achieve mathematical equivalence of both forms of Maxwell's equations, the differential form is supplemented boundary conditions, which must be satisfied by the electromagnetic field at the interface between two media. The integral form of Maxwell's equations contains these conditions. They have been considered before (see § 90, 134):

D 1 n = D 2 n , E 1  = E 2  , B 1 n = B 2 n , H 1  = H 2 

(the first and last equations correspond to cases where there are neither free charges nor conduction currents at the interface).

Maxwell's equations are the most general equations for electric and magnetic fields in resting environments. They play the same role in the theory of electromagnetism as Newton's laws in mechanics. It follows from Maxwell's equations that an alternating magnetic field is always associated with the electric field generated by it, and an alternating electric field is always associated with the magnetic field generated by it, that is, the electric and magnetic fields are inextricably linked with each other - they form a single electromagnetic field.

Maxwell's theory, being a generalization of the basic laws of electrical and magnetic phenomena, was able to explain not only already known experimental facts, which is also an important consequence of it, but also predicted new phenomena. One of the important conclusions of this theory was the existence of a magnetic field of displacement currents (see § 138), which allowed Maxwell to predict the existence electromagnetic waves- an alternating electromagnetic field propagating in space with a finite speed. Later it was proved that the speed of propagation of a free electromagnetic field (not related to charges and currents) in vacuum is equal to the speed of light c = 3 10 8 m/s. This conclusion and the theoretical study of the properties of electromagnetic waves led Maxwell to create the electromagnetic theory of light, according to which light is also electromagnetic waves. Electromagnetic waves were experimentally obtained by the German physicist G. Hertz (1857-1894), who proved that the laws of their excitation and propagation are completely described by Maxwell's equations. Thus, Maxwell's theory was experimentally confirmed.

To electromagnetic field only Einstein's principle of relativity is applicable, since the fact that electromagnetic waves propagate in vacuum in all frames of reference with the same speed With incompatible with Galileo's principle of relativity.

According to Einstein's principle of relativity mechanical, optical and electromagnetic phenomena in all inertial frames of reference proceed in the same way, that is, they are described by the same equations. Maxwell's equations are invariant under Lorentz transformations: their form does not change when passing

from one inertial system reference to another, although the values E, V,D, N they are converted according to certain rules.

It follows from the principle of relativity that a separate consideration of electric and magnetic fields has a relative meaning. So, if the electric field is created by a system of fixed charges, then these charges, being fixed with respect to one inertial frame of reference, move relative to another and, therefore, will generate not only an electric, but also a magnetic field. Similarly, a fixed-current conductor with respect to one inertial frame of reference, exciting a constant magnetic field at each point in space, moves relative to other inertial frames, and the alternating magnetic field created by it excites a vortex electric field. Thus, Maxwell's theory, its experimental confirmation, as well as Einstein's principle of relativity lead to a unified theory of electrical, magnetic and optical phenomena based on the idea of ​​an electromagnetic field.

Classifications of media in relation to the electromagnetic field

The properties of the medium with respect to the electromagnetic field are determined by the parameters

Medium conductivity

If these parameters depend on the magnitude of the field, then linear environment, and if at least 1 parameter depends on the field value, then the environment is non-linear.

Linear media are divided into 4 groups

1. Homogeneous, where these parameters do not depend on the coordinates.

2. Inhomogeneous, where these parameters depend on the coordinates.

3. Isotropic, the properties are the same in all directions.

4. Anisotropic, properties are different in all directions.

Maxwell's equations in differential, integral and complex forms

1 Maxwell equation in differential form: Electric charge is a source of electrical induction.

2 Maxwell equation. There are no magnetic charges

3 Maxwell's equation. The change in magnetic induction generates a vortex electric field

4 Maxwell equation. Electricity and a change in electrical induction generate a vortex magnetic field

In the same order, the integral notation

Electrical induction flow through a closed surface s proportional to the amount of free charge in the volume v that surrounds the surface s.

The flux of magnetic induction through a closed surface is zero (magnetic charges do not exist).

Change in the flux of magnetic induction passing through an open surface s, taken with the opposite sign, is proportional to the circulation of the electric field in a closed loop l s.

The total electric current of free charges and the change in the flow of electric induction through an open surface s, are proportional to the circulation of the magnetic field in a closed circuit l, which is the boundary of the surface s.

Maxwell's equations for complex amplitudes

3. Balance equation of instantaneous power values

As noted in 1.1, the electromagnetic field is one of the forms of matter. Like any other form of matter, it has energy. This energy can spread through space and be converted into other forms of energy.

Let us formulate the balance equation for instantaneous power values ​​in relation to a certain volume V, bounded by the surface S (Fig. 1.23). Let in volume V, filled with a homogeneous isotropic medium, there are third-party sources. From general physical concepts, it is obvious that the power released by third-party sources can be spent on Joule losses and on changing the energy of the electromagnetic field inside V, and can also be partially scattered, escaping into the surrounding space through the surface S. In this case, the equality

where R st is the power of third-party sources; R P - power of Joule losses inside the volume V; R Σ is the power passing through the surface S; W- energy of an electromagnetic field concentrated in a volume V, a dW/dt- power expended to change energy in volume v.

AT this section the equations of state (1.53) will be used. These equations do not allow taking into account the energy losses during polarization and magnetization of the medium. Therefore, the term R P in equality (1.120) actually determines the power of Joule losses in the volume V , caused by conduction current.

Equation (1.120) gives only a qualitative idea of ​​the energy relationships. To obtain quantitative relationships, you need to use Maxwell's equations. Consider the first Maxwell equation, taking into account external currents (1.111). All members of this equation are vector quantities having the dimension A/m 2 .

To obtain an equation similar to (1.120), you need to modify Maxwell's first equation (1.111) so that its terms become scalar quantities measured in watts. To do this, it suffices to multiply all the terms of the indicated equality scalarly by the vector E, and then integrate the resulting expression over the volume v. After scalar multiplication by a vector E we get

Using the div formula known from vector analysis = = H rot E - E rot H, we transform the left side of relation (1.121) and replace rot E with its value from the second Maxwell equation (1.39):

Substituting this expression into (1.121), we obtain

In the last term on the right side of (1.122), the order of factors in the scalar product of vectors is changed dB/dt and H. This is allowed because H dB/dt = dAT/dtH. This change is not fundamental and does not provide any advantages in deriving the balance equation considered here for instantaneous power values. However, with such a notation, in all terms of equation (1.122) the second factor (vectors j st, j, BDIDt and H) is a vector that was previously included in the first Maxwell equation. This circumstance will make it possible in the future (see 1.8.4) to somewhat simplify the derivation of the balance equation in the case of a monochromatic field (the balance equation of the complex power). Integrating term-by-term equation (1.122) over volume V, we get

where is the direction of the element dS coincides with the direction of the outer normal to the surface S. In passing from (1.122) to (1.123), the Ostrogradsky-Gauss theorem is used to translate the volume integral from div[ E, H] into the surface integral of the vector product [ E, H]. We introduce the notation

and transform the integrand in the last term on the right side of (1.123):

Substituting (1.124) and (1.125) into (1.123) and changing the order of integration and differentiation, we obtain

Let us find out the physical meaning of the expressions included in equation (1.126).

Consider the first term on the right side of (1.126). Let's imagine the volume V as a sum of infinitesimal cylinders of length dl, the ends of which ( dS ) perpendicular to the direction of current (vector j). Then EjdV=EjdV=(Edl)(jdS) = dUdl = dP n , where dl=jdS is the current flowing through the considered infinitesimal cylinder; dU = Edl- change in potential along the length dl, a dP n is the power of the Joule losses in the volume d V . Therefore, the term under consideration is the power of the Joule losses Р p in the volume v. Using the relation j = σЕ, for R P other representations can be obtained:

Formulas (1.127) can be considered as a generalized Joule-Lenz law valid for a conducting volume V arbitrary shape.

The integral on the left side of (1.126) differs from the first term on the right side only in that in the integrand instead of j included j c t. Therefore, it must determine the power of third-party sources. We will consider the positive power given off by external currents to the electromagnetic field. Electric current is an ordered movement of charged particles. The positive direction of the current is the direction of movement positive charges. The current gives off energy to the electromagnetic field when the charged particles that form it decelerate. For this, it is necessary that the electric field strength vector E had a component oriented opposite to the current direction, i.e. to dot product of vectors E and j st was negative ( Ej st<0). При этом левая часть равенства (1.126) будет поло­жительной величиной. Таким образом, мгновенное значение мощ­ности, отдаваемой сторонними токами электромагнитному полю в объеме V, is defined by the expression

To understand the physical meaning of the last term on the right side of equation (1.126), we consider a special case. Let's assume that the volume V surrounded by a perfectly conducting shell coinciding with the surface S. Then the tangent component of the vector E on the surface S will be equal to zero. Surface element dS coincides in direction with the outer normal n 0 . Consequently, the surface integral in equation (1.126) will be equal to zero, since the normal component of the vector product [ E, H] is determined by the tangent components of its Vectors. In addition, suppose that the environment within the volume V does not have conductivity σ = 0). In this case, there will be no Joule losses in the region under consideration, and the first integral on the right side of equation (1.126) will also be equal to zero. As a result, we get

Obviously, in the case under consideration, the power of external sources can only be spent on changing the energy of the electromagnetic field. Thus, the right side of equality (1.129) is the rate of change of the energy of the electromagnetic field stored in the volume V, those. corresponds to the term dW/dt in equation (1.126). It is natural to assume that the integral on the right side of (1.129) is equal to the energy of the electromagnetic field concentrated in the volume V:

Strictly speaking, this integral may differ from W to some function g = g(x, y, z) independent of time. It is easy to verify that the function d equals zero. Let us rewrite (1.130) as W \u003d W E + W M, where

Assume that the electric and magnetic fields are constant (do not depend on time). In this case, as is known from the course of physics (see also Chaps. 3 and 4), expressions (1.131) and (1.132) determine the energy of the electric and magnetic fields, respectively, in the volume v. But this means that g = 0 and these expressions determine the instantaneous values ​​of the energy of the electric and magnetic fields in the volume V for any dependence on time, their sum, determined by formula (1.130), is indeed equal to the instantaneous value of the energy of the electromagnetic field in the volume v.

It remains to clarify the physical essence of the surface integral in equation (1.126). We assume that in the volume V there are no losses and, in addition, the amount of electromagnetic energy remains constant (W= const). In this case, equation (1.126) takes the form

At the same time, it is obvious from physical representations that in this particular case, all the power of third-party sources should go into the surrounding space (R st = Р Σ). Therefore, the right side of equation (1.133) is equal to the energy flow through the surface S (the limit of the ratio of the amount of energy passing through S in the time Δt at Δt→0), those.

It is natural to assume that the vector P represents the energy flux density (the limit of the ratio of the energy flux through the area ∆S, located perpendicular to the direction of energy propagation, to ∆S at ∆S→0). Formally, mathematically, this assumption is not obvious, since the replacement of the vector P on the P 1 = P + rot a, where a- arbitrary vector, does not change the value R Σ . However, it is true and, in particular, follows directly from the relativistic theory of the electromagnetic field.

Thus, equality (1.126) is similar to (1.120) and represents the equation for the balance of instantaneous values ​​of the power of the electromagnetic field. It was obtained by Poynting in 1884 and is called Pointing's theorem. Accordingly, the vector P is called the Poynting vector. The names are also often used "Umov-Poynting theorem" and "Umov-Pointing vector" in order to emphasize the fact that the formulation of the law of conservation of energy in a general form with the introduction of the concept of an energy flux and a vector characterizing its density was first given by N.A. Umov in 1874.

Note that energy can enter the volume V not only from outside sources. For example, the energy flow through the surface S can be directed from the surrounding space into the volume v. At the same time, the power PΣ will be negative, since the energy flow leaving the volume is considered positive V into the surrounding space (element direction dS coincides with the direction of the outer normal to the surface S).

Third-party sources can not only give energy, but also receive it from the electromagnetic field. In this case, the power of third-party sources will be negative. Indeed, the electromagnetic field gives off energy to the conduction current if it accelerates the movement of charged particles that form the current. For this, the electric field strength vector E must have a component oriented along the streamlines, i.e. so that the scalar product of the vectors E and j st was greater than zero.

Let us consider in more detail the formulas that determine the energy of the electromagnetic field. Integrals in

can be interpreted as the instantaneous values ​​of the volumetric energy densities of the electric and magnetic fields, respectively, and their sum

As the volume density of the total energy of the electromagnetic field.

We emphasize that the principle of superposition, which is satisfied by the vectors of electric and magnetic fields, does not apply to energy. Indeed, let the field energies E 1, H 1 and E 2, H 2, existing separately in the area V, equal respectively W 1 and W2. Then the energy of the total field E \u003d E 1 + E 2, H \u003d H 1 + H 2 is determined by the expression

Mutual energy of fields. Mutual Energy W 12 can be both positive and negative. If the vectors E 1 and E 2, as well as H1 and H 2 mutually perpendicular, then W 12 = 0.

In the case of variable processes, the distribution of electromagnetic energy changes continuously. This change at any given point can be determined on the basis of equation (1.122), which is conveniently represented as

where p st \u003d- Ej st and p n = Ej- instantaneous values ​​of the power densities of third-party sources and the power of Joule losses, respectively. When passing from relation (1.122) to equation (1.136), formulas (1.125) and (1.135) are taken into account. Equation (1.136) is differential form of Poynting's theorem.

4 WAVE EQUATIONS

General case

When solving direct problems of electrodynamics, it is required to find the vectors E and H according to known (specified) third-party sources. Let us assume that external sources are located in an infinite homogeneous isotropic medium. To simplify the transformations, we assume that σ= 0. Writing the Maxwell equations for this particular case, we obtain

Definition of vectors E and H directly from the system of equations (2.25) is difficult. Therefore, it is advisable to transform it by eliminating either the vector E, or a vector H, i.e. obtain from it such a differential equation, which would include only one of the vectors E or H. To do this, we take the rotor from both parts of the second equation of system (2.25) and change the order of differentiation in time and in spatial coordinates. Taking into account the equality known from vector analysis

where Δ 2 ≡Δ-Laplace operator, and the third equality of the system under consideration, we arrive at the equation

Similarly, the equation for the vector is derived H:

Each of the vector equations (2.27) and (2.28) is equivalent to three scalar equations obtained by projecting the vector equation onto the axes X, Y and Z of the Cartesian coordinate system. These scalar equations are of the form

where w and f(x, y, z, f)-sought and given (known) functions, respectively. As is known, equations of the form (2.29) describe wave processes, and the parameter v equal to the speed of this process. Such equations are called nonhomogeneous d'Alembert equations or inhomogeneous wave equations. Equations (2.27) and (2.28) differ from (2.29) only in that the functions they contain are vector functions. This type of equation is called nonhomogeneous vector d'Alembert equations or inhomogeneous vector wave equations. Analogous equations whose right-hand sides are equal to zero are called homogeneous vector d'Alembert equations (homogeneous vector wave equations). Later it will be shown that the parameter entering into equations (2.27) and (2.28), which is an analogue of the parameter v in (2.29), in the case of a lossless medium, is also the propagation velocity of the electromagnetic field and is equal to the speed of light in the considered medium. This result is not unexpected, since light is electromagnetic waves of a certain frequency range.

Similar equations for vectors can be written without difficulty E and H and in the case when σ≠0 (see, for example, ).

monochromatic field

In the case of a monochromatic field, the complete system of Maxwell's equations in complex form, which takes into account external electrical sources, has the form

Let us assume that the medium filling the considered part of space is homogeneous and isotropic. Let us take the curl from both parts of the second equation of the system (2.30) and exclude the vector H, using the first equation. Taking into account formula (2.26) and the equality valid for a homogeneous isotropic medium, we arrive at the equation

where For vector H we obtain similarly

It is obvious that the same equations relate the complex amplitudes

If there are no external sources in the area under consideration, equations (2.31) and (2.32) are simplified:

To pass to the case of a lossless medium in equations (2.30)-(2.34) we must put . Each

from vector equations (2.33) and (2.34) is equivalent to three scalar equations of the same type for the Cartesian components of the corresponding vector: ∆ 2w+ k 2w= 0, where w- any of the components