The chemical potential of a substance. Chemical potential
When changing the number of particles in the system and necessary to describe the properties open systems(with a variable number of particles).
X. p. m i
i th component of a multicomponent system is equal to the partial derivative of any of the thermodynamic. potentials according to the number (number of particles) of this component at post. the values of the remaining thermodynamic. variables that determine this thermodynamic. potential, eg. m i = (dF/dN i) T,V,N (F-free energy, T-temp-ra, V-volume, ji). Thus, in systems with alternating the number of particles in the expression for the differential, for example. dF, add the value :
![]()
where R- pressure, S-entropy. Naib. just X. p. is associated with thermodynamic. potential G(cm. Gibbs energy):. For a one-component system X. n. m = G/N,
i.e., is the Gibbs energy per particle. Because of the additivity G, in addition to pressure and temperature-ry, X. p. depends only on the concentration of otd. components, but not on the number of particles in each component. In the simplest case ideal gases m i depends only on the concentration i-th component:
where is the total number of particles, m ~ i-X. n. clean i th
component. Often the values m i convenient to use as independent thermodynamic. variables instead N i. In variables T, V, m i the state of the system characterizes thermodynamic. potential
![]()
X. p. is thermodynamic. parameter in Gibbs grand canonical distribution for AC systems the number of particles. As a normalization constant X. p. enters the distributions of Boltzmann, Bose - Einstein and Fermi - Dirac for particles ideal gases(cm. statistical physics). In systems to which Boltzmann or Bose-Einstein statistics are applicable, X. p. is always negative. For Fermi gas X. p. at zero temperature is positive and determines the boundary Fermi energy(cm. Fermi surface)and degeneration temperature. If a
the total number of particles in the system is not fixed, but must be determined from the thermodynamic condition. equilibrium, such as for phonons in solid body or for photons in the case of equilibrium thermal, then the equilibrium is characterized by the equality to zero X. p.
The concept of x.p. allows us to formulate the conditions thermodynamic equilibrium. One of the conditions is that the X. p. of any component is the same in decomp. phases and in different places of one phase. This is due to the possibility of a redistribution of particles, leading to an equalization of X. p. For systems in a spatially inhomogeneous ext. the equilibrium field means that
![]()
where m i 0 - X. p. in the absence of a field, U i (r)-potential particle energy i th component in ext. field. For a gas in a gravitational field, this condition leads to a barometric filter for gas. In case of charging particles in electric. field (e.g. in semiconductors) value m i called electrochemical potential, leaving the name X. p. for m i 0 . The equality of the values of X.p. for particles of the same component that are in different phases determines the equilibrium conditions for phase transitions (
Thermodynamics of phase transitions. Definitions
Let us consider the thermodynamics of systems in which phase transitions. A thermodynamic system that can exchange matter with environment, is called open.
The thermodynamic system is called homogeneous or homogeneous, if in each small part of it physical properties substances and intensive thermodynamic parameters are the same or change in space in a continuous way.
Thermodynamic systems in which the physical properties of a substance and intensive parameters change abruptly on some surfaces inside the system are called heterogeneous. An example of a heterogeneous system is a boiling liquid.
Areas in a heterogeneous system with homogeneous or continuously changing properties and parameters are called phases. At equilibrium of a heterogeneous system in the absence of external fields, the intense parameters within each phase are constant.
But these intensive parameters need not be the same in different phases. A homogeneous system is thus single-phase.
Each of the phases, in the general case, can be a homogeneous mixture of chemically pure substances, between which chemical reactions. Chemically pure substances in a mixture are called components. Phases in the general case can exchange not only energy in the form of work or heat, but also matter. The transformation of matter from one phase state to another is called phase transition.
Let a one-component single-phase TD system be open, and only the substance that makes up the system can penetrate through the shell. And let the system be in equilibrium.
Change internal energy Such a system will occur not only due to the supply of heat and the performance of work on it, but also due to a change in its mass. The substance penetrating through the shell carries its inherent energy. Then the Gibbs equations for each of the four thermodynamic potentials(5.3) and (5.5) should be supplemented with one more term proportional to the change in the mass of the system, i.e.
Value μ , determined by partial derivatives
is called chemical potential and it makes sense to change the energy of a thermodynamic system when its mass changes by one, while maintaining a constant of one or another pair of independent parameters of the system.
Let's find the connection of the chemical potential with other potentials of the system. To do this, consider the fourth of the expressions in (4.12). Gibbs free energy Φ, entropy S and system volume V we write through their specific values:
Replacing the Gibbs free energy differential with its expression ![]() and rearranging the terms, we get:
and rearranging the terms, we get:
According to (4.5) for M= const = 1 kg ![]() , whence, in view of the arbitrariness of the mass differential d M, we find:
, whence, in view of the arbitrariness of the mass differential d M, we find:
those. The chemical potential of a substance is its specific Gibbs free energy.
4.6. Conditions for thermodynamic equilibrium of multiphase systems. Gibbs phase rule
Consider one-component system, consisting of two interacting phases. Let each of the phases be in its own internal equilibrium, i.e. each of them is characterized by its own set of parameters. Let us study the question of equilibrium between phases. To do this, we enclose the entire system in an insulating shell (Fig. 4.1). Then, with a small change in the state of each of the phases (subsystems), one can write for them the thermodynamic identities in accordance with (4.1)
 (4.15)
(4.15)
Due to the additivity of extensive quantities ![]() , the closedness of the system, and the reversibility of the process, we have
, the closedness of the system, and the reversibility of the process, we have
![]()
those. after summing equalities (4.5) we get:
By virtue of the arbitrariness of the differentials ![]() , the factors in parentheses at these differentials must be equal to zero, whence we obtain the conditions of thermodynamic equilibrium of the desired system:
, the factors in parentheses at these differentials must be equal to zero, whence we obtain the conditions of thermodynamic equilibrium of the desired system:
 (4.16)
(4.16)
The chemical potential, by definition, is itself a function of a natural pair of variables, thus the phase equilibrium condition can be written as
Type of functions from T and p in the general case is different for each of the phases, so condition (4.17) is not an identity. This is an algebraic equation relating temperature and pressure in an equilibrium system consisting of two coexisting interacting phases between which heat, work and matter are exchanged.
Thus, in a two-phase one-component system, temperature and pressure are uniquely related. The volume of the system can take on an arbitrary value depending on the ratio between the masses of the phases. The equilibrium state of a two-phase system is called the saturation state, and the temperature and pressure equal for the phases are called the saturation parameters T s , p s .
Consider the equilibrium three-phase one-component system. In this case:
 (4.18)
(4.18)
But for closed system:
taking into account what, adding equations (4.8), we obtain:
Since all differentials here are independent and their values are arbitrary, we find the equilibrium conditions:
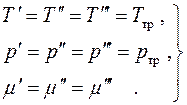 (4.19)
(4.19)
Chemical equilibrium, i.e. equality of the chemical potentials of the phases, can be written in the form of two algebraic equations
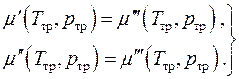 (4.20)
(4.20)
This is a system of two equations in two unknowns. An equilibrium one-component system can exist simultaneously in three phases only at strictly defined values of pressure and temperature. This state of the system is called triple point.
For an equilibrium four-phase one-component system:
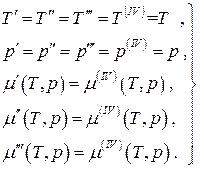 (4.21)
(4.21)
a system of three equations in two unknowns. Such a system of equations is inconsistent except for the case when any two of them are proportional to each other, i.e. when two of the four phases are actually indistinguishable, and this will already be a three-phase system. Thus, in an equilibrium one-component system, the simultaneous coexistence of no more than three phases is possible. If an equilibrium thermodynamic system is multicomponent, then the number of simultaneously coexisting phases can be more than three, namely
where n is the number of system components. This result is called Gibbs phase rules.
LECTURE PLAN:
1. The organizational part of the lecture: a report is received on the readiness of cadets for the lesson, absentees are noted in the journal (time 3-5 minutes).
2. Introduction to the section "Heat and Mass Transfer".
Lecture questions:
heat transfer mechanisms.
temperature field.
temperature gradient.
The basic law of heat conduction.
· Coefficient of thermal conductivity.
· Differential equation of heat conduction.
· Boundary conditions.
3. Conclusion.
For the next class, students must:
KNOW: differential equation thermal conductivity; determination of coefficients of heat and thermal diffusivity.
BE ABLE TO: apply boundary conditions when solving problems on the Fourier equation.
HAVE A REPRESENTATION: about the mechanisms of heat transfer in bodies of different structure and state of aggregation.
4. Tasks for self-training:
_____________/ professor Physics and Heat Transfer, Doctor of Physics and Mathematics, P.V. Skripov
The lecture was reviewed and approved at the meeting of the department
Protocol No. _______ dated "_____" ______ 2011
Head of the Department of Physics and Heat Transfer
professor, d.t.s. __________________ / N.M. barbin
"_____"______________ 2011
Free energy of the system (Gibbs energy G and Helmholtz energy F) depends on external conditions:
This dependence is complete for the simplest systems consisting of one component.
A thermodynamic system can consist of one or more components. Obviously, the value of the free energy of a multicomponent system will depend both on external conditions ( T,R, or V), and on the nature and quantity of substances that make up the system, i.e., free energy, like any thermodynamic function, is an extensive property of the system. If the composition of the system changes with time (i.e., a chemical reaction occurs in the system), it is necessary to take into account the effect of the change in composition on the value of the free energy of the system.
Consider a thermodynamic system consisting of k components. Let n 1 , n 2 , …, n k- the number of moles of the 1st, 2nd, ..., k th components. Then the Gibbs free energy is a function of the following variables:
G = f(p, T, n 1 , n 2 , …, n k )
Differentiate with respect to all variables:
 (2.1)
(2.1)
Let's introduce the notation:
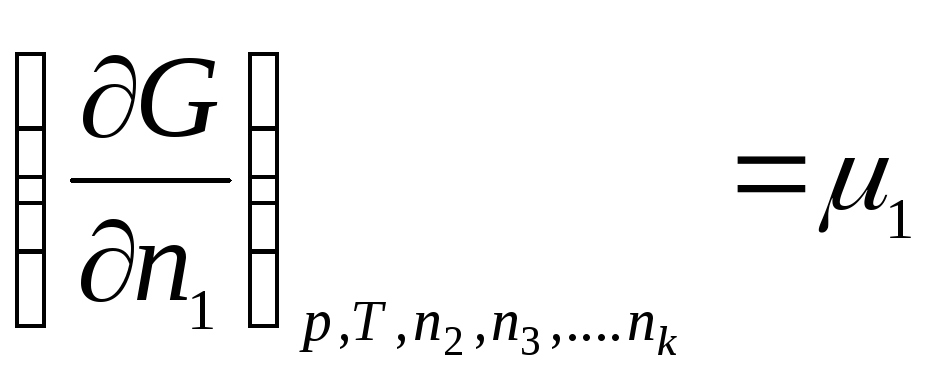

………………….
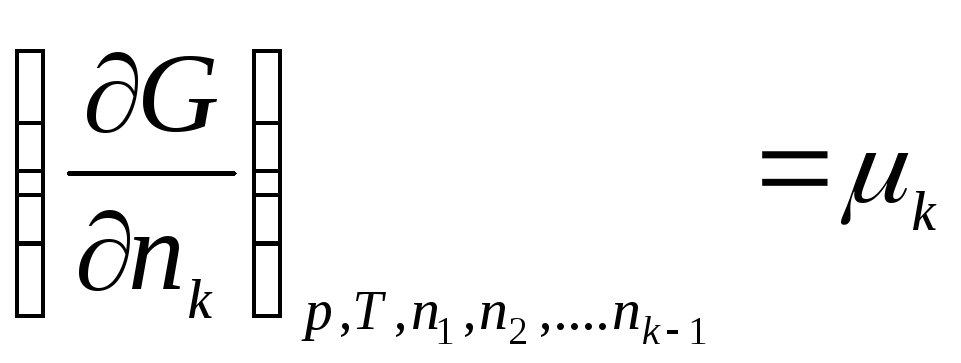 ,
,
where μ 1 , μ 2 , …, μ k– chemical potentials of the 1st, 2nd, …, k th components, respectively.
In general
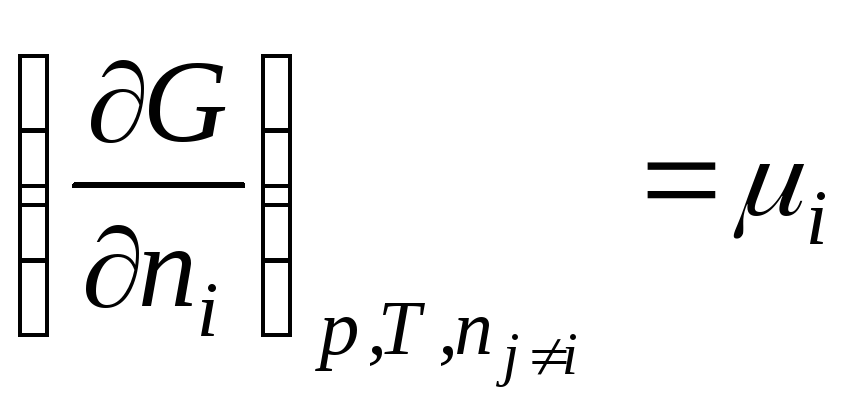 .
.
We obtain a similar expression for the Helmholtz free energy:
F = f(V, T, n 1 , n 2 , …, n k )
 .
.
In this way, chemical potential is the partial derivative of free energy with respect to the number of moles i-th component with the constancy of the corresponding external parameters and the number of moles of all other components. Thus, the chemical potential is the partial molar Gibbs energy (at R, T = const):
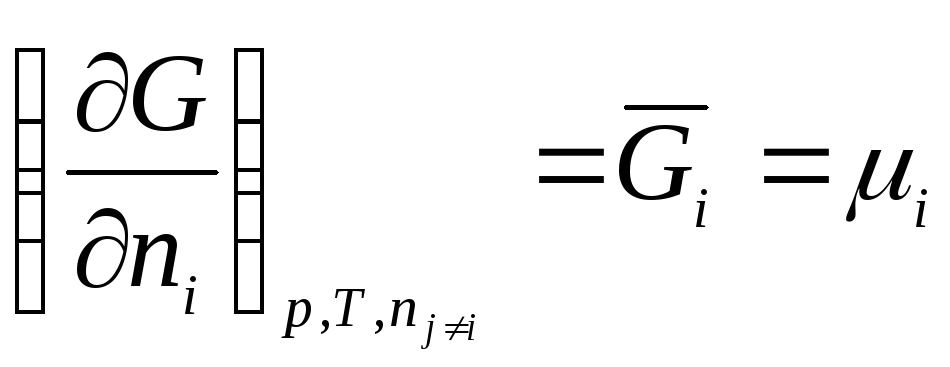 .
.
Free energy is common property systems, the chemical potential characterizes the properties of an individual component included in the system. The chemical potential is an intensive property of the system, since does not depend on the mass of the system.
At p, T =const equation (2.1) has the form:
![]() .
(2.2)
.
(2.2)
In this case, the change in the Gibbs energy, that is, the useful work of the system, is due only to a change in the composition of the system as a result of a chemical reaction or due to the exchange of matter between the system and the environment.
Equation (2.2) expresses the relationship between the general property of the system and the properties of each of its components. Assuming that the chemical potential is a constant value, we integrate equation (2.2):
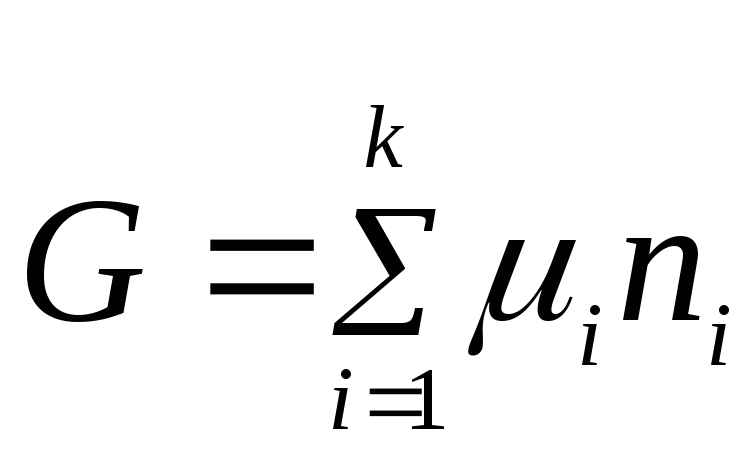 .
.
The integration constant is zero because if all n i= 0, the Gibbs energy is also equal to zero.
For an individual substance
 ,
,
those. the chemical potential of an individual substance is equal to the Gibbs molar energy.
At equilibrium dG = 0 and equation (2.1) takes the form:
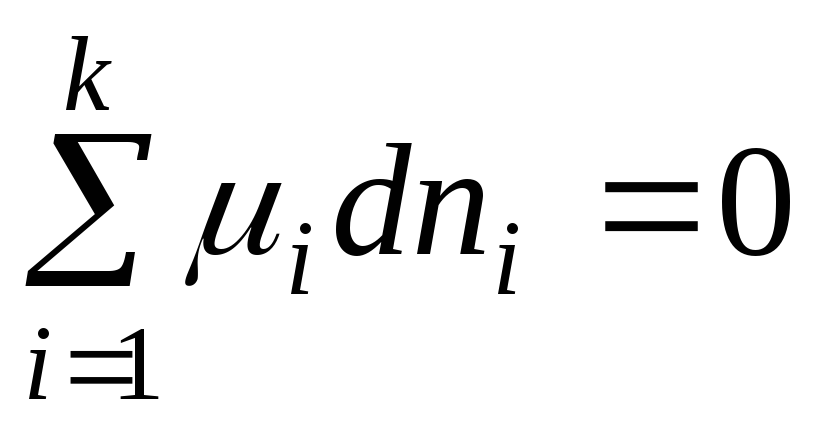 . (2.3)
. (2.3)
The resulting equation is a general equilibrium condition in a system with variable composition at R,T =const.
Chemical potential of an individual ideal gas.
Consider a thermodynamic system that is an ideal gas. Chemical potential ideal gas equals:
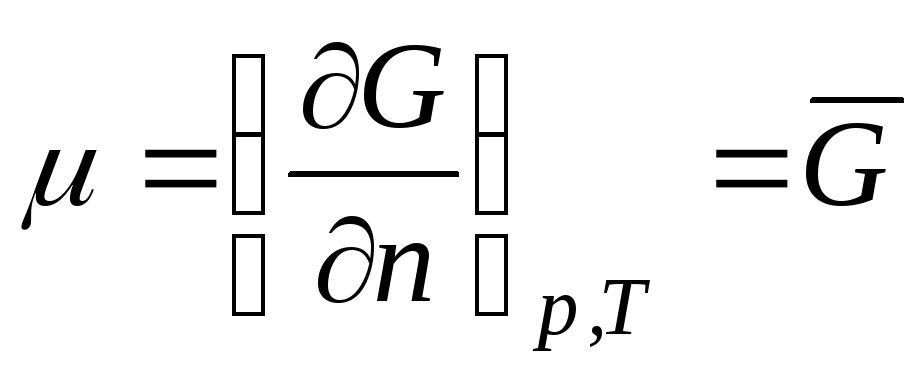 ,
,
where  is the Gibbs molar energy (isobaric potential of 1 mole of an ideal gas).
is the Gibbs molar energy (isobaric potential of 1 mole of an ideal gas).
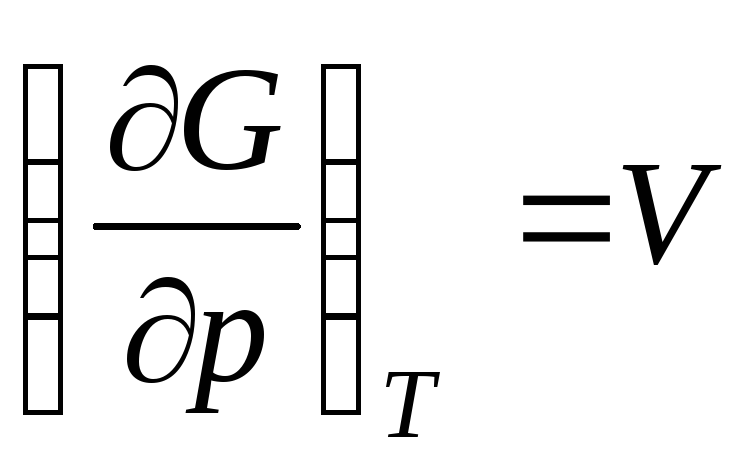 ,
,
then 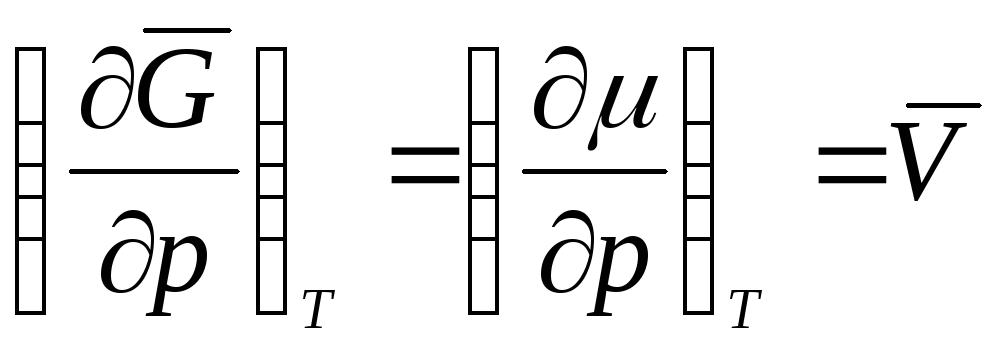 ,
,
where  is the molar volume of an ideal gas (the volume of 1 mol of gas).
is the molar volume of an ideal gas (the volume of 1 mol of gas).
If the process is running at T =const, the partial derivative can be replaced by the total. Then

The equation of state for 1 mole of an ideal gas is:
 ;
;
 ,
,
![]()
Let us integrate in the interval from R 0 before R:

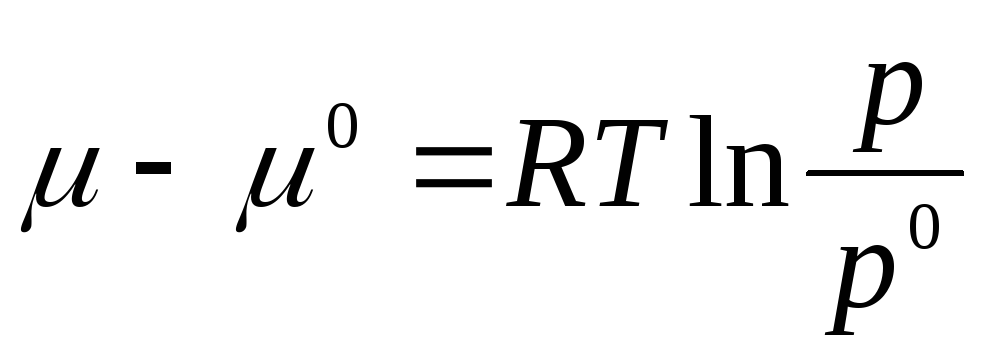
where μ 0 , R 0 is the chemical potential and pressure of an ideal gas in the standard state.
The standard state is taken to be the state of an ideal gas at R 0 = 1 atm.
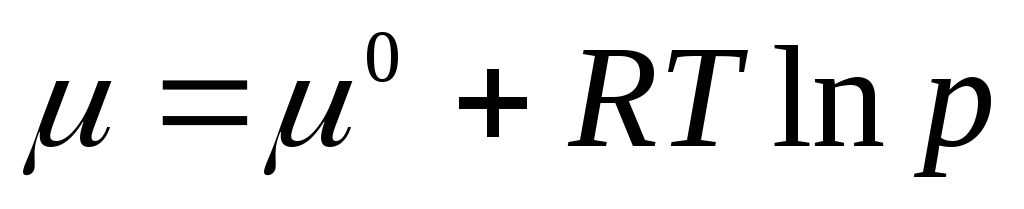 .
(2.3)
.
(2.3)
The standard chemical potential is the chemical potential at a gas pressure of 1 atm. Chemical potential in the standard state μ 0 depends only on temperature and does not depend on pressure, i.e. μ 0 = f(T). Equation (2.3) shows that under the sign of the logarithm is a dimensionless quantity equal to the pressure ratio R to standard pressure R 0 = 1 atm.
Because the μ
=
 , can be written
, can be written
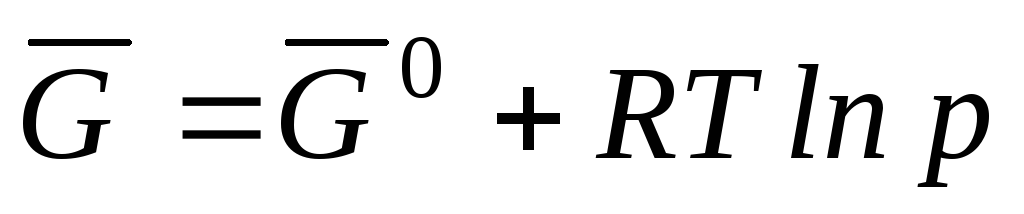
where  is the Gibbs standard molar energy.
is the Gibbs standard molar energy.
Chemical potential of a component of ideal solutions.
If the total pressure of the gas mixture is small, then each gas will exert its own pressure, moreover, such as if it alone occupied the entire volume. This pressure is called partial. Total observed pressure R is equal to the sum of the partial pressures of each gas (Dalton's law):
 .
.
The chemical potential of a component of an ideal gas mixture is:
 ,
,
where R i is the partial pressure of the gas.
Expressing the partial pressure of a gas R i through the total pressure and the mole fraction of the gas x i, get the expression for the dependence of the chemical potential i-th component from the mole fraction:
where  is the chemical potential of an ideal gas at x i= 1 (i.e. in the individual state) at pressure R and temperature T;
is the chemical potential of an ideal gas at x i= 1 (i.e. in the individual state) at pressure R and temperature T;
 depends on both temperature and pressure.
depends on both temperature and pressure.
For ideal liquid solutions applicable equation
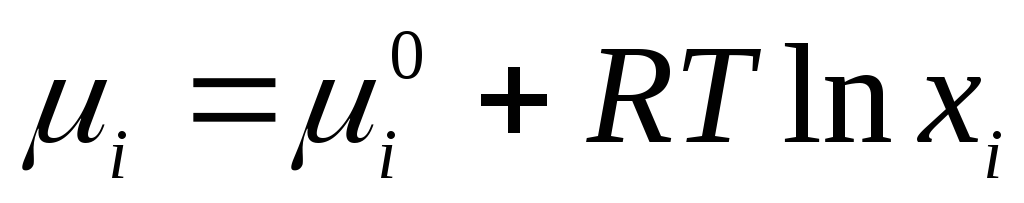 ,
,
where  is the standard chemical potential of an individual component in the liquid state (
is the standard chemical potential of an individual component in the liquid state (  ) depends on temperature and pressure; x i is the mole fraction of the component.
) depends on temperature and pressure; x i is the mole fraction of the component.
Chemical potential of a component of real solutions .
For real solutions, all the dependences considered are inapplicable. Chemical potential of the component real gas solution calculated using the Lewis method. In this case, to preserve the form of thermodynamic equations, instead of partial pressure, they introduce a fictitious quantity f i, which is called partial fugacity, or volatility. Then
![]() ,
,
where  is the chemical potential of a component of a real gas mixture in the standard state.
is the chemical potential of a component of a real gas mixture in the standard state.
The ratio of volatility to partial pressure real gas solution is called the volatility coefficient:
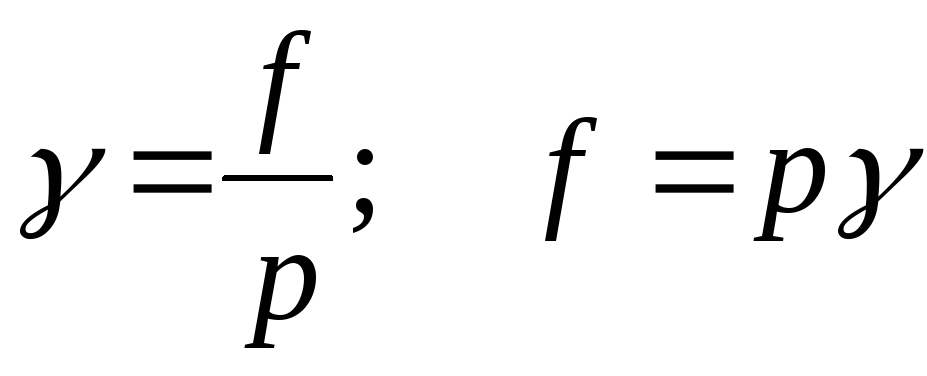 ;
;
Similarly, for liquid real solutions the actual concentration is replaced by the corresponding fictitious value - activity a i :
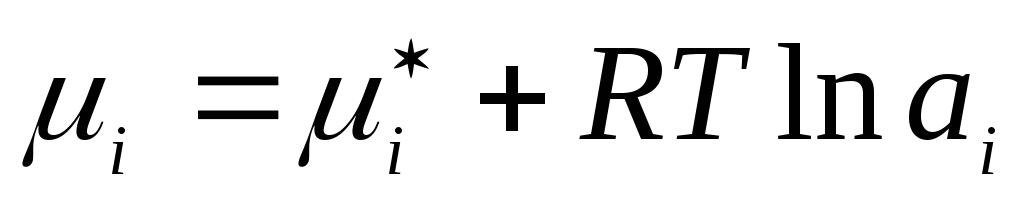 ,
,
where  is the chemical potential of a component of a real liquid solution in the standard state.
is the chemical potential of a component of a real liquid solution in the standard state.
Activity is related to concentration through the activity coefficient:
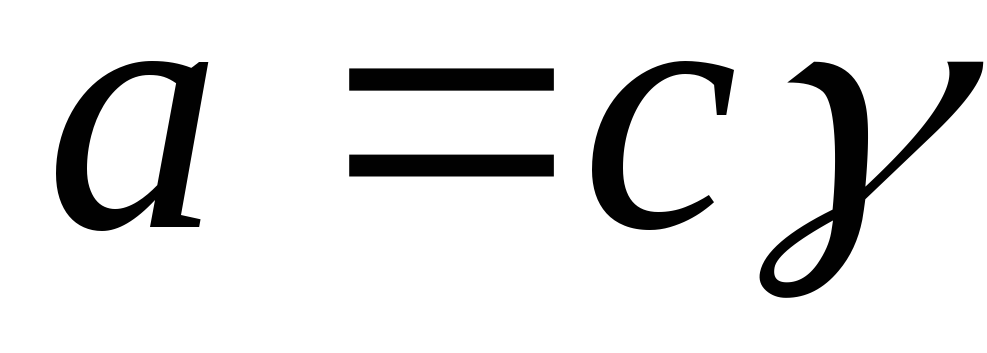 ,
,
where γ i is the activity coefficient.
Depending on the method of expressing the concentration of a solution, rational, molar and molal activity coefficients are distinguished:

The activity coefficient depends on the concentration of the solution. In infinitely dilute solutions γ → 1, a i and f i → c i and p i respectively.
Let us rewrite the equation for the chemical potential in the form
 ,
,
therefore, thermodynamic activity is the work of transfer of 1 mol i th component from the standard solution to the given real solution.
There are two main ways to choose standard condition- symmetrical and asymmetrical.
symmetrical way. The same standard state is chosen for the solvent and the solute - the state of the pure component at the temperature of the solution. Then in the standard state x i = 1, a i = 1and γ i = 1. This method is more often used for non-electrolyte solutions.
asymmetric way. A different standard state is selected for the solvent and the solute. For the solvent - as in the symmetrical method: x i → 1, a i → 1and γ i → 1. For a solute the standard state is the state of matter in an infinitely dilute solution: x i → 0, a i → x i and γ i → 1. The method is most often used in the thermodynamics of electrolyte solutions.






