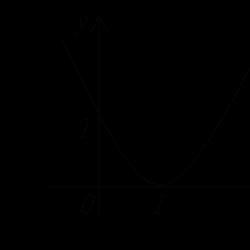
Cardano formülünü kullanarak kübik denklemlerin çözümü. Cardano'nun kübik denklem çözme formülü. Cardano'nun kübik denklem çözme formülü

Simonyan Albina

Makalede kübik denklemlerin çözümüne yönelik teknikler ve yöntemler ele alınmaktadır. Matematik sınavına hazırlıkta problemlerin çözümü için Cardano formülünün uygulanması.

İndirmek:

Ön izleme:

MOU DOD Çocuklar ve Gençler için Yaratıcılık Sarayı

Genç Araştırmacılar için Don Bilimler Akademisi

Bölüm: matematik - cebir ve sayılar teorisi

Araştırma

"Formüllerin dünyasına bakalım"

Bu konuda "3. Dereceden Denklemlerin Çözümü"

Danışman: matematik öğretmeni Babina Natalya Alekseevna

G.Salsk 2010

Giriş ……………………………………………………………………………….3
Ana bölüm…………………………………………………………………….4
Pratik kısım…………………………………………………………… 10-13
Sonuç…………………………………………………………………………….14
Edebiyat…………………………………………………………………………..15
Uygulamalar

1. Giriş

Genel eğitim okullarında alınan matematik eğitimi, modern insanın genel eğitiminin ve genel kültürünün en önemli bileşenidir. Bir insanı çevreleyen hemen hemen her şey şu ya da bu şekilde matematikle bağlantılıdır. Ve fizik, teknoloji ve bilgi teknolojisindeki en son başarılar, gelecekte de durumun aynı kalacağına dair hiçbir şüphe bırakmıyor. Bu nedenle, birçok pratik problemin çözümü, çözülmesinin öğrenilmesi gereken çeşitli denklem türlerinin çözümüne indirgenir. Birinci dereceden lineer denklemler, birinci sınıfta çözmemiz öğretildi ve onlara pek ilgi göstermedik. Doğrusal olmayan denklemler daha ilginçtir - büyük dereceli denklemler. Matematik düzeni, simetriyi ve kesinliği ortaya çıkarır ve bunlar güzelliğin en yüksek biçimleridir.

“Üçüncü dereceden kübik denklemlerin çözümü” konulu “Formüller dünyasına bakalım” projemin amacı, kübik denklemlerin nasıl çözüleceğine ilişkin bilgiyi sistematikleştirmek, denklemi bulmak için bir formülün varlığı gerçeğini ortaya koymaktır. üçüncü dereceden bir denklemin kökleri ve kübik bir denklemdeki kökler ve katsayılar arasındaki ilişki. Sınıfta hem kübik hem de derecesi 3'ün üzerinde olan denklemleri çözdük. Denklemleri farklı yöntemlerle çözerek katsayıları topladık, çıkardık, çarptık, böldük, kuvvetlerini yükselttik ve köklerini çıkardık, kısacası cebirsel işlemler yaptık. İkinci dereceden denklemleri çözmek için bir formül var. Üçüncü derecenin denklemini çözmek için bir formül var mı? köklerin elde edilebilmesi için katsayılarla birlikte hangi sıra ile hangi cebirsel işlemlerin yapılması gerektiğinin belirtilmesi. Ünlü matematikçilerin kübik denklemleri çözmeye uygun genel bir formül bulmaya çalışıp çalışmadıklarını bilmek bana ilginç geldi. Peki deneselerdi denklemin katsayıları cinsinden köklerin ifadesini elde edebilecekler miydi?

2. Ana gövde:

Bilgelerin bilinmeyen miktarlar içeren eşitlikler hakkında ilk düşünmeye başladıkları o uzak zamanlarda, muhtemelen henüz madeni para veya cüzdan yoktu. Mezopotamya'nın, Hindistan'ın, Çin'in, Yunanistan'ın eski matematik problemlerinde bilinmeyen nicelikler, bahçedeki tavus kuşlarının sayısını, sürüdeki boğaların sayısını, mal paylaşımında dikkate alınan şeylerin bütünlüğünü ifade ediyordu. Bize ulaşan kaynaklar, eski bilim adamlarının bilinmeyen niceliklerdeki problemleri çözmek için bazı genel yöntemlere sahip olduklarını gösteriyor. Ancak ne tek bir papirüs ne de tek bir kil tablet bu tekniklerin tanımını vermez. Bunun istisnası, Yunan matematikçi İskenderiyeli Diophantus'un (III. Yüzyıl) "Aritmetiği"dir - çözümlerinin sistematik bir sunumuyla denklemleri derlemek için bir görev koleksiyonu. Ancak 9. yüzyıldaki Bağdatlı bilim adamının çalışması, yaygın olarak bilinen sorunların çözümüne yönelik ilk el kitabı oldu. Muhammed bin Musa el-Harezmi.

“Formüllerin dünyasına bakalım…” projesini oluşturma fikri böyle ortaya çıktı, bu projenin temel soruları şunlardı:

kübik denklemlerin çözümü için bir formül olup olmadığının belirlenmesi;
Olumlu bir cevap olması durumunda, kübik bir denklemin köklerini, katsayıları üzerinde yapılan sonlu sayıda cebirsel işlem cinsinden ifade eden bir formül arayışı.

Ders kitaplarında ve matematikle ilgili diğer kitaplarda akıl yürütme ve kanıtların çoğu belirli örnekler üzerinde değil, genel olarak yapıldığından, fikrimi doğrulayan veya çürüten belirli örnekleri aramaya karar verdim. Kübik denklemleri çözmek için bir formül ararken, ikinci dereceden denklemleri çözmek için tanıdık algoritmaları izlemeye karar verdim. Örneğin denklemi çözmek x 3 + 2x 2 - 5x -6=0 (x + a) formülünü uygulayarak tam küpü seçtiniz 3 \u003d x 3 + 3x 2 a + 3a 2 x + a 3 . Aldığım denklemin sol tarafından tam bir küp seçmek için 2x'i ona çevirdim 2'si 3x2'de ve bunlar. Eşitliğin doğru olması için böyle bir şey arıyordum 2x 2 \u003d 3x 2 a . a = değerini hesaplamak kolaydı. Bu denklemin sol tarafını dönüştürdümşu şekilde: x 3 + 2x 2 -5x-6=0

(x 3 + 3x 2 a + 3x. +) - 3x. - - 5x - 6= (x+) 3 - 6x - 6 y \u003d x + yerine bir değişiklik yaptım, yani. x = y - y 3 - 6(y -) - 6=0; 3'te - 6y + 4- 6=0; Orijinal denklem şu şekli aldı: 3 - 6y - 2=0; Çok güzel bir denklem olmadığı ortaya çıktı, çünkü artık tamsayı katsayıları yerine kesirli katsayılara sahibim, ancak denklemin bilinmeyenin karesini içeren terimi ortadan kalktı! Hedefime daha yakın mıyım? Sonuçta bilinmeyenin ilk gücünü içeren terim kaldı. Belki - 5x teriminin ortadan kalkması için tam bir küp seçmek gerekiyordu? (x+a) 3 \u003d x 3 + 3x 2 a + 3a 2 x + a 3 . Bunun gibi bir şey buldum 3a 2 x \u003d -5x; onlar. 2'ye = - Ama sonra durum oldukça kötü çıktı - bu eşitlikte solda pozitif bir sayı, sağda ise negatif bir sayı var. Böyle bir eşitlik olamaz. Şu ana kadar denklemi çözemedim, sadece forma getirebildim 3 - 6y - 2=0.

Yani, ilk aşamada yaptığım çalışmanın sonucu: İkinci dereceyi içeren terimi kübik denklemden çıkarabildim, yani. kanonik denklem ax verilirse 3 +2'de + cx + d ise tamamlanmamış bir kübik denklem x'e indirgenebilir 3 +px+q=0. Ayrıca, farklı referans literatürüyle çalışarak şu formda bir denklem bulmayı başardım: x 3 + piksel \u003d q İtalyan matematikçi Dal Ferro'yu (1465-1526) çözmeyi başardı. Neden bu tür için de, bu tür için değil x 3 + piksel + q \u003d 0? Bu çünkü o zamanlar negatif sayılar henüz tanıtılmamıştı ve denklemler yalnızca pozitif katsayılarla dikkate alınıyordu. Ve negatif sayılar biraz sonra tanındı.Tarihsel referans:Dal Ferro, verilen ikinci dereceden denklemin köklerinin formülüne benzeterek çok sayıda seçenek seçti. Şöyle düşündü: İkinci dereceden denklemin kökü - ± yani. şu forma sahiptir: x=t ± . Bu, kübik denklemin kökünün aynı zamanda bazı sayıların toplamı veya farkı olması gerektiği ve muhtemelen aralarında üçüncü derecenin köklerinin olması gerektiği anlamına gelir. Tam olarak hangileri? Çok sayıda seçenekten birinin başarılı olduğu ortaya çıktı: Cevabı bir fark şeklinde buldu - t ve u'nun = olacak şekilde seçilmesi gerektiğini tahmin etmek daha da zordu. X yerine farkı - ve p yerine çarpımı koymak Alınan: (-) 3 +3 (-)=q. Parantezler açıldı: t - 3 +3- u+3- 3=q. Benzer terimleri getirdikten sonra şunu elde ederiz: t-u=q.

Ortaya çıkan denklem sistemi:

t sen = () 3 t-u=q. Sağa sola kaldıralımbirinci denklemin bölümlerinin karesini alın, ikinci denklemi 4 ile çarpın ve birinci ve ikinci denklemleri ekleyin. 4t 2 +2tu +u 2 =q 2 +4() 3 ; (t+u) 2 =4()+() 3 t+u =2 Yeni sistemden t+u=2 ; t -u=q elimizde: t= + ; u= - . İfadeyi x yerine koyarsak, şunu elde ederiz:Proje üzerinde çalışırken en ilginç malzemeleri öğrendim. Dal Ferro'nun bulduğu yöntemi yayınlamadığı ortaya çıktı, ancak öğrencilerinden bazıları bu keşiften haberdardı ve çok geçmeden içlerinden biri olan Antonio Fior bunu kullanmaya karar verdi.O yıllarda bilimsel konularda kamusal tartışmalar yaygındı. Bu tür tartışmaların galipleri genellikle iyi bir ödül aldı ve genellikle yüksek pozisyonlara davet edildiler.

Aynı zamanda, İtalya'nın Verona şehrinde Tartaglia (yani kekeme) lakaplı fakir bir matematik öğretmeni Nicolo (1499-1557) yaşıyordu. Çok yetenekliydi ve Dal Ferro'nun tekniğini yeniden keşfetmeyi başardı (Ek 1).Fiore ile Tartaglia arasında bir düello gerçekleşti. Koşula göre rakipler, çözümüne 50 gün süre verilen otuz sorunu paylaştı. Ama o zamandan beri Fior aslında yalnızca bir problem biliyordu ve bazı öğretmenlerin bunu çözemeyeceğinden emindi, sonra 30 problemin hepsinin aynı türde olduğu ortaya çıktı. Tartaglia onlarla 2 saat içinde ilgilendi. Fiore ise düşmanın önerdiği tek bir görevi bile çözemedi. Zafer İtalya genelinde Tartaglia'yı yüceltti, ancak sorun tam olarak çözülmedi. .

Bütün bunlar Gerolamo Cardano tarafından yapıldı. Dal Ferro tarafından keşfedilen ve Tartaglia tarafından yeniden keşfedilen formüle Cardano formülü denir (Ek 2).

Cardano Girolamo (24 Eylül 1501 - 21 Eylül 1576) İtalyan matematikçi, tamirci ve doktordu. Pavia'da doğdum. Pavia ve Padua üniversitelerinde okudu. Gençliğinde hekimlik yaptı. 1534'te Milano ve Bologna'da matematik profesörü oldu. Matematikte Cardano'nun adı genellikle kübik denklemlerin çözümü için N. Tartaglia'dan ödünç aldığı formülle ilişkilendirilir. Bu formül Cardano'nun Büyük Sanatı veya Cebir Kuralları Üzerine (1545) kitabında yayınlandı. O zamandan beri Tartaglia ve Cardano amansız düşmanlar haline geldi. Bu kitap, Cardano'nun başta kübik denklemler olmak üzere denklemleri çözmek için kullandığı modern yöntemleri sistematik olarak özetlemektedir. Cardano, kübik denklemi 2. dereceden terim içermeyen bir forma indirgemeyi mümkün kılan doğrusal bir dönüşüm gerçekleştirdi ve denklemin kökleri ile katsayıları arasındaki bağımlılığa, polinomun x – farkına bölünebilirliğine dikkat çekti. a, eğer a onun kökü ise. Cardano, Avrupa'da denklemlerin negatif köklerinin varlığını kabul eden ilk kişilerden biriydi. Eserlerinde ilk kez hayali büyüklükler karşımıza çıkıyor. Cardano, mekanik alanında kaldıraç ve ağırlık teorisini inceledi. Bir doğru parçasının dik açının kenarları boyunca yaptığı hareketlerden birine mekanikte karda yeni hareketi denir. Yani Cardano formülüne göre formdaki denklemler çözülebilir x 3 + px + q \u003d 0 (Ek 3)

Sorun çözülmüş gibi görünüyor. Kübik denklemleri çözmek için bir formül var.

İşte burada!

Kökün altındaki ifade - ayrımcı. D = () 2 + () 3 Denklemime geri dönmeye ve onu Cardano formülünü kullanarak çözmeye karar verdim: Denklemim: 3 - 6y - 2=0, burada p= - 6=-; q = - 2 = - . Bunu hesaplamak kolaydır () 3 ==- ve () 2 ==, () 2 + () 3 = = - = - . Peki sırada ne var? Bu kesrin payından kolayca kökü çıkardım, 15 çıktı. Peki paydayla ne yapmalı? Sadece kök tamamen çıkarılmamış değil, aynı zamanda onu çıkarmak için de - o zaman negatif bir sayıdan olması gerekir! Sorun ne? Bu denklemin köklerinin olmadığı varsayılabilir çünkü D için Böylece proje üzerinde çalışırken başka bir sorunla karşılaştım.Sorun ne? Kökleri olan ancak bilinmeyenin karesi terimini içermeyen denklemler yazmaya başladım:

kökü x \u003d - 4 olan bir denklem yaptı.

x 3 + 15x + 124 = 0 Ve gerçekten de kontrol ederek denklemin kökü -4 olduğuna ikna oldum. (-4) 3 +15*(-4)+124=- 64 – 60 +124=0,

Bu kökün Cardano formülünü kullanarak elde edilip edilemeyeceğini kontrol ettim x=+=+= =1- 5 =- 4

Alınan, x = -4.

gerçek kökü x \u003d 1: x olan ikinci bir denklem yaptı 3 + 3x - 4 = 0 ve formülü kontrol ettik.

Ve bu durumda formül kusursuz işledi.

x denklemini buldum 3 +6x+2=0, bunun bir irrasyonel kökü var.

Bu denklemi çözdükten sonra şu kökü elde ettim: x = - Ve sonra bir varsayımda bulundum: Denklemin yalnızca bir kökü varsa formül işe yaradı. Ve çözümü beni çıkmaza sokan denklemimin üç kökü vardı! Sebebini burada aramanız gerekiyor!Şimdi üç kökü olan bir denklem aldım: 1; 2; -3. x 3 – 7x +6=0 p= -7; q = 6. Diskriminant kontrol edildi: D = () 2 + () 3 = () 3 + (-) 3 = 9 -

Şüphelendiğim gibi karekökün yine negatif bir sayı olduğu ortaya çıktı. Şu sonuca vardım:x denkleminin üç köküne giden yol 3 +px+q=0 Negatif bir sayının karekökünü almak gibi imkansız bir işlemin yapılmasına yol açar.

Şimdi denklemin iki kökü olduğu durumda neyle karşılaşacağımı bulmak bana kalıyor. İki kökü olan bir denklem seçtim: x 3 - 12 x + 16 \u003d 0. p \u003d -12, q \u003d 16.

D=() 2 +() 3 =() 2 +() 3 \u003d 64-64 \u003d 0 D \u003d 64 - 64 \u003d 0. Artık formun kübik denkleminin kök sayısının olduğu sonucuna varılabilir. x 3 + piksel + q \u003d 0 diskriminantın işaretine bağlıdır D=() 2 +() 3 Aşağıdaki şekilde:

D>0 ise denklemin 1 çözümü vardır.

Eğer D

Eğer D=0 ise denklemin 2 çözümü vardır.

Sonucumun onayını matematik üzerine bir referans kitabında, yazar N.I. Bronshtein'de buldum. Yani benim sonucum: Kökün benzersiz olduğundan emin olduğumuzda Cardano'nun formülü kullanılabilir. Bana göre kübik bir denklemin köklerini bulmak için bir formül olduğunu tespit etmeyi başardı, ancak form için x 3 + piksel + q \u003d 0.

3. Pratik kısım.

Proje üzerinde çalışmak “… parametrelerle ilgili bazı problemleri çözerken bana çok yardımcı oldu. Örneğin:1. x denkleminin en küçük doğal değeri nedir? 3 -3x+4=a'nın 1 çözümü var mı? Denklem şu şekilde yeniden yazıldı: x 3 -3x+4-a=0; p= -3; q=4-a. Koşula göre 1 çözümü olmalıdır; D>0 D'yi bulun. D=() 2 +(-) 3 = +(-1) 3 = == a 2 -8a+12>0

A (-∞;2) (6;∞)

a'nın bu aralıktaki en küçük doğal değeri 1'dir.

Cevap. 1

2. Ne zaman a denklemi x parametresinin en büyük doğal değeri 3 + x 2 -8x+2-a=0'ın üç kökü var mı?

Denklem x 3 +3x 2 -24x + 6-3a = 0'ı y formuna getiriyoruz 3 + ru + q=0, burada a=1; =3'te; c=-24; d=6-3а burada q= - + ve 3 p = q=32-3a; p=-27. Bu tür denklem için D=() 2 + () 3 =() 2 +(-9) 3 = -729 =; D 2 -4 *9* (-1892) = 36864 + 68112 = 324 2 ve 1 = ==28 ve 2 == - = -7.

+_ . __-___ . _+

7 28

bir (-7; 28)

a'nın bu aralıktaki en büyük doğal değeri: 28.

Cevap.28

3. a parametresinin değerlerine bağlı olarak denklemin kök sayısını bulun x 3 - 3x - a \u003d 0

Çözüm. Denklemde p = -3; q = -a. D=() 2 + () 3 =(-) 2 +(-1) 3 = -1=.

_+ . __-__ . _+

a (-∞;-2) (2;∞) için denklemin 1 çözümü vardır;

a (-2; 2) olduğunda denklemin 3 kökü vardır;

a \u003d -2 olduğunda; Denklem 2'nin 2 çözümü vardır.

Testler:

1. Denklemlerin kaç kökü vardır:

1) x 3 -12x+8=0?

a) 1; b) 2; 3'te; d)4

2) x 3 -9x+14=0

a) 1; b) 2; 3'te; d)4

2. p denkleminin hangi değerlerinde x 3 +px+8=0'ın iki kökü var mı?

a) 3; b) 5; 3'te; d)5

Cevap: 1.d) 4

2.c) 3.

3.c)-3

Bizden 400 yıl önce Fransız matematikçi Francois Viet (1540-1603) (Ek 4) ikinci dereceden bir denklemin kökleri ile katsayıları arasında bağlantı kurmayı başarmıştı.

X 1 + x 2 \u003d -p;

X 1 ∙x 2 \u003d q.

Şunu öğrenmek benim için ilginç hale geldi: Üçüncü dereceden bir denklemin kökleri ile katsayıları arasında bir bağlantı kurmak mümkün mü? Evet ise bu bağlantı nedir? Mini projem bu şekilde ortaya çıktı. Sorunumu çözmek için mevcut ikinci dereceden becerilerimi kullanmaya karar verdim. benzetmeyle hareket edilir. x denklemini aldım 3 + piksel 2 +qх+r =0. Denklemin köklerini belirtirsek x 1, x 2, x 3 ise denklem (x-x) şeklinde yazılabilir. 1) (x-x 2) (x-x 3 )=0 Parantezleri genişlettiğimizde şunu elde ederiz: x 3 - (x 1 + x 2 + x 3) x 2 + (x 1 x 2 + x 1 x 3 + x 2 x 3) x - x 1 x 2 x 3 \u003d 0. Aşağıdaki sistemi aldım:

X 1 + x 2 + x 3 \u003d - p;

X 1 x 2 x 3 = - r.

Böylece, keyfi derecedeki denklemlerin kökleri katsayılarıyla ilişkilendirilebilir.Beni ilgilendiren soruda Vieta teoreminden ne çıkarılabilir?

1. Denklemin tüm köklerinin çarpımı serbest terimin modülüne eşittir. Denklemin kökleri tam sayı ise serbest terimin bölenleri olmalıdır.

X denklemine geri dönelim. 3 + 2x2 -5x-6=0. Tamsayılar şu kümeye ait olmalıdır: ±1; ±2; ±3; ±6. Sayıları sırayla denklemde değiştirerek kökleri elde ederiz: -3; -1; 2.

2. Bu denklemi çarpanlara ayırarak çözerseniz, Vieta teoremi bir "ipucu" verir:Genişletme için grupları derlerken, serbest terimin bölenleri olan sayıların ortaya çıkması gerekir. Hemen öğrenemeyeceğiniz açıktır çünkü tüm bölenler denklemin kökleri değildir. Ve ne yazık ki, hiç işe yaramayabilir - sonuçta denklemin kökleri tam sayılar olmayabilir.

Denklemi çöz x 3 +2x 2 -5x-6=0 çarpanlara ayırma. X 3 + 2x 2 -5x-6 \u003d x 3 + (3x 2 - x 2) -3x-2x-6 \u003d x 2 (x + 3) - x (x + 3) - 2 (x + 3) \u003d (x + 3) (x 2 -x-2) \u003d \u003d (x + 3) (x 2 + x -2x -2) \u003d (x + 3) (x (x + 1) -2 (x + 1)) \u003d (x + 2) (x + 1) (x-2) Orijinal denklem şu şekildedir: şuna eşdeğerdir: ( x+2)(x+1)(x-2)=0. Ve bu denklemin üç kökü var: -3; -1; 2. Vieta teoreminin "ipucunu" kullanarak aşağıdaki denklemi çözdüm: x 3 -12x+16=0 x 1 x 2 x 3 = -16. Serbest terimin bölenleri: ±1; ±2; ±4; ±8; ±16. X 3 -12x + 16 \u003d x 3 -4x-8x + 16 \u003d (x 3 -4x) - (8x-16) \u003d x (x 2) -4)-8(x-2)=x(x-2)(x+2)-8(x-2)=

\u003d (x-2) (x (x + 2) -8) \u003d (x-2) (x 2 + 2x-8) (x-2) (x 2 + 2x-8) \u003d 0 x- 2 \u003d 0 veya x 2 +2x-8=0 x=2 x 1 =-4; x 2 \u003d 2. Cevap. -4; 2.

3. Ortaya çıkan eşitlik sistemini bilerek, denklemin bilinmeyen katsayılarını denklemin köklerinden bulabilirsiniz..

Testler:

1. Denklem x 3 + piksel 2 + 19x - 12=0'ın kökleri 1, 3, 4'tür. p katsayısını bulun; Cevap. a) 12; b) 19; 12'de; d) -8 2. Denklem x 3 - 10x2 + 41x + r=0'ın kökleri 2, 3, 5'tir. r katsayısını bulun; Cevap. a) 19; b) -10; c) 30; d) -30.

Bu projenin sonuçlarının yeterli miktarda uygulanmasına yönelik görevler, M.I.Skanavi tarafından düzenlenen üniversiteye başvuranlar için kılavuzda bulunabilir. Vieta teoreminin bilinmesi bu tür problemlerin çözümünde paha biçilemez bir yardım sağlayabilir.

№6.354

4. Sonuç

1. Bir cebirsel denklemin köklerini denklemin katsayıları cinsinden ifade eden bir formül vardır: burada D==() 2 + () 3 D>0, 1 çözüm. Formül Cardano.

2. Kübik denklemin köklerinin özelliği

X 1 + x 2 + x 3 \u003d - p;

X 1. x 2 + x 1 x 3 + x 2 x 3 = q;

X 1 x 2 x 3 = - r.

Sonuç olarak kübik denklemlerin köklerini katsayıları cinsinden ifade eden bir formülün olduğu ve denklemin kökleri ile katsayıları arasında da bir bağlantı olduğu sonucuna vardım.

5. Literatür:

1. Genç bir matematikçinin ansiklopedik sözlüğü. A.P. Savin. –M.: Pedagoji, 1989.

2. Matematikte birleşik devlet sınavı - 2004. Görevler ve çözümler. V.G.Agakov, N.D.Polyakov, M.P.Urukova ve diğerleri.Cheboksary. Çuvaş yayınevi. un-ta, 2004.

3. Parametreli denklemler ve eşitsizlikler. V.V. Mochalov, Silvestrov V.V. Parametreli denklemler ve eşitsizlikler: Proc. ödenek. -Çeboksary: Çuvaş Yayınevi. Üniversite, 2004.

4. Matematikteki problemler. Cebir. Referans kılavuzu. Vavilov V.V., Olehnik S.N.-M.: Nauka, 1987.

5.M.I.Skanavi tarafından düzenlenen koleksiyonun matematikteki tüm rekabet problemlerinin Reshebnik'i. M.P. Bazhov'un adını taşıyan "Ukrayna Ansiklopedisi" yayınevi, 1993.

6. Bir cebir ders kitabının sayfalarının arkası. L.F. Pichurin.-M.: Aydınlanma, 1990.

Ön izleme:

Sunumların önizlemesini kullanmak için bir Google hesabı (hesap) oluşturun ve oturum açın: https://accounts.google.com

Slayt başlıkları:

Formüllerin dünyasına bakalım

denklem şu şekildedir (1) denklemi tam bir küp seçecek şekilde dönüştürürüz: denklemleri 3 ile çarparız (1) (2) dönüştürürüz (2) denklemleri elde ederiz aşağıdaki denklemi elde ederiz Denklemin sağ ve sol taraflarında (3) üçüncü kuvveti denklemin köklerini buluyoruz kübik denklemlerin çözüm örnekleri

İkinci dereceden denklemler diskriminantın gerçek sayılar arasında kökleri olmadığı formun denklemleri

Üçüncü derecenin denklemi

Tarihsel not: Bilge adamların bilinmeyen miktarlar içeren eşitlikler hakkında ilk kez düşünmeye başladıkları o uzak zamanlarda, muhtemelen henüz madeni para veya cüzdan yoktu. Mezopotamya'nın, Hindistan'ın, Çin'in, Yunanistan'ın eski matematik problemlerinde bilinmeyen nicelikler, bahçedeki tavus kuşlarının sayısını, sürüdeki boğaların sayısını, mal paylaşımında dikkate alınan şeylerin bütünlüğünü ifade ediyordu. Bize ulaşan kaynaklar, eski bilim adamlarının bilinmeyen niceliklerdeki problemleri çözmek için bazı genel yöntemlere sahip olduklarını gösteriyor. Ancak ne tek bir papirüs ne de tek bir kil tablet bu tekniklerin tanımını vermez. Bunun istisnası, Yunan matematikçi İskenderiyeli Diophantus'un (III. Yüzyıl) "Aritmetiği"dir - çözümlerinin sistematik bir sunumuyla denklemlerin derlenmesine yönelik bir problemler koleksiyonu. Ancak 9. yüzyıldaki Bağdatlı bilim adamının çalışması, yaygın olarak bilinen sorunların çözümüne yönelik ilk el kitabı oldu. Muhammed bin Musa el-Harezmi.

denklem (1) şeklindedir bulmayı seçerek formül 1'i uygularız ve aşağıdaki eşitlik sağlanacak şekilde denklemin (1) sol tarafını şu şekilde dönüştürürüz: elde ettiğimiz toplam olarak tam küpü seçeriz y için denklem (2) basitleştirin (2) denklemi ( 3) (3)'te, bilinmeyenin karesini içeren terim kayboldu, ancak bilinmeyenin birinci kuvvetini içeren terim kaldı 2) seçimle, öyle bir sayı bulun ki aşağıdaki eşitlik sağlanır.Bu eşitlik imkansızdır çünkü solda pozitif bir sayı, solda negatif bir sayı vardır.Bu tarafa gidersek takılıp kalırız.... Seçilen yolda başarısız oluruz. Henüz denklemi çözemedik.

Formun denkleminin kübik denklemleri burada (1) 1. Denklemleri a'ya bölerek basitleştiririz, daha sonra "x" katsayısı 1'e eşit olur, bu nedenle herhangi bir kübik denklemin çözümü toplam küp formülüne dayanır. : (2) Eğer denklem (1)'i alırsak, denklem (2)'den sadece x'teki katsayı ve serbest terim farklıdır. Denklem (1) ve (2)'yi toplayıp benzerlerini veriyoruz: Burada bir değişiklik yaparsak, y'ye göre terimiz kübik bir denklem elde ederiz:

Cardano Girolamo

Cardano Girolamo (24 Eylül 1501 - 21 Eylül 1576) İtalyan matematikçi, tamirci ve doktordu. Pavia'da doğdum. Pavia ve Padua üniversitelerinde okudu. Gençliğinde hekimlik yaptı. 1534'te Milano ve Bologna'da matematik profesörü oldu. Matematikte Cardano adı genellikle N. Tartaglia'dan ödünç aldığı kübik bir denklemi çözmek için kullanılan formülle ilişkilendirilir. Bu formül Cardano'nun Büyük Sanatı veya Cebir Kuralları Üzerine (1545) kitabında yayınlandı. O zamandan beri Tartaglia ve Cardano amansız düşmanlar haline geldi. Bu kitap, Cardano'nun başta kübik denklemler olmak üzere denklemleri çözmek için kullandığı modern yöntemleri sistematik olarak özetlemektedir. Cardano, kübik bir denklemi 2. dereceden terim içermeyen bir forma getirmeyi mümkün kılan doğrusal bir dönüşüm gerçekleştirdi; denklemin kökleri ve katsayıları arasındaki ilişkiye, bir polinomun x farkına bölünebilirliğine dikkat çekti. – a, eğer a onun kökü ise. Cardano, Avrupa'da denklemlerin negatif köklerinin varlığını kabul eden ilk kişilerden biriydi. Eserlerinde ilk kez hayali büyüklükler karşımıza çıkıyor. Cardano, mekanik alanında kaldıraç ve ağırlık teorisini inceledi. Bir parçanın dik açının kenarları boyunca yaptığı hareketlerden birine mekanikte kardan hareketi denir. Cardano Girolamo'nun Biyografisi

Aynı zamanda, İtalya'nın Verona şehrinde Tartaglia (yani kekeme) lakaplı fakir bir matematik öğretmeni Nicolo (1499-1557) yaşıyordu. Çok yetenekliydi ve Dal Ferro'nun tekniğini yeniden keşfetmeyi başardı. Fiore ile Tartaglia arasında bir düello gerçekleşti. Şarta göre rakipler, çözümüne 50 gün süre verilen 30 sorunu paylaştı. Ancak Fior özünde yalnızca bir sorunu bildiğinden ve bazı öğretmenlerin bunu çözemeyeceğinden emin olduğundan, 30 sorunun hepsinin aynı türde olduğu ortaya çıktı. Tartaglia onlarla iki saat içinde ilgilendi. Fiore ise düşmanın önerdiği görevlerin hiçbirini çözemedi. Zafer tüm İtalya'da Tartaglia'yı yüceltti, ancak sorun tamamen çözülmedi.Bilinmeyen bir değerin karesini içeren denklemin bir üyesiyle (tam bir küp seçerek) başa çıkmayı başardığımız bu basit numara henüz açık değildi ve Çeşitli türdeki denklemlerin çözümü sisteme getirilmemiştir. Fiora ile Tartaglia'nın düellosu

bu denklemden bir denklem formu a denklemin diskriminantını hesaplıyoruz Bu denklemin kökü tamamen çıkarılmamış olmakla kalmıyor, yine de negatif bir sayıdan çıkarılması gerekiyor. Sorun ne? Bu denklemin köklerinin olmadığı varsayılabilir çünkü D

Kübik bir denklemin kökleri diskriminantına bağlıdır denklemin 1 çözümü vardır denklemin 3 çözümü vardır denklemin 2 çözümü vardır Sonuç

denklem şu şekildedir: Cardano formülünü kullanarak denklemin köklerini bulun Cardano formülünü kullanarak kübik denklemleri çözme örnekleri

bu denklemden (1) formunda bir denklem ve koşula göre bu denklemin 1 çözümü olması gerektiğinden, denklemin diskriminantını (1) hesaplıyoruz + - + 2 6 Cevap: a'dan en küçük doğal değer bu aralık 1'dir. Bir denklemin 1 çözümü olan en küçük doğal değeri nedir?

Kübik denklemlerin Vieta yöntemiyle çözümü Denklemler şu şekildedir:

Vieta teoremine göre iki kökünün çarpımının 1'e eşit olduğu biliniyorsa ve koşulumuz varsa denklemi çözün veya değeri ilk denklemde yerine koyarız veya üçüncü denklemdeki değeri birinciye koyarız Denklemin köklerini veya cevabını bulacağız:

Kullanılan literatür: “Matematik. Eğitimsel ve metodik el kitabı » Yu.A. Gusman, A.O. Smirnov. Ansiklopedi “Dünyayı biliyorum. Matematik" - Moskova, AST, 1996. "Matematik. Öğretim yardımı » V.T. Lisichkin. M.I.Skanavi tarafından düzenlenen, üniversitelere başvuranlar için bir rehber. Matematikte Birleşik Devlet Sınavı - 2004

İlginiz için teşekkür ederiz

Formül Cardano

Köprü

Odessa

Orta Çağ'daki anlaşmazlıklar her zaman genç ve yaşlı aylak kasaba halkının ilgisini çeken ilginç bir gösteri olmuştur. Tartışmaların konuları çeşitliydi ama zorunlu olarak bilimseldi. Bilim aynı zamanda yedi özgür sanat olarak adlandırılan listede yer alan şeyin elbette teoloji olduğu anlamına geliyordu. Teolojik tartışmalar en sık görülen konulardı. Her şeyi tartıştılar. Örneğin, Kutsal Ruh'a bir farenin kutsal ayini yerse bağlanıp bağlanmayacağı, Cuma Sibyl'in İsa Mesih'in doğuşunu tahmin edip edemeyeceği, Kurtarıcı'nın erkek ve kız kardeşlerinin neden kanonlaştırılmadığı vb.

Ünlü matematikçi ile daha az ünlü olmayan doktor arasında çıkacak anlaşmazlık hakkında, kimse gerçekten bir şey bilmediğinden, yalnızca en genel tahminler ifade edildi. Birinin diğerini aldattığı söylendi (kim olduğu ve tam olarak kim olduğu bilinmiyor). Meydanda toplananların hemen hemen hepsinin matematikle ilgili en belirsiz fikirleri vardı ama herkes anlaşmazlığın başlamasını sabırsızlıkla bekliyordu. Her zaman ilginçti; haklı olsun ya da olmasın, kaybedene gülebiliyordunuz.

Belediye binasının saati beşi vurduğunda kapılar ardına kadar açıldı ve kalabalık katedralin içine akın etti. Girişi mihraba bağlayan orta hattın her iki yanında, iki yan sütunda tartışmacılar için iki uzun minber dikildi. Orada bulunanlar kilisede olmalarına aldırış etmeden yüksek bir ses çıkardılar. Sonunda, ikonostasisi orta nefin geri kalanından ayıran demir ızgaranın önünde, siyah ve mor pelerinli şehir tellalı belirdi ve şunu ilan etti: “Milano şehrinin saygıdeğer vatandaşları! Şimdi karşınızda Brenia'lı ünlü matematikçi Niccolò Tartaglia konuşacak. Rakibi ise matematikçi ve doktor Geronimo Cardano olacaktı. Niccolo Tartaglia, Cardano'yu "Ars magna" adlı kitabında kendisine ait olan 3. dereceden bir denklemi çözme yöntemini, yani Tartaglia'yı yayınlayan son kişi olmakla suçluyor. Ancak Cardano'nun kendisi anlaşmazlığa gelemedi ve bu nedenle öğrencisi Luige Ferrari'yi gönderdi. Böylece tartışma açık ilan edilir, katılımcıları sandalyelere davet edilir. Girişin solundaki minbere kanca burunlu, kıvırcık sakallı, beceriksiz bir adam tırmandı ve karşıdaki minbere yakışıklı, kendine güvenen yüzlü, yirmili yaşların başında bir genç çıktı. Bütün tavrı, her hareketinin ve her sözünün memnuniyetle karşılanacağına dair tam bir güven gösteriyordu.

Tartaglia başladı.

Sayın Baylar! Biliyorsunuz, 13 yıl önce 3. dereceden bir denklemi çözmenin bir yolunu bulmayı başardım ve ardından bu yöntemi kullanarak Fiori ile bir anlaşmazlığı kazandım. Yöntemim yurttaşınız Cardano'nun dikkatini çekti ve o, sırrı benden çıkarmak için tüm kurnaz sanatını kullandı. Aldatmaca ya da düpedüz sahtecilikle yetinmedi. Ayrıca Cardano'nun cebir kuralları hakkındaki kitabının 3 yıl önce Nürnberg'de yayınlandığını ve burada utanmadan çalınan yöntemimin herkesin kullanımına sunulduğunu da biliyorsunuz. Cardano ve öğrencisini bir yarışmaya davet ettim. Ben 31 problemi çözmeyi teklif ettim, aynı rakam bana rakiplerim tarafından da teklif edildi. Sorunların çözümü için süre 15 gündü. Cardano ve Ferrari'nin derlediği sorunların çoğunu 7 günde çözmeyi başardım. Bunları bastırdım ve kuryeyle Milano'ya gönderdim. Ancak sorunlarıma yanıt alana kadar tam beş ay beklemek zorunda kaldım. Doğru değillerdi. Bu bana her ikisini de kamusal bir tartışmaya davet etmem için sebep verdi.

Tartaglia sessizdi. Talihsiz Tartaglia'ya bakan genç adam şunları söyledi:

Sayın Baylar! Değerli rakibim, konuşmasının ilk kelimelerinde bana ve öğretmenime karşı o kadar çok iftira atmasına izin verdi ki, iddiası o kadar temelsizdi ki, ilkini çürütmek ve ikincisinin tutarsızlığını size göstermek bana neredeyse hiç zorluk çıkarmazdı. Öncelikle Niccolo Tartaglia yöntemini tamamen gönüllü olarak ikimizle de paylaşıyorsa nasıl bir aldatmacadan bahsedebiliriz? Ve işte Geronimo Cardano, cebir kuralının keşfinde rakibimin rolü hakkında şöyle yazıyor. İnsan zekasını ve insan ruhunun tüm yeteneklerini aşan, böylesine güzel ve şaşırtıcı bir şeyi keşfetme onuru Cardano'nun kendisine değil, arkadaşım Tartaglia'ya ait olduğunu söylüyor. Bu keşif gerçekten ilahi bir armağandır, onu kavrayan aklın gücünün o kadar mükemmel bir kanıtıdır ki, onun için hiçbir şeyin ulaşılmaz olduğu düşünülemez."

Rakibim beni ve öğretmenimi kendi sorunlarına yanlış çözüm bulmakla suçladı. Peki denklemin kökü, onu denklemde yerine koyarak ve bu denklemde belirtilen tüm eylemleri gerçekleştirerek bir özdeşliğe ulaşırsak nasıl yanlış olabilir? Ve eğer Senor Tartaglia tutarlı olmak istiyorsa, o zaman neden hırsızlık yapan bizlerin, onun icadıyla ve onu önerilen sorunları çözmek için kullanarak yanlış çözüme ulaştığımızın yorumuna cevap vermek zorundaydı. Ancak biz, öğretmenim ve ben, Sinyor Tartaglia'nın icadının önemsiz olduğunu düşünmüyoruz. Bu buluş harika. Üstelik ona çok güvenerek 4. derece denklemini çözmenin bir yolunu buldum ve "Ars magna"da öğretmenim bundan bahsediyor. Senor Tartaglia bizden ne istiyor? Tartışarak ne elde etmeye çalışıyor?

Beyler beyler, diye bağırdı Tartaglia, sizden beni dinlemenizi rica ediyorum! Genç düşmanımın mantık ve belagat konusunda çok güçlü olduğunu inkar etmiyorum. Ancak bu gerçek bir matematiksel kanıtın yerini alamaz. Cardano ve Ferrari'ye verdiğim görevler doğru bir şekilde çözülmedi ama bunu kanıtlayacağım. Aslında, örneğin onu çözenler arasında bir denklemi ele alalım. Biliniyor...

Kilisede, şanssız matematikçinin başlattığı cümlenin sonunu tamamen yutan, hayal edilemeyecek bir gürültü yükseldi. Devam etmesine izin verilmedi. Kalabalık onun çenesini kapatmasını ve sıranın Ferrari'ye verilmesini talep etti. Tartışmanın devamının tamamen faydasız olduğunu gören Tartaglia, aceleyle kürsüden indi ve kuzey verandasından meydana çıktı. Kalabalık, tartışmanın "kazananını", Luigi Ferrari'yi alkışladı.

... Bugün bile giderek daha fazla tartışmaya neden olmaya devam eden bu anlaşmazlık böylece sona erdi. 3. derece denklemi çözmenin yolu aslında kimin elinde? Şimdi konuşuyoruz - Niccolo Tartaglia. Keşfetti ve Cardano bu keşfi onun elinden aldı. Ve eğer şimdi 3. dereceden bir denklemin köklerini katsayıları aracılığıyla temsil eden formüle Cardano formülü dersek, bu tarihsel bir adaletsizliktir. Ancak haksızlık mı? Matematikçilerin her birinin keşfine katılım ölçüsü nasıl hesaplanır? Belki zamanla birisi bu soruyu kesin olarak cevaplayabilecektir, ya da belki bir sır olarak kalacaktır ...

Formül Cardano

Modern matematik dilini ve modern sembolizmi kullanırsak, Cardano formülünün türetilmesi aşağıdaki son derece temel hususlar kullanılarak bulunabilir:

3. dereceden genel bir denklem verelim:

balta 3 +3bx 2 +3cx+d=0 (1)

Eğer koyarsak

, sonra denklemi veriyoruz (1) akla

(2) , .

Yeni bir bilinmeyeni tanıtalım sen eşitliği kullanmak

Bu ifadeyi dahil ederek (2) , alıyoruz

(3) ,

buradan

İkinci terimin pay ve paydası ifadeyle çarpılırsa

ve elde edilen ifadeyi dikkate alın sen"+" ve "-" işaretlerine göre simetrik olduğu ortaya çıkarsa, sonunda şunu elde ederiz:

(Son eşitlikteki kübik radikallerin çarpımı eşit olmalıdır P).

Bu ünlü Cardano formülüdür. Eğer gidersen sen geri dönmek X, daha sonra 3. dereceden genel denklemin kökünü belirleyen bir formül elde ederiz.

Tartaglia'ya bu kadar acımasızca davranan genç adam, gösterişsiz bir gizemin haklarını anladığı kadar matematiği de kolaylıkla anlıyordu. Ferrari 4. derece denklemi çözmenin bir yolunu buluyor. Cardano bu yönteme kitabında yer verdi. Bu yöntem nedir?

(1)

– 4. derecenin genel denklemi.(2)

Nerede p,q,r bağlı olarak bazı katsayılar vardır a,b,c,d,e. Bu denklemin aşağıdaki biçimde yazılabileceğini görmek kolaydır:

(3)

Aslında parantezleri açmak yeterlidir, ardından aşağıdakileri içeren tüm üyeler T, birbirimizi iptal ederiz ve denkleme geri döneriz (2) .

Parametreyi seçelim T böylece denklemin sağ tarafı (3) açısından mükemmel bir kareydi sen. Bilindiği gibi bunun gerekli ve yeterli şartı, trinomialin katsayılarından diskriminantın sıfır olmasıdır. sen) Sağdaki.

BELEDİYE VII ÖĞRENCİ BİLİMSEL VE UYGULAMALI KONFERANSI "GENÇLİK: YARATICILIK, ARAMA, BAŞARI"

Anninsky belediye bölgesi

Voronej bölgesi

Bölüm:MATEMATİK

Ders:"Cardano Formülü: Tarih ve Uygulamalar"

MKOU Anninskaya ortaokul No. 3, 9 "B" sınıfı

Niccolò Fontana Tartaglia (1499-1557) İtalyan matematikçidir.

Genel olarak tarih, formülün ilk olarak Tartaglia tarafından keşfedildiğini ve zaten bitmiş haliyle Cardano'ya teslim edildiğini söylüyor, ancak Cardano'nun kendisi bu gerçeği reddetti, ancak Tartaglia'nın formülün yaratılmasındaki rolünü inkar etmedi.

Formülün arkasında, onu gerçekten açıklayan ve kamuoyuna sunan bilim adamının onuruna, "Cardano'nun formülü" adı köklü bir şekilde yer almaktadır.

Belediye binasının saati beşi vurduğunda kapılar ardına kadar açıldı ve kalabalık katedralin içine akın etti. Girişi mihraba bağlayan orta hattın her iki yanında, iki yan sütunda tartışmacılar için iki uzun minber dikildi. Orada bulunanlar kilisede olmalarına aldırış etmeden yüksek bir ses çıkardılar. Sonunda, ikonostasisi orta nefin geri kalanından ayıran demir ızgaranın önünde, siyah ve mor pelerinli şehir tellalı belirdi ve şunu ilan etti: “Milano şehrinin saygıdeğer vatandaşları! Şimdi karşınızda Brenia'lı ünlü matematikçi Niccolò Tartaglia konuşacak. Rakibi ise matematikçi ve doktor Geronimo Cardano olacaktı. Niccolo Tartaglia, Cardano'yu "Arsmagna" adlı kitabında kendisine ait olan 3. dereceden bir denklemi çözme yöntemini, yani Tartaglia'yı yayınlamakla suçluyor. Ancak Cardano'nun kendisi anlaşmazlığa gelemedi ve bu nedenle öğrencisi Luige Ferrari'yi gönderdi. Böylece tartışma açık ilan edilir, katılımcıları sandalyelere davet edilir. Girişin solundaki minbere kambur burunlu, kıvırcık sakallı, beceriksiz bir adam, karşıdaki minbere ise yakışıklı, kendine güvenen yüzlü, yirmili yaşlarının başında bir genç çıktı. Bütün tavrı, her hareketinin ve her sözünün memnuniyetle karşılanacağına dair tam bir güven gösteriyordu.

Tartaglia başladı.

Tartaglia sessizdi. Talihsiz Tartaglia'ya bakan genç adam şunları söyledi:

Sayın Baylar! Değerli rakibim, konuşmasının ilk kelimelerinde bana ve öğretmenime karşı o kadar çok iftira atmasına izin verdi ki, iddiası o kadar temelsizdi ki, ilkini çürütmek ve ikincisinin tutarsızlığını size göstermek bana neredeyse hiç zorluk çıkarmazdı. Öncelikle Niccolo Tartaglia yöntemini tamamen gönüllü olarak ikimizle de paylaşıyorsa nasıl bir aldatmacadan bahsedebiliriz? Ve işte Geronimo Cardano, cebir kuralının keşfinde rakibimin rolü hakkında şöyle yazıyor. İnsan zekasını ve insan ruhunun tüm yeteneklerini aşan, böylesine güzel ve şaşırtıcı bir şeyi keşfetme onuru Cardano'nun kendisine değil, arkadaşım Tartaglia'ya ait olduğunu söylüyor. Bu keşif gerçekten ilahi bir armağandır, onu kavrayan zihnin gücünün o kadar mükemmel bir kanıtıdır ki, onun için hiçbir şeyin ulaşılmaz olduğu düşünülemez.

Rakibim beni ve öğretmenimi kendi sorunlarına yanlış çözüm bulmakla suçladı. Peki denklemin kökü, onu denklemde yerine koyarak ve bu denklemde belirtilen tüm eylemleri gerçekleştirerek bir özdeşliğe ulaşırsak nasıl yanlış olabilir? Ve eğer Senor Tartaglia tutarlı olmak istiyorsa, o zaman onun deyimiyle buluşunu çalan ve onu önerilen sorunları çözmek için kullanan bizlerin neden yanlış çözümü bulduğumuz sorusuna cevap vermesi gerekiyordu. Ancak biz, öğretmenim ve ben, Sinyor Tartaglia'nın icadının önemsiz olduğunu düşünmüyoruz. Bu buluş harika. Üstelik ona çok güvenerek 4. derece denklemini çözmenin bir yolunu buldum ve "Arsmagna" da öğretmenim bundan bahsediyor. Senor Tartaglia bizden ne istiyor? Tartışarak ne elde etmeye çalışıyor?

Beyler beyler, diye bağırdı Tartaglia, sizden beni dinlemenizi rica ediyorum! Genç düşmanımın mantık ve belagat konusunda çok güçlü olduğunu inkar etmiyorum. Ancak bu gerçek bir matematiksel kanıtın yerini alamaz. Cardano ve Ferrari'ye verdiğim görevler yanlış çözüldü ama bunu kanıtlayacağım. Aslında, örneğin onu çözenler arasında bir denklemi ele alalım. Biliniyor...

Bugün giderek daha fazla anlaşmazlığa neden olmaya devam eden bu anlaşmazlık böylece sona erdi. 3. derece denklemi çözmenin yolu aslında kimin elinde? Şimdi konuşuyoruz - Niccolo Tartaglia. Keşfetti ve Cardano bu keşfi onun elinden aldı. Ve eğer şimdi 3. dereceden bir denklemin köklerini katsayıları aracılığıyla temsil eden formüle Cardano formülü dersek, bu tarihsel bir adaletsizliktir. Ancak haksızlık mı? Matematikçilerin her birinin keşfine katılım ölçüsü nasıl hesaplanır? Belki zamanla birisi bu soruyu kesin olarak cevaplayabilecektir, ya da belki bir sır olarak kalacaktır ...

Modern matematik dilini ve modern sembolizmi kullanırsak, Cardano formülünün türetilmesi aşağıdaki son derece temel hususlar kullanılarak bulunabilir:

3. dereceden genel bir denklem verelim:

X 3 + balta 2 + bx + C = 0,

(1)

Neredea, b, c – keyfi gerçek sayılar.

Denklem (1)'deki değişkeni değiştirelimX yeni bir değişkene senformüle göre:

X 3 +balta 2 +bx+c = (y ) 3 + a(y ) 2 + b(y ) + c = y 3 3 yıl 2 + 3 yıl+ a(y 2 2 yıl+tarafından =y 3 sen 3 + (b

o zaman denklem (1) şu formu alırsen 3 + ( B

Gösterimi tanıtırsakP = B, Q = ,

o zaman denklem şu şekli alacaktırsen 3 + py + Q = 0.

Bu ünlü Cardano formülüdür.

Kübik denklemin köklerisen 3 + py + Q = 0 ayrımcıya bağlı

EğerD> 0, o zamankübik bir polinomun üç farklı gerçek kökü vardır.

EğerD< 0, то kübik bir polinomun bir gerçek kökü ve iki karmaşık kökü vardır (bunlar karmaşık eşleniklerdir).

EğerD = 0, çoklu bir kökü vardır (ya çokluk 2'nin bir kökü ve çokluk 1'in bir kökü, her ikisi de gerçek; ya da çokluk 3'ün tek bir gerçek kökü).

2.4. Kübik denklemleri çözmenin evrensel yollarına örnekler

Cardan formülünü belirli denklemlerin çözümüne uygulamaya çalışalım.

Örnek 1: X 3 +15 X+124 = 0

BuradaP = 15; Q = 124.

Cevap:X

İçerik

Ayrıca bakınız: Vieta'nın trigonometrik formülü

Kübik bir denklemin indirgenmiş forma indirgenmesi

Kübik denklemi düşünün:
(1) ,
Nerede . Bunu ikiye ayıralım:
(2) ,
Nerede , , .
Ayrıca, ve -'nin gerçek sayılar olduğunu varsayıyoruz.

Denklemi (2) daha basit bir forma getirelim. Bunu yapmak için bir değişiklik yapalım
.
;
;
.
Katsayıyı sıfıra eşitleyelim. Bunun için belirledik
:
;
;
.
İndirgenmiş formun bir denklemini elde ederiz:
(3) ,
Nerede
(4) ; .

Cardano formülünün türetilmesi

Denklemi (3) çözüyoruz. Oyuncu değişikliği yapma
(5) :
;
;
;
.
Bu denklemi sağlamak için şunu belirledik:
(6) ;
(7) .

(7)'den elimizde:
.
(6)'da yerine koy:
;
.

İkinci dereceden bir denklemi çözüyoruz.
(8) .
Üstteki "+" işaretini alalım:
,
notasyonu nerede tanıttık
.
(6)'dan elimizde:
.

Böylece yukarıdaki denklemin çözümünü aşağıdaki biçimde bulduk:
(5) ;
(9) ;
(10) ;
(7) ;
(11) .
Böyle bir çözüm denir Cardano formülü.

Eğer (8)'deki karekökün işaretini seçerken alttaki işareti alırsak, o zaman yer değiştirecekler ve yeni bir şey elde edemeyiz. Değerler ve değerleri küp köklerine eşit olduğundan üç değere sahiptirler. Tüm olası çiftlerden denklemi (7) karşılayanları seçmek gerekir.

Yani, indirgenmiş kübik denklemi çözmek için algoritma
(3)
Sonraki.
1) Öncelikle karekökün herhangi bir değerini belirliyoruz.
2) Küp kökünün üç değerini hesaplayın.
3) Formül (7)'yi kullanarak her değer için değeri hesaplıyoruz:
.
Sonuç olarak, üç çift miktar elde ederiz ve .
4) Her değer çifti için ve formül (5)'e göre yukarıdaki denklemin (3) köklerinin değerlerini buluyoruz.
5) Orijinal denklemin (1) köklerinin değerlerini formüle göre hesaplıyoruz
.
Bu şekilde orijinal denklemin üç kökünün değerlerini elde ederiz. İki veya üç kökün katı (eşit) olması durumunda.

Bu algoritmanın 3. adımında farklı şekilde ilerlenebilir. Miktarın üç değerini formül (10) kullanarak hesaplayabiliriz. Ve sonra üç çift kök yapın ve böylece her çift için ilişki yerine gelsin
(7) .

Durum Q ≥ 0

Olayı ele alalım. Üstelik ve gerçek sayılardır. Gösterimi tanıtalım. Küp köklerinin gerçek değerleri olsun ve gösterelim.

Köklerin diğer değerlerini bulalım ve . Bunu aşağıdaki formda yazalım:
; ,
burada - bir tam sayıdır;
- hayali birim, .
Daha sonra
.
Değer atayarak üç kök elde ederiz:
, ;
, ;
, .
Benzer şekilde üç kök elde ederiz:
;
;
.

Şimdi her çift için ilişki olacak şekilde gruplayıp çiftlere ayırıyoruz.
(7) .
Çünkü o zaman
.
Daha sonra
.
Buradan ilk çifti alıyoruz: .
Daha sonra şunu fark ediyoruz
.
Bu yüzden
; .
Sonra ve iki çift daha var.

Şimdi yukarıdaki denklemin üç kökünü elde ediyoruz:
;
;
.
Ayrıca aşağıdaki biçimde de yazılabilirler:
(12) ; .
Bu formüllere Cardano formülü denir.

, tarihinde. İki kök katlardır:
; .
Çünkü her üç kök de katlardır:
.

Durum S< 0

Formül (12)'nin türetilmesini izlersek, türetmenin tamamının negatif bir değerle bile geçerli kalacağını görürüz. Yani karmaşık olabilirler. Daha sonra for ve one arasındaki ilişkinin herhangi bir küp kök değeri seçilebilir.
.

Cardano'nun kübik denklem çözme formülü

Böylece indirgenmiş kübik denklemin köklerinin olduğunu tespit ettik.
daha uygundurlar.

Referanslar:
N.M. Gunther, R.O. Kuzmin, Yüksek matematikte problemlerin toplanması, Lan, 2003.

Ayrıca bakınız:

Gerçek köklü katsayılar içeren kübik bir denklem, diğer ikisi karmaşık eşlenik çift olarak kabul edilir. Rasyonel köklerin araştırılmasının yanı sıra, iki terimli ve karşılıklı denklemler içeren denklemler de dikkate alınacaktır. Tüm bilgiler örneklerle desteklenecektir.

A x 3 + B = 0 formundaki iki terimli kübik denklemin çözümü

Binom içeren kübik bir denklem A x 3 + B = 0 biçimindedir. Sıfırdan farklı olan A'ya bölünerek x 3 + B A \u003d 0'a düşürülmelidir. Bundan sonra küp toplamının kısaltılmış çarpımı formülünü uygulayabilirsiniz. Bunu anlıyoruz

x 3 + B Bir = 0 x + B Bir 3 x 2 - B Bir 3 x + B Bir 2 3 = 0

İlk parantez sonucu x \u003d - B A 3 ve kare trinomial - x 2 - B A 3 x + B A 2 3 şeklini alacak ve yalnızca karmaşık köklerle.

örnek 1

2 x 3 - 3 = 0 kübik denkleminin köklerini bulun.

Çözüm

Denklemden x'i bulmanız gerekiyor. Hadi yaz:

2 x 3 - 3 = 0 x 3 - 3 2 = 0

Kısaltılmış çarpma formülünü uygulamak gerekir. O zaman bunu anlıyoruz

x 3 - 3 2 = 0 x - 3 3 2 6 x 2 + 3 3 2 6 x + 9 2 3 = 0

İlk parantezi genişletin ve x = 3 3 2 6 değerini elde edin. İkinci parantezin gerçek kökleri yoktur çünkü diskriminant sıfırdan küçüktür.

Cevap: x = 3 3 2 6 .

A x 3 + B x 2 + B x + A = 0 formundaki karşılıklı kübik denklemin çözümü

İkinci dereceden denklemin formu A x 3 + B x 2 + B x + A \u003d 0'dır; burada A ve B'nin değerleri katsayılardır. Gruplandırma gereklidir. Bunu anlıyoruz

A x 3 + B x 2 + B x + A = A x 3 + 1 + B x 2 + x = = A x + 1 x 2 - x + 1 + B x x + 1 = x + 1 A x 2 + x B-A+A

Denklemin kökü x \u003d - 1'dir, o zaman A x 2 + x B - A + A kare trinomialinin köklerini elde etmek için, diskriminantı bularak onu kullanmak gerekir.

Örnek 2

5 x 3 - 8 x 2 - 8 x + 5 = 0 gibi bir denklem çözün.

Çözüm

Denklem tersine çevrilebilir. Gruplandırma gereklidir. Bunu anlıyoruz

5 x 3 - 8 x 2 - 8 x + 5 = 5 x 3 + 1 - 8 x 2 + x = = = 5 x + 1 x 2 - x + 1 - 8 x x + 1 = x + 1 5 x 2 - 5 x + 5 - 8 x = = x + 1 5 x 2 - 13 x + 5 = 0

Eğer x \u003d - 1 denklemin kökü ise, o zaman verilen üç terimli 5 x 2 - 13 x + 5'in köklerini bulmanız gerekir:

5 x 2 - 13 x + 5 = 0 D = (- 13) 2 - 4 5 5 = 69 x 1 = 13 + 69 2 5 = 13 10 + 69 10 x 2 = 13 - 69 2 5 = 13 10 - 69 10

Cevap:

x 1 = 13 10 + 69 10 x 2 = 13 10 - 69 10 x 3 = - 1

Rasyonel köklü kübik denklemlerin çözümü

Eğer x \u003d 0 ise, o zaman A x 3 + B x 2 + C x + D \u003d 0 formundaki denklemin köküdür. Serbest terim D \u003d 0 ile denklem A x 3 + B x 2 + C x \u003d 0 formunu alır. X parantezden çıkarıldığında denklemin değiştiğini görüyoruz. Diskriminant veya Vieta aracılığıyla çözerken, x A x 2 + B x + C = 0 formunu alacaktır.

Örnek 3

Verilen denklemin köklerini bulun 3 x 3 + 4 x 2 + 2 x = 0.

Çözüm

İfadeyi sadeleştirelim.

3 x 3 + 4 x 2 + 2 x = 0 x 3 x 2 + 4 x + 2 = 0

X = 0 denklemin köküdür. 3 x 2 + 4 x + 2 formundaki kare bir trinomiyalin köklerini bulmalısınız. Bunu yapmak için sıfıra eşitlemek ve diskriminant kullanarak çözüme devam etmek gerekir. Bunu anlıyoruz

D \u003d 4 2 - 4 3 2 \u003d - 8. Değeri negatif olduğundan üçlü kök yoktur.

Cevap: x = 0.

A x 3 + B x 2 + C x + D = 0 denkleminin katsayıları tam sayı olduğunda cevapta irrasyonel kökler elde edilebilir. A ≠ 1 ise, denklemin her iki kısmı da A 2 ile çarpıldığında, değişkenlerde bir değişiklik gerçekleştirilir, yani y \u003d A x:

A x 3 + B x 2 + C x + D = 0 A 3 x 3 + B A 2 x 2 + C A A x + D A 2 = 0 y = A x ⇒ y 3 + B y 2 + C A y + D A 2

Kübik denklem formuna geliyoruz. Kökler tamsayı veya rasyonel olabilir. Aynı eşitliği elde etmek için, elde edilen denklemde bölenleri değiştirmek gerekir. O zaman ortaya çıkan y 1 kök olacaktır. Bu, x 1 = y 1 A formundaki orijinal denklemin kökünün olduğu anlamına gelir. A x 3 + B x 2 + C x + D polinomunu x - x 1'e bölmek gerekir. Daha sonra kare trinomialin köklerini bulabiliriz.

Örnek 4

Çözüm

Her iki parçayı da 2 2 ile çarparak ve y \u003d 2 x tipindeki bir değişkeni değiştirerek bir dönüşüm gerçekleştirmek gerekir. Bunu anlıyoruz

2 x 3 - 11 x 2 + 12 x + 9 = 0 2 3 x 3 - 11 2 2 x 2 + 24 2 x + 36 = 0 y = 2 x ⇒ y 3 - 11 y 2 + 24 y + 36 = 0

Serbest terim 36'dır, o zaman tüm bölenlerini düzeltmeniz gerekir:

± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 9 , ± 12 , ± 36

Formun kimliğini elde etmek için y 3 - 11 y 2 + 24 y + 36 = 0 yerine bir değişiklik yapmak gerekir

1 3 - 11 1 2 + 24 1 + 36 = 50 ≠ 0 (- 1) 3 - 11 (- 1) 2 + 24 (- 1) + 36 = 0

Buradan y \u003d - 1'in kök olduğunu görüyoruz. Yani x = y 2 = - 1 2.

Bizde buna sahibiz

2 x 3 - 11 x 2 + 12 x + 9 = x + 1 2 2 x 2 - 12 x + 18 = = 2 x + 1 2 x 2 - 6 x + 9

Bundan sonra, x 2 - 6 x + 9 formundaki ikinci dereceden denklemin köklerini bulmanız gerekir. Denklemin x 2 - 6 x + 9 \u003d x - 3 2 biçimine indirgenmesi gerektiğine sahibiz, burada x \u003d 3 onun kökü olacaktır.

Cevap: x 1 \u003d - 1 2, x 2, 3 \u003d 3.

Yorum

Algoritma karşılıklı denklemlere uygulanabilir. -1'in kökü olduğu görülebilir, bu da sol tarafın x + 1'e bölünebileceği anlamına gelir. Ancak o zaman kare üçlünün köklerini bulmak mümkün olacaktır. Rasyonel köklerin yokluğunda, polinomu çarpanlara ayırmak için diğer çözme yöntemleri kullanılır.

Cardano formülünü kullanarak kübik denklemleri çözme

Cardano formülünü kullanarak küp kökleri bulmak mümkündür. A 0 x 3 + A 1 x 2 + A 2 x + A 3 = 0 için B 1 = A 1 A 0, B 2 = A 2 A 0, B 3 = A 3 A 0'ı bulmanız gerekir.

O halde p = - B 1 2 3 + B 2 ve q = 2 B 1 3 27 - B 1 B 2 3 + B 3 .

Ortaya çıkan p ve q, Cardano formülüne dönüştürülür. Bunu anlıyoruz

y = - q 2 + q 2 4 + p 3 27 3 + - q 2 - q 2 4 + p 3 27 3

Küp köklerin seçimi çıktı değerini - p 3 - karşılamalıdır. O halde orijinal denklemin kökleri x = y - B 1 3'tür. Önceki örneği Cardano formülünü kullanarak çözmeyi düşünün.

Örnek 5

Verilen denklemin köklerini bulun 2 x 3 - 11 x 2 + 12 x + 9 = 0.

Çözüm

A 0 \u003d 2, A 1 \u003d - 11, A 2 \u003d 12, A 3 \u003d 9 olduğu görülebilir.

B 1 = A 1 A 0 = - 11 2, B 2 = A 2 A 0 = 12 2 = 6, B 3 = A 3 A 0 = 9 2'yi bulmak gerekir.

Dolayısıyla şu sonuç çıkıyor

p = - B 1 2 3 + B 2 = - - 11 2 2 3 + 6 = - 121 12 + 6 = - 49 12 q = 2 B 1 3 27 - B 1 B 2 3 + B 3 = 2 - 11 2 3 27 - - 11 2 6 3 + 9 2 = 343 108

Cordano formülünde bir değişiklik yaparız ve şunu elde ederiz:

y = - q 2 + q 2 4 + p 3 27 3 + - q 2 - - q 2 4 + p 3 27 3 = = - 343 216 + 343 2 4 108 2 - 49 3 27 12 3 3 + - 343 216 - 343 2 4 108 2 - 49 3 27 12 3 3 = = - 343 216 3 + - 343 216 3

343 216 3'ün üç anlamı vardır. Bunları aşağıda ele alalım.

343 216 3 \u003d 7 6 çünkü π + 2 π k 3 + i sin π + 2 π k 3, k \u003d 0, 1, 2

k \u003d 0 ise, o zaman - 343 216 3 \u003d 7 6 cos π 3 + i sin π 3 \u003d 7 6 1 2 + i 3 2

Eğer k = 1 ise - 343 216 3 = 7 6 cosπ + i sinπ = - 7 6

k \u003d 2 ise, o zaman - 343 216 3 \u003d 7 6 cos 5 π 3 + i sin 5 π 3 \u003d 7 6 1 2 - i 3 2

Çiftlere ayırmamız gerekiyor, o zaman - p 3 = 49 36 elde ederiz.

Sonra çiftler elde ederiz: 7 6 1 2 + i 3 2 ve 7 6 1 2 - i 3 2 , - 7 6 ve - 7 6 , 7 6 1 2 - i 3 2 ve 7 6 1 2 + i 3 2.

Cordano formülünü kullanarak dönüşüm yapalım:

y 1 = - 343 216 3 + - 343 216 3 = = = 7 6 1 2 + ben 3 2 + 7 6 1 2 - i 3 2 = 7 6 1 4 + 3 4 = 7 6 y 2 = - 343 216 3 + - 343 216 3 = - 7 6 + - 7 6 = - 14 6 y 3 = - 343 216 3 + - 343 216 3 = = 7 6 1 2 - i 3 2 + 7 6 1 2 + i 3 2 = 7 6 1 4 + 3 4 = 7 6

x 1 = y 1 - B 1 3 = 7 6 + 11 6 = 3 x 2 = y 2 - B 1 3 = - 14 6 + 11 6 = - 1 2 x 3 = y 3 - B 1 3 = 7 6 + 11 6 = 3

Cevap: x 1 \u003d - 1 2, x 2, 3 \u003d 3

Kübik denklemleri çözerken, Ferrari yöntemiyle 4. derece denklemlerin çözümüne indirgeme yapılabilir.

Metinde bir hata fark ederseniz, lütfen onu vurgulayın ve Ctrl+Enter tuşlarına basın.