Ağırlık merkezi, sonuçta ortaya çıkan temel yerçekimi kuvvetlerinin etki çizgisinin geçtiği noktadır. Paralel kuvvetlerin merkezi olma özelliğine sahiptir (E. M. Nikitin, § 42). Bu yüzden çeşitli cisimlerin ağırlık merkezinin konumunu belirlemek için formüller gibi görünmek:
x c = (∑ G ben x ben) / ∑ G ben ;
(1) y c = (∑ G ben y ben) / ∑ G ben;
z c = (∑ G ben z ben) / ∑ G ben .

Ağırlık merkezinin belirlenmesi gereken cisim, çizgilerden oluşan bir şekille tanımlanabiliyorsa (örneğin, Şekil 173'teki gibi telden yapılmış kapalı veya açık bir kontur), o zaman her bir segmentin ağırlığı G i li i bir ürün olarak temsil edilebilir
G i \u003d l i d,
burada d, şeklin tamamı için sabit olan malzemenin birim uzunluğunun ağırlığıdır.

Formüller (1) yerine G i değerleri l i d yerine yerleştirildikten sonra, pay ve paydanın her bir dönemindeki sabit faktör d parantezlerin dışına (toplam işaretinin dışına) çıkarılabilir ve azaltılabilir. Böylece, çizgi parçalarından oluşan bir şeklin ağırlık merkezinin koordinatlarını belirlemek için formüller, şu formu alacaktır:
x c = (∑ l ben x ben) / ∑ l ben ;
(2) y c = (∑ l ben y ben) / ∑ l ben ;
z c = (∑ l ben z ben) / ∑ l ben .

Gövde, çeşitli şekillerde yerleştirilmiş düzlemlerden veya kavisli yüzeylerden oluşan bir şekil biçimine sahipse (Şekil 174), o zaman her bir düzlemin (yüzeyin) ağırlığı aşağıdaki şekilde temsil edilebilir:
G ben = F ben p,
burada F i her yüzeyin alanıdır ve p, şeklin birim alanı başına ağırlığıdır.

G i'nin bu değerini formül (1)'e yerleştirdikten sonra şunu elde ederiz: alanlardan oluşan bir şeklin ağırlık merkezinin koordinatları için formüller:
x c = (∑ F ben x ben) / ∑ F ben ;
(3) y c = (∑ F ben y ben) / ∑ F ben ;
z c = (∑ F ben z ben) / ∑ F ben .

Homojen bir gövde belirli bir geometrik şeklin basit parçalarına bölünebiliyorsa (Şekil 175), o zaman her parçanın ağırlığı
G ben = V ben γ,
burada V i her bir parçanın hacmidir ve γ gövdenin birim hacmi başına ağırlığıdır.

G i değerlerini formül (1)'e yerleştirdikten sonra, şunu elde ederiz: homojen hacimlerden oluşan bir cismin ağırlık merkezinin koordinatlarını belirlemek için formüller:
x c = (∑ V ben x ben) / ∑ V ben ;
(4) y c = (∑ V ben y ben) / ∑ V ben;
z c = (∑ V ben z ben) / ∑ V ben .

Cisimlerin ağırlık merkezinin konumunu belirlemek için bazı problemleri çözerken, bazen bir daire yayının, dairesel bir sektörün veya bir üçgenin ağırlık merkezinin nerede olduğunu bilmek gerekir.

Yayın yarıçapı r ve yay tarafından daraltılan ve radyan cinsinden ifade edilen merkez açısı 2a biliniyorsa, o zaman C ağırlık merkezinin (Şekil 176, a) yayın O merkezine göre konumu şöyledir: formülle belirlenir:
(5) x c = (r sin α)/α.

Yayın AB=b akoru verilirse, formül (5)'te değiştirmeyi yapmak mümkündür.
sinα = b/(2r)
ve daha sonra
(5a) x c = b/(2α).

Yarım daire için özel bir durumda, her iki formül de şu şekli alacaktır (Şekil 176, b):
(5b) x c = OC = 2r/π = d/π.

Yarıçapı r verilirse (Şekil 176, c), dairesel sektörün ağırlık merkezinin konumu aşağıdaki formül kullanılarak belirlenir:
(6) x c = (2r sin α)/(3α).

Sektörün akoru verilirse, o zaman:
(6a) x c = b/(3α).

Yarım daire için özel bir durumda, her iki son formül de şu şekli alacaktır (Şekil 176, d)
(6b) x c = OC = 4r/(3π) = 2d/(3π).

Herhangi bir üçgenin alanının ağırlık merkezi, herhangi bir taraftan karşılık gelen yüksekliğin üçte birine eşit bir mesafede bulunur.

Dik bir üçgende ağırlık merkezi, dik açının üst kısmından sayılarak, bacakların uzunluğunun üçte biri kadar uzaklıkta bulunan noktalardan bacaklara yükseltilmiş dikmelerin kesişme noktasındadır (Şekil 177).

İnce çubuklardan (çizgilerden), plakalardan (alanlardan) veya hacimlerden oluşan herhangi bir homojen cismin ağırlık merkezinin konumunu belirlemeye yönelik problemleri çözerken, aşağıdaki sıraya uyulması tavsiye edilir:

1) ağırlık merkezinin konumunun belirlenmesi gereken bir gövde çizin. Genellikle tüm vücut ölçüleri bilindiğinden ölçeğe dikkat edilmelidir;

2) gövdeyi, ağırlık merkezlerinin konumu gövdenin boyutuna göre belirlenen bileşen parçalarına (çizgi parçaları veya alanlar veya hacimler) ayırın;

3) kurucu parçaların uzunluklarını, alanlarını veya hacimlerini belirlemek;

4) koordinat eksenlerinin konumunu seçin;

5) kurucu parçaların ağırlık merkezlerinin koordinatlarını belirlemek;

6) bireysel parçaların uzunluklarının, alanlarının veya hacimlerinin bulunan değerlerinin yanı sıra ağırlık merkezlerinin koordinatlarını uygun formüllerle değiştirin ve tüm vücudun ağırlık merkezinin koordinatlarını hesaplayın;

7) Bulunan koordinatlara göre, vücudun ağırlık merkezinin konumunu şekilde belirtin.

§ 23. İnce homojen çubuklardan oluşan bir gövdenin ağırlık merkezinin konumunun belirlenmesi

§ 24. Plakalardan oluşan şekillerin ağırlık merkezi konumunun belirlenmesi

Son problemde de bir önceki paragrafta verilen problemlerde olduğu gibi şekilleri bileşen parçalarına ayırmak çok fazla zorluk yaratmamaktadır. Ancak bazen şekil, onu çeşitli şekillerde bileşen parçalarına ayırmanıza izin veren bir forma sahiptir, örneğin üçgen kesimli ince dikdörtgen bir plaka (Şek. 183). Böyle bir plakanın ağırlık merkezinin konumu belirlenirken, alanı çeşitli şekillerde dört dikdörtgene (1, 2, 3 ve 4) ve bir dik üçgene (5) bölünebilir. Şekil 2'de iki seçenek gösterilmektedir. 183, a ve b.

En rasyonel olanı, şekli en az sayıda oluşan bileşen parçalarına bölme yoludur. Şekilde kesikler varsa, bunlar da şeklin bileşen parçalarının sayısına dahil edilebilir, ancak kesilen parçanın alanı negatif olarak kabul edilir. Bu nedenle bu bölmeye negatif alanlar yöntemi adı verilir.

Şekil 2'deki plaka. 183, c bu yöntemi kullanarak yalnızca iki parçaya bölünür: tüm plakanın alanını sanki bir bütünmüş gibi gösteren dikdörtgen 1 ve negatif olduğunu düşündüğümüz bir alanı olan üçgen 2.

§ 26. Basit geometrik şekle sahip parçalardan oluşan bir gövdenin ağırlık merkezinin konumunun belirlenmesi

Basit geometrik şekle sahip parçalardan oluşan bir cismin ağırlık merkezinin konumunu belirleme problemlerini çözmek için, çizgilerden veya alanlardan oluşan şekillerin ağırlık merkezinin koordinatlarını belirleme becerisine sahip olmak gerekir. .

Ders 4. Ağırlık merkezi.

Bu ders aşağıdaki soruları kapsamaktadır

1. Katı bir cismin ağırlık merkezi.

2. Homojen olmayan cisimlerin ağırlık merkezlerinin koordinatları.

3. Homojen cisimlerin ağırlık merkezlerinin koordinatları.

4. Ağırlık merkezlerinin koordinatlarını belirleme yöntemleri.

5. Bazı homojen cisimlerin ağırlık merkezleri.

Bu konuların incelenmesi gelecekte cisimlerin hareketinin dinamiklerini incelemek, kayma sürtünmesi ve yuvarlanma sürtünmesini, mekanik bir sistemin kütle merkezinin dinamiğini, kinetik momentleri dikkate alarak disiplindeki problemleri çözmek için gereklidir. "Materyallerin kuvveti".

Paralel kuvvetlerin getirilmesi.

Düz bir sistemin ve keyfi bir uzaysal kuvvetler sisteminin merkeze indirgenmesini düşündükten sonra, paralel kuvvetler sisteminin özel bir durumunun değerlendirilmesine yeniden dönüyoruz.

İki paralel kuvvetin getirilmesi.

Böyle bir kuvvetler sistemini değerlendirirken aşağıdaki üç indirgeme durumu mümkündür.

1. Doğrusal iki kuvvetin sistemi. İki paralel ve aynı yönde yönlendirilmiş kuvvetlerden oluşan bir sistem düşünün P Ve Q noktalarda uygulanan A Ve İÇİNDE. Kuvvetlerin bu segmente dik olduğunu varsayacağız (Şekil 1, A).

İLE, segmente ait AB ve koşulun sağlanması:

AC/GB = Q/P.(1)

Ana sistem vektörü RC = P + Q Modulo bu kuvvetlerin toplamına eşittir: RC = P + Q.

İLE(1)'in sıfıra eşit olduğu dikkate alındığında:MC = P ∙ AC- Q∙ GB = 0.

Böylece, oyuncu kadrosunun bir sonucu olarak şunu elde ettik: RC ≠ 0, MC= 0. Bu, ana vektörün indirgeme merkezinden geçen bileşiğe eşdeğer olduğu anlamına gelir, yani:

Doğrusal kuvvetlerin sonucu mutlak değer olarak toplamlarına eşittir ve etki çizgisi, bu kuvvetlerin dahili modülleriyle ters orantılı olarak uygulama noktalarını birleştiren segmenti böler.

Noktanın konumuna dikkat edin İLE kuvvetler değişmezse R Ve Q köşeden dönα. Nokta İLE Bu özelliğe sahip olana denir paralel kuvvetlerin merkezi.

2. İkili sistem doğrusal olmayan ve kuvvet modülü bakımından eşit değildir. kuvvetler olsun P Ve Q noktalarda uygulanan A Ve İÇİNDE, paralel, zıt yönlerde yönlendirilmiş ve modül açısından eşit olmayan (Şekil 1, B).

Noktayı referans merkezi olarak seçelim İLE, hala (1) ilişkisini karşılıyor ve aynı düz çizgi üzerinde ancak parçanın dışında yer alıyor AB.

Bu sistemin ana vektörü RC = P + Q modulo artık vektörlerin modülleri arasındaki farka eşit olacaktır: RC = Q - P.

Merkezle ilgili önemli an İLE hala sıfır:MC = P ∙ AC- Q∙ GB= 0, yani

Sonuç doğrusal olmayan Mutlak değeri eşit olmayan kuvvetler ise farklarına eşit olup, daha büyük bir kuvvete doğru yönlendirilir ve etki çizgisi, bu kuvvetlerin dış modülleri ile ters orantılı olarak uygulanma noktalarını birleştiren segmenti böler.

Şekil 1

3. İkili sistem doğrusal olmayan ve kuvvetlerin modülleri eşittir. Önceki indirgeme durumunu ilk durum olarak ele alalım. Gücü düzeltelim R ve kuvvet Q zorlamak için modulo'yu deneyelim R.

sonra Q → R formül (1)'deki oran AC/GB → 1. Bu şu anlama gelir: AC → GB yani mesafe AC →∞ .

Bu durumda ana vektörün modülü RC → 0 ve ana momentin modülü, indirgeme merkezinin konumuna bağlı değildir ve orijinal değere eşit kalır:

MC = P ∙ AC- Q∙ GB = P ∙ ( AC- GB) =P ∙ AB.

Böylece limitte bir kuvvetler sistemi elde ettik. RC = 0, MC≠ 0 ve indirgeme merkezi sonsuza kadar kaldırılır, bu da sonuçla değiştirilemez. Bu sistemde bir kuvvet çiftini bulmak zor değildir, dolayısıyla bir çift kuvvetin sonucu yoktur.

Paralel kuvvetler sisteminin merkezi.

Sistemi düşünün N kuvvetler Pi noktalarda uygulananbir ben (x ben , sen ben , z ben) ve eksene paralelYumurta vektör ile ben(İncir. 2).

Bir kuvvet çiftine eşdeğer bir sistem durumunu önceden hariç tutarsak, önceki paragrafa dayanarak onun bileşkesinin varlığını kanıtlamak zor değildir.R.

Merkezin koordinatlarını belirleyinC(X C, sen C, z C) paralel kuvvetler, yani bu sistemin sonucunun uygulama noktasının koordinatları.

Bu amaçla Varignon teoremini kullanıyoruz:

M0 (R) = Σ M0(Pi).

İncir. 2

Kuvvetin vektör momenti çapraz çarpım olarak temsil edilebilir, dolayısıyla:

M 0 (R) = uzaktan kumanda× R = Σ M0i(Pi) = Σ ( ri× Pi ).

Verilen R = Karavan ∙ ben, A Pi = Pvi ∙ ben ve vektör çarpımının özelliklerini kullanarak şunu elde ederiz:

uzaktan kumanda × Karavan ∙ ben = Σ ( ri × Pvi ∙ ben),

uzaktan kumanda ∙ R v × ben = Σ ( ri ∙ Pvi × ben) = Σ ( ri ∙ Pvi ) × ben,

veya:

[ r c R v - Σ ( ri Pvi )] × ben= 0.

Son ifade yalnızca köşeli parantez içindeki ifadenin sıfır olması durumunda geçerlidir. Bu nedenle endeksin atlanmasıvve sonucun göz önüne alındığındaR = Σ Pi buradan şunu elde ederiz:

uzaktan kumanda = (Σ Pi ri )/(Σ Pi ).

Son vektör eşitliğini koordinat eksenine yansıtarak istenen değeri elde ederiz. paralel kuvvetlerin merkezinin koordinatlarının ifadesi:

x c = (Σ Pi x ben)/(Σ Pi );

y c = (Σ Pi sen ben )/(Σ Pi );(2)

z c = (Σ Pi z ben )/(Σ Pi ).

Vücudun ağırlık merkezi

Homojen bir cismin ağırlık merkezlerinin koordinatları.

Sert bir cismin ağırlığını düşünün P ve hacim V koordinat sisteminde Oksiz eksenlerin nerede olduğu X Ve sen Dünya yüzeyi ve eksen ile bağlantılı z zirveye doğru yönlendirildi.

Vücudu hacimli temel parçalara ayırırsak∆ V Ben o zaman çekim kuvveti onun her bir parçasına etki edecektir.∆ Pidünyanın merkezine doğru yönlendirilir. Vücudun boyutlarının Dünya'nın boyutlarından çok daha küçük olduğunu varsayalım, o zaman vücudun temel kısımlarına uygulanan kuvvetler sisteminin yakınsak değil paralel olduğu düşünülebilir (Şekil 3) ve tüm sonuçlar önceki bölümdeki hükümler onun için geçerlidir.

Şek. 3

Tanım . Katı bir cismin ağırlık merkezi, bu cismin temel parçalarının paralel ağırlık kuvvetlerinin merkezidir.

Hatırlamak spesifik yer çekimi Vücudun temel kısmına ağırlığının oranı denir∆ Pi hacmine ∆ V Ben : γ Ben = ∆ Pi/ ∆ V Ben . Homojen bir cisim için bu değer sabittir:γ Ben = γ = P/ V.

(2) ∆ yerine koyma Pi = γ Ben ∙∆ V Ben yerine Pi, son açıklamayı dikkate alarak pay ve paydayı azaltarakG, alıyoruz homojen bir cismin ağırlık merkezinin koordinatları için ifadeler:

x c = (Σ ∆ Vi∙ x ben)/(Σ ∆ Vi);

y c = (Σ ∆ Vi∙ sen ben )/(Σ ∆ Vi);(3)

z c = (Σ ∆ Vi∙ z ben )/(Σ ∆ Vi).

Ağırlık merkezinin belirlenmesinde çeşitli teoremler faydalıdır.

1) Homojen bir cismin bir simetri düzlemi varsa ağırlık merkezi bu düzlemdedir.

Eğer eksenler X Ve en bu simetri düzlemine yerleştirildikten sonra koordinatları olan her nokta için. ve koordine etmek (3)'e göre sıfıra eşit olacaktır çünkü toplamda Tüm Zıt işaretli terimler çiftler halinde elenir. Yani ağırlık merkezi simetri düzleminde.

2) Homojen bir cismin simetri ekseni varsa cismin ağırlık merkezi bu eksen üzerinde bulunur.

Aslında bu durumda eksenzkoordinatları olan her nokta için simetri ekseni boyunca çizim yapınkoordinatları olan bir nokta bulabilirsiniz ve koordinatlar ve formül (3) ile hesaplanan sıfıra eşit olacaktır.

Üçüncü teorem de benzer şekilde kanıtlanmıştır.

3) Homojen bir cismin bir simetri merkezi varsa cismin ağırlık merkezi bu noktada bulunur.

Ve birkaç açıklama daha.

Birinci. Vücut, ağırlığı ve ağırlık merkezinin konumu bilinen parçalara bölünebiliyorsa, her noktayı dikkate almaya gerek yoktur, ancak formüllerde (3) Pi – İlgili parçanın ağırlığı olarak belirlenecek veağırlık merkezinin koordinatları olarak.

Saniye. Eğer vücut homojen ise ayrı bir kısmının ağırlığı, Nerede gövdenin yapıldığı malzemenin özgül ağırlığıdır ve Vi - vücudun bu kısmının hacmi. Ve formül (3) daha uygun bir biçim alacaktır. Örneğin,

Ve benzer şekilde nerede - tüm vücudun hacmi.

Üçüncü not. Vücudun alanlı ince bir plaka gibi görünmesine izin verin F ve kalınlık T uçakta yatmak Oksi. (3) yerine koyma∆ V Ben =T ∙ ∆F Ben , homojen bir plakanın ağırlık merkezinin koordinatlarını elde ederiz:

x c = (Σ ∆ F ben∙ x ben) / (Σ ∆ F ben);

y c = (Σ ∆ F ben∙ sen ben ) / (Σ ∆ F ben).

z c = (Σ ∆ F ben∙ z Ben ) / (Σ ∆ F ben).

Nerede – bireysel plakaların ağırlık merkezinin koordinatları;vücudun toplam alanıdır.

Dördüncü not. Uzunluğu olan ince eğrisel bir çubuk şeklindeki bir gövde için L kesit alanına sahip A temel hacim∆ V Ben = A ∙∆ L Ben , Bu yüzden ince eğrisel bir çubuğun ağırlık merkezinin koordinatları eşit olacaktır:

x c = (Σ ∆ L ben∙ x ben)/(Σ ∆ L ben);

y c = (Σ ∆ L ben∙ sen ben )/(Σ ∆ L ben);(4)

z c = (Σ ∆ L ben∙ z ben )/(Σ ∆ L ben).

Nerede – ağırlık merkezinin koordinatlarıBen-inci bölüm; .

Tanıma göre ağırlık merkezinin geometrik bir nokta olduğunu unutmayın; aynı zamanda belirli bir cismin (örneğin bir yüzük için) sınırlarının dışında da bulunabilir.

Not.

Dersin bu bölümünde yerçekimi, yerçekimi ve vücut ağırlığı arasında ayrım yapmıyoruz. Gerçekte yerçekimi, Dünya'nın yerçekimi ile dönmesinden kaynaklanan merkezkaç kuvveti arasındaki farktır.

Homojen olmayan cisimlerin ağırlık merkezlerinin koordinatları.

Ağırlık merkezi koordinatları homojen olmayan katı(Şekil 4) seçilen referans sisteminde şu şekilde tanımlanır:

Şekil 4

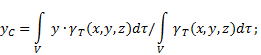
Nerede - birim vücut hacmi başına ağırlık (özgül ağırlık)

- tüm vücut ağırlığı.

pürüzlü yüzey(Şekil 5), daha sonra seçilen referans sistemindeki ağırlık merkezinin koordinatları aşağıdaki gibi belirlenir:

Şekil 5

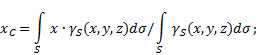
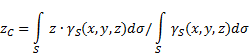
Nerede - vücudun birim alanı başına ağırlık

- tüm vücut ağırlığı.

Eğer katı ise heterojen çizgi(Şekil 6), daha sonra seçilen referans sistemindeki ağırlık merkezinin koordinatları aşağıdaki gibi belirlenir:

Şekil 6

Nerede - vücut uzunluğu birim ağırlığı,

Tüm vücut ağırlığı.

Ağırlık merkezinin koordinatlarını belirleme yöntemleri.

Yukarıda elde edilen genel formüllere dayanarak spesifik yöntemleri belirtmek mümkündür. cisimlerin ağırlık merkezlerinin koordinatlarının belirlenmesi.

1. Simetri. Homojen bir cismin bir düzlemi, ekseni veya simetri merkezi varsa (Şekil 7), ağırlık merkezi sırasıyla simetri düzleminde, simetri ekseninde veya simetri merkezinde bulunur.

Şekil 7

2. Bölünme. Gövde, her biri için ağırlık merkezinin konumu ve alanı bilinen sınırlı sayıda parçaya bölünmüştür (Şekil 8).

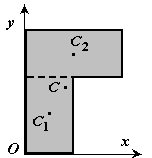
Şekil 8

S \u003d S 1 + S 2.

3.Negatif alanlar yöntemi. Bölümleme yönteminin özel bir durumu (Şekil 9). Kesiksiz gövdenin ve kesiksiz gövdenin ağırlık merkezleri biliniyorsa, kesikli gövdelere uygulanır. Kesikli bir plaka şeklindeki gövde, katı bir plakanın (kesiksiz) bir alanla birleşimi ile temsil edilir. S1 ve kesilen parçanın alanı S2.

Şekil 9

S \u003d S 1 - S 2.

4.gruplandırma yöntemi. Son iki yönteme iyi bir eklentidir. Şekli kurucu unsurlarına ayırdıktan sonra, bu grubun simetrisini hesaba katarak çözümü basitleştirmek için bazılarını tekrar birleştirmek uygun olabilir.

Bazı homojen cisimlerin ağırlık merkezleri.

1) Dairesel bir yayın ağırlık merkezi. Yayı düşünün AB yarıçapR merkezi açılı. Simetri nedeniyle bu yayın ağırlık merkezi eksen üzerinde yer alır.Öküz(Şekil 10).

Şekil 10

Koordinatını bulalım formüle göre . Bunu yapmak için yayı seçin AB eleman AA ’ uzunkonumu açıyla belirlenen. Koordinat X eleman MM' irade. Bu değerleri değiştirme X Ve D ben İntegralin yayın tüm uzunluğu boyunca uzatılması gerektiğini akılda tutarak şunu elde ederiz:

burada L, AB yayının uzunluğuna eşittir.

Buradan nihayet dairesel yayın ağırlık merkezinin merkezden belli bir mesafede simetri ekseni üzerinde bulunduğunu buluyoruz. Ah eşit

açı nerede radyan cinsinden ölçülür.

2) Bir üçgenin alanının ağırlık merkezi. Düzlemde yatan bir üçgen düşünün Oksi köşe koordinatları bilinen: Ai (x ben,sen ben ), (Ben= 1,2,3). Üçgeni kenara paralel dar şeritlere bölmek A 1 AŞekil 2'de üçgenin ağırlık merkezinin kenarortaya ait olması gerektiği sonucuna varıyoruz. A 3 M 3 (şek.11) .

Şekil 11

Üçgeni kenara paralel şeritlere ayırma A 2 A 3, medyanın üzerinde olması gerektiğinden emin olabilirsiniz A 1 M 1. Böylece, Bir üçgenin ağırlık merkezi kenarortaylarının kesiştiği noktadadır, bildiğiniz gibi, karşılık gelen taraftan sayılarak üçüncü kısmı her medyandan ayırır.

Özellikle ortanca için A 1 M 1 noktanın koordinatları verildiğinde elde ederiz M 1 - köşelerin koordinatlarının aritmetik ortalamasıdır A 2 ve A 3 :

x c = X 1 + (2/3) ∙ (XM 1 - X 1 ) = X 1 + (2/3) ∙ [(X 2 + X 3 )/2 - X 1 ] = (X 1 + X 2 + X 3 )/3.

Dolayısıyla üçgenin ağırlık merkezinin koordinatları, köşelerinin koordinatlarının aritmetik ortalamasıdır:

X C =(1/3) Σ x ben ; sen C =(1/3) Σ sen ben .

3) Dairesel sektörün alanının ağırlık merkezi. Yarıçaplı bir dairenin bir sektörünü düşünün R merkez açılı 2α eksen etrafında simetrik olarak yerleştirilmiş Öküz (Şekil 12) .

Açıkça görülüyor ki sen C = 0 ve bu sektörün kesildiği dairenin merkezinden ağırlık merkezine olan mesafe aşağıdaki formülle belirlenebilir:

Şekil 12

Bu integrali hesaplamanın en kolay yolu, entegrasyon alanını belirli bir açıyla temel sektörlere bölmektir. Dφ . Birinci dereceden sonsuz küçüklere kadar böyle bir sektör, tabanı eşit olan bir üçgenle değiştirilebilir. R × Dφ ve yükseklik R. Böyle bir üçgenin alanı dF =(1/2)R 2 ∙ Dφ ve ağırlık merkezi 2/3'tür. Rüstten, yani (5)'e şunu koyarız: X = (2/3)R∙ çünkü. (5) yerine koyma F= α R 2, şunu elde ederiz:

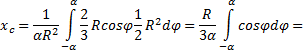
Son formülü kullanarak özellikle ağırlık merkezine olan mesafeyi hesaplıyoruz. yarım daire.

(2) α = π /2 yerine koyarsak şunu elde ederiz: X C = (4 R)/(3 π ) ≅ 0,4 R .

örnek 1Şekilde görülen homojen cismin ağırlık merkezini belirleyelim. 13.

Şekil 13

Çözüm.Gövde homojen olup simetrik şekle sahip iki parçadan oluşur. Ağırlık merkezlerinin koordinatları:

Hacimleri:

Bu nedenle vücudun ağırlık merkezinin koordinatları

Örnek 2 Dik açıyla bükülmüş bir plakanın ağırlık merkezini bulun. Boyutlar - çizimde (Şek. 14).

Şekil 14

Çözüm. Ağırlık merkezleri koordinatları:

0.

Kareler:

Bu yüzden:

Şekil 2'de gösterilen plakanın ağırlık merkezinin konumunu bulun. 16. Boyutlar santimetre cinsinden verilmiştir.

Şekil 16

Çözüm. Plakayı rakamlara bölüyoruz (Şek. 17), merkezler kimin ciddiyeti belli.

Bu şekillerin alanları ve ağırlık merkezlerinin koordinatları:

1) kenarları 30 ve 40 cm olan bir dikdörtgen,S 1 =30 ∙ 40=1200cm 2 ; x 1=15cm; en 1 \u003d 20 cm.

2) tabanı 50 cm ve yüksekliği 40 cm olan bir dik üçgen;S 2 =0,5 ∙ 50 ∙ 40= 1000cm 2 ; X 2 \u003d 30 + 50 / 3 \u003d 46,7 cm; y2 =40/3 =13,3 cm;

3) yarım daire daire yarıçapı R = 20 santimetre;S 3 =0,5 ∙π∙ 20 2 \u003d 628 cm 2 ; X 3 =4 R /3 π =8,5 cm; en

Çözüm. Fizikte bir cismin yoğunluğununρ ve özgül ağırlığıGoran ile ilişkilidir:γ = ρ G , NeredeG - yerçekimi ivmesi. Böyle homojen bir cismin kütlesini bulmak için yoğunluğu hacmiyle çarpmanız gerekir.

Şekil 19

"Doğrusal" veya "doğrusal" yoğunluk terimi, kiriş çubuğunun kütlesini belirlemek için doğrusal yoğunluğun bu çubuğun uzunluğuyla çarpılması gerektiği anlamına gelir.

Sorunu çözmek için bölümleme yöntemini kullanabilirsiniz. Belirli bir kafes kirişi 6 ayrı çubuğun toplamı olarak temsil edersek şunu elde ederiz:

NeredeL ben uzunlukBen çiftliğin -th çubuğu vex ben , sen ben - ağırlık merkezinin koordinatları.

Bu sorunun çözümü son 5 kafes çubuğunun gruplandırılmasıyla basitleştirilebilir. Bu çubuk grubunun ağırlık merkezinin bulunduğu dördüncü çubuğun ortasında simetri merkezi bulunan bir şekil oluşturduklarını görmek kolaydır.

Böylece, belirli bir kafes kiriş yalnızca iki grup çubuktan oluşan bir kombinasyonla temsil edilebilir.

Birinci grup birinci çubuktan oluşur, bunun içinL 1 = 4 m,X 1 = 0m,sen 1 = 2 m İkinci çubuk grubu beş çubuktan oluşur;L 2 = 20m,X 2 = 3m,sen 2 = 2 m.

Çiftliğin ağırlık merkezinin koordinatları aşağıdaki formülle bulunur:

X C = (L 1 ∙ X 1 + L 2 ∙ X 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2m;

sen C = (L 1 ∙ sen 1 + L 2 ∙ sen 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 m.

Merkezin olduğuna dikkat edin İLE bağlayan hatta yatıyor İLE 1 ve İLE 2 ve segmenti böler İLE 1 İLE 2 ile ilgili: İLE 1 İLE/SS 2 = (X C - X 1 )/(X 2 - X C ) = L 2 / L 1 = 2,5/0,5.

Kendi kendine muayene için sorular

Paralel kuvvetlerin merkezi nedir?

- Paralel kuvvetlerin merkezinin koordinatları nasıl belirlenir?

- Sonucu sıfır olan paralel kuvvetlerin merkezi nasıl belirlenir?

Paralel kuvvetlerin merkezinin özelliği nedir?

- Paralel kuvvetlerin merkezinin koordinatlarını hesaplamak için hangi formüller kullanılır?

Bir cismin ağırlık merkezi nedir?

- Vücudun bir noktasına etki eden Dünya'nın çekim kuvvetleri neden paralel kuvvetler sistemi olarak alınabilir?

- Homojen olmayan ve homojen cisimlerin ağırlık merkezinin konumunu belirleme formülünü, düz bölümlerin ağırlık merkezinin konumunu belirleme formülünü yazın?

- Basit geometrik şekillerin ağırlık merkezinin konumunu belirlemek için formülü yazın: dikdörtgen, üçgen, yamuk ve yarım daire?

Alanın statik momentine ne denir?

- Ağırlık merkezi vücudun dışında olan bir cismin örneğini verin.

- Cisimlerin ağırlık merkezlerinin belirlenmesinde simetri özelliklerinden nasıl yararlanılır?

- Negatif ağırlıklar yönteminin özü nedir?

Dairesel yayın ağırlık merkezi nerede bulunur?

Bir üçgenin ağırlık merkezini grafiksel olarak nasıl bulabilirsiniz?

- Dairesel sektörün ağırlık merkezini belirleyen formülü yazın.

- Bir üçgenin ve dairesel bir sektörün ağırlık merkezlerini belirleyen formülleri kullanarak, benzer bir formülü dairesel bir parça için türetin.

- Homojen cisimlerin, düz şekillerin ve çizgilerin ağırlık merkezlerinin koordinatlarını hesaplamak için hangi formüller kullanılır?

- Düz bir şeklin alanının eksene göre statik momentine ne denir, nasıl hesaplanır ve hangi boyuta sahiptir?

- Bireysel parçalarının ağırlık merkezlerinin konumu biliniyorsa, alanın ağırlık merkezinin konumu nasıl belirlenir?

- Ağırlık merkezinin konumunun belirlenmesinde hangi yardımcı teoremler kullanılır?

Mühendislik uygulamasında, ağırlık merkezinin konumu bilinen basit elemanlardan oluşan karmaşık bir düz şeklin ağırlık merkezinin koordinatlarını hesaplamak gerekli hale gelir. Bu görev, belirleme görevinin bir parçasıdır...

Kiriş ve çubukların kompozit kesitlerinin geometrik özellikleri. Çoğu zaman bu tür sorular, basınç merkezinin koordinatlarını belirlerken zımba kalıplarının tasarım mühendisleri, yükleri yerleştirirken çeşitli araçlar için yükleme şemaları geliştiricileri, elemanların bölümlerini seçerken metal yapı tasarımcıları ve elbette öğrenciler çalışırken karşı karşıya kalır. "Teorik Mekanik" ve "Malzemelerin Mukavemeti" disiplinleri.

Temel figürler kütüphanesi.

Simetrik düzlemsel şekiller için ağırlık merkezi simetri merkeziyle çakışır. Temel nesnelerin simetrik grubu şunları içerir: bir daire, bir dikdörtgen (kare dahil), bir paralelkenar (eşkenar dörtgen dahil), normal bir çokgen.

Yukarıdaki şekilde gösterilen on rakamdan sadece ikisi temeldir. Yani, üçgenleri ve daire sektörlerini kullanarak pratik açıdan ilgi çekici hemen hemen her şekli birleştirebilirsiniz. Herhangi bir rastgele eğri bölümlere ayrılabilir ve daire yayları ile değiştirilebilir.

Geriye kalan sekiz şekil en yaygın olanlardır ve bu nedenle bu tür bir kütüphaneye dahil edilmişlerdir. Bizim sınıflandırmamızda bu unsurlar temel değildir. Bir dikdörtgen, bir paralelkenar ve bir yamuk iki üçgenden oluşabilir. Altıgen dört üçgenin toplamıdır. Çemberin parçası, çemberin dilimi ile üçgen arasındaki farktır. Çemberin halka şeklindeki sektörü iki sektör arasındaki farktır. Daire, açısı α=2*π=360˚ olan bir dairenin sektörüdür. Yarım daire sırasıyla α=π=180˚ açısına sahip bir dairenin sektörüdür.

Bileşik bir şeklin ağırlık merkezinin koordinatlarının Excel'de hesaplanması.

Konuyu tamamen teorik hesaplamalar üzerinden incelemek yerine, bir örnek üzerinden bilgi aktarmak ve algılamak her zaman daha kolaydır. "Ağırlık merkezi nasıl bulunur?" Sorununun çözümünü düşünün. bu metnin altındaki şekilde gösterilen bileşik şekil örneğine göre.

Bileşik bölüm bir dikdörtgendir (boyutları A1 =80mm, B1 \u003d 40 mm), sol üste bir ikizkenar üçgenin eklendiği (taban boyutunda A2 =24 mm ve yükseklik H2 \u003d 42 mm) ve sağ üstten yarım daire kesilmiş (koordinatların olduğu noktada ortalanmış) X03 =50 mm ve sen03 =40 mm, yarıçap R3 =26 mm).

Hesaplamayı yapmanıza yardımcı olmak için programı dahil edeceğiz Microsoft Excel veya program Oo Calc . Bunlardan herhangi biri görevimizle kolayca başa çıkacak!

olan hücrelerde sarı doldurma yapılabilir yardımcı ön hazırlık hesaplamalar .

Açık sarı dolgulu hücrelerde sonuçları sayarız.

Mavi yazı tipi ilk veri .

Siyah yazı tipi orta seviye hesaplama sonuçları .

Kırmızı yazı tipi son hesaplama sonuçları .

Sorunu çözmeye başlıyoruz - bölümün ağırlık merkezinin koordinatlarını aramaya başlıyoruz.

İlk veri:

1. Bileşik bölümü oluşturan temel figürlerin adları buna göre girilecektir.

D3 hücresine: Dikdörtgen

E3 hücresine: Üçgen

F3 hücresine: Yarım daire

2. Bu makalede sunulan "Temel Şekiller Kütüphanesi" ni kullanarak kompozit bölümün elemanlarının ağırlık merkezlerinin koordinatlarını belirliyoruz. xci Ve yci keyfi olarak seçilen 0x ve 0y eksenlerine göre mm cinsinden yazın ve yazın

D4 hücresine: =80/2 = 40,000

xc 1 = A 1 /2

D5 hücresine: =40/2 =20,000

yc 1 = B 1 /2

E4 hücresine: =24/2 =12,000

xc 2 = A 2 /2

E5 hücresine: =40+42/3 =54,000

yc 2 = B 1 + H 2 /3

F4 hücresine: =50 =50,000

xc 3 = X03

F5 hücresine: =40-4*26/3/PI() =28,965

yc 3 = sen 03 -4* r3 /3/ π

3. Elemanların alanını hesaplayın F 1 , F 2 , F3 mm2 cinsinden, "Temel şekiller kitaplığı" bölümündeki formülleri tekrar kullanarak

D6 hücresinde: =40*80 =3200

F1 = A 1 * B1

E6 hücresinde: =24*42/2 =504

F2 = a2 *h2 /2

F6 hücresinde: =-PI()/2*26^2 =-1062

F3 =-π/2*r3 ^2

Üçüncü elemanın alanı - yarım daire - negatiftir çünkü bu kesik boş bir alandır!

Ağırlık merkezinin koordinatlarının hesaplanması:

4. Son şeklin toplam alanını belirleyin F0 mm2 cinsinden

birleştirilmiş D8E8F8 hücresinde: =D6+E6+F6 =2642

F0 = F 1 + F 2 + F3

5. Bileşik şeklin statik momentlerini hesaplayın Sx Ve Sy seçilen 0x ve 0y eksenlerine göre mm3 cinsinden

birleştirilmiş D9E9F9 hücresinde: =D5*D6+E5*E6+F5*F6 =60459

Sx = yc1 * F1 + yc2 *F2 + yc3 *F3

birleştirilmiş D10E10F10 hücresinde: =D4*D6+E4*E6+F4*F6 =80955

Sy = xc1 * F1 + xc2 *F2 + xc3 *F3

6. Son olarak kompozit bölümün ağırlık merkezinin koordinatlarını hesaplıyoruz. Xc Ve Yc seçilen koordinat sisteminde mm cinsinden 0x - 0y

birleştirilmiş D11E11F11 hücresinde: =D10/D8 =30,640

Xc = Sy / F0

birleştirilmiş D12E12F12 hücresinde: =D9/D8 =22,883

Yc=Sx/F0

Sorun çözüldü, Excel'deki hesaplama tamamlandı - üç basit öğe kullanılarak derlenen bölümün ağırlık merkezinin koordinatları bulundu!

Çözüm.

Makaledeki örnek, karmaşık bir bölümün ağırlık merkezini hesaplama metodolojisinin anlaşılmasını kolaylaştırmak amacıyla çok basit olacak şekilde seçilmiştir. Yöntem, herhangi bir karmaşık şeklin, ağırlık merkezleri bilinen konumlara sahip basit elemanlara bölünmesi ve tüm kesit için son hesaplamaların yapılması gerektiği gerçeğine dayanmaktadır.

Bölüm haddelenmiş profillerden - köşelerden ve kanallardan oluşuyorsa, bunları dairesel "π / 2" sektörlerle kesilmiş dikdörtgenlere ve karelere ayırmaya gerek yoktur. Bu profillerin ağırlık merkezlerinin koordinatları GOST tablolarında verilmiştir, yani kompozit kesit hesaplamalarınızda hem köşe hem de kanal temel temel unsurlar olacaktır (I-kirişler, borular hakkında konuşmanın bir anlamı yoktur) , çubuklar ve altıgenler - bunlar merkezi olarak simetrik bölümlerdir).

Koordinat eksenlerinin şeklin ağırlık merkezinin konumu üzerindeki konumu elbette etkilemez! Bu nedenle hesaplamalarınızı kolaylaştıracak bir koordinat sistemi seçin. Mesela örneğimizde koordinat sistemini saat yönünde 45˚ döndürseydim, dikdörtgen, üçgen ve yarım dairenin ağırlık merkezlerinin koordinatlarını hesaplamak, yapamayacağınız ayrı ve hantal bir hesaplama adımına dönüşürdü “ Kafanın içinde".

Aşağıda sunulan Excel hesaplama dosyası bu durumda bir program değildir. Daha ziyade, bir hesap makinesinin, bir algoritmanın, her durumda takip eden bir şablonun taslağıdır. parlak sarı dolgulu hücreler için kendi formül dizinizi oluşturun.

Artık herhangi bir bölümün ağırlık merkezini nasıl bulacağınızı biliyorsunuz! Rasgele karmaşık kompozit bölümlerin tüm geometrik özelliklerinin tam bir hesaplaması, "" başlığındaki sonraki makalelerden birinde ele alınacaktır. Blogdan haberleri takip edin.

İçin alma yeni makalelerin yayınlanması hakkında bilgi ve için çalışan program dosyalarını indirme Yazının sonunda yer alan pencerede veya sayfanın üst kısmında yer alan pencerede duyurulara abone olmanızı rica ediyorum.

E-posta adresinizi girip "Makale duyurularını al" butonuna tıkladıktan sonra UNUTMA ABONELİĞİ ONAYLA linke tıklayarak belirtilen postada size hemen gelecek bir mektupta (bazen - klasörde) « İstenmeyen e-posta » )!

Makalenin başındaki “ikon illüstrasyon”da tasvir edilen bir bardak, bir bozuk para ve iki çatal hakkında birkaç söz. Birçoğunuz, çocukların ve deneyimsiz yetişkinlerin hayranlık dolu bakışlarını uyandıran bu "numaraya" kesinlikle aşinasınız. Bu makalenin konusu ağırlık merkezidir. O ve dayanak noktası, bilincimiz ve deneyimimizle oynuyor, aklımızı kandırıyor!

"Çatal + madeni para" sisteminin ağırlık merkezi her zaman sabit mesafe dikey aşağı madalyonun kenarından, bu da dayanak noktasıdır. Bu istikrarlı bir denge konumudur!Çatalları sallarsanız sistemin eski stabil pozisyonunu almaya çalıştığı hemen anlaşılıyor! Bir sarkaç hayal edin - bir bağlantı noktası (= camın kenarındaki madalyonun destek noktası), sarkacın bir çubuk ekseni (= bizim durumumuzda eksen sanaldır, çünkü iki çatalın kütlesi uzayın farklı yönlerinde ayrılmıştır) ve eksenin altındaki yük (= tüm "çatal" sisteminin ağırlık merkezi + madeni para"). Sarkaçları herhangi bir yönde (ileri, geri, sola, sağa) dikeyden saptırmaya başlarsanız, yerçekiminin etkisi altında kaçınılmaz olarak orijinal konumuna geri dönecektir. kararlı denge durumu(aynı şey çatallarımızda ve bozuk paramızda da olur)!

Kim anlamadı ama anlamak istiyor - bunu kendin çöz. Kendinize "ulaşmak" çok ilginç! Roly-Get Up oyuncağında da aynı istikrarlı denge kullanma ilkesinin uygulandığını ekleyeceğim. Bu oyuncağın yalnızca ağırlık merkezi dayanak noktasının üzerinde, ancak destek yüzeyinin yarım küresinin merkezinin altında bulunur.

Yorumlarınızı her zaman bekliyoruz sevgili okuyucular!

Sormak, SAYGI yazarın çalışması, dosyayı indir ABONE OLDUKTAN SONRA makale duyuruları için.

Dairesel bir yayın ağırlık merkezi

Yayın bir simetri ekseni vardır. Ağırlık merkezi bu eksende yer alır, yani. sen C = 0 .

dl– yay elemanı, dl = Rdφ, R dairenin yarıçapıdır, x = Rcosφ, L= 2aR,

Buradan:

X C = R(sinα/α).

Dairesel sektörün ağırlık merkezi

Yarıçap sektörü R merkez açılı 2 α simetri ekseni vardır Öküz ağırlık merkezinin bulunduğu yer.

Sektörü üçgen sayılabilecek temel sektörlere ayırıyoruz. Temel sektörlerin ağırlık merkezleri, yarıçaplı bir dairenin yayında bulunur (2/3) R.

Sektörün ağırlık merkezi yayın ağırlık merkezi ile çakışıyor AB:

Yarım daire:

37. Kinematik. Nokta kinematiği. Bir noktanın hareketini belirleme yöntemleri.

Kinematik- maddi cisimlerin hareketinin, kütle ve onlara etki eden kuvvetler dikkate alınmadan geometrik açıdan incelendiği bir mekanik dalı. Bir noktanın hareketini belirleme yöntemleri: 1) doğal, 2) koordinat, 3) vektör.

Nokta kinematiği- maddi noktaların hareketinin matematiksel tanımını inceleyen kinematik bölümü. Kinematiğin temel görevi, bu harekete neden olan nedenleri açıklamadan, hareketi matematiksel bir aparat yardımıyla açıklamaktır.

doğal kaplıca. noktanın yörüngesi, bu yörünge boyunca hareketinin yasası, yay koordinatının başlangıcı ve yönü belirtilir: s=f(t) – noktanın hareketinin yasası. Doğrusal hareket için: x=f(t).

Koordinat sp. uzayda bir noktanın konumu üç koordinat tarafından belirlenir; değişiklikler noktanın hareket yasasını belirler: x=f 1 (t), y=f 2 (t), z=f 3 (t).

Hareket bir düzlemde ise iki hareket denklemi vardır. Hareket denklemleri yörünge denklemini parametrik biçimde tanımlar. Denklemlerden t parametresini çıkararak yörünge denklemini olağan biçimde elde ederiz: f (x, y) = 0 (bir düzlem için).

vektör spa. Bir noktanın konumu, bir merkezden çizilen yarıçap vektörü tarafından belirlenir. Bir vektörün sonuna çizilen eğriye denir. hodograf bu vektör. Onlar. yörünge yarıçap vektörünün hodografıdır.

38. Koordinat ve vektör arasındaki bağlantı, koordinat ve bir noktanın hareketini belirlemenin doğal yolları.

VEKTÖR YÖNTEMİNİN KOORDİNAT VE DOĞAL İLE İLİŞKİSİ ilişkilerle ifade edilir:

belirli bir noktada yörüngeye teğetin mesafe okumaya doğru yönlendirilmiş birim vektörü, belirli bir noktada eğrilik merkezine doğru yönlendirilmiş yörüngeye normalin birim vektörüdür (bkz. Şekil 3).

KOORDİNAT YÖNTEMİNİN DOĞAL OLAN İLE İLİŞKİSİ. Yörünge denklemi f(x, y)=z; f 1 (x, z)=y, koordinat formundaki hareket denklemlerinden t süresinin ortadan kaldırılmasıyla elde edilir. Bir noktanın koordinatlarını alabilen değerlerin ek analizi, eğrinin yörünge olan bölümünü belirler. Örneğin bir noktanın hareketi şu denklemlerle veriliyorsa: x=sin t; y=sin 2 t=x 2 ise, noktanın yörüngesi y=x 2 parabolünün -1≤x≤+1, 0≤x≤1 olduğu bölümü olur. Mesafeleri saymanın başlangıcı ve yönü keyfi olarak seçilir; bu ayrıca hızın işaretini ve başlangıç ​​mesafesinin (s0) büyüklüğünü ve işaretini belirler.

Hareket kanunu bağımlılıkla belirlenir:

+ veya - işareti, sayma mesafelerinin kabul edilen yönüne bağlı olarak belirlenir.

Nokta hızı söz konusu referans çerçevesindeki bu noktanın yarıçap vektörünün zamana göre türevine eşit olan hareketinin kinematik ölçüsüdür. Hız vektörü, hareket yönünde noktanın yörüngesine teğet olarak yönlendirilir

Hız vektörü (v) bir cismin birim zamanda belirli bir yönde kat ettiği mesafedir. Tanımın hız vektörü Tek bir önemli fark dışında hızın belirlenmesine çok benzer: Bir cismin hızı hareketin yönünü göstermez, ancak bir cismin hız vektörü hem hızı hem de hareketin yönünü gösterir. Bu nedenle cismin hız vektörünü tanımlayan iki değişkene ihtiyaç vardır: hız ve yön. Anlamı ve yönü olan fiziksel büyüklüklere vektör büyüklükleri denir.

Hız vektörü vücut zaman zaman değişebilir. Hızı veya yönü değişirse cismin hızı da değişir. Sabit hız vektörü, sabit bir hızı ve sabit bir yönü ifade ederken "sabit hız" terimi, yönden bağımsız olarak yalnızca sabit bir değeri ifade eder. "Hız vektörü" terimi sıklıkla "hız" terimi ile birbirinin yerine kullanılır. Her ikisi de vücudun birim zamanda kat ettiği mesafeyi ifade eder.

nokta ivmesi bu noktanın hızının zamana göre türevine veya zamandaki noktanın yarıçap vektörünün ikinci türevine eşit olan hızındaki değişimin bir ölçüsüdür. İvme, hız vektöründeki büyüklük ve yön değişimini karakterize eder ve yörüngenin içbükeyliğine doğru yönlendirilir.

Hızlanma vektörü

hızdaki değişimin, bu değişimin meydana geldiği zaman aralığına oranıdır. Ortalama ivme aşağıdaki formülle belirlenebilir:

Nerede - ivme vektörü.

İvme vektörünün yönü, hızdaki değişimin yönü Δ = - 0 ile çakışmaktadır (burada 0, başlangıç ​​hızıdır, yani vücudun hızlanmaya başladığı hızdır).

t1 anında (bkz. Şekil 1.8) cismin hızı 0'dır. T2 anında vücudun bir hızı vardır. Vektör çıkarma kuralına göre hız değişiminin vektörünü Δ = - 0 buluyoruz. O zaman ivme şu şekilde tanımlanabilir:

Bazı basit geometrik şekillerin ağırlık merkezleri

Sıklıkla ortaya çıkan bir şekle (üçgen, dairesel yay, sektör, segment) sahip cisimlerin ağırlık merkezlerini belirlemek için referans verilerinin kullanılması uygundur (tabloya bakınız).

Bazı homojen cisimlerin ağırlık merkezinin koordinatları

№	Şekil adı	Çizim
	bir dairenin yayı: Homojen bir daire yayının ağırlık merkezi simetri ekseni üzerindedir (koordinat) C R dairenin yarıçapıdır.
	Homojen dairesel sektör C= 0). burada α merkez açının yarısıdır; R dairenin yarıçapıdır.
	Segment: ağırlık merkezi simetri ekseninde bulunur (koordinat) C= 0). burada α merkez açının yarısıdır; R dairenin yarıçapıdır.
	Yarım daire:
	Üçgen: Homojen bir üçgenin ağırlık merkezi kenarortaylarının kesiştiği noktadadır. Nerede x1, y1, x2, y2, x3, y3üçgenin köşelerinin koordinatlarıdır
	Koni: Homojen dairesel bir koninin ağırlık merkezi koninin yüksekliğindedir ve koninin tabanından yüksekliğin 1/4'ü kadar uzaktadır.
	yarımküre: Ağırlık merkezi simetri ekseni üzerindedir.
	Trapez: şeklin alanıdır.
	- şeklin alanı;

Arabanın ağırlık merkezinin altında, tüm ağırlığının yoğunlaştığı koşullu bir nokta olduğu varsayılmaktadır. Ağırlık merkezinin konumu, aracın yol tutuşu ve dengesi üzerinde önemli bir etkiye sahiptir ve sürücünün bunu her zaman dikkate alması gerekir. Ağırlık merkezinin yükseklikteki konumu yükün ağırlığına ve niteliğine bağlıdır. Örneğin, bir binek otomobil yalnızca gövdede bulunan kargoyu taşıyorsa, ağırlık merkezi, kargoyu tavanın üzerinde bulunan bagajda taşırken olduğundan çok daha düşük olacaktır. Ancak yükün niteliği ve yerleşimi ne olursa olsun, yüklü bir makinenin ağırlık merkezi her zaman yüksüz olanınkinden daha yüksek olacaktır. Bunu göz önünde bulundurarak, birçok sürücünün yüklü bir aracın iyi stabilitesi (ve hatta devrilme olasılığının azaltılması) hakkındaki mevcut görüşü doğru değildir.

Makinenin ağırlık merkezinin yüksekliği, hızlanma ve frenleme sırasında ve ayrıca çekiş kütlesine ve buna bağlı olarak maksimum çekiş kuvvetine yansıyacak olan makineyi yatırırken tekerlekler üzerindeki normal reaksiyonların yeniden dağıtılmasını etkiler.

Aracın ağırlık merkezinin konumu büyük önem taşıyor. Makinenin devrilmeye karşı stabilitesini karakterize eder. Bu, ayakta yolcuların bulunduğu otobüslerde açıkça görülmektedir ve aynı zamanda büyük boyutlu kargo taşıyan otomobiller (karayolu trenleri), vanlar ve özel taşıma araçları (hava platformları, kamyon vinçleri vb.) için de daha geçerlidir.