SONSUZ KÜÇÜK FONKSİYONLAR VE ANA ÖZELLİKLERİ

İşlev y=f(x) isminde sonsuz küçük en x→a ya da ne zaman X→∞ eğer veya ise, yani Sonsuz küçük bir fonksiyon, belirli bir noktadaki limiti sıfır olan bir fonksiyondur.

Örnekler.

Aşağıdaki önemli ilişkiyi kuralım:

Teorem. Eğer fonksiyon y=f(x) temsil edilebilir x→a sabit bir sayının toplamı olarak B ve sonsuz derecede küçük α(x): f(x)=b+ α(x) O .

Tam tersine, eğer öyleyse f(x)=b+α(x), Nerede a(x) sonsuz derecede küçüktür x→a.

Kanıt.

Sonsuz küçük fonksiyonların temel özelliklerini ele alalım.

Teorem 1.İki, üç ve genel olarak herhangi bir sonlu sayıda sonsuz küçük sayının cebirsel toplamı sonsuz küçük bir fonksiyondur.

Kanıt. İki terim için bir kanıt verelim. İzin vermek f(x)=α(x)+β(x), Nerede ve . Keyfi olarak küçük ε için bunu kanıtlamamız gerekiyor. > 0 orada δ> 0, öyle ki X eşitsizliği tatmin etmek |x – a|<δ gerçekleştirilen |f(x)|< ε.

Böylece keyfi bir ε sayısını sabitliyoruz > 0. Teoremin hipotezine göre, a(x) sonsuz küçük bir fonksiyonsa δ 1 vardır > 0, hangisi |x – a|< δ 1 elimizde |α(x)|< ε / 2. Aynı şekilde, beri β(x) sonsuz küçükse, böyle bir δ 2 vardır > 0, hangisi |x – a|< δ 2 elimizde | β(x)|< ε / 2.

Hadi alalım δ=dak(δ1 , δ2 } .Sonra noktanın bir mahallesinde A yarıçap δ eşitsizliklerin her biri karşılanacak |α(x)|< ε / 2 ve | β(x)|< ε / 2. Bu nedenle bu mahallede

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,

onlar. |f(x)|< ε, kanıtlanması gerekiyordu.

Teorem 2. Sonsuz küçük bir fonksiyonun çarpımı a(x) sınırlı işlev için f(x) en x→a(ya da ne zaman x→∞) sonsuz küçük bir fonksiyondur.

Kanıt. Fonksiyondan beri f(x) sınırlıdır, o zaman bir sayı vardır Möyle ki tüm değerler için X bu noktanın bir mahallesinden a|f(x)|≤M. Ayrıca, beri a(x) için sonsuz küçük bir fonksiyondur x→a, o zaman keyfi ε için > 0 noktasının bir komşuluğu var A eşitsizliğin olduğu |α(x)|< ε /M. Daha sonra bu mahallelerden daha küçük olanında | αf|< ε /M= ε. Ve bu şu anlama geliyor af- sonsuz derecede küçük. Dava için x→∞ ispat da benzer şekilde gerçekleştirilir.

Kanıtlanmış teoremden şu sonuç çıkar:

Sonuç 1. Eğer ve ise o zaman.

Sonuç 2. Eğer c= const, o zaman .

Teorem 3. Sonsuz küçük bir fonksiyonun oranı a(x) fonksiyon başına f(x) Limiti sıfır olmayan bir sonsuz küçük fonksiyondur.

Kanıt. İzin vermek . sonra 1 /f(x) sınırlı bir işlevi vardır. Bu nedenle kesir sonsuz küçük bir fonksiyonun ve sınırlı bir fonksiyonun ürünüdür, yani fonksiyon sonsuz küçüktür.

SONSUZ KÜÇÜK VE SONSUZ BÜYÜK FONKSİYONLAR ARASINDAKİ İLİŞKİ

Teorem 1. Eğer fonksiyon f(x) sonsuz derecede büyüktür x→a, ardından işlev 1 /f(x) sonsuz derecede küçüktür x→a.

Kanıt. Rastgele bir sayı alın ε >0 ve bunu bazılarına göster δ>0 (ε'ya bağlı olarak) tümü için X, hangisi için |x – a|<δ eşitsizlik karşılanır ve bu şu anlama gelir: 1/f(x) sonsuz küçük bir fonksiyondur. Gerçekten de o zamandan beri f(x) için sonsuz büyük bir fonksiyondur x→a, o zaman var δ>0 öyle ki en kısa sürede |x – a|<δ , yani | f(x)|> 1/ ε. Ama sonra aynı şey için X.

Örnekler.

Ters teorem de kanıtlanabilir.

Teorem 2. Eğer fonksiyon f(x)- sonsuz derecede küçük x→a(veya x→∞) ve ortadan kaybolmaz, o zaman y= 1/f(x) sonsuz bir fonksiyondur.

Teoremi kendiniz kanıtlayın.

Örnekler.

Böylece sonsuz küçük ve sonsuz büyük fonksiyonların en basit özellikleri aşağıdaki koşullu ilişkiler kullanılarak yazılabilir: A≠ 0

LİMİTLER ÜZERİNE TEOREMLER

Teorem 1.İki, üç ve genellikle belirli sayıda fonksiyonun cebirsel toplamının limiti, bu fonksiyonların limitlerinin cebirsel toplamına eşittir;

Kanıt. İspatı iki terim için yapacağız çünkü herhangi bir sayıda terim için aynı şekilde yapılır. İzin vermek .Daha sonra f(x)=b+α(x) Ve g(x)=c+β(x), Nerede α Ve β sonsuz küçük fonksiyonlardır. Buradan,

f(x) + g(x)=(b + c) + (α(x) + β(x)).

Çünkü b+c bir sabittir ve α(x) + β(x) sonsuz küçük bir fonksiyondur, o zaman

Örnek. .

Teorem 2.İki, üç ve genel olarak sonlu sayıda fonksiyonun çarpımının limiti, bu fonksiyonların limitlerinin çarpımına eşittir:

Kanıt. İzin vermek . Buradan, f(x)=b+α(x) Ve g(x)=c+β(x) Ve

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

İş M.Ö sabit bir değerdir. İşlev bβ + cα + αβ Sonsuz küçük fonksiyonların özelliklerine dayanarak sonsuz küçük bir miktar vardır. Bu yüzden .

Sonuç 1. Sabit faktör limit işaretinden çıkarılabilir:

.

Sonuç 2. Derecenin sınırı, sınırın derecesine eşittir:

.

Örnek..

Teorem 3. Paydanın limiti sıfır değilse, iki fonksiyonun bölümünün limiti bu fonksiyonların limitlerinin bölümüne eşittir;

.

Kanıt. İzin vermek . Buradan, f(x)=b+α(x) Ve g(x)=c+β(x), Nerede α, β sonsuz küçüktür. Bölümü göz önünde bulundurun

Kesir sonsuz küçük bir fonksiyondur çünkü pay sonsuz küçük bir fonksiyondur ve paydanın bir limiti vardır c2 ≠0.

Örnekler.

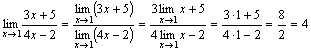
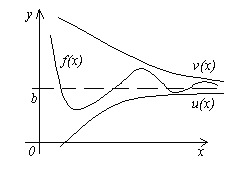
Teorem 4.Üç fonksiyon verilsin f(x), u(x) Ve v(x) u eşitsizliklerini tatmin etmek (x)≤f(x)≤v(x). Eğer işlevler sen(x) Ve v(x) aynı limite sahip x→a(veya x→∞), ardından fonksiyon f(x) aynı sınıra doğru eğilim gösterir, yani Eğer

, O .

Bu teoremin anlamı şekilden açıkça görülmektedir.

Teorem 4'ün kanıtı örneğin ders kitabında bulunabilir: Piskunov N. S. Diferansiyel ve integral hesap, cilt 1 - M .: Nauka, 1985.

Teorem 5. Eğer x→a(veya x→∞) işlev y=f(x) negatif olmayan değerler alır y≥0 ve sınıra doğru yöneliyor B ise bu sınır negatif olamaz: b≥0.

Kanıt. Kanıt çelişki yoluyla gerçekleştirilecektir. Öyleymiş gibi yapalım B<0 , Daha sonra |y – b|≥|b| ve bu nedenle farkın modülü sıfıra ulaşma eğiliminde değildir. x→a. Ama sonra sen sınıra gitmiyor B en x→a bu da teoremin koşuluyla çelişiyor.

Teorem 6. Eğer iki fonksiyon f(x) Ve g(x) argümanın tüm değerleri için X eşitsizliği gidermek f(x)≥ g(x) ve sınırları varsa, o zaman eşitsizliğimiz de olur b≥c.

Kanıt. Teoreme göre f(x)-g(x) ≥0, dolayısıyla Teorem 5'e göre , veya .

TEK TARAFLI LİMİTLER

Şu ana kadar bir fonksiyonun limitinin tanımını göz önünde bulundurduk. x→a keyfi olarak, yani fonksiyonun limiti, fonksiyonun nasıl olduğuna bağlı değildi. X karşı A, solunda veya sağında A. Bununla birlikte, bu koşul altında limiti olmayan fonksiyonlar bulmak oldukça yaygındır, ancak aşağıdaki durumlarda limitleri vardır: x→a, bir tarafta kalmak A, sol veya sağ (bkz. şekil). Bu nedenle tek taraflı limit kavramı ortaya çıkmıştır.

Eğer f(x) sınıra doğru gidiyor B en X bir sayı için çabalıyorum A Bu yüzden X yalnızca aşağıdaki değerleri alır A, ardından yazın ve arayın f(x) fonksiyonunun soldaki a noktasındaki sınırı.

Def.: Fonksiyon çağrılır sonsuz küçük eğer .

" " gösteriminde şunu varsayacağız: x0 nihai değer olarak alabiliriz: x0= İnşaat ve sonsuz: x0= ∞.

Sonsuz küçük fonksiyonların özellikleri:

1) Sonlu sayıda sonsuz küçük for fonksiyonun cebirsel toplamı sonsuz küçük bir fonksiyondur.

2) Sonlu sayıda sonsuz küçük fonksiyonların çarpımı sonsuz küçük bir fonksiyondur.

3) Sınırlı bir fonksiyon ile sonsuz küçük bir fonksiyonun çarpımı sonsuz küçük bir fonksiyondur.

4) Bir fonksiyondaki sonsuz küçük bir sayının, limiti sıfır olmayan bir fonksiyona bölünme bölümü, bir fonksiyondaki sonsuz küçük bir sayıdır.

Örnek: İşlev sen = 2 + X'da sonsuz küçüktür, çünkü .

Def.: Fonksiyon çağrılır sonsuz büyüklükte eğer .

Sonsuz büyük fonksiyonların özellikleri:

1) Fonksiyonlar için sonsuz büyüklerin toplamı, bir fonksiyon için sonsuz büyüktür.

2) Bir fonksiyon için sonsuz büyük bir değer ile limiti sıfır olmayan bir fonksiyonun çarpımı, bir fonksiyon için sonsuz büyük bir değerdir.

3) Sonsuz büyük bir fonksiyon ile sınırlı bir fonksiyonun toplamı sonsuz büyük bir fonksiyondur.

4) Bir fonksiyon için sonsuz büyüklükteki bir sayıyı, sonlu limiti olan bir fonksiyona bölme bölümü, bir fonksiyon için sonsuz büyüklüktedir.

Örnek: İşlev sen= için sonsuz büyüktür, çünkü .

Teorem.Sonsuz küçük ve sonsuz büyük miktarlar arasındaki ilişki. Bir fonksiyon noktasında sonsuz küçükse, o zaman fonksiyon noktasında sonsuz büyüktür. Tersine, eğer bir fonksiyon noktasında sonsuz büyükse, o zaman fonksiyon noktasında sonsuz küçüktür.

İki sonsuz küçükün oranı genellikle sembolüyle, iki sonsuz büyüğün oranı ise sembolüyle gösterilir. Her iki ilişki de, belirsiz ifadelerde yer alan belirli fonksiyonların türüne bağlı olarak, limitlerinin var olabileceği veya olamayacağı, belirli bir sayıya eşit olabileceği veya sonsuz olabileceği anlamında belirsizdir.

Biçimin belirsizlerine ve belirsizlere ek olarak aşağıdaki ifadeler de vardır:

Aynı işaretin sonsuz büyük olanlarının farkı;

Sonsuz küçük bir sayının sonsuz büyük bir sayı ile çarpımı;

Tabanı 1'e ve göstergesi -'ye eğilimli olan bir üstel güç fonksiyonu;

Tabanı sonsuz küçük ve üssü sonsuz büyük olan bir üstel kuvvet fonksiyonu;

Tabanı ve üssü sonsuz küçük olan üstel bir fonksiyon;

Tabanı sonsuz büyük ve üssü sonsuz küçük olan üstel bir fonksiyon.

Buna karşılık gelen türden bir belirsizliğin olduğu söyleniyor. Bu durumlarda limitin hesaplanması çağrılır. belirsizliğin açıklanması. Belirsizliği ortaya çıkarmak için limit işaretinin altındaki ifade belirsizlik içermeyen bir forma dönüştürülür.

Limitleri hesaplarken limitlerin özelliklerinin yanı sıra sonsuz küçük ve sonsuz büyük fonksiyonların özellikleri de kullanılır.

Çeşitli limitlerin hesaplama örneklerini düşünün.

1) . 2) .

4) , Çünkü sonsuz küçük bir fonksiyonun sınırlı bir fonksiyona göre çarpımı sonsuz küçüktür.

5) . 6) .

7) = =

. Bu durumda, polinomların çarpanlara ayrılması ve ortak bir çarpanla azaltılmasıyla çözülen tipte bir belirsizlik vardı.

= .

Bu durumda, türde bir belirsizlik vardı ve bu, pay ve paydanın formül kullanılarak ifadeyle çarpılması ve ardından kesrin (+1) azaltılmasıyla çözüldü.

9)
. Bu örnekte türün belirsizliği, kesrin pay ve paydasının terim terim en yüksek dereceye bölünmesiyle ortaya çıkmıştır.

Dikkate Değer Sınırlar

İlk harika sınır : .

Kanıt. Bir birim çember düşünün (Şekil 3).

Şek. 3. birim çember

İzin vermek X merkez açının radyan ölçüsüdür MOA(), Daha sonra OA = R= 1, MK= günah X, AT=tg X. Üçgenlerin alanlarının karşılaştırılması OMA, OTA ve sektörler OMA, şunu elde ederiz:

,

.

Son eşitsizliği günaha böl X, şunu elde ederiz:

.

Çünkü için, o zaman limitlerin 5) özelliğine göre

Nereden ve at'nin tersi kanıtlanacaktı.

Yorum: Eğer fonksiyon 'da sonsuz küçükse, yani. , o zaman ilk dikkate değer limit şu şekildedir:

.

İlk dikkate değer limiti kullanarak limit hesaplama örneklerini düşünün.

Bu limit hesaplanırken trigonometrik formül kullanıldı: .

.

İkinci dikkat çekici limiti kullanarak limit hesaplama örneklerini düşünün.

2) .

3) . Tip belirsizliği var. O zaman bir değişiklik yapalım; .

Sonsuz küçükler ve büyükler hesabı

Sonsuz küçük hesap- türetilmiş sonucun sonsuz olarak kabul edildiği, sonsuz küçük değerlerle yapılan hesaplamalar toplam sonsuz derecede küçük. Sonsuz küçükler hesabı genel bir kavramdır. diferansiyel Ve Integral hesabı modernliğin temelini oluşturan yüksek Matematik. Sonsuz küçük miktar kavramı, kavramla yakından ilgilidir. sınır.

Sonsuz küçük

Alt sıra A N isminde sonsuz küçük, Eğer . Örneğin bir sayı dizisi sonsuz derecede küçüktür.

Fonksiyon çağrılır bir noktanın komşuluğunda sonsuz küçük X 0 ise .

Fonksiyon çağrılır sonsuzda sonsuz küçük, Eğer veya .

Ayrıca sonsuz küçük, bir fonksiyon ile limiti arasındaki fark olan bir fonksiyondur, yani eğer , O F(X) − A = α( X) , .

sonsuz büyüklükte

Alt sıra A N isminde sonsuz büyüklükte, Eğer .

Fonksiyon çağrılır bir noktanın mahallesinde sonsuz derecede büyük X 0 ise .

Fonksiyon çağrılır sonsuzda sonsuz büyük, Eğer veya .

Her durumda, eşitlik sağındaki sonsuzluğun belirli bir işarete ("artı" veya "eksi") sahip olduğu varsayılır. Yani, örneğin, fonksiyon X günah X için sonsuz büyük değildir.

Sonsuz küçüklerin ve sonsuz küçüklerin özellikleri

Sonsuz küçüklerin karşılaştırılması

Sonsuz küçük miktarlar nasıl karşılaştırılır?
Sonsuz küçük miktarların oranı sözde oluşturur belirsizlik.

Tanımlar

Aynı α( değeri için sonsuz küçüklüğe sahip olduğumuzu varsayalım. X) ve β( X) (veya tanım açısından önemli olmayan sonsuz küçük diziler).

Bu limitleri hesaplamak için şunu kullanmak uygundur: L'Hopital'in kuralı.

Karşılaştırma örnekleri

Eşdeğer miktarlar

Tanım

Eğer ise sonsuz küçük miktarlara α ve β denir eş değer ().
Açıkçası, eşdeğer miktarlar aynı küçüklük derecesine sahip sonsuz küçük miktarların özel bir durumudur.

için aşağıdaki denklik ilişkileri geçerlidir: , , .

Teorem

Bu teorem limitlerin bulunmasında pratik öneme sahiptir (örneğe bakın).

Kullanım örneği

Tarihsel taslak

"Sonsuz küçük" kavramı eski çağlarda bölünemeyen atom kavramıyla bağlantılı olarak tartışılmış ancak klasik matematiğe girmemiştir. 16. yüzyılda ortaya çıkmasıyla yeniden canlanmıştır. "bölünmezler yöntemi"- incelenmekte olan şeklin sonsuz küçük bölümlere ayrılması.

Sonsuz küçükler hesabının cebirselleştirilmesi 17. yüzyılda gerçekleşti. Herhangi bir sonlu (sıfır olmayan) değerden küçük olan ancak yine de sıfıra eşit olmayan sayısal değerler olarak tanımlanmaya başlandı. Analiz sanatı sonsuz küçüklükleri içeren bir ilişki çizmekten ibaretti ( diferansiyeller) ve sonra - onun içinde entegrasyon.

Eski tarz matematikçiler bu kavramı konu edindiler sonsuz küçük Sert eleştiri. Michelle Rulo yeni hesabın şöyle olduğunu yazdı " bir takım parlak hatalar»; Voltaire Bu hesabın, varlığı kanıtlanamayan şeyleri hesaplama ve doğru olarak ölçme sanatı olduğuna öfkeyle işaret etti. Eşit Huygensüst düzey diferansiyellerin anlamını anlamadığını itiraf etti.

Kaderin bir ironisi olarak, yüzyılın ortasındaki görünüm düşünülebilir. standart dışı analiz Orijinal bakış açısının - gerçek sonsuz küçüklerin - aynı zamanda tutarlı olduğunu ve analizin temeli olabileceğini kanıtlayan kişi.

Ayrıca bakınız

Wikimedia Vakfı. 2010.

Diğer sözlüklerde "Sonsuz Büyük" ifadesinin ne olduğuna bakın:

Sonsuz küçük bir X'in tersi olan bir Y değişkeni, yani Y = 1/X ... Büyük Ansiklopedik Sözlük

Sonsuz küçük bir x'in tersi olan bir y değişkeni, yani y = 1/x. * * * SONSUZ BÜYÜK SONSUZ BÜYÜK, değişken değer Y, sonsuz küçük bir X değerinin tersi, yani Y = 1/X... ansiklopedik sözlük

Matematikte, belirli bir değişim sürecinde mutlak değeri önceden belirlenmiş herhangi bir sayıdan daha büyük olan ve bu değerde kalan bir değişken. B. çalışıyor. miktarlar sonsuz küçüklerin incelenmesine indirgenebilir (Bkz. ... ... Büyük Sovyet Ansiklopedisi

Sonsuz küçük fonksiyonlar

%%f(x)%% fonksiyonu çağrılıyor sonsuz küçük(b.m.) for %%x \to a \in \overline(\mathbb(R))%%, eğer argüman buna yöneldiğinde fonksiyonun limiti sıfıra eşitse.

B.m. kavramı. işlevi, argümanındaki bir değişikliğin göstergesiyle ayrılmaz bir şekilde bağlantılıdır. B.m hakkında konuşabiliriz. %%a \ ila a + %0 ve %%a \ ila a - %0 % için işlevler. Genellikle b.m. işlevler Yunan alfabesinin ilk harfleriyle gösterilir %%\alpha, \beta, \gamma, \ldots%%

Örnekler

1. %%f(x) = x%% fonksiyonu b.m'dir. %%x \to 0%%'de, çünkü %%a = 0%%'deki limiti sıfırdır. İki taraflı limit ile tek taraflı limit arasındaki bağlantıya ilişkin teoreme göre bu fonksiyon b.m'dir. hem %%x \to +0%% ile hem de %%x \to -0%% ile.
2. Fonksiyon %%f(x) = 1/(x^2)%% - b.m. %%x \to \infty%% ile (ayrıca %%x \to +\infty%% ve %%x \to -\infty%% ile).

Mutlak değeri ne kadar küçük olursa olsun, sıfır olmayan bir sabit sayı b.m değildir. işlev. Sabit sayılar için tek istisna sıfırdır, çünkü %%f(x) \equiv 0%% fonksiyonunun sıfır sınırı vardır.

Teorem

%%f(x)%% fonksiyonunun, genişletilmiş sayısal satırın %%a \in \overline(\mathbb(R))%% noktasında %%b%% sayısına eşit bir son sınırı vardır. eğer bu fonksiyon bu sayının %%b%% ve b.m'nin toplamına eşitse. %%x \to a%% ile %%\alpha(x)%% işlevleri veya $$ \exists~\lim\limits_(x \to a)(f(x)) = b \in \mathbb(R ) \Leftrightarrow \left(f(x) = b + \alpha(x)\right) \land \left(\lim\limits_(x \to a)(\alpha(x) = 0)\right). $$

Sonsuz küçük fonksiyonların özellikleri

Limite geçiş kurallarına göre, %%c_k = 1~ \forall k = \overline(1, m), m \in \mathbb(N)%% için aşağıdaki ifadeler aşağıdaki gibidir:

1. Son sayının toplamı b.m. %%x \to a%% için işlevler f.m. %%x \'den %%'ye kadar.
2. Herhangi bir sayıda b.m.'nin ürünü. %%x \to a%% için işlevler f.m. %%x \'den %%'ye kadar.

B.m.'nin ürünü. %%x \'den a%%'ye kadar olan fonksiyonlar ve a noktasının %%\stackrel(\circ)(\text(U))(a)%% delinmiş mahallesinde sınırlı bir fonksiyon, b.m'dir. %%x \ ile %% işlevine.

Sabit bir fonksiyonun ve b.m'nin çarpımının olduğu açıktır. %%x \to a%%'de b.m. var. %%x \'den %%'ye kadar işlev.

Eşdeğer sonsuz küçük fonksiyonlar

%%x \to a%% için sonsuz küçük %%\alpha(x), \beta(x)%% fonksiyonları çağrılır eş değer ve %%\alpha(x) \sim \beta(x)%% olarak yazılır, eğer

$$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\limits_(x \to a)(\frac(\beta(x) )(\alpha(x))) = 1. $$

B.m.'nin değiştirilmesine ilişkin teorem. işlevler eşdeğeri

%%\alpha(x), \alpha_1(x), \beta(x), \beta_1(x)%% b.m olsun. %%x \to a%% ve %%\alpha(x) \sim \alpha_1(x);'deki işlevler \beta(x) \sim \beta_1(x)%%, sonra $$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x)))) = \lim\ limitler_(x \to a)(\frac(\alpha_1(x))(\beta_1(x))). $$

Eşdeğer b.m. işlevler.

%%\alpha(x)%% b.m olsun. %%x \'den %%'ye kadar işlev, ardından

1. %%\sin(\alpha(x)) \sim \alpha(x)%%
2. %%\displaystyle 1 - \cos(\alpha(x)) \sim \frac(\alpha^2(x))(2)%%
3. %%\tan \alpha(x) \sim \alpha(x)%%
4. %%\arcsin\alpha(x) \sim \alpha(x)%%
5. %%\arctan\alpha(x) \sim \alpha(x)%%
6. %%\ln(1 + \alpha(x)) \sim \alpha(x)%%
7. %%\displaystyle\sqrt[n](1 + \alpha(x)) - 1 \sim \frac(\alpha(x))(n)%%
8. %%\displaystyle a^(\alpha(x)) - 1 \sim \alpha(x) \ln(a)%%

Örnek

$$ \begin(array)(ll) \lim\limits_(x \to 0)( \frac(\ln\cos x)(\sqrt(1 + x^2) - 1)) & = \lim\limits_ (x \to 0)(\frac(\ln(1 + (\cos x - 1)))(\frac(x^2)(4)))) = \\ & = \lim\limits_(x \to 0)(\frac(4(\cos x - 1))(x^2)) = \\ & = \lim\limits_(x \to 0)(-\frac(4 x^2)(2 x^ 2)) = -2 \end(array) $$

Sonsuz büyük işlevler

%%f(x)%% fonksiyonu çağrılıyor sonsuz büyüklükte(b.b.) for %%x \to a \in \overline(\mathbb(R))%%, eğer fonksiyon argümanın eğiliminde olduğu gibi sonsuz bir limite sahipse.

B.m. gibi b.b kavramını işler. işlevi, argümanındaki bir değişikliğin göstergesiyle ayrılmaz bir şekilde bağlantılıdır. B.b hakkında konuşabiliriz. %%x \ile a + %0'a ve %%x \ile a - %0'a kadar işlevler. "Sonsuz büyük" terimi, fonksiyonun mutlak değerini değil, dikkate alınan noktanın yakınındaki değişiminin niteliğini ifade eder. Mutlak değeri ne kadar büyük olursa olsun hiçbir sabit sayı sonsuz büyük değildir.

Örnekler

1. Fonksiyon %%f(x) = 1/x%% - b.b. %%x \'den %0'a kadar.
2. Fonksiyon %%f(x) = x%% - b.b. %%x \ile \infty%% arasında.

Tanımların koşulları $$ \begin(array)(l) \lim\limits_(x \to a)(f(x)) = +\infty, \\ \lim\limits_(x \to a)( ise f( x)) = -\infty, \end(array) $$

sonra konuşurlar pozitif veya olumsuz b.b. %%a%% işlevinde.

Örnek

%%1/(x^2)%% fonksiyonu pozitif b.b. %%x \'den %0'a kadar.

B.b. ve b.m. işlevler

Eğer %%f(x)%% b.b ise. %%x \to a%% bir işlevse, o zaman %%1/f(x)%% b.m'dir.

%%x \'den %%'ye kadar. Eğer %%\alpha(x)%% b.m. %%x için \to a%%, %%a%% noktasının bazı delinmiş komşuluklarında sıfır olmayan bir fonksiyondur, bu durumda %%1/\alpha(x)%% b.b'dir. %%x \'den %%'ye kadar.

Sonsuz büyük fonksiyonların özellikleri

B.b'nin çeşitli özelliklerini sunalım. işlevler. Bu özellikler doğrudan b.b'nin tanımından kaynaklanmaktadır. sonlu limitleri olan fonksiyonlar ve fonksiyonların özelliklerinin yanı sıra b.b. ve b.m. işlevler.

1. Sonlu bir sayının çarpımı b.b. %%x \to a%% için işlevler b.b. %%x \'den %%'ye kadar işlev. Aslında, eğer %%f_k(x), k = \overline(1, n)%% b.b'dir. %%x \'den a%%'ye kadar, ardından %%a%% %%f_k(x) \ne 0%% noktasının delinmiş bir komşuluğunda çalışır ve bağlantı teoremi ile b.b. ve b.m. işlevler %%1/f_k(x)%% - b.m. %%x \'den %%'ye kadar işlev. %%\displaystyle\prod^(n)_(k = 1) 1/f_k(x)%%, %%x \to a%% için bir b.m işlevidir ve %%\displaystyle\prod^( n )_(k = 1)f_k(x)%% — b.b. %%x \'den %%'ye kadar işlev.
2. B.b.'nin ürünü. %%x \ ile %% arasında bir fonksiyon ve %%a%% noktasının bazı delinmiş mahallelerinde mutlak değeri pozitif bir sabitten büyük olan bir fonksiyon bir b.b'dir. %%x \'den %%'ye kadar işlev. Özellikle b.b. %%x \to a%% noktasındaki fonksiyonlar ve %%a%% noktasında sıfırdan farklı sonlu limiti olan bir fonksiyon b.b olacaktır. %%x \'den %%'ye kadar işlev.

%%a%% ve b.b noktasının delinmiş bazı komşuluklarında sınırlanan bir fonksiyonun toplamı. %%x \'den a%%'ye kadar olan işlevler b.b. %%x \'den %%'ye kadar işlev.

Örneğin, %%x - \sin x%% ve %%x + \cos x%% - b.b. %%x \ile \infty%% arasında.

3. İki b.b'nin toplamı. %%x \'den %%'ye kadar olan işlevlerde belirsizlik vardır. Terimlerin işaretine bağlı olarak böyle bir toplamdaki değişimin niteliği çok farklı olabilir.

   Örnek

   %%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%% - b.b fonksiyonları olsun. %%x \ ila \infty%% aralığında çalışır. Daha sonra:

   • %%f(x) + g(x) = 3x%% - b.b. %%x \'den \infty%%'ye kadar işlev;
   • %%f(x) + h(x) = %0 - b.m. %%x \'den \infty%%'ye kadar işlev;
   • %%h(x) + v(x) = \sin x%%'nin %%x \to \infty%% arasında sınırı yoktur.