Definition of logarithm

The logarithm of the number b to the base a is the exponent to which you need to raise a to get b.

The number e in mathematics, it is customary to denote the limit to which the expression tends to

Number e is irrational number - a number incommensurable with one, it cannot be exactly expressed either as a whole or as a fraction rational number.

Letter e- first letter Latin word exonere- to flaunt, hence the name in mathematics exponential- exponential function.

Number e is widely used in mathematics, and in all sciences, one way or another using mathematical calculations for their needs.

Logarithms. Properties of logarithms

Definition: The base logarithm of a positive number b is the exponent c to which the number a must be raised to obtain the number b.

Basic logarithmic identity:

7) Formula for transition to a new base:

lna = log e a, e ≈ 2.718…

Tasks and tests on the topic “Logarithms. Properties of logarithms»

• Logarithms - Important topics for repeating the exam in mathematics

To successfully complete tasks on this topic, you must know the definition of the logarithm, the properties of logarithms, the basic logarithmic identity, the definitions of decimal and natural logarithms. The main types of tasks on this topic are tasks for calculating and converting logarithmic expressions. Let's consider their solution on the following examples.

Solution: Using the properties of logarithms, we get

Solution: using the properties of the degree, we get

1) (2 2) log 2 5 =(2 log 2 5) 2 =5 2 =25

Properties of logarithms, formulations and proofs.

Logarithms have a number of characteristic properties. In this article, we will analyze the main properties of logarithms. Here we give their formulations, write the properties of logarithms in the form of formulas, show examples of their application, and also give proofs of the properties of logarithms.

Page navigation.

Basic properties of logarithms, formulas

For ease of remembering and using, we present basic properties of logarithms as a list of formulas. In the next section, we give their formulations, proofs, examples of use, and necessary explanations.

Private logarithm property: , where a>0 , a≠1 , x>0 , y>0 .

Consequence: , where a>0 , a≠1 , n is a natural number greater than one, b>0 .

Corollary 1: , a>0 , a≠1 , b>0 , b≠1 .

Corollary 2: , a>0 , a≠1 , b>0 , p and q are real numbers, q≠0 , in particular, for b=a we have .

Statements and proofs of properties

We pass to the formulation and proof of the recorded properties of logarithms. All properties of logarithms are proved on the basis of the definition of the logarithm and the basic logarithmic identity that follows from it, as well as the properties of the degree.

Let's start with properties of the logarithm of unity. Its formulation is as follows: the logarithm of unity is equal to zero, that is, log a 1=0 for any a>0 , a≠1 . The proof is straightforward: since a 0 =1 for any a that satisfies the above conditions a>0 and a≠1 , then the proven equality log a 1=0 immediately follows from the definition of the logarithm.

Let's give examples of application of the considered property: log 3 1=0 , lg1=0 and .

Let's move on to the next property: the logarithm of a number equal to the base is equal to one, that is, log a a=1 for a>0 , a≠1 . Indeed, since a 1 =a for any a , then by the definition of the logarithm log a a=1 .

Examples of using this property of logarithms are log 5 5=1 , log 5.6 5.6 and lne=1 .

The logarithm of the power of a number equal to the base of the logarithm is equal to the exponent. This property of the logarithm corresponds to a formula of the form log a a p =p, where a>0 , a≠1 and p is any real number. This property follows directly from the definition of the logarithm. Note that it allows you to immediately specify the value of the logarithm, if it is possible to represent the number under the sign of the logarithm as a degree of base, we will talk more about this in the article calculating logarithms.

For example, log 2 2 7 =7 , log10 -4 =-4 and .

Logarithm of the product of two positive numbers x and y is equal to the product of the logarithms of these numbers: log a (x y)=log a x+log a y, a>0 , a≠1 . Let us prove the property of the logarithm of the product. Due to the properties of the degree a log a x + log a y =a log a x a log a y , and since by the main logarithmic identity a log a x =x and a log a y =y , then a log a x a log a y =x y . Thus, a log a x+log a y =x y , whence the required equality follows by the definition of the logarithm.

Let's show examples of using the property of the logarithm of the product: log 5 (2 3)=log 5 2+log 5 3 and .

The product logarithm property can be generalized to the product of a finite number n of positive numbers x 1 , x 2 , …, x n as log a (x 1 x 2 ... x n)= log a x 1 +log a x 2 +...+log a x n. This equality can be easily proved by the method of mathematical induction.

For example, the natural logarithm of a product can be replaced by the sum of three natural logarithms of the numbers 4 , e , and .

Logarithm of the quotient of two positive numbers x and y is equal to the difference between the logarithms of these numbers. The property of the quotient logarithm corresponds to a formula of the form , where a>0 , a≠1 , x and y are some positive numbers. The validity of this formula is proved like the formula for the logarithm of the product: since , then by the definition of the logarithm .

Here is an example of using this property of the logarithm: .

Let's move on to property of the logarithm of degree. The logarithm of a degree is equal to the product of the exponent and the logarithm of the modulus of the base of this degree. We write this property of the logarithm of the degree in the form of a formula: log a b p =p log a |b|, where a>0 , a≠1 , b and p are numbers such that the degree of b p makes sense and b p >0 .

We first prove this property for positive b . The basic logarithmic identity allows us to represent the number b as a log a b , then b p =(a log a b) p , and the resulting expression, due to the power property, is equal to a p log a b . So we arrive at the equality b p =a p log a b , from which, by the definition of the logarithm, we conclude that log a b p =p log a b .

It remains to prove this property for negative b . Here we note that the expression log a b p for negative b makes sense only for even exponents p (since the value of the degree b p must be greater than zero, otherwise the logarithm will not make sense), and in this case b p =|b| p . Then b p =|b| p =(a log a |b|) p =a p log a |b| , whence log a b p =p log a |b| .

For example, and ln(-3) 4 =4 ln|-3|=4 ln3 .

It follows from the previous property property of the logarithm from the root: the logarithm of the root of the nth degree is equal to the product of the fraction 1/n and the logarithm of the root expression, that is, where a>0, a≠1, n is a natural number greater than one, b>0.

The proof is based on an equality (see the definition of exponent with a fractional exponent), which is valid for any positive b , and the property of the logarithm of the degree: .

Here is an example of using this property: .

Now let's prove conversion formula to the new base of the logarithm kind . To do this, it suffices to prove the validity of the equality log c b=log a b log c a . The basic logarithmic identity allows us to represent the number b as a log a b , then log c b=log c a log a b . It remains to use the property of the logarithm of the degree: log c a log a b = log a b log c a . Thus, the equality log c b=log a b log c a is proved, which means that the formula for the transition to a new base of the logarithm is also proved .

Let's show a couple of examples of applying this property of logarithms: and .

The formula for moving to a new base allows you to move on to working with logarithms that have a “convenient” base. For example, it can be used to switch to natural or decimal logarithms so that you can calculate the value of the logarithm from a table of logarithms. The formula for the transition to a new base of the logarithm also allows in some cases to find the value of a given logarithm, when the values ​​of some logarithms with other bases are known.

Used frequently special case formulas for the transition to a new base of the logarithm for c=b of the form . This shows that log a b and log b a are mutually inverse numbers. For example, .

The formula is also often used, which is convenient when finding logarithm values. To confirm our words, we will show how the value of the logarithm of the form is calculated using it. We have . To prove the formula, it suffices to use the transition formula to the new base of the logarithm a: .

It remains to prove the comparison properties of logarithms.

Let's use the opposite method. Suppose that for a 1 >1 , a 2 >1 and a 1 2 and for 0 1 log a 1 b≤log a 2 b is true. By the properties of logarithms, these inequalities can be rewritten as and respectively, and from them it follows that log b a 1 ≤log b a 2 and log b a 1 ≥log b a 2, respectively. Then, by the properties of powers with the same bases, the equalities b log b a 1 ≥b log b a 2 and b log b a 1 ≥b log b a 2 must be satisfied, that is, a 1 ≥a 2 . Thus, we have arrived at a contradiction to the condition a 1 2 . This completes the proof.

Basic properties of logarithms

• Materials for the lesson
• Download all formulas

Logarithms, like any number, can be added, subtracted and converted in every possible way. But since logarithms are not quite ordinary numbers, there are rules here, which are called basic properties.

These rules must be known - no serious logarithmic problem can be solved without them. In addition, there are very few of them - everything can be learned in one day. So let's get started.

Addition and subtraction of logarithms

Consider two logarithms with the same base: log a x and log a y . Then they can be added and subtracted, and:

So, the sum of the logarithms is equal to the logarithm of the product, and the difference is the logarithm of the quotient. Please note: the key point here is - same grounds. If the bases are different, these rules do not work!

These formulas will help calculate the logarithmic expression even when its individual parts are not considered (see the lesson "What is a logarithm"). Take a look at the examples - and see:

A task. Find the value of the expression: log 6 4 + log 6 9.

Since the bases of logarithms are the same, we use the sum formula:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.

A task. Find the value of the expression: log 2 48 − log 2 3.

The bases are the same, we use the difference formula:
log 2 48 - log 2 3 = log 2 (48: 3) = log 2 16 = 4.

A task. Find the value of the expression: log 3 135 − log 3 5.

Again, the bases are the same, so we have:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.

As you can see, the original expressions are made up of "bad" logarithms, which are not considered separately. But after transformations quite normal numbers turn out. Based on this fact, many test papers. Yes, that control - similar expressions in all seriousness (sometimes - with virtually no changes) are offered at the exam.

Removing the exponent from the logarithm

Now let's complicate the task a little. What if there is a degree in the base or argument of the logarithm? Then the exponent of this degree can be taken out of the sign of the logarithm according to the following rules:

• log a x n = n log a x ;
• 
• 

It is easy to see that the last rule follows their first two. But it's better to remember it anyway - in some cases it will significantly reduce the amount of calculations.

Of course, all these rules make sense if the ODZ logarithm is observed: a > 0, a ≠ 1, x > 0. And one more thing: learn to apply all formulas not only from left to right, but also vice versa, i.e. you can enter the numbers before the sign of the logarithm into the logarithm itself. This is what is most often required.

A task. Find the value of the expression: log 7 49 6 .

Let's get rid of the degree in the argument according to the first formula:
log 7 49 6 = 6 log 7 49 = 6 2 = 12

A task. Find the value of the expression:

[Figure caption]

Note that the denominator is a logarithm whose base and argument are exact powers: 16 = 2 4 ; 49 = 72. We have:

[Figure caption]

I think the last example needs clarification. Where have logarithms gone? Until the very last moment, we work only with the denominator. They presented the base and the argument of the logarithm standing there in the form of degrees and took out the indicators - they got a “three-story” fraction.

Now let's look at the main fraction. The numerator and denominator have the same number: log 2 7. Since log 2 7 ≠ 0, we can reduce the fraction - 2/4 will remain in the denominator. According to the rules of arithmetic, the four can be transferred to the numerator, which was done. The result is the answer: 2.

Transition to a new foundation

Speaking about the rules for adding and subtracting logarithms, I specifically emphasized that they only work with the same bases. What if the bases are different? What if they are not exact powers of the same number?

Formulas for transition to a new base come to the rescue. We formulate them in the form of a theorem:

Let the logarithm log a x be given. Then for any number c such that c > 0 and c ≠ 1, the equality is true:

[Figure caption]

In particular, if we put c = x , we get:

[Figure caption]

It follows from the second formula that it is possible to interchange the base and the argument of the logarithm, but in this case the whole expression is “turned over”, i.e. the logarithm is in the denominator.

These formulas are rarely found in ordinary numerical expressions. It is possible to evaluate how convenient they are only when deciding logarithmic equations and inequalities.

However, there are tasks that cannot be solved at all except by moving to a new foundation. Let's consider a couple of these:

A task. Find the value of the expression: log 5 16 log 2 25.

Note that the arguments of both logarithms are exact exponents. Let's take out the indicators: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;

Now let's flip the second logarithm:

[Figure caption]

Since the product does not change from permutation of factors, we calmly multiplied four and two, and then figured out the logarithms.

A task. Find the value of the expression: log 9 100 lg 3.

The base and argument of the first logarithm are exact powers. Let's write it down and get rid of the indicators:

[Figure caption]

Now let's get rid of the decimal logarithm by moving to a new base:

[Figure caption]

Basic logarithmic identity

Often in the process of solving it is required to represent a number as a logarithm to a given base. In this case, the formulas will help us:

1. n = log a a n

2. In the first case, the number n becomes the exponent in the argument. The number n can be absolutely anything, because it's just the value of the logarithm.

   The second formula is actually a paraphrased definition. It's called the basic logarithmic identity.

   Indeed, what will happen if the number b is raised to such a power that the number b to this power gives the number a? That's right: this is the same number a . Read this paragraph carefully again - many people "hang" on it.

   Like the new base conversion formulas, the basic logarithmic identity is sometimes the only possible solution.

   [Figure caption]

   Note that log 25 64 = log 5 8 - just take the square of the base and the argument of the logarithm. Given the rules for multiplying powers with the same base, we get:

   [Figure caption]

   If someone is not in the know, this was a real task from the Unified State Examination 🙂

   Logarithmic unit and logarithmic zero

   In conclusion, I will give two identities that are difficult to call properties - rather, these are consequences from the definition of the logarithm. They are constantly found in problems and, surprisingly, create problems even for "advanced" students.

   1. log a a = 1 is the logarithmic unit. Remember once and for all: the logarithm to any base a from that base itself is equal to one.
   2. log a 1 = 0 is logarithmic zero. The base a can be anything, but if the argument is one - the logarithm is zero! Because a 0 = 1 is a direct consequence of the definition.

   That's all the properties. Be sure to practice putting them into practice! Download the cheat sheet at the beginning of the lesson, print it out - and solve the problems.

   Logarithm. Properties of the logarithm (addition and subtraction).

   Properties of the logarithm follow from its definition. And so the logarithm of the number b by reason a defined as the exponent to which a number must be raised a to get the number b(the logarithm exists only for positive numbers).

   From this formulation it follows that the calculation x=log a b, is equivalent to solving the equation ax=b. For example, log 2 8 = 3 because 8 = 2 3 . The formulation of the logarithm makes it possible to justify that if b=a c, then the logarithm of the number b by reason a equals With. It is also clear that the topic of logarithm is closely related to the topic of the power of a number.

   With logarithms, as with any numbers, you can perform addition, subtraction operations and transform in every possible way. But in view of the fact that logarithms are not quite ordinary numbers, their own special rules apply here, which are called basic properties.

   Addition and subtraction of logarithms.

   Take two logarithms with the same base: log x and log a y. Then remove it is possible to perform addition and subtraction operations:

   As we see, sum of logarithms equals the logarithm of the product, and difference logarithms- the logarithm of the quotient. And this is true if the numbers a, X and at positive and a ≠ 1.

   It is important to note that the main aspect in these formulas are the same bases. If the bases differ from each other, these rules do not apply!

   The rules for adding and subtracting logarithms with the same bases are read not only from left to right, but also vice versa. As a result, we have the theorems for the logarithm of the product and the logarithm of the quotient.

   Logarithm of the product two positive numbers is equal to the sum their logarithms ; paraphrasing this theorem, we get the following, if the numbers a, x and at positive and a ≠ 1, then:

   Logarithm of the quotient of two positive numbers is equal to the difference between the logarithms of the dividend and the divisor. In other words, if the numbers a, X and at positive and a ≠ 1, then:

   We apply the above theorems to solve examples:

   If numbers x and at are negative, then product logarithm formula becomes meaningless. So, it is forbidden to write:

   since the expressions log 2 (-8) and log 2 (-4) are not defined at all (the logarithmic function at= log 2 X defined only for positive values ​​of the argument X).

   Product theorem is applicable not only for two, but also for an unlimited number of factors. This means that for every natural k and any positive numbers x 1 , x 2 , . . . ,x n there is an identity:

   From quotient logarithm theorems one more property of the logarithm can be obtained. It is well known that log a 1= 0, therefore,

   So there is an equality:

   Logarithms of two mutually reciprocal numbers on the same basis will differ from each other only in sign. So:

   Logarithm. Properties of logarithms

   Logarithm. Properties of logarithms

   Consider equality. Let us know the values ​​and and we want to find the value of .

   That is, we are looking for the exponent to which we need to cock to get .

   Let the variable can take any real value, then the following restrictions are imposed on the variables: o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>

   If we know the values ​​\u200b\u200bof and , and we are faced with the task of finding the unknown, then for this purpose a mathematical operation is introduced, which is called logarithm.

   To find the value we take logarithm of a number on foundation :

   The logarithm of a number to the base is the exponent to which you need to raise to get .

   That is basic logarithmic identity:

   o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>

   is essentially a mathematical notation logarithm definitions.

   The mathematical operation logarithm is the inverse of exponentiation, so properties of logarithms are closely related to the properties of the degree.

   We list the main properties of logarithms:

   (o” title=”a>o”/> , 1″ title=”a1″/>, 0″ title=”b>0″/>, 0,

   d>0″/>, 1″ title=”d1″/>

   4.

   5.

   The following group of properties allows you to represent the exponent of the expression under the sign of the logarithm, or standing at the base of the logarithm as a coefficient before the sign of the logarithm:

   6.

   7.

   8.

   9.

   The next group of formulas allows you to go from a logarithm with a given base to a logarithm with an arbitrary base, and is called transition formulas to a new base:

   10.

   12. (corollary from property 11)

   

   The following three properties are not well known, but they are often used when solving logarithmic equations, or when simplifying expressions containing logarithms:

   13.

   14.

   15.

   Special cases:

   — decimal logarithm

   — natural logarithm

   When simplifying expressions containing logarithms, a general approach is applied:

   1. Introducing decimals in the form of ordinary.

   2. mixed numbers represented as improper fractions.

   3. The numbers at the base of the logarithm and under the sign of the logarithm are decomposed into prime factors.

   4. We try to bring all logarithms to the same base.

   5. Apply the properties of logarithms.

   Let's look at examples of simplifying expressions containing logarithms.

   Example 1

   Calculate:

   Let's simplify all the exponents: our task is to bring them to logarithms, the base of which is the same number as the base of the exponent.

   ==(by property 7)=(by property 6) =

   Substitute the indicators that we have obtained in the original expression. We get:

   Answer: 5.25

   Example 2 Calculate:

   

   We bring all logarithms to base 6 (in this case, the logarithms from the denominator of the fraction will “migrate” to the numerator):

   Let's decompose the numbers under the sign of the logarithm into prime factors:

   Apply properties 4 and 6:

   We introduce the replacement

   We get:

   Answer: 1

   Logarithm . Basic logarithmic identity.

   Properties of logarithms. Decimal logarithm. natural logarithm.

   logarithm positive number N in base (b > 0, b 1) called the exponent x to which you need to raise b to get N .

   This entry is equivalent to the following: b x = N .

   EXAMPLES: log 3 81 = 4 since 3 4 = 81 ;

   log 1/3 27 = – 3 because (1/3) - 3 = 3 3 = 27 .

   The above definition of the logarithm can be written as an identity:

   

   Basic properties of logarithms.

   2) log 1 = 0 because b 0 = 1 .

   3) The logarithm of the product is equal to the sum of the logarithms of the factors:

   4) The logarithm of the quotient is equal to the difference between the logarithms of the dividend and the divisor:

   5) The logarithm of the degree is equal to the product of the exponent and the logarithm of its base:

   The consequence of this property is the following: log root equals the logarithm of the root number divided by the power of the root:

   

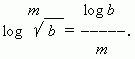
   6) If the base of the logarithm is a power, then the value the reciprocal of the exponent can be taken out of the rhyme log sign:

   

   The last two properties can be combined into one:

   

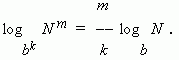
   7) The formula for the transition modulus (i.e. the transition from one base of the logarithm to another base):

   

   In a particular case, when N = a we have:

   

   Decimal logarithm called base logarithm 10. It is denoted lg, i.e. log 10 N= log N. Logarithms of numbers 10, 100, 1000, . p are 1, 2, 3, …, respectively, i.e. have so many positive

   units, how many zeros are in the logarithm number after one. Logarithms of numbers 0.1, 0.01, 0.001, . p are –1, –2, –3, …, respectively, i.e. have as many negative ones as there are zeros in the logarithm number before the one (including zero integers). The logarithms of the remaining numbers have a fractional part called mantissa. The integer part of the logarithm is called characteristic. For practical applications, decimal logarithms are most convenient.

   natural logarithm called base logarithm e. It is denoted by ln, i.e. log e N=ln N. Number e is irrational, its approximate value is 2.718281828. It is the limit towards which the number (1 + 1 / n) n with unlimited increase n(cm. first wonderful limit on the Number Sequence Limits page).
   Strange as it may seem, natural logarithms turned out to be very convenient when carrying out various operations related to the analysis of functions. Calculating base logarithms e much faster than any other basis.

• How to get a certificate of state registration of ownership of an apartment? In accordance with the Constitution of the Russian Federation, the state is entrusted with the function of guarantor of the right to private property. The state has its powers in this area […] Penalty for failure to submit reports SZV-M and RSV-1 to the FIU At the end of each reporting and settlement period, the insured must submit the necessary calculation to the Pension Fund in the RSV-1 form. If for any reason […]
• When and how to get the funded part of the pension in Sberbank? Sberbank is a partner bank of the state pension fund. On the basis of this, citizens who have issued a funded pension could transfer the funded […]
• How to get subsidies for utility bills (rent)? Subsidies for utility bills are provided to certain categories of citizens in accordance with the housing legislation of the Russian Federation. To learn more about the procedure […]
• Information free of charge by TIN or OGRN from the tax register throughout Russia - online On the Unified Portal of Tax Services, information on state registration of legal entities, individual entrepreneurs, […]
• Cesspool: sanitary and building codes and regulations For the arrangement of sewerage in a summer cottage or city plot, it is necessary to follow not only construction, but also legislative standards. Cesspool: norms and rules for its arrangement […]

In relation to

the task of finding any of the three numbers from the other two, given, can be set. Given a and then N is found by exponentiation. If N are given and then a is found by extracting the root of the power x (or exponentiation). Now consider the case when, given a and N, it is required to find x.

Let the number N be positive: the number a is positive and not equal to one: .

Definition. The logarithm of the number N to the base a is the exponent to which you need to raise a to get the number N; the logarithm is denoted by

Thus, in equality (26.1), the exponent is found as the logarithm of N to the base a. Entries

have the same meaning. Equality (26.1) is sometimes called the basic identity of the theory of logarithms; in fact, it expresses the definition of the concept of the logarithm. By this definition the base of the logarithm a is always positive and different from unity; the logarithmable number N is positive. Negative numbers and zero do not have logarithms. It can be proved that any number with a given base has a well-defined logarithm. Therefore equality entails . Note that the condition is essential here, otherwise the conclusion would not be justified, since the equality is true for any values ​​of x and y.

Example 1. Find

Solution. To get the number, you need to raise base 2 to the power Therefore.

You can record when solving such examples in the following form:

Example 2. Find .

Solution. We have

In examples 1 and 2, we easily found the desired logarithm by representing the logarithmable number as a degree of base with a rational exponent. In the general case, for example, for etc., this cannot be done, since the logarithm has an irrational value. Let us pay attention to one question related to this statement. In § 12 we gave the concept of the possibility of determining any real power of a given positive number. This was necessary for the introduction of logarithms, which, in general, can be irrational numbers.

Consider some properties of logarithms.

Property 1. If the number and base are equal, then the logarithm is equal to one, and, conversely, if the logarithm is equal to one, then the number and base are equal.

Proof. Let By the definition of the logarithm, we have and whence

Conversely, let Then by definition

Property 2. The logarithm of unity to any base is equal to zero.

Proof. By the definition of the logarithm (the zero power of any positive base is equal to one, see (10.1)). From here

Q.E.D.

The converse statement is also true: if , then N = 1. Indeed, we have .

Before stating the following property of logarithms, we agree to say that two numbers a and b lie on the same side of a third number c if they are both either greater than c or less than c. If one of these numbers is greater than c and the other is less than c, then we say that they lie on opposite sides of c.

Property 3. If the number and base lie on the same side of unity, then the logarithm is positive; if the number and base lie on opposite sides of unity, then the logarithm is negative.

The proof of property 3 is based on the fact that the degree of a is greater than one if the base is greater than one and the exponent is positive, or the base is less than one and the exponent is negative. The degree is less than one if the base is greater than one and the exponent is negative, or the base is less than one and the exponent is positive.

There are four cases to be considered:

We confine ourselves to the analysis of the first of them, the reader will consider the rest on his own.

Let then the exponent in equality be neither negative nor equal to zero, therefore, it is positive, i.e., which was required to be proved.

Example 3. Find out which of the following logarithms are positive and which are negative:

Solution, a) since the number 15 and the base 12 are located on the same side of the unit;

b) , since 1000 and 2 are located on the same side of the unit; at the same time, it is not essential that the base is greater than the logarithmic number;

c), since 3.1 and 0.8 lie on opposite sides of unity;

G) ; why?

e) ; why?

The following properties 4-6 are often called the rules of logarithm: they allow, knowing the logarithms of some numbers, to find the logarithms of their product, quotient, degree of each of them.

Property 4 (the rule for the logarithm of the product). The logarithm of the product of several positive numbers in a given base is equal to the sum of the logarithms of these numbers in the same base.

Proof. Let positive numbers be given.

For the logarithm of their product, we write the equality (26.1) defining the logarithm:

From here we find

Comparing the exponents of the first and last expressions, we obtain the required equality:

Note that the condition is essential; the logarithm of the product of two negative numbers makes sense, but in this case we get

In general, if the product of several factors is positive, then its logarithm is equal to the sum of the logarithms of the modules of these factors.

Property 5 (quotient logarithm rule). The logarithm of a quotient of positive numbers is equal to the difference between the logarithms of the dividend and the divisor, taken in the same base. Proof. Consistently find

Q.E.D.

Property 6 (rule of the logarithm of the degree). The logarithm of the power of any positive number is equal to the logarithm of that number times the exponent.

Proof. We write again the main identity (26.1) for the number :

Q.E.D.

Consequence. The logarithm of the root of a positive number is equal to the logarithm of the root number divided by the exponent of the root:

We can prove the validity of this corollary by presenting how and using property 6.

Example 4. Logarithm to base a:

a) (it is assumed that all values ​​b, c, d, e are positive);

b) (it is assumed that ).

Solution, a) It is convenient to pass in this expression to fractional powers:

Based on equalities (26.5)-(26.7) we can now write:

We notice that simpler operations are performed on the logarithms of numbers than on the numbers themselves: when multiplying numbers, their logarithms are added, when divided, they are subtracted, etc.

That is why logarithms have been used in computational practice (see Sec. 29).

The action inverse to the logarithm is called potentiation, namely: potentiation is the action by which this number itself is found by the given logarithm of a number. In essence, potentiation is not any special action: it comes down to raising the base to a power (equal to the logarithm of the number). The term "potentiation" can be considered synonymous with the term "exponentiation".

When potentiating, it is necessary to use the rules that are inverse to the rules of logarithm: replace the sum of logarithms with the logarithm of the product, the difference of logarithms with the logarithm of the quotient, etc. In particular, if there is any factor in front of the sign of the logarithm, then during potentiation it must be transferred to the indicator degrees under the sign of the logarithm.

Example 5. Find N if it is known that

Solution. In connection with the potentiation rule just stated, the factors 2/3 and 1/3, which are in front of the signs of logarithms on the right side of this equality, will be transferred to the exponents under the signs of these logarithms; we get

Now we replace the difference of logarithms with the logarithm of the quotient:

to obtain the last fraction in this chain of equalities, we freed the previous fraction from irrationality in the denominator (section 25).

Property 7. If the base is greater than one, then more has a larger logarithm (and a smaller one has a smaller one), if the base is less than one, then a larger number has a smaller logarithm (and a smaller one has a larger one).

This property is also formulated as a rule for the logarithm of inequalities, both parts of which are positive:

When taking the logarithm of inequalities to a base greater than one, the inequality sign is preserved, and when taking a logarithm to a base less than one, the sign of the inequality is reversed (see also item 80).

The proof is based on properties 5 and 3. Consider the case when If , then and, taking the logarithm, we obtain

(a and N/M lie on the same side of unity). From here

Case a follows, the reader will figure it out for himself.

What is a logarithm?

Attention!
There are additional
material in Special Section 555.
For those who strongly "not very..."
And for those who "very much...")

What is a logarithm? How to solve logarithms? These questions confuse many graduates. Traditionally, the topic of logarithms is considered complex, incomprehensible and scary. Especially - equations with logarithms.

This is absolutely not true. Absolutely! Don't believe? Good. Now, for some 10 - 20 minutes you:

1. Understand what is a logarithm.

2. Learn to solve a whole class of exponential equations. Even if you haven't heard of them.

3. Learn to calculate simple logarithms.

Moreover, for this you will only need to know the multiplication table, and how a number is raised to a power ...

I feel you doubt ... Well, keep time! Go!

First, solve the following equation in your mind:

If you like this site...

By the way, I have a couple more interesting sites for you.)

You can practice solving examples and find out your level. Testing with instant verification. Learning - with interest!)

you can get acquainted with functions and derivatives.

(from the Greek λόγος - "word", "relation" and ἀριθμός - "number") numbers b by reason a(log α b) is called such a number c, and b= a c, that is, log α b=c and b=ac are equivalent. The logarithm makes sense if a > 0, a ≠ 1, b > 0.

In other words logarithm numbers b by reason a formulated as an exponent to which a number must be raised a to get the number b(the logarithm exists only for positive numbers).

From this formulation it follows that the calculation x= log α b, is equivalent to solving the equation a x =b.

For example:

log 2 8 = 3 because 8=2 3 .

We note that the indicated formulation of the logarithm makes it possible to immediately determine logarithm value when the number under the sign of the logarithm is a certain power of the base. Indeed, the formulation of the logarithm makes it possible to justify that if b=a c, then the logarithm of the number b by reason a equals With. It is also clear that the topic of logarithm is closely related to the topic degree of number.

The calculation of the logarithm is referred to logarithm. Logarithm is the mathematical operation of taking a logarithm. When taking a logarithm, the products of factors are transformed into sums of terms.

Potentiation is the mathematical operation inverse to logarithm. When potentiating, the given base is raised to the power of the expression on which the potentiation is performed. In this case, the sums of terms are transformed into the product of factors.

Quite often, real logarithms with bases 2 (binary), e Euler number e ≈ 2.718 (natural logarithm) and 10 (decimal) are used.

At this stage, it is worth considering samples of logarithms log 7 2 , ln √ 5, lg0.0001.

And the entries lg (-3), log -3 3.2, log -1 -4.3 do not make sense, since in the first of them a negative number is placed under the sign of the logarithm, in the second - a negative number in the base, and in the third - and a negative number under the sign of the logarithm and unit in the base.

Conditions for determining the logarithm.

It is worth considering separately the conditions a > 0, a ≠ 1, b > 0. definition of a logarithm. Let's consider why these restrictions are taken. This will help us with an equality of the form x = log α b, called the basic logarithmic identity, which directly follows from the definition of the logarithm given above.

Take the condition a≠1. Since one is equal to one to any power, then the equality x=log α b can only exist when b=1, but log 1 1 will be any real number. To eliminate this ambiguity, we take a≠1.

Let us prove the necessity of the condition a>0. At a=0 according to the formulation of the logarithm, can only exist when b=0. And then accordingly log 0 0 can be any non-zero real number, since zero to any non-zero power is zero. To eliminate this ambiguity, the condition a≠0. And when a<0 we would have to reject the analysis of rational and irrational values ​​of the logarithm, since the exponent with rational and irrational exponent is defined only for non-negative bases. It is for this reason that the condition a>0.

And the last condition b>0 follows from the inequality a>0, since x=log α b, and the value of the degree with a positive base a always positive.

Features of logarithms.

Logarithms characterized by distinctive features, which led to their widespread use to greatly facilitate painstaking calculations. In the transition "to the world of logarithms", multiplication is transformed into a much easier addition, division into subtraction, and raising to a power and taking a root are transformed into multiplication and division by an exponent, respectively.

The formulation of logarithms and a table of their values ​​(for trigonometric functions) was first published in 1614 by the Scottish mathematician John Napier. Logarithmic tables, enlarged and detailed by other scientists, were widely used in scientific and engineering calculations, and remained relevant until electronic calculators and computers began to be used.

derived from its definition. And so the logarithm of the number b by reason a defined as the exponent to which a number must be raised a to get the number b(the logarithm exists only for positive numbers).

From this formulation it follows that the calculation x=log a b, is equivalent to solving the equation ax=b. For example, log 2 8 = 3 because 8 = 2 3 . The formulation of the logarithm makes it possible to justify that if b=a c, then the logarithm of the number b by reason a equals With. It is also clear that the topic of the logarithm is closely related to the topic of the power of a number.

With logarithms, as with any numbers, you can perform operations of addition, subtraction and transform in every possible way. But in view of the fact that logarithms are not quite ordinary numbers, their own special rules apply here, which are called basic properties.

Addition and subtraction of logarithms.

Take two logarithms with the same base: log x and log a y. Then remove it is possible to perform addition and subtraction operations:

log a x+ log a y= log a (x y);

log a x - log a y = log a (x:y).

log a(x 1 . x 2 . x 3 ... x k) = log x 1 + log x 2 + log x 3 + ... + log a x k.

From quotient logarithm theorems one more property of the logarithm can be obtained. It is well known that log a 1= 0, therefore,

log a 1 /b= log a 1 - log a b= -log a b.

So there is an equality:

log a 1 / b = - log a b.

Logarithms of two mutually reciprocal numbers on the same basis will differ from each other only in sign. So:

Log 3 9= - log 3 1 / 9 ; log 5 1 / 125 = -log 5 125.