Kretanje tijela po kosoj površini. Kretanje tijela po kosoj ravni
slučaju ubrzanog kretanja naniže
Kretanje tijela uzduž kosoj ravni
Kretanje tijela duž nagnute ravni je klasičan primjer gibanja tijela pod djelovanjem nekoliko neusmjerenih sila. Standardna metoda za rješavanje problema ove vrste kretanja je proširenje vektora svih sila na komponente usmjerene duž koordinatnih osa. Takve komponente su linearno nezavisne. Ovo omogućava da se zapiše drugi Newtonov zakon za komponente duž svake ose posebno. Dakle, drugi Newtonov zakon, koji je vektorska jednadžba, pretvara se u sistem od dvije (tri za trodimenzionalni slučaj) algebarskih jednačina.
Poreklo ovog poslednjeg, bez sumnje, mora biti u velikoj meri posledica rešenja pitanja centra oscilovanja na osnovu proširenja i ravnoteže sila; literatura pregledana u ovoj studiji sugerira da je liječenje šoka jednako pravedno. Znamo važnost spisa Pierrea Varignona za razvoj analitičke mehanike; Enciklopedija i Ugovor o dinamici pozivaju nas da ne ograničavamo svoj doprinos samo ovoj oblasti.
Za svaki dajemo relevantan odlomak i dajemo njegovu francusku verziju, izvučenu iz Enciklopedije kada je autor bio D'Alembert. Označavamo kada je članak potpisan "Kamera". Varignon je teoriju zraka razvijenu primijenio na teoriju centralnih sila; pošto, imajući radijus razvoja krive, možemo pronaći vrijednost središnje sile tijela koje se kreće duž ove krive, nalazi se u istoj tački gdje se greda završava; ili, obrnuto, s obzirom na centralnu silu, moguće je odrediti razvijeni polumjer. Vidi istoriju.
Zamislite tijelo koje klizi niz nagnutu ravan. U ovom slučaju na njega djeluju sljedeće sile:
- Gravitacija m g , usmjerena okomito prema dolje;
- Reakciona snaga podrške N , usmjeren okomito na ravan;
- sila trenja klizanja F tr, usmjeren suprotno brzini (gore duž nagnute ravni kada tijelo klizi)
sila trenja klizanja F tr = µN proporcionalna sili reakcije oslonca. Ovo vam omogućava da dobijete sledeći izraz za silu trenja: F tr = mmg cos( α ) . Ova sila je suprotna komponenti "vuče" gravitacije. Stoga, za telo klizi nadole , dobijamo izraze za ukupnu rezultantnu silu i ubrzanje:
F x= mg(grijeh( α
) – µ
cos( α
));
a x= g(grijeh( α
) – µ
cos( α
)).
Varignon je također dao dva opšte teoreme o ovoj temi u akad. memoarima. Varignon demonstrira kako je nekoherentno Kopernikovo raspoloženje povezano sa Nebeskim mehanizmom: Jer sile koje planete moraju da drže u svojim orbitama moraju se uvek udružiti da bi se kretale zaista različitim brzinama; u beskonačnom broju slučajeva, postoji samo jedna stvar po kojoj se mogu ravnomjerno kretati.
Gornji pasus koji se odnosi na Varignon ne pojavljuje se u prijevodu Enciklopedije. Ali to čini problem mnogo opštijim i zahteva ne samo da vizuelni uglovi budu jednaki, već i da se povećavaju ili smanjuju u bilo kom datom odnosu; pod uslovom da najveća vrijednost ne prelazi desni ugao. Oko, mora biti postavljeno bilo gdje, bilo na početku raspona, ili izvan njega, ili sa strane. Sve je ugrađeno, on pretpostavlja da će prva linija biti prava linija i traži šta bi linija trebala biti, koju on naziva krivulja raspona.
Nije teško to uočiti ako µ α) , tada izraz ima pozitivan predznak i radi se o ravnomjerno ubrzanom kretanju niz nagnutu ravan. Ako µ >tg( α ), tada će ubrzanje imati negativan predznak i kretanje će biti jednako sporo. Takvo kretanje je moguće samo ako je tijelu data početna brzina niz padinu. U tom slučaju tijelo će postepeno stati. Ako, podložno µ >tg( α ) objekt u početku miruje, a zatim neće početi kliziti prema dolje. Ovdje će statička sila trenja u potpunosti kompenzirati komponentu gravitacije koja "vuče".
Kada je koeficijent trenja tačno jednak tangentu ugla nagiba ravnine: µ
= tg( α
) , radi se o međusobnoj kompenzaciji sve tri sile. U ovom slučaju, prema prvom Newtonovom zakonu, tijelo može ili mirovati ili se kretati konstantnom brzinom (u ovom slučaju ravnomjerno kretanje je moguće samo prema dolje).
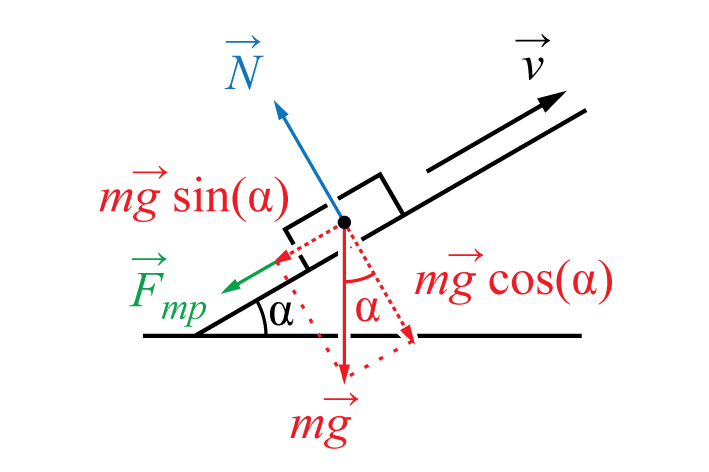
Sile koje djeluju na blok
klizanje po kosoj ravni:
gore slučaj usporenog snimanja
Ovo, po njegovom mišljenju, mora biti hiperbola da bi uglovi vida bili jednaki. Prave i hiperbolične linije biće prikazane paralelno sa beskonačnošću; a ako se doda suprotna poluhiperbola, imaćemo tri reda stabala, a sva tri su paralelna. Takođe nije potrebno da ova druga hiperbola bude suprotna prvoj, tj. e. iste vrste ili imaju istu poprečnu osu: Ovo je dovoljno ako ima isti centar, njegov vrh u istoj desnoj liniji i istu konjugiranu osu.
Dakle, dvije hiperbole mogu biti različite opcije; ali svi imaju isti efekat. Varignon kaže da ako Redukcija bude u određenom omjeru, koji on određuje; druga linija mora biti paralelna sa pravom linijom. Ali on ide još dalje; i pod pretpostavkom da prvi red ima bilo kakvu krivulju, traži drugu koja će učiniti da redovi imaju željeni efekat, tj. e. vidljivo pod bilo kojim uglom, jednakim, rastućim ili opadajućim. Mariotte i pokazao da dodaje "Obračun centra udaraljki" Galilejevom sistemu. - Poređenje centara gravitacije sa centrima udaraljki daje odličan pregled; i stavio celu Doktrinu u najprijatnije Svetlo.
Međutim, tijelo može voziti i po kosoj ravni. Primjer takvog pokreta je kretanje hokejaškog paka po ledenom toboganu. Kada se tijelo kreće prema gore, i sila trenja i komponenta gravitacije "vuče" su usmjerene naniže duž nagnute ravni. U ovom slučaju uvijek imamo posla s ravnomjerno usporenim kretanjem, jer je ukupna sila usmjerena u smjeru suprotnom brzini. Izraz za ubrzanje za ovu situaciju dobija se na sličan način i razlikuje se samo po predznaku. Dakle za tijelo koje klizi prema nagnutoj ravni , imamo:
a x= g(grijeh( α
) + µ
cos( α
)).
id="tabs-1">
Ovaj model je animirani dijagram klasične škole laboratorijski rad u fizici, za proučavanje ubrzanog kretanja tijela pod djelovanjem nekoliko sila na nagnutu ravan.
U ovom modelu možete postaviti sljedeće vrijednosti:
- Visina/ugao nagnute ravni (crvena tačka);
- Koeficijent trenja klizanja šipke po površini (gornji klizač);
- Početni položaj tijela (plava tačka M);
- Položaj senzora štoperice (crveni trokuti S 1 i S 1);
- Zastava za prikaz vektora sila koji djeluju na tijelo.
- Ugao nagiba nagnute ravni;
- Vrijeme kretanja tijela od prvog senzora štoperice do drugog:
- Prilikom računanja vremena ono se umjetno uvodi greška mjerenja vremena, distribuira se po normalnom zakonu!
- Koordinate senzora;
- Koordinate početne pozicije šipke;
- Konstruisani su vektori sila koje deluju na telo.
Upravljanje interaktivnim modelom
- Promjena skale: "CTRL + točak miša" ili "CTRL + "+""–"CTRL + "-""
- Promjena pozicije: prevucite držeći "CTRL + lijevi taster miša"
- Izbrišite sve "tragove": CTRL+F»
Preuzmite model
Varignon, uprkos činjenici da ima problema povezanih sa dijalektičkim poremećajima, popuni tablu donatora i odredi kvantitativna karakteristika. Vozilo u kojem možete pronaći tačne podatke koji se mogu koristiti za sigurnost i zaštitu od nezgoda.
Dakle, čini se da Galileov prijedlog i u ovom slučaju propada, a ipak ima dobre rezultate; samo sa nekim ograničenjem. Varignon je pokušao da razjasni šta je povezano sa brzinama padajućih tela; i postavio cijelu Majku u novo svjetlo: on i dalje vjeruje u prvi Galilejev sistem, da su brzine u drugačije vrijeme vertikalni pad - to je poput korijena odgovarajućih visina.
Modeli označeni sa © CC-BY-SA su autori pojedinaca navedenih na sajtu. Interaktivni modeli distribuirani pod licencom Creative Commons Attribution-Share Like 3.0
Attribution-Dijeli pod istim uvjetima (by-sa)- Licenca "Sa naznakom autorstva - Copyleft". Ova licenca omogućava drugima da prerađuju, ispravljaju i razvijaju djelo, čak i u komercijalne svrhe, pod uslovom da se da atribucija i da su izvedena djela licencirana pod sličnim uslovima. Ova licenca je copyleft licenca. Svi novi radovi zasnovani na onima licenciranim po njoj će imati istu licencu, tako da će se sva izvedena dela moći modifikovati i koristiti u komercijalne svrhe. Prilikom reprodukcije djela koja se distribuiraju pod ovom licencom, obavezan je link na stranicu!
Preuzmite model
Veliki Princip koristi da postigne svoj Kraj, ovo je složeni pokret. Varinon iz sastava ovih pokreta pokazuje da Telo, kada se susreće sa drugim Planom, gubi svoju brzinu; a posledica činjenice da na kraju jeseni neće biti isti kao što bi bio da je pao, produžila je prvu ravan: tako da "Procenat visinskih korena" koji je tvrdio Galileo ovde ne funkcioniše.
Razlog za gubitak brzine je taj što kretanje koje je bilo paralelno s prvom ravninom postaje koso u odnosu na drugu kako stvaraju ugao: to je kretanje koje je koso u odnosu na drugu ravninu, jer se zamišlja kao otežano da dio okomit na avion je izgubljen zbog svojih suprotnosti, kao i dio brzine zajedno s njim: Odnosno, što je ugao tupiji, tijelo manje gubi brzinu.
id="tabs-2">
Pitanja za samoispitivanje na temu "Kosa ravan"
- Kada je kretanje po nagnutoj ravni ravnomjerno sporo?
- Kada tijelo jednoliko klizi niz nagnutu ravan?
- Pri kojim vrijednostima ugla nagiba šipka može počivati na nagnutoj ravni?
- Zašto je pogodno odabrati kosi koordinatni sistem za nagnutu ravan?
- Kolika je sila trenja koja drži blok u mirovanju?
- Što se događa sa silom reakcije oslonca kada se kut nagiba poveća?
- Može li se tijelo ravnomjerno kretati po kosoj ravni?
          |
Slajdovi i tekst ove prezentacije
slajd 1
slajd 2
Plan za rješavanje zadataka u dinamici
1. Napravite crtež na kojem će se naznačiti smjer koordinatnih osa, ubrzanje i sve sile koje se primjenjuju na tijelo.
2. Za svako tijelo zapišite u vektorskom obliku jednadžbu drugog Newtonovog zakona, navodeći na njegovoj desnoj strani bilo kojim redom sve sile koje djeluju na tijelo
3. Zapišite jednačine dobijene u paragrafu 2 u projekciji na koordinatne ose.
5. Naći brojčanu vrijednost nepoznate veličine, ako to zahtijeva uvjet zadatka.
4. Iz rezultirajuće jednačine (sistema jednačina) izraziti nepoznata količina.
Školski pomoćnik "misteriozni konus" tipičan je pomagač koji će očarati široku okolinu. Međutim, ako ne želite da se ova pomoć ne sviđa vašim učenicima, imate dvije opcije: nabavite sponzora da kupi ili kupite ruku pomoći od svega što možete pronaći u školi. Ovaj bi vam članak trebao pomoći ako odaberete drugu opciju. Ako želite da napravite ovu pomoć, najbolje je da počnete tako što ćete odbaciti pomoć koju ste napravili i napraviti tačnu kopiju.
Pretpostavimo da smo napravili dvodimenzionalne korijene poznate veličine i tkanja, od kojih želimo stvoriti nagnutu ravan za kretanje s dva oka. Najlakši način za sastavljanje ovog šapavog materijala možete vidjeti na slici. Naš cilj je da dobijemo željene parametre iz poznatih parametara. Ako pobliže pogledamo kretanje dvojnika po nagnutoj ravni i snimimo kretanje njegovog testa, dobićemo sliku.
slajd 3
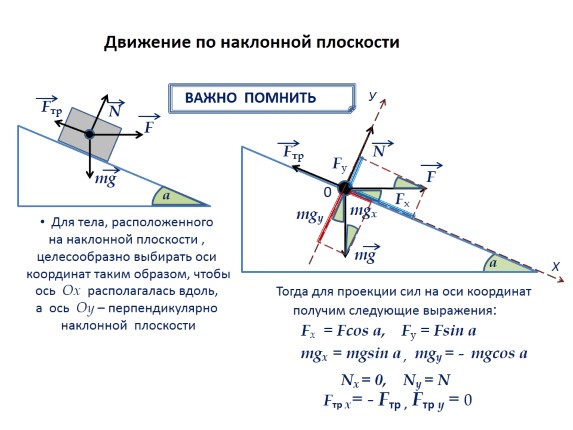
Kretanje po kosoj ravni
VAŽNO ZAPAMTITI
mg
N
F
Ftr.
Za tijelo koje se nalazi na kosoj ravni, preporučljivo je odabrati koordinatne ose na način da se os Ox nalazi duž, a os Oy okomita na nagnutu ravninu.
a
Tada za projekciju sila na koordinatne ose dobijamo sledeće izraze:
Fx. = Fcos a, Fu = Fsin a
mgx. = mgsin a, mgy = - mgcos a
Nx = 0,
Ny=N
Ftr x= - Ftr., Ftr y = 0 .
Za naredne proračune i odgovore svaki od segmenata označavamo na sljedeći način. Da bi se dvokrilac pomerio "gore" po kosoj ravni, mora da padne njegova tama. Stoga možemo proizvoljno definirati vrijednost Δ u ovom rasponu. Shvatimo, međutim, da promjenom proreza on smanjuje ne samo ugao δ, već i ugao γ. Ugao δ je naš parametar, koji karakterizira brzinu kretanja dvoglavog tipa.
Pokažimo valjanost ovih simpatija i šablona za slučaj prikazan na slici. Naravno, zbog opće valjanosti popusta i kalkulacija, veličine se mogu mijenjati prema raspoloživom materijalu, tako da možemo doprinijeti gotovo bilo kojoj veličini.
slajd 4
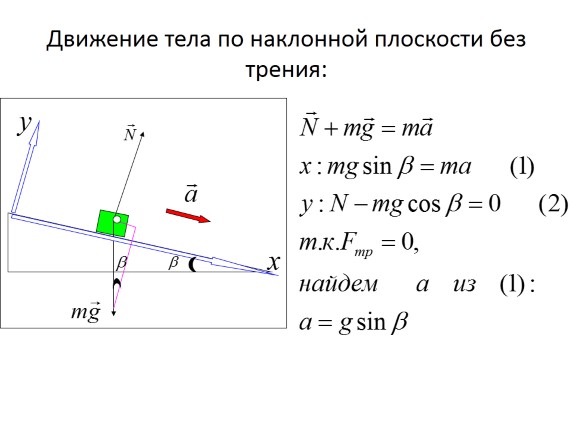
Kretanje tijela po kosoj ravni bez trenja:
slajd 5
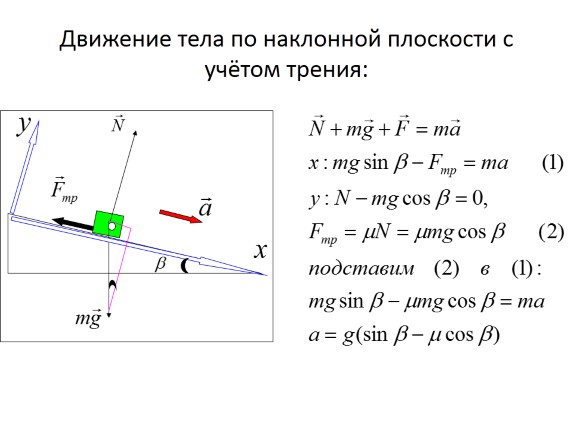
Kretanje tijela duž nagnute ravni, uzimajući u obzir trenje:
slajd 6
a
β
m1g
m2g
N1
N2
T
T
At
At
X
X
a
a
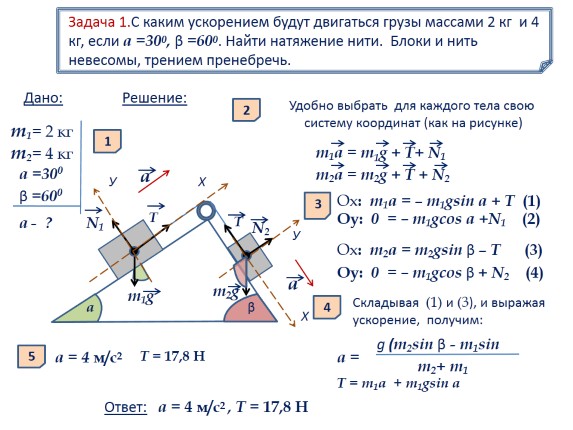
Zadatak 1. Kojim ubrzanjem će se kretati tereti masa 2 kg i 4 kg, ako je a = 300, β = 600. Pronađite napetost niti. Blokovi i konac su bestežinski, trenje je zanemareno.
m1= 2 kg
m2= 4 kg
Dato:
a = 300
β=600
a - ?
Rješenje:
1
2
Pogodno je odabrati za svako tijelo vlastiti koordinatni sistem (kao na slici)
m1a = m1g + T + N1
m2a = m2g + T + N2
3
Ox: m1a \u003d - m1gsin a + T (1)
Oy: 0 = - m1gcos a + N1 (2)
Ox: m2a = m2gsin β – T (3)
Oy: 0 = – m1gcos β + N2 (4)
4
Zbrajanjem (1) i (3) i izražavanjem ubrzanja dobijamo:
g (m2sin β - m1sin
Uz pretpostavku o stanju i općem rješenju, nazovimo unutrašnju udaljenost rešetke Δ = 150 mm. Za uslov treba da izaberemo ugao δ, koji karakteriše ubrzanje dvostruke krive na kosoj ravni. Tako imamo potrebne prekretnice i možemo ući u zgradu. Većina materijala se može naći kod nastavnika škole ili kod drugih instruktora ili učenika. Problematična oblast je proizvodnja dvostrukih oštrica. Za lijepljenje je korišteno epoksidno ljepilo. No, prava "zlatna zvijezda" okrenula je dvojnika.
Ne radi se čak ni na proizvodu, kao što je vezivanje za strug. Ako budete imali sreće, naići ćete na strug sa škarama koji će vam pomoći s jednostavnim alatima i može sve to podesiti. Preostala pomoć se mora dodati ratu koji ide prema dolje. Ili ćemo ga ponovo izgraditi, ili ćemo koristiti bilo koju rundu, ali bolje je pokupiti konus.
a =
m2+ m1
T = 17,8 H
T = m1a + m1gsin a
5
a = 4 m/s2
Odgovor: a \u003d 4 m / s2, T \u003d 17,8 H
Slajd 7
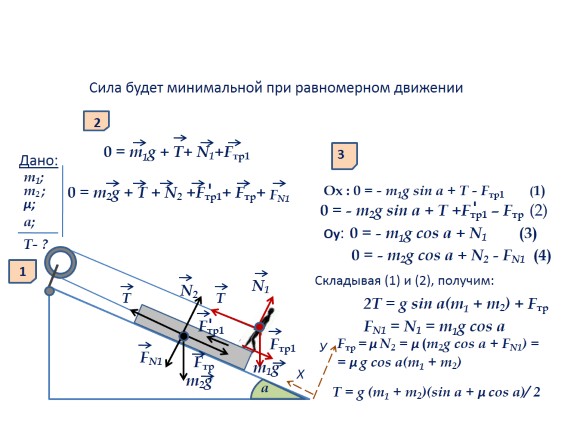
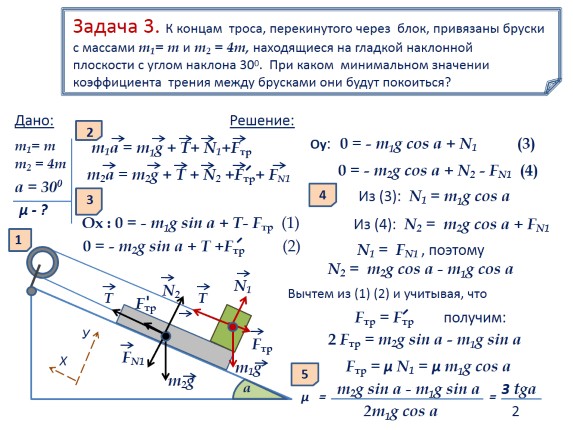
Zadatak 2. Čovjek mase m1, oslonjen nogama na kutiju mase m2, povlači je užetom prebačenim preko bloka duž nagnute ravni sa uglom nagiba a. Koja je minimalna sila potrebna za povlačenje užeta da bi se kutija povukla do bloka? Koeficijent trenja između jezgre i nagnute ravni μ






