Corpuscular-wave duality of light

Light is emitted, propagated and absorbed in the form of corpuscles - photons, which are particles of the electromagnetic field and carriers of quanta (portions) of energy. The value of the quantum of energy is determined by Planck's formula: Corpuscular characteristics of a photon () are supplemented by wave characteristics (), which confirms Bohr's complementarity principle.

Bothe's experience (1924). In this experiment, a thin metal foil F was illuminated by low-intensity X-rays, which caused weak X-ray fluorescence (afterglow) in the foil. X-ray radiation from the foil fell on two counters of ionizing radiation, Cch1 and Cch2 (Geiger counters). The sensitivity of such counters is so high that they can register individual x-ray quanta. When triggered, the counters actuated the mechanisms of the recorders M1 and M2, which make marks on the moving tape L. As a result, it was found that the marks on the tape from two recorders, associated with the moments of X-ray quanta hitting the counters, are absolutely random. This fact could only be explained by the random hit of X-ray quanta scattered by the foil either in one or the other direction, whereas, according to wave concepts, the radiation from the source should propagate uniformly in all directions.

Energy, mass and momentum of a photon.

Light is emitted, absorbed and propagated in discrete portions (quanta) called photons. Photon energy. Its mass is found from the law of the relationship between mass and energy: . Photon - elementary particle, which always (in any medium) moves at a speed c and has a rest mass equal to zero. Consequently, the mass of the photon differs from the mass of such el-tar particles as the electron, proton and neutron, which have a non-zero rest mass and can be at rest. The momentum of a photon is obtained if general form theory of relativity (E - total energy) put the rest mass of the photon: . Therefore, a photon, like any other particle, is characterized by energy, mass and momentum.

Photoelectric effect.

Planck's hypothesis, which solved the problem of the thermal radiation of a black body, was confirmed and further developed in explaining the photoelectric effect - a phenomenon whose discovery played an important theory in the development of quantum theory. There are external, internal and valve photoelectric effect. external photoelectric effect is called the emission of electrons in-tion under the influence of electromagnetic radiation (light). It is observed in solids(metals, semiconductors, dielectrics), as well as in gases on individual atoms and molecules. Internal photoelectric effect- These are the transitions of electrons inside a semiconductor or dielectric caused by electromagnetic radiation from bound states to free ones without escaping to the outside. In p-tate, the concentration of current carriers inside the body increases, which leads to the appearance of photoconductivity (an increase in the electrical conductivity of a semiconductor or dielectric when it is illuminated) or the appearance of an EMF. valve photoelectric effect- the occurrence of EMF (photo-EMF) when illuminating the contact of two different semiconductors or a semiconductor and a metal (in the absence of an external electric field). With the help of valve photoelectric effect, it is possible to directly convert solar energy into electrical energy. Einstein's equation for the external photoelectric effect: The energy of the incident photon is spent on doing the work of exit from the metal and on communicating kinetic energy to the photoelectron. According to the law of conservation of energy, .

The Compton effect and its theory.

In the Compton effect, the corpuscular properties of light are most fully manifested. Investigating the scattering of monochromatic X-ray radiation by substances with light atoms, Compton found that in the composition of the scattered radiation, along with the radiation of the initial wavelength, radiation of longer wavelengths is also observed. Experiments have shown that the difference Δλ \u003d λ '-λ does not depend on the wavelength λ of the incident radiation and the nature of the scattering substance, but is determined only by the magnitude of the scattering angle , where is the wavelength of the scattered radiation, is the Compton wavelength (when a photon is scattered by an electron = 2,426nm). The Compton effect is called the elastic scattering of short-wavelength radiation (X-ray and γ-radiation) on free (or weakly bound) electrons in the islands, accompanied by an increase in wavelength. If you count how it does quantum theory that radiation has a corpuscular nature, i.e. represents a stream of photons, then the Compton effect is the p-tat of the elastic collision of X-ray photons with free electrons in the islands (for light atoms, electrons are weakly bound to the nuclei of atoms, so they can be considered free). During this collision, the photon transfers part of its energy and momentum in accordance with the laws of their conservation.

The Compton effect cannot be observed in the visible region of the spectrum, since the photon energy visible light is comparable to the binding energy of an electron with an atom, and even the outer electron cannot be considered free. Eph. K. is observed not only in electrons, but also on charged particles, such as protons, however, due to the large mass of the proton, its recoil is “visible” only when photons of very high energies are scattered. Like ef. K. and the photoelectric effect based on quantum concepts are due to the interaction of photons with electrons. In the first case, the photon is scattered, in the second, it is absorbed. Scattering occurs when a photon interacts with a free electron, and the photoelectric effect with bound electrons. When a photon collides, as this is in conflict with the laws of conservation of momentum and energy. Therefore, when photons interact with free electrons, only their scattering can be observed, i.e. Compton effect.

Bremsstrahlung radiation.

An electron moving in some medium loses its speed. This creates a negative acceleration. According to Maxwell's theory, any accelerated the movement of a charged particle is accompanied by electromagnetic radiation. The radiation that occurs when an electron decelerates in the anode material is called bremsstrahlung X-rays.

Light pressure.

If the photon has momentum, then the light falling on the body must exert pressure on it. From the point of view of quantum theory, the pressure of light on the repetition is due to the fact that each photon, when colliding with the repetition, transfers its momentum to it. Let us calculate, from the point of view of quantum theory, the light pressure exerted on the surface of the body by a stream of monochromatic radiation (frequency ν) incident perpendicular to the surface. If N photons fall per unit time per unit area of ​​the surface of the body, then with a reflection coefficient ρ of light, ρ will be reflected from the surface of the body N photons, and (1− ρ )N- will be absorbed. Each absorbed photon transmits a second impulse , and each reflected - 2 =2 hν / c(when reflected, the momentum of a photon changes to ). The pressure of light on the loop is equal to the momentum that is transmitted by loops in 1 s of N photons:

is the energy of all photons falling per unit rep per unit time, i.e. energy illumination of the area, a / c=ω - volume density of radiation energy. Therefore, the pressure produced by light during normal incidence on the surface, .

6. Atomic spectra. serial formulas. Rutherford's experience. Bohr's postulates. The Frank-Hertz experiment. Elementary theory of the hydrogen atom. Significance of Bohr's theory. X-ray characteristic spectra. Moseley's law.

Atomic spectra.serial formulas.

Studies of the emission spectra of rarefied gases (i.e., the emission spectra of individual atoms) have shown that each gas has a well-defined line spectrum, consisting of individual spectral lines or groups of closely spaced lines. The most studied is the spectrum of the simplest atom - the hydrogen atom. Balmer (1825-1898) picked up an empirical formula describing all known at that time spectral lines hydrogen atom and the visible region of the spectrum ,(n = 3, 4, …) where R"is the Rydberg constant. Since ν = With/λ , then the f-la can be rewritten for frequencies: , where R= R"c is also the Rydberg constant. It follows from the obtained expressions that the spectral lines differing in different values ​​of n form a group or a series of lines, called the Balmer series. As n increases, the lines of the series approach each other; the value n = ∞ determines the boundary of the series, to which the continuous spectrum adjoins from the side of high frequencies. Subsequently, several more series were discovered in the spectrum of the hydrogen atom.

In the ultraviolet region of the spectrum is

Lyman series:

In the infrared region were found:

Paschen series:

bracket series:

Pfund series:

Humphy series:

All the above series in the spectrum of the hydrogen atom can be described by one f-loop, called the generalized Balmer f-loop: , where m has a constant value in each given series, m = 1, 2, 3, 4, 5, 6 (defines series), n - takes integer values, starting from m + 1 (defines the individual lines of this series).

Rutherford's experience.

In the development of ideas about the structure of the atom, the importance of Rutherford's experiments on the scattering of α-particles in matter. Alpha particles arise from radioactive transformations; they are positive charged particles with a charge of 2e and a mass approximately 7300 times greater than the mass of an electron. Beams of α-particles are highly monochromatic (for a given transformation they have practically the same speed (of the order of 10^7 m/s)). Rutherford, investigating the passage of α-particles in v-ve (through gold foil approximately 1 μm thick), showed that most of them experience minor deviations, but some α-particles (about one in 20,000) deviate sharply from their original direction (deflection angles even reached 180°). Because electrons cannot significantly change the motion of such heavy and fast particles as α-particles, then Rutherford concluded that the significant deviation of α-particles is due to their interaction with a positive charge of a large mass. However, only a few α particles experience significant deflection; therefore, only some of them pass near a given positive charge. This in turn means that positive charge of an atom is concentrated in a volume very small compared to the volume of an atom. Based on his experiments, Rutherford proposed a nuclear model of the atom. According to this model, put around the serial number of el-ta in the Mendeleev system, e is an elementary charge), the size is 10^(−15) −10^(−14) m and a mass practically equal to the mass of an atom, in a region with linear dimensions of the order 10^(−10) m electrons move in closed orbits, forming electron shell atom. Since the atoms are neutral, then the charge of the nucleus is equal to the total charge of the electrons, i.e. Z electrons must revolve around the nucleus.

Bohr's postulates.

The first attempt to build a qualitatively new - quantum - theory of the atom was undertaken by Bohr. He set himself the goal of linking into a single whole the empirical patterns of line spectra, Rutherford's nuclear model of the atom (According to this model, around a positive nucleus with a charge Ze (Z is the serial number of the element in the Mendeleev system, e is the elementary charge), size 10 ^(−15) −10^(−14) m and a mass practically equal to the mass of an atom, electrons move in closed orbits in a region with linear dimensions of the order of 10^(−10 m), forming the electron shell of an atom. Since atoms are neutral, then the charge of the nucleus is equal to the total charge of the electrons, i.e. Z electrons must rotate around the nucleus) and the quantum nature of the emission and absorption of light. Two postulates:

Bohr's first postulate(postulate of stationary states): there are stationary states in the atom in which it does not radiate energy. Stationary states of an atom correspond to stationary orbits along which electrons move. The motion of electrons in stationary orbits is not accompanied by the emission of electromagnetic waves. In the stationary state of an atom, an electron moving along a circular orbit must have discrete quantum values ​​of the angular momentum that satisfy the condition (n=1,2,3,…), where - mass of the electron, v - its speed along the n-th orbit of radius , = h/ 2π .

Second postulate(frequency rule): when an electron moves from one stationary orbit to another, one photon with energy is emitted (absorbed) equal to the energy difference of the corresponding stationary states ( and -- respectively, the energy of the stationary states of the atom before and after radiation (absorption)). At< a photon is emitted (the transition of an atom from a state with a higher energy to a state with a lower one, i.e. the transition of an electron from an orbit more distant from the nucleus to a nearby one), at > - its absorption (the transition of an atom to a state with a higher energy, i.e. the transition of an electron to an orbit more distant from the nucleus). The set of all possible discrete frequencies ν=( −)/h quantum transitions and determines the line spectrum of the atom.

The Frank-Hertz experiment.

By studying the method of retarding potential collisions of electrons with atoms of gases, it was experimentally proved that the values ​​of the energy of atoms are discrete. A schematic diagram of their installation is shown in fig. A vacuum tube filled with mercury vapor (pressure approximately equal to 13 Pa) contained a cathode (K), two grids (i) and an anode (A). The electrons emitted by the cathode were accelerated by the potential difference applied between the cathode and the grid. A small (about 0.5 V) retarding potential is applied between the grid and the anode. Electrons accelerated in region 1 enter region 2 between the grids, where they experience collisions with mercury vapor atoms. Electrons which, after collisions, have sufficient energy to overcome the retarding potential in region 3 reach the anode. In inelastic collisions of electrons with mercury atoms, the latter can be excited. According to Bohr's theory, each of the mercury atoms can receive only a very definite energy, while passing into one of the excited states. From experience it follows that with an increase in the accelerating potential up to 5 V, the anode current increases monotonically, its value passes through a maximum, then sharply decreases and increases again.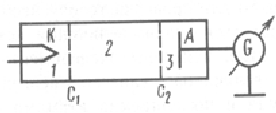

Moseley's law.

In 1913 English physicist Moseley measured wavelengths x-rays emitted by different metals in the cathode tube and plotted the reciprocal of the square root of the X-ray wavelength versus the element's atomic number. This graph (Fig. 1) shows that the serial number reflects some important characteristic of the element. Moseley suggested that this characteristic is the charge of the nucleus of an atom, and that it increases by one when moving from one element to the next one in order. He called the serial number atomic number - Z.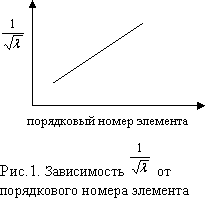

Moseley's law:

The square root of the reciprocal of the wavelength of X-rays emitted by atoms various elements, is in linear dependence from the serial number of the element. where is the wavelength, is a constant value, Z is the ordinal number of the element (nuclear charge).

Later it became known that the serial number is equal to the number of protons in the nucleus. Thus, the ordinal (atomic) number is equal to the charge of the nucleus and it also determines the presence of protons (positive particles) in it. And since atoms are neutral, the number of electrons in an atom must be equal to the number of protons. But the masses of atoms turned out to be greater than the total mass of protons. To explain the excess mass, the existence of neutrons was suggested.

7. De Broglie wavelength. Experimental substantiation of wave dualism. The Heisenberg uncertainty relation. Wave function and its statistical meaning. Schrödinger equation. Eigenfunctions and eigenvalues. Stationary Schrödinger equation. Quantum mechanical representation of a freely moving particle. Quantum mechanical description of a particle in an infinitely deep rectangular potential well.

De Broglie wavelength.

The French scientist Louis de Broglie (1892-1987), realizing the symmetry existing in nature and developing ideas about the dual corpuscular-wave nature of light, put forward in 1923 a hypothesis about universality of corpuscular-wave dualism. De Broglie argued that not only photons, but also electrons and any other particles of matter, along with corpuscular ones, also have wave properties. So, according to de Broglie, each micro-object connected, on the one hand, corpuscular characteristics - energy E and momentum p, and on the other hand, wave characteristics- frequency v and wavelength TO. Quantitative ratios connecting corpuscular and wave properties particles are the same as for photons: Thus, any particle with momentum is associated with a wave process with a wavelength determined by according to the de Broglie formula: This relation is valid for any particle with momentum R.

Experimental substantiation of wave dualism.

Soon de Broglie's hypothesis was confirmed experimentally. In 1927, the American physicist and K. Davisson (1881 - 1958) and L. Germer (1896 - 1971) discovered that an electron beam scattered from a natural diffraction grating - a nickel crystal - gives a distinct diffraction pattern. The diffraction maxima corresponded to the Wulff-Braggs formula (182.1), and the Bragg wavelength turned out to be exactly equal to the length wave, calculated by the formula. Later, de Broglie's formula was confirmed by the experiments of P. S. Tartakovsky and G. Thomson, who observed the diffraction pattern during the passage of a beam of fast electrons (energy "50 keV) through a metal foil (thickness x 1 micron). Since the diffraction pattern was studied for the flow of electrons, it was necessary to prove that the wave properties are inherent not only in the flow of a large set of electrons, but also in each electron separately. This was experimentally confirmed in 1948 by the Soviet physicist V. A. Fabrikant (b. 1907). He showed that even in the case of such a weak electron beam, when each electron passes through the device independently of the others (the time interval between two electrons is 10^4 times longer than the time the electron passes through the device), the diffraction pattern that occurs during long exposure does not differ from the diffraction patterns obtained with a short exposure for electron flows tens of millions of times more intense. Consequently, the wave properties of particles are not a property of their collective, but are inherent in each particle separately. Subsequently, diffraction phenomena were also discovered for neutrons, protons, atomic and molecular beams. This finally served as a proof of the presence of wave properties of microparticles and made it possible to describe the movement of microparticles in the form of a wave process characterized by a certain wavelength calculated by the de Broglie formula. The discovery of the wave properties of microparticles led to the emergence and development of new methods for studying the structure of substances, such as electron diffraction and neutron diffraction, as well as to the emergence of a new branch of science - electron optics.

The Heisenberg uncertainty relation.

According to the dual corpuscular-wave nature of matter particles, either wave or corpuscular representations are used to describe microparticles. Therefore, it is impossible to attribute to them all the properties of particles and all the properties of waves. V. Heisenberg, taking into account the wave properties of microparticles and the limitations in their behavior associated with wave properties, came to the conclusion in 1927 that it is impossible to characterize an object of the microworld simultaneously with any predetermined accuracy by both coordinate and momentum. According to the Heisenberg uncertainty relation, a microparticle (microobject) cannot simultaneously have a certain coordinate (x, y, z), and a certain corresponding momentum projection (px, ru, rg), moreover, the uncertainties of these quantities satisfy the conditions, i.e. the product of a coordinate and the corresponding momentum projection cannot be less than a value of the order h. It follows from the uncertainty relation that, for example, if a microparticle is in a state with an exact value of the coordinate (), then in this state the corresponding projection of its momentum turns out to be completely uncertain, and vice versa. Thus, for a microparticle there are no states in which its coordinates and momentum would have both exact values. This implies the actual impossibility to simultaneously measure the coordinate and momentum of a micro-object with any predetermined accuracy. Since in classical mechanics it is assumed that the measurement of position and momentum can be made with any accuracy, then the uncertainty relation is, thus, quantum limitation of the applicability of classical mechanics to micro-objects.

Wave function and its statistical meaning.

The German physicist M. Born in 1926 suggested that, according to the wave law, it is not the probability itself that changes, but the quantity called probability amplitude and denoted This value is also called wave function(or -function). The probability amplitude can be complex, and the probability W proportional to the square of its modulus: is a function complex conjugate to ). Thus, the description of the state of a microobject with the help of the wave function has statistical, probabilistic character: the square of the modulus of the wave function (the square of the modulus of the amplitude of the de Broglie waves) determines the probability of finding a particle at a time in the region with coordinates

Schrödinger equation.

Basic Equation non-relativistic quantum mechanics formulated in 1926 by E. Schrödinger. The Schrödinger equation, like all the basic equations of physics (for example, Newton's equations in classical mechanics and Maxwell's equations for the electromagnetic field), is not derived, but postulated. The correctness of this equation is confirmed by the agreement with the experience of the results obtained with its help, which, in turn, gives it the character of a law of nature. The Schrödinger equation has the form: , where m is the mass of the particle, is the Laplace operator, i- imaginary unit, U(x, y, z, t) -potential function of a particle in the force field in which it moves Ψ (x, y, z, t) is the desired wave function of the particle.

Eigenfunctions and eigenvalues. Stationary Schrödinger equation.

The equation called Schrödinger equation for stationary states. This equation includes the total energy as a parameter E particles. In the theory of differential equations, it is proved that such equations have an infinite set of solutions, from which, by imposing boundary conditions, solutions are selected that have physical meaning. For the Schrödinger equation, such conditions are the conditions of regularity of the wave functions: the wave functions must be finite, single-valued, and continuous together with their first derivatives. Thus, only solutions that are expressed by regular functions have real physical meaning y. But regular solutions do not take place for any values ​​of the parameter E, but only for a certain set of them, characteristic of a given task. These energy values ​​are called own. Solutions that match own energy values ​​are called own functions. Eigenvalues E can form both continuous and discrete series. In the first case, one speaks of continuous, or continuous, spectrum, in the second - about the discrete spectrum.

Quantum mechanical representation of a freely moving particle.

When a free particle moves (U(x) = 0) its total energy coincides with the kinetic one. For a free particle moving along the axis X, the Schrödinger equation for stationary states takes the form .Direct substitution can make sure that a particular solution of equation i is a function, where A=const and k = const, with energy eigenvalue The function is only the coordinate part of the wave function. Therefore, the time-dependent wave function, according to , (219.3) (here The function is a plane monochromatic de Broglie wave). It follows from the expression that the dependence of energy on momentum turns out to be common for nonrelativistic particles. Consequently, the energy of a free particle can take on any values ​​(since the wave number k can take any positive values), i.e. its energy spectrum is continuous. Thus, a free quantum particle is described by a plane monochromatic de Broglie wave. This corresponds to a time-independent probability density of detecting a particle at a given point in space.

Quantum mechanical description of a particle in an infinitely deep rectangular potential well.

Let us carry out a qualitative analysis of the solutions of the Schrödinger equation as applied to a particle in a one-dimensional rectangular "potential well" with infinitely high "walls". Such a “pit” is described by a potential energy of the form (for simplicity, we assume that the particle moves along the axis X) 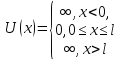where l- the width of the "pit", and the energy is measured from its bottom.

The Schrödinger equation for stationary states in the case of a one-dimensional problem can be written as

. At the boundaries of the "pit" (for x = 0 and x = l) the continuous wave function must also vanish. Therefore, the boundary conditions in this case have the form

General solution of the differential equation: Since . Then Condition performed only when P- integers, i.e. it is necessary that . It follows that i.e., the stationary Schrödinger equation describing the motion of a particle in a "potential well" with infinitely high "walls" is satisfied only for eigenvalues , "depending on an integer P. Consequently, the energy £n of a particle in a "potential well" with infinitely high "walls" takes only certain discrete values, i.e., quantized. Quantized Energy Values called energy levels, and the number P, which determines the energy levels of a particle is called principal quantum number. Thus, a microparticle in a "potential well" with infinitely high "walls" can only be at a certain energy level £n, or, as they say, the particle is in a quantum state P.

Wavelength is the distance between two adjacent points that oscillate in the same phase; as a rule, the concept of "wavelength" is associated with the electromagnetic spectrum. The method for calculating the wavelength depends on this information. Use the basic formula if you know the speed and frequency of the wave. If you need to calculate the wavelength of a light from a known photon energy, use the appropriate formula.

Steps

Part 1

Use the formula to calculate the wavelength. To find the wavelength, divide the speed of the wave by the frequency. Formula:

• In this formula λ (\displaystyle \lambda )(lambda, letter of the Greek alphabet) - wavelength.
• v (\displaystyle v) is the wave speed.
• f (\displaystyle f) is the frequency of the wave.

1. Use the appropriate units of measure. Speed ​​is measured in units metric system, for example, in kilometers per hour (km/h), meters per second (m/s), and so on (in some countries, speed is measured in British system, for example, in miles per hour). Wavelength is measured in nanometers, meters, millimeters, and so on. Frequency is usually measured in hertz (Hz).

   • Units end result must match the units of measurement of the source data.
   • If frequency is given in kilohertz (kHz), or wave speed in kilometers per second (km/s), convert these values ​​to hertz (10 kHz = 10000 Hz) and to meters per second (m/s).

2. Substitute the known values ​​into the formula and find the wavelength. Substitute the values ​​of the speed and frequency of the wave into the above formula. Dividing the speed by the frequency gives you the wavelength.

   • For example. Find the wavelength of a wave propagating at a speed of 20 m/s at an oscillation frequency of 5 Hz.
     • Wave length = Wave speed / Wave frequency
       λ = v f (\displaystyle \lambda =(\frac (v)(f)))
       λ = 20 5 (\displaystyle \lambda =(\frac (20)(5)))
       λ = 4 (\displaystyle \lambda =4) m.

3. Use the formula below to calculate speed or frequency. The formula can be rewritten in a different form and calculate the speed or frequency if the wavelength is given. To find the speed from a known frequency and wavelength, use the formula: v = λ f (\displaystyle v=(\frac (\lambda )(f))). To find the frequency from known speed and wavelength, use the formula: f = v λ (\displaystyle f=(\frac (v)(\lambda ))).

   • For example. Find the speed of wave propagation at an oscillation frequency of 45 Hz, if the wavelength is 450 nm. v = λ f = 450 45 = 10 (\displaystyle v=(\frac (\lambda )(f))=(\frac (450)(45))=10) nm/s.
   • For example. Find the oscillation frequency of a wave whose length is 2.5 m and the propagation speed is 50 m/s. f = v λ = 50 2 , 5 = 20 (\displaystyle f=(\frac (v)(\lambda ))=(\frac (50)(2,5))=20) Hz.

Part 2

1. Calculate the wavelength using the formula for calculating the energy of a photon. Formula for calculating photon energy: E = h c λ (\displaystyle E=(\frac (hc)(\lambda ))), where E (\displaystyle E) is the photon energy, measured in joules (J), h (\displaystyle h)- Planck's constant, equal to 6.626 x 10 -34 J∙s, c (\displaystyle c) is the speed of light in vacuum, equal to 3 x 10 8 m/s, λ (\displaystyle \lambda ) is the wavelength, measured in meters.

   • In the problem, the photon energy will be given.

2. Rewrite the formula presented to find the wavelength. To do this, perform a series of mathematical operations. Multiply both sides of the formula by the wavelength, and then divide both sides by the energy; you will get the formula: . If the energy of a photon is known, the wavelength of light can be calculated.

3. Substitute the known values ​​into the resulting formula and calculate the wavelength. Substitute only the energy value in the formula, because the two constants are constants, that is, do not change. To find the wavelength, multiply the constants and then divide the result by the energy.

   • For example. Find the wavelength of the light if the energy of the photon is 2.88 x 10 -19 J.
     • λ = h c E (\displaystyle \lambda =(\frac (hc)(E)))
       = (6 , 626 ∗ 10 − 34) (3 ∗ 10 8) (2 , 88 ∗ 10 − 19) (\displaystyle (\frac ((6,626*10^(-34))(3*10^(8)) )((2.88*10^(-19)))))
       = (19 , 878 ∗ 10 − 26) (2 , 88 ∗ 10 − 19) (\displaystyle =(\frac ((19.878*10^(-26)))((2.88*10^(-19) ))))
       = 6 , 90 ∗ 10 − 7 (\displaystyle =6.90*10^(-7)) m.
     • Convert the resulting value to nanometers by multiplying it by 10 -9. The wavelength is 690 nm.

Part 3

1. Check the answer. To do this, multiply the wavelength by the frequency. If you get this speed value, the solution is correct; otherwise check the calculations. If you are using a calculator, enter numbers correctly.

   • For example. Find the wavelength that propagates at a speed of 343 m/s at a frequency of 70 Hz.
     • Solve this problem as described above and get a value of 4.9 m.
     • Check your answer: 4.9 m x 70 Hz = 343 m/s. This is the speed given in the condition of the problem, so the solution is correct.

2. Use exponential notation to avoid rounding errors (in a calculator). Sometimes in the calculation of the wavelength involved very big numbers, especially when the speed of light is present. This can lead to rounding errors. Therefore, use exponential notation for numbers.

   • For example. Light travels through water at a speed of 225,000,000 m/s. Find the wavelength of a light wave if its frequency is 4 x 10 14 Hz.
     • Write down the speed of the wave in exponential form: 2.25 x 10 8 . The frequency of the wave is already given in exponential form.
     • λ = v f (\displaystyle \lambda =(\frac (v)(f)))
       = 2 , 25 ∗ 10 8 4 ∗ 10 14 = 2 , 25 4 ∗ 10 6 (\displaystyle =(\frac (2.25*10^(8))(4*10^(14)))=(\ frac(2,25)(4*10^(6))))
       = 0 , 563 ∗ 10 − 6 (\displaystyle =0.563*10^(-6))
     • The frequency will not change and will remain the same f.
     • The new wavelength is: (New speed / New frequency) = v 1 , 5 f = v 1 , 5 f (\displaystyle (\frac (\frac (v)(1,5))(f))=(\frac (v)(1,5f))).

13.2. Light and microparticles as objects of quantum theory

13.2.2. Photons, photon beams

Light - complex phenomenon, which has a dual corpuscular-wave nature.

In some cases, light manifests itself as electromagnetic waves, in others - as a stream of particles - photons.

Photons (quanta of light) are electrically neutral particles propagating in space at the speed of light.

Photons have the following characteristics:

• the rest mass of a photon is zero:

m 0γ = 0;

• photon charge is zero:

q γ = 0;

• the energy of a photon is related to its frequency and wavelength by the formulas:

where ν is the photon frequency, ν = c /λ; c is the speed of light in vacuum, c ≈ 3.0 ⋅ 10 8 m/s; h - Planck's constant, h = 6.626 ⋅ 10 −34 J ⋅ s; λ is the wavelength of the photon;

• photon speed in vacuum equal to the speed of light (in a vacuum):

c = 3 ⋅ 10 8 m/s;

• photon speed in the medium is determined by the relation

• the momentum of a photon is determined by the formulas:

p γ = h ν c ; p γ = h λ .

• mass of a moving photon is determined using the Einstein formula, which establishes the equivalence of the mass m and energy E , i.e. E=mc2:

m γ = E γ c 2 = h ν c 2 , or m γ = E γ c 2 = h λ c .

Photon beam energy(laser pulse) is equal to the sum of the energies of each photon separately:

E ˜ = N E γ ,

The energy of a photon is determined by its frequency (wavelength):

E γ = h ν, E γ = h c λ ,

where ν is the photon frequency, ν = c /λ; c is the speed of light in vacuum; λ is the wavelength of the photon; h is Planck's constant, h = 6.626 ⋅ 10 −34 J ⋅ s.

Pulsed laser energy(the energy of the light beam emitted by the laser) is determined by the product

E = n E˜ ,

where n is the number of pulses emitted by the laser for certain time; E ˜ - energy of one pulse.

Energy of one laser pulse(beam of photons) is equal to the sum of the energies of each photon separately:

E ˜ = N E γ ,

where N is the number of photons in the beam; E γ - energy of one (each) photon.

The energy of a photon is determined by its frequency (wavelength):

E γ = h ν, E γ = h c λ ,

where ν is the photon frequency, ν = c /λ; λ is the wavelength of the photon; c is the speed of light in vacuum; h is Planck's constant, h = 6.626 ⋅ 10 −34 J ⋅ s.

Photon beam power is determined by the relation

P = E ˜ t = N E γ t ,

where E ˜ is the energy of the photon beam (laser pulse), E ˜ = N E γ ; N /t is the number of photons emitted by the laser every second; E γ - photon energy, E γ = h ν = hc /λ; ν is the photon frequency; λ is the wavelength of the photon; c is the speed of light in vacuum; h - Planck's constant, h = 6.626 ⋅ 10 −34 J ⋅ s; t is the time during which the photon beam is emitted.

Pulsed laser power(the power of the light beam emitted by the pulsed laser) is determined by the relation

P = E t = n E ˜ t ,

where n /t is the number of pulses emitted by the laser every second; E ˜ - energy of one pulse, E ˜ = N E γ ; N is the number of photons in the beam; E γ - photon energy, E γ = h ν = hc /λ; ν is the photon frequency; λ is the wavelength of the photon; c is the speed of light in vacuum; h is Planck's constant, h = 6.626 ⋅ 10 −34 J ⋅ s.

Coefficient useful action ( Efficiency ) of the laser connects electrical power laser and the power of the photon beam (power of the light beam) emitted by the laser:

η = P sv P el ⋅ 100% ,

where P St is the power of the light beam; P el - electrical (consumed) power of the laser.

AT quantum physics it turns out to be convenient to measure the energy in electronvolts: 1 electronvolt (1 eV) is equal to the energy of an electron that has passed a potential difference of 1 volt (1 V):

1 eV = 1.6 ⋅ 10 −19 C ⋅ 1 V = 1.6 ⋅ 10 −19 J.

Energy transfer is carried out according to the following formulas:

• from electronvolts to joules (SI) -

E (eV) ⋅ 1.6 ⋅ 10 −19 = E (J),

where E (eV) - energy in electron volts; E (J) - energy in joules;

• from joules (SI) to electronvolts -

E (J) 1.6 ⋅ 10 − 19 = E (eV) .

In calculations, the Planck constant h = 6.626 ⋅ 10 −34 J ⋅ s should be taken with an accuracy corresponding to the accuracy of the rest of the data of the problem being solved.

Example 3. Determine the wavelength of a photon whose energy is equal to the kinetic energy of an electron that has passed a potential difference of 6.6 V.

Solution . The photon and electron energies are determined by the following formulas:

• photon -

E γ = h c λ ,

where h is Planck's constant, h = 6.6 ⋅ 10 −34 J ⋅ s; c is the speed of light in vacuum, c = 3.0 ⋅ 10 8 m/s; λ is the wavelength of the photon;

• an electron that has passed the indicated potential difference, -

E e = | q e | Δφ ,

where q e is the electron charge, q e = −1.6 ⋅ 10 −19 C; Δφ - potential difference, Δφ = 6.6 V.

According to the condition of the problem, the energies of an electron and a photon are:

E e = E γ ,

or explicitly

| q e | Δφ = h c λ .

We express from here the desired wavelength of the photon:

λ = h c | q e | Δφ.

Let's calculate:

λ = 6.6 ⋅ 10 − 34 ⋅ 3.0 ⋅ 10 8 1.6 ⋅ 10 − 19 ⋅ 6.6 = 1.9 ⋅ 10 − 7 m = 0.19 µm.

The photon wavelength is 0.19 µm.

Example 4. At what temperature is the average kinetic energy thermal motion of an ideal monatomic gas molecule is equal to the energy of a photon with a wavelength of 3.31 ⋅ 10 −6 m?

Solution . The average kinetic energy of the thermal motion of an ideal monatomic gas molecule is determined by the expression

E mol \u003d 3 2 k T ,

where k is the Boltzmann constant, k = 1.38 ⋅ 10 −23 J/K; T is the required gas temperature.

The energy of a photon with a certain wavelength is the ratio

E γ = h c λ ,

where h is Planck's constant, h ≈ 6.63 ⋅ 10 −34 J ⋅ s; c is the speed of light in vacuum, c ≈ 3.00 ⋅ 10 8 m/s; λ is the wavelength of the photon, λ = 3.31 ⋅ 10 −6 m.

According to the condition of the problem, the average kinetic energy of the thermal motion of a molecule of an ideal monatomic gas and the energy of a photon are equal to:

E mol \u003d E γ,

or explicitly

3 2 k T = h c λ .

The desired temperature is determined by the expression

T = 2 h c 3 λ k .

The calculation gives the value:

T = 2 ⋅ 6.63 ⋅ 10 − 34 ⋅ 3.00 ⋅ 10 8 3 ⋅ 3.31 ⋅ 10 − 6 ⋅ 1.38 ⋅ 10 − 23 ≈ 2900 K.

The desired temperature is approximately 2900 K.

Example 5. Bundle laser radiation with a wavelength of 6.63 ⋅ 10 −7 m is used to heat 500 g of water. How long will it take for the water to heat up by 10.0 K if the laser emits 1.00 ⋅ 10 21 photons every second and all of them are absorbed by the water? The specific heat capacity of water is 4.20 ⋅ 10 3 J/(kg ⋅ K).

Solution . To heat water, the amount of heat required is determined by the formula

Q = c sp m ∆T ,

where c ud - specific heat water, c beats = 4.20 ⋅ 10 3 J/(kg ⋅ K); m is the mass of water, m = 500 g; ΔT - change in water temperature, ΔT = 10.0 K.

The laser beam for a certain time transfers to the water an energy equal to the energy of the photons emitted during this time:

E = NE γ ,

where N is the number of photons absorbed by water during the specified time; E γ - energy of one photon, E γ = hc /λ; h - Planck's constant, h = 6.63 ⋅ 10 −34 J ⋅ s; c is the speed of light in vacuum, c = 3.00 ⋅ 10 8 m/s; λ is the wavelength of the photon, λ = 6.63 ⋅ 10 −7 m.

Since all photons are absorbed by water, the energy of the laser beam and the heat required to heat the water are the same:

E = Q

or explicitly

N h c λ = c beat m Δ T .

The written equality does not contain the desired value (time). Let's transform it by dividing both parts by the time t:

N t ⋅ h c λ = c beat m Δ T t ,

where N /t is the number of photons emitted by the laser every second, N /t = 1.00 ⋅ 10 21 s −1 ; t is the time required to heat the water.

We express the desired value

t = c sp m Δ T λ (N / t) h c

and calculate:

t = 4.20 ⋅ 10 3 ⋅ 500 ⋅ 10 − 3 ⋅ 10.0 ⋅ 6.63 ⋅ 10 − 7 1.00 ⋅ 10 21 ⋅ 6.63 ⋅ 10 − 34 ⋅ 3.00 ⋅ 10 8 = 70 0 s

Therefore, to heat water by 10 K, it is necessary that the laser work for 70 s.