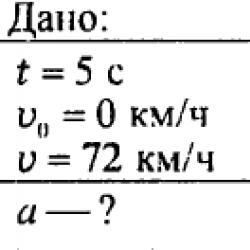Gauss yöntemi Doğrusal cebirsel denklem sistemlerini (SLAE'ler) çözmek için mükemmeldir. Diğer yöntemlere göre bir takım avantajları vardır:

• öncelikle tutarlılık açısından denklem sistemini incelemeye gerek yoktur;
• ikinci olarak, Gauss yöntemi yalnızca denklem sayısının bilinmeyen değişkenlerin sayısıyla çakıştığı ve sistemin ana matrisinin tekil olmadığı SLAE'leri değil, aynı zamanda denklem sayısının bilinmeyen değişkenlerle çakışmadığı denklem sistemlerini de çözebilir. bilinmeyen değişkenlerin sayısı veya ana matrisin determinantı sıfıra eşittir;
• üçüncüsü, Gauss yöntemi nispeten az sayıda hesaplama işlemiyle sonuçlara yol açar.

Makaleye kısa genel bakış.

Öncelikle gerekli tanımları verip notasyonları tanıtıyoruz.

Daha sonra, en basit durum için Gauss yönteminin algoritmasını açıklayacağız, yani doğrusal cebirsel denklem sistemleri için, bilinmeyen değişkenlerin sayısıyla çakışan denklemlerin sayısı ve sistemin ana matrisinin determinantı şöyledir: sıfıra eşit değil. Bu tür denklem sistemlerini çözerken, Gauss yönteminin özü en açık şekilde görülebilir; bu, bilinmeyen değişkenlerin sıralı olarak ortadan kaldırılmasıdır. Bu nedenle Gauss yöntemine bilinmeyenlerin sıralı olarak yok edilmesi yöntemi de denir. Birkaç örneğin ayrıntılı çözümlerini göstereceğiz.

Sonuç olarak, ana matrisi dikdörtgen veya tekil olan lineer cebirsel denklem sistemlerinin Gauss yöntemiyle çözümünü ele alacağız. Bu tür sistemlerin çözümü, örneklerle detaylı olarak inceleyeceğimiz bazı özelliklere sahiptir.

Sayfada gezinme.

Temel tanımlar ve gösterimler.

N bilinmeyenli (p, n'ye eşit olabilir) p doğrusal denklemden oluşan bir sistemi düşünün:

Bilinmeyen değişkenler, sayılar (gerçek veya karmaşık) ve serbest terimlerdir.

Eğer , o zaman doğrusal cebirsel denklemler sistemi denir homojen, aksi takdirde - heterojen.

Sistemin tüm denklemlerinin özdeşlik haline geldiği bilinmeyen değişkenlerin değerleri kümesine denir SLAU'nun kararı.

Bir doğrusal cebirsel denklem sisteminin en az bir çözümü varsa buna denir. eklem yeri, aksi takdirde - ortak olmayan.

Bir SLAE'nin benzersiz bir çözümü varsa buna denir. kesin. Birden fazla çözüm varsa sistem çağrılır. belirsiz.

Sistemin yazılı olduğunu söylüyorlar koordinat formu, eğer formu varsa
.

Bu sistemdeki matris formu kayıtlar şu forma sahiptir: burada - SLAE'nin ana matrisi, - bilinmeyen değişkenler sütununun matrisi, - serbest terimler matrisi.

A matrisine (n+1)'inci sütun olarak serbest terimlerden oluşan bir matris sütunu eklersek, sözde elde ederiz. genişletilmiş matris Doğrusal denklem sistemleri. Tipik olarak, genişletilmiş bir matris T harfiyle gösterilir ve serbest terimler sütunu, kalan sütunlardan dikey bir çizgi ile ayrılır;

A kare matrisi denir dejenere determinantı sıfır ise. Eğer ise A matrisi denir dejenere olmayan.

Aşağıdaki noktaya dikkat edilmelidir.

Aşağıdaki işlemleri bir doğrusal cebirsel denklem sistemiyle gerçekleştirirseniz

• iki denklemin yerini değiştirin,
• herhangi bir denklemin her iki tarafını keyfi ve sıfır olmayan bir gerçek (veya karmaşık) sayı k ile çarpın,
• herhangi bir denklemin her iki tarafına başka bir denklemin karşılık gelen kısımlarını rastgele bir k sayısıyla çarparak ekleyin,

o zaman aynı çözümlere sahip (veya tıpkı orijinal sistem gibi hiçbir çözümü olmayan) eşdeğer bir sistem elde edersiniz.

Bir doğrusal cebirsel denklem sisteminin genişletilmiş matrisi için bu eylemler, satırlarla temel dönüşümlerin gerçekleştirilmesi anlamına gelecektir:

• iki satırı değiştirerek,
• T matrisinin herhangi bir satırının tüm elemanlarını sıfırdan farklı bir k sayısıyla çarpmak,
• Bir matrisin herhangi bir satırının elemanlarına, başka bir satırın karşılık gelen elemanlarının rastgele bir k sayısıyla çarpılmasıyla eklenmesi.

Artık Gauss yönteminin açıklamasına geçebiliriz.

Denklem sayısının bilinmeyenlerin sayısına eşit olduğu ve sistemin ana matrisinin tekil olmadığı doğrusal cebirsel denklem sistemlerini Gauss yöntemini kullanarak çözme.

Bir denklem sistemine çözüm bulma görevi bize verilseydi okulda ne yapardık? .

Bazıları bunu yapardı.

Birinci denklemin sol tarafını ikinci denklemin sol tarafına, sağ tarafını da sağ tarafına ekleyerek bilinmeyen x 2 ve x 3 değişkenlerinden kurtulabileceğinizi ve hemen x 1'i bulabileceğinizi unutmayın:

Bulunan x 1 =1 değerini sistemin birinci ve üçüncü denklemlerinde yerine koyarız:

Sistemin üçüncü denkleminin her iki tarafını -1 ile çarpıp birinci denklemin karşılık gelen kısımlarına eklersek bilinmeyen x 3 değişkeninden kurtuluruz ve x 2'yi bulabiliriz:

Ortaya çıkan x 2 = 2 değerini üçüncü denklemde yerine koyarız ve kalan bilinmeyen değişken x 3'ü buluruz:

Diğerleri farklı yapardı.

Sistemin ilk denklemini bilinmeyen x 1 değişkenine göre çözelim ve elde edilen ifadeyi sistemin ikinci ve üçüncü denklemlerinde bu değişkeni hariç tutmak için yerine koyalım:

Şimdi sistemin ikinci denklemini x 2 için çözelim ve elde edilen sonucu üçüncü denklemde yerine koyarak bilinmeyen x 2 değişkenini ortadan kaldıralım:

Sistemin üçüncü denkleminden x 3 =3 olduğu açıktır. Bulduğumuz ikinci denklemden ve elde ettiğimiz ilk denklemden.

Tanıdık çözümler, değil mi?

Buradaki en ilginç şey, ikinci çözüm yönteminin esasen bilinmeyenlerin sıralı olarak yok edilmesi yöntemi yani Gauss yöntemi olmasıdır. Bilinmeyen değişkenleri (ilk x 1, sonraki aşamada x 2) ifade edip sistemin geri kalan denklemlerine yerleştirdiğimizde onları dışarıda bırakmış oluyoruz. Son denklemde tek bir bilinmeyen değişken kalana kadar yok etme işlemi yaptık. Bilinmeyenlerin sırayla ortadan kaldırılması işlemine ne ad verilir? doğrudan Gauss yöntemi. İleriye doğru hamleyi tamamladıktan sonra son denklemde bulunan bilinmeyen değişkeni hesaplama fırsatına sahip oluyoruz. Onun yardımıyla sondan bir önceki denklemden bir sonraki bilinmeyen değişkeni buluruz vb. Son denklemden birinciye geçerken bilinmeyen değişkenleri sırayla bulma işlemine denir Gauss yönteminin tersi.

İlk denklemde x 1'i x 2 ve x 3 cinsinden ifade ettiğimizde ve elde edilen ifadeyi ikinci ve üçüncü denklemlerde değiştirdiğimizde, aşağıdaki eylemlerin aynı sonuca yol açacağına dikkat edilmelidir:

Aslında böyle bir prosedür, bilinmeyen değişken x 1'in sistemin ikinci ve üçüncü denklemlerinden çıkarılmasını da mümkün kılar:

Sistem denklemleri bazı değişkenler içermediğinde, Gauss yöntemi kullanılarak bilinmeyen değişkenlerin ortadan kaldırılmasıyla ilgili nüanslar ortaya çıkar.

Örneğin, SLAU'da birinci denklemde bilinmeyen x 1 değişkeni yoktur (yani önündeki katsayı sıfırdır). Dolayısıyla bu bilinmeyen değişkeni kalan denklemlerden çıkarmak için sistemin ilk denklemini x 1 için çözemeyiz. Bu durumdan çıkmanın yolu sistemin denklemlerini değiştirmektir. Ana matrislerin determinantları sıfırdan farklı olan lineer denklem sistemlerini ele aldığımız için her zaman ihtiyacımız olan değişkenin bulunduğu bir denklem vardır ve bu denklemi ihtiyacımız olan konuma yeniden düzenleyebiliriz. Örneğimiz için sistemin birinci ve ikinci denklemlerinin yer değiştirmesi yeterlidir. , ardından x 1 için ilk denklemi çözebilir ve onu sistemin geri kalan denklemlerinden hariç tutabilirsiniz (her ne kadar x 1 artık ikinci denklemde mevcut olmasa da).

Ana fikri anladığınızı umuyoruz.

Hadi tarif edelim Gauss yöntemi algoritması.

n bilinmeyen değişkenli n doğrusal cebirsel denklemden oluşan bir sistemi çözmemiz gerektiğini varsayalım. ve ana matrisinin determinantının sıfırdan farklı olmasına izin verin.

Bunu her zaman sistemin denklemlerini yeniden düzenleyerek başarabileceğimiz için bunu varsayacağız. Bilinmeyen değişken x 1'i ikinciden başlayarak sistemin tüm denklemlerinden çıkaralım. Bunu yapmak için sistemin ikinci denklemine birincisini çarptığımız denklemi, üçüncü denklemine birincisini ekliyoruz ve bu şekilde devam ederek n'inci denkleme birincisini çarpıyoruz. Bu tür dönüşümlerden sonra denklem sistemi şu şekli alacaktır:

Nerede ve .

Sistemin ilk denkleminde x 1'i diğer bilinmeyen değişkenler cinsinden ifade edip, elde edilen ifadeyi diğer tüm denklemlerde yerine koysaydık aynı sonuca ulaşırdık. Böylece x 1 değişkeni ikinciden başlayarak tüm denklemlerin dışında bırakılır.

Daha sonra benzer şekilde ilerliyoruz, ancak yalnızca sonuçtaki sistemin şekilde işaretlenmiş kısmıyla

Bunu yapmak için sistemin üçüncü denklemine ikinciyi çarpıyoruz, dördüncü denkleme ikinciyi ekliyoruz ve bu şekilde devam ederek n'inci denkleme ikinciyi çarpıyoruz. Bu tür dönüşümlerden sonra denklem sistemi şu şekli alacaktır:

Nerede ve . Böylece x2 değişkeni üçüncüden başlayarak tüm denklemlerin dışında bırakılır.

Daha sonra sistemin şekilde işaretlenen kısmı ile benzer şekilde hareket ederek bilinmeyen x 3'ü ortadan kaldırmaya devam ediyoruz.

Böylece sistem şu formu alana kadar Gauss yönteminin doğrudan ilerlemesine devam ediyoruz:

Bu andan itibaren Gauss yönteminin tersini başlatırız: son denklemden x n'yi şu şekilde hesaplarız, elde edilen x n değerini kullanarak sondan bir önceki denklemden x n-1'i buluruz ve bu şekilde devam ederek ilk denklemden x 1'i buluruz .

Bir örnek kullanarak algoritmaya bakalım.

Örnek.

Gauss yöntemi.

Çözüm.

a 11 katsayısı sıfır değildir, bu nedenle Gauss yönteminin doğrudan ilerlemesine, yani bilinmeyen x 1 değişkeninin birincisi hariç sistemin tüm denklemlerinden hariç tutulmasına geçelim. Bunu yapmak için, ikinci, üçüncü ve dördüncü denklemlerin sol ve sağ taraflarına, birinci denklemin sol ve sağ taraflarını sırasıyla ile çarparak ekleyin. Ve :

Bilinmeyen x 1 değişkeni elendi, şimdi x 2'yi yok etmeye geçelim. Sistemin üçüncü ve dördüncü denklemlerinin sol ve sağ taraflarına, ikinci denklemin sol ve sağ taraflarını sırasıyla çarparak ekleriz. Ve :

Gauss yönteminin ileri ilerlemesini tamamlamak için sistemin son denkleminden bilinmeyen x3 değişkenini çıkarmamız gerekir. Dördüncü denklemin sol ve sağ taraflarına sırasıyla üçüncü denklemin sol ve sağ taraflarını çarparak ekleyelim. :

Gauss yönteminin tersinden başlayabilirsiniz.

Elimizdeki son denklemden ,
elde ettiğimiz üçüncü denklemden,
ikinciden itibaren,
ilkinden.

Kontrol etmek için bilinmeyen değişkenlerin elde edilen değerlerini orijinal denklem sistemine değiştirebilirsiniz. Tüm denklemlerin özdeşliğe dönüşmesi Gauss yöntemini kullanan çözümün doğru bulunduğunu gösterir.

Cevap:

Şimdi aynı örneğe matris gösteriminde Gauss yöntemini kullanarak bir çözüm verelim.

Örnek.

Denklem sisteminin çözümünü bulun Gauss yöntemi.

Çözüm.

Sistemin genişletilmiş matrisi şu şekildedir: . Her sütunun üstünde matrisin elemanlarına karşılık gelen bilinmeyen değişkenler bulunur.

Gauss yönteminin buradaki doğrudan yaklaşımı, sistemin genişletilmiş matrisinin temel dönüşümler kullanılarak yamuk biçime indirilmesini içerir. Bu işlem, sistemle koordinat formunda yaptığımız bilinmeyen değişkenlerin ortadan kaldırılmasına benzer. Şimdi bunu göreceksiniz.

Matrisi, ikinci sütundan başlayarak ilk sütundaki tüm öğeler sıfır olacak şekilde dönüştürelim. Bunu yapmak için, ikinci, üçüncü ve dördüncü satırların elemanlarına, birinci satırın karşılık gelen elemanlarını ile çarparak ekleriz, ve buna göre:

Daha sonra, ortaya çıkan matrisi, ikinci sütunda üçüncüden başlayarak tüm öğelerin sıfır olacağı şekilde dönüştürüyoruz. Bu, bilinmeyen x 2 değişkeninin ortadan kaldırılmasına karşılık gelecektir. Bunu yapmak için, üçüncü ve dördüncü satırların elemanlarına, matrisin ilk satırının karşılık gelen elemanlarını sırasıyla çarparak ekleriz. Ve :

Geriye bilinmeyen x3 değişkenini sistemin son denkleminden hariç tutmak kalır. Bunu yapmak için, elde edilen matrisin son satırının elemanlarına, sondan bir önceki satırın karşılık gelen elemanlarını şununla çarparak ekleriz: :

Bu matrisin bir doğrusal denklem sistemine karşılık geldiğine dikkat edilmelidir.

ileri bir hamleden sonra daha erken elde edildi.

Geri dönmenin zamanı geldi. Matris gösteriminde, Gauss yönteminin tersi, sonuçtaki matrisin, şekilde işaretlenen matris olacak şekilde dönüştürülmesini içerir.

köşegen oldu, yani şeklini aldı

bazı sayılar nerede?

Bu dönüşümler Gauss yönteminin ileri dönüşümlerine benzer ancak ilk satırdan sonuncuya değil, sondan birinciye doğru gerçekleştirilir.

Üçüncü, ikinci ve birinci satırların elemanlarına son satırın karşılık gelen elemanlarını şununla çarparak ekleyin: , durmadan sırasıyla:

Şimdi ikinci ve birinci satırların elemanlarına üçüncü satırın karşılık gelen elemanlarını sırasıyla ve ile çarparak ekleyin:

Ters Gauss yönteminin son adımında, ilk satırın elemanlarına ikinci satırın karşılık gelen elemanlarını şununla çarparak ekleriz:

Ortaya çıkan matris denklem sistemine karşılık gelir bilinmeyen değişkenleri bulduğumuz yerden.

Cevap:

NOT.

Doğrusal cebirsel denklem sistemlerini çözmek için Gauss yöntemini kullanırken, tamamen yanlış sonuçlara yol açabileceğinden yaklaşık hesaplamalardan kaçınılmalıdır. Ondalık sayıları yuvarlamamanızı öneririz. Ondalık kesirlerden sıradan kesirlere geçmek daha iyidir.

Örnek.

Gauss yöntemini kullanarak üç denklemden oluşan bir sistemi çözme .

Çözüm.

Bu örnekte bilinmeyen değişkenlerin farklı bir atamaya sahip olduğuna dikkat edin (x 1, x 2, x 3 değil, x, y, z). Sıradan kesirlere geçelim:

Bilinmeyen x'i sistemin ikinci ve üçüncü denklemlerinden çıkaralım:

Ortaya çıkan sistemde, bilinmeyen değişken y ikinci denklemde yok, ancak üçüncü denklemde y mevcut, bu nedenle ikinci ve üçüncü denklemleri yer değiştirelim:

Bu, Gauss yönteminin doğrudan ilerleyişini tamamlar (bu bilinmeyen değişken artık mevcut olmadığından y'yi üçüncü denklemden çıkarmaya gerek yoktur).

Ters harekete başlayalım.

Bulduğumuz son denklemden ,
sondan bir öncekinden


elimizdeki ilk denklemden

Cevap:

X = 10, y = 5, z = -20.

Denklem sayısının bilinmeyenlerin sayısıyla örtüşmediği veya sistemin ana matrisinin tekil olduğu doğrusal cebirsel denklem sistemlerinin Gauss yöntemini kullanarak çözülmesi.

Ana matrisi dikdörtgen veya kare tekil olan denklem sistemlerinin çözümü olmayabilir, tek çözümü olabilir veya sonsuz sayıda çözümü olabilir.

Şimdi Gauss yönteminin bir doğrusal denklem sisteminin uyumluluğunu veya tutarsızlığını belirlememize ve uyumlu olması durumunda tüm çözümleri (veya tek bir çözümü) belirlememize nasıl izin verdiğini anlayacağız.

Prensip olarak, bu tür SLAE'ler durumunda bilinmeyen değişkenleri ortadan kaldırma süreci aynı kalır. Ancak ortaya çıkabilecek bazı durumlar hakkında detaya inmekte fayda var.

Gelelim en önemli aşamaya.

Dolayısıyla, Gauss yönteminin ileri ilerlemesini tamamladıktan sonra doğrusal cebirsel denklemler sisteminin şu şekli aldığını varsayalım: ve tek bir denklem bile indirgenmedi (bu durumda sistemin uyumsuz olduğu sonucuna varırdık). Mantıklı bir soru ortaya çıkıyor: "Bundan sonra ne yapmalı?"

Ortaya çıkan sistemin tüm denklemlerinde ilk sırada yer alan bilinmeyen değişkenleri yazalım:

Örneğimizde bunlar x 1, x 4 ve x 5'tir. Sistemin denklemlerinin sol taraflarında yalnızca yazılı bilinmeyen değişkenler x 1, x 4 ve x 5'i içeren terimleri bırakıyoruz, geri kalan terimler ters işaretle denklemlerin sağ tarafına aktarılıyor:

Denklemlerin sağ tarafında yer alan bilinmeyen değişkenlere keyfi değerler verelim; - keyfi sayılar:

Bundan sonra SLAE'mizin tüm denklemlerinin sağ tarafları sayılar içerir ve Gauss yönteminin tersine ilerleyebiliriz.

Sistemin sahip olduğumuz son denkleminden, bulduğumuz sondan bir önceki denklemden, elde ettiğimiz ilk denklemden

Bir denklem sisteminin çözümü, bilinmeyen değişkenlerin değerlerinin bir kümesidir

Numara Vermek Farklı değerler alarak denklem sistemine farklı çözümler elde edeceğiz. Yani denklem sistemimizin sonsuz sayıda çözümü vardır.

Cevap:

Nerede - keyfi sayılar.

Malzemeyi pekiştirmek için birkaç örneğin daha çözümlerini ayrıntılı olarak analiz edeceğiz.

Örnek.

Homojen bir doğrusal cebirsel denklem sistemini çözün Gauss yöntemi.

Çözüm.

Bilinmeyen x değişkenini sistemin ikinci ve üçüncü denklemlerinden hariç tutalım. Bunu yapmak için ikinci denklemin sol ve sağ taraflarına sırasıyla birinci denklemin sol ve sağ taraflarını ile çarparak, üçüncü denklemin sol ve sağ taraflarına ise sol ve sağ taraflarını ekliyoruz. ilk denklemin sağ tarafları şununla çarpılır:

Şimdi ortaya çıkan denklem sisteminin üçüncü denkleminden y'yi hariç tutalım:

Ortaya çıkan SLAE, sisteme eşdeğerdir .

Sistem denklemlerinin sol tarafında yalnızca bilinmeyen x ve y değişkenlerini içeren terimleri bırakıp, bilinmeyen değişken z'yi içeren terimleri sağ tarafa taşıyoruz:

Carl Friedrich Gauss - Alman matematikçi, aynı isimli SLAE'leri çözme yönteminin kurucusu

Carl Friedrich Gauss ünlü bir büyük matematikçiydi ve bir zamanlar “Matematiğin Kralı” olarak tanındı. Her ne kadar "Gauss'un yöntemi" adı genel olarak kabul edilse de, Gauss onun yazarı değildir: Gauss'un yöntemi ondan çok önce biliniyordu. İlk tanımı 2. yüzyıl arasında derlenen “Dokuz Kitapta Matematik” adlı Çin eserinde yer almaktadır. M.Ö e. ve ben yüzyıl. N. e. ve 10. yüzyıl civarında yazılmış eski eserlerin bir derlemesidir. M.Ö e.

– bilinmeyenlerin tutarlı bir şekilde hariç tutulması. Bu yöntem ikinci dereceden doğrusal cebirsel denklem sistemlerini çözmek için kullanılır. Denklemler Gauss yöntemi kullanılarak kolayca çözülebilse de öğrenciler çoğu zaman işaretler (artı ve eksiler) konusunda kafaları karıştığı için doğru çözümü bulamazlar. Bu nedenle SLAE'leri çözerken son derece dikkatli olmanız gerekir ve ancak o zaman en karmaşık denklemi bile kolayca, hızlı ve doğru bir şekilde çözebilirsiniz.

Doğrusal cebirsel denklem sistemlerinin çeşitli avantajları vardır: Denklemin önceden tutarlı olması gerekmez; denklem sayısının bilinmeyen değişkenlerin sayısıyla çakışmadığı veya ana matrisin determinantının sıfıra eşit olduğu denklem sistemlerini çözmek mümkündür; Nispeten az sayıda hesaplama işlemiyle sonuçlara ulaşmak için Gauss yöntemini kullanmak mümkündür.

Daha önce de belirtildiği gibi Gauss yöntemi öğrenciler için bazı zorluklara neden olmaktadır. Ancak yöntemi ve çözüm algoritmasını öğrenirseniz çözümün inceliklerini hemen anlayacaksınız.

Öncelikle doğrusal denklem sistemleri hakkındaki bilgileri sistematize edelim.

Not!

Bir SLAE, unsurlarına bağlı olarak aşağıdakilere sahip olabilir:

1. Bir çözüm;
2. birçok çözüm;
3. hiçbir çözümü yok.

İlk iki durumda SLAE uyumlu, üçüncü durumda ise uyumsuz olarak adlandırılır. Bir sistemin tek çözümü varsa kesin, birden fazla çözümü varsa belirsiz olarak adlandırılır.

Gauss yöntemi - teorem, çözüm örnekleri güncellenme tarihi: 22 Kasım 2019: Bilimsel Makaleler.Ru

Bir doğrusal denklem sistemini çözmenin en basit yollarından biri, determinantların hesaplanmasına dayanan bir tekniktir ( Cramer kuralı). Avantajı, çözümü anında kaydetmenize izin vermesidir; özellikle sistemin katsayılarının sayı değil, bazı parametreler olduğu durumlarda kullanışlıdır. Dezavantajı, çok sayıda denklem durumunda hesaplamaların zahmetli olmasıdır; ayrıca Cramer kuralı, denklem sayısının bilinmeyenlerin sayısıyla çakışmadığı sistemlere doğrudan uygulanamaz. Bu gibi durumlarda genellikle kullanılır Gauss yöntemi.

Çözüm kümeleri aynı olan lineer denklem sistemlerine denir. eş değer. Açıkçası, herhangi bir denklem değiştirilirse, denklemlerden biri sıfırdan farklı bir sayıyla çarpılırsa veya bir denklem diğerine eklenirse, doğrusal bir sistemin çözüm kümesi değişmeyecektir.

Gauss yöntemi (bilinmeyenlerin sıralı eliminasyonu yöntemi) temel dönüşümlerin yardımıyla sistemin adım tipinde eşdeğer bir sisteme indirgenmesidir. İlk olarak 1. denklemi kullanarak ortadan kaldırırız. X Sistemin sonraki tüm denklemlerinden 1'i. Daha sonra 2. denklemi kullanarak ortadan kaldırırız. X 3. ve sonraki tüm denklemlerden 2. Bu süreç adı verilir doğrudan Gauss yöntemi, son denklemin sol tarafında tek bir bilinmeyen kalana kadar devam eder xn. Bundan sonra yapılır Gauss yönteminin tersi– son denklemi çözerek şunu buluruz: xn; bundan sonra, bu değeri kullanarak hesapladığımız sondan bir önceki denklemden xn–1 vb. Sonuncuyu buluyoruz Xİlk denklemden 1.

Gauss dönüşümlerini, denklemlerin kendisiyle değil, katsayılarının matrisleri ile dönüşümler gerçekleştirerek gerçekleştirmek uygundur. Matrisi düşünün:

isminde sistemin genişletilmiş matrisi,çünkü sistemin ana matrisine ek olarak bir de serbest terimler sütunu içerir. Gauss yöntemi, sistemin genişletilmiş matrisinin temel satır dönüşümlerini (!) kullanarak sistemin ana matrisini üçgen forma (veya kare olmayan sistemlerde yamuk forma) indirgemeye dayanır.

Örnek 5.1. Sistemi Gauss yöntemini kullanarak çözün:

Çözüm. Sistemin genişletilmiş matrisini yazalım ve ilk satırı kullanarak ardından kalan elemanları sıfırlayacağız:

ilk sütunun 2., 3. ve 4. satırlarında sıfırlar alıyoruz:

Şimdi 2. satırın altındaki ikinci sütundaki tüm elemanların sıfıra eşit olmasına ihtiyacımız var. Bunun için ikinci satırı –4/7 ile çarpıp 3. satıra ekleyebilirsiniz. Ancak kesirlerle uğraşmamak için ikinci sütunun 2. satırında bir birim oluşturalım ve sadece

Şimdi üçgen bir matris elde etmek için 3. sütunun dördüncü satırının elemanını sıfırlamanız gerekir, bunun için üçüncü satırı 8/54 ile çarpıp dördüncüye ekleyebilirsiniz. Ancak kesirlerle uğraşmamak için 3. ve 4. satırları ve 3. ve 4. sütunları değiştireceğiz ve ancak bundan sonra belirtilen elemanı sıfırlayacağız. Sütunları yeniden düzenlerken karşılık gelen değişkenlerin yer değiştirdiğini ve bunun hatırlanması gerektiğini unutmayın; sütunlarla diğer temel dönüşümler (bir sayıyla toplama ve çarpma) gerçekleştirilemez!

Son basitleştirilmiş matris, orijinaline eşdeğer bir denklem sistemine karşılık gelir:

Buradan Gauss yönteminin tersini kullanarak dördüncü denklemi buluruz. X 3 = –1; üçüncüden X 4 = –2, ikinciden itibaren X 2 = 2 ve ilk denklemden X 1 = 1. Matris formunda cevap şu şekilde yazılır:

Sistemin kesin olduğu durumu değerlendirdik, yani. tek bir çözüm olduğunda. Bakalım sistem tutarsız veya belirsiz olursa ne olacak?

Örnek 5.2. Gauss yöntemini kullanarak sistemi keşfedin:

Çözüm. Sistemin genişletilmiş matrisini yazıp dönüştürüyoruz

Basitleştirilmiş bir denklem sistemi yazıyoruz:

Burada son denklemde 0=4 olduğu ortaya çıktı, yani. çelişki. Sonuç olarak sistemin bir çözümü yoktur, yani. o uyumsuz. à

Örnek 5.3. Gauss yöntemini kullanarak sistemi keşfedin ve çözün:

Çözüm. Sistemin genişletilmiş matrisini yazıyoruz ve dönüştürüyoruz:

Dönüşümler sonucunda son satırda yalnızca sıfırlar yer alıyor. Bu, denklem sayısının bir azaldığı anlamına gelir:

Böylece basitleştirmelerden sonra geriye iki denklem ve dört bilinmeyen kalıyor; iki bilinmeyen "ekstra". Bırakın "gereksiz" olsunlar, ya da dedikleri gibi, serbest değişkenler, irade X 3 ve X 4. Daha sonra

İnanmak X 3 = 2A Ve X 4 = B, alıyoruz X 2 = 1–A Ve X 1 = 2B–A; veya matris formunda

Bu şekilde yazılan çözüme denir genelçünkü parametreleri vermek A Ve B Farklı değerler, sistemin tüm olası çözümlerini tanımlayabilir. A

Bu yazımızda:

• Gauss yöntemini tanımlayalım,
• Denklem sayısının bilinmeyen değişkenlerin sayısıyla çakıştığı ve determinantın sıfıra eşit olmadığı doğrusal denklemleri çözmek için eylem algoritmasını analiz edelim;
• SLAE'leri dikdörtgen veya tekil bir matrisle çözmek için eylem algoritmasını analiz edelim.

Gauss yöntemi - nedir bu?

Tanım 1

Gauss yöntemi doğrusal cebirsel denklem sistemlerinin çözümünde kullanılan ve aşağıdaki avantajlara sahip bir yöntemdir:

• tutarlılık açısından denklem sistemini kontrol etmeye gerek yoktur;
• Denklem sistemlerini aşağıdaki durumlarda çözmek mümkündür:
• Belirleyicilerin sayısı bilinmeyen değişkenlerin sayısıyla örtüşür;
• Belirleyicilerin sayısı bilinmeyen değişkenlerin sayısıyla örtüşmüyor;
• determinant sıfırdır.
• sonuç nispeten az sayıda hesaplama işlemiyle üretilir.

Temel tanımlar ve gösterimler

örnek 1

N bilinmeyenli p doğrusal denklem sistemi vardır (p, n'ye eşit olabilir):

a 11 x 1 + a 12 x 2 +. . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 ⋯ a p 1 x 1 + a p 2 x 2 + . . . + a p n x n = b p,

burada x 1 , x 2 , . . . . , x n - bilinmeyen değişkenler, a i j, i = 1, 2. . . , p, j = 1, 2. . . , n - sayılar (gerçek veya karmaşık), b 1 , b 2 , . . . , b n - serbest terimler.

Tanım 2

Eğer b 1 = b 2 = ise. . . = b n = 0 ise böyle bir doğrusal denklem sistemine denir homojen, eğer tersi ise - heterojen.

Tanım 3

SLAE çözümü - bilinmeyen değişkenlerin değerleri kümesi x 1 = a 1, x 2 = a 2, . . . , x n = a n , sistemin tüm denklemleri birbiriyle aynı hale gelir.

Tanım 4

Ortak SLAU - En az bir çözüm seçeneğinin bulunduğu sistem. Aksi takdirde tutarsız denir.

Tanım 5

Tanımlanmış SLAU - Bu, benzersiz bir çözümü olan bir sistemdir. Birden fazla çözüm varsa, böyle bir sistem belirsiz olarak adlandırılacaktır.

Tanım 6

Koordinat kaydı türü:

a 11 x 1 + a 12 x 2 +. . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 ⋯ a p 1 x 1 + a p 2 x 2 + . . . + a p n x n = b p

Tanım 7

Matris gösterimi: A X = B, burada

A = a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a p 1 a p 2 ⋯ a p n - SLAE'nin ana matrisi;

X = x 1 x 2 ⋮ x n - bilinmeyen değişkenlerin sütun matrisi;

B = b 1 b 2 ⋮ b n - serbest terimlerin matrisi.

Tanım 8

Genişletilmiş Matris - serbest terimlerden oluşan bir matris sütununun (n + 1) sütun olarak eklenmesiyle elde edilen ve T olarak gösterilen bir matris.

T = a 11 a 12 ⋮ a 1 n b 1 a 21 a 22 ⋮ a 2 n b 2 ⋮ ⋮ ⋮ ⋮ ⋮ a p 1 a p 2 ⋮ a p n b n

Tanım 9

Tekil kare matris A - determinantı sıfıra eşit olan bir matris. Determinant sıfıra eşit değilse, böyle bir matrise dejenere olmayan denir.

Eşit sayıda denklem ve bilinmeyenle SLAE'leri çözmek için Gauss yöntemini kullanmaya yönelik algoritmanın açıklaması (Gauss yönteminin ters ve ileri ilerlemesi)

Öncelikle Gauss yönteminin ileri ve geri hareket tanımlarına bakalım.

Tanım 10

İleri Gauss hareketi - bilinmeyenlerin sıralı olarak ortadan kaldırılması süreci.

Tanım 11

Gauss ters çevrilmesi - son denklemden birinciye kadar bilinmeyenleri sırayla bulma süreci.

Gauss yöntemi algoritması:

Örnek 2

n bilinmeyen değişkenli n doğrusal denklem sistemini çözüyoruz:

a 11 x 1 + a 12 x 2 + a 13 x 3 +. . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + . . . + a 2 n x n = b 2 a 31 x 1 + a 32 x 2 + a 33 x 3 + . . . + bir 3 n x n = b 3 ⋯ bir n 1 x 1 + bir n 2 x 2 + bir n 3 x 3 + . . . + a n n x n = b n

Matris determinantı sıfıra eşit değil .

1. 11 sıfıra eşit değildir - bu her zaman sistemin denklemlerini yeniden düzenleyerek başarılabilir;
2. x 1 değişkenini ikinciden başlayarak sistemin tüm denklemlerinden hariç tutuyoruz;
3. Sistemin ikinci denklemine - a 21 a 11 ile çarpılan ilk denklemi, üçüncü denkleme - a 21 a 11 ile çarpılan ilk denklemi ekleyelim, vb.

Bu adımlardan sonra matris şu şekli alacaktır:

a 11 x 1 + a 12 x 2 + a 13 x 3 +. . . + a 1 n x n = b 1 a (1) 22 x 2 + a (1) 23 x 3 + . . . + a (1) 2 n x n = b (1) 2 a (1) 32 x 2 + a (1) 33 x 3 + . . . + a (1) 3 n x n = b (1) 3 ⋯ a (1) n 2 x 2 + a (1) n 3 x 3 + . . . + a (1) n n x n = b (1) n ,

burada a ben j (1) = a i j + a 1 j (- a ben 1 a 11), i = 2, 3, . . . , n , j = 2 , 3 , . . . , n , b ben (1) = b ben + b 1 (- a ben 1 a 11) , i = 2 , 3 , . . . , N.

a 11 x 1 + a 12 x 2 + a 13 x 3 +. . . + a 1 n x n = b 1 a (1) 22 x 2 + a (1) 23 x 3 + . . . + a (1) 2 n x n = b (1) 2 a (1) 32 x 2 + a (1) 33 x 3 + . . . + a (1) 3 n x n = b (1) 3 ⋯ a (1) n 2 x 2 + a (1) n 3 x 3 + . . . + a (1) n n x n = b (1) n

22(1)'in sıfıra eşit olmadığına inanılmaktadır. Böylece, üçüncüden başlayarak bilinmeyen değişken x 2'yi tüm denklemlerden çıkarmaya devam ediyoruz:

• sistemin üçüncü denklemine - a (1) 42 a (1) 22 ile çarpılan ikinciyi ekliyoruz;
• dördüncüye ikinciyi ekliyoruz - a (1) 42 a (1) 22 vb.

Bu tür manipülasyonlardan sonra SLAE sonraki görünüm :

a 11 x 1 + a 12 x 2 + a 13 x 3 +. . . + a 1 n x n = b 1 a (1) 22 x 2 + a (1) 23 x 3 + . . . + a (1) 2 n x n = b (1) 2 a (2) 33 x 3 + . . . + a (2) 3 n x n = b (2) 3 ⋯ a (2) n 3 x 3 + . . . + a (2) n n x n = b (2) n ,

burada a ben j (2) = a (1) i j + a 2 j (- a (1) i 2 a (1) 22), i = 3, 4, . . . , n , j = 3 , 4 , . . . , n , b ben (2) = b (1) i + b (1) 2 (- a (1) i 2 a (1) 22) , i = 3 , 4 , . . . , N. .

Böylece x2 değişkeni üçüncüden başlayarak tüm denklemlerin dışında bırakılır.

a 11 x 1 + a 12 x 2 + a 13 x 3 +. . . + a 1 n x n = b 1 a (1) 22 x 2 + a (1) 23 x 3 + . . . + a (1) 2 n x n = b (1) 2 a (2) 33 x 3 + . . . + a (2) 3 n x n = b (2) 3 ⋯ a (n - 1) n n x n = b (n - 1) n

Not

Sistem bu formu aldıktan sonra başlayabilirsiniz. Gauss yönteminin tersi :

• son denklemden x n'yi şu şekilde hesaplayın: x n = b n (n - 1) a n n (n - 1) ;
• ortaya çıkan x n'yi kullanarak, sondan bir önceki denklemden x n - 1'i buluruz, vb., ilk denklemden x 1'i buluruz.

Örnek 3

Gauss yöntemini kullanarak denklem sistemine bir çözüm bulun:

Nasıl karar verilir?

a 11 katsayısı sıfırdan farklıdır, dolayısıyla doğrudan çözüme geçiyoruz, yani. x 11 değişkeninin ilki hariç sistemin tüm denklemlerinden hariç tutulması. Bunu yapmak için 2., 3. ve 4. denklemlerin sol ve sağ taraflarına birincinin sol ve sağ taraflarını - a 21 a 11 ile çarpıyoruz:

1 3, - a 31 a 11 = - - 2 3 = 2 3 ve - a 41 a 11 = - 1 3.

3 x 1 + 2 x 2 + x 3 + x 4 = - 2 x 1 - x 2 + 4 x 3 - x 4 = - 1 - 2 x 1 - 2 x 2 - 3 x 3 + x 4 = 9 x 1 + 5 x 2 - x 3 + 2 x 4 = 4 ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = - 2 x 1 - x 2 + 4 x 3 - x 4 + (- 1 3) (3 x 1 + 2 x 2 + x 3 + x 4) = - 1 + (- 1 3) (- 2) - 2 x 1 - 2 x 2 - 3 x 3 + x 4 + 2 3 (3 x 1 + 2 x 2 + x 3 + x 4) = 9 + 2 3 (- 2) x 1 + 5 x 2 - x 3 + 2 x 4 + (- 1 3) (3 x 1 + 2 x 2 + x 3 + x 4) = 4 + (- 1 3) (- 2 ) ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = - 2 - 5 3 x 2 + 11 3 x 3 - 4 3 x 4 = - 1 3 - 2 3 x 2 - 7 3 x 3 + 5 3 x 4 = 23 3 13 3 x 2 - 4 3 x 3 + 5 3 x 4 = 14 3

Bilinmeyen x 1 değişkenini eledik, şimdi x 2 değişkenini elemeye geçiyoruz:

A 32 (1) a 22 (1) = - - 2 3 - 5 3 = - 2 5 ve a 42 (1) a 22 (1) = - 13 3 - 5 3 = 13 5:

3 x 1 + 2 x 2 + x 3 + x 4 = - 2 - 5 3 x 2 + 11 3 x 3 - 4 3 x 4 = - 1 3 - 2 3 x 2 - 7 3 x 3 + 5 3 x 4 = 23 3 13 3 x 2 - 4 3 x 3 + 5 3 x 4 = 14 3 ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = - 2 - 5 3 x 2 + 11 3 x 3 - 4 3 x 4 = - 1 3 - 2 3 x 2 - 7 3 x 3 + 5 3 x 4 + (- 2 5) (- 5 3 x 2 + 11 3 x 3 - 4 3 x 4) = 23 3 + (- 2 5) (- 1 3) 13 3 x 2 - 4 3 x 3 + 5 3 x 4 + 13 5 (- 5 3 x 2 + 11 3 x 3 - 4 3 x 4) = 14 3 + 13 5 (- 1 3) ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = - 2 - 5 3 x 2 + 11 3 x 3 - 4 3 x 4 = - 1 3 - 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 - 9 5 x 4 = 19 5

Gauss yönteminin ileri ilerlemesini tamamlamak için, x 3'ü sistemin son denkleminden hariç tutmak gerekir - a 43 (2) a 33 (2) = - 41 5 - 19 5 = 41 19:

3 x 1 + 2 x 2 + x 3 + x 4 = - 2 - 5 3 x 2 + 11 3 x 3 - 4 3 x 4 = - 1 3 - 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 - 9 5 x 4 = 19 5 ⇔

3 x 1 + 2 x 2 + x 3 + x 4 = - 2 - 5 3 x 2 + 11 3 x 3 - 4 3 x 4 = - 1 3 - 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 - 9 5 x 4 + 41 19 (- 19 5 x 3 + 11 5 x 4) = 19 5 + 41 19 39 5 ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = - 2 - 5 3 x 2 + 11 3 x 3 - 4 3 x 4 = - 1 3 - 19 5 x 3 + 11 5 x 4 = 39 5 56 19 x 4 = 392 19

Gauss yöntemini tersine çevirin:

• elimizdeki son denklemden: x 4 = 392 19 56 19 = 7;
• 3. denklemden şunu elde ederiz: x 3 = - 5 19 (39 5 - 11 5 x 4) = - 5 19 (39 5 - 11 5 × 7) = 38 19 = 2;
• 2'den itibaren: x 2 = - 3 5 (- 1 3 - 11 3 x 4 + 4 3 x 4) = - 3 5 (- 1 3 - 11 3 × 2 + 4 3 × 7) = - 1 ;
• 1.'den itibaren: x 1 = 1 3 (- 2 - 2 x 2 - x 3 - x 4) = - 2 - 2 × (- 1) - 2 - 7 3 = - 9 3 = - 3 .

Cevap : x1 = -3; x2 = -1; x3 = 2; x 4 = 7

Örnek 4

Matris gösteriminde Gauss yöntemini kullanarak aynı örneğe bir çözüm bulun:

3 x 1 + 2 x 2 + x 3 + x 4 = - 2 x 1 - x 2 + 4 x 3 - x 4 = - 1 - 2 x 1 - 2 x 2 - 3 x 3 + x 4 = 9 x 1 + 5 x 2 - x 3 + 2 x 4 = 4

Nasıl karar verilir?

Sistemin genişletilmiş matrisi şu şekilde sunulur:

x 1 x 2 x 3 x 4 3 2 1 1 1 - 1 4 - 1 - 2 - 2 - 3 1 1 5 - 1 2 - 2 - 1 9 4

Bu durumda Gauss yönteminin doğrudan yaklaşımı, temel dönüşümler kullanılarak genişletilmiş matrisin yamuk forma indirgenmesini içerir. Bu süreç, koordinat formundaki bilinmeyen değişkenlerin ortadan kaldırılması sürecine çok benzemektedir.

Matris dönüşümü tüm elemanların sıfıra çevrilmesiyle başlar. Bunu yapmak için, 2., 3. ve 4. satırların elemanlarına, 1. satırın karşılık gelen elemanlarını - a 21 a 11 = - 1 3 , - a 31 a 11 = - - 2 3 = ile çarparak ekleriz. 2 3 ben n a - a 41 a 11 = - 1 3 .

Diğer dönüşümler aşağıdaki şemaya göre gerçekleşir: 3. sıradan başlayarak 2. sütundaki tüm öğeler sıfır olur. Bu süreç bir değişkenin ortadan kaldırılması sürecine karşılık gelir. Bu eylemi gerçekleştirmek için, 3. ve 4. satırların elemanlarına, matrisin 1. satırının karşılık gelen elemanlarını - a 32 (1) a 22 (1) = - 2 ile çarpmak gerekir. 3 - 5 3 = - 2 5 ve - a 42 (1) a 22 (1) = - 13 3 - 5 3 = 13 5:

x 1 x 2 x 3 x 4 3 2 1 1 | - 2 0 - 5 3 11 3 - 4 3 | - 1 3 0 - 2 3 - 7 3 5 3 | 23 3 0 13 3 - 4 3 5 3 | 14 3 ~

x 1 x 2 x 3 x 4 ~ 3 2 1 1 | - 2 0 - 5 3 11 3 - 4 3 | - 1 3 0 - 2 3 + (- 2 5) (- 5 3) - 7 3 + (- 2 5) 11 3 5 3 + (- 2 5) (- 4 3) | 23 3 + (- 2 5) (- 1 3) 0 13 3 + 13 5 (- 5 3) - 4 3 + 13 5 × 11 3 5 3 + 13 5 (- 4 3) | 14 3 + 13 5 (- 1 3) ~

x 1 x 2 x 3 x 4 ~ 3 2 1 1 | - 2 0 - 5 3 11 3 - 4 3 | - 1 3 0 0 - 19 5 11 5 | 39 5 0 0 41 5 - 9 5 | 19 5

Şimdi x 3 değişkenini son denklemden hariç tutuyoruz - matrisin son satırının elemanlarına son satırın karşılık gelen elemanlarını ekliyoruz, bu da 43 (2) a 33 (2) = - 41 5 ile çarpılıyor - 19 5 = 41 19.

x 1 x 2 x 3 x 4 3 2 1 1 | - 2 0 - 5 3 11 3 - 4 3 | - 1 3 0 0 - 19 5 11 5 | 39 5 0 0 41 5 - 9 5 | 19 5 ~

x 1 x 2 x 3 x 4 ~ 3 2 1 1 | - 2 0 - 5 3 11 3 - 4 3 | - 1 3 0 0 - 19 5 11 5 | 39 5 0 0 41 5 + 41 19 (- 19 5) - 9 5 + 41 19 × 11 5 | 19 5 + 41 19 × 39 5 ~

x 1 x 2 x 3 x 4 ~ 3 2 1 1 | - 2 0 - 5 3 11 3 - 4 3 | - 1 3 0 0 - 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19

Şimdi ters yöntemi uygulayalım. Matris gösteriminde matrisin dönüşümü, görüntüde renkli olarak işaretlenen matrisin şu şekilde olacağı şekildedir:

x 1 x 2 x 3 x 4 3 2 1 1 | - 2 0 - 5 3 11 3 - 4 3 | - 1 3 0 0 - 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19

diyagonal hale geldi, yani aşağıdaki formu aldı:

x 1 x 2 x 3 x 4 3 0 0 0 | a 1 0 - 5 3 0 0 | a 2 0 0 - 19 5 0 | 3 0 0 0 56 19 | 392 19, burada 1, 2 ve 3 bazı sayılardır.

Bu tür dönüşümler ileri harekete benzer, yalnızca dönüşümler denklemin 1. satırından değil son satırından gerçekleştirilir. 3., 2. ve 1. satırların elemanlarına, son satırın karşılık gelen elemanlarını çarparak ekleriz.

11 5 56 19 = - 209 280, - - 4 3 56 19 = 19 42 ve - 1 56 19 = 19 56.

x 1 x 2 x 3 x 4 3 2 1 1 | - 2 0 - 5 3 11 3 - 4 3 | - 1 3 0 0 - 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19 ~

x 1 x 2 x 3 x 4 ~ 3 2 1 1 + (- 19 56) 56 19 | - 2 + (- 19 56) 392 19 0 - 5 3 11 3 - 4 3 + 19 42 × 56 19 | - 1 3 + 19 42 × 392 19 0 0 - 19 5 11 5 + (- 209 280) 56 19 | 39 5 + (- 209 280) 392 19 0 0 0 56 19 | 392 19 ~

x 1 x 2 x 3 x 4 ~ 3 2 1 0 | - 9 0 - 5 3 11 3 0 | 9 0 0 - 19 5 0 | - 38 5 0 0 0 56 19 | 392 19

11 3 - 19 5 = 55 57 ve - 1 - 19 5 = 5 19.

x 1 x 2 x 3 x 4 3 2 1 0 | - 9 0 - 5 3 11 3 0 | 9 0 0 - 19 5 0 | - 38 5 0 0 0 56 19 | 392 19 ~

x 1 x 2 x 3 x 4 ~ 3 2 1 + 5 19 (- 19 5) 0 | - 9 + 5 19 (- 38 5) 0 - 5 3 11 3 + 55 57 (- 19 5) 0 | 9 + 55 57 (- 38 5) 0 0 - 19 5 0 | - 38 5 0 0 0 56 19 | 392 19 ~

x 1 x 2 x 3 x 4 ~ 3 2 1 0 | - 11 0 - 5 3 0 0 | 5 3 0 0 - 19 5 0 | - 38 5 0 0 0 56 19 | 392 19

Son aşamada - 2 - 5 3 = 6 5 ile çarptığımız 1. sıranın karşılık gelen elemanlarına 2. sıranın elemanlarını ekliyoruz.

x 1 x 2 x 3 x 4 3 2 1 0 | - 11 0 - 5 3 0 0 | 5 3 0 0 - 19 5 0 | - 38 5 0 0 0 56 19 | 392 19 ~

x 1 x 2 x 3 x 4 ~ 3 2 + 6 5 (- 5 3) 0 0 | - 11 + 6 5 × 5 3) 0 - 5 3 0 0 | 5 3 0 0 - 19 5 0 | - 38 5 0 0 0 56 19 | 392 19 ~

x 1 x 2 x 3 x 4 ~ 3 0 0 0 | - 9 0 - 5 3 0 0 | 5 3 0 0 - 19 5 0 | - 38 5 0 0 0 56 19 | 392 19

Ortaya çıkan matris denklem sistemine karşılık gelir

3 x 1 = - 9 - 5 3 x 2 = 5 3 - 19 5 x 3 = - 38 5 56 19 x 4 = 392 19, buradan bilinmeyen değişkenleri buluyoruz.

Cevap: x 1 = - 3, x 2 = - 1, x 3 = 2, x 4 = 7. ​

Farklı sayıda denklem ve bilinmeyene veya dejenere matris sistemine sahip SLAE'leri çözmek için Gauss yöntemini kullanmaya yönelik algoritmanın açıklaması

Tanım 2

Temel matris kare veya dikdörtgen ise denklem sistemlerinin tek bir çözümü olabilir, çözümleri olmayabilir veya sonsuz sayıda çözümü olabilir.

Bu bölümde SLAE'lerin uyumluluğunu veya uyumsuzluğunu belirlemek için Gauss yönteminin nasıl kullanılacağını ve ayrıca uyumluluk durumunda sistem için çözüm sayısını belirlemeyi öğreneceğiz.

Prensip olarak bu tür SLAE'ler için bilinmeyenleri ortadan kaldırma yöntemi aynı kalır ancak vurgulanması gereken birkaç nokta vardır.

Örnek 5

Bilinmeyenlerin elenmesinin bazı aşamalarında bazı denklemler 0=0 özdeşliğine dönüşür. Bu durumda denklemler güvenli bir şekilde sistemden çıkarılabilir ve Gauss yönteminin doğrudan ilerlemesine devam edilebilir.

2. ve 3. denklemlerden x 1'i çıkarırsak durum şu şekilde ortaya çıkar:

x 1 + 2 x 2 - x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 - 2 x 3 + 6 x 4 = 14 x - x + 3 x + x = - 1 ⇔

x 1 + 2 x 2 - x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 - 2 x 3 + 6 x 4 + (- 2) (x 1 + 2 x 2 - x 3 + 3 x 4) = 14 + (- 2) × 7 x - x + 3 x + x + (- 1) (x 1 + 2 x 2 - x 3 + 3 x 4) = - 1 + (- 1) × 7 ⇔

⇔ x 1 + 2 x 2 - x 3 + 3 x 4 = 7 0 = 0 - 3 x 2 + 4 x 3 - 2 x 4 = - 8

Buradan 2. denklemin sistemden güvenli bir şekilde çıkarılabileceği ve çözüme devam edilebileceği sonucu çıkmaktadır.

Gauss yönteminin doğrudan ilerleyişini gerçekleştirirsek, bir veya daha fazla denklem sıfırdan farklı belirli bir sayı biçimini alabilir.

Bu da 0=λ eşitliğine dönüşen denklemin değişkenlerin hiçbir değeri için eşitliğe dönüşemeyeceğini göstermektedir. Basitçe söylemek gerekirse, böyle bir sistem tutarsızdır (çözüm yoktur).

Sonuç:

• Gauss yönteminin ileri ilerlemesini gerçekleştirirken, bir veya daha fazla denklem 0 = λ formunu alırsa, burada λ sıfırdan farklı belirli bir sayıdır, bu durumda sistem tutarsızdır.
• Gauss yönteminin ileriye doğru ilerlemesinin sonunda, denklem sayısı bilinmeyenlerin sayısıyla çakışan bir sistem elde edilirse, o zaman böyle bir sistem tutarlı ve tanımlanır: bunun tersiyle hesaplanan benzersiz bir çözümü vardır. Gauss yönteminin çalıştırılması.
• Gauss yönteminin ileri gidişinin sonunda sistemdeki denklemlerin sayısı bilinmeyenlerin sayısından az çıkarsa, böyle bir sistem tutarlıdır ve sonsuz sayıda çözüme sahiptir. Gauss yönteminin ters çalışması.

Metinde bir hata fark ederseniz, lütfen onu vurgulayın ve Ctrl+Enter tuşlarına basın.

Bilinmeyenleri olan bir doğrusal cebirsel denklem sistemi (SLAE) verilmiştir. Bu sistemi çözmek gerekiyor: kaç çözümü olduğunu (hiç, bir veya sonsuz sayıda) belirlemek ve en az bir çözümü varsa bunlardan herhangi birini bulmak.

Resmi olarak Sorun şu şekilde ifade ediliyor: sistemi çözün:

katsayılar nerede ve biliniyor ve değişkenler - istenen bilinmeyenler.

Bu problemin matris gösterimi uygundur:

katsayılardan oluşan bir matris ve yüksekliğin sütun vektörleridir.

SLAE'nin gerçek sayılar alanı üzerinde değil, alan üzerinde olabileceğini belirtmekte fayda var. modulo herhangi bir sayı, yani:

— Gauss algoritması bu tür sistemler için de çalışır (ancak bu durum aşağıda ayrı bir bölümde tartışılacaktır).

Gauss algoritması

Açıkça konuşursak, aşağıda açıklanan yönteme doğru bir şekilde "Gauss-Jordan eleme" yöntemi adı verilir, çünkü bu, araştırmacı Wilhelm Jordan tarafından 1887'de tanımlanan Gauss yönteminin bir varyasyonudur (Wilhelm Jordan'ın her ikisinin de yazarı olmadığını belirtmekte fayda var). Ürdün teoremi eğrileri veya Ürdün cebiri - bunların hepsi aynı adı taşıyan üç farklı bilim adamıdır; ayrıca, görünüşe göre, "Ürdün" transkripsiyonu daha doğrudur, ancak "Ürdün" yazımı Rus literatüründe zaten oluşturulmuştur). Jordan'la eş zamanlı olarak (ve bazı verilere göre ondan da önce) bu algoritmanın B.-I. Clasen tarafından icat edildiğini belirtmek de ilginçtir.

Temel şema

Kısaca konuşursak, algoritma tutarlı dışlama Her denklemde yalnızca bir değişken kalana kadar her denklemdeki değişkenler. Eğer öyleyse, Gauss-Jordan algoritmasının sistem matrisini birim matrise indirgemeye çalıştığını söyleyebiliriz - sonuçta, matris birim matris haline geldikten sonra sistemin çözümü açıktır - çözüm benzersizdir ve belirtilmiştir elde edilen katsayılara göre.

Bu durumda, algoritma sistemin iki basit eşdeğer dönüşümüne dayanır: birincisi, iki denklem değiştirilebilir ve ikinci olarak, herhangi bir denklem, bu satırın (sıfır olmayan katsayılı) doğrusal bir kombinasyonu ile değiştirilebilir ve diğer satırlar (keyfi katsayılarla).

İlk adımda Gauss-Jordan algoritması ilk satırı bir katsayıya böler. Daha sonra algoritma, ilk satırı, ilk sütundaki katsayıları sıfıra dönecek şekilde katsayılarla kalan satırlara ekler - bunun için, açıkçası, ilk satırı -'inci satıra eklerken, onu ile çarpmanız gerekir. Bir matrisle yapılan her işlem için (bir sayıya bölme, bir satıra başka bir tane ekleme), karşılık gelen işlemler vektörle gerçekleştirilir; bir bakıma matrisin inci sütunu gibi davranıyor.

Sonuç olarak, ilk adımın sonunda, matrisin ilk sütunu bir olacak (yani, ilk satırda bir ve geri kalanında sıfırlar içerecek).

Algoritmanın ikinci adımı da benzer şekilde gerçekleştirilir, yalnızca şimdi ikinci sütun ve ikinci satır dikkate alınır: önce ikinci satır bölünür ve ardından ikinci sütunu sıfırlayacak katsayılarla diğer tüm satırlardan çıkarılır. matris.

Dönen arama

Elbette yukarıda açıklanan diyagram eksiktir. Yalnızca her -'inci adımda öğe sıfırdan farklıysa çalışır - aksi takdirde mevcut sütunda kalan katsayıların -'inci satırı ekleyerek sıfırlanmasını sağlayamayız.

Bu gibi durumlarda algoritmanın çalışmasını sağlamak için tam olarak bir süreç vardır. bir referans elemanı seçme(İngilizce'de buna tek kelimeyle "dönme" denir). İstenilen öğenin sıfırdan farklı bir sayı içermesi için matrisin satırlarının ve/veya sütunlarının yeniden düzenlenmesinden oluşur.

Bilgisayarda satırları yeniden düzenlemenin, sütunları yeniden düzenlemeye göre çok daha kolay olduğunu unutmayın: Sonuçta, iki sütunu değiştirirken, bu iki değişkenin yer değiştirdiğini hatırlamanız gerekir, böylece daha sonra yanıtı geri yüklerken hangi yanıtı doğru bir şekilde geri yükleyebilirsiniz. hangi değişkene aittir? Satırları yeniden düzenlerken bu tür ek eylemlerin gerçekleştirilmesine gerek yoktur.

Neyse ki, yöntemin doğru olması için satır değişimleri tek başına yeterlidir (hem satırlar hem de sütunlar değiştirildiğinde "tam dönme" yerine "kısmi dönme" adı verilir). Peki takas için hangi diziyi seçmelisiniz? Ve referans eleman aramasının yalnızca mevcut eleman sıfır olduğunda yapılması gerektiği doğru mu?

Bu sorunun genel bir cevabı yok. Çeşitli buluşsal yöntemler vardır ancak bunlardan (basitlik ve etki açısından) en etkili olanı şudur: sezgisel: Modülü en büyük olan eleman referans eleman olarak alınmalı ve referans elemanın aranıp onunla değiştirilmesi gerekmektedir. Her zaman ve yalnızca gerektiğinde değil (yani yalnızca olduğunda değil).

Başka bir deyişle, Gauss-Jordan algoritmasının . aşamasını kısmi dönme sezgiseli ile yürütmeden önce, . sütunda indeksleri maksimum moduloya kadar olan elemanlar arasından bulmak ve bu elemanla olan satırı th ile değiştirmek gerekir. sıra.

İlk olarak, bu buluşsal yöntem, çözüm sırasında element olsa bile SLAE'yi çözmenize izin verecektir. İkinci olarak ve oldukça önemlisi, bu buluşsal yöntem, sayısal kararlılık Gauss-Jordan algoritması.

Bu buluşsal yöntem olmadan, sistem her aşamada Gauss-Jordan algoritmasının çalışacağı şekilde olsa bile, sonuçta biriken hata o kadar büyük olabilir ki, hata boyutundaki matrisler için bile hatanın kendisi cevabı aşabilir. .

Dejenere vakalar

Dolayısıyla, kısmi dönme ile Gauss-Jordan algoritmasında durursak, o zaman sistemin dejenere olmaması (yani sıfırdan farklı bir determinantı olması, yani benzersiz bir çözümü olması) durumunda algoritmanın tartışılacağı ileri sürülür. Yukarıda anlatılanlar tamamen çalışacak ve birim matrise gelecektir (bunun kanıtı yani her zaman sıfır olmayan bir destek elemanının bulunacağının kanıtı burada verilmemiştir).

Şimdi düşünelim Genel dava- ne zaman ve mutlaka eşit değildir. 3. adımda destek elemanının bulunmadığını varsayalım. Bu, inci sütunda mevcut satırdan başlayan tüm satırların sıfır içerdiği anlamına gelir. Bu durumda bu değişkenin tanımlanamayacağı belirtiliyor ve bağımsız değişken(herhangi bir değeri alabilir). Gauss-Jordan algoritmasının sonraki tüm değişkenler için çalışmaya devam edebilmesi için, böyle bir durumda mevcut satırın sayısını artırmadan mevcut -'inci sütunu atlamanız yeterlidir (sanal olarak -'yi kaldırdığımızı söyleyebiliriz). matrisin inci sütunu).

Yani algoritmanın çalışması sırasında bazı değişkenlerin bağımsız olduğu ortaya çıkabilmektedir. Değişken sayısı denklem sayısından büyük olduğunda en azından değişkenlerin bağımsız bulunacağı açıktır.

Genel olarak, eğer en az bir bağımsız değişken bulunursa, o zaman isteğe bağlı bir değer alabilir, geri kalan (bağımlı) değişkenler ise onun aracılığıyla ifade edilecektir. Bu, reel sayılar alanında çalıştığımızda sistemin potansiyel olarak sahip olduğu anlamına gelir. sonsuz sayıda çözüm(Eğer bir SLAE modülünü dikkate alırsak, o zaman çözümlerin sayısı bu modülün bağımsız değişken sayısının kuvvetine eşit olacaktır). Ancak dikkatli olunmalıdır: bağımsız değişkenler keşfedilse bile yine de SLAE'nin hiçbir çözümü olmayabilir. Bu, kalan işlenmemiş denklemlerin (Gauss-Jordan algoritmasının ulaşamadığı denklemler, yani bunlar yalnızca bağımsız değişkenlerin kaldığı denklemler) sıfırdan farklı en az bir serbest terime sahip olması durumunda gerçekleşir.

Ancak bulunan çözümü açıkça değiştirerek bunu kontrol etmek daha kolaydır: tüm bağımsız değişkenlere sıfır değerler atayın, bulunan değerleri bağımlı değişkenlere atayın ve bu çözümü mevcut SLAE'ye değiştirin.

Uygulama

Burada Gauss-Jordan algoritmasının kısmi dönme buluşsal yöntemiyle (sütundaki maksimum olarak bir referans elemanı seçerek) bir uygulamasını sunuyoruz.

Sistem matrisinin kendisi fonksiyon girişine iletilir. Matrisin son sütunu, eski gösterimimizde, serbest katsayılar sütunudur (bu, programlamaya kolaylık sağlamak için yapıldı - çünkü algoritmanın kendisinde, serbest katsayılarla yapılan tüm işlemler, matrisle işlemleri tekrarlar).

İşlev, çözümlerin sayısını sisteme (, veya) döndürür (sonsuzluk, kodda herhangi bir büyük değere ayarlanabilecek özel bir sabitle gösterilir). En az bir çözüm varsa, o zaman vektörde döndürülür.

int gauss (vektör< vector< double >> a, vektör< double >& ans) ( int n = (int ) a.size () ; int m = (int ) a[ 0 ] .size () - 1 ; vektör< int >< m && row< n; ++ col) { int sel = row; for (int i= row; i< n; ++ i) if (abs (a[ i] [ col] ) >abs (a[ sel] [ sütun] ) ) sel = i; if (abs (a[ sel] [ sütun] )< EPS) continue ; for (int i= col; i<= m; ++ i) swap (a[ sel] [ i] , a[ row] [ i] ) ; where[ col] = row; for (int i= 0 ; i< n; ++ i) if (i ! = row) { double c = a[ i] [ col] / a[ row] [ col] ; for (int j= col; j<= m; ++ j) a[ i] [ j] - = a[ row] [ j] * c; } ++ row; } ans.assign (m, 0 ) ; for (int i= 0 ; i< m; ++ i) if (where[ i] ! = - 1 ) ans[ i] = a[ where[ i] ] [ m] / a[ where[ i] ] [ i] ; for (int i= 0 ; i< n; ++ i) { double sum = 0 ; for (int j= 0 ; j< m; ++ j) sum + = ans[ j] * a[ i] [ j] ; if (abs (sum - a[ i] [ m] ) >EPS) dönüş 0 ; ) for (int i= 0 ; i< m; ++ i) if (where[ i] == - 1 ) return INF; return 1 ; }

İşlev, geçerli sütuna ve geçerli satıra yönelik iki işaretçiyi destekler.

Ayrıca her değişken için hangi satırda yer alması gerektiğinin yazıldığı bir vektör de oluşturulur (yani her sütun için bu sütunun sıfırdan farklı olduğu satırın numarası yazılır). Bu vektör gereklidir çünkü bazı değişkenler çözüm sırasında "tanımlanmamış" olabilir (yani bunlar isteğe bağlı bir değer atanabilen bağımsız değişkenlerdir - örneğin yukarıdaki uygulamada bunlar sıfırdır).

Uygulama kısmi döndürme tekniğini kullanır, maksimum modül elemanına sahip satırı arar ve ardından bu satırı konumuna göre yeniden düzenler (her ne kadar açık satır yeniden düzenlemesi bazı dizilerde iki endeksin değiştirilmesiyle değiştirilebilirse de, pratikte bu gerçek bir kazanç sağlamayacaktır) , çünkü değişim işlemleri boşa gider).

Uygulamada, basitlik adına, mevcut satır baş elemana bölünmez - böylece algoritmanın sonunda matris bir birim matris değil köşegen bir matris haline gelir (ancak, görünüşe göre, satırı öncü öğeye bölmek, ortaya çıkan hataları bir miktar azaltmamıza olanak tanıyor).

Çözüm bulduktan sonra sistemin en az bir çözümü olup olmadığını kontrol etmek için matrise tekrar eklenir. Bulunan çözümün doğrulanması başarılıysa, işlev en az bir bağımsız değişkenin olup olmadığına bağlı olarak veya - değerini döndürür.

Asimptotikler

Ortaya çıkan algoritmanın asimptotik davranışını tahmin edelim. Algoritma, her birinde aşağıdakilerin gerçekleştiği aşamalardan oluşur:

Açıkçası, ilk nokta ikinciden daha küçük bir asimptotik davranışa sahiptir. Ayrıca ikinci noktanın birden fazla kez (SLAE'de bağımlı değişkenlerin olabileceği sayıda) gerçekleştirilmediğine dikkat edin.

Böylece, son asimptotikler algoritma şeklini alır.

Bu tahmin dönüştüğünde .

SLAE gerçek sayılar alanında değil, modülo iki alanında dikkate alındığında, sistemin çok daha hızlı çözülebileceğini unutmayın - buna aşağıdaki "SLAE modulo çözme" bölümünde bakın.

Eylem sayısının daha doğru tahmini

Zaten bildiğimiz gibi, tüm algoritmanın çalışma süresi aslında mevcut denklemin geri kalanından çıkarılması için harcanan süre ile belirlenir.

Bu, mevcut denklemin diğerlerine eklenmesiyle adımların her birinde gerçekleşebilir. Ekleme sırasında iş, mevcut olandan başlayarak yalnızca sütunlarla yapılır. Yani toplam işlemlerdir.

Eklentiler

Algoritmanın hızlandırılması: ileri ve geri vuruşlara bölünmesi

Algoritmanın ileri ve geri aşamalara bölündüğü, daha klasik olan başka bir versiyonunu dikkate alarak algoritmanın iki kat hızlanmasını sağlayabilirsiniz.

Genel olarak, yukarıda açıklanan algoritmanın aksine, matrisi köşegen forma değil, şu şekle indirgemek mümkündür: üçgen görünüm- ana köşegenin kesinlikle altındaki tüm öğeler sıfıra eşit olduğunda.

Üçgen matrisli bir sistem önemsiz bir şekilde çözülür - ilk önce, son değişkenin değeri son denklemden hemen bulunur, daha sonra bulunan değer sondan bir önceki denklemde ikame edilir ve sondan bir önceki değişkenin değeri bulunur ve böylece Açık. Bu süreç denir geri viteste Gauss algoritması.

Düz vuruş Gauss algoritması, bir istisna dışında yukarıda açıklanan Gauss-Jordan algoritmasına benzer bir algoritmadır: mevcut değişken tüm denklemlerin dışında tutulmaz, yalnızca mevcut değişkenden sonraki denklemlerden çıkarılır. Bunun sonucu aslında köşegen değil, üçgen bir matristir.

Aradaki fark ileri vuruşun işe yaramasıdır Daha hızlı Gauss-Jordan algoritması - ortalama olarak bir denklemin diğerine yarısı kadar ekleme yaptığı için. Ters vuruş, her durumda ileri vuruştan asimptotik olarak daha hızlıdır.

Böylece, eğer , o zaman bu algoritma zaten Gauss-Jordan algoritmasının yarısı kadar olan işlemleri gerçekleştirecektir.

SLAE modülünün çözümü

Modulo SLAE'leri çözmek için yukarıda açıklanan algoritmayı kullanabilirsiniz; algoritma doğruluğunu korur.

Elbette artık bir referans elemanı seçmek için herhangi bir karmaşık teknik kullanmak gereksiz hale geliyor; mevcut sütunda sıfır olmayan herhangi bir elemanı bulmak yeterlidir.

Modül basitse, hiçbir zorluk ortaya çıkmaz - Gauss algoritmasının çalışması sırasında meydana gelen bölünmeler herhangi bir özel sorun yaratmaz.

Özellikle dikkat çekici ikiye eşit modül: Onun için matrisle yapılan tüm işlemler çok verimli bir şekilde gerçekleştirilebiliyor. Örneğin, bir diziyi diğer modülo ikiden çıkarmak aslında onların simetrik farkıdır (“xor”). Böylece, tüm matrisin bit maskeleri halinde sıkıştırılması ve yalnızca bunlarla çalışılmasıyla algoritmanın tamamı önemli ölçüde hızlandırılabilir. Gauss-Jordan algoritmasının ana bölümünün standart C++ "bitset" kapsayıcısını kullanan yeni bir uygulaması:

int gauss (vektör< bitset< N>> a, int n, int m, bit kümesi< N>& cevap) (vektör< int >burada (m, -1 ) ; for (int sütun= 0, satır= 0; sütun< m && row< n; ++ col) { for (int i= row; i< n; ++ i) if (a[ i] [ col] ) { swap (a[ i] , a[ row] ) ; break ; } if (! a[ row] [ col] ) continue ; where[ col] = row; for (int i= 0 ; i< n; ++ i) if (i ! = row && a[ i] [ col] ) a[ i] ^ = a[ row] ; ++ row; }

Gördüğünüz gibi, eski uygulamadan çok daha hızlı olmasına rağmen, yani bit sıkıştırması nedeniyle birkaç kat daha hızlı olmasına rağmen uygulama biraz daha kısa hale geldi. Ayrıca, modülo iki sistem çözümünün pratikte çok hızlı çalıştığına da dikkat edilmelidir, çünkü bir satırdan diğerini çıkarmanın gerekli olduğu durumlar oldukça nadiren meydana gelir (seyrek matrislerde, bu algoritma, kare sırasına göre bir zamanda çalışabilir). küp yerine boyut).

Eğer modül keyfi(mutlaka basit olması gerekmez), o zaman her şey biraz daha karmaşık hale gelir. Çin kalan teoremini kullanarak, rastgele bir modülle ilgili sorunu yalnızca "asallık derecesi" biçimindeki modüllere indirgeyeceğimiz açıktır. [daha fazla metin gizlendi çünkü Bu doğrulanmamış bir bilgidir - belki de çözmenin yanlış yolu ]

Son olarak soruya bakalım SLAE çözümlerinin sayısı modulo. Bunun cevabı oldukça basittir: Çözüm sayısı eşittir, burada modül ve bağımsız değişken sayısıdır.

Bir destek elemanı seçmenin farklı yolları hakkında biraz

Yukarıda da belirttiğimiz gibi bu sorunun net bir cevabı yok.

Geçerli sütundaki maksimum öğeyi bulmayı içeren "kısmi dönme" buluşsal yöntemi pratikte oldukça iyi çalışıyor. Ayrıca, pivot elemanı geçerli satırdan ve geçerli sütundan başlayarak tüm alt matrisin elemanları arasında arandığında "tam dönme" ile neredeyse aynı sonucu verdiği ortaya çıktı.

Ancak bu maksimum öğe buluşsal yöntemlerinin her ikisinin de aslında orijinal denklemlerin nasıl ölçeklendirildiğine oldukça bağlı olduğunu belirtmek ilginçtir. Örneğin sistemin denklemlerinden biri bir milyonla çarpılırsa, ilk adımda bu denklem neredeyse kesinlikle önde gelen denklem olarak seçilecektir. Bu oldukça garip görünüyor, bu yüzden biraz daha karmaşık bir buluşsal yönteme geçmek mantıklıdır - sözde "örtük dönme".

Örtülü dönmenin buluşsal yöntemi, farklı satırların öğelerinin, sanki her iki satır da içlerindeki maksimum öğe bire eşit olacak şekilde normalleştirilmiş gibi karşılaştırılmasıdır. Bu tekniği uygulamak için, her satırdaki mevcut maksimum değeri korumanız yeterlidir (veya her satırı, içindeki maksimum mutlak değerde bire eşit olacak şekilde koruyun, ancak bu, birikmiş hatanın artmasına neden olabilir).

Bulunan yanıtın iyileştirilmesi

Çünkü çeşitli buluşsal yöntemlere rağmen Gauss-Jordan algoritması - mertebesinde boyutlarda bile özel matrislerde hala büyük hatalara yol açabilir.

Bu bağlamda, Gauss-Jordan algoritmasıyla elde edilen cevap, buna bazı basit sayısal yöntemlerin (örneğin, basit yineleme yöntemi) uygulanmasıyla geliştirilebilir.

Böylece çözüm iki adımlı bir çözüme dönüşür: Önce Gauss-Jordan algoritması çalıştırılır, ardından ilk adımda elde edilen çözümü başlangıç ​​verisi olarak alan bazı sayısal yöntemler gerçekleştirilir.

Bu teknik, Gauss-Jordan algoritması tarafından çözülen problemler kümesini kabul edilebilir bir hatayla bir miktar genişletmemize olanak tanır.

Edebiyat

• William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery. Sayısal Tarifler: Bilimsel Hesaplama Sanatı
• Anthony Ralston, Philip Rabinowitz. Sayısal analizde ilk ders