2020-yil iyul oyida NASA Marsga ekspeditsiyani boshlaydi. Koinot kemasi Marsga ekspeditsiyaning barcha ro‘yxatdan o‘tgan a’zolarining ismlari yozilgan elektron tashuvchini yetkazadi.

Ishtirokchilarni ro'yxatga olish ochiq. Marsga chiptani ushbu havola orqali oling.

Agar ushbu post muammoingizni hal qilgan bo'lsa yoki sizga shunchaki yoqqan bo'lsa, unga havolani ijtimoiy tarmoqlardagi do'stlaringiz bilan baham ko'ring.

Ushbu kod variantlaridan birini nusxalash va veb-sahifa kodingizga joylashtirish kerak, yaxshisi teglar orasiga yoki tegdan keyin. Birinchi variantga ko'ra, MathJax tezroq yuklanadi va sahifani kamroq sekinlashtiradi. Ammo ikkinchi variant MathJax-ning so'nggi versiyalarini avtomatik ravishda kuzatib boradi va yuklaydi. Agar siz birinchi kodni kiritsangiz, uni vaqti-vaqti bilan yangilab turish kerak bo'ladi. Agar siz ikkinchi kodni joylashtirsangiz, sahifalar sekinroq yuklanadi, lekin siz MathJax yangilanishlarini doimiy ravishda kuzatib borishingiz shart emas.

MathJax-ni ulashning eng oson yo'li Blogger yoki WordPress-da: saytni boshqarish paneliga uchinchi tomon JavaScript kodini kiritish uchun mo'ljallangan vidjetni qo'shing, unga yuqoridagi yuklash kodining birinchi yoki ikkinchi versiyasini nusxalang va vidjetni yaqinroq joylashtiring. shablonning boshlanishi (Aytgancha, bu umuman kerak emas, chunki MathJax skripti asinxron ravishda yuklangan). Ana xolos. Endi MathML, LaTeX va ASCIIMathML belgilash sintaksisini o'rganing va siz matematik formulalarni veb-sahifalaringizga joylashtirishga tayyorsiz.

Yana bir yangi yil kechasi... sovuq ob-havo va deraza oynasidagi qor parchalari... Bularning barchasi meni yana... fraktallar va Volfram Alfa bu haqda nima bilishi haqida yozishga undadi. Shu munosabat bilan qiziqarli maqola bor, unda ikki o'lchovli fraktal tuzilmalarning misollari mavjud. Bu erda biz uch o'lchovli fraktallarning yanada murakkab misollarini ko'rib chiqamiz.

Fraktalni geometrik shakl yoki jism sifatida ko'rish (ta'riflash) mumkin (ya'ni ikkalasi ham to'plam, bu holda nuqtalar to'plami), uning tafsilotlari asl shaklning o'zi bilan bir xil shaklga ega. Ya'ni, bu o'ziga o'xshash tuzilma bo'lib, uning tafsilotlarini hisobga olsak, kattalashganda, biz kattalashtirilmagan shaklni ko'ramiz. Oddiy geometrik figuraga (fraktal emas) kelsak, kattalashganda, biz asl figuraning o'zidan oddiyroq shaklga ega bo'lgan tafsilotlarni ko'ramiz. Masalan, etarlicha yuqori kattalashtirishda ellipsning bir qismi to'g'ri chiziq segmentiga o'xshaydi. Fraktallar bilan bu sodir bo'lmaydi: ulardagi har qanday o'sish bilan biz yana bir xil murakkab shaklni ko'ramiz, bu har bir o'sish bilan yana va yana takrorlanadi.

Fraktallar fanining asoschisi Benua Mandelbrot o'zining "Fraktallar va fan uchun san'at" maqolasida shunday deb yozgan edi: "Fraktallar umumiy shaklida bo'lgani kabi, tafsilotlari jihatidan ham murakkab geometrik shakllardir. Ya'ni, fraktal irodaning bir qismi bo'lsa. butunning o'lchamiga kattalashtirilsa, u butunga o'xshaydi, yoki aniq, yoki ehtimol, engil deformatsiya bilan ko'rinadi.

Ta'rif. Ikki o'zgaruvchili funktsiyaning ekstremum nuqtalari Bu funksiyaning minimal va maksimal nuqtalari. Ekstremum nuqtalardagi funktsiyaning o'zi qiymatlari deyiladi ikki o'zgaruvchili funktsiyaning ekstremasi .

Ta'rif. Nuqta P(x 0 , y 0) deyiladi z = z(x, y), agar funktsiyaning bu nuqtadagi qiymati uning qo'shni nuqtalaridagidan katta bo'lsa. Funksiyaning maksimal nuqtadagi qiymati deyiladi ikkita o'zgaruvchining funksiyasining maksimali .

Ta'rif. Nuqta P(x 0 , y 0) deyiladi ikkita o'zgaruvchili funktsiyaning maksimal nuqtasi z = z(x, y), agar funktsiyaning bu nuqtadagi qiymati uning qo'shni nuqtalaridagidan katta bo'lsa. Funktsiya qiymati maksimal nuqtada ikki o‘zgaruvchili funksiyaning maksimali deyiladi .

Teorema (ikki o'zgaruvchining funksiyasi ekstremumining zaruriy mezoni). Agar nuqta P(x 0 , y 0 ) - ikkita o'zgaruvchili funktsiyaning ekstremum nuqtasi z = z(x, y), u holda funktsiyaning birinchi qisman hosilalari ("x" va "y" ga nisbatan) bu nuqtada nolga teng yoki mavjud emas:

Ta'rif. Ikki o‘zgaruvchi funksiyaning birinchi qisman hosilalari nolga teng bo‘lgan nuqta deyiladi. statsionar nuqtalar .

Ta'rif. Ikki o'zgaruvchining funksiyasining birinchi qisman hosilalari nolga teng yoki mavjud bo'lmagan nuqta deyiladi. tanqidiy nuqtalar .

Bitta o'zgaruvchili funktsiyada bo'lgani kabi, ikkita o'zgaruvchining funktsiyasi ekstremumining mavjudligi uchun zarur shart etarli emas. Funktsiyaning birinchi qisman hosilasi nolga teng yoki mavjud bo'lmagan juda ko'p funktsiyalar mavjud, ammo tegishli nuqtalarda ekstremallar yo'q. Har bir ekstremal nuqta tanqidiy nuqtadir, lekin har bir tanqidiy nuqta ekstremum emas .

Ikki o'zgaruvchili funktsiyaning ekstremum mavjudligi uchun etarli mezon. Shu nuqtada P Ikki o‘zgaruvchili funksiyaning ekstremumi mavjud bo‘ladi, agar shu nuqtaga yaqin joyda funksiyaning umumiy o‘sish belgisi o‘zgarmasa. Kritik nuqtada birinchi umumiy differentsial nolga teng bo'lganligi sababli, funktsiyaning o'sishi ikkinchi to'liq differentsialni aniqlaydi.

Umumiy differensialni qo'llashni eng yaxshi tushunish ushbu darsning ikkinchi nuqtasidan keyingi ikkita o'zgaruvchili funktsiyaning ekstremallarini topish algoritmining 3 va 4-bosqichlarini o'rganish va mashq qilishdan kelib chiqadi.

Ikki o'zgaruvchili funktsiya ekstremasining mahalliy tabiati. Funksiyaning taʼrif sohasining istalgan qismidagi ikkita oʻzgaruvchidan iborat funksiyaning maksimali barcha taʼrif sohasi uchun maksimal boʻlishi shart emas, xuddi har qanday boʻlimdagi minimal ham butun taʼrif sohasida minimal boʻlmaganidek. Keling, dengizning qirg'oq zonasidagi to'lqinlarning balandligini ko'rib chiqaylik (hudud hududdan kichikroq). Keyin ushbu bo'limda biz eng yuqori to'lqin balandligini (hech bo'lmaganda vizual ravishda) tuzatishimiz mumkin. Ammo shamol kattaroq to'lqin balandligini keltirib chiqaradigan boshqa qismda biz minimal to'lqin balandligini o'rnatamiz. Bu birinchi qismdagi maksimal to'lqin balandligi ikkinchi qismdagi minimal to'lqin balandligidan kamroq bo'lishi mumkinligini anglatadi. Shuning uchun, bitta o'zgaruvchining funksiyasining ekstremumidagi kabi, bu tushunchaga aniqlik kiritish va ekstremalarni ikki o'zgaruvchili funktsiyaning mahalliy ekstremasi sifatida gapirish kerak.

Ikki o'zgaruvchili funktsiyaning ekstremasini topish algoritmi katta qiziqish uyg'otadi, chunki birinchidan, u bitta o'zgaruvchining funksiyasining ekstremasini topish algoritmidan farq qiladi, ikkinchidan, unga o'xshashlik bo'yicha algoritm tuzish mumkin. uchta o'zgaruvchining funksiyasini topish uchun. Xususan, determinantlarni hisoblash kerak bo'ladi.

Shunday qilib, ikkita o'zgaruvchili funktsiyaning ekstremalini topish algoritmi.

Ikki o'zgaruvchining funktsiyasi berilgan.

2-qadam. Ushbu hosilalarning tengliklaridan nolga tenglamalar tizimini tuzamiz (ularning nolga tengligi ekstremum mavjudligining zaruriy belgisidir):

Bu tenglamalar tizimining yechimlari mumkin bo'lgan ekstremum nuqtalari - kritik nuqtalardir.

3-qadam. 2-bosqichda topilgan kritik nuqta bo‘lsin. Unda ikkita o‘zgaruvchi funksiyasining ekstremumi borligiga ishonch hosil qilish uchun ikkinchi tartibli qisman hosilalarni topamiz.

1-bosqichda topilgan birinchi tartibli qisman hosilalarning qisman hosilalari sifatida.

4-qadam. 3-bosqichda topilgan ikkinchi tartibli qisman hosilalarni harf belgilariga belgilaymiz:

4-qadam. Aniqlovchini toping:

, ya'ni topilgan kritik nuqtada ekstremum yo'q,

va, ya'ni topilgan kritik nuqtada ikkita o'zgaruvchining minimal funktsiyasi mavjud,

va, ya'ni topilgan kritik nuqtada ikkita o'zgaruvchining maksimal funktsiyasi mavjud.

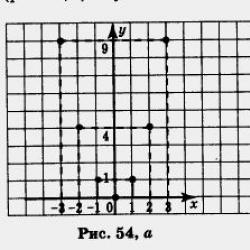
Keling, y \u003d x 3 - 3x 2 funktsiyasining grafigiga murojaat qilaylik. x = 0 nuqtasining qo'shniligini ko'rib chiqing, ya'ni. bu nuqtani o'z ichiga olgan ba'zi interval. X \u003d 0 nuqtasining shunday qo'shnisi borligi mantiqan to'g'ri, bu qo'shnilikdagi y \u003d x 3 - 3x 2 funktsiyasi x \u003d 0 nuqtasida eng katta qiymatni oladi. Masalan, intervalda (- 1; 1) 0 ga teng bo'lgan eng katta qiymat, funktsiya x = 0 nuqtada oladi. x = 0 nuqtasi bu funktsiyaning maksimal nuqtasi deyiladi.

Xuddi shunday, x \u003d 2 nuqtasi x 3 - 3x 2 funktsiyasining minimal nuqtasi deb ataladi, chunki bu nuqtada funktsiyaning qiymati x \u003d 2 nuqtasi yaqinidagi boshqa nuqtadagi qiymatidan katta emas. , masalan, mahalla (1,5; 2,5).

Shunday qilib, x 0 nuqtasi f (x) funksiyaning maksimal nuqtasi deyiladi, agar x 0 nuqtaning qo'shnisi bo'lsa - shundayki f (x) ≤ f (x 0) tengsizlik bundan barcha x uchun qanoatlantiriladi. Turar joy dahasi.

Masalan, x 0 \u003d 0 nuqtasi f (x) \u003d 1 - x 2 funktsiyasining maksimal nuqtasidir, chunki f (0) \u003d 1 va f (x) ≤ 1 tengsizlik barcha qiymatlar uchun to'g'ri. x dan.

Agar x 0 nuqtaning shunday qo'shnisi mavjud bo'lsa, f (x) funktsiyaning minimal nuqtasi x 0 nuqtasi deb ataladi, bu qo'shnilikdagi barcha x uchun f (x) ≥ f (x 0) tengsizlik qanoatlantiriladi.

Masalan, x 0 \u003d 2 nuqtasi f (x) \u003d 3 + (x - 2) 2 funktsiyasining minimal nuqtasidir, chunki barcha x uchun f (2) \u003d 3 va f (x) ≥ 3 .

Ekstremal nuqtalar minimal nuqtalar va maksimal nuqtalar deb ataladi.

X 0 nuqtaning qaysidir qo'shnisida aniqlangan va shu nuqtada hosilasi bo'lgan f(x) funksiyaga murojaat qilaylik.

Agar x 0 differensiallanuvchi f (x) funksiyaning ekstremum nuqtasi bo'lsa, u holda f "(x 0) \u003d 0. Bu bayonot Ferma teoremasi deb ataladi.

Ferma teoremasi aniq geometrik ma'noga ega: ekstremum nuqtada tangens x o'qiga parallel va shuning uchun uning qiyaligi.
f "(x 0) nolga teng.

Masalan, f (x) \u003d 1 - 3x 2 funktsiyasi x 0 \u003d 0 nuqtasida maksimalga ega, uning hosilasi f "(x) \u003d -2x, f "(0) \u003d 0.

f (x) \u003d (x - 2) 2 + 3 funktsiyasi x 0 \u003d 2, f "(x) \u003d 2 (x - 2), f "(2) \u003d 0 nuqtasida minimal qiymatga ega. .

E'tibor bering, agar f "(x 0) \u003d 0 bo'lsa, bu x 0 f (x) funktsiyasining ekstremum nuqtasi ekanligini ta'kidlash uchun etarli emas.

Masalan, agar f (x) \u003d x 3 bo'lsa, f "(0) \u003d 0. Biroq, x \u003d 0 nuqtasi ekstremum nuqta emas, chunki x 3 funktsiyasi butun haqiqiy o'qda ortadi.

Demak, differensiallanuvchi funksiyaning ekstremum nuqtalarini faqat tenglamaning ildizlari orasidan izlash kerak.
f "(x) \u003d 0, lekin bu tenglamaning ildizi har doim ham ekstremal nuqta emas.

Statsionar nuqtalar - bu funktsiyaning hosilasi nolga teng bo'lgan nuqtalar.

Shunday qilib, x 0 nuqta ekstremum nuqta bo'lishi uchun uning statsionar nuqta bo'lishi kerak.

Statsionar nuqta ekstremum nuqtasi bo'lishi uchun etarli shartlarni ko'rib chiqing, ya'ni. statsionar nuqta funktsiyaning minimal yoki maksimal nuqtasi bo'lgan shartlar.

Agar statsionar nuqtaning chap tomonidagi hosila ijobiy bo'lsa, o'ngda esa salbiy bo'lsa, ya'ni. hosilaviy o'zgarishlar bu nuqtadan o'tayotganda "+" belgisini "-" belgisiga qo'yadi, keyin bu statsionar nuqta maksimal nuqta hisoblanadi.

Haqiqatan ham, bu holda, statsionar nuqtaning chap tomonida, funktsiya ortadi va o'ngda, u kamayadi, ya'ni. bu nuqta maksimal nuqtadir.

Agar lotin statsionar nuqtadan o'tganda "-" belgisini "+" belgisiga o'zgartirsa, u holda bu statsionar nuqta minimal nuqta hisoblanadi.

Agar lotin statsionar nuqtadan o'tganda belgisini o'zgartirmasa, ya'ni. lotin statsionar nuqtaning chap va o'ng tomonida ijobiy yoki salbiy bo'lsa, bu nuqta ekstremum nuqta emas.

Keling, muammolardan birini ko'rib chiqaylik. f (x) \u003d x 4 - 4x 3 funktsiyasining ekstremum nuqtalarini toping.

Yechim.

1) hosilani toping: f "(x) \u003d 4x 3 - 12x 2 \u003d 4x 2 (x - 3).

2) Statsionar nuqtalarni toping: 4x 2 (x - 3) \u003d 0, x 1 \u003d 0, x 2 \u003d 3.

3) Intervalli usuldan foydalanib, f "(x) \u003d 4x 2 (x - 3) hosilasi x\u003e 3 uchun ijobiy, x uchun salbiy ekanligini aniqlaymiz.< 0 и при 0 < х < 3.

4) x 1 \u003d 0 nuqtasidan o'tayotganda hosilaning belgisi o'zgarmasligi sababli, bu nuqta ekstremum nuqta emas.

5) hosila x 2 \u003d 3 nuqtadan o'tayotganda "-" belgisini "+" belgisiga o'zgartiradi. Shuning uchun x 2 \u003d 3 minimal nuqtadir.

sayt, materialni to'liq yoki qisman nusxalash bilan, manbaga havola talab qilinadi.

Funktsiya va uning xususiyatlarini o'rganish zamonaviy matematikaning asosiy boblaridan birini egallaydi. Har qanday funktsiyaning asosiy komponenti nafaqat uning xossalarini, balki ushbu funktsiya hosilasining parametrlarini ham tasvirlaydigan grafiklardir. Keling, ushbu qiyin mavzuni ko'rib chiqaylik. Xo'sh, funktsiyaning maksimal va minimal nuqtalarini topishning eng yaxshi usuli qanday?

Qaysidir ma'noda boshqa miqdorning qiymatlariga bog'liq bo'lgan har qanday o'zgaruvchini funktsiya deb atash mumkin. Masalan, f(x 2) funktsiyasi kvadratik bo'lib, butun x to'plamining qiymatlarini aniqlaydi. Aytaylik, x = 9, u holda bizning funktsiyamizning qiymati 9 2 = 81 ga teng bo'ladi.

Funktsiyalar turli xil bo'ladi: mantiqiy, vektor, logarifmik, trigonometrik, raqamli va boshqalar. Ularni o'rganish bilan Lakroix, Lagranj, Leybnits va Bernulli kabi buyuk aql egalari shug'ullangan. Ularning yozuvlari funktsiyalarni o'rganishning zamonaviy usullarida qo'rg'on bo'lib xizmat qiladi. Minimal nuqtalarni topishdan oldin, funktsiya va uning hosilasining ma'nosini tushunish juda muhimdir.

Barcha funktsiyalar o'z o'zgaruvchilariga bog'liq, ya'ni ular istalgan vaqtda o'z qiymatini o'zgartirishi mumkin. Grafikda bu y o'qi bo'ylab tushadigan yoki ko'tariladigan egri chiziq sifatida tasvirlanadi (bu grafikning vertikali bo'ylab "y" raqamlarining butun to'plami). Shunday qilib, maksimal va minimal funktsiya nuqtasining ta'rifi aynan shu "tebranishlar" bilan bog'liq. Keling, bu munosabatlar nima ekanligini tushuntiramiz.

Har qanday funksiyaning hosilasi uning asosiy xarakteristikalarini o‘rganish va funksiyaning qanchalik tez o‘zgarishini (ya’ni “x” o‘zgaruvchisiga qarab qiymatini o‘zgartirishini) hisoblash uchun chiziladi. Funksiya oshgan paytda uning hosilasi grafigi ham ortadi, lekin istalgan soniyada funktsiya pasayishni boshlashi mumkin, keyin esa hosila grafigi kamayadi. Hosila minusdan plyusga o'tadigan nuqtalar minimal nuqtalar deb ataladi. Minimal ballarni qanday topishni bilish uchun siz yaxshiroq tushunishingiz kerak

Ta'rif va funktsiyalardan bir nechta tushunchalarni nazarda tutadi Umuman olganda, hosilaning ta'rifini quyidagicha ifodalash mumkin: bu funktsiyaning o'zgarish tezligini ko'rsatadigan qiymat.

Ko'pgina talabalar uchun uni aniqlashning matematik usuli murakkab ko'rinadi, lekin aslida hamma narsa ancha sodda. Har qanday funktsiyaning hosilasini topish uchun faqat standart rejaga amal qilish kerak. Quyida funktsiyaning minimal nuqtasini differentsiallash qoidalarini qo'llamasdan va hosilalar jadvalini yodlamasdan qanday topish mumkinligi tasvirlangan.

Maktab matematika dasturida funksiyaning minimal nuqtasini ikki usulda topish mumkin. Biz allaqachon grafik yordamida birinchi usulni tahlil qildik, lekin lotinning raqamli qiymatini qanday aniqlash mumkin? Buni amalga oshirish uchun siz lotinning xususiyatlarini tavsiflovchi va "x" kabi o'zgaruvchilarni raqamlarga aylantirishga yordam beradigan bir nechta formulalarni o'rganishingiz kerak bo'ladi. Quyidagi usul universaldir, shuning uchun uni deyarli barcha turdagi funktsiyalarga (ham geometrik, ham logarifmik) qo'llash mumkin.

Funksiya va uning hosilasini o‘rganishda eng asosiy komponent bu differentsiallanish qoidalarini bilishdir. Faqat ularning yordami bilan noqulay ifodalarni va katta murakkab funktsiyalarni o'zgartirish mumkin. Keling, ular bilan tanishamiz, ular juda ko'p, lekin ularning barchasi kuch va logarifmik funktsiyalarning muntazam xususiyatlari tufayli juda oddiy.

Biz allaqachon minimal nuqtalarni qanday topishni muhokama qildik, ammo funktsiyaning maksimal nuqtalari tushunchasi mavjud. Agar minimal funktsiya minusdan plyusga o'tadigan nuqtalarni bildirsa, u holda maksimal nuqtalar x o'qidagi nuqtalar bo'lib, bunda funktsiya hosilasi plyusdan teskarisiga - minusga o'zgaradi.

Siz uni yuqorida tavsiflangan usul yordamida topishingiz mumkin, faqat shuni hisobga olish kerakki, ular funktsiya pasayishni boshlaydigan joylarni bildiradi, ya'ni lotin noldan kichik bo'ladi.

Matematikada ikkala tushunchani umumlashtirish, ularni "ekstrema nuqtalari" iborasi bilan almashtirish odatiy holdir. Vazifa ushbu nuqtalarni aniqlashni so'rasa, bu ushbu funktsiyaning hosilasini hisoblash va minimal va maksimal nuqtalarni topish kerakligini anglatadi.

Funksiyaning ekstremum nuqtasi funksiyaning qiymati minimal yoki maksimal qiymatni qabul qiladigan funktsiya sohasi nuqtasidir. Ushbu nuqtalardagi funktsiya qiymatlari funktsiyaning ekstremal (minimal va maksimal) deb ataladi.

Ta'rif. Nuqta x 1 funksiya doirasi f(x) deyiladi funktsiyaning maksimal nuqtasi, agar funktsiyaning ushbu nuqtadagi qiymati unga etarlicha yaqin bo'lgan, uning o'ng va chap tomonida joylashgan nuqtalardagi funktsiya qiymatlaridan katta bo'lsa (ya'ni, tengsizlik) f(x 0 ) > f(x 0 + Δ x) x 1 maks.

Ta'rif. Nuqta x 2 ta funksiya doirasi f(x) funktsiyaning minimal nuqtasi deyiladi, agar funktsiyaning ushbu nuqtadagi qiymati unga etarlicha yaqin bo'lgan, uning o'ng va chap tomonida joylashgan nuqtalardagi funktsiya qiymatlaridan kichik bo'lsa (ya'ni tengsizlik). f(x 0 ) < f(x 0 + Δ x)). Bu holda funksiya nuqtada mavjud deyiladi x 2 minimal.

Keling, fikrni aytaylik x 1 - funksiyaning maksimal nuqtasi f(x). Keyin gacha bo'lgan oraliqda x 1 funktsiya ortib bormoqda, shuning uchun funktsiyaning hosilasi noldan katta ( f "(x) > 0 ) va undan keyingi oraliqda x 1 funktsiya kamayib bormoqda, shuning uchun funktsiyaning hosilasi noldan kichik ( f "(x) < 0 ). Тогда в точке x 1

Keling, fikrni ham taxmin qilaylik x 2 - funktsiyaning minimal nuqtasi f(x). Keyin gacha bo'lgan oraliqda x 2 funktsiya kamayib bormoqda va funktsiyaning hosilasi noldan kichik ( f "(x) < 0 ), а в интервале после x 2 funktsiya ortib bormoqda va funktsiyaning hosilasi noldan katta ( f "(x) > 0). Bu holatda ham nuqtada x 2 funksiyaning hosilasi nolga teng yoki mavjud emas.

Ferma teoremasi (funksiya ekstremumining mavjudligi uchun zaruriy mezon). Agar nuqta x 0 - funktsiyaning ekstremum nuqtasi f(x), u holda bu nuqtada funktsiyaning hosilasi nolga teng ( f "(x) = 0 ) yoki mavjud emas.

Ta'rif. Funktsiyaning hosilasi nolga teng yoki mavjud bo'lmagan nuqtalar deyiladi tanqidiy nuqtalar .

Misol 1. Funktsiyani ko'rib chiqing.

Shu nuqtada x= 0 funktsiyaning hosilasi nolga teng, shuning uchun nuqta x= 0 kritik nuqtadir. Biroq, funktsiyaning grafigida ko'rinib turganidek, u ta'rifning butun sohasida ortadi, shuning uchun nuqta x= 0 bu funksiyaning ekstremum nuqtasi emas.

Shunday qilib, nuqtadagi funktsiya hosilasi nolga teng yoki mavjud bo'lmagan shartlar ekstremum uchun zarur shartlardir, lekin etarli emas, chunki bu shartlar qondiriladigan funktsiyalarga boshqa misollar keltirilishi mumkin, lekin funktsiya. tegishli nuqtada ekstremumga ega emas. Shuning uchun ma'lum bir tanqidiy nuqtada ekstremum mavjudligini va qaysi biri - maksimal yoki minimal ekanligini aniqlash uchun etarli belgilarga ega bo'lish kerak.

Teorema (funksiya ekstremumining mavjudligi uchun birinchi etarli mezon). Kritik nuqta x 0 f(x) , agar funktsiyaning hosilasi bu nuqtadan o'tganda ishorani o'zgartirsa va ishora "ortiqcha" dan "minus" ga o'zgartirilsa, u holda maksimal nuqta, "minus" dan "ortiqcha" ga o'tsa, minimal nuqta. .

Agar nuqtaga yaqin bo'lsa x 0 , uning chap va o'ng tomonida hosila o'z belgisini saqlab qoladi, bu funktsiya nuqtaning ba'zi qo'shnilarida faqat kamayadi yoki faqat ortadi degan ma'noni anglatadi. x 0 . Bunday holda, nuqtada x 0 ekstremum yo'q.

Shunday qilib, funktsiyaning ekstremum nuqtalarini aniqlash uchun siz quyidagilarni bajarishingiz kerak :

2-misol. Funksiyaning ekstremallarini toping .

Yechim. Funktsiyaning hosilasini topamiz:

Kritik nuqtalarni topish uchun hosilani nolga tenglang:

.

"X" ning har qanday qiymatlari uchun maxraj nolga teng bo'lmaganligi sababli, hisoblagichni nolga tenglashtiramiz:

Bitta muhim nuqta bor x= 3. Ushbu nuqta bilan chegaralangan oraliqlarda hosilaning belgisini aniqlaymiz:

minus cheksizlikdan 3 gacha - minus belgisi, ya'ni funktsiya kamayadi,

3 dan ortiqcha cheksizlik oralig'ida - ortiqcha belgisi, ya'ni funktsiya ortadi.

Ya'ni nuqta x= 3 - minimal nuqta.

Funksiyaning minimal nuqtadagi qiymatini toping:

Shunday qilib, funksiyaning ekstremum nuqtasi topiladi: (3; 0) va u minimal nuqtadir.

Teorema (funksiya ekstremumining mavjudligi uchun ikkinchi etarli mezon). Kritik nuqta x 0 - funksiyaning ekstremum nuqtasi f(x), agar funktsiyaning bu nuqtadagi ikkinchi hosilasi nolga teng bo'lmasa ( f ""(x) ≠ 0 ), bundan tashqari, agar ikkinchi hosila noldan katta bo'lsa ( f ""(x) > 0 ), u holda maksimal nuqta va agar ikkinchi hosila noldan kichik bo'lsa ( f ""(x) < 0 ), то точкой минимума.

Izoh 1. Agar biror nuqtada x 0 bo'lsa, birinchi va ikkinchi hosilalar yo'qoladi, keyin bu nuqtada ikkinchi etarli belgisi asosida ekstremum mavjudligini hukm qilish mumkin emas. Bunday holda, siz funktsiyaning ekstremumi uchun birinchi etarli mezondan foydalanishingiz kerak.

Izoh 2. Birinchi hosila statsionar nuqtada mavjud bo'lmaganda (keyin ikkinchi hosila ham mavjud emas) funksiya ekstremumining ikkinchi yetarli mezoni ham qo'llanilmaydi. Bunda funksiyaning ekstremumi uchun birinchi yetarli mezondan ham foydalanish kerak.

Yuqoridagi ta'riflardan kelib chiqadiki, funktsiyaning ekstremumi mahalliy xususiyatga ega - bu eng yaqin qiymatlarga nisbatan funktsiyaning eng katta va eng kichik qiymati.

Aytaylik, siz bir yil ichida daromadingizni ko'rib chiqasiz. Agar may oyida siz 45 000 rubl, aprel oyida 42 000 rubl va iyun oyida 39 000 rubl ishlagan bo'lsangiz, may oyidagi daromad eng yaqin qiymatlarga nisbatan daromad funktsiyasining maksimal ko'rsatkichidir. Ammo oktyabr oyida siz 71 000 rubl, sentyabrda 75 000 rubl va noyabrda 74 000 rubl ishlab oldingiz, shuning uchun oktyabr oyidagi daromadlar yaqin qiymatlarga nisbatan daromad funktsiyasining minimalidir. Va aprel-may-iyun oylaridagi qiymatlar orasidagi maksimal sentyabr-oktyabr-noyabr oylarining minimalidan kamroq ekanligini osongina ko'rishingiz mumkin.

Umuman olganda, funktsiya oraliqda bir nechta ekstremallarga ega bo'lishi mumkin va funktsiyaning istalgan minimali har qanday maksimaldan katta bo'lishi mumkin. Shunday qilib, yuqoridagi rasmda ko'rsatilgan funktsiya uchun.

Ya'ni, funktsiyaning maksimal va minimal qiymatlari ko'rib chiqilayotgan butun segment bo'yicha mos ravishda uning maksimal va minimal qiymatlari deb o'ylamaslik kerak. Maksimal nuqtada funktsiya barcha nuqtalarda maksimal nuqtaga etarlicha yaqin bo'lgan qiymatlarga nisbatan eng katta qiymatga ega bo'ladi va minimal nuqtada faqat shu qiymatlarga nisbatan eng kichik qiymatga ega. uning barcha nuqtalarida minimal nuqtaga etarlicha yaqin bo'lishi.

Shuning uchun biz yuqorida berilgan funksiyaning ekstremum nuqtalari tushunchasini takomillashtirishimiz va minimal nuqtalarni mahalliy minimal nuqtalar, maksimal nuqtalarni esa mahalliy maksimal nuqtalar deb atashimiz mumkin.

3-misol

Yechish.Funksiya butun sonlar qatorida aniqlangan va uzluksiz. Uning hosilasi butun son qatorida ham mavjud. Shuning uchun, bu holda, faqat o'shalar, ya'ni tanqidiy nuqtalar bo'lib xizmat qiladi. , qaerdan va . Kritik nuqtalar va funksiyaning butun sohasini uchta monotonlik oralig'iga bo'ling: . Ularning har birida bitta nazorat nuqtasini tanlaymiz va shu nuqtada hosila belgisini topamiz.

Interval uchun mos yozuvlar nuqtasi bo'lishi mumkin: biz topamiz. Intervaldagi nuqtani olib, biz ga ega bo'lamiz va oraliqdagi nuqtani olamiz. Shunday qilib, intervallarda va , va intervalda . Ekstremumning birinchi yetarli belgisiga koʻra nuqtada ekstremum yoʻq (chunki hosila oraliqda oʻz belgisini saqlab qoladi) va funksiya nuqtada minimumga ega (chunki hosila oʻtishda ishorani minusdan plyusga oʻzgartiradi. bu nuqta orqali). Funktsiyaning mos qiymatlarini toping: , va . Intervalda funktsiya kamayadi, chunki bu oraliqda , va intervalda u ortadi, chunki bu oraliqda.

Grafikni qurishni aniqlashtirish uchun uning koordinata o'qlari bilan kesishish nuqtalarini topamiz. Funktsiya grafigining ildizlari va , ya'ni ikkita nuqtasi (0; 0) va (4; 0) topilgan tenglamani olganimizda. Qabul qilingan barcha ma'lumotlardan foydalanib, biz grafik tuzamiz (misolning boshiga qarang).

Hisob-kitoblar paytida o'z-o'zini tekshirish uchun siz onlayn lotin kalkulyatoridan foydalanishingiz mumkin.

4-misol. Funksiyaning ekstremal qismini toping va uning grafigini tuzing.

Funktsiyaning sohasi nuqtadan tashqari butun son chizig'idir, ya'ni. .

Tadqiqotni qisqartirish uchun biz ushbu funktsiyaning juft bo'lishidan foydalanishimiz mumkin, chunki . Shuning uchun uning grafigi o'qga nisbatan simmetrikdir Oy va tadqiqot faqat interval uchun amalga oshirilishi mumkin.

Hosilini topish va funktsiyaning muhim nuqtalari:

1) ;

2) ,

lekin funksiya bu nuqtada tanaffusga uchraydi, shuning uchun u ekstremal nuqta bo'la olmaydi.

Shunday qilib, berilgan funksiya ikkita kritik nuqtaga ega: va. Funksiyaning paritetini hisobga olib, biz faqat nuqtani ekstremumning ikkinchi yetarli belgisi bilan tekshiramiz. Buning uchun biz ikkinchi hosilani topamiz va uning belgisini aniqlang: olamiz. Chunki va , keyin funksiyaning minimal nuqtasi, while .

Funksiya grafigi haqida toʻliqroq tasavvurga ega boʻlish uchun uning taʼrif sohasi chegaralaridagi xatti-harakatlarini bilib olaylik:

(bu erda belgi istakni bildiradi x o'ngda nolga, va x ijobiy bo'lib qoladi; xuddi shunday intilishni anglatadi x chap tomonda nolga, va x salbiy bo'lib qoladi). Shunday qilib, agar , keyin . Keyingi, biz topamiz

,

bular. bo'lsa, keyin.

Funktsiya grafigida o'qlar bilan kesishish nuqtalari yo'q. Rasm misolning boshida.

Hisob-kitoblar paytida o'z-o'zini tekshirish uchun siz onlayn lotin kalkulyatoridan foydalanishingiz mumkin.

8-misol. Funksiyaning ekstremal qismini toping.

Yechim. Funktsiya sohasini toping. Tengsizlik o'rinli bo'lishi kerakligi sababli, biz dan olamiz.

Funktsiyaning birinchi hosilasi topilsin.