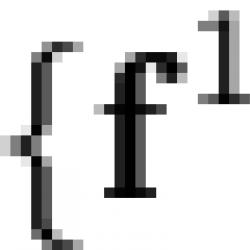Do baze (e 1, ..., e n)modul U odnosu na oblik f – takva osnova (c 1, ..., c p) modul E,Što

gdje je E slobodni K-modul nad komutativnim prstenom K s identitetom, a f je nesingularan na E.

Neka E*-modul povezan s E, a (e* 1,. . ., f*n) - osnova E*, konjugiran na izvornu bazu E: e i* (npr ja)=1, e i* (npr ja) = 0, . Tada svakoj bilinearnoj formi f na E odgovaraju preslikavanja j f, g f: definirano jednakostima

Ako je f nesingularan, tada svako od preslikavanja , j f g f je izomorfizam, i obrnuto. Štoviše, dual na ( e 1, ..., e str)osnova ( c i . . ., s n) karakterizira svojstvo da

E. N. Kuzmin.

Matematička enciklopedija. - M.: Sovjetska enciklopedija. I. M. Vinogradov. 1977-1985.

Pogledajte što je "DVOJNA OSNOVA" u drugim rječnicima:

Skupa X je minimalni podskup B koji ga generira. Generiranje znači da se primjenom operacija određene klase na elemente dobiva bilo koji element. Ovaj koncept je povezan s konceptom ovisnosti: elementi od X stavljaju se u ... ... Matematička enciklopedija

U matematici, Casimirova invarijanta, ili Casimirov operator, značajan je element središta univerzalne ovojne algebre Liejeve algebre. Primjer je kvadrat operatora kutnog momenta, koji je Casimirova invarijanta 3-dimenzionalne grupe... ... Wikipedia

Ili je dualni prostor prostor linearnih funkcionala na danom linearnom prostoru. Sadržaj 1 Definicija linearno konjugiranog prostora 2 Svojstva ... Wikipedia

Ne smije se miješati s "simpleksnom metodom", metodom za optimiziranje proizvoljne funkcije. Vidi metodu Nelder Mead Simpleks metoda je algoritam za rješavanje problema optimizacije linearnog programiranja nabrajanjem vrhova konveksnog poliedra u... ... Wikipedia

Planarni graf, graf koji dopušta pravilno polaganje na ravninu (vidi Polaganje grafa). Drugim riječima, graf G se zove ravna ako se može prikazati na ravnini na način da vrhovi odgovaraju različitim točkama na ravnini, a pravci... ... Matematička enciklopedija

Biografija. Marxova učenja. Filozofski materijalizam. Dijalektika. Materijalističko shvaćanje povijesti. Klasna borba. Marxova ekonomska učenja. Cijena. Višak vrijednosti. Socijalizam. Taktika klasne borbe proletarijata... Književna enciklopedija

Diferencijalno algebarska metoda za proučavanje sustava diferencijalnih jednadžbi i varijeteta s različitim strukturama. Algebarski Metoda se temelji na Grassmannovoj algebri. Neka je V 2n-dimenzionalni vektorski prostor nad proizvoljnim... ... Matematička enciklopedija

Jacobian, algebarska krivulja S je načelno polarizirana Abelova varijanta povezana s ovom krivuljom. Ponekad je Yam jednostavno komutativna algebra. skupina. Ako je S glatka projektivna krivulja roda. preko polja C ili, klasično... ... Matematička enciklopedija

ODNOSI DRUŠTVENI odnosi, uključujući kao njihove elemente: 1) subjekte sa svojim statusima i ulogama, vrijednostima i normama, potrebama i interesima, poticajima i motivima; 2) sadržaj aktivnosti subjekata i njihove interakcije,... ... Filozofska enciklopedija

Sadržaj: I. R. Moderna; II. Povijest grada R.; III. Rimska povijest prije pada Zapadnog Rimskog Carstva; IV. rimsko pravo. I. Rim (Roma) glavni grad talijanskog kraljevstva, na rijeci Tiber, u takozvanoj rimskoj Kampaniji, na 41°53 54 sjeverno... ... Enciklopedijski rječnik F.A. Brockhaus i I.A. Efron

Dvojna osnova

Često se tenzor predstavlja kao višedimenzionalna tablica (gdje d- dimenzija vektorskog prostora nad kojim je zadan tenzor, a broj faktora koincidira s “valentnošću tenzora”), ispunjen brojevima ( komponente tenzora).

Takav prikaz (s izuzetkom tenzora nulte valencije - skalara) moguć je tek nakon izbora baze (ili koordinatnog sustava), pri čemu se pri promjeni baze komponente tenzora na određeni način mijenjaju. Štoviše, sam tenzor kao “geometrijski entitet” ne ovisi o izboru baze. To se može vidjeti na primjeru vektora, koji je poseban slučaj tenzora: komponente vektora se mijenjaju kada se mijenjaju koordinatne osi, ali sam vektor - čija vizualna slika može biti jednostavno nacrtana strelica - mijenja ne promijeniti.

Pojam "tenzor" također se često skraćuje za pojam "tenzorsko polje", što je proučavanje tenzorskog računa.

Definicije

Moderna definicija

Tenzor ranga ( n,m) iznad d-dimenzionalni vektorski prostor V postoji element tenzorskog produkta m prostorima V I n konjugirani prostori V* (odnosno, prostori linearnih funkcionala (1-formi) na V )

Zbroj brojeva n + m nazvao valencija tenzor (koji se često naziva i rang). Tenzor ranga ( n,m) također se naziva n jednom kovarijantni I m jednom kontravarijantni.

Tenzor kao polilinearna funkcija

Kao što se kovarijantni tenzor ranga (1,0) može prikazati kao linearni funkcional, tenzor τ ranga ( n,0) pogodno je zamisliti kao funkciju od n vektorskih argumenata, koji je linearan u svakom argumentu v ja(takve funkcije nazivamo multilinearnim), odnosno za bilo koju konstantu c s polja F(nad kojim je definiran vektorski prostor)

Na isti način, tenzor τ proizvoljnog ranga ( n,m) predstavljen je multilinearnim funkcionalom od n vektori i m kovektori:

Komponente tenzora

Birajmo u prostoru V osnovu, i prema tome - dvojna osnova u konjugiranom prostoru V* (to je , gdje je Kroneckerov simbol).

Zatim u tenzorskom umnošku prostora osnova nastaje prirodno

Ako tenzor definiramo kao multilinearnu funkciju, tada su njegove komponente određene vrijednostima ove funkcije na temelju:

Nakon toga, tenzor se može napisati kao linearna kombinacija produkata baznog tenzora:

Indeksi komponenta tenzori se nazivaju kovarijantni, a gornji kontravarijantni. Na primjer, proširenje nekog dvostruko kovarijantnog tenzora h bit će ovako:

O klasičnoj definiciji

Klasični pristup definiranju tenzora, češći u literaturi iz fizike, počinje predstavljanjem tenzora u komponentama. Tenzor je definiran kao geometrijski objekt koji je opisan višedimenzionalnim nizom, odnosno skupom brojeva indeksiranih s nekoliko indeksa, ili, drugim riječima, tablicom (općenito govoreći, n-dimenzionalno, gdje n - valencija tenzor (vidi gore)).

Glavne tenzorske operacije su zbrajanje, koje se u ovom pristupu svodi na pokomponentno zbrajanje, slično vektorima, i konvolucija - s vektorima, međusobno i sami sa sobom, generalizirajuće množenje matrica, skalarni umnožak vektora i uzimanje traga matrice. Množenje tenzora brojem (skalarom) može se po želji smatrati posebnim slučajem konvolucije; svodi se na komponentno množenje.

Brojčane vrijednosti u nizu, ili komponente tenzora, ovise o koordinatnom sustavu, ali u isto vrijeme i sam tenzor, npr geometrijski entitet, ne ovisi o njima. Manifestacije ove geometrijske suštine mogu se shvatiti kao mnoge stvari: razne skalarne invarijante, simetrija/antisemetrija indeksa, odnosi između tenzora i drugo. Na primjer, skalarni produkt i duljina vektora ne mijenjaju se kada se osi okreću, a metrički tenzor uvijek ostaje simetričan. Konvolucije bilo kojeg tenzora sa samim sobom i/ili drugim tenzorima (uključujući vektore), ako kao rezultat toga nema preostalog indeksa, su skalari, to jest, invarijante pod promjenom koordinata: ovo je opći način konstruiranja skalarnih invarijanti.

Pri zamjeni koordinatnog sustava komponente tenzora se transformiraju prema određenom linearnom zakonu.

Poznavajući komponente tenzora u jednom koordinatnom sustavu, uvijek možete izračunati njegove komponente u drugom ako je dana matrica transformacije koordinata. Stoga se drugi pristup može sažeti kao formula:

Treba primijetiti da to implicira da se svi tenzori (svi tenzori u jednom vektorskom prostoru), bez obzira na njihov rang (to jest, uključeni vektori), transformiraju kroz istu matricu transformacije koordinata (i njezinu dualnu, ako postoje indeksi i indeksi ). Komponente tenzora se tako transformiraju prema istom zakonu kao i odgovarajuće komponente tenzorskog umnoška vektora (u iznosu jednakom valenciji tenzora), uzimajući u obzir kovarijantnost-kontravarijantnost komponenata.

Na primjer, komponente tenzora

transformira se na isti način kao i komponente tenzorskog umnoška triju vektora, odnosno kao umnožak komponenata tih vektora

Budući da je poznata transformacija vektorskih komponenti, na ovaj se način lako može formulirati najjednostavnija verzija klasične definicije tenzora.

Primjeri

Kao što proizlazi iz definicije, komponente tenzora se moraju mijenjati na određeni način sinkrono s komponentama vektora prostora na kojem je definiran pri transformaciji koordinata. Zato Ne svaka tablica ili vrijednost s indeksima koja izgleda kao da predstavlja tenzor zapravo predstavlja tenzor.

• Jednostavan, iako općenito pomalo umjetan, primjer takve tablete je Ne predstavljanje tenzora može biti tablica čije komponente predstavljaju skup proizvoljnih brojeva koji se ni na koji način ne mijenjaju pod proizvoljnim transformacijama koordinata. Takav objekt ne predstavlja tenzor, ili, u svakom slučaju, ne predstavlja tenzor na linearnom prostoru u kojem se dogodila transformacija koordinata. Dakle, skup od tri broja ne predstavlja trodimenzionalni vektor osim ako se ti brojevi ne transformiraju prilikom zamjene koordinata na vrlo specifičan način.

• Također u općem slučaju, podskup komponenti tenzora najvišeg ranga Ne je tenzor najnižeg ranga.
• Ne Tenzor također predstavlja objekt čije su sve komponente nula u barem jednom nedegeneriranom koordinatnom sustavu (u punoj bazi), dok je u drugom barem jedna komponenta različita od nule. Ova činjenica je posljedica (poli-)linearnosti tenzora.

Postoje objekti koji nisu samo slični tenzorima, već za koje su tenzorske operacije definirane (i imaju razumno i ispravno značenje) (konvolucija s drugim tenzorima, posebno s vektorima), ali u isto vrijeme koji nisu tenzori:

• Prije svega same matrice (Jacobijeve matrice) koordinatne transformacije, koja je poseban slučaj difeomorfizma između dviju mnogoznačnika, uz pomoć koje se uvodi klasična definicija tenzora, iako po mnogim svojim svojstvima nalikuju tenzor, ne pripadaju tenzorima. Za njih također možete unijeti gornje i donje indekse, operacije množenja, zbrajanja i konvolucije. Međutim, za razliku od tenzora, čije komponente ovise samo o koordinatama na zadanoj mnogostrukosti, komponente Jacobijeve matrice ovise i o koordinatama na mnogostrukosti slike. Ova razlika je očita u slučaju kada se razmatraju Jacobijeve matrice difeomorfizma dviju proizvoljnih mnogoznačnika, ali kada se mnogoznačnik preslikava u samu sebe, može se zanemariti, budući da su tangentni prostori slike i praslike izomorfni (ne kanonski). Međutim, ustraje. Analogija između Jacobijevih matrica i tenzora može se razviti ako uzmemo u obzir proizvoljne vektorske snopove nad mnogoznačnikom i njihove produkte, a ne samo tangentne i kotangensne snopove.

Tenzorske operacije

Tenzori dopuštaju sljedeće algebarske operacije:

• Množenje skalarom - kao vektor ili skalar (posebni slučajevi tenzora);

• Zbrajanje tenzora iste valencije i sastava indeksa (zbroj se može računati komponentu po komponentu, kao i za vektore);
  • Prisutnost množenja skalarom i zbrajanja tenzora čini prostor tenzora iste vrste linearnim prostorom.

Simetrije

U raznim primjenama, tenzori se često pojavljuju s određenim svojstvom simetrije.

Tenzor koji zadovoljava sljedeći zahtjev naziva se simetričnim u odnosu na dva ko-(kontra-)varijantna indeksa:

ili u komponentama

Linearni operatori kvantne mehanike, naravno, također se mogu tumačiti kao tenzori nad određenim apstraktnim prostorima (prostorima stanja), ali ovo je tradicionalna uporaba termina tenzor praktički se ne koristi, baš kao što se općenito iznimno rijetko koristi za opisivanje linearnih operatora nad beskonačnodimenzionalnim prostorima. Općenito, u fizici pojam tenzor nastoji se primijeniti samo na tenzore nad običnim fizičkim 3-dimenzionalnim prostorom ili 4-dimenzionalnim prostor-vremenom, ili, najviše, nad najjednostavnijim i najizravnijim generalizacijama tih prostora, iako načelna mogućnost njegove primjene u općenitijim slučajevima nije tajna.

Primjeri tenzora u fizici su:

• metrički tenzor nad pseudo-Riemannovim 4-dimenzionalnim mnogoznačnikom, koji je u općoj teoriji relativnosti razvoj koncepta Newtonovog gravitacijskog potencijala.
• Riemannov tenzor zakrivljenosti izražen kroz njega i njegove konvolucije, povezan u istoj teoriji s energijom gravitacijskog polja i izravno uključen u glavnu jednadžbu teorije.
• tenzor elektromagnetskog polja nad prostorom Minkowskog, koji sadrži jakosti električnog i magnetskog polja i glavni je predmet klasične elektrodinamike u 4-dimenzionalnom zapisu. Konkretno, Maxwellove jednadžbe napisane su pomoću njega u obliku jedne 4-dimenzionalne jednadžbe.
• naprezanja i deformacije u teoriji elastičnosti opisuju se tenzorima nad 3-dimenzionalnim euklidskim prostorom. Isto vrijedi i za veličine kao što su moduli elastičnosti.
• Gotovo većina veličina koje su skalarne karakteristike tvari u slučaju izotropije potonje su tenzori u slučaju anizotropne tvari. Točnije, odnosi se na značajne koeficijente koji povezuju vektorske količine ili stoje ispred umnožaka (osobito kvadrata) vektora. Primjeri uključuju električnu vodljivost (također njen inverzni otpor), toplinsku vodljivost, dielektričnu osjetljivost i permitivnost, brzinu zvuka (ovisno o smjeru), itd.
• u mehanici krutog tijela najvažniju ulogu ima tenzor tromosti koji povezuje kutnu brzinu s kutnom količinom gibanja i kinetičkom energijom rotacije. Ovaj tenzor se razlikuje od većine drugih tenzora u fizici, koji su, općenito govoreći, tenzorska polja, po tome što jedan tenzor karakterizira jedno apsolutno kruto tijelo, u potpunosti određujući, uz masu, i njegovu tromost.
• tenzori uključeni u multipolnu ekspanziju imaju slično svojstvo: samo jedan tenzor u cijelosti predstavlja trenutak raspodjele naboja odgovarajućeg reda u određenom trenutku.
• često koristan u fizici je Levi-Civita pseudotenzor, koji je uključen, na primjer, u koordinatni zapis vektora i mješovitih proizvoda vektora. Komponente ovog tenzora uvijek se pišu gotovo identično (do skalarnog faktora ovisno o metrici), au desnoj ortonormiranoj bazi uvijek se pišu potpuno isto (svaka je jednaka 0, +1 ili −1).

Lako je uočiti da većina tenzora u fizici (bez skalara i vektora) ima samo dva indeksa. Tenzore koji imaju višu valenciju (kao što je Riemannov tenzor u općoj teoriji relativnosti) nalazimo u pravilu samo u teorijama koje se smatraju dosta složenima, a i tada se često pojavljuju uglavnom u obliku svojih vijuga niže valencije. Većina je simetrična ili antisimetrična.

Najjednostavnija ilustracija koja nam omogućuje razumijevanje fizičkog (i dijelom geometrijskog) značenja tenzora, točnije simetričnih tenzora drugog reda, vjerojatno će biti razmatranje (specifičnog) tenzora električne vodljivosti σ. Intuitivno, anizotropni medij, poput kristala ili čak nekog posebno proizvedenog umjetnog materijala, općenito neće jednako lako provoditi struju u svim smjerovima (na primjer, zbog oblika i orijentacije molekula, atomskih slojeva ili nekih supramolekularnih struktura - možemo zamisliti, na primjer, tanke žice od visoko vodljivog metala, jednako orijentirane i spojene u slabo vodljivi medij). Uzmimo kao osnovu za jednostavnost i specifičnost najnoviji model (dobro vodljive žice u slabo vodljivom mediju). Električna vodljivost duž žica bit će velika, nazovimo je σ 1, a poprečno će biti mala, nazovimo je σ 2. (Jasno je da će se u općem slučaju (na primjer, kada su žice spljoštene u poprečnom presjeku i to spljoštenje također jednako orijentirano za sve žice), električna vodljivost σ 3 razlikovati od σ 2, ali u slučaju okruglog ravnomjerno raspoređenih žica - σ 2 = σ 3, ali nisu jednaki σ 1). Sasvim netrivijalna u općem slučaju, ali sasvim očita u našem primjeru, činjenica je da postoje tri međusobno okomita pravca za koje veza između vektor gustoće struje i jakost električnog polja koje ga uzrokuje bit će povezani jednostavno numeričkim faktorom (u našem primjeru - to je smjer duž žica, drugi - duž njihove spljoštenosti, a treći je okomit na prva dva) .Ali bilo koji vektor može se rastaviti na komponente duž ovih prikladnih smjerova:

tada za svaku komponentu možemo napisati:

I vidjet ćemo da za bilo koji smjer koji se ne poklapa s 1, 2 i 3, vektor se više neće poklapati u smjeru s osim ako barem dva od σ 1, σ 2 i σ 3 nisu jednaka.

Prelaskom na proizvoljne kartezijeve koordinate koje se ne podudaraju s ovim odabranim smjerovima, bit ćemo prisiljeni uključiti matricu rotacije za transformaciju koordinata, pa će stoga u proizvoljnom koordinatnom sustavu odnos između i izgledati ovako:

odnosno tenzor električne vodljivosti prikazat će se simetričnom matricom.

Definicija 10.1. Preslikavanje f: L → R koje je definirano na linearni prostor L i uzima realne vrijednosti, tzv linearna funkcija (također linearni oblik, linearni funkcional) , ako zadovoljava dva uvjeta:

a) f(x + y) = f(x) + f(x), x,y ∈ L;

b) f(λx) = λf(x), x ∈ L,λ ∈ R.

Uspoređujući ovu definiciju s definicijom 4.1 linearni operator, vidjet ćemo puno toga zajedničkog. Ako skup realnih brojeva promatramo kao jednodimenzionalni linearni prostor, tada možemo reći da je linearna funkcija linearni operator čiji je prostor slike jednodimenzionalan.

Odaberimo neku bazu e = (e 1 ... e n) u linearnom prostoru L. Tada za bilo koji vektor x ∈ L s koordinatama x = (x 1 ; ... x n) T

f(x) = f(x 1 e 1 +... + x n e n) = xi 1 f(e 1) + ... + x n f(e n) = a 1 x 1 + ... + a n x n = ax,

gdje je a = (ai ... an), a* = /(e*), i = 1, n. Stoga je linearna funkcija jednoznačno određena svojim vrijednostima na baznim vektorima. Naprotiv, ako je funkcija /(x) kroz koordinate x vektora x izražena u obliku /(x) = az, tada je ova funkcija linearna, a niz a je sastavljen od vrijednosti ovog funkcija na baznim vektorima. Tako se uspostavlja korespondencija jedan na jedan između skupa linearnih formi definiranih na linearnom prostoru £ i nizova duljine n.

Linearni oblici se mogu zbrajati i množiti realnim brojevima prema pravilima:

(f + g)(x)=f(x)+g(x), (λf)(x) = λf(x).

Ovako uvedene operacije pretvaraju skup linearnih formi u prostoru L u linearni prostor. Taj se linearni prostor naziva konjugirani prostor u odnosu na linearni prostor L i označimo L*.

Na temelju baze e odabrane u prostoru L konstruiramo bazu u dualnom prostoru L*. Za svaki vektor e i iz baze e, razmotrimo linearni oblik fi, za koji je f i (e i) = 1 i f i (e j)= 0 za sve vektore e j osim e i. Dobivamo sustav linearnih oblika f1, ..., /” e C*. Pokažimo da je to linearno neovisan sustav. Neka neka linearna kombinacija ovih oblika bude jednaka nultom linearnom obliku / = aif1 +... + anfn = 0. Oblik / poprima nulte vrijednosti na svim baznim vektorima. Ali

Nulte vrijednosti f na baznim vektorima ekvivalentne su jednakosti α i = 0, i = 1,n, pa je stoga sustav linearnih oblika f 1, ..., f n linearno neovisan.

Sustav linearnih formi f 1, ..., f n je baza u dualnom prostoru. Doista, budući da se radi o linearno neovisnom sustavu linearnih formi, dovoljno je dokazati da je svaka linearna forma iz L* njihova linearna kombinacija. Izaberimo proizvoljan linearni oblik f iz L* i neka su a 1 ... i n vrijednosti oblika f na baznim vektorima. Ove vrijednosti jedinstveno definiraju linearni oblik. Ali linearna kombinacija f" = a 1 f i +... + a n f n također je linearna forma, koja na baznim vektorima poprima iste vrijednosti a 1, ... i n. To znači da ove dvije linearne forme podudaraju, te dobivamo jednakost f = f" = a 1 f 1 +... + a n f n, tj. proširenje proizvoljno odabrane linearne forme u sustav formi f 1, ..., f n

Gornje razmišljanje pokazuje da dualni prostor L* ima isto dimenzija, kao L. Baza koju smo konstruirali f 1, ..., f n ovisi o izboru baze e u prostoru L.

Definicija 10.2. Baze e 1, ..., e n i f 1, ..., f n linearni prostor L i dualni prostor L* nazivaju se biortogonalan, odnosno recipročan , Ako

Ako su baze e 1, ..., e n i f 1, ..., f n međusobne, tada su koordinate proizvoljnog oblika f u bazi f 1, ..., f n vrijednosti ovog oblika na vektore međusobne baze e 1, .. ., e n . Kada se zajedno razmatraju linearni prostor L i dualni prostor L*, elementi svakog od ovih prostora nazivaju se vektori, ali se elementi dualnog prostora L* nazivaju kovarijantni vektori (kovektori) , te elementi iz linearnog prostora L - kontravarijantni vektori (ili samo vektori). Koordinate obaju određuju se primarno u međusobnim bazama, pri čemu koordinate kontravarijantnih vektora imaju indeks na vrhu, a za kovarijantne vektore indeks na dnu.

Oznaku f(x) možemo promatrati na dva načina. Nakon što smo fiksirali oblik f, mijenjamo vektor x, dobivajući sve moguće vrijednosti linearnog oblika. Ali ako fiksiramo vektor x i mijenjamo linearnu formu f, dobit ćemo funkciju definiranu na dualnom prostoru L*. Lako je provjeriti da je ova funkcija linearna, jer prema definiciji zbroja linearnih oblika i umnoška linearnog oblika s brojem,

(f + g)(x) = f(x) + g(x), (λf)(x) = λf(x)

Dakle, svaki vektor x ∈ L odgovara linearnoj formi na dualnom prostoru L, odnosno elementu dvostruko konjugirani prostor (L*)* = L**. Dobivamo preslikavanje φ: L → L**. Lako je provjeriti da ovo prikazati linearno i što je to injektivno. Iz injektivnosti slijedi da je dimimφ = dimL = n. Ali dualni prostor L* ima istu dimenziju kao L, i dimL** = dimL* = dimL. Dakle, dimenzija linearnog potprostora imφ u L** podudara se s dimenzijom cijelog dvostruko konjugiranog prostora. To znači imφ = L** i preslikavanje φ je izomorfizam. Napomenimo da ovaj izomorfizam nije vezan uz izbor bilo koje baze. Stoga je prirodno identificirati linearne forme definirane na L* s elementima prostora L. To znači da se dvostruki dualni prostor podudara s izvornim linearnim prostorom: L** = L. Ako je L* dualan na L, tada je L je dualan na L*.

Uzajamnost linearnog prostora i njegovog konjugiranog prostora ukazuje na simetričnost odnosa između vektora i kovektora. Stoga je umjesto pisanja f(x) prikladnije koristiti drugi oblik zapisa, simetrični: (f,x). Linearne forme sada ćemo također označiti podebljanim kurzivom: (f,x). Usvojeni zapis sličan je zapisu za skalarni umnožak, ali za razliku od potonjeg, argumenti u novom zapisu preuzeti su iz različitih prostora. Sam zapis (f, x) može se smatrati zapisom preslikavanja definiranog na skupu L*×L, koji paru kovektora i vektora dodjeljuje realni broj. U ovom slučaju, naznačeno preslikavanje je linearno u svakom od argumenata.

Teorem 10.1. Neka su b i c dvije baze n-dimenzionalni linearni prostor L,U - matrica prijelaza iz b u c. Baze b* i c* dualnog prostora L*, međusobno s bazama b odnosno c, međusobno su povezane relacijama

c* = b*(U T) -1 b* =c*U T

Koordinate f c = (f c 1 ... f c n) linearne forme f u bazi c* su vrijednosti ove forme na baznim vektorima c = (c 1 ... c n). Otkrijmo kako su koordinate oblika f povezane u dvije baze c* i b*.

Baze b i c međusobno su povezane prijelaznom matricom matričnom relacijom c = bU (vidi 1.8). Ova relacija predstavlja jednakost nizova duljine n, sastavljenih od vektora. Iz jednakosti nizova vektora slijedi da nizovi vrijednosti linearne forme f na ovim vektorima su jednaki:

((f,c 1) ... (f,c n)) = ((f,b 1) ... (f,b n))U,

gdje su f b i f c oznake koordinatnih pravaca oblika f u bazama b* odnosno c*. Transponiranjem ove jednakosti dobivamo prihvaćeni oblik povezivanja koordinata elemenata linearnog prostora u kojem su koordinate ispisane u stupcima:

(f c) T = U T (f b) T .

Ova relacija znači da je matrica U T matrica prijelaza s baze c*, koja u formuli ima ulogu stare, na bazu b*, koja ima ulogu nove. Prema tome, b* = c*U T, odakle množenjem s matricom (U T) -1 dobivamo c* = b*(U T) -1.

Ako je linearni prostor L euklidski, tada skalarni produkt generira izomorfizam između L i l*, neovisno o bazi, što nam omogućuje identificiranje euklidskog prostora s njegovim konjugatom. Zaista, za bilo koji vektor a ∈ L preslikavanje x → (a,x) je linearna forma u L, budući da je skalarni umnožak linearan u drugom svom argumentu. Pojavljuje se preslikavanje ψ koje vektoru a ∈ L pridružuje linearni oblik f a (x) - (a,x). Ovo preslikavanje je linearno zbog svojstava skalarnog produkta i injektivno je. Injektivnost slijedi iz činjenice da ako je (a,x) = 0 za bilo koji x ∈ L, onda je (a,a) = 0, tj. a = 0. Budući da su linearni prostori L i L* konačnodimenzionalni i imaju iste dimenzije, preslikavanje ∈ je bijektivno i ostvaruje izomorfizam tih prostora. Dakle, za euklidski prostor L* = L. U tom smislu, euklidski prostor je “samopridružen” prostor.