What is mechanical energy with an example. total mechanical energy. Strength bond

The value that equates to half of the product of the mass of a given body and the speed of this body squared is called in physics the kinetic energy of the body or the energy of action. The change or inconstancy of the kinetic or driving energy of the body for some time will be equal to the work that has been done for a given time by a certain force acting on a given body. If the work of any force along a closed trajectory of any type is equal to zero, then a force of this kind is called potential power. The work of such potential forces will not depend on the trajectory along which the body moves. Such work is determined by the initial position of the body and its final position. The starting point or zero for the potential energy can be chosen absolutely arbitrarily. The value that will be equal to the work done by the potential force to move the body from a given position to the zero point is called in physics the potential energy of the body or the energy of the state.

For various kinds forces in physics, there are various formulas for calculating the potential or stationary energy of a body.

The work done by potential forces will be equal to the change in this potential energy, which must be taken in the opposite sign.

If we add the kinetic and potential energy body, you get a value called the total mechanical energy body. In a position where a system of several bodies is conservative, the law of conservation or constancy of mechanical energy is valid for it. A conservative system of bodies is such a system of bodies that is subject to the action of only those potential forces that do not depend on time.

The law of conservation or constancy of mechanical energy is as follows: "During any processes that occur in a certain system of bodies, its total mechanical energy always remains unchanged." Thus, the total or all mechanical energy of any body or any system of bodies remains constant if this system of bodies is conservative.

The law of conservation or constancy of total or all mechanical energy is always invariant, that is, its form of writing does not change, even when the starting point of time is changed. This is a consequence of the law of homogeneity of time.

When dissipative forces begin to act on the system, for example, such as a gradual decrease or decrease in the mechanical energy of this closed system. This process is called energy dissipation. A dissipative system is a system in which the energy can decrease over time. During dissipation, the mechanical energy of the system is completely converted into another. This is fully consistent with the universal law of energy. Thus, there are no completely conservative systems in nature. One or another dissipative force will necessarily take place in any system of bodies.

The total mechanical energy characterizes the movement and interaction of bodies, therefore, it depends on the speeds and relative position of the bodies.

The total mechanical energy of a closed mechanical system is equal to the sum of the kinetic and potential energies of the bodies of this system:

Law of energy conservation

The law of conservation of energy is a fundamental law of nature.

In Newtonian mechanics, the law of conservation of energy is formulated as follows:

The total mechanical energy of an isolated (closed) system of bodies remains constant.

In other words:

Energy does not arise from nothing and does not disappear anywhere, it can only pass from one form to another.

Classical examples of this statement are: a spring pendulum and a pendulum on a thread (with negligible damping). In the case of a spring pendulum, in the process of oscillation, the potential energy of a deformed spring (having a maximum in the extreme positions of the load) is converted into kinetic energy load (reaching a maximum at the moment the load passes the equilibrium position) and vice versa. In the case of a pendulum on a thread, the potential energy of the load is converted into kinetic energy and vice versa.

2 Equipment

2.1 Dynamometer.

2.2 Laboratory stand.

2.3 Load weighing 100 g - 2 pcs.

2.4 Measuring ruler.

2.5 Piece soft tissue or felt.

3 Theoretical background

The scheme of the experimental setup is shown in Figure 1.

The dynamometer is fixed vertically in the foot of the tripod. A piece of soft cloth or felt is placed on a tripod. When hanging loads from the dynamometer, the tension of the dynamometer spring is determined by the position of the pointer. In this case, the maximum elongation (or static displacement) of the spring X 0 occurs when the elastic force of a spring with stiffness k balances the force of gravity of the load with the mass t:

kx 0 =mg, (1)

where g = 9.81 - free fall acceleration.

Consequently,

The static displacement characterizes the new equilibrium position O" of the lower end of the spring (Fig. 2).

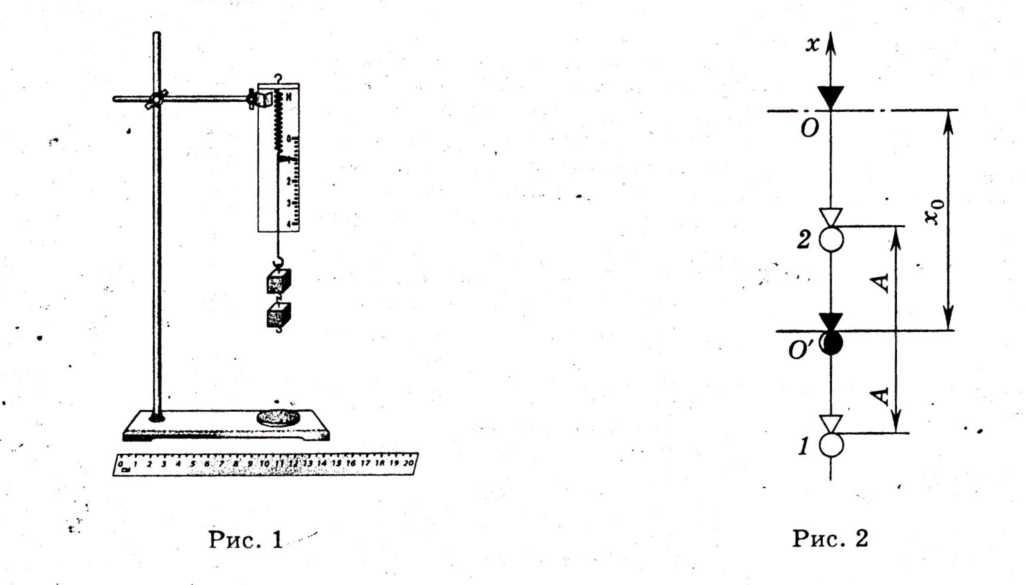
If the load is pulled down a distance BUT from point O" and release at point 1, then periodic oscillations of the load occur. At points 1 and 2, called turning points, the load stops, reversing the direction of movement. Therefore, at these points, the speed of the load v = 0.

Max Speed v m ax the load will have at the midpoint O". Two forces act on the oscillating load: the constant force of gravity mg and variable elastic force kx. Potential energy of a body in a gravitational field at an arbitrary point with coordinate X is equal to mgx. The potential energy of the deformed body, respectively, is equal to .

In this case, the point X = 0, corresponding to the position of the pointer for an unstretched spring.

The total mechanical energy of the load at an arbitrary point is the sum of its potential and kinetic energy. Neglecting the forces of friction, we use the law of conservation of total mechanical energy.

Let us equate the total mechanical energy of the load at point 2 with the coordinate -(X 0 -BUT) and at point O" with coordinate -X 0 :

Expanding the brackets and performing simple transformations, we bring formula (3) to the form

Then the module of the maximum speed of loads

The stiffness of a spring can be found by measuring the static displacement X 0 . As follows from formula (1),

The total mechanical energy characterizes the movement and interaction of bodies, therefore, it depends on the speeds and relative position of the bodies.

The total mechanical energy of a closed mechanical system is equal to the sum of the kinetic and potential energies of the bodies of this system:

Law of energy conservation

The law of conservation of energy is a fundamental law of nature.

In Newtonian mechanics, the law of conservation of energy is formulated as follows:

The total mechanical energy of an isolated (closed) system of bodies remains constant.

In other words:

Energy does not arise from nothing and does not disappear anywhere, it can only pass from one form to another.

Classical examples of this statement are: a spring pendulum and a pendulum on a thread (with negligible damping). In the case of a spring pendulum, in the process of oscillation, the potential energy of a deformed spring (having a maximum in the extreme positions of the load) is converted into the kinetic energy of the load (reaching a maximum at the moment the load passes the equilibrium position) and vice versa. In the case of a pendulum on a thread, the potential energy of the load is converted into kinetic energy and vice versa.

2 Equipment

2.1 Dynamometer.

2.2 Laboratory stand.

2.3 Load weighing 100 g - 2 pcs.

2.4 Measuring ruler.

2.5 A piece of soft cloth or felt.

3 Theoretical background

The scheme of the experimental setup is shown in Figure 1.

kx 0 =mg, (1)

where g = 9.81 - free fall acceleration.

Consequently,

The static displacement characterizes the new equilibrium position O" of the lower end of the spring (Fig. 2).

In this case, the point X = 0, corresponding to the position of the pointer for an unstretched spring.

Let us equate the total mechanical energy of the load at point 2 with the coordinate -(X 0 -BUT) and at point O" with coordinate -X 0 :

Expanding the brackets and performing simple transformations, we bring formula (3) to the form

Then the module of the maximum speed of loads

The stiffness of a spring can be found by measuring the static displacement X 0 . As follows from formula (1),

Page 1

The total mechanical energy of the body does not change. Energy only changes from one form to another.

The total mechanical energy of a body, which is not affected by the forces of friction and resistance, remains unchanged during its motion.

The total mechanical energy of a body is the sum of its kinetic and potential energies. Consider full energy freely falling body at different times.

Does the total mechanical energy of the body change when it falls.

What is called the total mechanical energy of the body.

Thus, the total mechanical energy of a body performing harmonic oscillations is proportional to the square of the oscillation amplitude. Therefore, the amplitude A of oscillations also does not depend on time.

As can be seen from (44.13), the total mechanical energy of the body during damped oscillations decreases with time according to an exponential law.

The sum of kinetic and potential energies forms the total mechanical energy of the body.

An absolutely elastic impact is such an impact at which the total mechanical energy of the bodies is conserved. First, the kinetic energy is partially or completely converted into the potential energy of elastic deformation. Then the bodies return to their original shape, repelling each other. As a result, the potential energy of elastic deformation again turns into kinetic energy and the bodies fly apart with velocities determined by two conditions - conservation of total energy and total impulse tel.

An absolutely elastic impact is such an impact at which the total mechanical energy of the bodies is conserved. First, the kinetic energy is partially or completely converted into the potential energy of elastic deformation. Then the bodies return to their original shape, repelling each other. As a result, the potential energy of elastic deformation again turns into kinetic energy and the bodies fly apart with velocities determined by two conditions - the conservation of the total energy and the total momentum of the bodies.

An absolutely elastic impact is such an impact at which the total mechanical energy of the bodies is conserved. First, the kinetic energy is partially or completely converted into the potential energy of elastic deformation. Then the bodies return to their original shape, repelling each other. As a result, the potential energy of elastic deformation again turns into kinetic energy and the bodies fly apart with speeds determined by two conditions - the conservation of the total energy and the total momentum of the bodies.

This work is spent on dissipating energy or changing the total mechanical energy of the body.

According to the law of energy change (see § 28), the work of the resistance force (external force) is equal to the increment of the total mechanical energy of the body.

This result is predictable, since the elastic force under which the body moves is conservative, therefore, the energy conservation law is fulfilled - the total mechanical energy of the body is conserved.

Mechanical energy characterizes the ability of a body to perform mechanical work. The total mechanical energy of a body is the sum of kinetic and potential energy.

Energy is the reserve of the system's operability. Mechanical energy is determined by the speeds of movements of bodies in the system and their mutual arrangement; hence, it is the energy of movement and interaction.

The kinetic energy of a body is the energy of its mechanical movement, which determines the ability to do work. In translational motion, it is measured by half the product of the mass of the body and the square of its speed:

At rotary motion the kinetic energy of the body has the expression:

The potential energy of a body is the energy of its position, due to the mutual relative position of bodies or parts of the same body and the nature of their interaction. Potential energy in the field of gravity:

where G is the force of gravity, h is the difference between the levels of the initial and final positions above the Earth (relative to which the energy is determined). Potential energy of elastically deformed body:

where C is the modulus of elasticity, delta l is the deformation.

Potential energy in the field of gravity depends on the location of the body (or system of bodies) relative to the Earth. The potential energy of an elastically deformed system depends on the relative arrangement of its parts. Potential energy arises due to kinetic energy (lifting the body, stretching the muscle) and when changing position (falling the body, shortening the muscle), it passes into kinetic energy.

The kinetic energy of the system during plane-parallel motion is equal to the sum of the kinetic energy of its CM (assuming that the mass of the entire system is concentrated in it) and the kinetic energy of the system in its rotational motion relative to the CM:

The total mechanical energy of the system is equal to the sum of the kinetic and potential energy. In the absence of external forces, the total mechanical energy of the system does not change.

Change in kinetic energy material system on some path is equal to the sum of the work of external and internal forces along the same path:

The kinetic energy of the system is equal to the work of the braking forces that will be produced when the system's velocity decreases to zero.

In human movements, one type of movement passes into another. At the same time, energy as a measure of the motion of matter also passes from one form to another. So, the chemical energy in the muscles is converted into mechanical energy (internal potential of elastically deformed muscles). The muscle traction force generated by the latter does work and converts potential energy into kinetic energy of the moving parts of the body and external bodies. The mechanical energy of external bodies (kinetic) is transferred during their action on the human body to the links of the body, is converted into potential energy of stretched antagonist muscles and into dissipated thermal energy (see Chapter IV).