Quantum energy and wavelengths of various natural radiations. Heisenberg uncertainty relations. Quantum: difference from electron
From small causes come great
consequences: yes, biting off a burr
gave my friend cancer.
Kozma Prutkov
What experimental data led to the hypothesis about the discrete properties of the field? What is a quantum electromagnetic radiation? What parameters characterize a photon as a wave and as a particle? What are corpuscular properties electromagnetic field?
Lesson-lecture
To late XIX in. there was an idea that our world consists of particles and fundamental fields - two components of matter. There were only small "flaws" to overcome which it was necessary to make some efforts.
However, of these small "flaws" at the turn of the XIX-XX centuries. a new, revolutionary theory arose in physics, which radically changed the ideas about particles and fields, that is, about matter. A new theory based on experimental facts, which later became known as quantum theory, began to describe particles and fields in a unified way. In accordance with its main provisions, the fields, which were previously considered as continuous objects, acquired discrete properties - the properties of particles. And vice versa, particles (substance), for which a discrete description was previously used, acquired continuous properties - the properties of fields or waves.
HYPOTHESIS OF ELECTROMAGNETIC FIELD QUANTUM. The beginning of a new theory was laid by a theoretical model describing the radiation of a completely black body. The fact that an absolutely black body should absorb all electromagnetic waves equally well (see § 20) meant that there should not be any regularity in the movement of charged particles. It must be chaotic, like the movement of particles of a molecular gas. Such a motion is practically realized on stars, which is why the spectrum of stars is close to the radiation spectrum of a completely black body.
The theory of blackbody radiation was developed by John Rayleigh and James Jeans. However, while agreeing well with experiment in the region of long wavelengths, it completely unsatisfactorily described the radiation in the region of short wavelengths (Fig. 18). While the experimental curve went to zero at small λ, the theoretical curve tended to infinity.
Rice. 18. Experimental radiation spectrum of a black body (1) and a curve corresponding to the Rayleigh-Jeans theory (2)
The mismatch between theory and experiment has been called " ultraviolet catastrophe” (ultraviolet radiation is short-wave radiation).
In 1900, Max Planck managed to build a theory consistent with experiment based on the assumption that an electromagnetic wave is emitted and absorbed not continuously, but in portions - quanta. Moreover, the quantum energy is proportional to the wave frequency: E = hv. Planck obtained the value of the coefficient of proportionality h by fitting the theoretical spectrum to the experimental data. The hypothesis of energy transfer by quanta was a bold assumption. since no experimental data obtained by that time gave any grounds for such an assumption. Despite the dissatisfaction with the result, Planck received a new, fundamental constant, which was later named after him - Planck's constant The value of this constant h = 6.62x10 -34 J*s corresponds to the values of the microcosm.
The theory of radiation of a completely black body, developed by M. Planck, for the first time included the provision on corpuscular properties fields.
PHOTO EFFECT. PHOTONS AS FIELD PARTICLES. The next step in the development of quantum theory is related to the explanation of the features of the photoelectric effect.
The scheme for observing the photoelectric effect is illustrated in Figure 19.
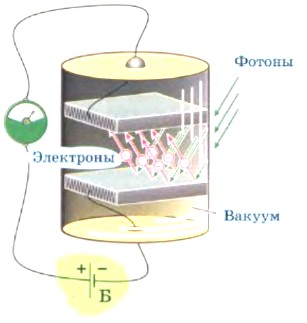
Rice. 19 Scheme for observing the phenomenon of the photoelectric effect
A voltage is applied between the anode and cathode. In the absence of light, there is practically no current, since there are no free charged particles in vacuum that can, moving between the cathode and anode, create an electric current. A beam of light, falling on the cathode, knocks out electrons from it, as a result of which a current arises.
What features of the photoelectric effect could be expected on the basis of classical ideas about the properties of the field? The energy of the light incident on the cathode is proportional to the intensity of the electromagnetic wave. The energy of the ejected electrons is proportional to the number of electrons and the energy (kinetic) of one electron, i.e., with increasing light intensity, the number of ejected electrons and, consequently, the force electric current, as well as the kinetic energy of the electrons. For a given intensity, these quantities should not depend on the frequency of the electromagnetic wave.
The results of the experiment turned out to be somewhat different. The current actually increased with increasing intensity. Concerning kinetic energy electrons, then it turned out to depend not on the intensity of light, but on its frequency. These quantities turned out to be connected by a linear dependence (Fig. 20), and when the light frequency was lowered below a certain critical value (vcr), the photoelectric effect disappeared. This critical frequency has been called red border photo effect(it really matched the red light).

Rice. 20. Dependence of the kinetic energy of electrons ejected from the cathode on the frequency of light
The phenomenon of the photoelectric effect is that, under the action of light, free electrons fly out of the metal.
A photon is both an electromagnetic wave and a particle of the electromagnetic field. As a wave, a photon is characterized by frequency V. As a particle, a photon is characterized by the fact that it has zero mass, always moves at the speed of light, has an energy equal to hv, and an impulse equal to h/λ.
It turned out to be impossible to explain the photoelectric effect on the basis of the classical theory of the interaction of light and matter, but from the dependence shown in the figure, a linear relationship between the energy and frequency of light was clearly traced (as in Planck's formula). The phenomenon of the photoelectric effect in 1905 was explained by A. Einstein, taking Planck's hypothesis as a basis. Assuming that one light quantum leads to the emission of one electron, the energy conservation law can be written as hv = Ekin + Aout.
This formula matches linear dependence, shown in Figure 20. The constant, which was called the work function, has the meaning of the energy that must be expended in order to knock out an electron from the metal. The existence of the red boundary of the photoelectric effect was explained in a natural way. It corresponded to the zero kinetic energy of the ejected electron: hv cr = A out.
Einstein went even further in understanding the concept of a quantum: he introduced the concept of a radiation particle (a particle of an electromagnetic field), which he called a photon. Like all other particles, a photon is able to move in space. The speed of the photon, of course, coincides with the speed of light. The energy of this particle is determined by Planck's formula. The mass of a photon, in accordance with Einstein's theory of relativity, must be equal to zero, and its momentum is related to the frequency by the relation ρ = hv/s. Given the relationship between wavelength and frequency, the expression for momentum can be written as ρ = h/λ.
Modern ideas about fields fully confirm the provisions put forward by Planck and Einstein. At the same time, particles corresponding to fields - field quanta - are present not only in the electromagnetic field, but also in other fundamental fields. The concept of "quantum" thus became general concept for various fields, and the concept of "photon" was assigned to the quantum of the electromagnetic field.
In accordance with modern concepts, any real electromagnetic field can be represented as a collection of photons. In this case, the classical description of the field remains valid only for a large number of photons involved in the process under consideration.
- What are the discrete properties of the electromagnetic field?
- What is a photon - a wave or a particle?
- About 10 billion photons come from the brightest stars to 1 m 2 of the Earth's surface in 1 s. How many photons enter the lens of a telescope with a diameter of 10 m in 1 s from a star whose intensity of light incident on Earth is 10 billion times less?
1.Absolutely black body. Laws of radiation of absolutely black body.
Ab. h. the body is the body to-e completely absorb. radiation incident on it (not reflective). A.h. model body can serve as a small hole in a hollow sphere.
Received Analysis experiment. natural. allowed formulas. radiation laws.
Stefan-Boltzmann R e \u003dT 4, post. St-B. =5.71*10 -8 if the body is not A.ch. then R e \u003d kT 4, where k is a certain coefficient. called degree of non-blackness 0<=k<=1
Wien's displacement law max =b/T, b–1st post. Guilt b=2.898*10 –3, max is the wavelength per k–th arrival. max emissivity A.h.body.
2nd Wine's law 0 ( max, T) \u003d b 1 T 5, b 1 -2nd post. Wine b \u003d 1.29 * 10 -5,
An attempt to give an explanation. experimental curve (,T) on the basis of classical physics led to dependence: (,T)~1/ (Rayleigh–Jeans).
Formula R.–D. agrees with the experimental curve only in the region of long wavelengths at 0 => (,T).
Divergence f. R.–D. with an experimental curve in the region of short wavelengths was called the “ultraviolet catastrophe”. Classic physics proved unable to explain the radiation. heated. tel. Get theory. dependence (, T) succeeded Max Planck by abandoning the theory of continuous. radiated. energy is heated. tel.
2.Planck's hypothesis
By the end of the 19th century, the question of the distribution of the radiation energy of blackbody radiation over wavelengths was experimentally studied, i.e. addiction r λ = f(λ , T) Physicists were faced with the task of finding a formula that would reflect this functional dependence. Based on the laws of classical physics and based on the concept of continuous radiation of energy by an atom, Rayleigh and Jeans obtained a formula that determines the form of the function f(λ , T):
r λ = f(λ , T) = 2πλ/ λ 2 *kT
where k is the Boltzmann constant. The curve obtained from this formula is shown in fig. 25 dotted. It gave good agreement in the region of long waves, but did not correspond at all to the experimental data in the ultraviolet part of the spectrum. It was necessary to revise the provisions of the classical theory. This situation in physics has been called "ultraviolet catastrophe". The way out of the disaster was found by M. Planck, who put forward a hypothesis in 1900: the atoms of the body do not radiate energy continuously, but in the form of separate portions of radiation quanta, later called photons. The energy of each quantum (photon) is proportional to its frequency: E= hν. Taking into account the formulas ν = With/ λ, ω = 2 πν , we get: E= hν= hc/ λ=ω/2π= h ω , (2.10)
where ν is the radiation frequency, c is the speed of light.
Planck's constants.
And 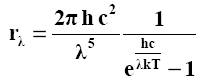 It can be seen from formula (2.10) that the shorter the wavelength, the greater the energy of the quantum; therefore, quantum limitations are most pronounced when emitting short waves. So, ultraviolet light can be emitted either in large quanta if the body temperature is high, for example, the surface of the Sun, or not emitted at all if the energy of the thermal motion of the body's atoms is not enough for it to emit a radiation quantum. This is a qualitative explanation of the drop in the radiation intensity at λ
→ 0
and resolution of ultraviolet catastrophe. Planck, using quantum concepts, theoretically obtained a formula describing the dependence r λ
= f(λ , T) called Planck's formula:
It can be seen from formula (2.10) that the shorter the wavelength, the greater the energy of the quantum; therefore, quantum limitations are most pronounced when emitting short waves. So, ultraviolet light can be emitted either in large quanta if the body temperature is high, for example, the surface of the Sun, or not emitted at all if the energy of the thermal motion of the body's atoms is not enough for it to emit a radiation quantum. This is a qualitative explanation of the drop in the radiation intensity at λ
→ 0
and resolution of ultraviolet catastrophe. Planck, using quantum concepts, theoretically obtained a formula describing the dependence r λ
= f(λ , T) called Planck's formula:
This formula gives very good agreement with the experimental data at all frequencies and at all temperatures. By integrating the equation, the Stefan-Boltzmann law can be obtained, and by differentiation, the Wien displacement law. Planck's hypothesis about the discrete nature of electromagnetic radiation marked the beginning of the quantum theory of light.
3. External photoelectric effect and its laws. Einstein's equation.
AT 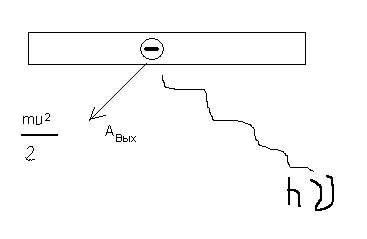 The external photoelectric effect is the emission of electrons from the surface of a metal under the action of incident light. It was experimentally found that external photoelectric effect subject to the following laws:
The external photoelectric effect is the emission of electrons from the surface of a metal under the action of incident light. It was experimentally found that external photoelectric effect subject to the following laws:
 1. The maximum speed of electrons emitted from the metal surface does not depend on the intensity of the incident light, but depends on its frequency.
1. The maximum speed of electrons emitted from the metal surface does not depend on the intensity of the incident light, but depends on its frequency.
2. There is a limiting wavelength characteristic of each substance, above which the photoelectric effect is not observed (simple boundary of the Photoelectric effect).
These regularities, observed experimentally, could not be explained by considering light as a wave; the corpuscular nature of light operates in the photoelectric effect.
Einstein developed Planck's quantum hypothesis. Light propagates in the form of separate portions (photons).
This shows that the speed of electrons during the photoelectric effect depends only on the frequency of the incident light. hv=A out +mv 2 /2.
The intensity of light is determined by the number of photons incident on the cathode. Consequently, the number of photoelectrons is determined only by the intensity of the incident light and does not depend on its frequency. In order to hold the photocurrent, it is necessary to apply a delay voltage to the anode. Its value can be determined by the formula: mv 2 /2=eU,U is the retarding voltage at the anode.
Therefore, hv \u003d A out + eU. The work A out is determined by the type of matter from which the photocathode is made. With a decrease in the frequency of the incident light, the energy of the emitted electrons will decrease hv cr =A out => λ cr =hc/ A out. Thus ur–e Einsch. allows you to explain all the experts. obs. law. Ur-e Einsch. built on the basis of one. approximations. And out of each specific. email did not hang. from the output of other e-in from the photocathode.
3. Photoelectric effect. Basic laws of the photoelectric effect
The photoelectric effect is the emission of electrons by a substance under the influence of electromagnetic radiation (photons). The photoelectric effect was discovered by Heinrich Hertz in 1887. Distinguish: an external photoelectric effect, in which the absorption of photons is accompanied by the escape of electrons outside the body, and an internal photoelectric effect, in which electrons, remaining in the body, are redistributed among energy levels.
The internal photoelectric effect manifests itself in a change in the electrical conductivity, dielectric constant of a substance or in the appearance at its boundaries electromotive force called photo emf. The photoelectric effect can be investigated using the following setup (Fig. 26). The tank is under high vacuum. Light enters through the quartz window O and illuminates the cathode K. The electrons emitted by the cathode due to the photoelectric effect move under the action of electric field to the anode A. As a result, a current will flow in the circuit, measured by a galvanometer D. The voltage U between the anode and cathode can be changed using a rheostat R. The graph (Fig. 27) shows the dependence of the photocurrent I on the voltage U for two values of the luminous flux Ф, and F2 > F1. The analysis of this dependence and the experiments carried out on the installation allow us to draw the following conclusions:
1. The photocurrent appears 10–8 s after the start of irradiation, i.e. the photoelectric effect is practically inertialess.
2. At a certain voltage, the photocurrent reaches saturation, i.e. all the electrons emitted by the cathode hit the anode (horizontal section of the graph in Fig. 27).
3 . When the voltage between the cathode and anode decreases to 0, the photocurrent does not disappear. Consequently, electrons knocked out by light from the cathode have a certain initial speed and can reach the anode without an external field. In order for the photocurrent to become equal to zero, it is necessary to apply a retarding voltage Uz in reverse direction. At this voltage, all electrons, even those with the highest velocity υmax during their flight, fail to overcome the retarding field and reach the anode. Therefore, based on the law of conservation of energy, we can equate the maximum kinetic energy of electrons Wmax to the work of the field forces eU3 in their retention:
. When the voltage between the cathode and anode decreases to 0, the photocurrent does not disappear. Consequently, electrons knocked out by light from the cathode have a certain initial speed and can reach the anode without an external field. In order for the photocurrent to become equal to zero, it is necessary to apply a retarding voltage Uz in reverse direction. At this voltage, all electrons, even those with the highest velocity υmax during their flight, fail to overcome the retarding field and reach the anode. Therefore, based on the law of conservation of energy, we can equate the maximum kinetic energy of electrons Wmax to the work of the field forces eU3 in their retention:
where e , m are the charge and mass of the electron.
4. From fig. 27 shows that an increase in the incident flux does not affect the magnitude of the retarding potential.
The following three laws of the external photoelectric effect have been experimentally established:
1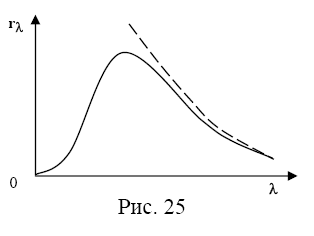 . Stoletov's law: at a fixed frequency of the incident light, the value of the saturation photocurrent is directly proportional to the incident light flux. The intensity of light is the luminous flux passing through a single area perpendicular to the direction of light. That's why the number of photoelectrons ejected from the cathode per unit time is proportional to the light intensity.
. Stoletov's law: at a fixed frequency of the incident light, the value of the saturation photocurrent is directly proportional to the incident light flux. The intensity of light is the luminous flux passing through a single area perpendicular to the direction of light. That's why the number of photoelectrons ejected from the cathode per unit time is proportional to the light intensity.
2 .The maximum initial speed of photoelectrons is determined by the frequency of light and does not depend on its intensity.
.The maximum initial speed of photoelectrons is determined by the frequency of light and does not depend on its intensity.
3
 .For every substance there is a minimum frequencyν0
light at which the external photoelectric effect is still possible. This minimum frequencyν0
(or maximum wavelengthλ0
) depends on the chemical nature of the substance, the state of its surface and is called the red boundary of the photoelectric effect. It is called red because for many substances it is in the red light region. For example, potassium does not give a photoelectric effect when illuminated with red light and begins to emit photoelectrons, starting with orange rays.
.For every substance there is a minimum frequencyν0
light at which the external photoelectric effect is still possible. This minimum frequencyν0
(or maximum wavelengthλ0
) depends on the chemical nature of the substance, the state of its surface and is called the red boundary of the photoelectric effect. It is called red because for many substances it is in the red light region. For example, potassium does not give a photoelectric effect when illuminated with red light and begins to emit photoelectrons, starting with orange rays.
The second and third laws of the photoelectric effect are in conflict with the idea of classical physics about the wave nature of light. Indeed, the greater the luminous flux, the greater the energy carried by the light wave, i.e. the more energy the photoelectrons should have received.
Quantum theory of the photoelectric effect. Einstein's equation
A. Einstein showed that all the laws of the photoelectric effect are explained if we assume that light is absorbed in the same portions (quanta, photons) as it is emitted according to Planck's hypothesis. According to Einstein, the photon energy E=hν received by an electron is assimilated by it entirely. Let us consider the photoelectric effect in metals from the quantum point of view. An electron is held in a metal by attraction. positive ions crystal lattice. In order to leave the metal, the electron must do the work function Aout. If the energy received by the electron is E = hν > Aout, then it will have kinetic energy upon departure. The value of this energy is maximum if the electron leaves the metal from the surface, and not from some depth. In this case, in accordance with the law of conservation of energy, a relation is fulfilled, which is called the Einstein equation for the external photoelectric effect:
E = hν = Aout + W max .
It can be seen from Einstein's formula that the photoelectric effect from the surface of a given substance is observed only at frequencies that satisfy the condition hν ≥ Aout. Then the red boundary of the photoelectric effect (ν0 or λ0) can be determined from the equation hν0 = Aout, i.e.

From formulas (2.12) and (2.13) it follows that U3 is a linear function of the frequency ν of the incident light (Fig. 28):
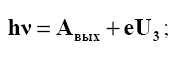
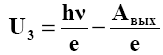

Intersection point U f(ν) 3 . = with the abscissa axis (U3 0 =) gives the value of the red border of the photoelectric effect ν0 . Extrapolating the straight line to the intersection with the y-axis, one can determine Aout for a given metal. On the basis of the photoelectric effect, photocells work - radiation receivers that convert radiation energy into electrical energy. They are used in various automation, signaling, communication systems, etc. Silicon solar cells are used to create solar panels.
6. Corpuscular-wave dualism of the properties of matter. De Broglie's hypothesis. Electron diffraction.
In 1924, Louis de Broglie proposed a hypothesis according to which the dualism (duality) of saints is inherent not only in optical phenomena, but also in matter in general. In particular, a wave process is associated with the flow of electrons, which affects the behavior of an electron as a particle, the charge and mass of which are localized in a small volume of space so that it behaves like a point charge. D-Broille showed how the wavelength of an electron wave can be determined by analogy with the wavelength of a photon.
Pf=m(index f)c=hνc/c (c.2)=hν/c=h/λ; λ(index c)=h/P(index e)=h/m(index c) v(index c) (1). The wavelength defined by (1) is called the de Broglie wavelength. D-Broil tried to explain Bohr's 1st postulate - the postulate of quantization. According to d-Brogle, stationary are those orbits of an electron, in which an integer number of d-Brogle waves fit along the perimeter. Those. a standing wave is established along the orbit. 2πr = nλ(index c), 2πr = nh/mv;
mvr = nh/2π=nh(c).
Jamer and Davison were the first to discover the diffraction of electrons by scattering them on monochromatic nickel. The electrons, accelerated by the potential difference U, flew out of the email. guns in the form of a narrow beam, and were focused on a klistal plate. Scattered electrons were captured by a Faraday cup trap connected to a sensitive galvanometer.
The electrons gave their charge to the trap, and the dependence of J on √U was established. The current strength J is a measure of the electrons reflected from the plate, and √U is a measure of their speed.
mv 2 /2=eU; √U~v. That. only electrons of certain velocities are reflected from the crystal. The crystal is a spatial diffraction grating in which the sources of secondary waves, i.e. particles in the nodes of the crystal lattice are located at strictly defined distances along the coordinate axes. When passing through a crystal of electromagnetic radiation, the particles at the nodes of the crystal lattice emit secondary waves, which, superimposed, form a maximum and minimum of diffraction. The fact that only electrons of certain velocities were reflected from the crystal meant that radiation, which is a wave process, falls on the crystal, and its selective reflection is the result of diffraction.
7. Bohr's postulates.
The first attempt to create a new - quantum - theory of the nucleus was carried out by N. Bohr. He set the goal of linking into a single whole the empirical regularities of line spectra, Rutherford's nuclear model of the atom, and the quantum nature of the emission and absorption of light. Bohr based his new theory on two postulates.
Bohr's first postulate (postulate of stationary states). In an atom, there are stationary (not changing with time) states in which it does not radiate energy. Stationary states of an atom correspond to stationary circular orbits along which electrons move. The motion of electrons in stationary orbits is not accompanied by the emission of electromagnetic waves.
In the stationary state of the atom, the electron has discrete values angular momentum, satisfying the condition
where  is the mass of the electron, v- its speed n th orbit radius
is the mass of the electron, v- its speed n th orbit radius 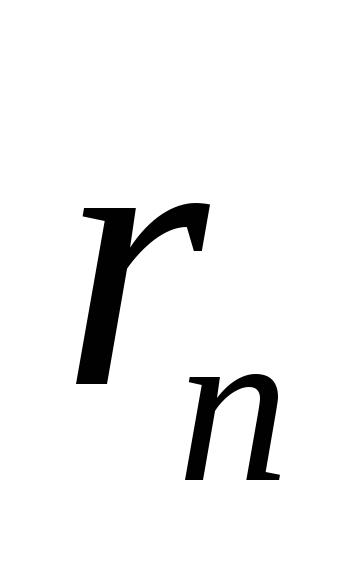 .
.
Bohr's second postulate (frequency rule). When an electron moves from one stationary orbit to another, one photon with energy is emitted (absorbed)
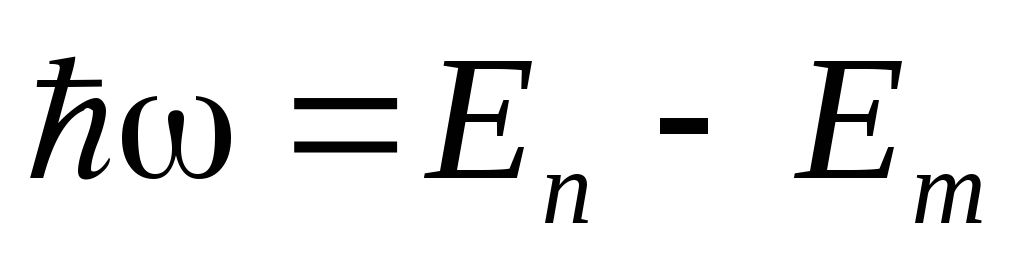 ,(2)
,(2)
where  and
and  are, respectively, the energies of the stationary states of the atom before and after radiation (absorption). The set of possible discrete frequencies of quantum transitions determines line spectrum atom.
are, respectively, the energies of the stationary states of the atom before and after radiation (absorption). The set of possible discrete frequencies of quantum transitions determines line spectrum atom.
T  Bohr's theory of the hydrogen-like atom. Bohr's postulates make it possible to calculate the spectrum of the hydrogen atom and hydrogen-like ions, consisting of a nucleus Ze and one electron, and theoretically calculate the Rydberg constant. Consider the motion of an electron in a field atomic nucleus. The electron motion equation has the form
Bohr's theory of the hydrogen-like atom. Bohr's postulates make it possible to calculate the spectrum of the hydrogen atom and hydrogen-like ions, consisting of a nucleus Ze and one electron, and theoretically calculate the Rydberg constant. Consider the motion of an electron in a field atomic nucleus. The electron motion equation has the form
 .(3)
.(3)
Excluding v from equations (1) and (3), we obtain an expression for the radii of admissible orbits
 .(4)
.(4)
For a hydrogen atom ( Z=1) the radius of the first orbit is called Bohr radius. Its value is
 .(5)
.(5)
The total energy of an electron in a hydrogen-like atom is the sum of its kinetic energy and potential energy interactions with the core

(Formula (3) was used in its preparation). Taking into account the quantization of radii (4), we obtain that the electron energy takes on discrete values
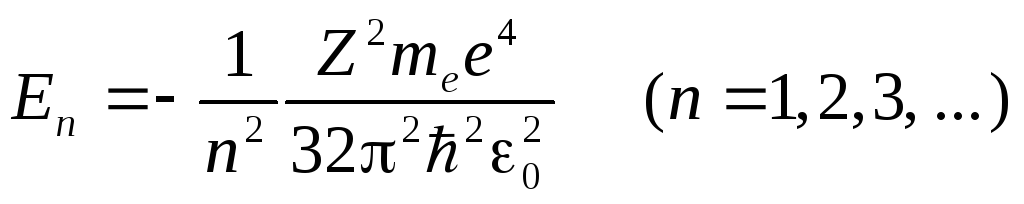 .(6)
.(6)
According to Bohr's second postulate, during the transition of a hydrogen atom from the state n into a state m a photon is emitted
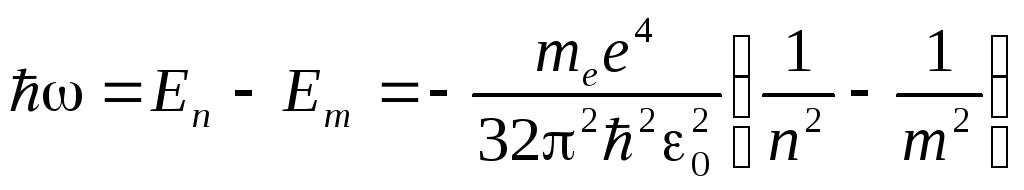 ,
,
whence the radiation frequency
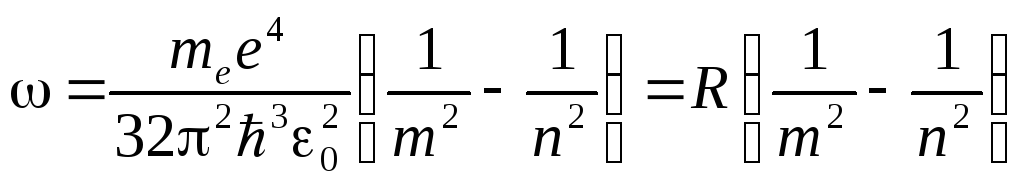 .
.
Thus, the Bohr theory leads to the generalized Balmer formula, and for the Rydberg constant the value 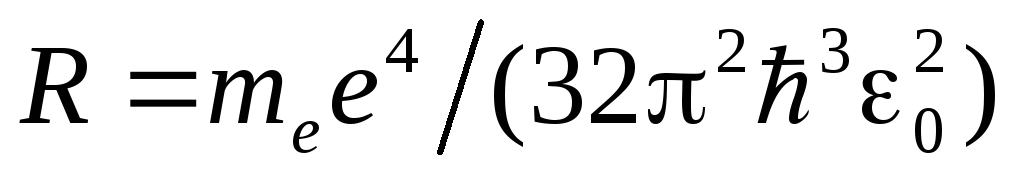 . When the values of the universal constants are substituted into this expression, a value is obtained that is in excellent agreement with the experimental value of the Rydberg constant.
. When the values of the universal constants are substituted into this expression, a value is obtained that is in excellent agreement with the experimental value of the Rydberg constant.
Bohr's theory was a major step in the development of the theory of the atom. She clearly showed that the processes in the microworld are described not by classical, but by other, quantum laws.
8. Experiments of Frank and Hertz.
The existence of discrete energy levels of the atom is confirmed by the experiments of Frank and Hertz. The scheme of their installation is shown in fig. The tube filled with mercury vapor under low pressure (~1 mmHg) contained three electrodes: a cathode To, grid FROM and anode BUT. The thermoelectrons emitted from the cathode were accelerated by the potential difference U applied between the cathode and the grid. A weak electric field (potential difference of about 0.5 V) was created between the grid and the anode, which slowed down the movement of electrons to the anode. In the experiment, the dependence of the current strength I in the anode circuit from voltage U between cathode and grid. The current-voltage characteristic characteristic of such experiments is shown in Fig.
The course of the curve can be explained as follows. When an electron collides with mercury atoms, two types of interaction are possible: 1) elastic collision, as a result of which the energy of electrons practically does not change, only the direction of motion changes; 2) inelastic collision electron with a mercury atom. In this case, the energy of the electrons decreases due to its transfer to the mercury atom.
In accordance with Bohr's postulates, a mercury atom can absorb energy in the form of a portion  and move into an excited state at a higher energy level. The first excited state of the mercury atom corresponds to an energy of 4.9 eV. At U< 4,9 В
электроны испытывают только упругое
взаимодействие с атомами ртути и,
поэтому, с увеличением напряжения
анодный ток возрастает.
and move into an excited state at a higher energy level. The first excited state of the mercury atom corresponds to an energy of 4.9 eV. At U< 4,9 В
электроны испытывают только упругое
взаимодействие с атомами ртути и,
поэтому, с увеличением напряжения
анодный ток возрастает.
Upon reaching U= 4.9 V, the energy of the electrons is compared with the energy of the first excited level of the mercury atom. There are inelastic collisions of electrons with mercury atoms, which receive a portion of energy  = 4.9 eV and go into an excited state. An electron that has lost energy cannot overcome the retarding potential. Therefore, when U= 4.9 V, the anode current decreases. A similar phenomenon is observed when U= 24.9 V, U\u003d 34.9 Vetc., when electrons can experience two, three, etc. inelastic collisions with mercury atoms. Having lost all (or almost all) energy, the electron will not be able to reach the anode, the retarding field will throw it back to the grid. As a result, there is a drop in current at these voltages and a general sawtooth course of the current-voltage characteristic.
= 4.9 eV and go into an excited state. An electron that has lost energy cannot overcome the retarding potential. Therefore, when U= 4.9 V, the anode current decreases. A similar phenomenon is observed when U= 24.9 V, U\u003d 34.9 Vetc., when electrons can experience two, three, etc. inelastic collisions with mercury atoms. Having lost all (or almost all) energy, the electron will not be able to reach the anode, the retarding field will throw it back to the grid. As a result, there is a drop in current at these voltages and a general sawtooth course of the current-voltage characteristic.
Mercury vapor atoms, having received energy from electrons, pass into an excited state, from which, after 10–8 s, they spontaneously return to the ground state. In this case, a photon with a wavelength of l»255 nm should be emitted. In the experiment, indeed, one ultraviolet line with such a wavelength is found. Thus, the experiments of Frank and Hertz experimentally confirm Bohr's postulates.
9. Electron spin. Spin quantum number. Experimental confirmation of the existence of a spin in an electron.
Was delivered experiment, for which atoms were taken, the cat's number of electrons is odd, and the mechanical and magnetic moments of the cat's are mutually compensated in pairs. Such atoms are the atoms of elements in the 1st group of the periodic table. An important feature of the element in this group is that the element in the ground state has l=0, M l =0 P l =0. A source of atoms was taken; field. Because Since the magnetic and mechanical moments of the atoms were = 0, then these atoms should not have been deflected by the magnetic field, and 1 spot should have been observed on the screen. The experiment showed: the atoms are deflected and give 2 max on the screen. Because the mechanical and magnetic moments of an electron in an atom due to its movement around the nucleus were equal to 0, and the atoms still deviated magnetically. field, it was assumed that an electron in an atom has its own mechanical M s and corresponding magnetic P s moments, which were called mechanical magnetic spin moments. Electron spin is considered to be the same fundamental property as charge and mass. The value of the spin mechanical moment m\b is calculated by the formula: M s =ħ  , where s- spin quantum number, which can take 2 values: s=1/2, s=-1/2.
, where s- spin quantum number, which can take 2 values: s=1/2, s=-1/2.
12. Band structure of intrinsic semiconductors. Intrinsic conductivity of semiconductors and its dependence on temperature.
Semipr-ki - islands, for which the width of the band gap is about 1 eV. At low temperatures, semi-conductors do not conduct electricity and are an insulator. Chemical-ski clean in-va is their own semi-pr-kami. Consider the 4-valent semipr-to Ge (germanium). Four bonds with neighboring atoms are formed by eight electrons (four from each atom). Each e-n acquires a connection with oppositely directed spins. When the temperature is low, all communications turn out to be staffed with emails and there are no free emails in the semi-pr-ke. When the temperature is increased, due to the energy of the chemical-th dv-I, the e-news are separated from one of the bonds. At the same time, in place of the departed electron, there remains an uncompensated positive charge called a hole. The hole is localized on some one bond in the crystal and cannot move freely through the crystal. The e-mail that has come off can freely move along the circle.
E  If you apply an external email field, then the email will move against the field. The hole can be occupied by an email from a neighboring connection. Through such jumps, the hole will move across the field, and the email will move against the field. Two holes can be considered as two positions of the particle charge. When free e-n takes the place of a hole, both free e-n and the hole disappear at the same time. This process is called recombination. That is, in chemically pure semi-pr-kah, a free electron and a hole appear at the same time, and their number is the same. The conductivity of chemically pure semi-conductors of the so-called properties is electron-hole. With tz zone theory, e-n involved in the creation of chemical bonds in the crystal-le nah-Xia in the valence band.
If you apply an external email field, then the email will move against the field. The hole can be occupied by an email from a neighboring connection. Through such jumps, the hole will move across the field, and the email will move against the field. Two holes can be considered as two positions of the particle charge. When free e-n takes the place of a hole, both free e-n and the hole disappear at the same time. This process is called recombination. That is, in chemically pure semi-pr-kah, a free electron and a hole appear at the same time, and their number is the same. The conductivity of chemically pure semi-conductors of the so-called properties is electron-hole. With tz zone theory, e-n involved in the creation of chemical bonds in the crystal-le nah-Xia in the valence band.
When sufficient energy is imparted to it, it overcomes the forbidden band and passes into the conduction band. In this case, a hole is formed in the valence band. Such a transition will be carried out primarily from the upper levels of the valence band. As the energy increases, electrons from ever deeper levels of the valence band will move into the conduction band. Therefore, the energy of a hole is greater, the deeper it is in the valence band. El-n in the conduction band and a hole in the valence band can be considered as free charge carriers in their own semi-pr-ke. It is clear that as the temperature increases, the number of such carriers will increase. The Fermi level in its own semi-pr-kah nah-Xia in the middle of the forbidden zone.
15. Spontaneous and stimulated emission.
The radiation in the cavity is a collection of quanta with energy 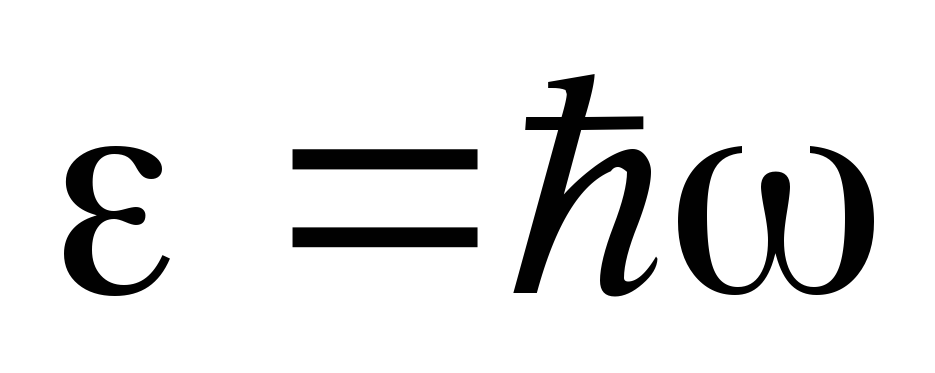 . Quanta can be absorbed by atoms, which in this case pass to a higher energy level with energy
. Quanta can be absorbed by atoms, which in this case pass to a higher energy level with energy 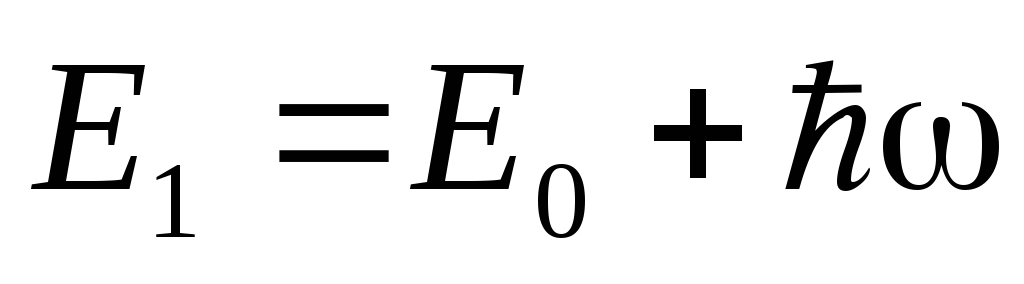 , where
, where  is the initial energy level of the atom. When an atom passes from the level
is the initial energy level of the atom. When an atom passes from the level  on the
on the  a quantum with energy is emitted
a quantum with energy is emitted  . Let's designate these levels with indices 0 and 1 (Fig.) and call them the lower and upper levels, respectively.
. Let's designate these levels with indices 0 and 1 (Fig.) and call them the lower and upper levels, respectively.
There is a constant exchange of energy between material bodies (cavity walls) and radiation. Dynamic equilibrium between them occurs when the exchange of quanta is balanced for each frequency. Therefore, only one frequency is considered below. For other frequencies, all arguments are similar.
Transitions from the lower level to the upper one are possible only with the absorption of an energy quantum, i.e. under the influence of the incident radiation. Such transitions are called forced. Transitions from the upper to the lower level can be either forced, under the influence of the incident on radiation atom, and spontaneous occurring independently of the radiation incident on the atom.
Denote  probability of spontaneous transition 1®0 per second,
probability of spontaneous transition 1®0 per second,  is the concentration of atoms at the upper level. Then the frequency of spontaneous transitions
is the concentration of atoms at the upper level. Then the frequency of spontaneous transitions
 .
.
The frequency of forced transitions is proportional to the number of incident photons or the spectral density of the radiation  . Denote
. Denote  and
and ![]() probabilities of forced transitions 1®0 and 0®1 per second under the action of radiation with
probabilities of forced transitions 1®0 and 0®1 per second under the action of radiation with  ;
;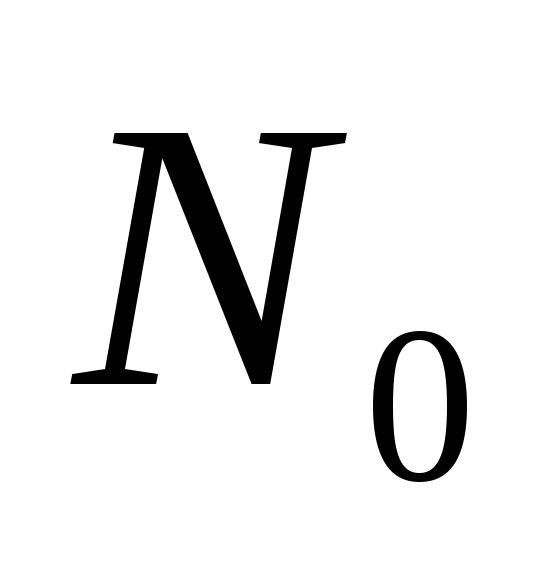 is the concentration of atoms at the lower level. Then for the frequency of forced transitions we can write
is the concentration of atoms at the lower level. Then for the frequency of forced transitions we can write
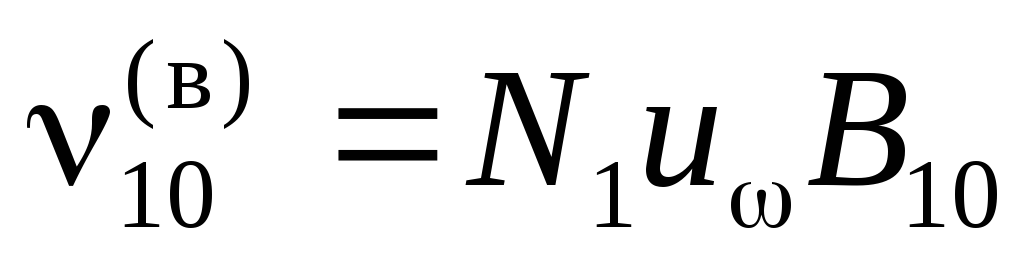 ,
,
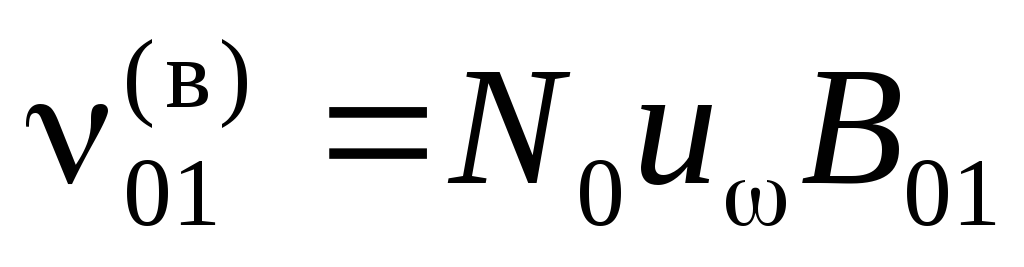 .
.
The dynamic equilibrium condition has the form 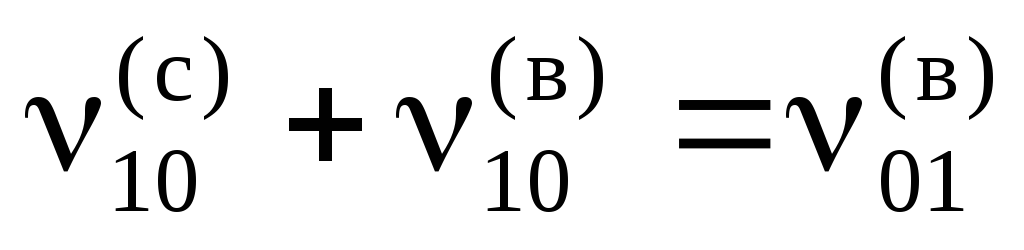 or
or
In the equilibrium state, the Boltzmann distribution is fulfilled, which for atomic concentrations has the form
 ,
,
 ,(2)
,(2)
where A is the normalization constant. Substituting (2) into (1), we find
Quantities  ,
, and
and  called Einstein coefficients.
called Einstein coefficients.
From physical considerations, it follows that  should be
should be  . Then it follows from the passage to the limit in (3) that
. Then it follows from the passage to the limit in (3) that
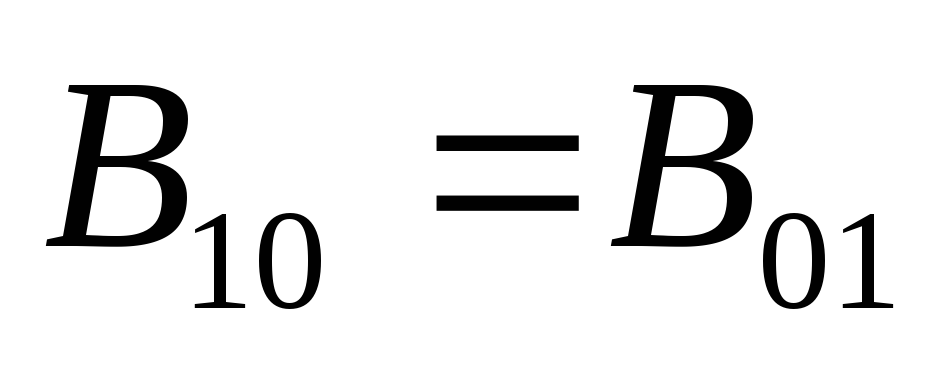 .(4)
.(4)
Therefore, relation (3) can be written as
 ,(5)
,(5)
where  . Meaning
. Meaning  can be found if we take into account that (5) at low frequencies should coincide with the Rayleigh-Jeans formula. At
can be found if we take into account that (5) at low frequencies should coincide with the Rayleigh-Jeans formula. At  and (5) takes the form
and (5) takes the form
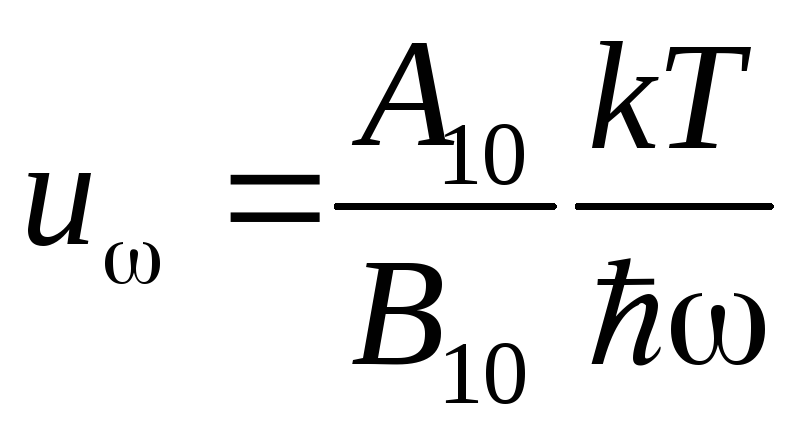 .
.
Comparing the resulting expression with the Rayleigh-Jeans formula, we find
 .
.
As a result, formula (5) takes the form
 .(6)
.(6)
Relation (6) is the Planck formula.
Spontaneous emission has a random propagation direction, random polarization and random phase. Stimulated emission differs from spontaneous emission in this respect. Direction of propagation stimulated emission coincides exactly with the direction of the driving radiation. The same applies to the frequency, phase, and polarization of stimulated and excitatory radiation. Consequently, stimulated and induced radiation turn out to be strictly coherent. This feature of stimulated emission underlies the operation of amplifiers and light generators called lasers.
16. Rutherford's model of the atom and its shortcomings. Bohr's postulates. Bohr model of the atom.
In all macroscopic systems, an electron behaves like a particle localized in a small volume, having a certain coordinate and speed. When an electron moves in an atom, its wave properties are manifested to a greater extent, as in all microscopic particles, but the wave is not localized in space, but is unlimited.
Let the electrons move in the direction OA with a velocity Vx and meet a narrow slot BC with a width a. DE is the screen on which the electrons will fall. Because electrons have wave properties, then when passing through a narrow slit they diffract, as a result of which the electrons will fall not only at the screen points DE located directly behind the slit, but will be distributed over the entire screen. Imagine that an electron is a classical particle. It is characterized by coordinate and momentum. It is possible to characterize the coordinate of an electron at the moment of passage of the gap as the coordinate of the gap. In such a definition of the coordinate, however, there is an inaccuracy due to the width of the slot. Let's denote this uncertainty by ∆x=a. After passing through the slit, the pulse component Px≠0, because changes in speed due to diffraction. The component of the electron momentum cannot be determined exactly, but only with some error ∆Px≥Psinφ1=Pλ/a=hλ/λa=h/a; ∆Px*∆x≥h (1) is the Heisenberg uncertainty relation.
The first attempt to formulate the laws governing the movement of electrons in an atom was made by Bohr on the basis of the notion that the atom is a stable system and that the energy that an atom can emit or absorb.
1) In the atom, there are stationary stable orbits, being on which the atom does not emit or absorb energy.
2) Bohr suggested that the emission or absorption of energy by an atom occurs when an atom passes from one stationary state to another. At each such transition, a quantum of energy is emitted, equal to the energy difference between bodies of stationary states, between which a quantum jump of an electron occurs, hν=En – Em (2) (n>m, radiation, n At the heart of his theory is an attempt to link into a single whole, firstly, the nuclear model of the Resenford atom, secondly, the quantum nature of the radiation and absorption of energy in atoms, and thirdly, the empirical laws of line spectra in the atom. Bohr's theory is applicable not only to the hydrogen atom, but also to one-electron He+ ions. The charge of the nucleus of such a system is ze, and around the nucleus is 1e(c). The Bohr model retains the main features of the classical Resenford model, i.e. .electron rotates in one of the circular orbits around a positively charged nucleus. Bohr's theory she pointed out the unacceptability of classical physics to describe the motion of an electron in an atom and the dominant role of quantum physics. DISADVANTAGES: 1) it was not completely non-classical, non-quantum. On the one hand, it allowed the orbital motion of an electron according to the law of classical physics, and on the other hand, it proceeded from the discreteness of energy levels, the quantization of energy and momentum, which contradicts the ideas of classical physics. 2) The rule of selection of stationary orbits is unreasonable. 3) The reason for the quantization of physical quantities is not clear: energy, momentum. 18. The structure of atomic nuclei. Mass and charge number. Nucleons. Core models: drip, shell. The nucleus of an atom is the center of the part in which the entire positive charge of the atom and almost all of its mass is concentrated. According to the present day, the atomic nucleus consists of protons and neutrons, which are considered to be 2 charge states - nucleons. A Z X , where Z is the charge number of the nucleus, coinciding with the number in Table Mend. A - mass number coincides with the atomic mass of the chemical element expressed in atomic mass unit. A express the total number of nucleons in the nucleus, since the atom of the chemical element is neutral, then the e-n (posit) db is exactly equal to the charge of the e-on in its e-shell. Therefore, the number of protons in the nucleus (+e): N p =Z. Number of neutrons: N n =A-Z. There are several kernel models. None of them is universal, but each of them is used when considering a particular nuclear process. Consider two of them: drip and shell drip model. Some properties of the nucleus and liquid drop are similar. The drip model is based on this similarity. The same density of nuclear matter indicates its extremely low compressibility, just like that of a liquid. According to this model, nucleons move intensively, randomly, experiencing numerous collisions. Each such collision is accompanied by a strong interaction of nucleons. Therefore, the energy received by the nucleus is quickly redistributed between the nucleons. Subsequent numerous collisions of nucleons can lead to the concentration of energy on a surface particle, for example,
α
-particle. If its energy is greater than its binding energy in the nucleus, then it can exit the nucleus. According to the drop model, the ejection of a particle from a nucleus is similar to the evaporation of molecules from a liquid. However, unlike a drop of liquid, an excited nucleus can pass into the ground state by emitting γ-quanta. So called photons of nuclear origin. The droplet model made it possible, in particular, to explain the process of nuclear fission. Shell model. According to this model, nucleons are filled in shells in accordance with the Pauli principle, just like electrons in an atom. With a completely filled nucleon shell, especially stable nuclei are formed. Based on experiments, these are nuclei in which the number of protons or the number of neutrons is: 2, 8, 20, 28, 50, 82, 126. These numbers are called magic. The first nucleon shell is filled with helium and consists of two protons and neutrons, the second with oxygen, and so on. According to the shell model, a nucleon moves in the field of other nucleons. When a nucleus is excited, one or more nucleons go to excited levels. Their transitions to the ground state are accompanied by the emission of γ-quanta. The article reveals the essence of the quantum properties of light. Talks about how they were discovered, and what it led to. In the late nineteenth and early twentieth centuries, it was believed in scientific circles that absolutely everything was clear in physics. The most advanced knowledge at that time was Maxwell's equations and the study of various phenomena associated with electricity. Young people who aspired to do science were not recommended to go into physics: after all, there could only be routine studies that did not provide any breakthroughs. However, ironically, it was precisely this study of the properties of a long-familiar phenomenon that opened the way to new horizons of knowledge. The wave and quantum properties of light began with the discovery of Max Planck. He studied the spectrum of an absolute black body and tried to find the most appropriate mathematical description of its radiation. As a result, he came to the conclusion that a certain minimum indivisible quantity, which he called the "quantum of action", should be introduced into the equation. And, since it was just a way to "cut the corner" for a simpler mathematical formula, he did not give this quantity any physical meaning. However, other scientists, for example, A. Einstein and E. Schrödinger, noticed the potential of such a phenomenon as a quantum, and gave development to a new branch of physics. I must say that Planck himself did not fully believe in the fundamental nature of his discovery. The scientist, trying to refute the quantum properties of light, briefly rewrote his formula, indulging in various mathematical tricks to get rid of this quantity. But nothing came of it: the genie had already been let out of the bottle. After Planck's discovery, the already known fact that light has wave properties was supplemented by another: a photon is a quantum of an electromagnetic field. That is, light consists of very small indivisible packets of energy. Each of these packets (photon) is characterized by frequency, wavelength and energy, and all these quantities are interconnected. The speed of light in a vacuum is the fastest in the known universe, at about 300,000 kilometers per second. It should be noted that other quantities are also quantized (that is, they are divided into the smallest indivisible parts): You should not think that in each type of field there is a certain smallest quantity, which is called a quantum: in the electromagnetic scale there are both very small and high-energy waves (for example, X-rays), and very large, but at the same time “weak” ones (for example, radio waves ). It's just that each quantum travels through space as a whole. Photons, it is worth noting, are able to lose some of their energy when interacting with insurmountable potential barriers. This phenomenon is called "tunneling". After such a bright opening, questions rained down: The main thing is that the phenomenon of light pressure has been proven. This fact gave a new reason for reflection: it means that the photon had momentum and mass. The corpuscular-wave dualism of microparticles adopted after that greatly facilitated the understanding of the madness happening in this world: the results did not fit into any logic that existed before. Further research only confirmed the quantum properties of light. The photoelectric effect showed how the energy of a photon is transferred to matter. Along with reflection and absorption, illumination is capable of pulling electrons from the surface of a body. How does this happen? The photon transfers its energy to the electron, which becomes more mobile and gains the ability to overcome the force of bonding with the nuclei of matter. The electron leaves its native element and rushes somewhere outside the familiar environment. The phenomenon of the photoelectric effect, which confirms the quantum properties of light, has different types and depends on which solid body the photon collides with. If it collides with a conductor, then the electron leaves the substance, as already described above. This is the essence of the external photoelectric effect. But if a semiconductor or dielectric is illuminated, then the electrons do not leave the body, but are redistributed, facilitating the movement of charge carriers. Thus, the phenomenon of improving conductivity when illuminated is called the intrinsic photoelectric effect. Oddly enough, but the internal photoelectric effect is very difficult to understand. It is necessary to know the band theory of the field, understand transitions through the band gap and understand the essence of the electron-hole conductivity of semiconductors in order to fully realize the importance of this phenomenon. In addition, the internal photoelectric effect is not so often used in practice. Confirming the quantum properties of light, the formulas for the external photoelectric effect limit the layer from which light is able to pull out electrons. where h is Planck's constant, ν is a quantum of light of a certain wavelength, A is the work that an electron does to leave matter, W is the kinetic energy (and hence the speed) with which it flies out. Thus, if all the energy of a photon is spent only on the exit of an electron from the body, then on the surface it will have zero kinetic energy and will actually not be able to escape. Thus, the internal photoelectric effect also takes place in a sufficiently thin external word of the illuminated substance. This severely limits its application. There is a possibility that an optical quantum computer will still use the internal photoelectric effect, but such technology does not yet exist. At the same time, the quantum properties of light are not entirely useless: the photoelectric effect and its laws make it possible to create a source of electrons. While these laws were formulated in full by Einstein (for which he received the Nobel Prize), various prerequisites arose much earlier than the twentieth century. The appearance of a current when an electrolyte was illuminated was first observed already at the beginning of the nineteenth century, in 1839. There are three laws in total: All these patterns are logical, but they should be considered in more detail. The first law means the following: the more photons fall on one square meter of surface area per second, the more electrons this light is able to “take away” from the illuminated substance. Basketball is an example: the more often a player throws the ball, the more often he will hit. Of course, if the player is good enough and not injured during the match. The second law actually gives the frequency response of the emitted electrons. The frequency and wavelength of a photon determine its energy. Red light has the lowest energy in the visible spectrum. And no matter how many red photons the lamp sends to matter, they are able to transfer only low energy to electrons. Therefore, even if they were pulled out from the surface itself and did almost no work of exit, then their kinetic energy cannot be higher than a certain threshold. But if we illuminate the same substance with violet rays, then the speed of the fastest electrons will be much higher, even if there are very few violet quanta. The third law has two components - the red border and the state of the surface. Many factors depend on whether the metal is polished or rough, whether it has pores or whether it is smooth: how many photons will be reflected, how they will be redistributed over the surface (obviously, less light will get into the pits). So you can compare different substances with each other only with the same surface condition. But the energy of a photon, which is still able to tear off an electron from a substance, depends only on the type of substance. If the nuclei do not attract charge carriers very strongly, then the photon energy can be lower, and, consequently, the red border is deeper. And if the nuclei of a substance hold their electrons tightly and do not want to part with them so easily, then the red border shifts to the green side. In physics for grade 11 (Kasyanov V.A., 2002), thermal radiation Completely black body thermal radiation- electromagnetic radiation emitted by heated bodies due to its internal energy. Completely black body- a body that absorbs all the energy of radiation incident on it of any frequency at an arbitrary temperature. Spectral density of energy luminosity is the energy of electromagnetic radiation emitted per unit of time per unit area of the body surface in a unit frequency interval. Unit of spectral density of energy luminosity J/m 2 . The energy of a radiation quantum is directly proportional to the frequency v of the radiation: where h = 6.6 10 -34 J s is Planck's constant. Photon- microparticle, quantum of electromagnetic radiation. Laws of Thermal Radiation: Wien's Displacement Law Stefan-Boltzmann law: The integral luminosity of a black body is proportional to the fourth power of its absolute temperature: photoelectric effect the phenomenon of ejection of electrons from solid and liquid substances under the action of light. Laws of the photoelectric effect 1. The saturation photocurrent is directly proportional to the intensity of the light incident on the cathode. 2. The maximum kinetic energy of photoelectrons is directly proportional to the frequency of light and does not depend on its intensity. 3. For each substance there is a minimum frequency of light, called the red limit of the photoelectric effect, below which the photoelectric effect is impossible. Einstein's equation for the photoelectric effect: red border photo effect Corpuscular-wave dualism - manifestation in the behavior of the same object of both corpuscular and wave properties. Corpuscular-wave dualism is a universal property of any material objects. wave theory correctly describes the properties of light at high intensities, i.e. when the number of photons is large. Quantum theory is used to describe the properties of light at low intensities, i.e. when the number of photons is small. Any particle with momentum p Answer
the de Broglie wavelength is: The state of the micro-object changes during the measurement process. Simultaneous precise determination of the position and momentum of a particle is impossible. Heisenberg uncertainty relations: 1. The product of the uncertainty of the particle's coordinate and the uncertainty of its momentum is not less than Planck's constant: Bohr's postulates: 1. In a stable atom, an electron can only move along special, stationary orbits, without radiating electromagnetic energy 2. The emission of light by an atom occurs during the transition of an atom from a stationary state with a higher energy E k to a stationary state with a lower energy Е n . The energy of the emitted photon is equal to the difference between the energies of the stationary states: Bohr's orbit quantization rule: On the circumference of each stationary orbit fits an integer n of de Broglie wavelengths, with Answer
corresponding to the motion of an electron Ground state of the atom is the state of minimum energy. Luminescence- non-equilibrium radiation of matter. Spectral analysis- a method for determining the chemical composition and other characteristics of a substance by its spectrum. Basic radiative processes of atoms: absorption of light, spontaneous and stimulated emission. light absorption is accompanied by the transition of the atom from the ground state to the excited state. Spontaneous emission- radiation emitted during the spontaneous transition of an atom from one state to another. stimulated emission- radiation of an atom that occurs when it passes to a lower energy level under the influence of external electromagnetic radiation. Laser- source of radiation amplified as a result of induced radiation. Inverse population of energy levels- non-equilibrium state of the medium, in which the concentration of atoms in the excited state is greater than the concentration of atoms in the ground state. Metastable state- the excited state of the atom, in which it can be much longer than in other states. Electromagnetic radiation with energies up to 250 keV is commonly called x-rays
, and above that - g radiation
. The radiation of radioactive isotopes, regardless of energy, is usually denoted as All other types of AI have a corpuscular nature, representing elementary particles. The mechanism of energy transfer of all charged particles is approximately the same. When passing through matter, a charged particle loses its energy, causing ionization and excitation of atoms until the total energy supply decreases to such an extent that the particle loses its ionizing ability and is usually captured by some atom to form an ion. The energy lost by a charged particle per unit of its path is called linear energy loss.
Depending on this, all ionizing radiation is divided into rarely-
and densely ionizing
. Rarely ionizing radiation includes all types of electromagnetic radiation and electrons, and densely ionizing radiation includes protons, deuterons and heavier particles. Rice. 11. Rutherford's experience. The first of them deviates slightly towards the negatively charged plate, and the other strongly deviates towards the positively charged plate. These components he called alpha rays and beta rays. Since most of the space in an atom is empty, fast a-particles can almost freely penetrate significant layers of matter containing several thousand layers of atoms. The scattering of charged particles observed by Rutherford is explained by such a distribution of charges in the atom. In collisions with individual electrons, a-particles deviate by very small angles, since the mass of the electron is small. However, in those rare cases when it flies at a close distance from one of the atomic nuclei, under the influence of a strong electric field of the nucleus, a deflection by a large angle can occur. A year later, P. Willard found that the composition of radioactive radiation also includes a third component: gamma rays, which are not deflected by either magnetic or electric fields. It was found that radioactive nuclei can emit particles of three types: positively and negatively charged and neutral. Until the nature of these radiations was clarified, the rays that deviated towards the negatively charged plate were conventionally called alpha particles
, deviated towards a positively charged plate - beta rays
, and the rays that did not deviate at all were called gamma rays
(Fig. 12.). Rice. 12. Components of radioactive radiation. K - lead container, R - radioactive preparation, Alpha particles (a) are the nuclei of the helium atom and consist of two protons and two neutrons. They have a double positive charge and a relatively large mass of 4.0003 amu. For each isotope, the energy of alpha particles is constant. The range of alpha particles in air is, depending on the energy, 2–10 cm, and in biological tissues it is several tens of microns. Since alpha particles are massive and have high energy, their path in matter is straightforward; they cause strongly pronounced effects of ionization and fluorescence. Alpha radiation when it enters the human body is extremely dangerous, since all the energy of a-particles is transferred to the cells of the body. Beta radiation (b) represents the stream of particles (electrons or positrons) emitted by nuclei during beta decay. The physical characteristic of the electrons of nuclear origin is the same as that of the electrons of the atomic shell. Beta particles are denoted by the symbol b - (electronic decay), b + (positron decay). Unlike alpha particles, beta particles of the same radioactive element have different amounts of energy. This is explained by the fact that during beta decay, neutrinos and beta particles are emitted from the atomic nucleus simultaneously. The energy released during each decay event is distributed between the beta particle and the neutrino. This is an electrically neutral particle that moves at the speed of light, has no rest mass and has a large penetrating power; making it difficult to register. If a b-particle is emitted with a large amount of energy, then a neutrino is emitted with a low energy level and vice versa. The range of beta particles in the same medium is not the same. The path in the substance of such particles is tortuous, they easily change the direction of movement under the action of the electric fields of oncoming atoms. Beta particles have less of an ionizing effect than alpha particles. Their range in air can be up to 25 cm, and in biological tissues - up to 1 cm. Different radioactive isotopes differ in the energy of beta particles. Their maximum energy has wide limits from 0.015–0.05 MeV (soft beta radiation) to 3–12 MeV (hard beta radiation). Gamma radiation (g) is a stream of electromagnetic waves; it's like radio waves, visible light, ultraviolet and infrared rays, and x-rays. Rice. 13. Scheme of the formation of gamma radiation Different types of radiation differ in the conditions of formation and certain properties. X-ray radiation occurs when fast electrons decelerate in the electric field of the nucleus of atoms of a substance (bremsstrahlung) or when the electron shells of atoms are rearranged during ionization and excitation of atoms and molecules (characteristic x-ray radiation). During various transitions from an excited state to an unexcited state, emission of visible light, infrared and ultraviolet rays can occur. Gamma quanta are emitted by the nuclei of atoms during the alpha and beta decay of natural and artificial radionuclides in those cases when an excess of energy is found in the daughter nucleus that is not captured by corpuscular radiation. Gamma rays have no rest mass, no charge, and therefore do not deviate in an electric or magnetic field. In matter and in vacuum, gamma radiation propagates in a straight line and uniformly in all directions. The energy of a gamma quantum is proportional to the oscillation frequency and is determined by the formula: Еg = h × ν, (1.16)
where h is Planck's universal constant (4.13 × 10 –21 MeV/s); n is the frequency of oscillations per second. The oscillation frequency is related to the wavelength. The longer the wavelength, the lower the oscillation frequency and vice versa, i.e. the frequency is inversely proportional to the wavelength. The energy of gamma radiation varies from a few keV to 2–3 MeV. The composition of the gamma radiation flux often includes quanta of various energy values. However, their set is constant for each isotope. Gamma quanta, having no charge and rest mass, cause a weak ionizing effect, but have a high penetrating power. The path in the air reaches 100–150 m (see Fig. 14). Rice. 14. Penetrating ability of alpha, beta and gamma particles. Neutrons. Unlike charged particles, neutrons do not carry an electric charge, which allows them to freely penetrate deep into atoms; colliding with the latter, they are either absorbed by it or repelled. As a result of elastic scattering, strongly ionizing high-energy protons are formed, and when neutrons are absorbed by atomic nuclei, protons, alpha particles and g-quanta are emitted from the latter, which also produce ionization. Thus, under neutron irradiation, the final biological effect is associated with ionization produced indirectly by secondary particles or g-quanta. The contribution of one or another nuclear interaction of neutrons depends on the composition of the irradiated substance and on their energy. According to the energy value, four types of neutrons are distinguished: fast, intermediate, slow and thermal (see Fig. 15). Neutrons are classified as densely ionizing radiation, since the range of the recoil protons they form is small. However, they occur at great depths due to the high penetrating power of neutrons. Negative p mesons- negatively charged particles with a mass 273 times the mass of an electron. They are obtained by artificial means. These particles have a unique ability to interact with the nuclei of atoms. Negative pimesons with energies on the order of 25–100 MeV travel all the way through matter until complete deceleration with almost no nuclear interactions. At the end of the run, they are captured with 100% probability by the nuclei of tissue atoms. Rice. 15. Types of neutrons. 1.3.2. Interaction of radioactive radiations First, purely physical the stage of interaction, which takes place in millionths of a second, consists in the transfer of a part of the photon energy to one of the electrons of the atom, followed by ionization and excitation. Ions and excited atoms, which have excess energy, are therefore characterized by increased chemical reactivity, they are able to enter into reactions that are not possible for ordinary, unexcited atoms. Second, physical and chemical, the stage proceeds depending on the composition and structure of the irradiated substance. Of fundamental importance is the presence of water and oxygen. If they are absent, then the possibilities of chemical interaction of atoms activated by radiation are limited, localized. Interaction of alpha and beta particles.
Charged particles, passing through matter, gradually lose energy as a result of interaction with the electrons of atoms, as well as with the electric field of the nucleus. The kinetic energy of a- and b-particles is wasted on ionization, that is, on the detachment of electrons from an atom, and on the excitation of atoms and molecules. Interacting with the electric field of the nucleus, the charged particle is slowed down and changes the direction of its movement, while the emission of radiation occurs, which in its characteristics is close to X-ray and is called bremsstrahlung X-ray radiation. The quantity that determines the energy side of the ionization process is ionization work
is the average work spent on the formation of one pair of ions. Charged particles, different in nature, but with the same energy, form almost the same number of pairs of ions. However ionization density
, i.e. the number of pairs of ions per unit path of a particle in a substance will be different. The ionization density increases with an increase in the charge of the particle and with a decrease in its velocity. Passing through matter, charged particles gradually lose energy and speed, so the ionization density along the path of the particle increases and reaches a value at the end of the path. At the end of the path, the a-particle attaches two electrons to itself and turns into a helium atom, and The path taken by an a- or b-particle in a substance, during which it produces ionization, is called particle range
. The range of an alpha particle in air can reach 10 cm, and in soft biological tissue - several tens of microns. The range of beta particles in the air reaches 25 m, and in tissues up to 1 cm. Alpha particles propagate in matter in a straight line and change direction only when they collide with the nuclei of oncoming atoms. Beta particles, having a small mass, high speed and negative charge, deviate significantly from their original direction as a result of collisions with orbiting electrons and nuclei of oncoming atoms. (scattering effect).
By undergoing multiple scattering, beta particles can even move in the opposite direction - backscattering. Due to the significant scattering of b-particles, the true path length in matter is 1.5–4 times greater than their range. Another difference is in the passage of a- and b-particles through matter. Since all alpha particles emitted by an isotope have relatively equal energy and move rectilinearly in the substance, their number in the beam passing through unit surface of the absorber drops sharply to zero only at the end of the run. The spectrum of beta particles is continuous, therefore, with an increase in the thickness of the absorber, the number of beta particles in a beam passing through a unit surface decreases gradually. The weakening of the intensity of the flow of b-particles in matter approximately obeys the exponential dependence: N \u003d N 0 × e - m a, (1.17)
where N is the number of beta particles that have passed through the absorber layer d cm, N 0 is the number of beta particles arriving in 1 s at the absorber area equal to 1 cm 2; e is the base of natural logarithms; m is the linear radiation attenuation coefficient characterizing the relative attenuation of the intensity of the b-particle flux after passing through an absorber 1 cm thick. Interaction of gamma radiation with matter.
During the radioactive decay of a nucleus, g-quanta with different energies are emitted. When passing through matter, they lose energy practically due to three effects: photoelectric absorption, Compton scattering, and the formation of electron-positron pairs. At photoelectric effect
the energy of the incident quantum is completely absorbed by the substance, as a result, free electrons appear that have a certain kinetic energy, the value of which is equal to the energy of the radiation quantum minus the work function of the given electron from the atom. A free electron, associating with one of the neutral atoms, generates a negative ion. The photoelectric effect is characteristic only for long-wavelength X-rays. Its probability depends on the atomic number and is proportional to Z 5 . The process of the photoelectric effect is impossible on weakly bound and free electrons (not bound to the nucleus), since they cannot absorb g-quanta. At Compton effect
g-quanta, colliding with electrons, transfer to them not all of their energy, but only part of it, and after the collision change their direction of motion. The electrons formed as a result of collision with g-quanta acquire significant kinetic energy and waste it on the ionization of matter (secondary ionization). That. as a result of the Compton effect, the intensity of gamma radiation is weakened due to the fact that g-quanta, interacting with the electrons of the medium, scatter in different directions and go beyond the primary beam, as well as due to the transfer of part of their energy to the electrons. Pairing. Some g-quanta with an energy of at least 1.02 MeV, passing through matter, are converted under the action of a strong electric field near the nucleus into an electron-positron pair. In this case, there is a transition from one form of matter - gamma radiation to another - into particles of matter. The formation of such a pair of particles is possible only at photon energies not less than the energy equivalent to the mass of both particles - an electron and a positron. The resulting electron-positron pair subsequently disappears, turning into two secondary g-quanta with an energy equal to the energy equivalent of the rest mass of particles - 0.511 MeV. The probability of pair formation increases with an increase in the energy of g-quanta and in the density of the absorber. The law of attenuation of gamma radiation by matter differs significantly from the law of attenuation of a- and b-particles. The g-ray beam is absorbed continuously as the thickness of the absorber increases. Those. Whatever the thickness of the substance layer, it is impossible to completely absorb the flow of g-rays, but only to weaken its intensity by any given number of times. This is the essential difference between the nature of the attenuation of g-rays and the attenuation of a- and b-particles, for which it is always possible to choose a layer of matter in which the flux of a- or b-particles is completely absorbed. The g-ray beam attenuation law has the following form: I \u003d I 0 × e - m a, (1.18)
where I is the intensity of the g-ray beam that has passed through the absorber layer; I 0 is the intensity of the incident beam of gamma rays; m is the linear attenuation coefficient, equal to the relative decrease in the intensity of the gamma-ray beam after passing through the absorber layer 1 cm thick. The linear attenuation coefficient is the total coefficient that takes into account the attenuation of the gamma-ray beam due to all three processes: photoelectric effect (t f), Compton effect (t k) and pair formation (t p): m \u003d t f + t k + t p (1.19)
Section 2 (lectures #3–4) FUNDAMENTALS OF RADIOECOLOGYPlanck and quantum
Light is a quantum of the electromagnetic field

Quantum: difference from electron
The interaction of light and matter

Energy transfer
Types of photoelectric effect

External photoelectric formula

Laws of the external photoelectric effect

Explanation of the laws of the photoelectric effect

a task №87
to chapter " Quantum theory of electromagnetic radiation. MAIN PROVISIONS». where λm is the wavelength at which the maximum spectral density of the blackbody energy luminosity falls, T is the temperature of the blackbody, b ≈ 3000 µm K is Wien's constant.
where λm is the wavelength at which the maximum spectral density of the blackbody energy luminosity falls, T is the temperature of the blackbody, b ≈ 3000 µm K is Wien's constant. where σ =
5.67 10 -8 W / (m 2 K 4) - Stefan-Boltzmann constant.
where σ =
5.67 10 -8 W / (m 2 K 4) - Stefan-Boltzmann constant.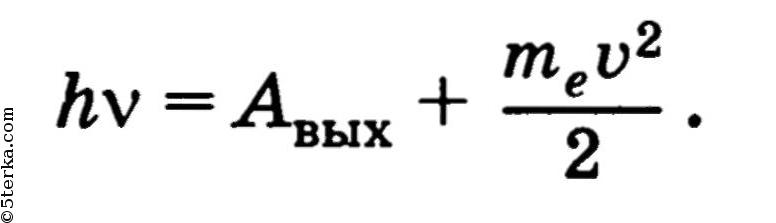 The energy of the photon is used to perform the work function and to communicate the kinetic energy to the emitted photoelectron. The work function is the minimum work that must be done to remove an electron from a metal.
The energy of the photon is used to perform the work function and to communicate the kinetic energy to the emitted photoelectron. The work function is the minimum work that must be done to remove an electron from a metal.

 2. The product of the uncertainty of the energy of a particle and the uncertainty of the time of its measurement is not less than Planck's constant:
2. The product of the uncertainty of the energy of a particle and the uncertainty of the time of its measurement is not less than Planck's constant: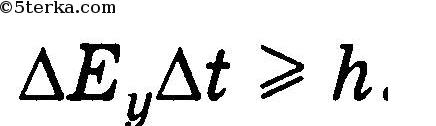


g-rays
.
The nature of the emitted radiation was studied by its absorption in matter and by the deflection of these rays in a magnetic and electric field.
In 1899, E. Rutherford, studying the behavior of radioactive radiation in an electric field, found that it consists of two components (see Fig. 11). 
Ф – photographic plate, – magnetic field.


with substance
b-particle (electron) can be included in one of the atoms of the medium.






