Rayleigh-Jeans formula. Ultraviolet disaster
Wien's first and second laws
Wien's first law is written as a formula:
u v
ν
- radiation frequency,
T
f is a function that depends only on frequency and temperature. The form of this function cannot be determined from thermodynamic considerations alone.
This is a formula for calculating the radiation density of any frequency.
Wien's second law is written as a formula:
![]()
u v is the radiation energy density,
ν
- radiation frequency,
T
is the temperature of the radiating body,
C1,C2- constants.
This formula is used to calculate the energy density of short wave radiation.
ultraviolet catastrophe- physical term, which describes the paradox of classical physics, which consists in the fact that the total power of thermal radiation of any heated body must be infinite. The name of the paradox was due to the fact that the spectral power density of the radiation had to increase indefinitely as the wavelength shortened. In fact, this paradox showed, if not the internal inconsistency of classical physics, then at least an extremely sharp (absurd) discrepancy with elementary observations and experiment .Since this is inconsistent with experimental observation, at the end of the 19th century, difficulties arose in describing the photometric characteristics of bodies. The problem was solved using quantum theory Max Planck radiation in 1900.
30. Planck's hypothesis. Way out of ultraviolet catastrophe.
Planck's hypothesis- a hypothesis put forward on December 14, 1900 by Max Planck and consisting in the fact that during thermal radiation, energy is emitted and absorbed not continuously, but in separate quanta (portions). Each such portion-quantum has an energy proportional to the frequency ν of radiation: where h or is the coefficient of proportionality, later called Planck's constant. On the basis of this hypothesis, he proposed a theoretical derivation of the relationship between the temperature of a body and the radiation emitted by this body - Planck's formula. Later, Planck's hypothesis was experimentally confirmed. The advancement of this hypothesis is considered the moment of the birth of quantum mechanics.
So, ultraviolet light can be emitted either in large quanta if the temperature of the body is high, for example, the surface of the Sun, or not emitted at all if the energy of the thermal motion of the atoms of the body is not enough for it to emit a radiation quantum. This is a qualitative explanation of the drop in the radiation intensity at λ → 0 and resolution of ultraviolet catastrophe. Planck, using quantum concepts, theoretically obtained a formula describing the dependence r λ= f(λ , T) called Planck's formula:
This formula gives very good agreement with the experimental data at all frequencies and at all temperatures. By integrating the equation, the Stefan-Boltzmann law can be obtained, and by differentiation, the Wien displacement law. Planck's hypothesis about the discrete nature of electromagnetic radiation marked the beginning of the quantum theory of light.
Unit 4: Quantum Physics
thermal radiation. external photoelectric effect.
Light pressure. Compton effect
1. Thermal radiation. Completely black body
2. Laws of thermal radiation
2.1. Kirchhoff's law
2.2. Laws of Wine
2.3. Stefan-Boltzmann law
3. Ultraviolet disaster
4. Quantum hypothesis and Planck's formula
5. Optical pyrometry
6. External photoelectric effect. Einstein's equation
7. Photons: energy, momentum
8. Light pressure
9 Compton Effect
1. Thermal radiation. Completely black body
The radiation of a body due to the thermal motion of molecules is called thermal, since it occurs due to the energy of the thermal motion of molecules (atoms). Any body with a temperature T≠0 radiates, and the radiation spectrum is continuous. Thermal radiation is the only radiation capable of being in thermodynamic equilibrium with matter. If the decrease in the energy of the body during radiation is replenished due to the absorption of radiation incident on the body from the environment, then the radiation is called balanced.
The thermal radiation of bodies can be characterized by the following quantities:
1) Integrated radiation intensity http://pandia.ru/text/78/094/images/image002_12.gif" width="115 height=52" height="52"> . (20.1)
This quantity is also called full energy luminosity. It depends on absolute temperature body. Dimension :
6. External photoelectric effect. Einstein's equation
Another phenomenon that can be explained only on the basis of quantum concepts is - photoelectric effect. Light, falling on a body (solid or liquid), knocks out electrons from its surface. The external photoelectric effect is the emission of electrons by a substance under the action of light..
The photoelectric effect was discovered by G. Hertz in 1887: when a negative electrode is illuminated with ultraviolet light, a gas discharge between the electrodes occurs at m e lower voltage. studied the photoelectric effect in the years. and found that when illuminated, the metal cathode loses negative charges. The basic laws of the photoelectric effect were experimentally discovered by Stoletov BEFORE THE DISCOVERY OF THE ELECTRON by J. Thomson in 1897. Systematic studies of the photoelectric effect were carried out in 1900 by F. Lennard using an apparatus, the scheme of which is given in fig. 20.7. Light enters the cathode through a quartz window. Electrons escaping from the cathode as a result of the photoelectric effect reach the anode. The voltage between the cathode and the anode can be changed in magnitude, as well as change its polarity using a switch.
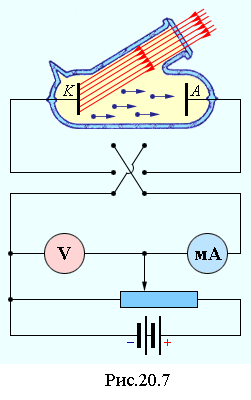 On fig. 20.8 shows the current-voltage characteristics of the photocell. In the absence of voltage, there is current in the circuit, since the most energetic electrons reach the anode. With an increase in voltage, the current in the photocell circuit first grows: electric field also less energetic electrons..gif" width="20" height="19 src="> saturation current increases.
On fig. 20.8 shows the current-voltage characteristics of the photocell. In the absence of voltage, there is current in the circuit, since the most energetic electrons reach the anode. With an increase in voltage, the current in the photocell circuit first grows: electric field also less energetic electrons..gif" width="20" height="19 src="> saturation current increases.
When switched on again (on the cathode - plus, on the anode - minus), the electric field between the cathode and the anode "drives" the electrons back to the cathode, and only the most energetic ones are able to overcome this retarding field and reach the anode..gif" width="65" height \u003d "28"\u003e Photon, falling on the cathode, is absorbed by the electron and transfers its energy to it.
1) The saturation current is directly proportional to the luminous flux and does not depend on the frequency of the light.:
Explanation: the more photons hit the cathode, the more electrons will be knocked out, and all of them, with sufficient voltage, will hit the cathode, regardless of the initial speed of the electrons. The strength of the saturation current does not depend on the energy of the electrons, but only on their number.
2) The maximum kinetic energy of photoelectrons depends linearly on the frequency of light and does not depend on its intensity. The energy of a photon is transferred to an electron. Part of the energy the electron spends on the work function, part remains with it in the form kinetic energy, and a part can be transferred to the crystal lattice. Therefore, electrons fly out of the cathode at different speeds, and only for those that have not transferred part of the energy to the lattice, the energy conservation law can be written:
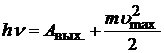 . (20.22)
. (20.22)
From (20.22) linear dependence 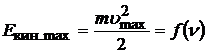 obvious. The speed (and energy) of a photoelectron does not depend on the intensity of light, since it is determined by the energy of one photon, and not by the number of photons.
obvious. The speed (and energy) of a photoelectron does not depend on the intensity of light, since it is determined by the energy of one photon, and not by the number of photons.
The retarding voltage does not allow even the most energetic electrons to reach the anode, that is, the photoelectrons spend all the energy to overcome the retarding voltage:
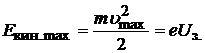 (20.23)
(20.23)
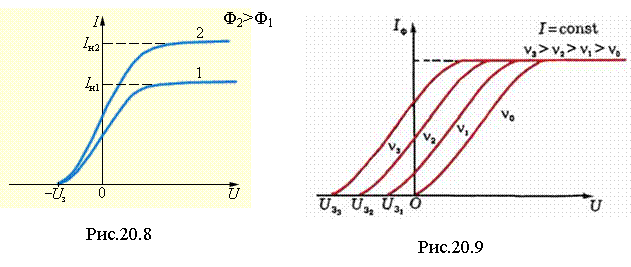 |
When the frequency changes, the light will change and (see the family of characteristics in Fig. 20.9):
http://pandia.ru/text/78/094/images/image071_1.gif" width="21" height="25 src="> , at which the photo effect starts: at http://pandia.ru/text/78/094/images/image073_1.gif" width="51" height="25">no photoelectric effect. The red border is different for each cathode substance.
The photoelectric effect is possible only if the energy of the photon is enough for the work function of the electron. The minimum energy of a photon that causes the photoelectric effect is equal to
where does the red border come from:
. (20.24)
Red border wavelength:
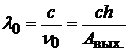 ; (20.25)
; (20.25)
Moreover, the photoelectric effect is present at and absent at .
Einstein's equation can also be written like this:
http://pandia.ru/text/78/094/images/image080_1.gif" width="128" height="25 src=">
http://pandia.ru/text/78/094/images/image082_1.gif" width="117" height="52 src=">
4) The photoelectric effect is inertialess. This was noticed even by Stoletov.
The laws of the photoelectric effect cannot be explained wave theory. For example, the existence of a red boundary does not fit into the wave theory: a light wave of low frequency (energy) could also “rock” an electron (only for a longer time) and it could fly out of the metal. The inertialessness is also inexplicable by the wave theory (it takes time to “build up” an electron by a wave), and from the point of view of quantum theory, the process of interaction of a photon with an electron occurs almost instantly. If light is absorbed as a wave, then the independence of the photoelectron energy from its amplitude, that is, the intensity of light, is inexplicable.
Computer model of the photoelectric effect:
http://www. *****/images/9/9f/Fot_7.swf
7. Photons: energy, momentum
So light:
a) emitted in discrete portions - quanta, photons (an explanation of the laws of thermal radiation led to this);
b) is also absorbed by quanta (photoelectric effect).
Energy photon is
http://pandia.ru/text/78/094/images/image084_1.gif" width="69" height="48 src=">. (20.26a)
Photons are massless particles:
http://pandia.ru/text/78/094/images/image086_1.gif" width="147" height="32 src=">.
Hence for a photon:
http://pandia.ru/text/78/094/images/image088_1.gif" width="73" height="28 src=">;
DIV_ADBLOCK62">
http://pandia.ru/text/78/094/images/image091_0.gif" align="left" width="221 height=288" height="288"> Since photons have momentum, when light falls on a surface it receives an impulse, that is, a pressure force acts on the surface.For the first time, a Russian physicist measured the pressure of light around 1900. To eliminate the influence of air flows on the movement of light wings, a vacuum is created in the vessel (Fig. 20.10).Light pressure was calculated from the angle of twisting of the quartz threads of a very sensitive torsion balance, to which the wings were suspended.The quantitative result obtained in Lebedev's experiments coincided with an accuracy of 2% with that predicted by Maxwell's theory for an electromagnetic field.
The expression for light pressure here will be obtained based on quantum concepts.
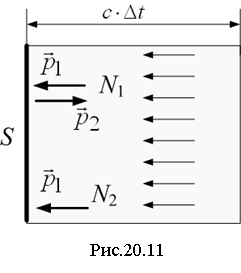 Let light normally fall on a surface with a reflection coefficient ρ (Fig. 20.11). For a period of time Δ t to the site S hits N photons. Of these, the number of photons reflected is equal to N 1=ρ N, and absorbed N 2=(1–ρ) N photons. The momentum of one photon is
Let light normally fall on a surface with a reflection coefficient ρ (Fig. 20.11). For a period of time Δ t to the site S hits N photons. Of these, the number of photons reflected is equal to N 1=ρ N, and absorbed N 2=(1–ρ) N photons. The momentum of one photon is
http://pandia.ru/text/78/094/images/image094_0.gif" width="113" height="28 src=">
directed along the normal to the site and equal in magnitude
http://pandia.ru/text/78/094/images/image096_0.gif" width="23" height="25 src="> – momentum of the incident photon, – reflected).
Change of momentum absorbed photon is equal to the magnitude of the momentum itself:
![]() .
.
According to the law of conservation of momentum, the total change in the photon momentum is equal to the momentum received by the site.
They call it thermal electromagnetic radiation, which is emitted by heated bodies due to their internal energy. Thermal radiation reduces internal energy body, and hence its temperature. The spectral characteristic of thermal radiation is the spectral density of energy luminosity.
2. What body is called absolutely black? Give examples of absolutely black bodies.
An absolutely black body is a body that absorbs all the energy of radiation of any frequency incident on it at an arbitrary temperature (a black hole).
3. What is an ultraviolet catastrophe? Formulate Planck's quantum hypothesis.
The discrepancy between the experimental results and the classical wave theory is called an ultraviolet catastrophe. Planck's quantum hypothesis: energy and frequency of radiation are related to each other. Radiation by molecules and atoms of matter occurs in separate portions - quanta.
4. What microparticle is called a photon? List the main physical characteristics of a photon.
Photon is a quantum of electromagnetic radiation.
1) its energy is proportional to the frequency of electromagnetic radiation.
3) its speed in all reference systems is equal to the speed of light in vacuum.
4) its rest mass is 0.
5) the momentum of a photon is equal to:
6) Pressure electromagnetic radiation.
Do you remember how in your wonderful fairy tale " The little Prince» Antoine de Saint-Exupery is sincerely surprised: unimaginative adults cannot understand at all that the hat drawn by the boy is actually a boa constrictor that swallowed an elephant? Adults, especially physicists, are always like this: they need unity of form and content...
Researchers called it "ultraviolet catastrophe". A discrepancy that could not be eliminated in any way. But among the scientists who struggled to solve this problem, there were very famous physicists- Lord Rayleigh, Wilhelm Wien, James Gine, Moscow professor V. A. Mikhelson. And they were based on the repeatedly verified position of classical physics, which says: in any direction, any emitter that is in thermal equilibrium with environment, continuously emits the same amount of energy.
Maxwell and Boltzmann, whose authority in science is deservedly great, used this position with success in their works. Indeed, it is not for nothing that today the famous theoretical physicist Robert Feynman notes in his lectures: “In the history of mankind (if you look at it, say, in ten thousand years), the most significant event of the 19th century will undoubtedly be the discovery by Maxwell of the laws of electrodynamics. Against the backdrop of this important scientific discovery Civil War in America in the same decade will look like a small provincial incident.
For physicists late XIX century there was no doubt about the correctness of the classical provisions.
But... further logical and justified mathematical calculations invariably led to formulas, the conclusions from which were completely at odds with the experiment. From these formulas, it followed that a red-hot furnace should, over time, give off more and more heat to the surrounding space and the brightness of its glow should increase more and more!
A contemporary of the "ultraviolet catastrophe", the physicist Lorentz sadly remarked: "The equations of classical physics turned out to be unable to explain why the fading furnace does not emit yellow rays along with radiation of large wavelengths ..."
Rayleigh and Jeans made an attempt to determine the emissivity of a black body based on the theorem of classical statistics on the equipartition of energy over degrees of freedom. According to this theorem, each electromagnetic oscillation has an average energy equal to the electric and magnetic energy of the wave. Finally, they came up with the formula
![]() , (1.20)
, (1.20)
![]() . (1.21)
. (1.21)
This formula satisfactorily agrees with the experimental curve only for long wavelengths and diverges sharply from it for short wavelengths (Fig. 1.6). In addition, the integration of expression (1.21) over within the range from 0 to gives an infinitely large value for the energy luminosity.
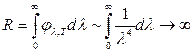 (1.22)
(1.22)
This result is called the ultraviolet catastrophe. The sharp discrepancy between theory and experiment indicated that some incorrect assumptions were used in the derivation of the Rayleigh Jeans formula.

Planck's formula for the emissivity of a black body.
The correct dependence of the emissivity of a black body on frequency was obtained by Planck. To do this, he had to make an assumption that is completely alien to classical concepts, namely, to assume that electromagnetic radiation is emitted in the form of separate portions of energy - quanta, the magnitude of which is proportional to the frequency of radiation
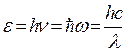 , (1.23)
, (1.23)
where ![]() is Planck's constant, and .
is Planck's constant, and .
Let us discuss in more detail the difference between classical continuous radiation and radiation by quanta. The energy of a classical oscillator is determined by two parameters, the oscillation amplitude and frequency. This means that for a given frequency, the oscillator energy can vary smoothly from zero to arbitrarily of great importance with a gradual increase in the oscillation amplitude. In this sense, they say that the energy of a classical oscillator is emitted continuously. According to formula (1.23), the radiation energy in the quantum case depends only on the frequency and is the minimum portion of energy that can be emitted by the oscillator. If the energy of the oscillating system becomes larger, then it can only take values that are multiples of this value
where are integers.
The calculation shows that with a discrete nature of the radiation, the average energy per each electromagnetic oscillation will no longer be equal to , as in the case of continuous radiation. The average energy of radiation in a state of thermal equilibrium at a temperature can be calculated as follows.
where is the probability that the vibration energy has the value .
This probability is obviously
where is the number of oscillators with energy , is the total number of oscillators.
In a state of thermal equilibrium, the energy distribution of oscillations obeys the Boltzmann law
where is the normalization factor satisfying the condition
![]() . (1.28)
. (1.28)
From here we find the normalization factor
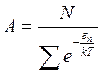 . (1.29)
. (1.29)
Substituting expression (1.29) into (1.27), we obtain
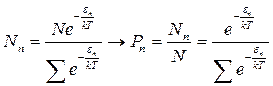 . (1.30)
. (1.30)
Then we obtain the average energy value by substituting the probability into expression (1.25)
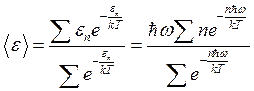 . (1.31)
. (1.31)
The summation in (1.31) can be performed, resulting in an expression for the average energy of thermal radiation at a temperature
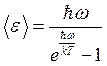 (1.32)
(1.32)
Note that if , then formula (1.32) transforms into the classical expression . Indeed, using the relation valid for , we obtain
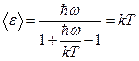 (1.33)
(1.33)
Thus, if the energy were emitted continuously, then its average value would coincide with the classical result.






