How to find the maximum kinetic energy of photoelectrons formula. Tutor-online - preparation for DT
In photoelectron spectroscopy solids the kinetic energy of electrons emitted when solids are irradiated by monoenergetic photons with energy is analyzed. The corresponding energy conservation equation has the form
where is Epol - total energy initial state; E - kinetic energy of photoelectrons; is the total final energy of the system after the emission of photoelectrons from the level. The contribution of the recoil energy can be neglected (see problem 8.5). Only for the lightest atoms is the value significant in comparison with the measured widths of the photoelectron spectra. The binding energy of a photoelectron is defined as the energy required to move it to infinity at zero kinetic energy. In XPS measurements, the binding energy of an electron at a level with respect to a local vacuum level is defined as
Substitution (9.1) into (9.2) leads to the photoelectric effect equation
The binding energies are counted from the conditional level. In photoemission from the gas phase, the binding energies are measured with respect to the vacuum level. When studying solids, the Fermi level is used as a reference level.
In the case of a solid sample, the spectrometer is connected to it by an electrical contact. For metal samples, the arising energy levels shown in fig. 9.6. Since the sample and the spectrometer are in thermodynamic equilibrium, their electrochemical potentials or Fermi levels are equal. Passing from the surface of the sample to the spectrometer, the photoelectron "feels" a potential equal to the difference between the work function of the spectrometer Фspeck and the work function of the sample . Thus, the kinetic energy of electrons on the sample surface
where is the binding energy with respect to the Fermi level. Note that this expression does not include the work function , but the work function of the spectrometer is included.
In the study of non-conducting samples, great care is required due to the possibility of charge accumulation on the sample and the uncertainty of the position of the Fermi level within the band gap. One solution to the problem is sputtering a thin film of gold (or other metal)
on the surface of the sample and the use of known atomic levels gold to determine the energy scale. Another way is to use highly visible features electronic structure, such as the edge of the valence band, which can be determined from the XPS spectra.
In what follows, the symbol will denote the binding energy regardless of the reference level. In metals and metal compounds, such as silicides, the Fermi level is most commonly used. In semiconductors and dielectrics, a well-defined reference level has never been found. This uncertainty, along with the buildup of charge on the sample, indicates that caution is required when obtaining spectra.
13.3. Photoelectric Effect: Wave and Quantum Theories
13.3.2. Einstein's equation for external photoelectric effect
In 1905, A. Einstein explained the photoelectric effect from quantum positions.
Scheme of the appearance of the external photoelectric effect shown in fig. 13.4:
Rice. 13.4
- a photon with energy E γ , falling on a substance, transfers part of its energy to an electron located near the surface of the substance;
- energy is expended to remove an electron, equal to work electron exit from substance A out;
- the emitted electron has a kinetic energy T e max .
The phenomenon of the photoelectric effect is described Einstein's equation, which is a mathematical representation of the law of conservation of energy for the photoelectric effect:
E γ \u003d A out + T e max,
where E γ - photon energy; A out - work function; T e max - maximum kinetic energy of photoelectrons.
The photon energy E γ is calculated by the formulas:
E γ = h ν, E γ = h c λ ,
where h is Planck's constant, h = 6.626 ⋅ 10 −34 J ⋅ s; ν - photon frequency, ν = c /λ; λ is the wavelength of the photon; c is the speed of light in vacuum, c ≈ 3.0 ⋅ 10 8 m/s.
Work function of electrons from the substance A out is a constant (reference) value for this substance, independent of the characteristics of the radiation; it is determined only by the type of substance and the degree of processing / cleanliness of its surface.
Maximum kinetic energy of photoelectrons T e max is calculated by the formulas:
T e max = m v max 2 2 , T e max = | e | U s,
where m is the electron mass, m = 9.1 ⋅ 10 −31 kg; v max - maximum speed of a photoelectron; |e| - electron charge modulus, |e | = 1.6 ⋅ 10 −19 C; U C - delaying potential difference.
The plot of the dependence of the maximum kinetic energy of photoelectrons on the frequency of the radiation incident on the surface is shown in fig. 13.5, and a graph of the dependence of the retarding voltage on the specified frequency is in fig. 13.6.
Rice. 13.5
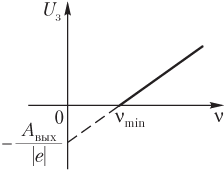
Rice. 13.6
Quantum theory fully explains the laws of the photoelectric effect:
1) the number of photoelectrons ejected from the surface is proportional to the number of photons absorbed by the surface, i.e. radiation intensity;
2) the maximum kinetic energy of photoelectrons depends linearly on the frequency of light (see Fig. 13.4):
T e max = h ν − A out,
where T e max - maximum energy photoelectrons; h - Planck's constant, h = 6.626 ⋅ 10 −34 J ⋅ s; A out - work function; ν is the photon frequency;
3) the photoelectric effect begins when the energy of a photon is enough to pull an electron out of the surface of a substance (E γ = A out); the minimum energy corresponds to the minimum frequency of light ν 0, called the "red border" of the photoelectric effect (see Fig. 13.4);
4) the absorption of photon energy by an electron occurs almost instantaneously, which explains the inertia of the photoelectric effect.
Example 7. The wavelength of light incident on metal plate, decreased from 500 to 420 nm. Determine the work function of an electron if it is known that the maximum kinetic energy of photoelectrons has increased by a factor of 2.50.
Solution . When the learning modes change, the work function of electrons from the substance does not change:
A out = const.
Let's write the Einstein equation twice:
E γ1 = A out + T e 1 ,
where E γ1 - photon energy, E γ1 = hc /λ 1 ; h - Planck's constant, h = 6.63 ⋅ 10 −34 J ⋅ s; c is the speed of light in vacuum, c = 3.00 ⋅ 10 8 m/s; T e 1 - maximum kinetic energy of photoelectrons in the first case;
- light with a wavelength λ 2 -
E γ2 = A out + T e 2 ,
where E γ2 is the photon energy, E γ2 = hc /λ 2 ; T e 2 - maximum kinetic energy of photoelectrons in the second case.
From the Einstein equation, we express the maximum kinetic energy photoelectrons:
- for light with wavelength λ 1 -
T e 1 = E γ1 − A out;
- light with a wavelength λ 2 -
T e 2 = E γ2 − A out.
According to the task
T e 2 \u003d 2.5 T e 1,
or taking into account the explicit form of expressions for T e 1 and T e 2:
E γ2 − A out = 2.5(E γ1 − A out).
Let us express from this the work function of electrons leaving the substance:
A out \u003d 2.5 E γ 1 - E γ 2 1.5 \u003d 2.5 h c λ 1 - h c λ 2 1.5 \u003d h c (2.5 λ 2 - λ 1) 1.5 λ 1 λ 2.
Let's calculate:
A out = 6.63 ⋅ 10 − 34 ⋅ 3.00 ⋅ 10 8 (2.5 ⋅ 420 ⋅ 10 − 9 − 500 ⋅ 10 − 9)
3.47 ⋅ 10 − 19 J.
Let's translate the obtained value of the work function from joules to electronvolts:
A out ≈ 3.47 ⋅ 10 − 19 1.6 ⋅ 10 − 19 = 2.17 eV.
The work function of electrons from the surface of this substance is 2.17 eV.
The maximum kinetic energy of photoelectrons increases linearly with increasing light frequency and does not depend on light intensity.
hν \u003d A out + E k (max)
The energy of the incident photon is spent on overcoming the work function of the electron from the substance and imparting kinetic energy to the electrons
The work function of electrons from a metal is equal to the minimum energy that an electron must have in order to be released from the surface of a substance.
There is an external and internal photoelectric effect.
1. The photoelectric effect is impossible if the energy of the incident photon is not enough to overcome the work function, hν< А вых
2. If hν min \u003d And out - the threshold of the photoelectric effect.
Frequency and wavelength of the red border of the photoelectric effect:
ν min \u003d A out / hλ max \u003d hc / A out
| THE QUANTUM PHYSICS | ||
| Quanta | According to Planck, any radiation (including light) consists of separate quanta. As a consequence, the radiation energy is always equal to the energy of an integer number of quanta. However, the energy of an individual quantum depends on the frequency. | |
| Quantum energy, or energy quantum | — radiation frequency, J s — Planck's constant | |
| Radiation quanta, frequencies (or wavelengths), which correspond to the area visible light are called light quanta. | ||
| Relationship between energy and mass | is the mass corresponding to the energy W, m/s is the speed of light in vacuum | |
| Photon | Energy quantization means that radiation is a stream of particles. These particles are called photons, but they are not particles in the sense of classical physics. | |
| Photon mass | J s is Planck's constant, is the frequency of radiation, is the wavelength of radiation, s is the speed of light in vacuum | |
| Photons always move at the speed of light; they do not exist at rest, their rest mass is zero | ||
| photon momentum |  |
|
| photoelectric effect | The emission of electrons by a substance under the action of light electromagnetic radiation. | |
| Laws of the photoelectric effect | ||
| I. At a fixed frequency of the incident light, the number of photoelectrons escaping from the cathode per unit time is proportional to the light intensity (Stoletov's law). | ||
| II. The maximum initial speed (maximum kinetic energy) of photoelectrons does not depend on the intensity of the incident light, but is determined only by its frequency | ||
| III. For each substance there is a red border of the photoelectric effect, i.e. the minimum frequency of light (depending on the chemical nature of the substance and the state of its surface), below which the photoelectric effect is impossible. | ||
Four students were asked to draw general form graph of the maximum kinetic energy of electrons emitted from the plate as a result of the photoelectric effect, on the intensity / incident light. Which drawing is correct?   |
The maximum kinetic energy of photoelectrons does not depend on the intensity of the incident light. Therefore, figure 4) is correctly executed. | |
| Scheme for studying the photoelectric effect |  |
|
| Volt-ampere characteristic of the photoelectric effect |  Photocurrent dependence I, formed by the flow of electrons emitted under the influence of light, from the voltage U between electrodes. - saturation photocurrent. It is determined by this value u, at which all the electrons emitted by the cathode reach the anode. |
|
| - holding voltage. At , none of the electrons, even if they have the maximum velocity when leaving the cathode, can overcome the retarding field and reach the anode. | ||
| The Uz value does not depend on the intensity of the incident light flux. Careful measurements have shown that the blocking potential increases linearly with increasing frequency ν of the light. |  The dependence of the blocking potential Uz on the frequency ν of the incident light |
|
The photocell is illuminated with light with a certain frequency and intensity. The figure shows a graph of the dependence of the strength of the photocurrent in this photocell on the voltage applied to it. 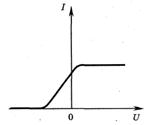 If the frequency is increased without changing the intensity of the incident light, the graph will change. Which of the following figures correctly shows the change in the graph?     |
At a constant intensity, the magnitude of the photocurrent does not depend on the frequency. When the frequency changes, the blocking voltage changes. Figure 1 corresponds to these conditions. | |
| Einstein's equation for the photoelectric effect | 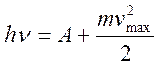 A is the electron work function. The energy of the incident photon is spent on the energy of the electron leaving the metal and on communicating the maximum kinetic energy to the outgoing electron. |
|
| This equation was derived on the basis of the quantum theory of the photoelectric effect, according to which light with a frequency v not only emitted, but also propagated in space and absorbed by matter in separate portions (quanta), the energy of which | ||
The calcium oxide layer is irradiated with light and emits electrons. The figure shows a graph of the change in the maximum kinetic energy of photoelectrons depending on the frequency of the incident light.  What is the work function of photoelectrons from calcium oxide? |
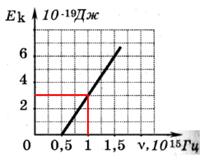 According to the graph we find: At ν = 1 10 15 Hz E k = 3 10 -19 J From the Einstein equation A = hν - E k A= 6.6 10 - 34 1 10 15 - 3 10 -19 = 3.6 10 -19 J = = 3.6 10 -19 / 1.6 10 -19 = 2.25 eV |
|
The graph shows the dependence of the photocurrent on the applied reverse voltage when a metal plate (photocathode) is illuminated with radiation with an energy of 4 eV.  What is the work function for this metal? |
 The photocurrent stops when U h = 1.5 V. Therefore, the maximum kinetic energy of a photoelectron is E k = 1.6·10 -19 C·1.5 V/1.6·10 -19 J = = 1.5 eV. The work function of an electron from the surface of the plate A= hν - E k = 4 - 1.5 = 2.5 eV |
|
| red border photo effect |  |
|
 is the maximum wavelength of the incident light (respectively, the minimum frequency) at which the photoelectric effect is still possible. |
||
| The work function is expressed in electronvolts | 1 eV = 1.6 10 -19 J | |
 |
||
Which graph corresponds to the dependence of the maximum kinetic energy of photoelectrons E on the frequency of photons incident on matter during the photoelectric effect (see figure)?  |
Photoelectrons acquire maximum kinetic energy when the frequency of incident photons exceeds the red border of the photoelectric effect. On the graph, the red border corresponds to the point BUT.  Therefore, schedule 3 corresponds to the conditions of the problem. |
|
| The pressure produced by light when it is normally incident on a surface |  - reflection coefficient; is the energy of all photons incident on a unit surface per unit time. |
|
| Explanation of light pressure | ||
| based on quantum theory | The pressure of light on the surface is due to the fact that each photon, when colliding with the surface, transfers its momentum to it. | |
| based on wave theory | The pressure of light on the surface is due to the action of the Lorentz force on the electrons of the substance, which oscillate under the action electric field electromagnetic wave. | |
Red border photoelectric effect for potassium λ 0 = 0.62 µm. What is the wavelength of light incident on a potassium photocathode if the maximum speed of photoelectrons v= 580 km/s? Give your answer in microns.
Solution.
The energy of the incident photon is spent on overcoming the work function and increasing the kinetic energy of the photoelectron where is the frequency corresponding to the red border of the photoelectric effect. Then the wavelength of the incident light is
Answer: 0.42 microns.
Answer: 0.42
Source: Unified State Examination in Physics 05/05/2014. Early wave. Option 3.
A metal plate is irradiated monochromatic light, whose wavelength is 2/3 of the wavelength corresponding to the red border of the photoelectric effect for this metal. The work function of electrons for the metal under study is 4 eV. Determine the maximum kinetic energy of photoelectrons emitted from a metal plate under the action of this light. Give your answer in electronvolts.
Solution.
Answer: 2.
Answer: 2
Source: StatGrad: Diagnostic work in physics 03/12/2015 Variant PHI10901.
What is the wavelength of light that knocks out photoelectrons from a metal plate, the maximum kinetic energy of which is 25% of the work function of electrons from this metal? The red border of the photoelectric effect for this metal corresponds to a wavelength of 500 nm. Give your answer in nm, rounded to the nearest integer.
Solution.
At a wavelength equal to the red border of the photoelectric effect, the energy of the wave is equal to the work done from the metal. Therefore, where
Answer: 400.
Answer: 400
Source: StatGrad: Diagnostic work in physics 03/12/2015 Variant PHI10902.
Falls on a fixed nickel plate electromagnetic radiation, whose photon energy is 8 eV. In this case, as a result of the photoelectric effect, electrons with a maximum kinetic energy of 3 eV fly out of the plate. What is the work function of electrons in nickel? (Give your answer in electronvolts.)
Solution.
Photoelectric effect equation: where is the photon energy.
We express from the formula
Answer: 5.
Answer: 5
Source: StatGrad: Thematic diagnostic work in physics 04/17/2015 Variant PHI10704
A photon with a wavelength corresponding to the red border of the photoelectric effect knocks out an electron from a metal plate (cathode) of a vessel from which air is pumped out. An electron is accelerated by a uniform electric field of strength. To what speed will an electron accelerate in this field, having flown a path? Relativistic effects are ignored.
Solution.
In accordance with the Einstein equation for the photoelectric effect, the initial velocity of the emitted electron v 0 = 0.
The formula relating the change in the kinetic energy of a particle with the work of the force from the electric field:
The work of the force is related to the field strength and the path traveled:
Answer:
Source: StatGrad: Rehearsal work in physics 05/17/2015 Variant PHI10801
Novel 19.06.2016 16:53
Hello.
It seems to me that there is an error in degrees (in the answer). If not right, then sorry.
Here is a numerical calculation showing a result that is approximately equal to 3*10^5
http://imageshack.com/a/img922/2749/hfsxdi.jpg
Anton
There is a typo in this formula: it should be instead of 104.
A beam of light from a laser was directed onto a metal plate, causing a photoelectric effect. Intensity laser radiation gradually increase without changing its frequency. How do the number of photoelectrons emitted per unit time and their maximum kinetic energy change as a result of this?
1) increase
2) decrease
3) will not change
Write down the chosen numbers for each physical quantity. Numbers in the answer may be repeated.
Solution.
The intensity of laser radiation is the number of photons that have passed through a unit area per unit time. This means that with increasing intensity, the number of photons will increase and the number of photoelectrons will increase. According to the second law of the photoelectric effect, the kinetic energy of photoelectrons depends on the work function of the material and on the photon energy. As the intensity increases, the photon energy does not change, which means that the maximum kinetic energy of photoelectrons remains unchanged.
Answer: 13.
Answer: 13
There are two calcium electrodes in vacuum, to which a 4000 pF capacitor is connected. When the cathode is illuminated with light for a long time, the photocurrent between the electrodes, which appeared at the beginning, stops, and a charge of 5.5 × 10–9 C appears on the capacitor. The "red border" of the photoelectric effect for calcium λ 0 = 450 nm. Determine the frequency of the light wave illuminating the cathode. Ignore the capacitance of the electrode system.
Solution.
Einstein's equation for the photoelectric effect: hν = A out + E to where E k - maximum kinetic energy of photoelectrons,
The photocurrent stops when E k = EU, where U- the voltage between the electrodes, or the voltage across the capacitor.
Capacitor charge q = CU.
As a result, we get:
Answer:
Source: Demo version of the USE-2016 in physics.
λ λ 2 λ 1 . How do the maximum kinetic energy of electrons emitted from the photocathode and the work function of the photocathode material change in the second experiment compared to the first?
For each value, determine the appropriate nature of the change:
1) increases;
2) decreases;
3) does not change.
Write in the table the selected numbers for each physical quantity. Numbers in the answer may be repeated.
Solution.
According to the photoelectric effect equation, the energy of the absorbed photon goes to the work function and to impart kinetic energy to the electron:
A decrease in the wavelength will lead to an increase in the energy of the incident radiation, which means that the maximum kinetic energy of photoelectrons will increase.
The work function is a characteristic of the photocathode material only and does not depend on the wavelength of the incident photons.
Answer: 13.
Answer: 13
Source: Training work in physics 02/16/2017, variant PHI10303
In the first experiment, the photocathode is illuminated with light with a wavelength λ 1, and the photoelectric effect is observed. In the second experiment, the photocathode is illuminated with light with a wavelength λ 2 > λ one . How do the maximum kinetic energy of electrons emitted from the photocathode and the work function of the photocathode material change in the second experiment compared to the first?
The photoelectric effect is the phenomenon of pulling out electrons under the action of light from liquid and solid substances.
2. Describe the concept of Stoletov's experiment. What is photocurrent and photoelectrons?
Two electrodes, a cathode and an anode, were placed in a vacuum tube and connected to a voltage source. There was no current in the circuit without cathode illumination. When illuminated, the electrons ejected from the cathode are attracted to the anode.
The photocurrent is the current arising in the circuit under the action of light, and the photoelectrons are the ejected electrons.
3. Formulate three laws of the photoelectric effect and explain the current-voltage characteristic of the photoelectric effect. How will it look with more light intensity?
Laws of the photoelectric effect:
1) the saturation photocurrent is proportional to the intensity of the light that falls on the cathode.
2) the maximum kinetic energy of photoelectrons does not depend on the intensity of light and is directly proportional to its frequency.
3) there is a minimum frequency of light for each substance, below which the photoelectric effect is not possible. It is called the red border of the photoelectric effect.
At low voltages, only part of the photoelectrons reaches the anode. The greater the potential difference, the greater the photocurrent. At a certain voltage value, it becomes maximum, it is called the voltage photocurrent. With a higher light intensity, the saturation photocurrent will be higher, and the graph will go higher.
4. Write and explain Einstein's equation for the photoelectric effect. What is the value of the work function?
The energy of the photon is used to communicate kinetic energy to the emitted photoelectron and to perform the work function. The work function is the minimum work that must be done to remove an electron from a metal. Red border photo effect:
5. Explain the graph of the dependence of the kinetic energy of photoelectrons on the frequency of light. How is the red border of the photoelectric effect calculated?
The kinetic energy of a photoelectron depends linearly on the frequency of light:
It is always greater than zero, and the photoelectric effect does not occur below the red border.
