Learn to take derivatives of functions. The derivative characterizes the rate of change of a function at a certain point lying on the graph of this function. In this case, the graph can be either a straight line or a curved line. That is, the derivative characterizes the rate of change of the function at a particular point in time. Remember the general rules by which derivatives are taken, and only then proceed to the next step.

• Read the article.
• How to take the simplest derivatives, for example, the derivative of an exponential equation, is described. The calculations presented in the following steps will be based on the methods described there.

Learn to distinguish between problems in which the slope needs to be calculated in terms of the derivative of a function. In tasks, it is not always suggested to find the slope or derivative of a function. For example, you may be asked to find the rate of change of a function at point A(x, y). You may also be asked to find the slope of the tangent at point A(x, y). In both cases, it is necessary to take the derivative of the function.

Take the derivative of the given function. You don't need to build a graph here - you only need the equation of the function. In our example, take the derivative of the function f (x) = 2 x 2 + 6 x (\displaystyle f(x)=2x^(2)+6x). Take the derivative according to the methods outlined in the article mentioned above:

Substitute the coordinates of the point given to you into the found derivative to calculate the slope. The derivative of the function is equal to the slope at a certain point. In other words, f "(x) is the slope of the function at any point (x, f (x)). In our example:

Convenient for, having given a specific value of the independent variable x (argument), calculate the corresponding value of the dependent variable y. For example, if a function is given y \u003d x 2, i.e. f (x) \u003d x 2, then for x \u003d 1 we get y \u003d 1 2 \u003d 1; in short, it is written as follows: f (1) \u003d 1. For x \u003d 2 we get f (2) \u003d 2 2 \u003d 4, i.e., y \u003d 4; with x \u003d - 3 we get f (- 3) \u003d (- Z) 2 \u003d 9, that is, y \u003d 9, etc.

Already in the 7th grade, we began to understand that in the equality y \u003d f (x) the right side, i.e. the expression f(x) is not limited to the four cases listed above (C, kx, kx + m, x 2).

For example, we have already met piecewise functions, i.e. functions given by different formulas on different intervals. Here is one such function: y = f(x), where

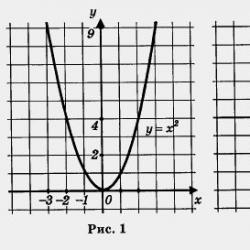
Do you remember how to plot such functions? First you need to build a parabola y \u003d x 2 and take its part at x< 0 (левая ветвь параболы, рис. 1), затем надо построить прямую у = 2х и взять ее часть при х >0 (Fig. 2). And, finally, both selected parts must be combined in one figure, i.e., built on the same coordinate plane (see Fig. 3).

Now our task is as follows: to replenish the stock of learned functions. In real life, there are processes described by various mathematical models of the form y \u003d f (x), not only those that we listed above. In this section, we will consider the function y = kx 2 , where coefficient k - any non-zero number.

In fact, the function y = kx 2 is somewhat familiar to you in one case. See: if k \u003d 1, then we get y \u003d x 2; you studied this function in the 7th grade and probably remember that its graph is a parabola (Fig. 1). Let us discuss what happens for other values ​​of the coefficient k.

Consider two functions: y \u003d 2x 2 and y \u003d 0.5x 2. Let's make a table of values ​​for the first function y \u003d 2x 2:

Construct points (0; 0), (1; 2), (-1; 2), (2; 8), (-2; 8), (1.5; 4.5), (-1.5; 4.5) on coordinate plane(Fig. 4); they outline some line, let's draw it (Fig. 5).

Let's make a table of values ​​for the second function y \u003d 0.5x 2:

Construct points (0; 0), (1; 0.5), (-1; 0.5), (2; 2), (-2; 2), C; 4.5), (-3; 4.5) on the coordinate plane (Fig. 6); they outline some line, let's draw it (Fig. 7)

.

The points shown in fig. 4 and 6 are sometimes referred to as control points for the corresponding function graph.

Compare figures 1, 5 and 7. Isn't it true that the lines drawn are similar? Each of them is called a parabola; in this case, the point (0; 0) is called the vertex of the parabola, and the y-axis is called the axis of symmetry of the parabola. The value of the coefficient k determines the "speed of aspiration" of the branches of the parabola upwards or, as they say, the "degree of steepness" of the parabola. This is clearly seen in Fig. 8, where all three parabolas constructed above are located on the same coordinate plane.

The situation is exactly the same with any other function of the form y \u003d kx 2, where k\u003e 0. Its graph is a parabola with a vertex at the beginning coordinates, the branches of the parabola are directed upwards, and the steeper, the greater the coefficient k. The y-axis is the axis of symmetry of the parabola. By the way, for the sake of brevity, mathematicians often instead of the long phrase “parabola serving as a graph of the function y \u003d kx 2”, they say “parabola y \u003d kx 2”, and instead of the term “axis of symmetry of the parabola”, they use the term “parabola axis”.

Do you notice that there is an analogy with the function y = kx? If k > 0, then the graph of the function y \u003d kx is a straight line passing through the origin (remember, we said briefly: straight line y \u003d kx), and here the “steepness” of the straight line depends on the value of the coefficient k. This is clearly seen in Fig. 9, where in one coordinate system are shown charts linear functions y = kx for three values ​​of the coefficient

Let's return to the function y \u003d kx 2. Let us find out how things stand in the case of a negative coefficient ft. Let's build, for example, a graph of the function

y \u003d - x 2 (here k \u003d - 1). Let's make a table of values:

Note the points (0; 0), (1; -1), (-1; -1), (2; -4), (-2; -4), (3; -9), (- 3; - 9) on the coordinate plane (Fig. 10); they outline some line, let's draw it (Fig. 11). This is a parabola with a vertex at the point (0; 0), the y-axis is the axis of symmetry, but unlike the case when k> 0, this time the branches of the parabola are directed downwards. The situation is similar for other negative values ​​of the coefficient k.

So, the graph of the function is a parabola with a vertex at the origin; the y-axis is the axis of the parabola; the branches of the parabola are directed upwards for k>0 u downwards for k<0.

We also note that the parabola y \u003d kx 2 touches the x-axis at the point (0; 0), i.e., one branch of the parabola smoothly passes into the other, as if clinging to the x-axis.

If you build in one coordinate system function graphs y \u003d x 2 and y \u003d - x2, then it is easy to see that these parabolas are symmetrical to each other about the x axis, which is clearly seen in Fig. 12. In the same way, the parabolas y \u003d 2x 2 and y \u003d - 2x 2 are symmetrical to each other about the x axis (do not be lazy, build these
two parabolas in the same coordinate system and verify the validity of the statement made).

In general, the graph of the function y \u003d - f (x) is symmetrical to the graph of the function y \u003d f (x) about the x-axis.

Properties of the function y \u003d kx 2 for k > 0

Describing the properties of this function, we will rely on its geometric model - a parabola (Fig. 13).

1. Since for any value of x by the formula y \u003d kx 2 you can calculate the corresponding value of y, the function is defined at any point x (for any value of the argument x). In short, this is written as follows: the domain of the function is (-oo, +oo), that is, the entire coordinate line.

2. y \u003d 0 for x \u003d 0; y > O at . This can also be seen from the graph of the function (it is all located above the x-axis), but it can be justified without the help of the graph: if

Then kx 2 > O as the product of two positive numbers k and x 2.

3. y = kx 2 is a continuous function. Recall that we consider this term so far as a synonym for the sentence "the graph of a function is a solid line that can be drawn without lifting the pencil from the paper." In the upper grades, a more precise mathematical interpretation of the concept of the continuity of a function will be given, not based on a geometric illustration.

4.y/ naim = 0 (achieved at x = 0); nai6 does not exist.

Recall that (/naim is the smallest value of the function, and Unib. is the largest value of the function on a given interval; if the interval is not specified, then unaim- and y naib, respectively, are the smallest and largest values ​​of the function in the domain of definition.

5. The function y \u003d kx 2 increases for x\u003e O and decreases for x< 0.

Recall that in the 7th grade algebra course, we agreed to call a function whose graph on the interval under consideration goes from left to right, as it were, “uphill”, increasing, and function, the graph of which on the interval under consideration goes from left to right, as if “downhill”, - decreasing. More precisely, we can say this: the function y \u003d f (x) is called increasing on the interval X, if on this interval a larger value of the argument corresponds to a larger value of the function; the function y = f (x) is called decreasing on the interval X if on this interval the larger value of the argument corresponds to the smaller value of the function.

In the Algebra-7 textbook, we called the process of listing the properties of a function reading a graph. The process of reading the graph will gradually become richer and more interesting for us - as we study new properties of functions. Those five properties that are listed above, we discussed in the 7th grade for the functions studied there. Let's add one new property.

A function y = f(x) is called bounded from below if all values ​​of the function are greater than a certain number. Geometrically, this means that the graph of the function is located above some straight, parallel to the x-axis.

Now look: the graph of the function y \u003d kx 2 is located above the straight line y \u003d - 1 (or y \u003d - 2, it doesn't matter) - it is drawn in Fig. 13. Hence, y - kx2 (k > 0) is a function bounded below.

Along with functions bounded from below, functions bounded from above are also considered. The function y - f(x) is called bounded from above if all values ​​of the function are less than a certain number. Geometrically, this means that the graph of the function is located below some straight line parallel to the x-axis.
Is there such a line for the parabola y = kx 2 , where k > 0? No. This means that the function is not bounded from above.

So, we got one more property, let's add it to the five that are listed above.

6. The function y = kx 2 (k > 0) is bounded from below and unbounded from above.

Properties of the function y \u003d kx 2 for k< 0

When describing the properties of this function, we rely on its geometric model- parabola (Fig. 14).

1. Function definition area - (-oo, +oo).

2. y \u003d 0 for x \u003d 0; at< 0 при .

Z.y \u003d kx 2 is a continuous function.
4. y nau6 = 0 (achieved at x = 0), unaim does not exist.

5. The function increases at x< 0, убывает при х > 0.

6. The function is limited from above and not limited from below.

Let us explain the last property: there is a line parallel to the x-axis (for example, y = 1, it is drawn in Fig. 14), such that the entire parabola lies below this line; this means that the function is bounded from above. On the other hand, it is impossible to draw a line parallel to the x-axis so that the entire parabola is located above this line; this means that the function is not bounded below.

The order of moves used above when listing the properties of a function is not a law as long as it has developed chronologically just like that.

We will develop a more or less definite order of moves gradually and unify it in the 9th grade algebra course.

Example 1 Find the smallest and largest values ​​of the function y \u003d 2x 2 on the segment: a) ; b) [- 2, - 1]; c) [- 1, 1.5].

a) Let's build a graph of the function y \u003d 2x 2 and select its part on the segment (Fig. 15). We notice that 1/naim. = 0 (reached at x = 0), and y max = 8 (reached at x = 2).

b) Let's build a graph of the function y \u003d 2x 2 and select its part on the segment [- 2, - 1] (Fig. 16). Note that 2/naim = 2 (achieved at x = - 1), and y max = 8 (achieved at x = - 2).

c) Let's build a graph of the function y \u003d 2x 2 and select its part on the segment [- 1, 1.5] (Fig. 17). We note that unanm = 0 (reached at x = 0), and y is reached at the point x = 1.5; let's calculate this value: (1.5) = 2-1.5 2 = 2-2.25 = 4.5. So, y max = 4.5.

Example 2 Solve the equation - x 2 \u003d 2x - 3.

Solution. In the Algebra-7 textbook, we developed algorithm graphic solution of equations, recall it.

To graphically solve the equation f (x) = g (x), you need:

1) consider two functions y \u003d -x 2 and y \u003d 2x -3;
2) build a graph of the function i/ = / (x) ;
3) build a graph of the function y \u003d g (x);
4) find the intersection points of the constructed graphs; abscissa
The sums of these points are the roots of the equation f(x) = g(x).

Let's apply this algorithm to the given equation.
1) Consider two functions: y \u003d - x2 and y \u003d 2x - 3.
2) Let's build a parabola - a graph of the function y \u003d - x 2 (Fig. 18).

3) Let's build a graph of the function y \u003d 2x - 3. This is a straight line, to build it, it is enough to find any two points on the graph. If x \u003d 0, then y \u003d - 3; if x = 1, then y = -1. So, we found two points (0; -3) and (1; -1). The straight line passing through these two points (the graph of the function y \u003d 2x - 3) is shown in the same drawing (see Fig. 18).

4) According to the drawing, we find that the straight line and the parabola intersect at two points A (1; -1) and B (-3; -9). This means that this equation has two roots: 1 and - 3 are the abscissas of points A and B.

Answer: 1, -3.

Comment. Of course, you can not blindly trust graphic illustrations. Maybe it just seems to us that point A has coordinates (1; - 1), but in fact they are different, for example (0.98; - 1.01)?

So it's always good to check yourself. So, in the considered example, you need to make sure that the point A (1; -1) belongs to the parabola y \u003d - x 2 (this is easy - just substitute the coordinates of the point A in the formula y \u003d - x 2; we get - 1 \u003d - 1 2 - correct numerical equality) and the straight line y \u003d 2x - 3 (and this is easy - just substitute the coordinates of point A into the formula y \u003d 2x - 3; we get - 1 \u003d 2-3 - the correct numerical equality). The same must be done for point 8. This check shows that in the considered equation, graphical observations led to the correct result.

Example 3 Solve the system

Solution. Let's transform the first equation of the system to the form y \u003d - x 2. The graph of this function is the parabola shown in Fig. 18.

We transform the second equation of the system to the form y \u003d 2x - 3. The graph of this function is the straight line shown in fig. 18.

The parabola and the straight line intersect at points A (1; -1) and B (- 3; - 9). The coordinates of these points serve as solutions to the given system of equations.

Answer: (1; -1), (-3; -9).

Example 4. Given a function y - f (x), where

Required:

a) calculate f(-4), f(-2), f(0), f(1.5), f(2), f(3);

b) build a graph of the function;

c) using a graph, list the properties of a function.

a) The value x = - 4 satisfies the condition -, therefore, f (-4) must be calculated from the first line of the function definition. We have f (x) = - 0.5x2, which means f (-4) = -0.5 . (-4) 2 = -8.

Similarly, we find:

f(-2) = -0.5 . (-2) 2 =-2;
f(0) = -0.5 . 0 2 = 0.

The value satisfies the condition , so it must be calculated from the second line of the function definition. We have f(x) = x + 1, so The value x = 1.5 satisfies condition 1< х < 2, т. е. f(1,5) надо вычислять по третьей строке задания функции. Имеем f (х) = 2х 2 , значит, f(1,5) = 2-1,5 2 = 4,5.
Similarly, we get f(2)= 2 . 2 2 =8.

The value x = 3 does not satisfy any of the three conditions for specifying the function, and therefore f(3) cannot be calculated in this case, the point x = 3 does not belong to the domain of the function. The assignment to compute f(3) is incorrect.

b) We can build a graph “piece by piece”. First, we construct a parabola y = -0.5x 2 and select its part on the segment [-4, 0] (Fig. 19). Then we construct a straight line y \u003d x + 1 u. we select its part on the half-interval (0, 1] (Fig. 20). Next, we construct the parabola y = 2x 2 and select its part on the half-interval (1, 2] (Fig. 21).

Finally, all three "pieces" will be depicted in the same coordinate system; we get the graph of the function y \u003d f (x) (Fig. 22).

c) Let's list the properties of the function or, as we agreed to say, read the graph.

1. The scope of the function is the segment [-4, 2].

2. y \u003d 0 for x \u003d 0; y > 0 at 0<х<2;у<0 при - 4 < х < 0.

3. The function undergoes a break at x = 0.

4. The function increases on the segment [-4, 2].

5. The function is limited both from below and from above.

6. y naim = -8 (achieved at x = -4); y nai6 . = 8 (achieved at x = 2).

Example 5 The function y \u003d f (x) is given, where f (x) \u003d Zx 2. Find.

Linear function y = kx + m when m = 0 becomes y = kx . In this case, you can see that:

1. If x = 0, then y = 0. Therefore, the graph of the linear function y = kx passes through the origin, regardless of the value of k .
2. If x = 1, then y = k.

Consider different values ​​of k and how this changes y .

If k is positive (k > 0), then the straight line (function graph), passing through the origin, will lie in the I and III coordinate quarters. After all, for positive k, when x is positive, then y will also be positive. And when x is negative, y will also be negative. For example, for a function y = 2x , if x = 0.5, then y = 1; if x = –0.5, then y = –1.

Now, under the condition of positive k, consider three different linear equations. Let it be: y = 0.5x and y = 2x and y = 3x . How does the value of y change with the same x ? Obviously it increases with k : the more k , the more y . And this means that the straight line (function graph) with a larger value of k will have a larger angle between the x-axis (abscissa axis) and the function graph. Thus, it depends on k at what angle the straight axis intersects x, and hence k is spoken of as slope of the linear function.

Now let's study the situation when k x is positive, then y will be negative; and vice versa: if x y > 0. Thus, the graph of the function y = kx for when k

Suppose there are linear equations y = –0.5x, y = –2x, y = –3x. For x = 1, we get y = –0.5, y = –2, y = –3. For x = 2, we get y = –1, y = –2, y = –6. Thus, the larger k, the larger y if x is positive.

However, if x = –1, then y = 0.5, y = 2, y = 3. For x = –2, we get y = 1, y = 4, y = 6. Here, as the value of k decreases, y increases at x

Graph of the function for k

Graphs of functions like y = kx + m differ from graphs y = km only by a parallel shift.

Class: 8

Presentation for the lesson

Back forward

Attention! The slide preview is for informational purposes only and may not represent the full extent of the presentation. If you are interested in this work, please download the full version.

Lesson type: lesson in discovering new knowledge.

Basic goals:

• form an idea of ​​the function y = kx 2 , its properties and graphics;
• repeat and pin: feature details y = x 2 , the properties of the function, known in the course of the 7th grade.

Demo material:

1) algorithm for constructing a graph of a function:

2) The rule for determining the location of the graph depending on the coefficient k:

3) independent work: On fig. graphs of functions y \u003d kx are shown 2 .

For each graph, indicate the corresponding value of the coefficient To.

4) a sample for self-examination of independent work.

Handout:

1) card:

1, 2 group:

Plot Functions y= 2X 2 , y = 4X

3, 4 group:

Plot Functions y=– 2X 2 , y = - 4X 2 and determine in which coordinate quarters the graphs of these functions are located. Draw a conclusion about the coefficient k.

2) reflection card:

DURING THE CLASSES

1. Motivation for learning activities

Goals:

• organize the actualization of the requirements for the student from the side of educational activities;
• organize the activities of students to set the thematic framework: we continue to work with functions;
• create conditions for the emergence of the student's internal need for inclusion in educational activities.

Organization of the educational process at stage 1:

- Hello! What interesting things have you learned in previous lessons? (We studied the function y = | x |, the graph of this function and its properties.)
– Today you will continue to get acquainted with new features.
- How will you work today? (With nice mood).
- I wish you success!

2. Actualization of knowledge and fixation of difficulties in individual activity

Goals:

• to update the educational content, necessary and sufficient for the perception of new material.
• fix updated methods of action in speech and in signs;
• organize a synthesis of updated methods of action;
• motivate to complete an individual task;
• to organize independent fulfillment of an individual task for new knowledge;
• organize the fixation of individual difficulties in the performance by students of an individual task or in its justification.

Organization of the educational process at stage 2:

Analyze several slides 2-5 and answer the question:

What schedule will you work with today? (With a parabola).

– Choose which function graph the parabola is at = X + 2, at = 2/X, y = x 2 ?(y=x 2 . We studied this function in the 7th grade).

- Name the numerical coefficient of the function y = x 2 . (It is equal to 1)

- In what coordinate quarters does the graph of the function lie? y = x 2 , what is the domain of definition and range of this function, the intervals of increase and decrease? (Graph of the function y = x 2 lies in 1 and 2 coordinate quarters or in the upper half-plane, the domain of definition is the entire number line, the range of values ​​is the function y \u003d x 2 takes non-negative values; increases at x > 0, decreasing at x < 0.)

Let's discuss what happens at other values ​​of the coefficient.

- Formulate the topic of the lesson. (Function y = kx 2 , its properties and graph).

1) A table is prepared on the board. Find the corresponding function values:

- Fill the table. 4 students are called to the board in succession.

2) Function Graph y = kx 2 passes through point A(2;8). Determine the value of the coefficient. Write down the function. (k = 2, y = 2x 2 ).

3) According to what plan do you usually build function graphs? Slide 7.

(Necessary -
1. Fill in the table of values
2. Construct points on the coordinate plane
3. Connect the constructed points with a smooth line
4. Sign the name of the function.)

- What did you repeat?

- And now, using everything that you have just repeated and learned, I suggest that you complete the following task:
Plot Functions y= 2X 2 , y = - 4X 2 and determine in which coordinate quarters the graphs of these functions are located. Make a conclusion about how the graph is located depending on the coefficient k.

Students work on graph paper.

Who doesn't get results?
What couldn't you do? (I could not__________________)
- Show the results, who completed the construction.
How can you prove that you did the right thing? (I must___________)
What will you use for proof? (____________.)
What couldn't you do?
What rule did you use when building?
- That you can not do?

3. Identifying the causes of the difficulty

Goals:

• organize the correlation of their actions with the standards used (algorithm, concept, etc.);
• on this basis, organize the identification and fixation in external speech of the cause of the difficulty - those specific knowledge and skills that are lacking to solve the original problem.

Organization of the educational process at stage 3:

What task did you have to complete?
What did you use to complete the task?
- Where did the problem arise?
- What is the cause of the difficulty? (We have no way to determine how the graph of the function y \u003d kx2 is located depending on the coefficient k.)

4. Problematic explanation of new knowledge

Goals:

• organize the goal setting of the lesson;
• organize the clarification and coordination of the topic of the lesson;
• organize a leading or encouraging dialogue on the problematic introduction of new knowledge;
• organize the use of subject actions with models, schemes, properties, etc.;
• organize the fixation of a new mode of action in speech;
• organize the fixation of a new mode of action in signs;
• correlation of new knowledge with the rule in a textbook, reference book, dictionary, etc.
• organize the fixation of overcoming the difficulty.

Organization of the educational process at stage 4:

- State the purpose of your activity. (Find a way to determine how the graph of the function y \u003d kx is located 2 depending on the coefficient k.)

- Specify the topic of the lesson. (Function y = kx 2 , its properties and graph). slide 6.

- And now you will work in groups: Slide 8.

1, 2 group:

Plot Functions y= 2X 2 , y = 4X 2 and determine in which coordinate quarters the graphs of these functions are located. Draw a conclusion about the coefficient k.

3, 4 group:

Plot Functions y = - 2X 2 ,y = - 4X 2 and determine in which coordinate quarters the graphs of these functions are located. Draw a conclusion about the coefficient k.

Each group is given a card. (Students may use a textbook or reference book if they have difficulty.)

- Present your version of the algorithm.

Each of the groups presents its own version, the rest complement, clarify. After agreement, the rule is posted on the board:

The teacher adds:

- Each of the lines you draw is called a parabola. In this case, the point (0;0) is called the vertex of the parabola, and the axis at is the axis of symmetry of the parabola.
The “speed of aspiration” of the branches of the parabola up (down), the “degree of steepness” of the parabola depends on the value of the coefficient k.
What have you discovered now?
- What should you do now?

5. Primary consolidation in external speech

Target: organize the assimilation by children of a new mode of action with their pronunciation in external speech.

Organization of the educational process at stage 5:

- In what coordinate quarters are the graphs of functions at = 1/5X 2 , at = X 2 /2, at = – X 2 /2, at = 3X 2 ?

The task is performed in pairs, one pair works at the blackboard.

6. Independent work with self-examination according to the sample

Goals:

• to organize independent performance by students of standard tasks for a new mode of action;
• based on the results of independent work, organize the identification and correction of errors;
• based on the results of independent work, create a situation of success.

Organization of the educational process at stage 6:

For independent work, a task on a card is offered. slide 9.

On fig. graphs of functions are shown at = kx 2 .

For each graph, indicate the value of the coefficient k corresponding to it.

After completing the work, students check it according to the model: Slide 10.

What rules did you use to complete the task?
- Who has difficulty - how to determine the sign of the coefficient k?
- Who had difficulty in determining the value of the coefficient k?
Who did the job right?

7. Inclusion in the knowledge system and repetition

Goals:

• train the skills of using new content in conjunction with previously studied material;
• review the learning content that will be required in the following lessons:

Organization of the educational process at stage 7:

The task from GIA-9 is performed at the blackboard. Slides 11-16.

- Identify the term that was repeated many times today in the lesson. (Graph)

1. The graph of which of these functions is a parabola located in the lower half-plane?

3. Find the range of the function y \u003d - 5x2

A) at = –15X 2 b) at = – 9X 2 V) at = – X 2 G) at = – 5X 2

c uh f and

5. Indicate the intervals of increasing the function y \u003d - 5x 2

a) at X > 0 b) when X < 0 c) at X< 0 d) at X > 0

h O And T

6. Specify the smallest value of the function y \u003d - 5x 2

a) 0 b) does not exist at 5 d) 5

s To d V.

Physics tasks: slide 17.

The path traveled by the body in the first t seconds of free fall is calculated by the formula: H = gt 2 /2, where g\u003d 9.8 m / s 2. Find from the graph the dependence of H on t:

A) the distance that a falling stone will fly in the first 6 seconds;
B) the time during which the stone will fly the first 250 m?

8. Reflection of activities in the lesson

Goals:

• organize the fixation of new content studied in the lesson;
• organize the fixation of the degree of compliance with the set goal and the results of activities;
• organize verbal fixation of steps to achieve the goal;
• based on the results of the analysis of the work in the lesson, organize the fixation of directions for future activities;
• organize self-assessment by students of work in the lesson;
• organize discussion and record homework.

Organization of the educational process at stage 8:

- What did you study today?
- What new did you learn at the lesson?
- What goals did you set for yourself?
– Have you achieved your goals?
- What helped you cope with difficulties?
- Review your work in class.

Students work with reflection cards (P).

Homework: slide 18.

• paragraph P.17 of the textbook read
• №17.2,
• №17.3,
• №17.11.

Bibliography:

1. A.G. Mordkovich. Algebra, class 8. In two parts. Textbook for students of educational institutions. M.: Mnemozina. 2011.
2. Internet resources.