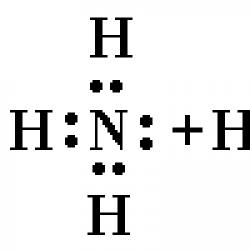Neka se po hrapavoj podlozi giba tijelo težine P pod djelovanjem sile T. S jedne strane, podloga ne dopušta tijelu da padne pod utjecajem gravitacije P. S druge strane, podloga sprječava slobodno kretanje tijela pod utjecajem sile T. Dakle, sila trenja F također, poput normalne reakcije, oživljava površina, tj. Sila trenja je također reakcija. Normalna reakcija i sila trenja zbrajaju ukupnu reakciju R, koja je od normale otklonjena za kut c. Taj se kut naziva kutom trenja. Pomoću Sl. Lako je izračunati koliko je tangens kuta trenja jednak tgts=F/N=µN/N=µ, tj. tangens kuta trenja je brojčano jednak koeficijentu trenja.

Sada zamislite da rotirate ukupnu reakciju oko normale površine. U tom slučaju sila R opisuje stožac koji se naziva stožac trenja. Zanimljivo je po tome što područje ograničeno tarnim stošcem određuje ravnotežno područje za tijelo: ako na tijelo unutar tarnog stošca djeluje sila, ona neće pomaknuti tijelo, ma koliko velika bila; ako sila djeluje na tijelo izvan tarnog stošca, ona pokreće tijelo, ma koliko mala bila (slika 19).

Riža. 19.

Pogledajmo zašto se to događa (slika 20).

Riža. 20.

Ako unutar tarnog stošca djeluje sila Q, tada je posmična sila Q 1 = Qsinb. Izračunajmo silu trenja:

F=µN=µQcosb=Qcosbtgsñ.

Faktor sigurnosti F-Q 1 =Q(cosb tgts-sin b) = Qsin(ts-b)/troškovi. Stoga je sigurnosna granica proporcionalna Q, budući da je sin(c-b)/coss konstantna vrijednost. Što je veća sila Q, veća je i sila držanja F-Q 1.

Zbog toga morate znati izgraditi tarni konus.

Jednom se u Münchenu srušio most, a krivac nije bio orkanski vjetar, niti puk vojnika koji je marširao u korak, već... trenje.

Taj je most na jednom kraju bio pričvršćen šarkom, a na drugom kraju bio je postavljen na valjke (slika 21). Most je uvijek osiguran na način da se ne iskrivi zbog temperaturnih oscilacija. Šarka je bila ispunjena pastom koja ju je štitila od korozije. Vrućeg ljetnog dana pasta se rastopila i smanjila joj se viskoznost. Priroda trenja se promijenila - također se smanjila. Stožac trenja se suzio, a sila pritiska na oslonac prešla je stožac.

Riža. 21.

Ravnoteža je prekinuta i most se srušio. Inženjeri često moraju konstruirati stožac trenja kako bi odredili hoće li određena struktura biti u ravnoteži ili ne. No inženjeri nisu jedini koji se bave tarnim konusom. Svatko se od nas svakodnevno susreće s ovim fizičkim fenomenom.

Da dođete do izlaza u prepunom autobusu ili trolejbusu, morate se migoljiti kao zmija noge. To radimo nesvjesno, ne razmišljajući da na taj način izlazimo iz tarnih čunjeva na mjestima kontakta s drugim putnicima.

Bilo da klizamo, idemo na posao ili okrećemo stranicu u knjizi, posvuda se susrećemo s trenjem, a posebno sa stožcem trenja.

Predavanje 3. Proračun rešetki. Trenje klizanja i kotrljanja.

Ovo predavanje pokriva sljedeća pitanja

1. Izračun rešetki.

2. Pojam farme.

3. Analitički proračun ravnih rešetki.

4. Grafički proračun ravnih rešetki.

5. Trenje.

6. Zakoni trenja klizanja.

7. Reakcije grubih veza.

8. Kut trenja.

9. Ravnoteža uz prisustvo trenja.

10. Trenje kotrljanja i vrtnje.

11. Moment sile u odnosu na središte kao vektor.

12. Moment para sila kao vektor.

13. Moment sile oko osi.

14. Odnos momenata sile u odnosu na središte i u odnosu na os.

15. Dovođenje prostornog sustava sila u zadano središte.

16. Uvjeti ravnoteže proizvoljnog prostornog sustava sila.

17. Problemi ravnoteže tijela pod utjecajem prostornog sustava sila.

Proučavanje ovih pitanja nužno je u budućnosti za proučavanje dinamike gibanja tijela uzimajući u obzir trenje klizanja i kotrljanja, dinamiku gibanja središta mase mehaničkog sustava, kinetičke momente, za rješavanje problema u disciplina “Čvrstoća materijala”.

Izračun farmi. Koncept farme. Analitički proračun ravnih rešetki.

Fermoy naziva krutu strukturu ravnih šipki spojenih na krajevima šarkama. Ako sve šipke rešetke leže u istoj ravnini, rešetka se naziva ravna. Spojne točke rešetkastih šipki nazivaju se čvorovi. Sva vanjska opterećenja na rešetku primjenjuju se samo na čvorovima. Pri proračunu rešetke zanemaruju se trenje u čvorovima i težina šipki (u usporedbi s vanjskim opterećenjem) ili se težine šipki raspoređuju po čvorovima. Tada će na svaku od rešetkastih šipki djelovati dvije sile koje djeluju na njezine krajeve, a koje u ravnoteži mogu biti usmjerene samo duž šipke. Stoga možemo pretpostaviti da rešetkaste šipke rade samo na napetost ili kompresiju. Ograničit ćemo se na razmatranje krutih ravnih rešetki, bez dodatnih šipki formiranih od trokuta. U takvim rešetkama broj šipki k i broj čvorova n povezani su relacijom

Proračun rešetke svodi se na određivanje reakcija potpore i sila u njezinim šipkama.

Reakcije potpore mogu se pronaći konvencionalnim statičkim metodama, uzimajući u obzir rešetku kao cjelinu kao kruto tijelo. Prijeđimo na određivanje sila u štapovima.

Metoda rezanja čvorova. Ova metoda je prikladna za korištenje kada trebate pronaći sile u svim šipkama rešetke. Svodi se na sekvencijalno razmatranje uvjeta ravnoteže sila koje konvergiraju u svakom od čvorova rešetke. Postupak izračuna objasnit ćemo na konkretnom primjeru.

Sl.23

Razmotrimo onaj prikazan na sl. 23,a rešetka oblikovana od identičnih jednakokračnih pravokutnih trokuta; sile koje djeluju na rešetku su paralelne s osi x i jednaki su: F 1 = F 2 = F 3 = F = 2.

Broj čvorova u ovoj farmi je n= 6, a broj šipki k= 9. Dakle, odnos je zadovoljen i rešetka je kruta, bez dodatnih šipki.

Sastavljajući jednadžbe ravnoteže za farmu kao cjelinu, nalazimo da su reakcije oslonaca usmjerene kao što je prikazano na slici i brojčano jednake;

Prijeđimo na određivanje sila u štapovima.

Označimo čvorove rešetke rimskim brojevima, a šipke arapskim brojevima. Označit ćemo potrebne napore S 1 (u šipki 1), S 2 (u šipki 2), itd. Mentalno odrežimo sve čvorove zajedno sa šipkama koje se u njima skupljaju od ostatka rešetke. Djelovanje odbačenih dijelova štapova zamijenit ćemo silama koje će biti usmjerene duž odgovarajućih štapova i brojčano jednake traženim silama S 1 , S 2, ... Prikazujemo sve te sile odjednom na slici, usmjeravajući ih iz čvorova, tj. uzimajući u obzir sve šipke koje treba rastegnuti (sl. 23, a; prikazanu sliku treba zamisliti za svaki čvor kao što je prikazano na Slika 23, b za čvor III). Ako se kao rezultat izračuna veličina sile u bilo kojoj šipki pokaže negativnom, to će značiti da ta šipka nije istegnuta, već stisnuta. Nema slovnih oznaka za sile koje djeluju duž šipki na sl. 23 ne ulaze, jer je jasno da su sile koje djeluju duž šipke 1 brojčano jednake S 1, duž šipke 2 - jednako S 2, itd.

Sada za sile koje konvergiraju u svakom čvoru, sekvencijalno sastavljamo jednadžbe ravnoteže

Počinjemo od čvora 1, gdje se susreću dvije šipke, budući da se samo dvije nepoznate sile mogu odrediti iz dviju jednadžbi ravnoteže.

Sastavljanjem jednadžbi ravnoteže za čvor 1 dobivamo

F 1 +S 2 cos45 0 =0, N+S 1 +S 2 sin45 0 =0.

Odavde nalazimo

Sada znajući S 1, idite na čvor II. Za njega jednadžbe ravnoteže daju

S 3 +F 2 =0, S 4 -S 1 =0,

S3=-F=-2H, S4=S1=-1H.

Utvrdivši S 4, sastavljamo na sličan način jednadžbe ravnoteže, prvo za čvor III, a zatim za čvor IV. Iz ovih jednadžbi nalazimo:

Na kraju, da izračunamo S 9 sastavljamo jednadžbu ravnoteže za sile koje konvergiraju u čvoru V, projicirajući ih na os By. Dobivamo Y A +S 9 cos45 0 =0 odakle

Druga jednadžba ravnoteže za čvor V i dvije jednadžbe za čvor VI mogu se sastaviti kao jednadžbe provjere. Za pronalaženje sila u šipkama ove jednadžbe nisu bile potrebne, jer su umjesto njih korištene tri jednadžbe ravnoteže za cijelu rešetku kao cjelinu za određivanje N, X A i Y A.

Konačni rezultati izračuna mogu se sažeti u tablici:

Kao što pokazuju znakovi napora, šipka 5 je rastegnuta, preostale šipke su stisnute; štap 7 nije opterećen (nulti štap).

Prisutnost nulte šipke u rešetki, slično šipki 7, odmah se detektira, jer ako se tri šipke konvergiraju u čvoru koji nije opterećen vanjskim silama, od kojih su dvije usmjerene duž iste ravne linije, tada sila u trećoj šipki je nula. Ovaj rezultat se dobiva iz jednadžbe ravnoteže u projekciji na os okomitu na dva spomenuta štapa.

Ako tijekom izračuna naiđete na čvor za koji je broj nepoznanica veći od dva, tada možete koristiti metodu presjeka.

Metoda presjeka (Ritterova metoda). Ova metoda je prikladna za određivanje sila u pojedinačnim rešetkastim šipkama, posebno za provjeru proračuna. Ideja metode je da je rešetka podijeljena na dva dijela s dijelom koji prolazi kroz tri šipke u kojima (ili u jednoj od kojih) treba odrediti silu, a razmatra se ravnoteža jednog od tih dijelova . Djelovanje odbačenog dijela zamjenjuje se odgovarajućim silama, usmjeravajući ih duž izrezanih šipki iz čvorova, tj. smatrajući da su šipke istegnute (kao kod metode rezanja čvorova). Zatim se konstruiraju jednadžbe ravnoteže, uzimajući središta momenata (ili osi projekcija) tako da svaka jednadžba uključuje samo jednu nepoznatu silu.

Grafički proračun ravnih rešetki.

Proračun rešetke izrezivanjem čvorova može se izvršiti grafički. Da biste to učinili, prvo odredite reakcije podrške. Zatim, uzastopno odsijecajući svaki od njegovih čvorova od rešetke, pronalaze sile u šipkama koje konvergiraju u tim čvorovima, konstruirajući odgovarajuće zatvorene poligone sila. Sve konstrukcije izvode se u mjerilu koje je potrebno unaprijed odabrati. Proračun počinje s čvorom u kojem se susreću dvije šipke (inače neće biti moguće odrediti nepoznate sile).

Sl.24

Kao primjer, razmotrite farmu prikazanu na sl. 24, a. Broj čvorova u ovoj farmi je n= 6, a broj šipki k= 9. Dakle, odnos je zadovoljen i rešetka je kruta, bez dodatnih šipki. Reakcije potpore i za rešetku koja se razmatra prikazane su zajedno sa silama i kao što je poznato.

Određivanje sila u štapovima počinjemo razmatranjem štapova koji konvergiraju u čvoru I (čvorove označavamo rimskim, a štapove arapskim brojevima). Nakon što smo mentalno odrezali ostatak rešetke od ovih šipki, odbacujemo njezino djelovanje i mentalno nadomještamo odbačeni dio silama i , koje bi trebale biti usmjerene duž šipki 1 i 2. Od sila koje konvergiraju u čvoru I gradimo zatvoreni trokut (Slika 24, b). Da bismo to učinili, najprije nacrtamo poznatu silu u odabranom mjerilu, a zatim kroz njen početak i kraj povučemo ravne linije, paralelne sa štapovima 1 i 2. Na taj način ćemo pronaći sile i koje djeluju na štapove 1 i 2. Zatim razmatramo ravnotežu štapova koji konvergiraju u čvoru II. Mentalno zamjenjujemo djelovanje na te šipke odbačenog dijela rešetke sa silama , , i , usmjerenim duž odgovarajućih šipki; Štoviše, sila nam je poznata, budući da je jednakost akcije i reakcije. Konstruiranjem zatvorenog trokuta od sila koje konvergiraju u čvoru II (počevši od sile), nalazimo vrijednosti S 3 i S 4 (u ovom slučaju S 4 = 0). Sile u ostalim štapovima nalaze se na sličan način. Odgovarajući poligoni sila za sve čvorove prikazani su na slici. 24, b. Posljednji poligon (za čvor VI) je konstruiran za provjeru, budući da su sve sile uključene u njega već pronađene.

Iz izgrađenih poligona, poznavajući mjerilo, nalazimo veličinu svih napora. Predznak sile u svakom štapu određuje se na sljedeći način. Nakon što smo mentalno izrezali čvor duž šipki koje se u njemu skupljaju (na primjer, čvor III), primjenjujemo pronađene sile na rubove šipki (slika 25); sila usmjerena iz čvora (na slici 25.) rasteže štap, a sila usmjerena prema čvoru (i na slici 25.) sabija ga.

Sl.25

Prema prihvaćenom stanju vlačnim silama dodijelimo predznak “+”, a tlačnim predznak “-”. U razmatranom primjeru (slika 25) šipke 1, 2, 3, 6, 7, 9 su komprimirane, a šipke 5, 8 istegnute.

Trenje.

Zašto žica violine zvuči kada se po njoj svira gudalo? Uostalom, gudalo se kreće, a vibracije žice su periodične. Kako automobil ubrzava, a koja ga sila usporava pri kočenju? Zašto auto proklizava na skliskoj cesti? Odgovore na sva ova i mnoga druga važna pitanja vezana uz gibanje tijela daju zakoni trenja.

Vidite kako se trenje manifestira na razne i ponekad neočekivane načine u okolini oko nas. Trenje je uključeno, i to vrlo značajno, tamo gdje to niti ne slutimo. Kada bi trenje iznenada nestalo iz svijeta, mnoge obične pojave odvijale bi se na potpuno drugačiji način.

Francuski fizičar Guillaume vrlo slikovito piše o ulozi trenja:

“Svi smo morali izlaziti u ledenim uvjetima; koliko nam je truda trebalo da se održimo da ne padnemo, koliko smo smiješnih pokreta morali napraviti da bismo stali! To nas tjera da shvatimo da obično tlo po kojem hodamo ima dragocjenu kvalitetu koja nam omogućuje da održimo ravnotežu bez puno napora. Ista misao javlja nam se kada vozimo bicikl po skliskom kolniku ili kada se konj posklizne na asfaltu i padne. Proučavanjem takvih pojava dolazimo do otkrića do kakvih posljedica trenje dovodi. Inženjeri ga nastoje eliminirati u automobilima što je više moguće - i rade dobar posao. U primijenjenoj mehanici o trenju se govori kao o krajnje nepoželjnoj pojavi i to je točno, ali samo u uskom, specijaliziranom području. U svim ostalim slučajevima trebamo biti zahvalni trenju: ono nam daje priliku hodati, sjediti i raditi bez straha da će knjige i tintarnica pasti na pod, da će stol kliziti dok ne udari u kut, a pero iskliznuti nam iz prstiju.

Trenje je toliko česta pojava da ga, uz rijetke iznimke, ne moramo zvati u pomoć: ono nam dolazi samo.

Trenje potiče stabilnost. Stolari izravnavaju pod tako da stolovi i stolice ostaju tamo gdje su postavljeni. Tanjurići, tanjuri, čaše postavljeni na stol ostaju nepomični bez ikakve posebne brige s naše strane, osim ako se to ne dogodi na parnom brodu tijekom ljuljanja.

Zamislimo da se trenje može potpuno eliminirati. Tada se nikakva tijela, bila ona veličine kamenog bloka ili mala kao zrnca pijeska, neće moći nasloniti jedno na drugo: sve će kliziti i kotrljati se dok ne završi na istoj razini. Da nema trenja, Zemlja bi bila kugla bez nepravilnosti, poput tekućine.”

Tome možemo dodati da bi u nedostatku trenja čavli i vijci klizili iz zidova, ništa se nije moglo držati u rukama, nijedan vihor nikada ne bi prestao, nijedan zvuk ne bi prestao, nego bi odjekivao u beskraj, odjekivao neprestano, na primjer, sa zidova sobe.

Objektivnu lekciju koja nas uvjerava u ogromnu važnost trenja svaki put nam daje crni led. Uhvaćeni od nje na ulici, nalazimo se bespomoćni i uvijek u opasnosti od pada. Evo poučnog izvatka iz novina (prosinac 1927.):

“London 21. Zbog jakog leda, ulični i tramvajski promet u Londonu je vrlo otežan. Oko 1400 ljudi primljeno je u bolnice sa slomljenim rukama, nogama itd.

“U sudaru kod Hyde Parka eksplozijom benzina uništena su tri automobila i dva tramvaja...”

"Pariz 21. Led u Parizu i njegovim predgrađima izazvao brojne nesreće..."

Međutim, zanemarivo trenje na ledu može se tehnički uspješno iskoristiti. Već obične saonice služe kao primjer za to. O tome još bolje svjedoče takozvane ledene ceste, koje su bile uređene za prijevoz drva od sječišta do željeznice ili do splava. Na takvoj cesti, koja ima glatke ledene tračnice, dva konja vuku saonice natovarene sa 70 tona balvana.

Trenje mirovanja, trenje klizanja.

Ranije se smatralo da mehanizam trenja nije kompliciran: površina je prekrivena neravninama, a trenje je rezultat podizanja kliznih dijelova na tim neravninama; ali to je pogrešno, jer tada ne bi bilo gubitka energije, ali zapravo se energija gubi na trenje.

Mehanizam gubitaka je drugačiji. I ovdje se pokazalo krajnje neočekivanim da se empirijski ovo trenje može približno opisati jednostavnim zakonom. Sila potrebna za svladavanje trenja i povlačenje jednog tijela po površini drugog ovisi o sili usmjerenoj normalno na dodirne površine.

Površina čvrstog tijela obično ima nepravilnosti. Na primjer, čak i kod vrlo dobro poliranih metala, pod elektronskim mikroskopom vidljive su "planine" i "doline" veličine 100-1000A. Kada su tijela sabijena, dolazi do kontakta samo na najvišim mjestima i površina stvarnog kontakta je znatno manja od ukupne površine dodirnih površina. Pritisak na kontaktnim točkama može biti vrlo visok i tu dolazi do plastične deformacije. U tom se slučaju povećava kontaktna površina i pada tlak. To se nastavlja sve dok tlak ne dosegne određenu vrijednost na kojoj prestaje deformacija. Stoga se ispostavlja da je stvarna kontaktna površina proporcionalna sili pritiska.

Na mjestu kontakta djeluju sile molekularne adhezije (zna se npr. da se vrlo čiste i glatke metalne površine lijepe jedna za drugu).

Ovaj model sila suhog trenja (tzv. trenja između čvrstih tijela) je naizgled blizak stvarnom stanju u metalima.

Ako tijelo, na primjer, jednostavno leži na vodoravnoj podlozi, tada na njega ne djeluje sila trenja. Trenje se javlja ako pokušate pomaknuti tijelo ili na njega primijeniti silu. Sve dok veličina te sile ne prijeđe određenu vrijednost, tijelo ostaje u stanju mirovanja, a sila trenja jednaka je po veličini i suprotnog smjera primijenjenoj sili. Tada počinje kretanje.

Možda se čini iznenađujuće, ali statička sila trenja je ta koja ubrzava automobil. Uostalom, kada se automobil kreće, kotači ne klize u odnosu na cestu, a između guma i površine ceste nastaje statička sila trenja. Kao što je lako vidjeti, usmjeren je u smjeru kretanja automobila. Veličina ove sile ne može prijeći najveću vrijednost statičkog trenja. Stoga, ako naglo pritisnete gas na skliskoj cesti, automobil će početi kliziti. Ali ako pritisnete kočnice, rotacija kotača će prestati i automobil će kliziti po cesti. Sila trenja će promijeniti smjer i početi usporavati automobil.

Sila trenja pri klizanju čvrstih tijela ne ovisi samo o svojstvima površina i sili pritiska (ta je ovisnost kvalitativno ista kao kod statičkog trenja), već i o brzini gibanja. Često, s povećanjem brzine, sila trenja prvo naglo opada, a zatim ponovno počinje rasti.

Ova važna značajka sile trenja klizanja objašnjava zašto violinska žica zvuči. U početku nema klizanja između gudala i strune, a tetiva se hvata gudalom. Kada sila statičkog trenja dostigne maksimalnu vrijednost, struna pukne, a zatim vibrira gotovo kao da je slobodna, zatim je opet zarobi gudalo itd.

Slične, ali već štetne vibracije mogu se pojaviti pri obradi metala na tokarilici zbog trenja između uklonjenih strugotina i rezača. A ako se luk trlja kolofonijom kako bi se oštrija ovisnost sile trenja o brzini, tada pri obradi metala morate učiniti suprotno (odabrati poseban oblik rezača, mazivo itd.). Stoga je važno poznavati zakone trenja i znati ih koristiti.

Uz suho trenje postoji i tzv. tekuće trenje, koje se javlja pri gibanju krutih tijela u tekućinama i plinovima, a povezano je s njihovom viskoznošću. Sile trenja tekućine proporcionalne su brzini gibanja i nestaju kada se tijelo zaustavi. Stoga u tekućini možete pokrenuti tijelo primjenom čak i vrlo male sile. Na primjer, čovjek može pokrenuti tešku teglenicu na vodi odgurujući se od dna motkom, ali na kopnu, naravno, ne može pomaknuti takav teret. Ova važna značajka sila tekućeg trenja objašnjava, na primjer, činjenicu zašto automobil "klizi" na mokroj cesti. Trenje postaje tekuće, pa čak i male neravnine na cesti koje stvaraju bočne sile dovode do "klizanja" automobila.

Rezimirajući gore navedeno, možemo zaključiti da je pojava trenja posljedica, prije svega, hrapavosti površina, što stvara otpor kretanju, te prisutnosti adhezije između tijela pritisnutih jedno na drugo. Proučavanje svih značajki fenomena trenja prilično je složen fizički i mehanički problem, čije razmatranje nadilazi okvir tečaja teorijske mehanike.

U inženjerskim izračunima obično polaze od niza općih načela utvrđenih eksperimentalno, koja odražavaju glavne značajke fenomena trenja s dovoljnom točnošću za praksu. Ovi zakoni, koji se nazivaju zakoni trenja klizanja u mirovanju (Coulombovi zakoni), mogu se formulirati na sljedeći način:

1. Prilikom pokušaja pomicanja jednog tijela duž površine drugog u ravnini kontakta tijela, nastaje sila trenja (ili sila prianjanja), čija veličina može uzeti bilo koju vrijednost od nule do vrijednosti F pr, koja se naziva krajnja sila trenja.

Sila trenja klizanja (ili jednostavno trenjem) je komponenta sile reakcije sprega koja leži u tangentnoj ravnini na površine tijela u dodiru.

Sila trenja usmjerena je u smjeru suprotnom od onoga u kojem sile koje djeluju nastoje pomaknuti tijelo.

U teorijskoj mehanici se pretpostavlja da nema maziva između površina tijela u kontaktu.

Suho trenje naziva se trenje kada između površina tijela u dodiru nema maziva.

Razmotrit ćemo dva slučaja: trenje kada tijelo miruje ili je u ravnoteži i trenje klizanja kada se jedno tijelo giba po površini drugoga određenom relativnom brzinom.

U mirovanju sila trenja ovisi samo o aktivnim silama. Uz odabrani smjer tangente na mjestu dodira površina tijela, sila trenja se izračunava po formuli:

Slično, s odabranim smjerom normale, normalna reakcija se izražava u terminima zadanih sila:

Kada se jedno tijelo giba po površini drugoga, sila trenja je stalna vrijednost.

2. Veličina krajnje sile trenja jednaka je umnošku statičkog koeficijenta trenja i normalnog tlaka ili normalne reakcije:

Statički koeficijent trenja - apstraktni broj 0< <1; он опре­деляется опытным путем и зависит от материала соприкасающихся тел и состояния поверхностей (характер обработки, температура, влажность, смазка и т. п.). Считается, что коэффициент трения не зависит от скорости движения.

3. Maksimalna sila trenja klizanja, pod jednakim uvjetima, ne ovisi o kontaktnoj površini površina za trljanje. Iz ovog zakona proizlazi da je za pomicanje, na primjer, cigle potrebno djelovati istom silom, bez obzira na kojoj je strani postavljena na površinu, širokoj ili uskoj.

Kombinirajući prvi i drugi zakon zajedno, dobivamo da u ravnoteži statička sila trenja (sila prianjanja)

Reakcije grubih veza. Kut trenja.

Do sada smo pri rješavanju problema statike zanemarivali trenje i smatrali da su vezne površine glatke i da su njihove reakcije usmjerene duž normala na te površine. Reakcija prave (grube) veze sastojat će se od dvije komponente: normalne reakcije i sile trenja okomite na nju. Posljedično, ukupna reakcija će biti odstupljena od normale na površinu za neki kut. Kada se sila trenja promijeni od nule do F, promijenit će se sila R od N do R, a njezin će kut s normalom porasti od nule do određene granične vrijednosti (slika 26).

Sl.26

Najveći kut koji ukupna reakcija hrapave veze čini s normalom na površinu naziva se kut trenja. Iz crteža je jasno da

Budući da , odavde nalazimo sljedeći odnos između kuta trenja i koeficijenta trenja:

U ravnoteži potpuna reakcija je R, ovisno o silama smicanja, može proći bilo gdje unutar kuta trenja. Kada ravnoteža postane ograničavajuća, reakcija će odstupiti od normale za kut .

Frikcijski konus naziva se stožac opisan maksimalnom reakcijskom silom hrapave veze oko smjera normalne reakcije.

Ako na tijelo koje leži na hrapavoj podlozi djeluje sila R, tvoreći kut s normalom (sl. 27), tada će se tijelo gibati samo kada je posmična sila Psin veća (uzimamo u obzir N=Pcos, zanemarujući težinu tijela). Ali nejednakost , u kojem se , izvršava samo kada , i.e. u . Prema tome, nikakva sila koja s normalom tvori kut manji od kuta trenja ne može pomaknuti tijelo duž zadane površine. To objašnjava dobro poznate pojave zaglavljivanja ili samokočenja tijela.

Sl.27

Za ravnotežu krutog tijela na hrapavoj podlozi potrebno je i dovoljno da linija djelovanja rezultantnih aktivnih sila koje djeluju na kruto tijelo prolazi unutar tarnog stošca ili duž njegove generatrise kroz njegov vrh.

Tijelo ne može biti izbačeno iz ravnoteže nikakvim modulom aktivne sile ako njegova linija djelovanja prolazi unutar tarnog stošca.

Fenomen trenja klizanja prvi put je eksperimentalno proučavan krajem 17. stoljeća. Francuski fizičar Amonton (1663-1705), zakone trenja formulirao je gotovo sto godina kasnije Coulomb (1736-1806).

1. Sila trenja leži u ravnini tangenti na dodirne površine tijela koja se trljaju.

2. Sila trenja ne ovisi o području kontakta između tijela.

3. Najveća vrijednost sile trenja proporcionalna je normalnom tlaku N tijelo na ravninu (u slučaju koji se razmatra N=P):

F max = fN

Na tjelesnu težinu P ležeći na vodoravnom stolu (slika 13) djelovat ćemo vodoravnom silom S. Zanemarujemo dimenzije tijela, smatrajući ga materijalnom točkom (u nastavku se govori o slučaju tijela konačnih dimenzija). Ako S =0, tijelo će biti u ravnoteži (u ovom slučaju, u mirovanju u odnosu na stol); ako sila S ako se počnemo povećavati, tijelo će i dalje ostati u mirovanju; dakle, horizontalna komponenta reakcije stola, koja se naziva sila trenja Ftr uravnotežuje primijenjenu silu S i raste s njim dok se ravnoteža ne poremeti. To će se dogoditi u trenutku kada sila trenja postigne najveću vrijednost.

F max = fN(1.17)

i koeficijent proporcionalnosti f, koji se naziva koeficijent trenja klizanja, određuje se eksperimentalno i pokazalo se da ovisi o materijalu i stanju (hrapavosti) površina tijela koja se trljaju. Brojčana vrijednost koeficijenta trenja klizanja za različite materijale može se pronaći u referentnim knjigama. Uz koeficijent trenja f Uvedimo u razmatranje kut trenja φ definirajući ga relacijom . Podrijetlo ove jednadžbe i naziv "kut trenja" bit će objašnjeni u nastavku. Kada R dostići će vrijednost Fmax, doći će kritični (okidački) trenutak ravnoteže; Ako S ostat će jednaki Fmax, tada se ravnoteža neće poremetiti, već je dovoljan i najbeznačajniji prirast napora S tako da se tijelo kreće. Možete primijetiti da čim se tijelo pomakne, sila trenja se odmah nešto smanjuje; pokusi su pokazali da je trenje pri međusobnom gibanju tijela nešto manje od trenja pri međusobnom mirovanju. Važno je napomenuti da je prije kritičnog trenutka, tj. dok tijelo miruje, sila trenja jednaka primijenjenoj sili i može se reći samo da F≤ N. Znak jednakosti odnosi se na kritični trenutak ravnoteže. Smjer sile trenja mirovanja suprotan je smjeru sile S a mijenja se s promjenom smjera ove sile.

Koeficijent trenja f ovisi o brzini tijela, opadajući za većinu materijala kako se brzina povećava. (Kao iznimku možemo istaknuti slučaj trljanja kože o metal; ovdje f raste s porastom relativne brzine.). Relacija (17) sasvim dobro odgovara opažanjima pri trenju suhih ili slabo podmazanih tijela; teorija trenja u prisutnosti sloja maziva, koju su stvorili N. P. Petrov i O. Reynolds, predstavlja poseban dio hidrodinamike viskozne tekućine.

Kut trenja, konus trenja.

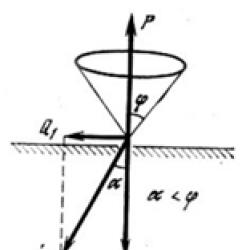
Uzimajući u obzir statičko trenje, pretpostavimo da se sila primjenjuje na tijelo koje počiva na horizontalnoj hrapavoj ravnini Q, čineći kut α s normalom na ravninu (slika 14). Kreirajmo jednadžbe ravnoteže. Za konvergentni sustav sila dovoljno je napisati dvije jednadžbe

.

Napisane jednadžbe određuju silu trenja i normalnu reakciju. Da se tijelo pod djelovanjem primijenjene sile ne bi pomaknulo s mjesta potrebno je da ili . Dobivenu nejednakost podijelimo s , imamo , ili uvođenjem kuta trenja dobivamo α ≤φ . Prema tome, ovisno o materijalu i prirodi površine trljajućih tijela, moguće je odrediti takav kut iz zadanog koeficijenta trenja φ , što ako je sila koja djeluje na tijelo nagnuta prema normali za kut manji od kuta φ, onda bez obzira koliko velika ova sila bila, tijelo će ostati u ravnoteži. Ovo objašnjava naziv kuta φ kut trenja. Područje unutar segmenata s kutom 2φ(“područje trenja”) predstavlja područje sa izvanrednim svojstvom: bez obzira koliki je intenzitet sile, čija se linija djelovanja nalazi unutar ovog područja, ta sila neće pokrenuti tijelo koje počiva na ravnini.

Ako uzmemo u obzir tijelo koje ima sposobnost kretanja u bilo kojem smjeru duž ravnine, tada će područje trenja biti ograničeno površinom stošca s kutom rastvaranja jednakim 2φ(tzv. tarni konus). Prisutnost područja trenja objašnjava fenomen zaglavljivanja ili, kako se kaže, "zaglavljivanja" dijelova stroja, kada nikakva sila unutar konusa ne može pomaknuti odgovarajući dio stroja. Koeficijent trenja može imati različite vrijednosti za različite smjerove na ravnini (na primjer, kada se trlja po drvu uzduž i poprijeko vlakana, kada se trlja po valjanom željezu duž i okomito na smjer kotrljanja). Stoga tarni stožac ne predstavlja uvijek ravni okrugli stožac.

Varlamov A.A. Stožac trenja // Quantum. - 1986. - br. 1. - str. 24-25.

Po posebnom dogovoru s uredništvom i uredništvom časopisa "Kvant"

Ako uzmemo u obzir uvjete ravnoteže tijela na nagnutoj ravnini, čiji se kut nagiba može mijenjati, tada je lako dobiti (učinite to sami) da će tijelo početi kliziti s ravnine pod kutom φ takav da

\(~\imeoperatora(tg) \varphi = \mu\) ,

Gdje μ - koeficijent trenja tijela o ravninu. Ne čudi li vas da taj kut ne ovisi o tjelesnoj težini?

Isti izraz za kut φ može se dobiti na drugi, možda jednostavniji način. Ali da biste to učinili, prvo se morate upoznati s pojmom "frikcijski konus".

Neka se tijelo, koje se može smatrati materijalnom točkom, nalazi na gruboj horizontalnoj ravnini. Sila teže \(~m \vec g\) pritišće tijelo na podlogu, a podloga "odgovara", djelujući na tijelo silom normalnog tlaka \(~\vec N\). Ako na tijelo djeluje i neka vodoravna sila, tada se s površine pojavljuje druga sila - sila trenja. Sve dok veličina vodoravne sile ne premaši najveću vrijednost sile statičkog trenja F tr.p. max = μN, tijelo miruje. Kada se postigne ta vrijednost, tijelo se počinje gibati, a površina na njega djeluje silom trenja klizanja koja sprječava kretanje

\(~F_(tr.sk.) = F_(tr.p.max) = \mu N\) .

I normalnu reakcijsku silu i silu trenja generira površina, tako da možemo govoriti o ukupnoj reakcijskoj sili površine. U slučaju kada se tijelo pod utjecajem vanjske sile (naravno, uključujući i silu teže) giba po površini (slika 1), ukupna sila reakcije je

\(~\vec R = \vec N + \vec F_(tr.sk)\) .

Ova sila je usmjerena pod kutom φ na normalu, što je lako odrediti:

\(~\imeoperatora(tg) \varphi = \frac(F_(tr.sk))(N) = \mu ; \varphi = \imeoperatora(arctg) \mu\) .

Kutak φ naziva kut trenja.

Sada ćemo mentalno rotirati vektor \(~\vec R\) oko normale na površinu bez promjene kuta φ između njih. U ovom slučaju, vektor će opisati stožac (s kutom od 2 φ na vrhu), tzv tarni konus. Ima sljedeće izvanredno svojstvo. Bez obzira koliko velika vanjska sila djeluje na tijelo, ako ono leži unutar tarnog stošca, tijelo ostaje u stanju mirovanja. Ako ta sila prijeđe stožac trenja, tijelo se počinje gibati, bez obzira na to koliko je mala.

Nije teško provjeriti valjanost ove tvrdnje. Doista, neka vanjska sila \(~\vec F\) (vidi sl. 1) djeluje na tijelo tako da njezina linija djelovanja čini kut α s normalom na površinu. Tada je sila koja "pomiče" tijelo po površini jednaka F grijeh α , a normalna sila reakcije jednaka je F cos α . Dakle, najveća moguća sila statičkog trenja koja drži tijelo na mjestu je

\(~F_(tr.p.max) = \mu N = \mu F \cos \alpha = F \operatorname(tg) \varphi \cos \alpha\) .

Dok sila \(~\vec F\) leži unutar stošca trenja, α < φ i stoga F grijeh α < F tg φ cos α . Tijelo miruje. Međutim, čim kut α kut trenja postaje veći φ , posljednja nejednakost je povrijeđena. Sada trenje više ne može držati tijelo na mjestu i ono počinje kliziti. Vratimo se na tijelo lijevo s početka članka na kosoj ravnini i konstruirajmo za njega tarni stožac (slika 2).

Vanjska sila ovdje je sila teže \(~m \vec g\) usmjerena okomito prema dolje. Pozdrav α < φ , prema onome što je gore rečeno, tijelo će mirovati. Ali čim kut α prelazi kut φ - pokret će započeti. Stoga odmah dobivamo uvjet da tijelo počne kliziti iz nagnute ravnine:

\(~\imeoperatora(tg) \alpha > \mu ; \alpha > \imeoperatora(arctg) \mu\) .

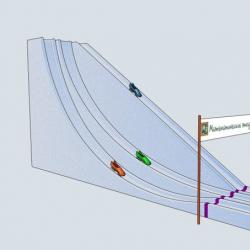
Imajte na umu da koncept tarnog stošca koriste inženjeri pri proračunu određene strukture. Na primjer, čak i kada dizajnirate stolac, trebali biste imati na umu konus trenja.

Zamislite tabure čije su noge šarkama povezane sa sjedalom (slika 3). Naravno, u stvarnosti to nitko ne bi učinio, ali takav sustav pričvršćivanja omogućit će nam lakše razumijevanje uloge tarnog konusa. Postavimo takav tabure na pod tako da kut α , koji noge čine s normalom na pod, bio je manji od kuta trenja φ . U ovom slučaju, bez obzira na to kako opteretimo stolicu, njene noge se neće razmaknuti - sila kojom svaka noga djeluje na pod leži unutar odgovarajućeg stošca trenja. Ako kut α napraviti više kuta φ , tada će sila kojom noga djeluje na pod prijeći granice tarnog stošca, noge će se razdvojiti i stolica će pasti.

Kod pravog taburea noge nisu šarkama spojene sa sjedalom, već su zalijepljene ili ušrafljene u njega.

Međutim, ako napravite kut α premašio kut trenja φ , tada na spoju nogu stolice sa sjedalom može doći do značajnog naprezanja i stolica će se slomiti.

U stvarnosti ne postoje apsolutno glatke površine. Sve su površine tijela u jednom ili drugom stupnju hrapave. Dakle, sila reakcije hrapave površine kada je tijelo u ravnoteži ovisi o aktivnim silama ne samo u brojčanoj vrijednosti, već iu smjeru.

Rastavimo reakcijsku silu hrapave površine na komponente: jednu ćemo usmjeriti po zajedničkoj normali na dodirnu površinu, a drugu u tangentnoj ravnini na te površine.

Sila trenja klizanje (ili jednostavno sila trenja) je komponenta sile reakcije veze koja leži u tangentnoj ravnini na površine tijela u dodiru.

Snagom normalne reakcije veza je komponenta sile reakcije veze, koja je usmjerena duž zajedničke normale na površine tijela koja se dodiruju.

Priroda sile trenja je vrlo složena i ne dotičemo je. U teorijskoj mehanici se pretpostavlja da nema maziva između površina tijela u kontaktu.

Suho trenje naziva se trenje kada između površina tijela u dodiru nema maziva.

Razmotrit ćemo dva slučaja: trenje kada tijelo miruje ili je u ravnoteži i trenje klizanja kada se jedno tijelo giba po površini drugoga određenom relativnom brzinom.

U mirovanju sila trenja ovisi samo o aktivnim silama. Uz odabrani smjer tangente na mjestu dodira površina tijela, sila trenja se izračunava po formuli:

Slično, s odabranim smjerom normale, normalna reakcija se izražava u terminima zadanih sila:

Kada se jedno tijelo giba po površini drugoga, sila trenja je stalna vrijednost.

Inženjerski izračuni obično se temelje na nizu eksperimentalno utvrđenih uzoraka koji odražavaju glavne značajke fenomena suhog trenja s dovoljnom točnošću za praksu. Ti se zakoni nazivaju zakoni trenja klizanja ili Coulombovi zakoni.

Coulombovi zakoni

1. Sila trenja klizanja nalazi se u zajedničkoj tangentnoj ravnini dodirnih površina tijela i usmjerena je u smjeru suprotnom od smjera mogućeg klizanja tijela pod djelovanjem aktivnih sila. Sila trenja ovisi o aktivnim silama, a njen modul je između nule i maksimalne vrijednosti, koja se postiže u trenutku kada tijelo napusti ravnotežni položaj, odnosno:

Nazvana krajnja sila trenja .

2. Maksimalna sila trenja klizanja, pod jednakim uvjetima, ne ovisi o području kontakta trljajućih površina. Iz ovog zakona proizlazi da je za pomicanje, na primjer, cigle potrebno djelovati istom silom, bez obzira na kojoj je strani postavljena na površinu, širokoj ili uskoj.

3. Granična sila trenja klizanja proporcionalna je normalnoj reakciji (normalnom tlaku) tj

gdje se bezdimenzionalni koeficijent naziva koeficijent trenja klizanja; neovisno je o normalnoj reakciji.

4. Koeficijent trenja klizanja ovisi o materijalu i agregatnom stanju površina koje se trljaju, odnosno o veličini i prirodi hrapavosti, vlažnosti, temperaturi i drugim uvjetima. Koeficijent trenja određuje se eksperimentalno.

Smatra se da koeficijent trenja ne ovisi o brzini kretanja.

Kut trenja. Uvjeti ravnoteže.

Mnogi problemi uključuju balansiranje tijela na gruboj površini, tj. u prisutnosti trenja, pogodno je riješiti geometrijski. Da bismo to učinili, uvodimo koncept kuta i stošca trenja.

Reakcija prave (grube) veze sastoji se od dvije komponente: normalne reakcije i sile trenja okomite na nju. Posljedično, reakcija veze odstupa od normale na površinu za određeni kut. Kada se sila trenja promijeni od nule do maksimuma, sila reakcije se mijenja od nule do , a njezin kut s normalom raste od nule do određene granične vrijednosti j.

Kut trenja naziva se najveći kut između najveće sile reakcije hrapave veze i normalne reakcije.

Kut trenja ovisi o koeficijentu trenja.

Frikcijski konus naziva se stožac opisan maksimalnom reakcijskom silom hrapave veze oko smjera normalne reakcije.

Primjer.

Ako na tijelo koje leži na hrapavoj podlozi djeluje sila P koja s normalom tvori kut, tada će se tijelo gibati samo kada je posmična sila  veća od granične sile trenja.  (ako zanemarimo težinu tijela, onda je ali nejednakost

Izvršava se samo kada , tj. u ,

Prema tome, nijedna sila koja s normalom tvori kut manji od kuta trenja  ne može pokrenuti tijelo po zadanoj površini.

Za ravnotežu krutog tijela na hrapavoj podlozi potrebno je i dovoljno da linija djelovanja rezultantnih aktivnih sila koje djeluju na kruto tijelo prolazi unutar tarnog stošca ili duž njegove generatrise kroz njegov vrh.

Tijelo ne može biti izbačeno iz ravnoteže nikakvim modulom aktivne sile ako njegova linija djelovanja prolazi unutar tarnog stošca.

Primjer.

Promotrimo tijelo koje ima vertikalnu ravninu simetrije. Presjek tijela ove ravnine ima oblik pravokutnika. Širina tijela je 2a.

Na tijelo u točki C, koja leži na osi simetrije, djeluje okomita sila, a u točki A, koja leži na udaljenosti h od podnožja, djeluje horizontalna sila. Reakcija osnovne ravnine (reakcija veze) svodi se na normalnu reakciju i silu trenja. Linija djelovanja sile je nepoznata. Označimo udaljenost od točke C do linije djelovanja sile s x. (). Kreirajmo tri jednadžbe ravnoteže:

Prema Coulombovom zakonu, tj. . (1)

Budući da je , tada (2)

Analizirajmo rezultate:

Povećat ćemo svoju snagu.

1) Ako , tada će se ravnoteža odvijati dok sila trenja ne dosegne svoju graničnu vrijednost, uvjet (1) će se pretvoriti u jednakost. Daljnje povećanje sile uzrokovat će klizanje tijela po površini.

2) Ako , tada će se ravnoteža odvijati sve dok sila trenja ne dosegne vrijednost , uvjet (2) će se pretvoriti u jednakost. Vrijednost x bit će jednaka h. Daljnje povećanje sile uzrokovat će naginjanje tijela oko točke B (neće biti klizanja).

Trenje kotrljanja

Trenje kotrljanja je otpor koji se javlja kada se jedno tijelo kotrlja po površini drugog.

Promotrimo cilindrični valjak radijusa r na horizontalnoj ravnini. Ispod valjka i ravnine na mjestu kontakta mogu se pojaviti reakcije koje djelovanjem aktivnih sila sprječavaju kotrljanje valjka po ravnini. Zbog deformacije površina, ne samo klizanje, već i kotrljanje.

Aktivne sile koje djeluju na valjke u obliku kotača obično se sastoje od gravitacije, horizontalne sile koja djeluje na središte valjka i nekoliko sila s momentom koji teži kotrljati kotač. Kotač se u ovom slučaju zove sljedbenik-vođa. Ako je , a , tada se kotač poziva rob. Ako je , a , tada se kotač poziva vodeći.