The postulates put forward by Bohr made it possible to calculate the spectrum of the hydrogen atom and hydrogen-like systems- systems consisting of a nucleus with a charge Ze and one electron (for example, He +, Li 2+ ions), as well as theoretically calculate the Rydberg constant.

Following Bohr, let us consider the motion of an electron in a hydrogen-like system, confining ourselves to circular stationary orbits. Solving together equation (208.1) m e v 2 /r=Zе 2 /(4 0 r 2) proposed by Rutherford and equation (210.1), we obtain an expression for the radius of the n-th stationary orbit:

where n=1, 2, 3, ... . From expression (212.1) it follows that the radii of the orbits grow in proportion to the squares of integers.

For a hydrogen atom (Z=1), the radius of the first electron orbit at n=1, called first Bohr radius(a), equals

which corresponds to calculations based on the kinetic theory of gases. Since the radii of stationary orbits cannot be measured, in order to test the theory it is necessary to turn to such quantities that can be measured experimentally. This quantity is the energy emitted and absorbed by hydrogen atoms.

The total energy of an electron in a hydrogen-like system is the sum of its kinetic energy (m e v 2 /2) and potential energy in the electrostatic field of the nucleus (-Ze 2 / (4 0 r)):

(we took into account that m e v 2 /2 = 1 / 2 Ze2(4 0 r) (see.

(208.1)). Taking into account the values ​​(212.1) quantized for the radius of the n-th stationary orbit, we obtain that the electron energy can take only the following allowed discrete values:

where the minus sign means that the electron is in a bound state.

It follows from formula (212.3) that the energy states of an atom form a sequence of energy levels that change depending on the value P. Integer n in expression (212.3), which determines the energy levels of an atom, is called principal quantum number. The energy state with n=1 is basic (normal) state; states with /r > 1 are excited. The energy level corresponding to the ground state of an atom is called basic (normal) level; all other levels are excited.

Giving n different integer values, we get for the hydrogen atom

(Z=1), according to formula (212.3), the possible energy levels, schematically presented in fig. 294. The energy of the hydrogen atom with increasing n increases (its negative value decreases) and the energy levels approach the boundary corresponding to the value n=  . The hydrogen atom thus has the lowest energy (E 1 = - 13.55 eV) at n= 1 and maximum (E 1 \u003d 0) at n \u003d  (when an electron is removed from an atom). Therefore, the value E  =0 corresponds to ionization atom (tear off an electron from it).

According to Bohr's second postulate (see (210.2)), during the transition of the hydrogen atom (Z=1) from the stationary state nWith higher energy into the stationary state m with lower energy a quantum is emitted

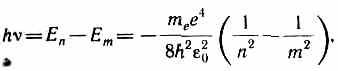
whence the radiation frequency

R=m e e 4 /(8h 3  2 0 ).

Using in the calculation R modern values ​​of the universal constants, we obtain a value that coincides with the experimental value of the Rydberg constant in the empirical formulas for the hydrogen atom (see §209). This coincidence convincingly proves the correctness of the formula obtained by Bohr

(212.3) for the energy levels of a hydrogen-like system.

Substituting, for example, into the formula

(212.4) m=1 and n=2, 3, 4, ..., we obtain a group of lines forming the Lyman series (see § 209) and corresponding to transitions of electrons from excited levels (n=2, 3, 4, .. .) on the main one (m=1). Similarly, when substituting m=2, 3, 4, 5,

6 and their corresponding values n we obtain the series of Balmer, Paschen, Bracket, Pfund and Humphrey (some of them are schematically shown in Fig. 294), described in § 209. Therefore, according to Bohr's theory, which quantitatively explained the spectrum of the hydrogen atom, the spectral series correspond to the radiation resulting from the transition of the atom to a given state from excited states located above the given one.

The absorption spectrum of the hydrogen atom is line-like, but contains only the Lyman series. It is also explained by Bohr's theory. Since free hydrogen atoms are usually in the ground state (stationary state with the lowest energy at n= 1), then when a certain energy is imparted to atoms from outside, only transitions can be observed

atoms from the ground state to the excited ones (the Lyman series arises).

Bohr's theory was a major step in the development of atomic physics and was an important step in the creation of quantum mechanics. However, this theory has internal contradictions (on the one hand, it applies the laws of classical physics, and on the other hand, it is based on quantum postulates). She examined the spectra of the hydrogen atom and hydrogen-like systems and calculated the frequencies spectral lines, however, could not explain their intensity and answer the question: why do certain transitions occur? A serious shortcoming of Bohr's theory was the impossibility of using it to describe the spectrum of the helium atom, one of the simplest atoms immediately following the hydrogen atom.

test questions

Why did the nuclear model of the atom fail?

Why was the Balmer series among the various series of spectral lines of the hydrogen atom the first to be studied?

What is the meaning of the numbers m and n in the generalized Balmer formula?

What is the radiation frequency of the hydrogen atom corresponding to the short-wavelength boundary of the Bracket series?

Explain the meaning of Bohr's postulates. How do they explain line spectrum atom? On which parts of the curve in Fig. 293 are elastic and on which inelastic collisions of electrons with atoms observed?

What are the main inputs that can be drawn from the experiments of Frank and Hertz? Using the Bohr model, indicate the spectral lines that can appear when a hydrogen atom goes into states with n=3 and n=4.

Plot on the wavelength scale three lines of each of the first two spectral series of the hydrogen atom.

Why does the absorption spectrum of the hydrogen atom contain only the Lyman series? Show that formula (212.3) can be written as E n =-13.55/n 2 , where E is expressed in electron volts.

Tasks

27.1. Determine the maximum and minimum photon energies in the ultraviolet series of the spectrum of the hydrogen atom (Lyman series).

27.2. Determine the wavelength corresponding to the boundary of the Balmer series.

27.3. Using Bohr's theory, determine the orbital magnetic moment of an electron moving along the second orbit of a hydrogen atom.

27.4. Using the Bohr theory, determine the change in the orbital mechanical momentum of an electron during its transition from an excited state (n=2) to the ground state with the emission of a photon with a wavelength =1.212 10 -7 m. [L = h=1.05 10 -3 4 J s]

27.5. Determine the ionization potential of the hydrogen atom.

27.6. Based on the fact that the ionization energy of the hydrogen atom E i \u003d 13.6 eV, determine the second excitation potential of this atom.

27.7 . Based on the fact that the ionization energy of the hydrogen atom is £" = 13.6 eV, determine in electron volts the photon energy corresponding to the longest wavelength line of the Lyman series.

* I. Rydberg (1854-1919) - Swedish scientist, specialist in the field of spectroscopy.

Studies of the emission spectra of rarefied gases (i.e., the emission spectra of individual atoms) have shown that each gas has a well-defined line spectrum, consisting of individual spectral lines or groups of closely spaced lines. The most studied is the spectrum of the simplest atom - the hydrogen atom.

The Swiss scientist I. Balmer (1825-1898) picked up an empirical formula describing all the spectral lines of the hydrogen atom known at that time in visible region of the spectrum:

where R "= 1.10 10 7 m -1 - constantRydberg . Since v = c/, then the formula

(209.1) can be rewritten for frequencies:

where R \u003d R "c \u003d 3.29 10 15 s -1 is also the Rydberg constant.

From expressions (209.1) and (209.2) it follows that spectral lines differing in different values n, form a group or series of lines called Balmer series. With the increase n the lines of the series are approaching; meaning n=  defines series border, to which the continuous spectrum adjoins from the side of high frequencies.

Later (at the beginning of the 20th century), several more series were discovered in the spectrum of the hydrogen atom. AT ultraviolet region of the spectrum located Lyman series:

AT infrared spectrum were also found: Paschen series

Bracket series

Pfund series

Humphrey series

All the above series in the spectrum of the hydrogen atom can be described by a single formula, called by the generalized Balmer formula:

where m has a constant value in each given series, m= 1, 2, 3, 4, 5, 6 (defines the series), n takes integer values ​​starting from m+1 (defines the individual lines of this series).

The study of more complex spectra - the spectra of vapors of alkali metals (for example, Li, Na, K) - showed that they are represented by a set of irregularly arranged lines. Rydberg managed to divide them into three series, each of which is located like the lines of the Balmer series.

The above serial formulas were selected empirically and for a long time had no theoretical justification, although they were confirmed experimentally with very high accuracy. The above form of serial formulas, the amazing repetition of integers in them, the universality of the Rydberg constant testify to a deep physical sense found regularities, which was impossible to reveal within the framework of classical physics.

§210. Bohr's postulates

The first attempt to build a qualitatively new - quantum - theory of the atom was made in 1913 by the Danish physicist Niels Bohr (1885-1962). He set himself the goal of linking into a single whole the empirical laws of line spectra, Rutherford's nuclear model of the atom, and the quantum nature of the emission and absorption of light. Bohr based his theory on two postulates.

Bohr's first postulate (stationary state postulate): in an atom, there are stationary (not changing with time) states in which it does not radiate energy. Stationary states of an atom correspond to stationary orbits along which electrons move. The motion of electrons in stationary orbits is not accompanied by the emission of electromagnetic waves.

In the stationary state of an atom, an electron moving along a circular orbit must have discrete quantized values ​​of the angular momentum that satisfy the condition

m e vr n = h(n= 1, 2, 3, ...), (210.1)

where m e is the mass of the electron, v- its speed along the n-th orbit of radius r n , h=h/(2). Bohr's second postulate (frequency rule): when an electron moves from one stationary orbit to another, one photon is emitted (absorbed) with energy

h =E n -E m , (210.2)

equal to the energy difference of the corresponding stationary states ( E n and E m - respectively, the energies of the stationary states of the atom before and after radiation (absorption)). At E m < E n a photon is emitted (the transition of an atom from a state with a higher energy to a state with a lower energy, i.e., the transition of an electron from an orbit more distant from the nucleus to a more nearby one), at E m > E n- its absorption (the transition of an atom to a state with a higher energy, i.e., the transition of an electron to an orbit more distant from the nucleus). Set of possible discrete frequencies v = = (E n -E m )/h quantum transitions and determines the line spectrum of the atom.

Its spectral series are the most well studied. They obey Rydberg's formula well:

where R= 109 677 cm −1 is the Rydberg constant for hydrogen, n'- the main level of the series.

Spectral lines that appear during transitions to the main energy level are called resonant, other - subordinate.

Physics of Spectral Series

The hydrogen atom consists of an electron revolving around the nucleus. The electromagnetic force between the electron and the proton of the nucleus causes the presence of a set quantum states electron, each of which has its own energy. These states are depicted in the Bohr model as separate electron orbits. Each orbit or state corresponds to an integer n .

Spectral emission occurs when an electron changes from a higher energy state to a lower one. The lower energy state is denoted n′ and the higher energy state n. The energy of the emitted photon corresponds to the difference between the two states. Since the energy of each state is always the same, the difference between them is also always the same, and the transition will always emit a photon with constant energy.

The spectral lines are grouped in series by n'. The lines are named sequentially from the lowest frequency in Greek letters. For example, the line 2 → 1 is called the Lyman-alpha (Ly-α) line, and 7 → 3 Paschen-delta (Pa-δ).

Hydrogen has lines that do not fall into these series, such as the 21 centimeter line. These lines correspond to rarer processes in the atom, such as hyperfine transitions. Fine structure also entails uniform spectral lines appearing as two or more closely clustered fine lines due to relativistic effects.

Lyman series

open T. Lyman in 1906. All lines of the series are in the ultraviolet range. The series corresponds to the Rydberg formula for n' = 1 and n = 2, 3, 4, … ; the line L α = 1216 Å is the resonance line of hydrogen. The series boundary is 911.8 Å.

Balmer series

Discovered by I. Ya. Balmer in 1885. The first four lines of the series are in the visible range and were known long before Balmer, who proposed an empirical formula for their wavelengths and on its basis predicted the existence of other lines of this series in the ultraviolet region. The series corresponds to the Rydberg formula for n' = 2 and n = 3, 4, 5, … ; line H α = 6565 Å , series boundary - 3647 Å .

Paschen Series

Brackett Series

Discovered by F.S. Bracket in 1922. All lines of the series are in the near infrared range. The series corresponds to the Rydberg formula for n' = 4 and n = 5, 6, 7, … ; line B α = 40 522 Å. The series boundary is 14,588 Å.

Pfund series

Discovered by A. G. Pfund in 1924. The lines of the series are in the near (part of the middle) infrared range. The series corresponds to the Rydberg formula for n' = 5 and n = 6, 7, 8, … ; line Pf α = 74 598 Å . The series boundary is 22,794 Å.

Spectral lines of hydrogen

The first attempt to explain the line spectrum of hydrogen in the visible range was made in 1885 by schoolteacher and mathematician Johann Balmer (1825–1898). Balmer noticed that the frequencies f these lines in the visible part of the spectrum can be described by the formula

f ~(1/2 2)-(1/n 2).

The symbol ~ means proportional, that is, indicates the presence of a constant factor, which is discussed below. In this equation n - an integer greater than 2, i.e. 3, 4, 5, etc.

These lines in the visible part of the spectrum are called the Balmer series. Later, lines were discovered in the ultraviolet and infrared parts of the spectrum. They were named the Lyman and Paschen series, respectively, after their discoverers - American physicist and the spectroscopist Theodor Lyman (1874–1954) and the German physicist Louis Carl Heinrich Friedrich Paschen (1865–1947). In 1888, the Swedish physicist and spectroscopist Johannes Rydberg (1854–1919) published a formula that described all the spectral lines visible in the emission of a hydrogen arc lamp and in the absorption spectra of solar and stellar light. The Rydberg formula for the frequency of spectral lines of hydrogen has the form

f =R H [(1/ n 1 2)-(1/n 2 2)],

where n 1 are integers starting from 1, and n 2 - other integers that must be greater n one . Meaning n 1 =1 gives the Lyman series, n 1 \u003d 2 - Balmer, n 1 \u003d 3 - Pashen's series.

Constant R H is called the Rydberg constant for the hydrogen atom. Its value is R H=109677.6 cm-1 and expressed by the number of waves ( cm-one). When using this value in the Rydberg formula, the frequencies of spectral lines, determined by integers n 1 and n 2 are expressed by wave numbers. To translate the result into hertz, you need to multiply the resulting value by the speed of light, that is, by 3 10 10 cm/sec. To find the wavelength of a spectral line, one must take the reciprocal of the frequency expressed in the number of waves, that is, divide one by the frequency expressed in the number of waves. For example, if n 1 =2, and n 2 =3, then

f =R H[(1/2 2)-(1/3 2)] = R H[(1/4)-(1/9)] = 1.52 10 4 cm -1

is the frequency expressed as the number of waves. The reciprocal of this number is 6.56 10 -5 cm = 656 10 -9 m = = 656 nm. So the wavelength is 656 nm is the red line in the Balmer series shown in Fig. 9.2.

When discussing Fig. 8.7 we have already discussed the discreteness of optical transitions between quantum energy levels for a particle in a box. On fig. 8.7 shows the transitions between the states of a particle in a box, in which n =1 turns into n =2 and n =1 turns into n =3. In this regard, it should not come as a big surprise that optical transitions in the hydrogen atom can correspond to a discrete set of frequencies that depend on integers. However, in 1888, when the Rydberg formula was obtained, there were still 12 years left before the idea of ​​quantizing the energy levels, which are connected by means of integers according to the Rydberg formula, can be understood as optical transitions between discrete energy levels associated with the hydrogen atom.

Rice. 9.3. Diagrams of some energy levels generating the Lyman and Balmer series of hydrogen emission lines. Downward arrows show how light is emitted by hydrogen, such as in an arc lamp. Upon absorption, which gives dark lines in Fig. 9.2, the arrows would point upwards. The intervals between levels are shown conventionally, not to scale.

Some of the energy levels that give rise to the Lyman and Balmer series are shown in Fig. 9.3. Here, the arrows pointing down correspond to the emission lines that are observed in a hydrogen arc lamp. The hydrogen atom, which is initially at a higher energy level, eventually moves to a lower level. Energy is conserved through the emission of a photon. To conserve energy, a photon must carry an energy equal to the difference between the original, higher energy level and a lower energy final level. Smallest possible value n 1 in the Rydberg formula is equal to 1, and n 2 should be more n one . The arrow labeled 2–1 corresponds to the emission from the level n =2 per level n =1.

The next largest radiation energy in the Lyman series is obtained by going from the level n =3 per level n =1. In the Rydberg formula, the next possible value for n 1 equals 2 and n 2 should be more n one . Therefore, the lowest energy of the emission line in the Balmer series is marked as 3–2. When a hydrogen atom is at the level n =3, goes to the level n =2, energy conservation is ensured by the emission of a photon with a wavelength of 656 nm. When light falls on hydrogen atoms, absorption occurs, which could be depicted in the same diagram by arrows pointing upwards.