Svojstva fizička tijela a objekti su opisani fizičke veličine . Jedna od ovih količina za električno polje je tenzija. U skladu s prethodno formuliranom definicijom, opisuje djelovanje sile polja na nabijena tijela u određenoj tački električnog polja. Ako je polje nehomogeno, onda je intenzitet in različite tačke polja su različita. A da bi se opisali svojstva polja u mnogim tačkama, potrebno je dostaviti veliki broj vrijednosti intenziteta. Ovo otežava proučavanje polja i sprečava stvaranje u ljudskoj mašti ideje polja u svakom konkretnom slučaju.

Jačina električnog polja je njegova moćna karakteristika.

Pomaže da se bolje predstavi struktura električnog polja grafička metoda. U srcu metode grafičkog predstavljanja strukture električnog polja leže stvarni fenomeni koji se mogu posmatrati u eksperimentima.

Neka se mala čestica tvari, koja također ima pozitivan naboj, unese u električno polje pozitivno nabijene lopte. Ako je ova čestica slobodna i djelovanje gravitacijskog polja je neznatno, onda će se pod utjecajem električne sile udaljiti od lopte. Slično će se uočiti u bilo kojoj tački u polju nabijene lopte (slika 4.20).

Nakon što je prikazao putanje kretanja mnogih pozitivno nabijenih čestica u električnom polju i pokazao im smjer operativna snaga, dobijamo sliku koja se zove spektra ovom polju.

Linije koje formiraju spektar električnog polja nazivaju se linije napetosti električno polje, ili dalekovodi.

koncept linija polja prvi je u nauku uveo M. Faraday na osnovu znanja stečenog tokom eksperimentalnih istraživanja.

Eksperimenti poznati M. Faradayu mogu se izvesti u savremenim uslovima.

Uzmimo metalni provodnik na koji su pričvršćene papirne trake i spojimo ga na provodnik elektrofora. Ako ga stavimo u akciju, tada će se sve trake papira razilaziti u različitim smjerovima zbog međusobnog odbijanja (slika 4.21). Rezultati ovog eksperimenta (i drugih sličnih) omogućavaju konstruisanje spektra električnog polja jednog naelektrisanog tijela. To je prikazano na sl. 4.22. Strelice na linijama sile pokazuju smjer sile koja će djelovati na pozitivno nabijeno tijelo koje se nalazi u datoj tački polja.

Dakle, linije sile "napuštaju" pozitivno naelektrisano telo i "ulaze" u negativno naelektrisano telo (slika 4.22). Treba imati na umu da oni "izlaze" i "ulaze" okomito na površinu tijela.

Linije jačine električnog polja su okomite na površinu naelektrisanog tijela na mjestima gdje počinju.materijal sa sajta

Uzmimo dva metalna provodnika sa papirnim trakama i spojimo ih na provodnike elektrofor mašine. Uključujemo elektrofor mašinu i videćemo da će papirne trake početi da se privlače (slika 4.23). Shodno tome, polje dvaju suprotno naelektrisanih tela imaće spektar prikazan na sl. 4.24.

Krivolinijski oblik linija napetosti objašnjava se činjenicom da na pozitivno nabijenu česticu djeluju dvije sile sa strane svakog tijela. Rezultanta ovih sila u svakoj tački polja je tangenta na linije napetosti.

Prave tangente na koje u bilo kojoj tački pokazuju smjer sile koja djeluje na pozitivno nabijeno tačkasto tijelo nazivaju se dalekovodi.

Smjerovi sila koje će djelovati u različitim tačkama polja dvaju nabijenih tijela prikazani su na sl. 4.25.

Budući da su linije napetosti uvijek okomite na površinu, spektri polja tijela različitog oblika bit će različiti (slika 4.26).

Na ovoj stranici materijal o temama:

• Spectra el. polja različitih naelektrisanih tela

• Grafička slika apstraktnog električnog polja

• Slike linija električnog polja u eksperimentima

• a b

  

  Poznavajući vektor intenziteta elektrostatičkog polja u svakoj njegovoj tački, ovo polje se može vizualizirati uz pomoć linija intenziteta sile (linije vektora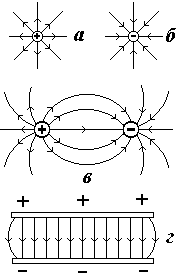 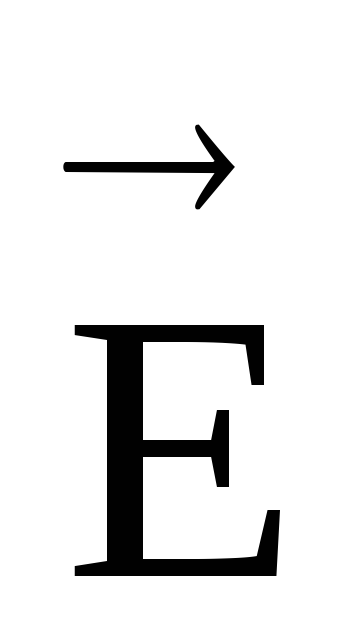). linije sile napetosti se povlače tako da se tangenta na njih u svakoj tački poklapa sa smjerom vektora napetosti (Sl. 1.4, a).

  Broj linija koje prodiru u jedno područje dS, okomito na njih, crta se proporcionalno modulu vektora (Sl. 1.4, b).

  Linijama sile je dodijeljen smjer koji se poklapa sa smjerom vektora . Rezultirajući obrazac raspodjele linija napetosti omogućava suđenje konfiguracije datog električnog polja u njegovim različitim tačkama. Linije polja počinju u pozitivnih naboja i završavaju negativnim nabojima. Na sl. 1.5 prikazuje linije napetosti tačkastih naboja (sl. 1.5, a, b); sistema dva suprotna naelektrisanja (slika 1.5, in) - primjer nehomogenog elektrostatičkog polja i dvije paralelne suprotno nabijene ravni (slika 1.5, G) je primjer jednolikog električnog polja.

  1.5. Raspodjela naplate

  U nekim slučajevima, da bi se pojednostavili matematički proračuni, zgodno je zamijeniti pravu distribuciju diskretnih tačkastih naboja fiktivnom kontinuiranom distribucijom. U prelasku na kontinuiranu distribuciju naelektrisanja koristi se koncept gustine naelektrisanja - linearni , površinski  i volumetrijski , tj.

  
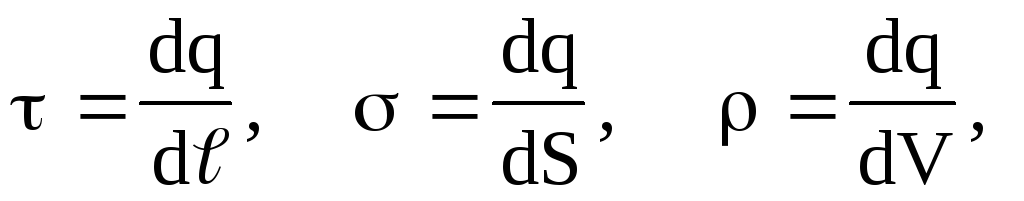  (1.12)

  gdje je dq naboj raspoređen prema elementu dužine
  
  , element površine dS i element volumena dV.

  Uzimajući u obzir ove distribucije, formula (1.11) se može napisati u drugačijem obliku. Na primjer, ako je naboj raspoređen po volumenu, tada umjesto q i trebate koristiti dq = dV i zamijeniti simbol zbira integralom, a zatim

  
  . (1.13)

  1.6. električni dipol

  Da bi se objasnili fenomeni povezani s nabojima u fizici, koristi se koncept električni dipol.

  Sistem od dva jednaka po veličini suprotna tačkasta naboja, među kojima je udaljenost mnogo manja od udaljenosti do proučavanih tačaka u prostoru, naziva se električni dipol. Prema definiciji dipola, +q=q= q.

  

  Prava linija koja povezuje suprotne naboje (polove) naziva se osa dipola; tačka 0 - centar dipola (slika 1.6). Karakteriziran je električni dipol dipol arm: vektor , usmjeren od negativnog na pozitivan naboj. Glavna karakteristika dipola je električni dipolni moment = q . (1.14)

  Po apsolutnoj vrijednosti

  p = q 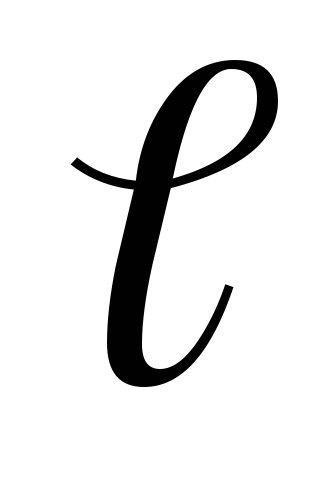. (1.15)

  U SI, električni dipolni moment se mjeri u kulonima puta po metru (C m).

  Izračunajmo potencijal i jačinu električnog polja dipola, smatrajući ga tačkom, ako 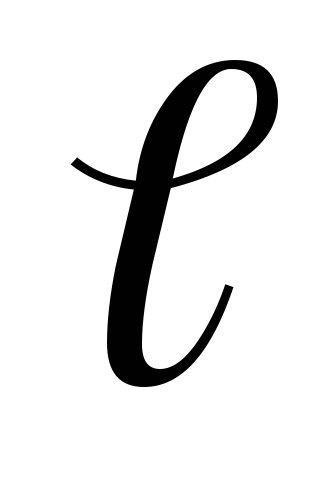 r.

  Potencijal električnog polja stvorenog sistemom tačkastih naboja u proizvoljnoj tački koju karakteriše radijus vektor 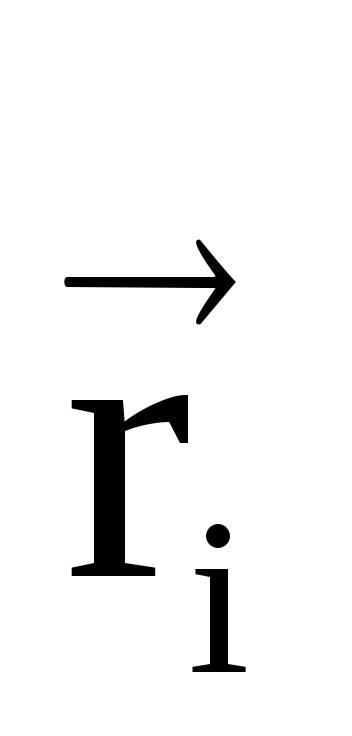, pišemo u obliku: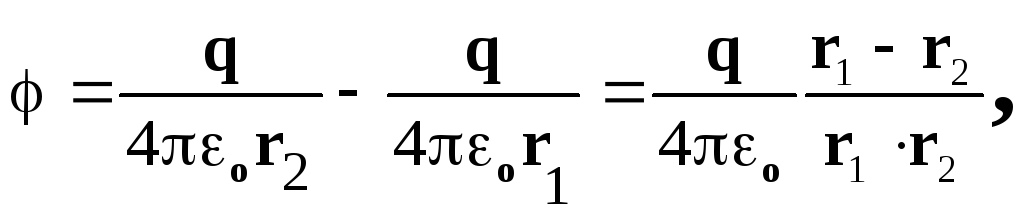

  
  

  gdje je r 1 r 2  r 2 , r 1  r 2  r =
  
  , jer 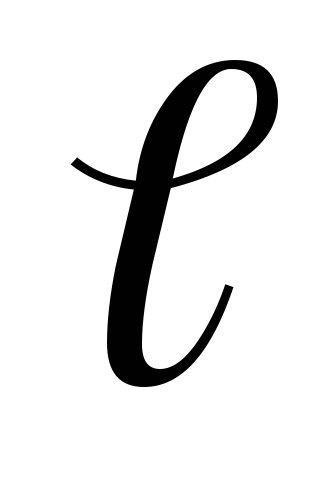r;   ugao između radijus vektora i (Sl. 1.6) . Imajući ovo na umu, dobijamo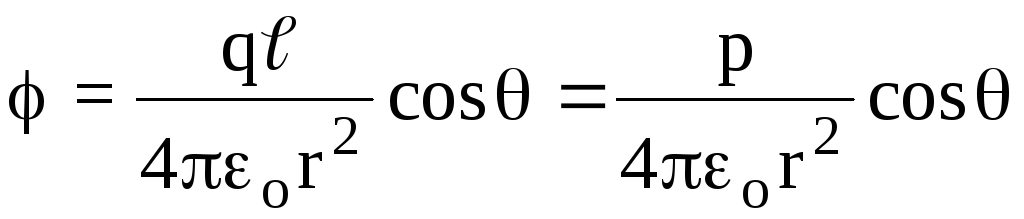

  
  . (1.16)

  Koristeći formulu koja povezuje gradijent potencijala sa intenzitetom, nalazimo intenzitet koji stvara električno polje dipola. Hajde da dekomponujemo vektor električni dipolno polje na dvije međusobno okomite komponente, tj.
  
  (Sl. 1. 6).

  Prvi od njih je određen kretanjem tačke koju karakteriše radijus vektor (za fiksnu vrijednost ugla ), tj. vrijednost E  nalazimo diferencijacijom (1.81) u odnosu na r, tj.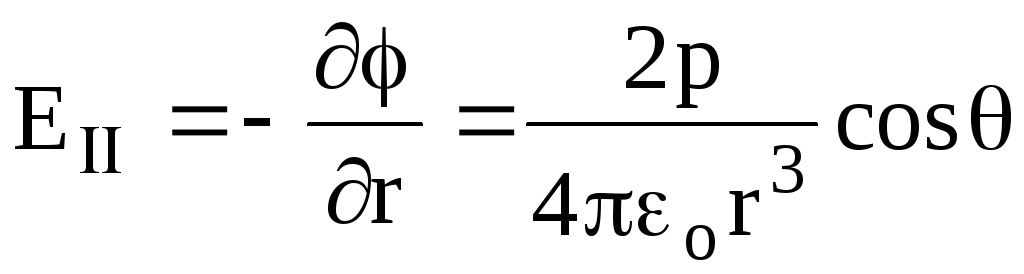

  
  . (1.17)

  Druga komponenta je određena kretanjem tačke povezanom sa promjenom ugla  (za fiksni r), tj. E  nalazimo diferenciranjem (1.16) u odnosu na :
  
  , (1.18)

  gdje
  
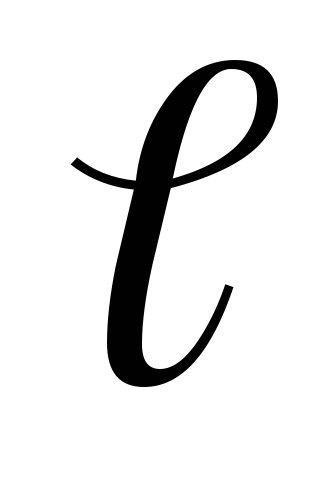  ,d = rd.

  Rezultirajuća napetost E 2 \u003d E  2 + E  2 ili nakon zamjene
  
  . (1.19)

  Komentar: Na  = 90 o
  
  , (1.20)

  tj., intenzitet u tački na pravoj liniji koja prolazi kroz centar dipola (tj. O) i okomita na osu dipola.

  Kada je  = 0 oko
  
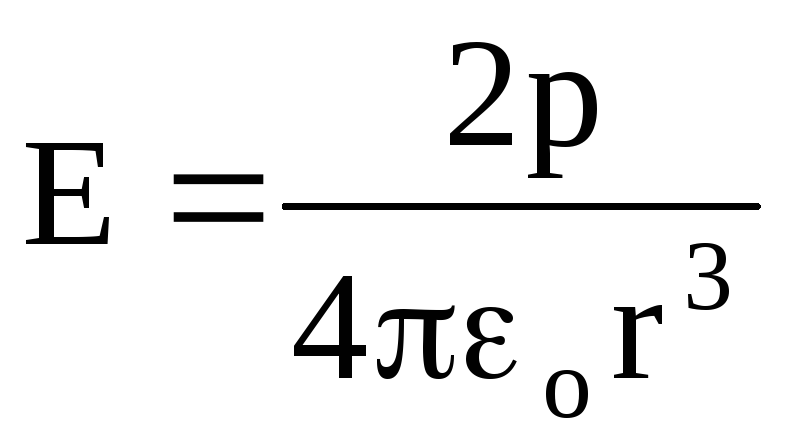  , (1.21)

  tj. u tački na nastavku prave linije koja se poklapa sa osom dipola.

  Analiza formula (1.19), (1.20), (1.21) pokazuje da se jačina električnog polja dipola smanjuje sa rastojanjem obrnuto proporcionalnim r 3 , odnosno brže nego za tačkasto naelektrisanje (obrnuto proporcionalno r 2).

  Radi veće jasnoće, električno polje se često prikazuje pomoću linija sile i ekvipotencijalnih površina.

  linije sile – to su neprekidne linije, tangente na koje se u svakoj tački kroz koju prolaze poklapaju sa vektorom jakosti električnog polja (slika 1.5). Gustoća linija polja (broj linija polja koje prolaze kroz jedinicu površine) proporcionalna je jačini električnog polja.

  Ekvipotencijalne površine (ekvipotencijale) – površine jednakog potencijala. To su površine (linije) pri kretanju duž kojih se potencijal ne mijenja. Inače, razlika potencijala između bilo koje dvije točke ekvipotencijalne površine jednaka je nuli. Linije sile su okomite na ekvipotencijalne površine i usmjerene u smjeru najoštrijeg pada potencijala. Ova činjenica proizilazi iz jednačine (1.10) i dokazana je u toku matematičke analize, odjeljak "Skalarna i vektorska polja".

  Razmotrimo, kao primjer, električno polje generirano na udaljenosti 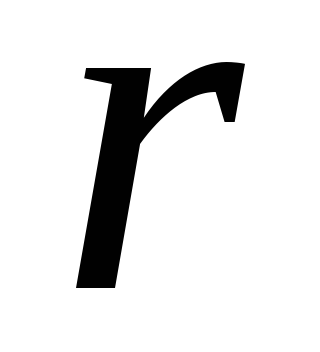od punjenja. Prema (1.11,b), vektor intenziteta se poklapa sa smjerom vektora ako je naelektrisanje pozitivno i suprotno ako je naelektrisanje negativno. Posljedično, linije sile odstupaju radijalno od naboja (sl. 1.6, a, b). Gustoća linija polja, kao i intenzitet, obrnuto je proporcionalna kvadratu udaljenosti (
  
  ) za punjenje. Ekvipotencijalne površine električnog polja tačkastog naelektrisanja su sfere sa središtem na mestu naelektrisanja.

  

  

  Na sl. 1.7 prikazuje električno polje sistema dva tačkasta naboja jednaka po apsolutnoj vrijednosti, ali suprotnog predznaka. Ovaj primjer ostavljamo čitateljima da sami analiziraju. Napominjemo samo da linije sile uvijek počinju na pozitivnim nabojima i završavaju na negativnim. U slučaju električnog polja sa jednim tačkastim naelektrisanjem (slika 1.6, a, b), pretpostavlja se da se linije sile prekidaju na veoma udaljenim naelektrisanjama suprotnog predznaka. Vjeruje se da je svemir u cjelini neutralan. Dakle, ako postoji naboj jednog znaka, onda će negdje sigurno postojati naboj drugog znaka koji mu je jednak u apsolutnoj vrijednosti.

  1.6. Gaussova teorema za električno polje u vakuumu

  Glavni zadatak elektrostatike je problem pronalaženja jačine i potencijala električnog polja u svakoj tački prostora. U odjeljku 1.4 riješili smo problem polja tačkastog naelektrisanja, a takođe smo razmotrili polje sistema tačkastih naelektrisanja. U ovom dijelu ćemo se fokusirati na teoremu koja nam omogućava da izračunamo električno polje složenijih naelektrisanih objekata. Na primjer, nabijena duga nit (prava linija), nabijena ravan, nabijena sfera i drugi. Nakon što se izračuna jačina električnog polja u svakoj tački u prostoru, koristeći jednačine (1.12) i (1.13), može se izračunati potencijal u svakoj tački ili razlika potencijala između bilo koje dvije tačke, tj. rješavaju osnovni problem elektrostatike.

  Za matematički opis uvodimo pojam toka vektora intenziteta ili toka električnog polja. Vektor fluksa (F). električno polje preko ravne kvadratne površine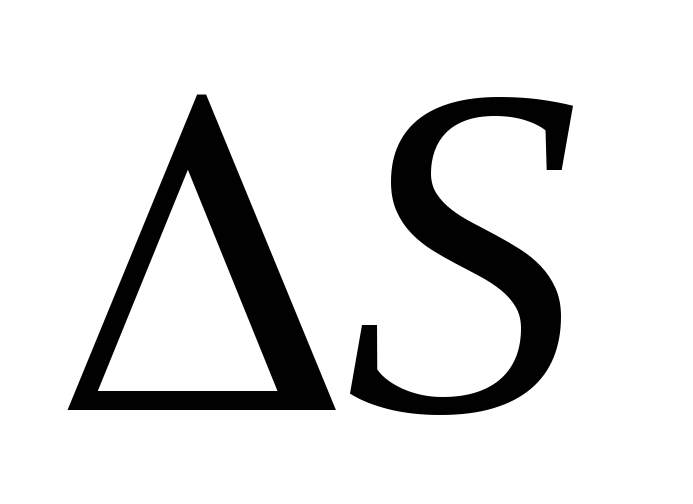
  
  količina se zove:

  
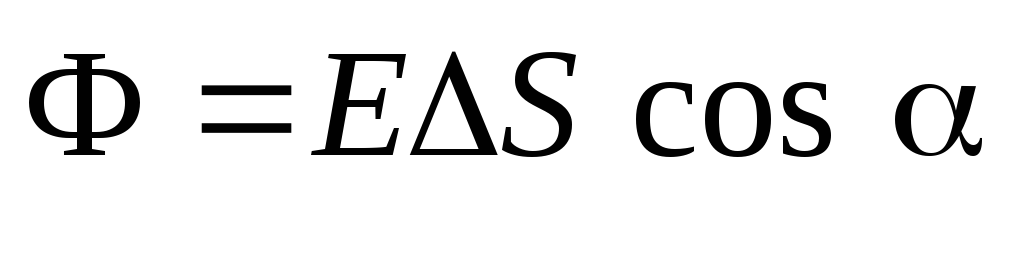  , (1.16)

  

  gdje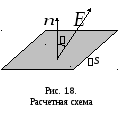 je jačina električnog polja, za koju se pretpostavlja da je konstantna unutar lokacije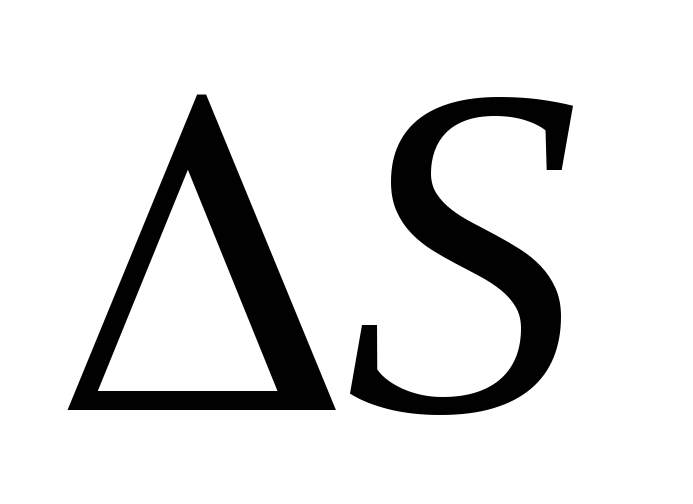
  
  ;
  
  je ugao između smjera vektora i jedinični normalni vektor 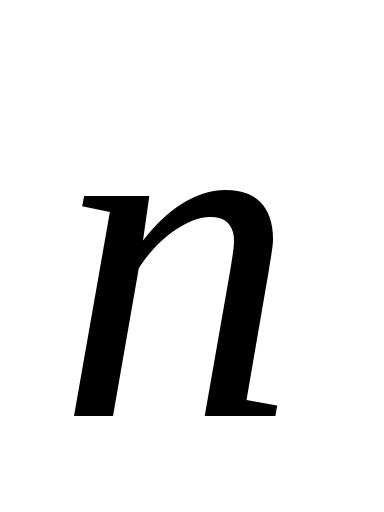na stranicu
  
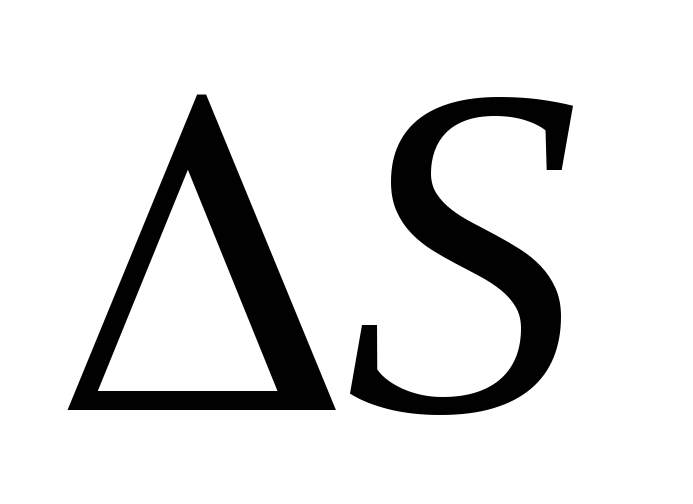  (Sl. 1.8). Formula (1.16) se može napisati koristeći koncept skalarnog proizvoda vektora:

  
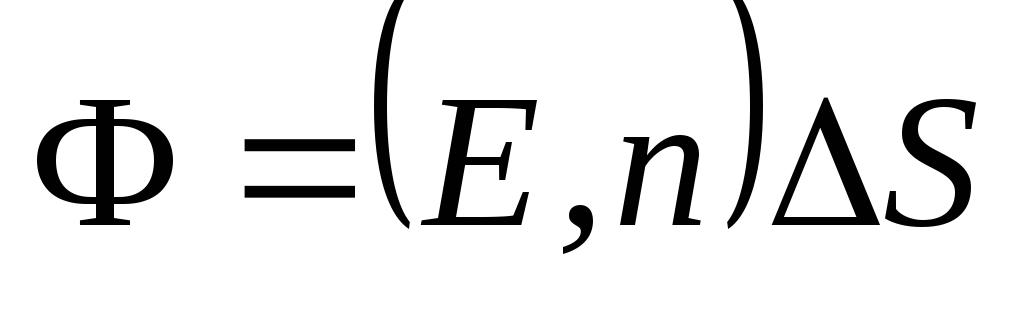  . (1.15,a)

  U slučaju površine nije ravan, da bi se izračunao protok mora se podijeliti na male dijelove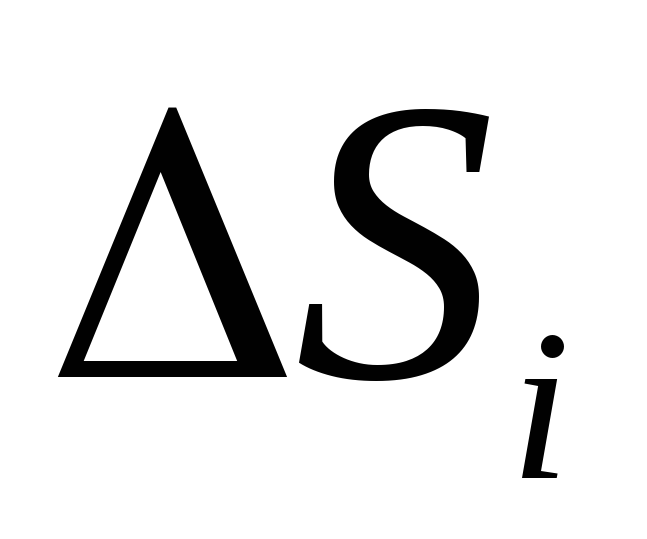
  
  , koji se približno može smatrati ravnim, a zatim zapišite izraz (1.16) ili (1.16, a) za svaki komad površine i dodajte ih. U granici kada je površina S i vrlo male (
  
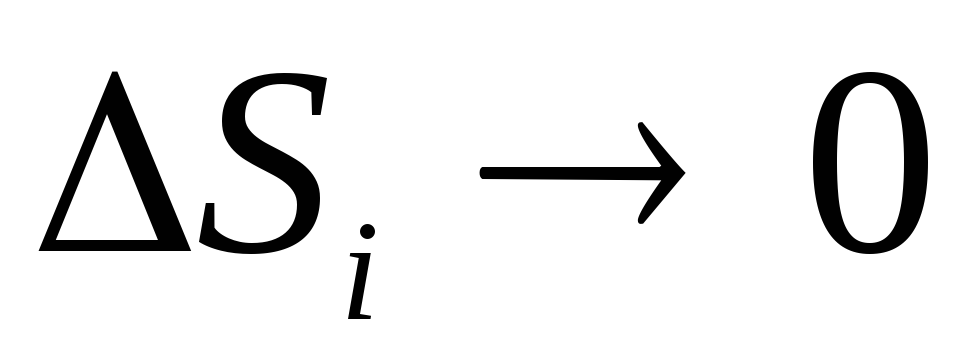  ), takav zbir naziva se površinski integral i označava
  
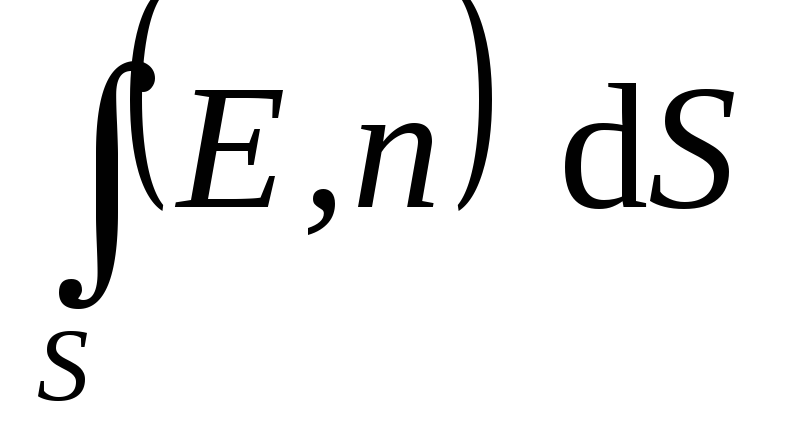  . Dakle, tok vektora jakosti električnog polja kroz proizvoljnu površinu je definisan izrazom:

  
  . (1.17)

  Kao primjer, razmotrite sferu polumjera 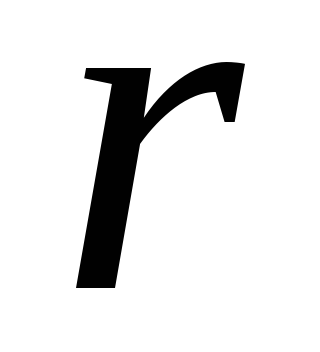, centriran na pozitivnom naboju , i odrediti tok električnog polja kroz površinu ove sfere. Linije sile (vidi, na primjer, sliku 1.6, a) koje izlaze iz naboja su okomite na površinu sfere, a u svakoj tački sfere modul jačine polja je isti

  
  .

  Područje sfere
  
  ,

  onda
  
  
  
  
  
  .

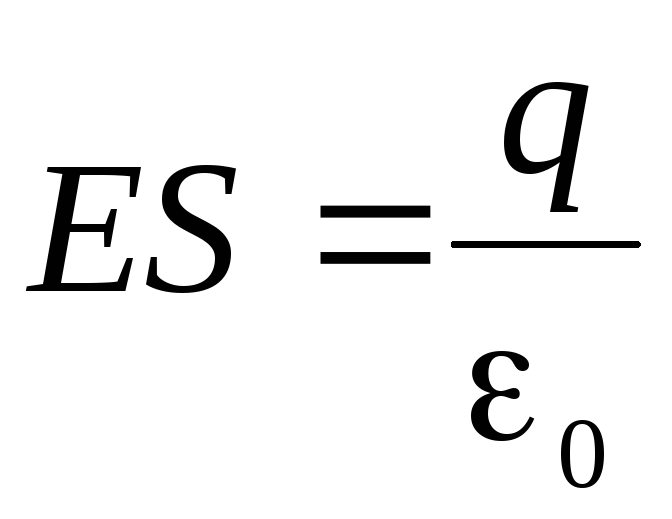  Vrijednost
  
  i predstavlja tok električnog polja kroz površinu sfere. Dakle, dobijamo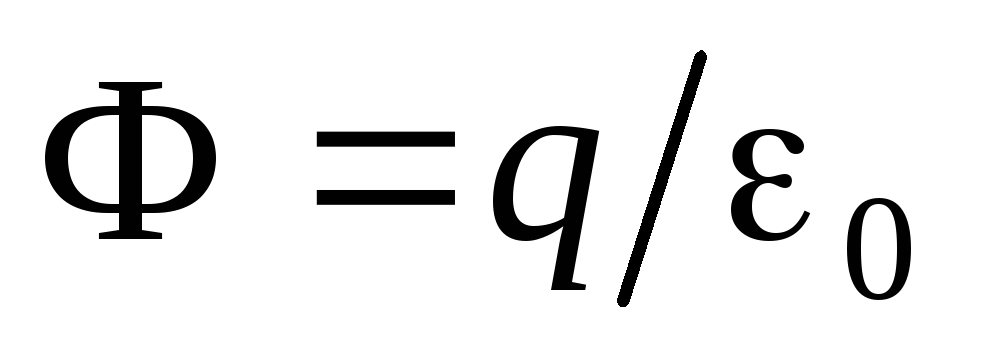
  
  . Vidi se da tok kroz površinu sfere električnog polja ne zavisi od poluprečnika sfere, već zavisi samo od samog naboja . Stoga, ako nacrtate niz koncentričnih sfera, tada će tok električnog polja kroz sve te sfere biti isti. Očigledno je da će i broj linija sile koje prelaze ove sfere biti isti. Dogovorili smo se da uzmemo broj linija sile koje izlaze iz naboja jednak protoku električnog polja:
  
  .

  Ako se sfera zamijeni bilo kojom drugom zatvorenom površinom, tada se tok električnog polja i broj linija sile koje ga prelaze neće promijeniti. Osim toga, protok električnog polja kroz zatvorenu površinu, a time i broj linija sile koje prodiru kroz ovu površinu, jednak je
  
  ne samo za polje tačkastog naelektrisanja, već i za polje stvoreno bilo kojim skupom tačkastih naelektrisanja, posebno naelektrisanog tela. Zatim vrijednost treba posmatrati kao algebarski zbir čitavog skupa naboja koji se nalaze unutar zatvorene površine. Ovo je suština Gaussove teoreme, koja je formulisana na sledeći način:

  Protok vektora jakosti električnog polja kroz proizvoljanzatvoreno površina jednaka
  
  , gdje
  
   algebarski iznos priloženih naknadaunutra ovu površinu.

  Matematički, teorema se može napisati kao

  
  . (1.18)

  Imajte na umu da ako na nekoj površini S vektor konstantan i paralelan vektoru 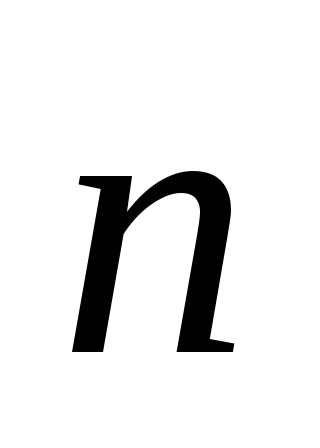, zatim strujanje kroz takvu površinu. Transformirajući prvi integral, prvo smo iskoristili činjenicu da su vektori i 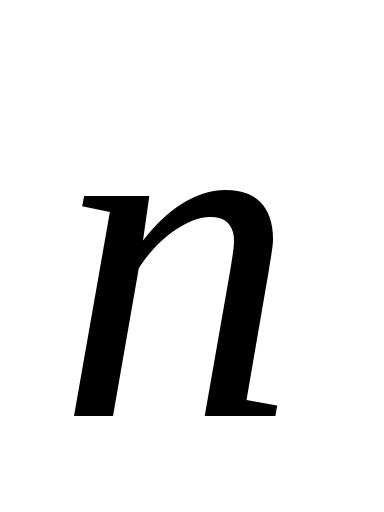paralelno, što znači
  
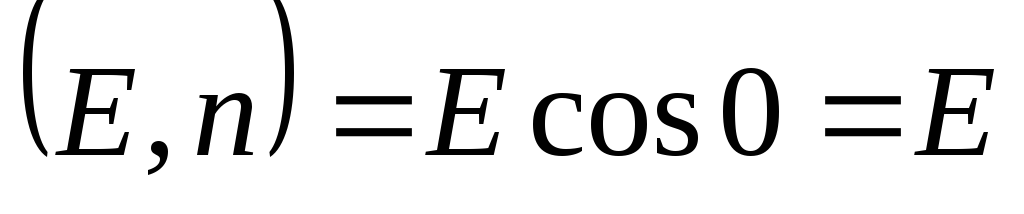  . Zatim je izvadio vrijednost za predznak integrala zbog činjenice da je konstantan u bilo kojoj tački sfere . Primjenjujući Gaussovu teoremu za rješavanje specifičnih problema, pokušavaju odabrati površinu za koju su zadovoljeni gore opisani uvjeti kao proizvoljnu zatvorenu površinu.

  Dajemo nekoliko primjera primjene Gaussove teoreme.

  Primjer 1.2. Izračunajte jačinu električnog polja jednolično nabijene beskonačne niti. Odredite razliku potencijala između dvije tačke u takvom polju.

  Rješenje. Pretpostavimo radi određenosti da je nit pozitivno nabijena. Zbog simetrije problema, može se tvrditi da će linije sile biti prave linije koje se radijalno odvajaju od ose niti (slika 1.9), čija gustina opada sa rastojanjem od niti prema nekom zakonu. Prema istom zakonu smanjit će se i veličina električnog polja 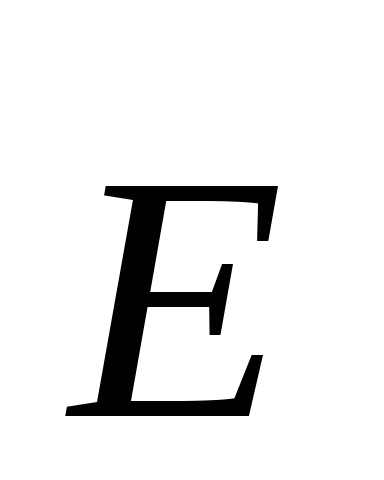. Ekvipotencijalne površine će biti cilindrične površine sa osom koja se poklapa sa navojem.

  Neka je naboj po jedinici dužine konca . Ova vrijednost se naziva linearna gustina naboja i mjeri se u SI jedinicama [C/m]. Za izračunavanje jačine polja primjenjujemo Gaussovu teoremu. Za to, kao proizvoljna zatvorena površina izaberite cilindar radijusa 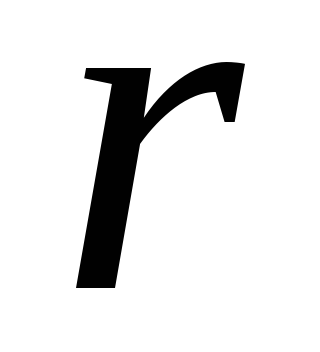i dužina , čija se os poklapa sa navojem (slika 1.9). Izračunajmo tok električnog polja kroz površinu cilindra. Ukupni protok je zbir protoka bočna površina cilindar i protok kroz baze

  Kako god,
  
  , budući da u bilo kojoj tački na bazi cilindra
  
  . To znači da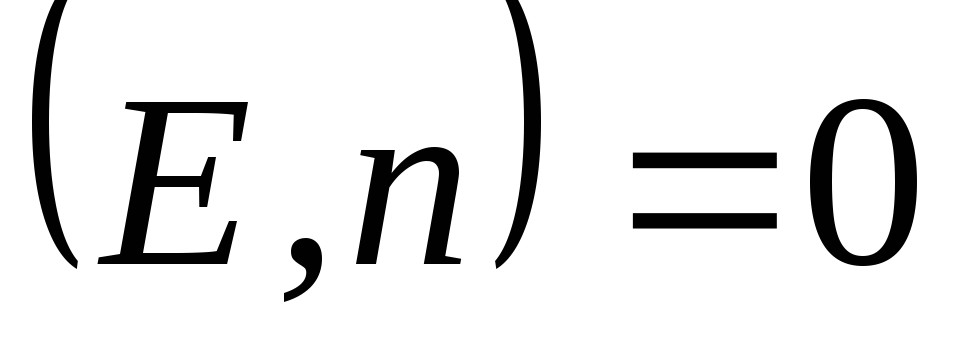
  
  na ovim tačkama. Protok kroz bočnu površinu
  
  . Prema Gaussovoj teoremi, ovaj ukupni protok je jednak
  
  . Dakle, dobili smo

  
  .

  Zbir naboja unutar cilindra izražen je u terminima linearne gustine naboja :
  
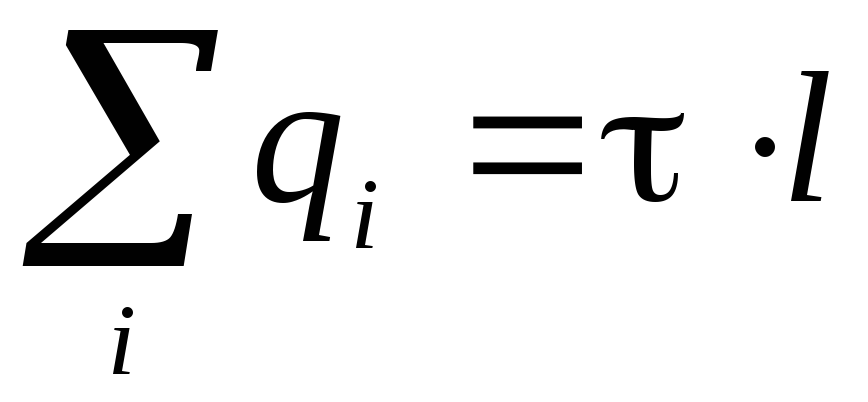  . S obzirom na to
  
  , dobijamo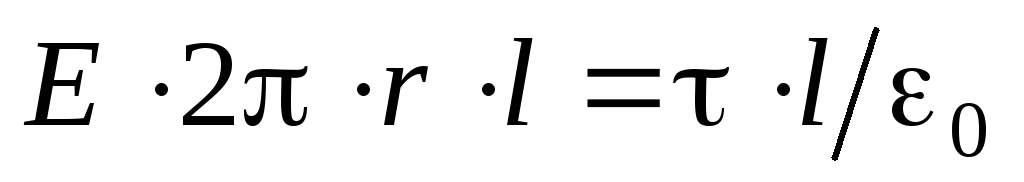

  
  ,

  
  , (1.19)

  one. intenzitet i gustina linija električnog polja jednolično nabijenog beskonačnog filamenta opada obrnuto s rastojanjem (
  
  ).

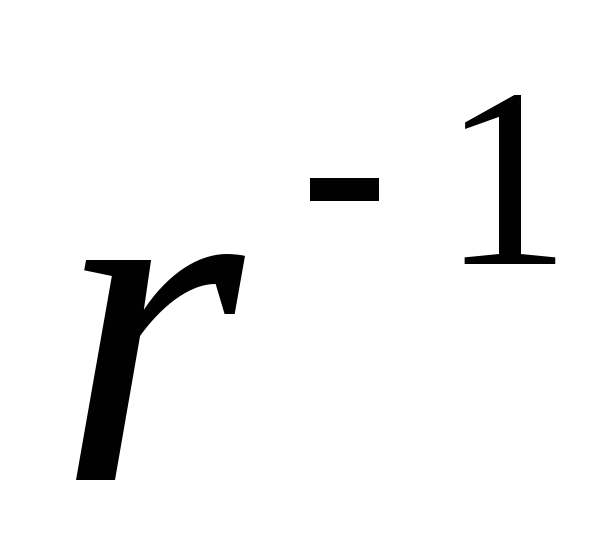  Pronađite razliku potencijala između tačaka koje se nalaze na udaljenostima 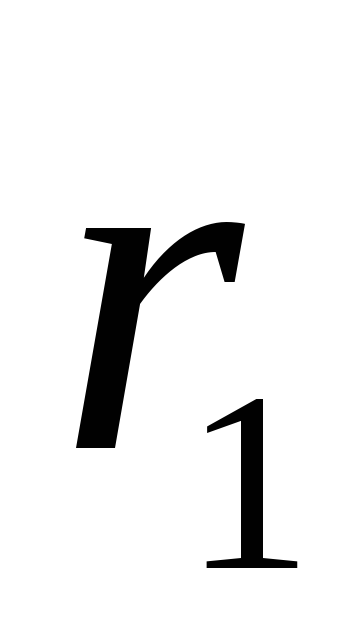i 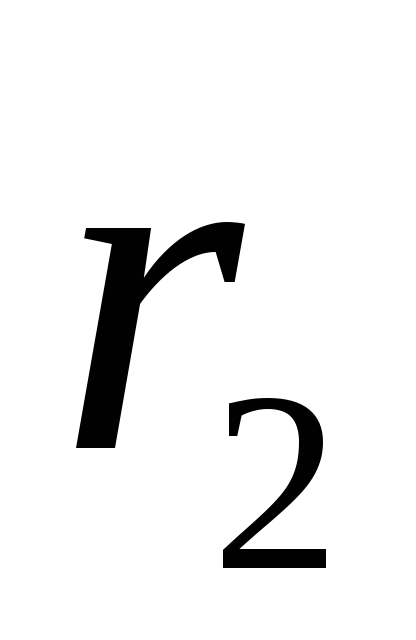od navoja (koji pripadaju ekvipotencijalnim cilindričnim površinama poluprečnika 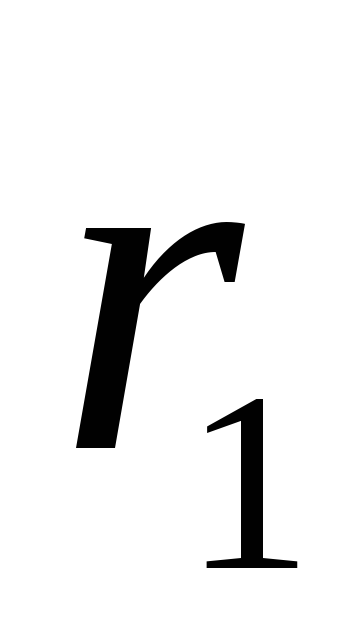i 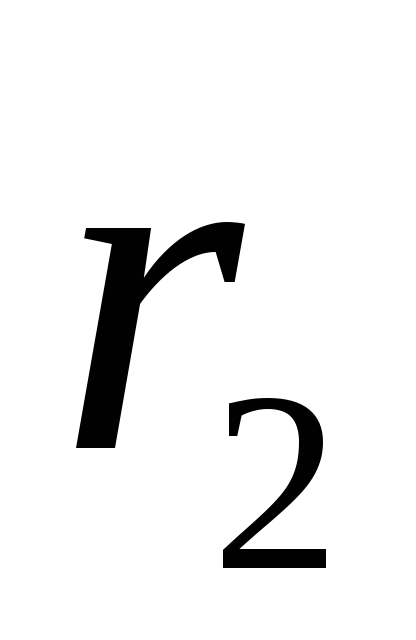). Da bismo to učinili, koristimo vezu između jakosti električnog polja i potencijala u obliku (1.9, c):
  
  . Uzimajući u obzir izraz (1.19), dobijamo diferencijalnu jednačinu sa odvojivim varijablama:

  
  
  
  
  
  
  
  

  
  
  
  
  
  .

  

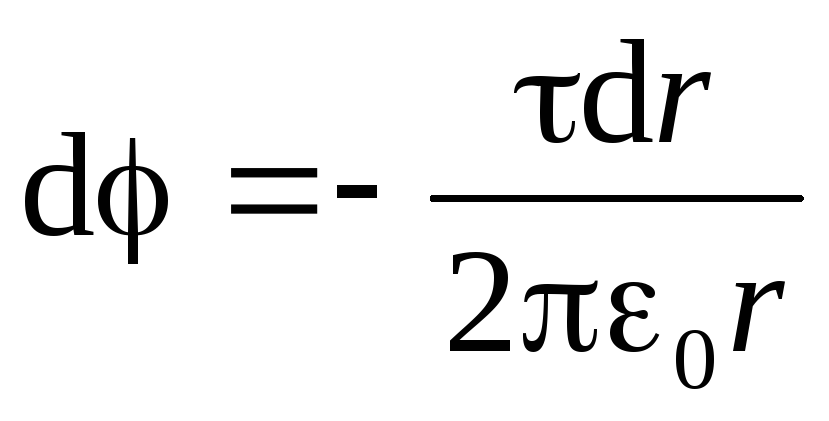
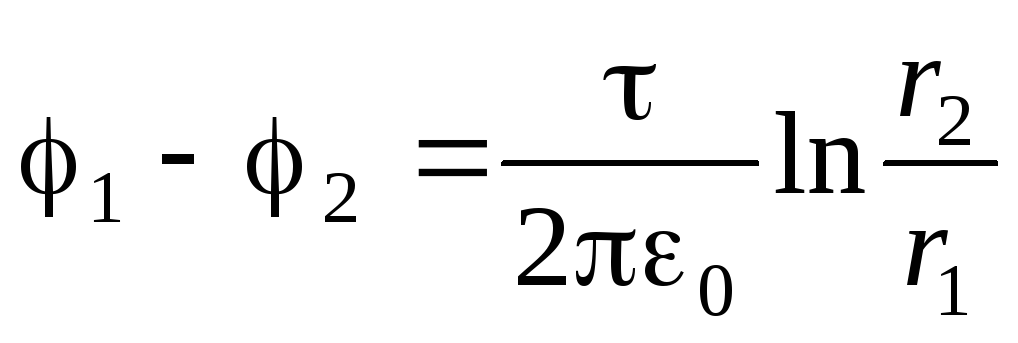  Primjer 1.3. Izračunajte jačinu električnog polja jednoliko nabijene ravni. Odredite razliku potencijala između dvije tačke u takvom polju.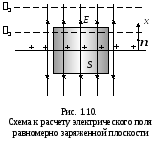

  Rješenje. Električno polje jednoliko nabijene ravni prikazano je na sl. 1.10. Zbog simetrije, linije sile moraju biti okomite na ravan. Stoga odmah možemo zaključiti da se gustina linije, a samim tim i jačina električnog polja neće mijenjati s rastojanjem od ravnine. Ekvipotencijalne površine su ravni paralelne datoj naelektrisanoj ravni. Neka naboj po jedinici površine aviona bude . Ova vrijednost se naziva površinska gustina naboja i mjeri se u SI u jedinicama [C/m 2 ].

  Primijenimo Gaussovu teoremu. Za to, kao proizvoljna zatvorena površina odaberite cilindar dužine 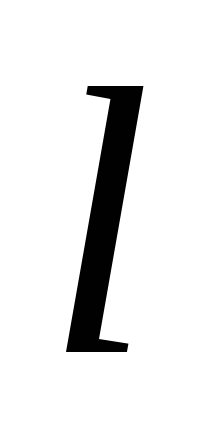, čija je osa okomita na ravan, a baze su jednako udaljene od nje (slika 1.10). Ukupni tok električnog polja
  
  . Protok kroz bočnu površinu je nula. Protok kroz svaku od baza je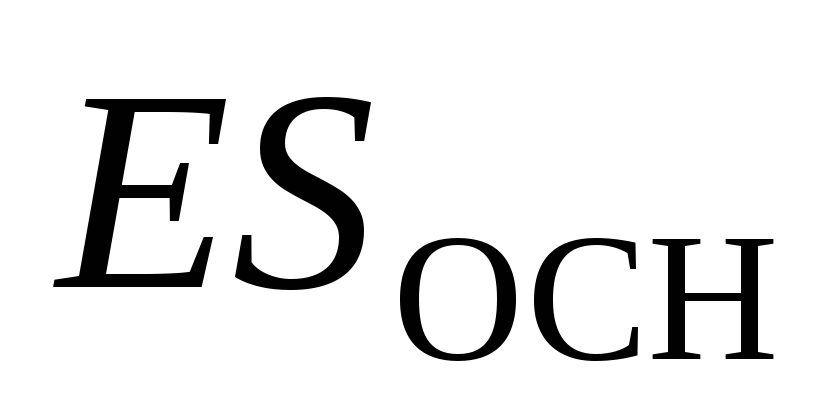
  
  , zbog toga
  
  . Prema Gaussovoj teoremi, dobijamo: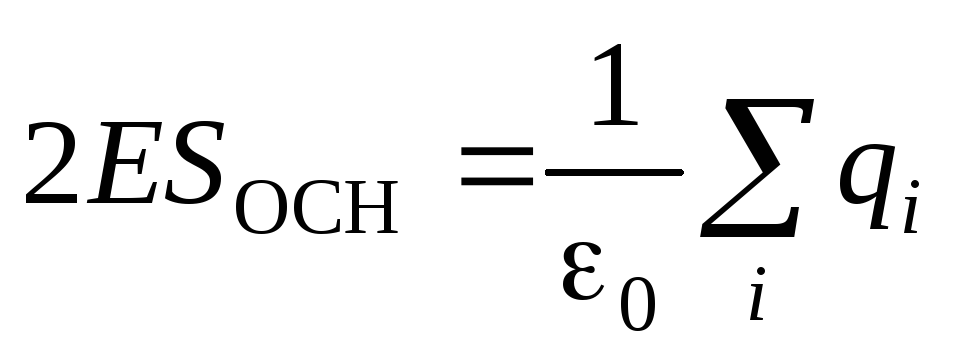

  
  .

  Zbir naelektrisanja unutar cilindra , nalazimo preko površinske gustine naboja :
  
  . Onda odakle:

  
  . (1.20)

  Iz dobijene formule se vidi da jačina polja jednolično nabijene ravni ne zavisi od udaljenosti do nabijene ravni, tj. u bilo kojoj tački prostora (u jednoj poluravni) je isti i po apsolutnoj vrijednosti i po smjeru. Takvo polje se zove homogena. linije sile uniformno polje paralelno, njihova gustina se ne mijenja.

  Nađimo razliku potencijala između dvije tačke homogenog polja (koje pripadaju ekvipotencijalnim ravnima i koja leži u jednoj poluravni u odnosu na nabijenu ravan (slika 1.10)). Usmjerimo osu 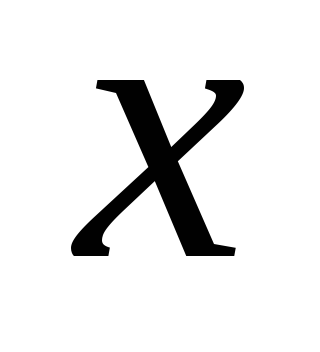vertikalno prema gore, tada je projekcija vektora napetosti na ovu os jednaka modulu vektora napetosti
  
  . Koristimo jednačinu (1.9):

  
  
  
  
  
  
  
  
  
  
  
  
  
  .

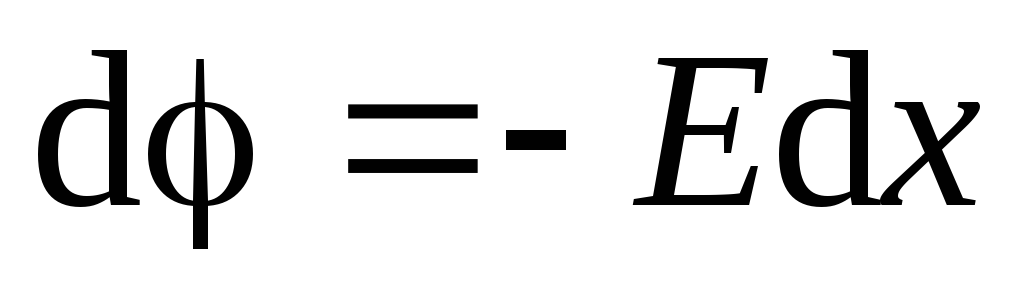
  Konstantna vrijednost (polje je homogeno) može se izvaditi ispod znaka integrala: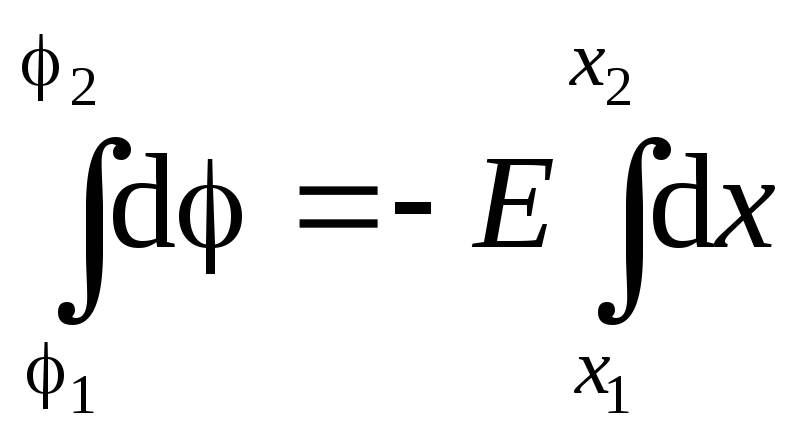
  
  . Integracijom dobijamo: . Dakle, potencijal homogenog polja linearno zavisi od koordinate.

  Razlika potencijala između dvije tačke električnog polja je napon između ovih tačaka ( ). Označimo udaljenost između ekvipotencijalnih ravni
  
  . Tada to možemo napisati u jednoličnom električnom polju:

  
  . (1.21)

  Još jednom naglašavamo da pri korištenju formule (1.21) moramo imati na umu da je veličina - ne rastojanje između tačaka 1 i 2, već rastojanje između ekvipotencijalnih ravni kojima ove tačke pripadaju.

  Primjer 1.4. Izračunajte jačinu električnog polja dvije paralelne ravni jednoliko nabijene površinskom gustoćom naboja
  
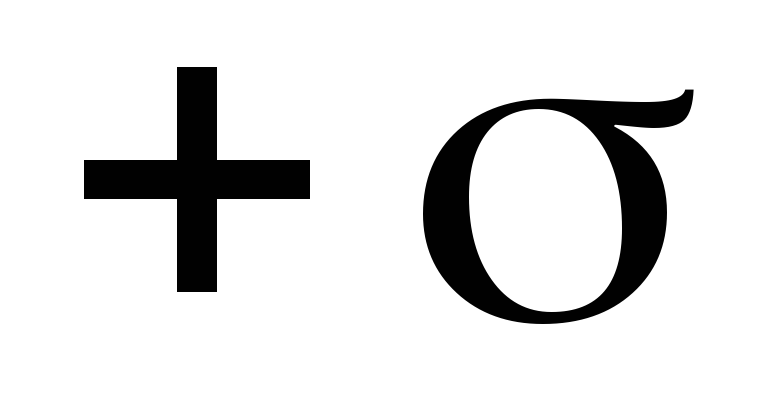  i
  
  .

  Rješenje. Koristimo rezultat primjera 1.3 i princip superpozicije. Prema ovom principu, rezultirajuće električno polje u bilo kojoj tački u prostoru
  
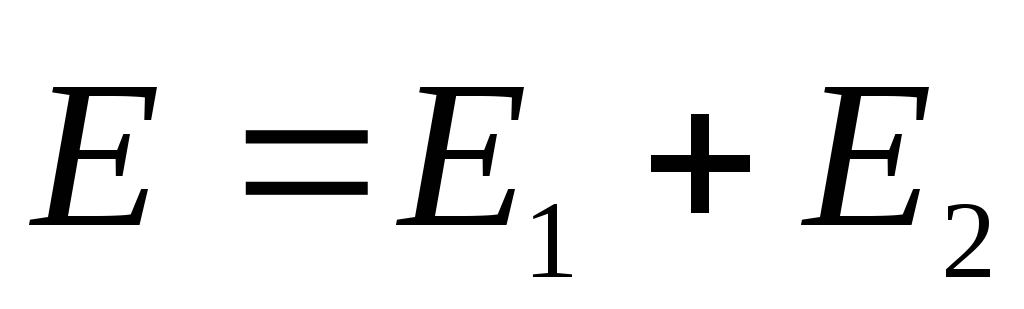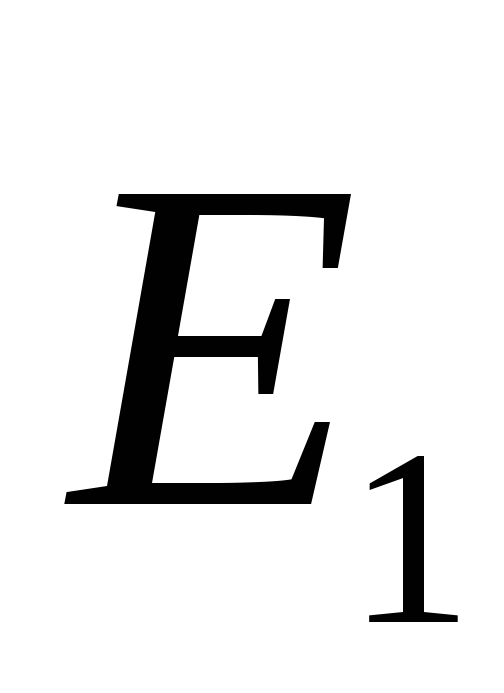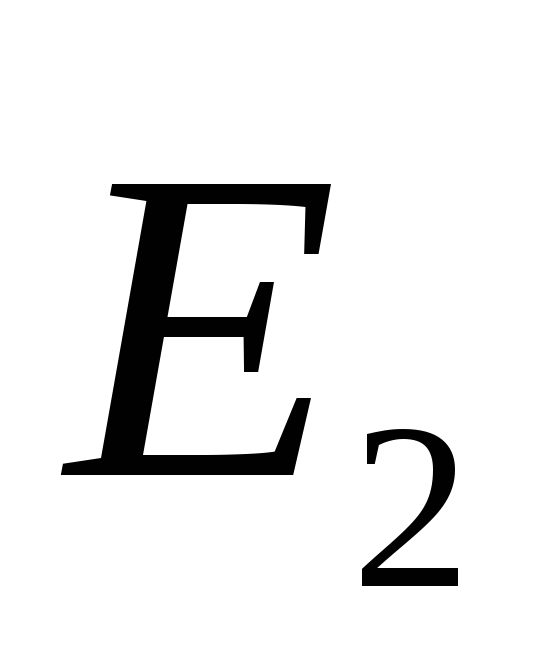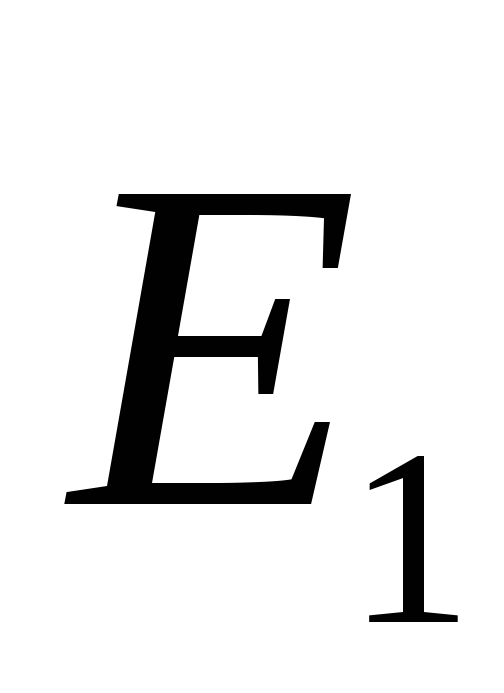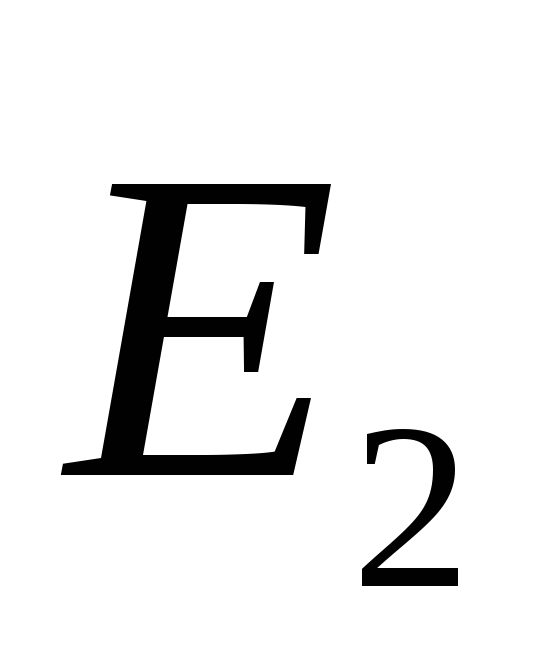  , gdje i - jačine električnog polja prve i druge ravni. U prostoru između vektorskih ravni i usmjerena u jednom smjeru, pa modul rezultirajuće jačine polja. U vanjskom prostoru vektora 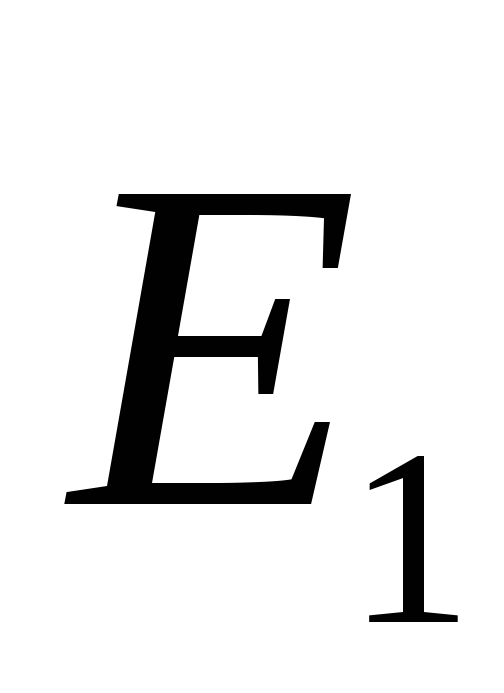i 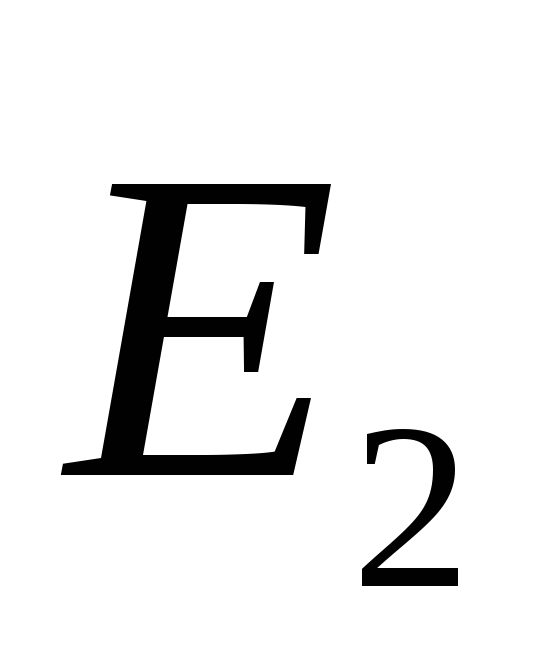usmjerene u različitim smjerovima, dakle (slika 1.11). Dakle, električno polje postoji samo u prostoru između ravnina. Homogen je, jer je zbir dva homogena polja.

  Primjer 1.5. Odrediti snagu i potencijal električnog polja jednolično nabijene kugle. Ukupan naboj sfere je , a polumjer sfere je .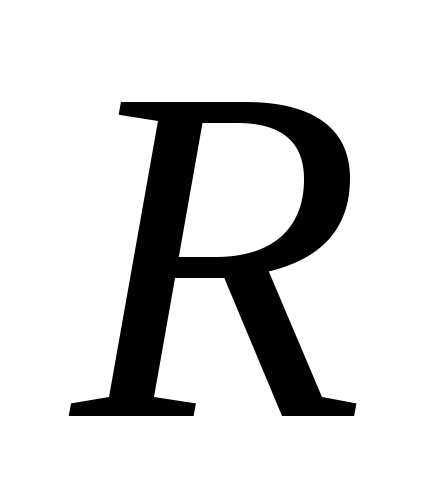

  Rješenje. Zbog simetrije raspodjele naboja, linije sile moraju biti usmjerene duž polumjera sfere.

  Razmotrite oblast unutar sfere. Kao proizvoljna površina izaberite sferu poluprečnika
  
  , čiji se centar poklapa sa centrom nabijene sfere. Zatim strujanje električnog polja kroz sferu S:
  
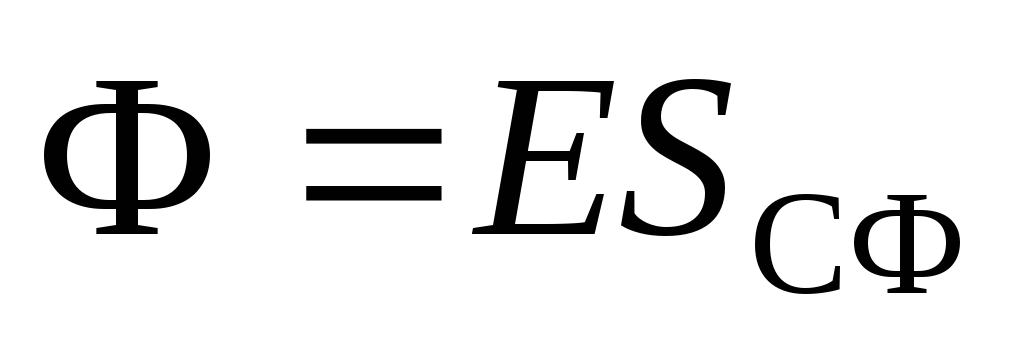  . Zbir naelektrisanja unutar sfere radijus 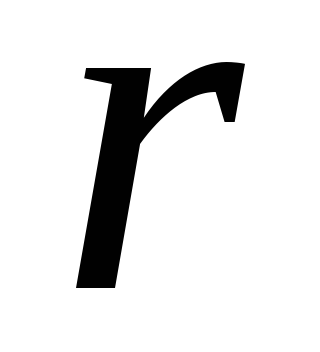jednaka je nuli, jer se sva naelektrisanja nalaze na površini sfere poluprečnika
  
  . Zatim po Gaussovom teoremu: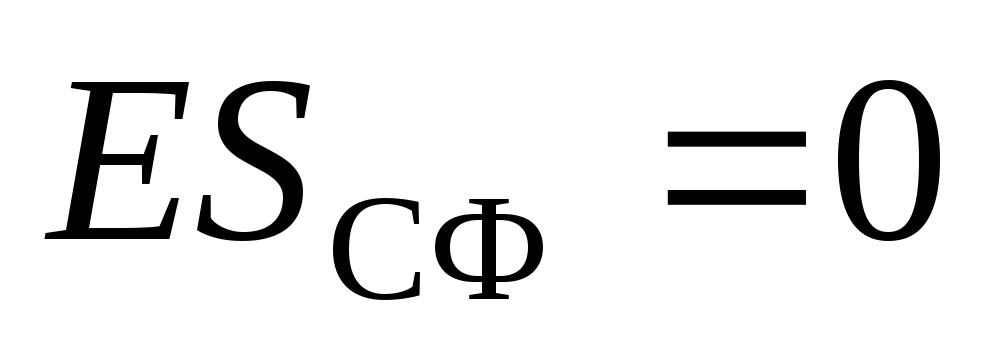
  
  . Zbog
  
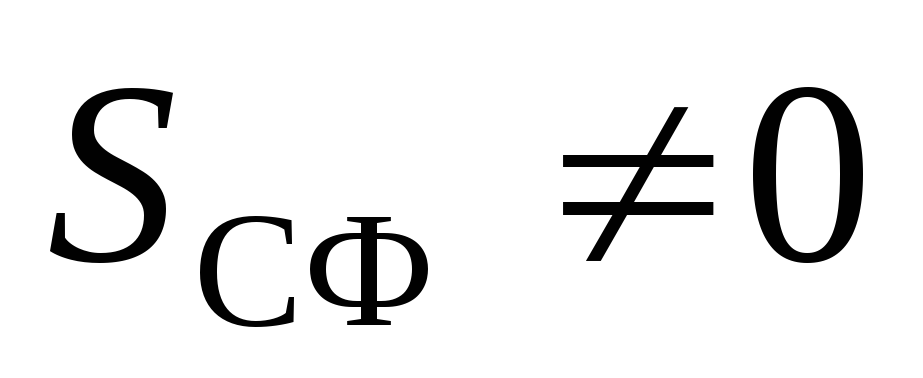  , onda
  
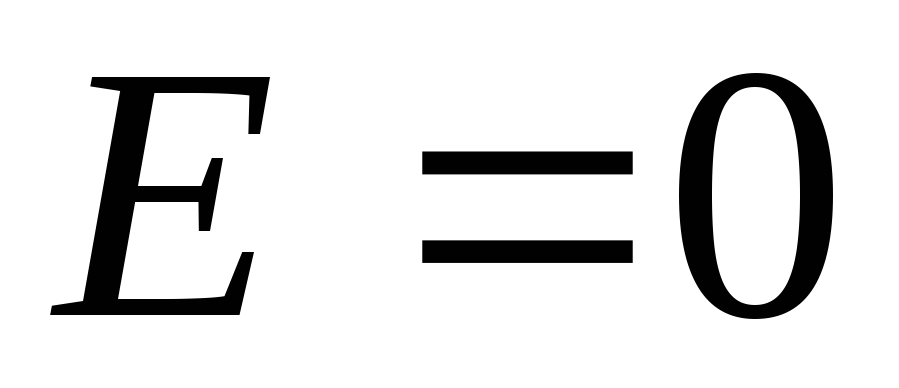  . Dakle, ne postoji polje unutar jednolično nabijene sfere.

  Razmotrite regiju izvan sfere. Kao proizvoljna površina izaberite sferu poluprečnika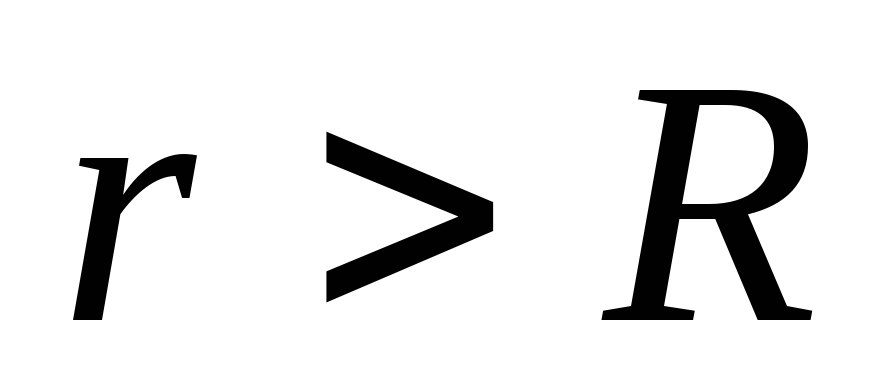
  
  , čiji se centar poklapa sa centrom nabijene sfere. Protok električnog polja kroz kuglu :
  
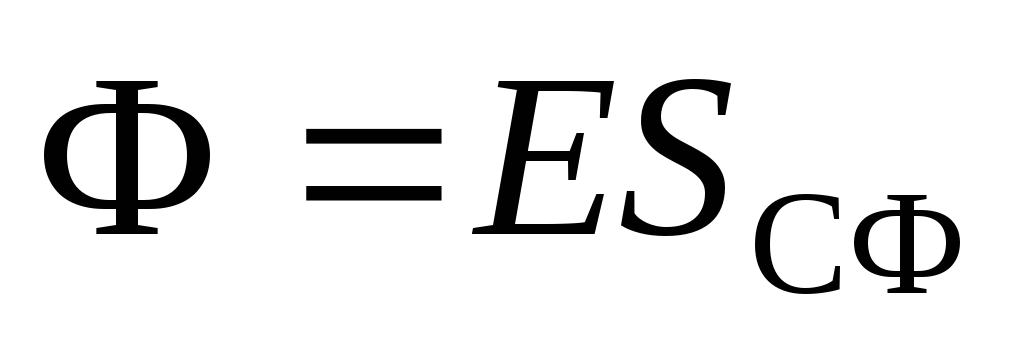  . Zbir naelektrisanja unutar sfere jednak je ukupnom naelektrisanju naelektrisana sfera poluprečnika 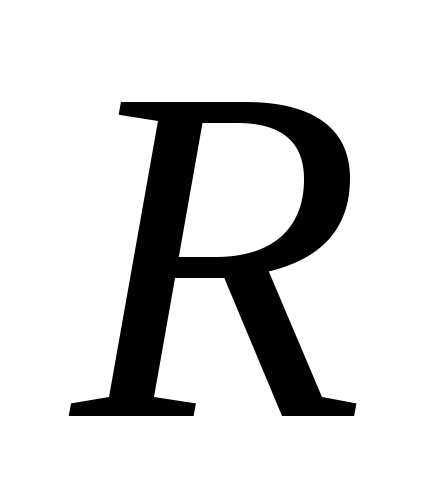. Zatim po Gaussovom teoremu:
  
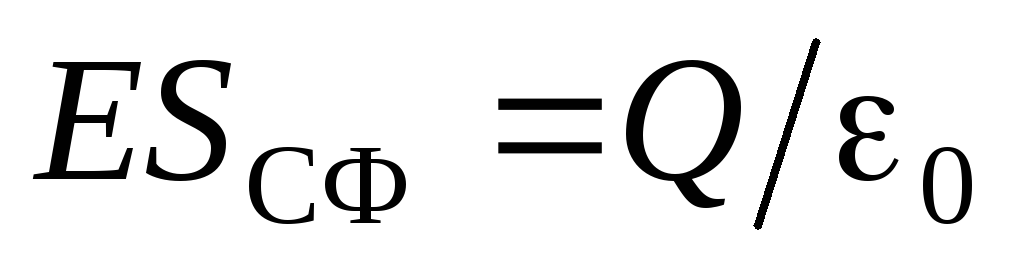  . S obzirom na to
  
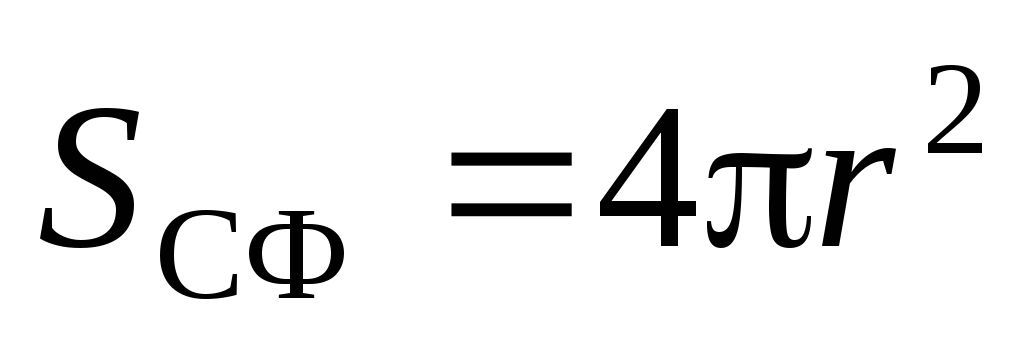  , dobijamo:

  
  .

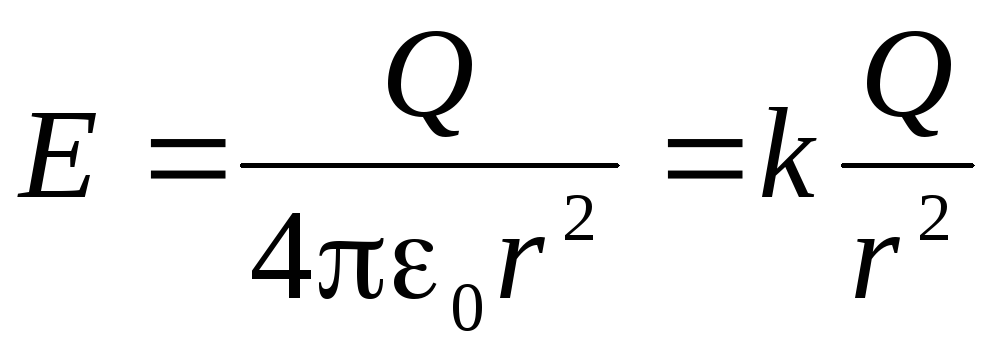  Izračunajmo potencijal električnog polja. Pogodnije je početi od vanjskog područja
  
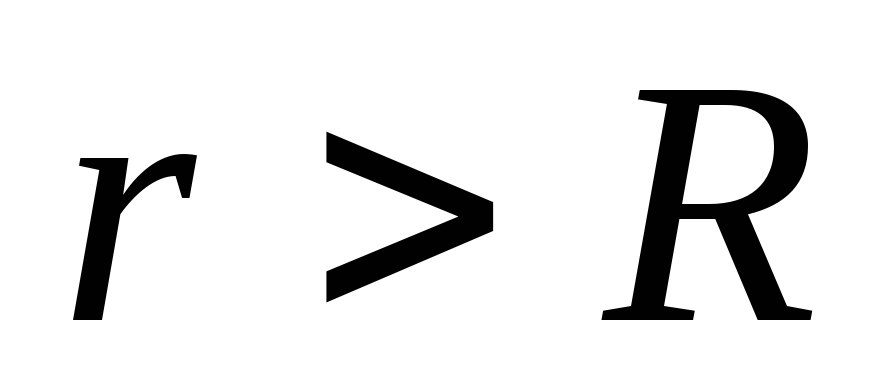  , pošto znamo da se na beskonačnoj udaljenosti od centra sfere pretpostavlja da je potencijal jednak nuli. Koristeći jednačinu (1.11, a) dobijamo diferencijalnu jednačinu sa odvojivim varijablama:

  
  
  
  
  
  
  
  
  
  
  
  
  
  .

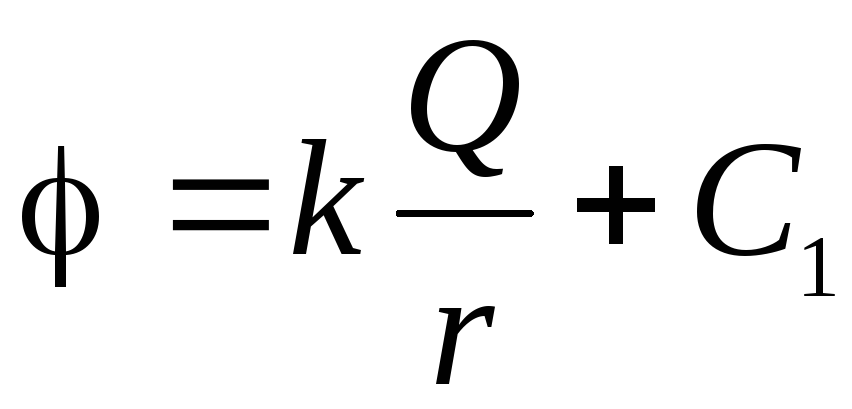  Konstantno
  
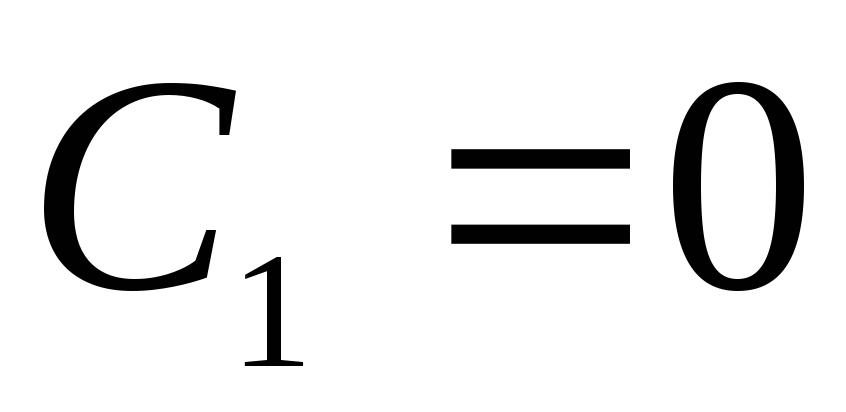  , zbog
  
  at
  
  . Dakle, u svemiru (
  
  ):
  
  .

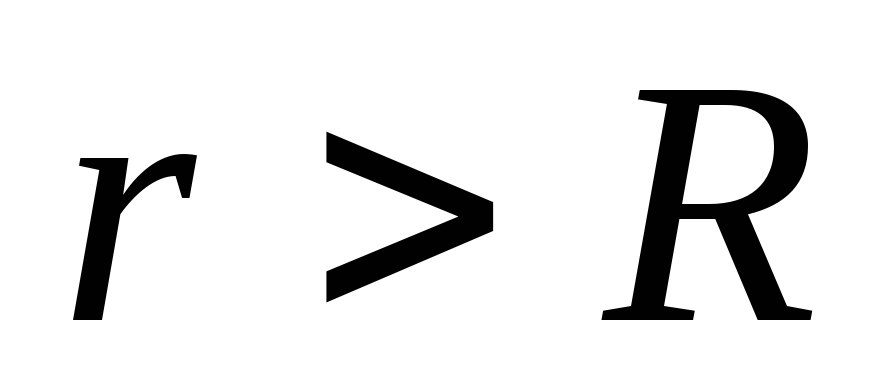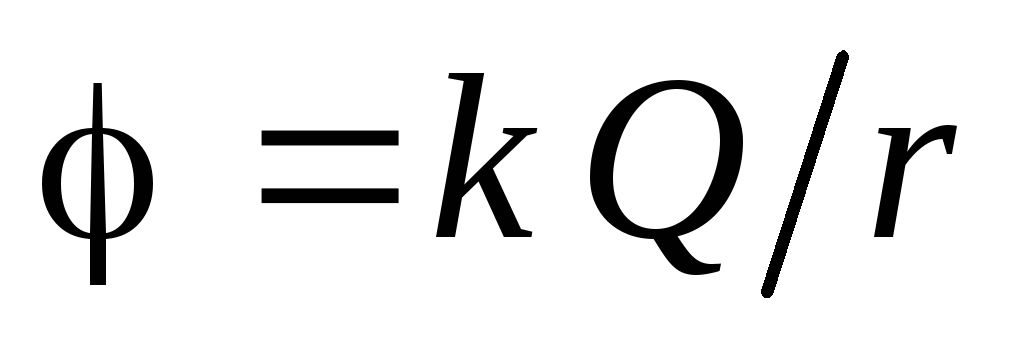  Tačke na površini nabijene sfere (
  
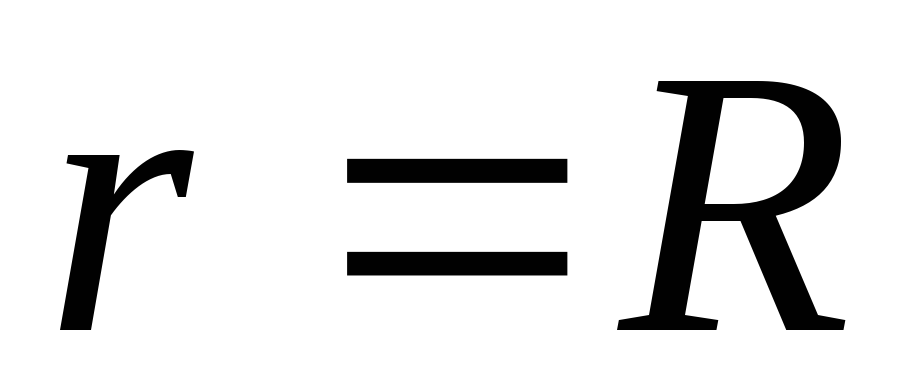  ) će imati potencijal
  
  .

  Razmotrite područje
  
  . U ovoj regiji
  
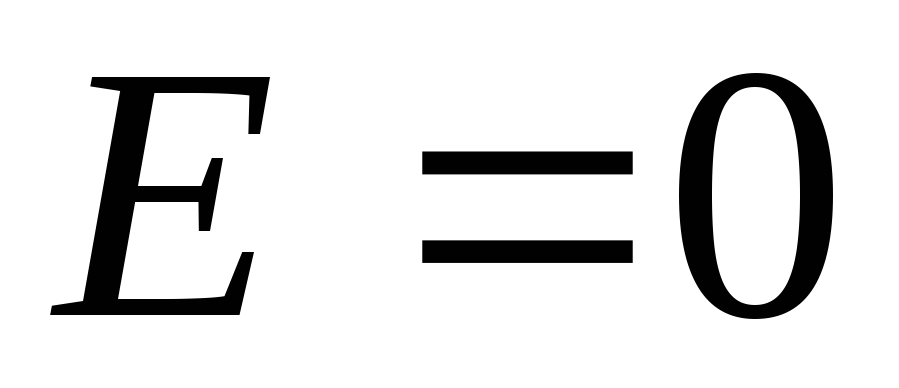  , dakle, iz jednačine (1.11, a) dobijamo: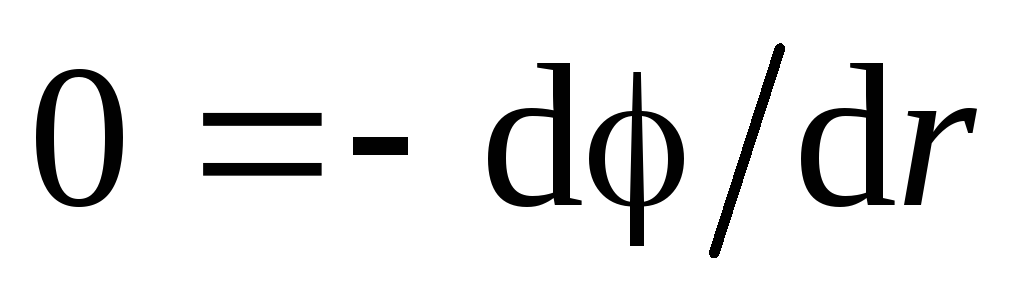
  
  
  
  
  
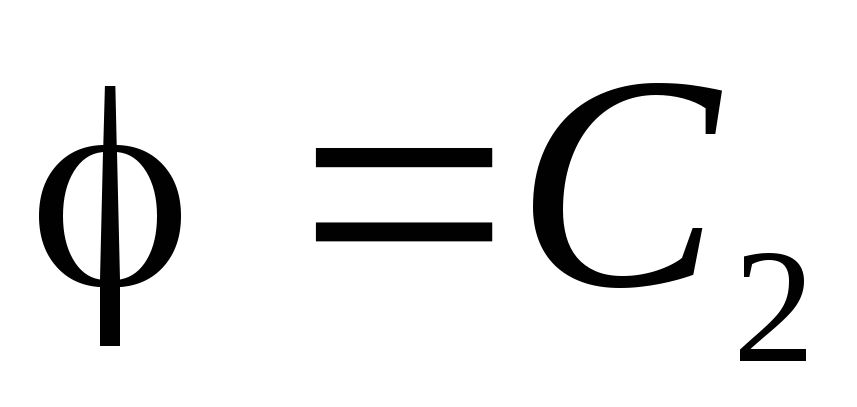  . Zbog kontinuiteta funkcije
  
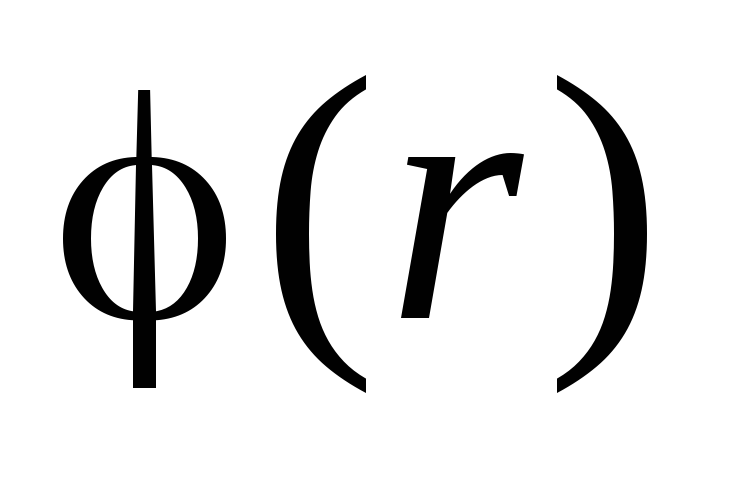  konstantan mora biti jednak vrijednosti potencijala na površini nabijene sfere: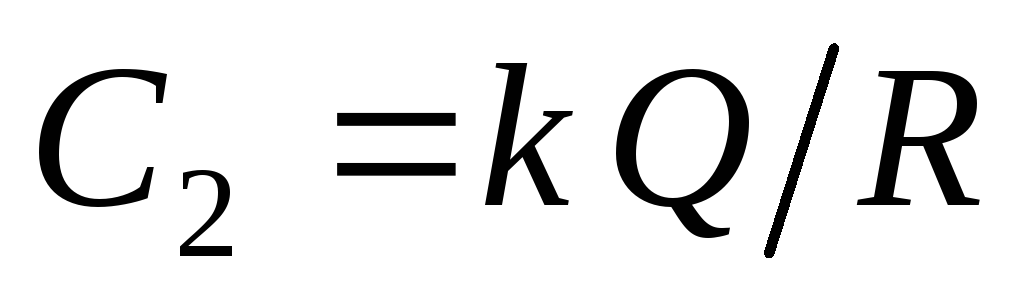
  
  . Dakle, potencijal u svim tačkama unutar sfere je:
  
  .

  

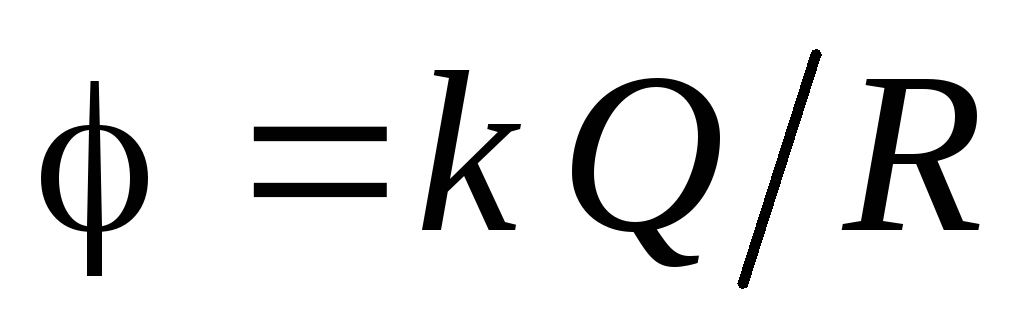  Dakle, dobili smo da su jačina i potencijal električnog polja koje stvara jednolično naelektrisana sfera izvan sfere jednaki jačini i potencijalu polja koje stvara tačka naboj iste veličine , što je naboj sfere postavljene u centar sfere. U unutrašnjem prostoru nema polja, a potencijal je isti u svim tačkama. Električno polje (linije polja i ekvipotencijalne površine) nabijene sfere prikazano je na sl. 1.12. Pretpostavlja se da je sfera pozitivno nabijena. Izvan sfere, linije sile i raspoređene su u prostoru na potpuno isti način kao i linije sile tačkastog naboja.

  

  Na sl. 1.13 prikazuje grafove zavisnosti
  
  i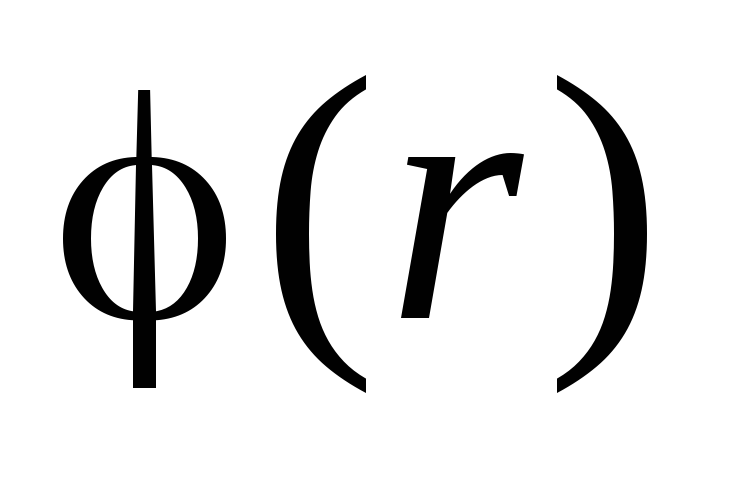
  
  . Funkcija
  
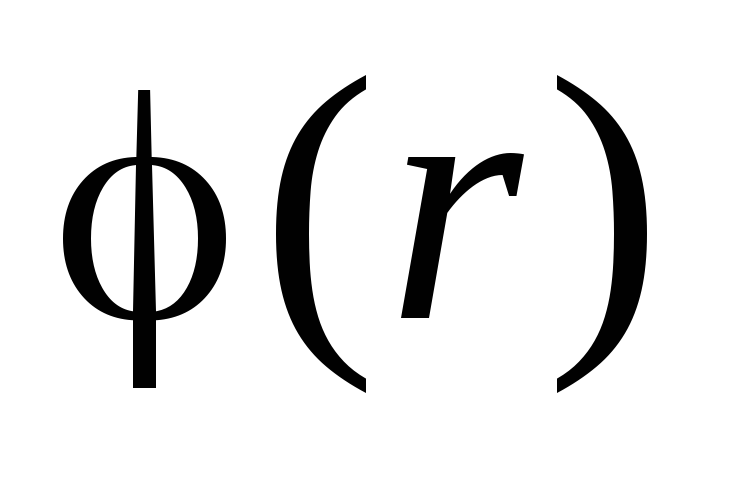  je kontinuirana, a funkcija
  
  naglo se mijenja prilikom prolaska kroz granicu nabijene sfere. Vrijednost skoka je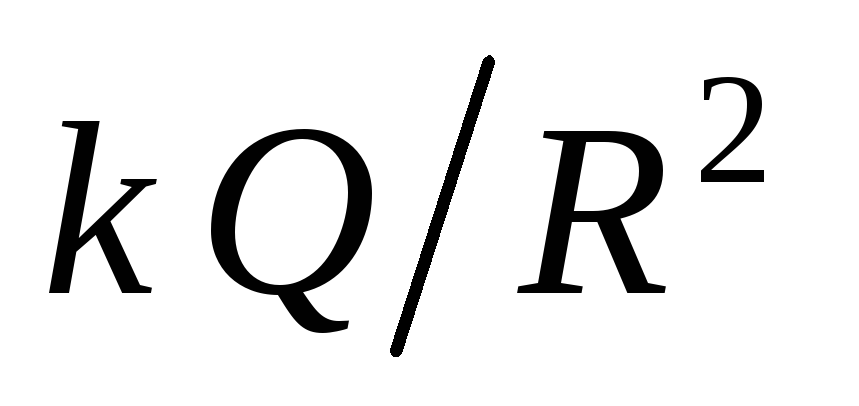
  
  . Zaista, blizu nabijene sfere (
  
  ) jačina polja u svemiru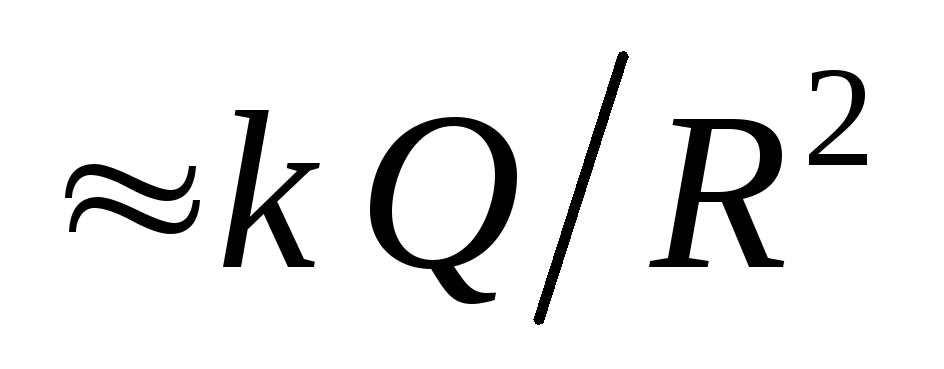
  
  , dok je unutra jednaka nuli.

  Veličina skoka može se izraziti u smislu površinske gustine naboja na sferi:

  
  .

  Imajte na umu da ovo zajedničko vlasništvo elektrostatičko polje: na nabijenoj površini, projekcija intenziteta na smjer normale uvijek doživi skok
  
  bez obzira na oblik površine. Preporučujemo da se ovaj princip proveri za polje jednoliko naelektrisane ravni i polje dve paralelno naelektrisane ravni (primeri 1.3, 1.4).

  Sa stanovišta matematike, kontinuitet potencijala u tačkama naelektrisane površine znači da
  
  . Sa stanovišta fizike, kontinuitet funkcije
  
  može se objasniti na sljedeći način. Ako bi potencijal na granici određenog područja imao skok (diskontinuitet), onda sa beskonačno malim pomakom određenog naboja od tačke 1, koja leži na jednoj strani granice, do tačke 2, koja leži na drugoj strani, izvršio bi se konačni rad
  
  , gdje i  potencijali tačaka 1 i 2, respektivno, i vrijednost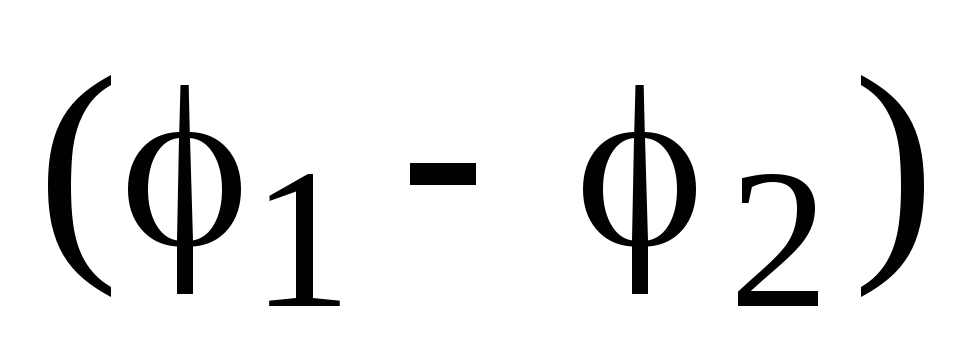
  
  jednak je potencijalnom skoku na granici regije. Konačni rad obavljen na beskonačno malom pomaku znači da bi na granicu djelovale beskonačno velike sile, što je nemoguće.

  Jačina električnog polja, za razliku od potencijala, na granici područja može se vrlo oštro promijeniti (skokovi).

  Primjer 1.6. Dvije koncentrične sfere polumjera i (
  
  ) su jednoliko naelektrisani sa jednakim naelektrisanjem po veličini, ali suprotnog predznaka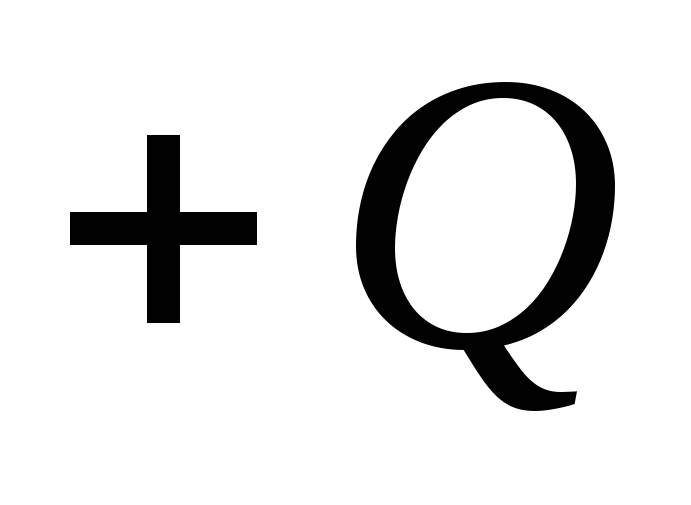
  
  i
  
  (sferni kondenzator). Odredite snagu i potencijal električnog polja u prostoru.

  Rješenje. Rješenje ovog problema moglo bi početi i primjenom Gaussove teoreme. Međutim, koristeći rezultate prethodnog primjera i princip superpozicije (1.13, 1.14), odgovor se može dobiti brže.

  Na vanjskim tačkama prostora (
  
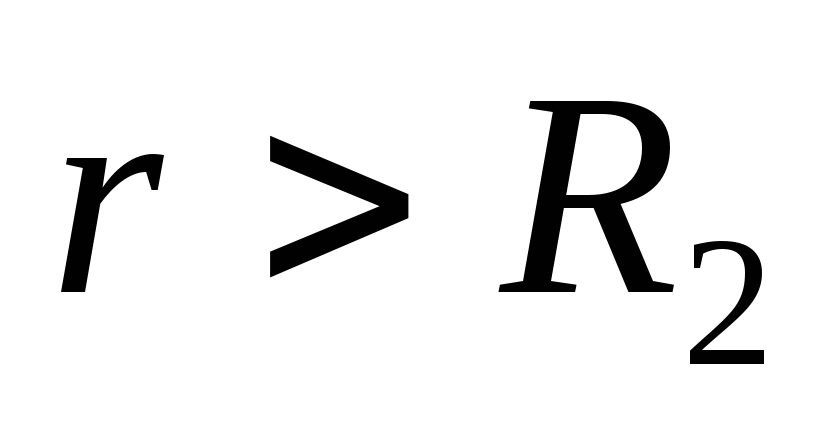  ) električno polje stvaraju naboji obje sfere. Veličina jačine polja prve sfere
  
  i usmjeren je od sfera duž polumjera. Veličina jačine polja druge sfere je ista
  
  , ali u suprotnom smjeru. Prema tome, prema principu superpozicije, neće biti električnog polja u svim vanjskim tačkama u prostoru.
  
  .

  Razmotrite tačke prostora između sfera (
  
  ). Ove tačke su unutrašnje za negativno nabijenu sferu, dakle u ovoj oblasti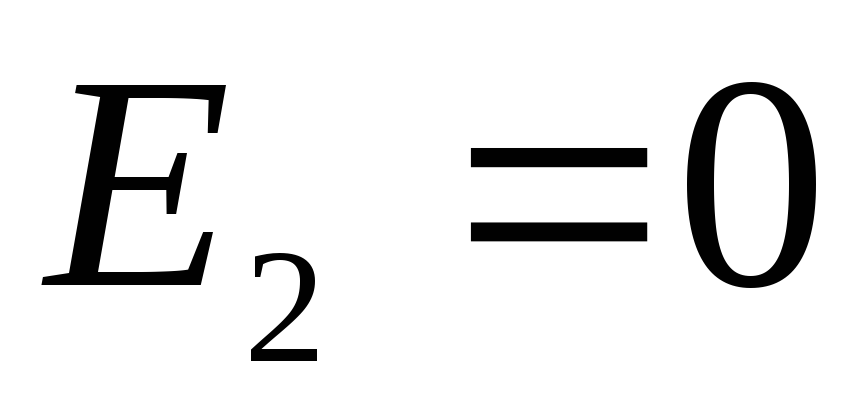
  
  (vidi primjer 1.5). Za pozitivno nabijenu sferu ove tačke su vanjske, dakle
  
  . Dakle, veličina jačine polja u ovoj regiji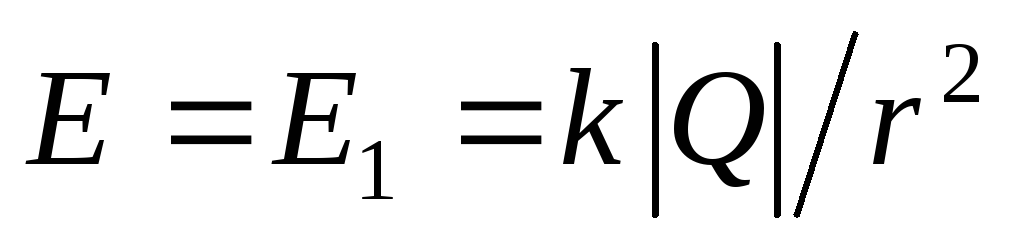
  
  . Ovdje polje stvaraju samo naboji manje sfere.

  Konačno, na unutrašnjim tačkama prostora (
  
  )
  
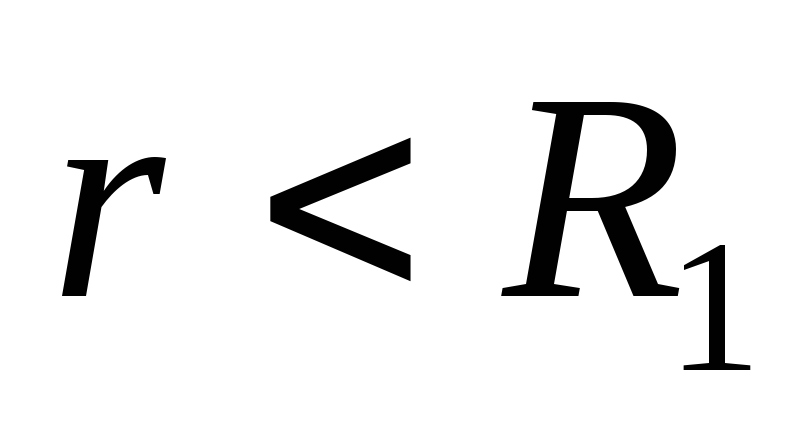  i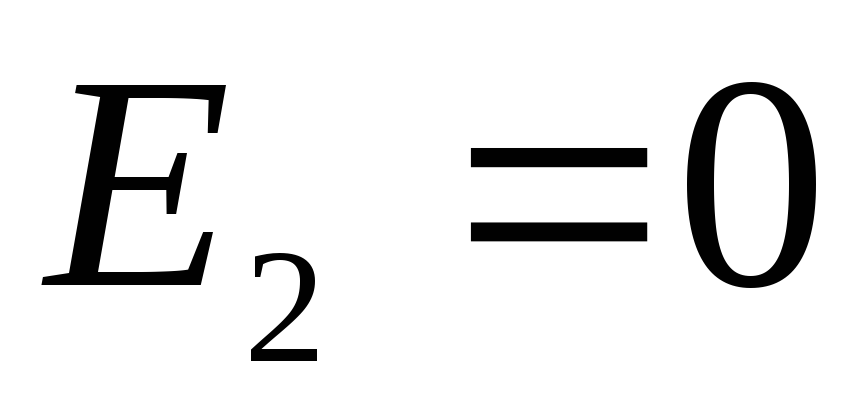
  
  , tako da u ovim tačkama nema električnog polja.

  Slično, princip superpozicije se može primijeniti na potencijale. Dobijaju se sljedeći rezultati:

  
  :
  
  ;

  
  :
  
  ;

  
  :
  
  .

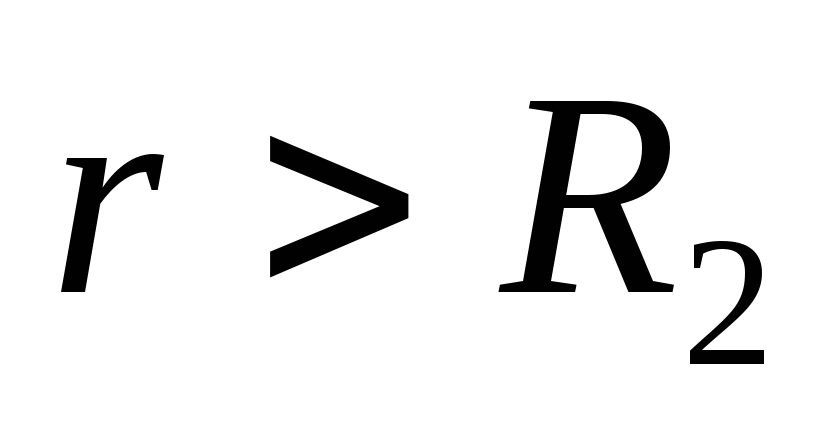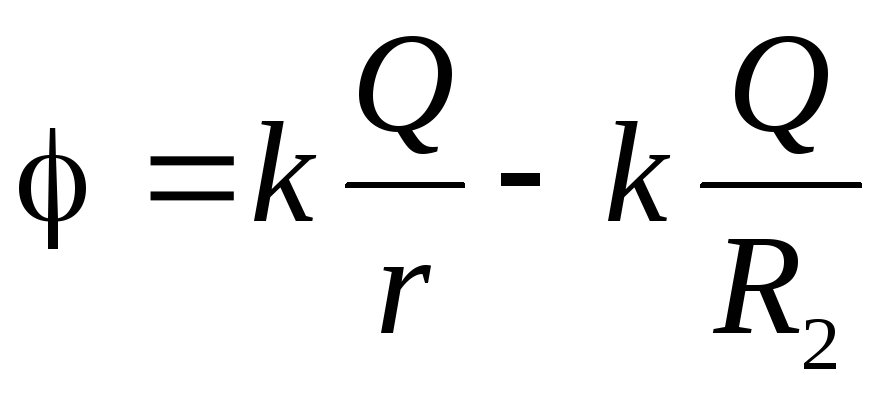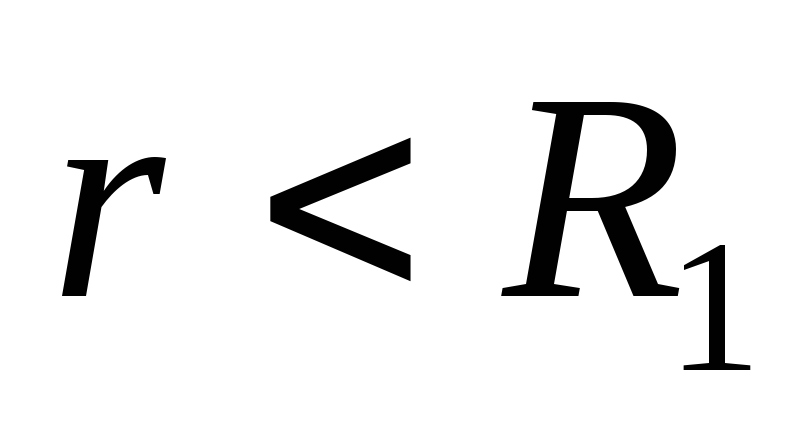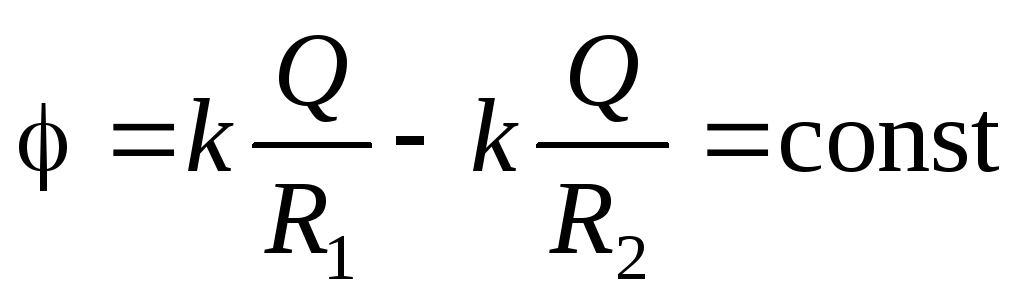  Preporučujemo da samostalno dobijete ove rezultate, kao i da shematski prikažete električno polje i izgradite grafikone
  
  i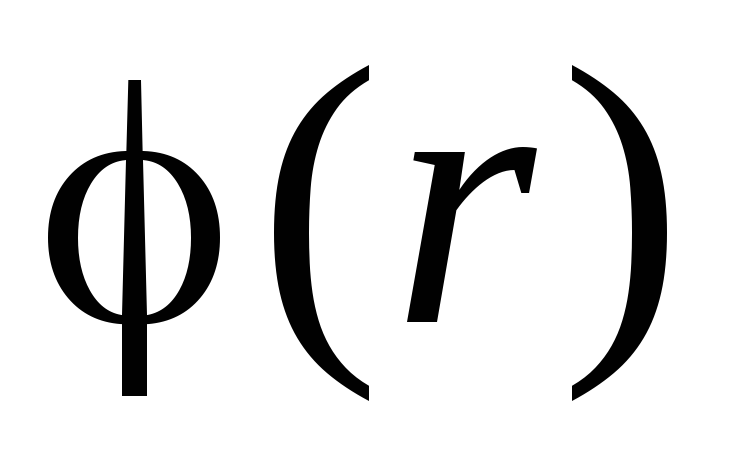
  
  .