Деформированное упругое тело (например, растянутая или сжатая пружина) способно, возвращаясь в недеформированное состояние, совершить работу над соприкасающимися с ним телами. Следовательно, упруго деформированное тело обладает потенциальной энергией. Она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина, зависит от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к нерастянутому состоянию, т. е. найдем потенциальную энергию растянутой пружины.

Пусть растянутая пружина закреплена одним концом, а второй конец, перемещаясь, совершает работу. Нужно учитывать, что сила, с которой действует пружина, не остается постоянной, а изменяется пропорционально растяжению. Если первоначальное растяжение пружины, считая от нерастянутого состояния, равнялось /> , то первоначальное значение силы упругости составляло , где - коэффициент пропорциональности, который называют жесткостью пружины. По мере сокращения пружины эта сила линейно убывает от значения до нуля. Значит, среднее значение силы равно . Можно показать, что работа равна этому среднему, умноженному на перемещение точки приложения силы:

Таким образом, потенциальная энергия растянутой пружины

Такое же выражение получается для сжатой пружины.

В формуле (98.1) потенциальная энергия выражена через жесткость пружины и через ее растяжение . Заменив на , где - упругая сила, соответствующая растяжению (или сжатию) пружины , получим выражение

которое определяет потенциальную энергию пружины, растянутой (или сжатой) силой . Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, т.е. чем больше ее упругость, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной растягивающей, силе. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на перемещение точки приложения силы, т. е. работа.

Эта закономерность имеет большое значение, например, при устройстве различных рессор и амортизаторов: при посадке на землю самолета амортизатор шасси, сжимаясь, должен произвести большую работу, гася вертикальную скорость самолета. В амортизаторе с малой жесткостью сжатие будет больше, зато возникающие силы упругости будут меньше и самолет будет лучше предохранен от повреждений. По той же причине при тугой накачке шин велосипеда дорожные толчки ощущаются резче, чем при слабой накачке.

Согласно выражению (3.12), потенциальная энергия системы есть максимальная положительная работа, которую могут совершить действующие в системе внутренние силы.

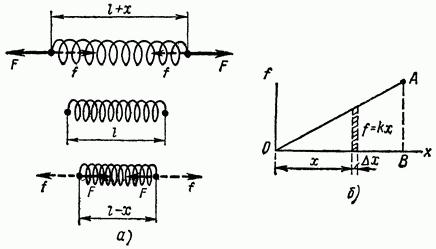
Рассчитаем потенциальную энергию сжатой или растянутой упругой пружины; внутренние силы действующие на концах пружины, направлены против внешних деформирующих сил и по величине пропорциональны деформации (рис. 1.27, а):

где коэффициент упругости пружины. Вычислим работу, которую могут совершать внутренние силы при переходе пружины из деформированного состояния в нормальное (недеформированное); эта работа всегда положительная. При изменении длины пружины на очень малую величину силы можно считать почти постоянными, а их работа будет равна Графически эта работа изображается площадкой, заштрихованной на рис. 1.27, б. Полная работа внутренних сил при переходе в нормальное состояние представлена, очевидно, площадью треугольника Эта работа и есть потенциальная энергия деформированной пружины

Для скрученной спиральной пружины аналогичный расчет дает где коэффициент упругости на кручение, а - угол скручивания. Заметим, что в состоянии с нулевой потенциальной энергией внутренние силы равны нулю.

Для упругодеформированного сплошного тела (или среды) можно рассчитать потенциальную энергию, содержащуюся в единице объема. Применим формулу к стержню длиной I и сечением Тогда будет относительным удлинением тела под действием силы нормальным механическим напряжением. Воспользуемся законом Гука (см. формулу и выразим потенциальную энергию всего стержня (см. (3.14)) в зависимости или от относительного

удлинения или от напряжения

где объем тела; модуль продольной упругости.

Таким образом, величина

есть энергия упругой деформации, (растяжения или сжатия), содержащаяся в единице объема тела или упругой среды. Для данной среды с определенным модулем продольной упругости энергия в единице объема прямо пропорциональна квадрату относительной деформации или квадрату напряжения а. При данной относительной деформации эта энергия пропорциональна модулю продольной упругости. Аналогичные выражения получаются и для других видов упругих деформаций.

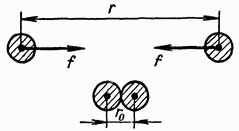
Рассчитаем потенциальную энергию двух тел с массами притягивающихся друг к другу по закону тяготения. Силы взаимного притяжения будут совершать положительную работу, если тела приближаются, и отрицательную работу, если тела удаляются. Допустим, что в начальном состоянии эти тела находятся на расстоянии а при сближении наименьшее возможное расстояние между ними (при соприкосновении) равно (рис. 1.28). Тогда положительная работа, которая совершается силами тяготения при этом сближении, может быть подсчитана как сумма элементарных работ т. е.

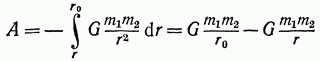
(знак минус перед интегралом появился вследствие того, что при уменьшении расстояния между телами величина как разность между новым и начальным значениями отрицательная, в то время как работа положительная, так как перемещение тел происходит в направлении действия сил). В частном случае, когда расстояния велики, а их разность мала, как это имеет место при падении тела на поверхность Земли с небольшой высоты, можно произведение заменить на и тогда

Работу, которую может при своем падении совершить тело весом расположенное на высоте называют потенциальной энергией этого тела в поле тяготения Земли По мере приближения

тела к Земле сила тяжести совершает положительную работу и потенциальная энергия тела уменьшается.

Однако если потенциальную энергию системы из двух притягивающихся тел приравнивать работе рассчитанной по формуле (3.15), то потенциальная энергия системы будет равна нулю при Но наименьшее расстояние между телами не всегда есть определенная величина. Это обстоятельство побудило выбрать другое, более определенное состояние системы, при котором ее потенциальная энергия равна нулю; а именно условились считать, что потенциальная энергия любой системы равна нулю, если ее составные части удалены друг от друга на бесконечно большие расстояния; при этом силы взаимодействия между телами равны нулю.

Из этого условия следует, что потенциальная энергия системы притягивающихся тел должна быть отрицательной величиной (а системы отталкивающихся тел - положительной величиной). Действительно, если из начального состояния, когда расстояние между телами бесконечно большое и тела начнут сближаться, например до расстояния то силы притяжения совершают положительную работу и поэтому потенциальная энергия должна уменьшаться и, следовательно, станет меньше нуля. Таким образом,

Следовательно,

Для системы, состоящей из двух взаимодействующих электрических зарядов и потенциальная энергия выражается такой же формулой:

где постоянная величина. Если заряды имеют различные знаки, то потенциальная энергия получается отрицательной; для системы зарядов одинакового знака потенциальная энергия - положительная величина. На рис. 1.29 приведены графики функции показывающие изменение потенциальной энергии системы притягивающихся (1) и отталкивающихся (2) тел с изменением расстояния между ними.

Для более сложной системы, содержащей, например, взаимодействующих тел, потенциальная энергия будет представлять собою функцию от координат всех этих тел: Как и в случае простой системы из двух тел, эта функция подбирается таким образом, чтобы при изменении координат взаимодействующих тел работа сил взаимодействия была равна Для двух тел следовательно,

Для сложной системы, состоящей из многих взаимодействующих между собой тел, сила, действующая на тело в направлении,

например, оси равна частной производной:

Допустим, что при графическом изображении функции для некоторой физической системы начало координат О помещено внутри системы, а ось ориентирована в каком-нибудь интересующем нас направлении (рис. 1.30). имеет отрицательный знак, т. е. она направлена к точке О и будет препятствовать удалению частицы из системы; в точке В сила имеет противоположное направление.

При удалении от точки О потенциальная энергия будет возрастать, следовательно, кинетическая энергия частицы должна убывать. Если в точке О кинетическая энергия частицы была равна то она

сделается равной нулю в точке А. Здесь частица остановится, после чего действующие на нее силы сообщат ей обратное движение; частица не сможет преодолеть потенциальный барьер и удалиться из системы. Это будет возможно только при достаточно большой кинетической энергии, например равной

В сложных системах взаимодействующих тел могут образоваться также потенциальные ямы (рис. 1.31). Если частица оказалась на участке то при перемещении в любом направлении потенциальная энергия возрастает, следовательно, кинетическая энергия убывает (сила, действующая на частицу, направлена к точке С). Поэтому если кинетическая энергия частицы внутри «ямы» мала, то она не сможет покинуть ее и будет совершать колебательное движение в окрестности точки С.

Обозначим через х растяжение пружины, т.е. разность длин пружины в деформированном и недеформированном состояниях.

При возвращении пружины из деформированного состояния в недеформированное сила совершает работу.

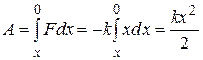. (12)

Таким образом, потенциальная энергия упруго деформированной пружины

4.5.2. Потенциальная энергия гравитационного притяжения двух материальных точек

На рис. 5 изображены две материальные точки массы m 1 и m 2 . Положение их характеризуется радиусами-векторами и соответственно. Элементарная работа, совершаемая силами гравитационного притяжения этих точек , где – сила, действующая на первую материальную точку со стороны второй, а – сила, действующая на вторую материальную точку со стороны первой; согласно 3-му закону Ньютона =-; и – элементарные перемещения материальных точек. С учетом этого , где . Учитывая, что и противоположно направлены и что величина , находим . Полная работа

где R 1 и R 2 – начальное и конечное расстояние между материальными точками.

Эта работа равна изменению потенциальной энергии A=W n 1 -W n 2 . Учитывая (14), находим, что потенциальная энергия гравитационного притяжения двух материальных точек

или (15)

где R или r – расстояние между материальными точками.

Конец работы -

Эта тема принадлежит разделу:

Физика будет изучаться в течение 4-х семестров: в первом: – физические основы классической и релятивистской механики

ВВЕДЕНИЕ... ФИЗИКА по гречески ПРИРОДА это наука изучающая простейшие и вместе с тем наиболее общие закономерности явлений...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Л Е К Ц И Я № 1. К И Н Е М А Т И К А
Кинематика – это раздел механики, в котором изучается движение тел без рассмотрения причин, вызывающих движение. Движением тела называют изменение его положения относительно другого тела в

Кинематика материальной точки. Путь, перемещение, скорость и ускорение
Рис. 1 Изуч

Закон движения дается векторным уравнением
. (1) При координатном способе положение точки А определяется координатами x, y, z, а зако

Скорость
Мгновенная скорость материальной точки определяется соотношением

Ускорение
Для характеристики быстроты изменения скорости вводится векторная физическая величина, называемая ускорением

Угловая скорость и угловое ускорение
Рассмотрим движение материальной точки по окружности радиуса R (рис. 5). Пусть за время

Л Е К Ц И Я № 2 . Д И Н А М И К А М А Т Е Р И А Л Ь Н О Й Т О Ч К И
Динамика – это раздел механики, посвященный изучению движения материальных тел под действием приложенных к ним сил. В основе динамики лежат 3 закона Ньютона, сформулированные в 1687 г. Они

Второй закон Ньютона
Для того, чтобы его сформулировать введем понятие силы. Силой называется векторная величина, характеризующая воздействие на данное тело со стороны других тел. Сила

Третий закон Ньютона
Воздействие тел друг на друга всегда носит характер взаимодействия. Если тело 2 действует на тело 1 с силой

Силы трения
Они появляются при перемещении соприкасающихся тел или их частей друг относительно друга. Трение, воз

Л Е К Ц И Я № 3. З А К О Н С О Х Р А Н Е Н И Я И М П У Л Ь С А
Совокупность тел, выделенных для рассмотрения, называется механической системой. Тела системы могут взаимодействовать как между собой, так и с телами, не входящими в систему. В соо

Закон сохранения импульса
Рассмотрим систему, состоящую из n материальных точек. Обозначим через силу, с которой материальная точка

Центр масс и закон его движения
В динамике широко используется понятие центра масс системы материальных то чек, который обычно обозначают буквой С. Положение центра масс определяется радиусом-вектором

Реактивное движение. Движение тел с переменной массой
Имеется много явлений, в основе которых лежит закон сохранения импульса. Например, полет ракет (и работа реактивных двигателей) основаны на том, что в результате выбрасывания из сопла газов, ракете

Консервативные и неконсервативные силы
Все силы, встречающиеся в механике, принято разделять на консервативные и неконсервативные. Сила, дейс

Потенциальная энергия системы материальных точек
Рассмотрим систему, состоящую из многих материальных точек. Если задано положение каждой материальной точки, то этим определено и положение всей системы или ее конфигурация. Если силы, действующие

Потенциальная энергия тела в однородном поле силы тяжести Земли
Формула (15) справедлива также для однородных сферических тел; в этом случае r – расстояние между центрами масс таких тел. В частности, потенциальная энергия тела массы т, находящегос

Кинетическая энергия
Напишем уравнение движения материальной точки (частицы) массы m, движущейся под действием сил, результирующая которых равна

Закон сохранения энергии в механике
Рассмотрим систему из n материальных точек, на которые действуют как консервативные так и неконсервативные силы. Найдем работу, которую совершают эти силы при перемещении системы из одной ко

Упругое и неупругое соударения
При соударении тел они в большей либо меньшей мере деформируются. При этом кинетическая энергия тел частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энерг

Абсолютно неупругий удар
Интересным примером, где имеет место потеря механической энергии под действием диссипативных сил, является абсолютно неупругий удар, при котором потенциальная энергия упругой деформации не возникае

Абсолютно упругий удар
Это такой удар, при котором полная механическая энергия тел сохраняется. Сначала кинетическая энергия частично или полностью переходит в потенциальную энергию упругой деформации. Затем тела возвращ

Общефизический закон сохранения энергии
Классическая механика учитывает только кинетическую энергию макроскопического движения тел и их макроскопических частей, а также их потенциальную энергию. Но она полностью отвлекается от внутреннег

Момент силы и момент импульса относительно неподвижного начала
Пусть О – какая-либо неподвижная точка в инерциальной системе отсчета. Ее называют началом или полюсом. Обозначим через

Уравнение моментов
Предположим, что точка О неподвижна. В случае одной материальной точки, дифференцируя (3), получаем.

Закон сохранения момента импульса
Если система замкнута (т. е. внешних сил нет), то и, следовательно, согласно уравнению (6) вектор

Движение в поле центральных сил
Если на материальную точку действует сила вида, (8) то говорят, что материальная точка находит

Степени свободы. Обобщенные координаты
Положение точки в пространстве можно задать некоторым числом независимых координат, например, тремя координатами х, у, z декартовой системы. Но это можно сделать и иначе. Например, вместо пр

Число степеней свободы твердого тела
Абсолютно твердым телом в механике называют идеализированную систему материальных точек, все расстояния между которыми при движении системы не изменяются с течением времени. Чтобы однознач

Уравнение движения и равновесия твердого тела
Так как твердое тело является механической системой с шестью степенями свободы, то для описания его движения требуется шесть независимых числовых уравнений или два независимых векторных уравнения.

Теорема Штейнера
В механике твердое тело обычно рассматривают как механическую систему, масса т которой непрерывно распределена по объему V тела, так что при вычислении момента инерции тела, суммирова

Кинетическая энергия при плоском движении
Плоским (плоскопараллельным) называется такое движение, при котором все точки тела движутся в параллельных плоскостях. Представим плоское движение тела как поступательное движение со скоростью

Просуммировав по всем материальным точкам, получим
или, (12)

Таким образом, если разбить плоское движение тела на поступательное со
скоростью центра масс Vc и вращательное с угловой скоростью w вокруг оси, проходящей через центр масс тела, то кинетическая энергия распадается на два независимых слагаемых

Мощность
. (16) Сопоставим основные величины и уравнения поступательного и вращательного движений

Преобразования Галилея. Принцип относительности Галилея
Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одной из них справедлив 1- й закон Ньютона, то эти системы являются инерциальными. Галилей установил:

Постулаты частной теории относительности
Исторически именно закон сложения скоростей (5) показал ограниченность галилеевых представлений о свойствах пространства и времени. Действительно, согласно этому закону по отношению к сист

Преобразования Лоренца
Постулаты Эйнштейна требовали коренного пересмотра представлений о свойствах пространства, времени и движения. Покажем это на простом примере. Представим себе, что движущейся системой отсч

Закон сложения скоростей в релятивистской механике
Дифференцируя (11) по, а (12) по

Масса в ньютоновской и релятивистской механике
При изучении движения тел, скорости vкоторых пренебрежимо малы по сравнению со скоростью света с (v/c → 0), имеет место нерелятивистское приближение. В этом случ

Энергия, импульс в релятивистской механике
Если тело движется со скоростью v относительно инерциальной системы отсчета (ИСО) K, то помимо энергии покоя

Основное уравнение релятивистской динамики
Согласно (20), релятивистский импульс, при этом обе формулы справедливы для «тяжелых», т.е. имеющих не н

Кинетическая энергия релятивистской частицы
Согласно (19), полная энергия тела (частицы) в релятивистской механике, она складывается из энер

Гармонические колебания
Рис. 1 Изуч

Потенциальная и кинетическая энергии
Установим изменение потенциальной и кинетической энергий колеблющейся системы. Известно, что потенциальная энергия упруго деформированного тела равна

Векторная диаграмма гармонического колебания
Гармоническое колебание можно представить в виде проекции вектора

Комплексная форма представления колебаний
Согласно формуле Эйлера для комплексных чисел

Сложение одинаково направленных колебаний
Рассмотрим сложение двух гармонических колебаний одинаковой частоты, смещения которых и

Математический маятник
Это материальная точка, подвешенная на невесомой, нерастяжимой нити. Хорошим приближением к мате

Пружинный маятник
Это груз массой т, подвешенный на абсолютно упругой пружине и совершающий колебания около положения равновесия, рис. 1. Он был рассмотрен в параграфе 1. Для него

Свободные затухающие колебания
Кроме силы упругости F = - kx на тело действуют также сила сопротивления, которая при медленных движениях пропорциональна скорости, т. е.

Логарифмический декремент затухания
Натуральный логарифм отношения отклонения системы в моменты времени t и называется логарифмическим декрем

Вынужденные колебания
Они возникают при действии на систему внешней периодически изменяющейся силы (вынуждающей силы) , (22)