16. Теорема Штерна .

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы т тела на квадрат расстояния а между осями:

17. Уравнение динамики вращательного движения твердого тела .

Iε = M. Это и есть основное уравнение динамики вращательного движения твердого тела. Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими. Обычно за положительное направление вращения принимают направление против часовой стрелки.

Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины, определяются как векторы, направленные по оси вращения. При изучении поступательного движения тел вводится понятие импульса тела. Аналогично, при изучении вращательного движения вводится понятие момента импульса. Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L: Момент импульса всего тела определяется как векторная сумма Li. L = Iω. Это уравнение, полученное здесь для случая, когда I = const, справедливо и в общем случае, когда момент инерции тела изменяется в процессе движения.

18. Кинетическая энергия вращательного тела .

Рассмотрим абсолютно твердое тело (см. § 1), вращающееся около неподвижной оси z, проходящей через него (рис. 24). Мысленно разобьем это тело на маленькие объемы с элементарными массами т 1 , т 2 ,..., т n , находящиеся на расстоянии r 1 , r 2 ,..., r n от оси.

При вращении твердого тела относительно неподвижной оси отдельные его элементар­ные объемы массами m i опишут окружности различных радиусов r i , и имеют различные линейные скорости v i . Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова: (17.1) Кинетическую энергию вращающегося тела найдем как сумму кинетических энер­гий его элементарных объемов:

или Используя выражение (17.1), получаем

где J z - момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела (17.2)

Из сравнения формулы (17.2) с выражением (12.1) для кинетической энергии тела движущегося поступательно (T=mv 2 /2), следует, что момент инерции - мера инертности тела при вращательном движении. Формула (17.2) справедлива для тела вращающегося вокруг неподвижной оси. В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения: где m - масса катящегося тела; v c - скорость центра масс тела; Jc - момент инер­ции тела относительно оси, проходящей через его центр масс; w - угловая скорость тела. Работа внешней силы по вращению тела F=Fi+Fr+Fk. Работа силы вращающегося тела A=M* ∆φ

19. Гравитационное поле .

Гравитационное взаимодействие между телами осуществляется с помощью поля тяготения, или гравитационного поля. Это поле порождается телами и является формой существования материи. Основное свойство поля тяготения заключается в том, что на всякое тело массой т, внесенное в это поле, действует сила тяготения, т. е. (24.1)

Вектор g не зависит от m и называется напряженностью поля тяготения. Напряженность поля тяготения определяется силой, действующей со стороны поля на материальную точку единичной массы, и совпадает по направлению с действующей силой. Напряжен­ность есть силовая характеристика поля тяготения. Поле тяготения называется однородным, если его напряженность во всех точках одинакова, и центральным, если во всех точках поля векторы напряженности направ­лены вдоль прямых, которые пересекаются в одной точке (А), неподвижной по отноше­нию к какой-либо инерциальной системе отсчета (рис. 38). Для графического изображения силового поля используются силовые линии (линии напряженности). Силовые линии выбираются так, что вектор напряженности поля направлен по касательной к силовой линии.

Величина является энергетической характеристикой поля тяготения и называется потенциалом. Потенциал поля тяготения j - скалярная величина, определяемая потенциальной энер­гией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точки поля в бесконечность. Таким образом, потенциал поля тяготения, создаваемого телом массой М, равен (25.4) где R - расстояние от этого тела до рассматриваемой точки. Из формулы (25.4) вытекает, что геометрическое место точек с одинаковым потен­циалом образует сферическую поверхность (R =const). Такие поверхности, для которых потенциал постоянен, называются эквипотенциальными. Рассмотрим взаимосвязь между потенциалом (j ) поля тяготения и его напряжен­ностью (g). Из выражений (25.1) и (25.4) следует, что элементарная работа dA, совершаемая силами поля при малом перемещении тела массой т, равна

20. Давление в жидкостях и газах. Законы Паскаля и Архимеда .

Единица давления -паскаль (Па): 1 Па равен давлению, создаваемому силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1м 2 (1 Па=1 Н/м 2).

Давление при равновесии жидкостей (газов) подчиняетсязакону Паскаля: давле­ние в любом месте покоящейся жидкости одинаково по воем направлениям, при­чем давление одинаково передается по всему объему, занятому покоящейся жидкос­тью. Рассмотрим, как влияет вес жидкости на распределение давления внутри покоящей­ся несжимаемой жидкости. При равновесии жидкости давление по горизонтали всегда одинаково, иначе не было бы равновесия. Поэтому свободная поверхность покоящейся жидкости всегда горизонтальна вдали от стенок сосуда. Если жидкость несжимаема, то ее плотность не зависит от давления. Тогда при поперечном сечении S столба жид­кости, его высоте h и плотности r вес P=rgSh, а давление на нижнее основание

(28.1) т. е. давление изменяется линейно с высотой. Давление rgh называетсягидростатичес­ким давлением. Согласно формуле (28.1), сила давления на нижние слои жидкости будет больше, чем на верхние, поэтому на тело, погруженное в жидкость, действует сила, определя­емая законом Архимеда: на тело, погруженное в жидкость (газ), действует со стороны этой жидкости направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости (газа): F А =PgV, где р - плотность жидкости, V- объем погруженного в жидкость тела.

21. Линия и трубка тока. Теорема о неразрывности струи .

Движение жидкостей называется течением, а совокупность частиц движущейся жид­кости - потоком. Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 45). Линии тока проводятся так, чтобы густота их, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Таким образом, по картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т. е. можно определить состояние движения жидкости. Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.

Рассмотрим какую-либо трубку тока. Выберем два ее сечения S 1 и S 2 , перпен­дикулярные направлению скорости (рис. 46). За время Dt через сечение S проходит объем жидкости Sv Dt; следовательно, за 1 с через S 1 пройдет объем жидкости S 1 v 1 , где v 1 - скорость течения жидкости в месте сечения S 1 . Через сечение S 2 за 1 с пройдет объем жидкости S 2 v 2 , где v 2 - скорость течения жидкости в месте сечения S 2 . Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (r=const), то через сечение S 2 пройдет такой же объем жидкости, как и через сечение S 1 , т. е. (29.1) Следовательно, произведение скорости течения несжимаемой жидкости на попереч­ное сечение трубки тока есть величина постоянная для данной трубки тока. Соотноше­ние (29.1) называется уравнением неразрывности для несжимаемой жидкости.

Уравнение Бернулли

Согласно уравнению неразрывности для несжимаемой жидкости , объем, занимаемый жидкостью, остается постоянным, т. е. Разделив выражение (30.5) на DV, получим где р - плотность жидкости. Но так как сечения выбирались произвольно, то можем записать (30.6)

Выражение (30.6) выведено швейцарским физиком Д. Бернулли и называется уравнением Бернулли. Как видно из его вывода, уравнение Бернулли - выражение закона сохранения энергии применительно к устано­вившемуся течению идеальной жидкости. Оно хорошо выполняется и для реальных жидкостей, внутреннее трение которых не очень велико. Величина р в формуле (30.6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела), величина rv 2 / 2 - динамическим давлением. Как уже указывалось выше, величина rgh представляет собой гидростатическое давление.

Для горизонтальной трубки тока (h 1 =h 2 ) выражение (30.6) принимает вид (30.7)

где p+rv 2 / 2 называется полным давлением. Из уравнения Бернулли (30.7) для горизонтальной трубки тока и уравнения нераз­рывности (29.1) следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давле­ние больше в более широких местах, т. е. там, где скорость меньше. Это можно продемонстрировать, установив вдоль трубы ряд манометров (рис. 48).

23. Формула Торричелли .

Рассмотрим цилиндрический сосуд с жид­костью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие (рис. 51). Рассмотрим два сечения (на уровне h 1 свободной поверхности жидкости в сосуде и на уровне h 2 выхода ее из отверстия) и напишем уравнение Бернулли:

Так как давления р 1 и р 2 в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р 1 =р 2 , то уравнение будет иметь вид

Из уравнения неразрывности (29.1) следует, что v 2 /v 1 =S 1 /S 2 , где S 1 и S 2 - площади поперечных сечений сосуда и отверстия. Если S 1 >>S 2 , то членом v /2 можно пренебречь и

Это выражение получило название формулы Торричелли. Формула для скорости истечения жидкости из отверстия в открытом сосуде

24. Вязкость, закон Ньютона. Режимы течения .

Вязкость (внутреннее трение) - это свойство реальных жидкостей оказывать сопротив­ление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявля­ется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медлен­нее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.

Сила внутреннего трения F тем больше, чем больше рассматриваемая площадь поверхности слоя S (рис. 52), и зависит от того, насколько быстро меняется скорость течения жидкости при переходе от слоя к слою. Направление, в котором отсчитывается расстояние между слоями, перпендикулярно скорости течения слоев. Величина показывает, как быстро меняется скорость при переходе от слоя к слою в направлении х, перпендикулярном направле­нию движения слоев, и называется градиентом скорости. Таким образом, модуль силы внутреннего трения (31.1), где коэффициент пропорциональности m , зависящий от природы жидкости, называется динамической вязкостью (или просто вязкостью). Единица вязкости - паскаль-секунда (Па×с). Чем больше вязкость, тем сильнее жидкость отличается от идеальной, тем большие силы внутреннего трения в ней возникают. Существует два режима течения жидкостей. Течение называется ламинарным (слоис­тым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними, и турбулентным (вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости (газа). Ламинарное течение жидкости наблюдается при небольших скоростях ее движения. Внешний слой жидкости, примыкающий к поверхности трубы, в которой она течет, из-за сил молекулярного сцепления прилипает к ней и остается неподвижным. Профиль усредненной скорости при турбулентном течении в трубах (рис. 53) отличается от параболического профиля при ламинарном течении более быстрым возрастанием скорости у стенок трубы и меньшей кривизной в центральной части течения. Характер течения зависит от безразмерной величины, называемойчислом Рейнольдса : где n = h/p- кинематическая вязкость; р- плотность жидкости; <v >-средняя по сечению трубы скорость жидкости; d - характерный линейный размер, например диаметр трубы. При малых значениях числа Рейнольдса наблюдается ламинарное тече­ние, переход от ламинарного течения к турбулентному происходит в области а при (для гладких труб) течение-турбулентное.

26. Формула Пуазейля. Методы определения вязкости.

Метод Стокса. Этот метод определения вязкости основан на измерении скорости медленно движущихся в жидкости небольших тел сферической формы. На шарик, падающий в жидкости вертикально вниз, действуют три силы: сила тяжести Р= 4 / 3 pr 3 rg (r - плотность шарика), сила Архимеда Р= 4 / 3 pr 3 r"g (r" - пло­тность жидкости) и сила сопротивления, эмпирически установленная Дж. Стоксом: F= 6phrv, где r - радиус шарика, v - его скорость. При равномерном движении шарика откуда

Измерив скорость равномерного движения шарика, можно определить вязкость жид­кости (газа). Метод Пуазейля. Этот метод основан на ламинарном течении жидкости в тонком капилляре. Рассмотрим капилляр радиусом R и длиной l . В жидкости мысленно выделим цилиндрический слой радиусом r и толщиной dr (рис. 54). Сила внутреннего трения (см. (31.1)), действующая на боковую поверхность этого слоя, где dS - боковая поверхность цилиндрического сло я; знак минус означает, что при возрастании радиуса скорость уменьшается. После интегрирования, полагая, что у стенок имеет место прилипание жидкости, т. е. скорость на расстоянии R от оси равна нулю, получаем За время t из трубы вытечет жидкость, объем которой откуда вязкость

27. Уравнение свободных гармонических колебаний для маятников .

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воз­действий на колебательную систему (систему, совершающую колебания). Простейшим типом колебаний являются гармонические колебания - колебания, при которых колеб­лющаяся величина изменяется со временем по закону синуса (косинуса). Пружинный маятник - это груз массой т , подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = –kx, где k - жесткость пружины. Уравнение движения маятника

Из выражений следует, что пружинный маятник совершает гармоничес­кие колебания по закону х=А соs (w 0 t + j ) с циклической частотой (142.2) и периодом (142.3) Формула (142.3) справедлива для упругих колебаний в пределах, в которых выполняет­ся закон Гука, т. е. когда масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника равна Физический маятник - это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О , не совпадающую с центром масс С тела (рис. 201). Если маятник отклонен из положения равновесия на некоторый угол a, то в соот­ветствии с уравнением динамики вращательного движения твердого тела (18.3) момент M возвращающей силы можно записать в виде (142.4) где J - момент инерции маятника относительно оси, проходящей через точку подве­са О, l – расстояние между ней и центром масс маятника, F t = –mg sina » –mga. - возвращающая сила (знак минус обусловлен тем, что направления F t и a всегда противоположны; sina »a соответствует малым колебаниям маятника, т.е. малым отклонениям маятника из положения равновесия). При малых колебаниях физический маятник совершает гармонические колебания с циклической частотой w 0 и периодом

Где L=J/ (ml ) - приведенная длина физического маятника.

Математический маятник - это идеализированная система, состоящая из материальной точки массой т, подвешенной на нерастяжимой невесомой нити, и колеб­лющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити. Момент инерции математического маятника

(142.8) где l - длина маятника. Так как математический маятник можно представить как частный случай физичес­кого маятника, предположив, что вся его масса сосредоточена в одной точке - центре масс, то, подставив выражение (142.8) в формулу (1417), получим выражение для периода малых колебаний математического маятника (142.9) Сравнивая формулы (142.7) и (142.9), видим, что если приведенная длина L физичес­кого маятника равна длине l математического маятника, то периоды колебаний этих маятников одинаковы. Следовательно, приведенная длина физического маятника - это длина такого математического маятника, период колебаний которого совпадает с пери­одом колебаний данного физического маятника.

28. Кинематика свободных гармонических колебаний .

Механическое гармоническое колебание - это прямолинейное неравномерное движение, при котором координаты колеблющегося тела (материальной точки) изменяются по закону косинуса или синуса в зависимости от времени. Согласно этому определению, закон изменения координаты в зависимости от времени имеет вид: , где wt - величина под знаком косинуса или синуса; w- коэффициент, физический смысл которого раскроем ниже; А - амплитуда механических гармонических колебаний. Уравнения (4.1) являются основными кинематическими уравнениями механических гармонических колебаний.

для материальной точки, совершающей гармонические механические колебания, величину w можно интерпретировать как количество колебаний за определенный цикл времени, равный 2л. Поэтому величину w назвали циклической (или круговой) частотой. Если точка М начинает свое движение не из точки 1 а из точки 2, то уравнение (4,1) примет вид: Величину ф0 называют начальной фазой.

29. Затухающие колебания .

Рассмотрим свободные затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются. Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде

(146.1), где s – колеблющаяся величина, описывающая тот или иной физический процесс, d=const - коэффициент затухания, w 0 - циклическая частота свободных незатуха­ющих колебаний той же колебательной системы, т. е. при d= 0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.

- амплитуда затухающих колебаний, а А 0 - начальная амплитуда. Если A(t) и А (t + Т) - амплитуды двух последовательных колебаний, соответст­вующих моментам времени, отличающимся на период, то отношение называетсядекрементом затухания, а его логарифм (146.7)- логарифмическим декрементом затухания; N e - число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания - по­стоянная для данной колебательной системы величина. Для характеристики колебательной системы пользуются понятиемдобротности Q, которая при малых значениях логарифмического декремента равна (146.8). Из формулы (146.8) следует, что добротность пропорциональна числу колебаний N e , совершаемых системой за время релаксации.

30. Вынужденные колебания, резонанс .

Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с., называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями. Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты w . Меха­нические и электромагнитные колебания будем рассматривать одновременно, называя колеблющуюся величину либо смещением (х) колеблющегося тела из положения равновесия, либо зарядом (Q) конденсатора.

Из формулы (147.8) следует, что амплитуда А смещения (заряда) имеет максимум. Чтобы определить резонансную частоту w рез, - частоту, при которой амплитуда А сме­щения (заряда) достигает максимума, - нужно найти максимум функции (147.8), или, что то же самое, минимум подкоренного выражения. Продифференцировав подкорен­ное выражение по w и приравняв его нулю, получим условие, определяющее w рез: Это равенство выполняется при w =0, ± , у которых только лишь положи­тельное значение имеет физический смысл. Следовательно, резонансная частота (148.1) Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к ча­стоте, равной или близкой собственной частоте колебательной системы, называется резонансом (соответственно механическим или электрическим). При значение w рез практически совпадает с собственной частотой w 0 колебательной системы. Подста­вляя (148.1) в формулу (147.8), получим (148.2)

На рис. 210 приведены зависимости амплитуды вынужденных колебаний от часто­ты при различных значениях d. Из (148.1) и (148.2) вытекает, что чем меньше d , тем выше и правее лежит максимум данной кривой. Если w ® 0, то все кривые (см. также (147.8)) достигают одного в того же, отличного от нуля, предельного значения , которое называют статическим отклонением. В случае механических колебаний , в случае электромагнитных – U m / (L ). Если w ®¥, то вое кривые асимптотически стремятся к нулю. Приведенная совокупность кривых называется резонансными кривыми.

Закон сохранения энергии утверждает, что энергия тела никогда не исчезает и не появляется вновь, она может лишь превращаться из одного вида в другой. Этот закон универсален. В различных разделах физики он имеет свою формулировку. Классическая механика рассматривает закон сохранения механической энергии.

Полная механическая энергия замкнутой системы физических тел, между которыми действуют консервативные силы, является величиной постоянной. Так формулируется закон сохранения энергии в механике Ньютона.

Замкнутой, или изолированной, принято считать физическую систему, на которую не действуют внешние силы. В ней не происходит обмена энергией с окружающим пространством, и собственная энергия, которой она обладает, остаётся неизменной, то есть сохраняется. В такой системе действуют только внутренние силы, и тела взаимодействуют друг с другом. В ней могут происходить лишь превращения потенциальной энергии в кинетическую и наоборот.

Простейший пример замкнутой системы – снайперская винтовка и пуля.

Виды механических сил

Силы, которые действуют внутри механической системы, принято разделять на консервативные и неконсервативные.

Консервативными считаются силы, работа которых не зависит от траектории движения тела, к которому они приложены, а определяется только начальным и конечным положением этого тела. Консервативные силы называют также потенциальными . Работа таких сил по замкнутому контуру равна нулю. Примеры консервативных сил – сила тяжести, сила упругости .

Все остальные силы называются неконсервативными . К ним относятся сила трения и сила сопротивления . Их называют также диссипативными силами. Эти силы при любых движениях в замкнутой механической системе совершают отрицательную работу, и при их действии полная механическая энергия системы убывает (диссипирует). Она переходит в другие, не механические виды энергии, например, в теплоту. Поэтому закон сохранения энергии в замкнутой механической системе может выполняться, только если неконсервативные силы в ней отсутствуют.

Полная энергия механической системы состоит из кинетической и потенциальной энергии и является их суммой. Эти виды энергий могут превращаться друг в друга.

Потенциальная энергия

Потенциальную энергию называют энергией взаимодействия физических тел или их частей между собой. Она определяется их взаимным расположением, то есть, расстоянием между ними, и равна работе, которую нужно совершить, чтобы переместить тело из точки отсчёта в другую точку в поле действия консервативных сил.

Потенциальную энергию имеет любое неподвижное физическое тело, поднятое на какую-то высоту, так как на него действует сила тяжести, являющаяся консервативной силой. Такой энергией обладает вода на краю водопада, санки на вершине горы.

Откуда же эта энергия появилась? Пока физическое тело поднимали на высоту, совершили работу и затратили энергию. Вот эта энергия и запаслась в поднятом теле. И теперь эта энергия готова для совершения работы.

Величина потенциальной энергии тела определяется высотой, на которой находится тело относительно какого-то начального уровня. За точку отсчёту мы можем принять любую выбранную нами точку.

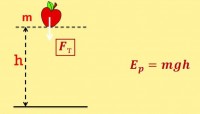
Если рассматривать положение тела относительно Земли, то потенциальная энергия тела на поверхности Земли равна нулю. А на высоте h она вычисляется по формуле:

Е п = m ɡ h ,

где m – масса тела

ɡ - ускорение свободного падения

h – высота центра масс тела относительно Земли

ɡ = 9,8 м/с 2

При падении тела c высоты h 1 до высоты h 2 сила тяжести совершает работу. Эта работа равна изменению потенциальной энергии и имеет отрицательное значение, так как величина потенциальной энергии при падении тела уменьшается.

A = - ( E п2 – E п1) = - ∆ E п ,

где E п1 – потенциальная энергия тела на высоте h 1 ,

E п2 - потенциальная энергия тела на высоте h 2 .

Если же тело поднимают на какую-то высоту, то совершают работу против сил тяжести. В этом случае она имеет положительное значение. А величина потенциальной энергии тела увеличивается.

Потенциальной энергией обладает и упруго деформированное тело (сжатая или растянутая пружина). Её величина зависит от жёсткости пружины и от того, на какую длину её сжали или растянули, и определяется по формуле:

Е п = k·(∆x) 2 /2 ,

где k – коэффициент жёсткости,

∆x – удлинение или сжатие тела.

Потенциальная энергии пружины может совершать работу.

Кинетическая энергия

В переводе с греческого «кинема» означает «движение». Энергия, которой физическое тело получает вследствие своего движения, называется кинетической. Её величина зависит от скорости движения.

Катящийся по полю футбольный мяч, скатившиеся с горы и продолжающие двигаться санки, выпущенная из лука стрела – все они обладают кинетической энергией.

Если тело находится в состоянии покоя, его кинетическая энергия равна нулю. Как только на тело подействует сила или несколько сил, оно начнёт двигаться. А раз тело движется, то действующая на него сила совершает работу. Работа силы, под воздействием которой тело из состояния покоя перейдёт в движение и изменит свою скорость от нуля до ν , называется кинетической энергией тела массой m .

Если же в начальный момент времени тело уже находилось в движении, и его скорость имела значение ν 1 , а в конечный момент она равнялась ν 2 , то работа, совершённая силой или силами, действующими на тело, будет равна приращению кинетической энергии тела.

∆ E k = E k 2 - E k 1

Если направление силы совпадает с направлением движения, то совершается положительная работа, и кинетическая энергия тела возрастает. А если сила направлена в сторону, противоположную направлению движения, то совершается отрицательная работа, и тело отдаёт кинетическую энергию.

Закон сохранения механической энергии

Е k 1 + Е п1 = Е k 2 + Е п2

Любое физическое тело, находящееся на какой-то высоте, имеет потенциальную энергию. Но при падении оно эту энергию начинает терять. Куда же она девается? Оказывается, она никуда не исчезает, а превращается в кинетическую энергию этого же тела.

Предположим, на какой-то высоте неподвижно закреплён груз. Его потенциальная энергия в этой точке равна максимальному значению. Если мы отпустим его, он начнёт падать с определённой скоростью. Следовательно, начнёт приобретать кинетическую энергию. Но одновременно начнёт уменьшаться его потенциальная энергия. В точке падения кинетическая энергия тела достигнет максимума, а потенциальная уменьшится до нуля.

Потенциальная энергия мяча, брошенного с высоты, уменьшается, а кинетическая энергия возрастает. Санки, находящиеся в состоянии покоя на вершине горы, обладают потенциальной энергией. Их кинетическая энергия в этот момент равна нулю. Но когда они начнут катиться вниз, кинетическая энергия будет увеличиваться, а потенциальная уменьшаться на такую же величину. А сумма их значений останется неизменной. Потенциальная энергия яблока, висящего на дереве, при падении превращается в его кинетическую энергию.

Эти примеры наглядно подтверждают закон сохранения энергии, который говорит о том, что полная энергия механической системы является величиной постоянной . Величина полной энергии системы не меняется, а потенциальная энергия переходит в кинетическую и наоборот.

На какую величину уменьшится потенциальная энергия, на такую же увеличится кинетическая. Их сумма не изменится.

Для замкнутой системы физических тел справедливо равенство
E k1 + E п1 = E k2 + E п2 ,
где E k1 , E п1 - кинетическая и потенциальная энергии системы до какого-либо взаимодействия, E k2 , E п2 - соответствующие энергии после него.

Процесс преобразования кинетической энергии в потенциальную и наоборот можно увидеть, наблюдая за раскачивающимся маятником.

Нажать на картинку

Находясь в крайне правом положении, маятник словно замирает. В этот момент его высота над точкой отсчёта максимальна. Следовательно, максимальна и потенциальная энергия. А кинетическая равна нулю, так как он не движется. Но в следующее мгновение маятник начинает движение вниз. Возрастает его скорость, а, значит, увеличивается кинетическая энергия. Но уменьшается высота, уменьшается и потенциальная энергия. В нижней точке она станет равной нулю, а кинетическая энергия достигнет максимального значения. Маятник пролетит эту точку и начнёт подниматься вверх налево. Начнёт увеличиваться его потенциальная энергия, а кинетическая будет уменьшаться. И т.д.

Для демонстрации превращений энергии Исаак Ньютон придумал механическую систему, которую называют колыбелью Ньютона или шарами Ньютона .

Нажать на картинку

Если отклонить в сторону, а затем отпустить первый шар, то его энергия и импульс передадутся последнему через три промежуточных шара, которые останутся неподвижными. А последний шар отклонится с такой же скоростью и поднимется на такую же высоту, что и первый. Затем последний шар передаст свою энергию и импульс через промежуточные шары первому и т. д.

Шар, отведенный в сторону, обладает максимальной потенциальной энергией. Его кинетическая энергия в этот момент нулевая. Начав движение, он теряет потенциальную энергию и приобретает кинетическую, которая в момент столкновения со вторым шаром достигает максимума, а потенциальная становится равной нулю. Далее кинетическая энергия передаётся второму, затем третьему, четвёртому и пятому шарам. Последний, получив кинетическую энергию, начинает двигаться и поднимается на такую же высоту, на которой находился первый шар в начале движения. Его кинетическая энергия в этот момент равна нулю, а потенциальная равна максимальному значению. Далее он начинает падать и точно так же передаёт энергию шарам в обратной последовательности.

Так продолжается довольно долго и могло бы продолжаться до бесконечности, если бы не существовало неконсервативных сил. Но в реальности в системе действуют диссипативные силы, под действием которых шары теряют свою энергию. Постепенно уменьшается их скорость и амплитуда. И, в конце концов, они останавливаются. Это подтверждает, что закон сохранения энергии выполняется только в отсутствии неконсервативных сил.

Полная механическая энергия характеризует движение и взаимодействие тел, следовательно, зависит от скоростей и взаимного расположения тел.

Полная механическая энергия замкнутой механической системы равна сумме кинетической и потенциальной энергии тел этой системы:

Закон сохранения энергии

Закон сохранения энергии - фундаментальный закон природы.

В ньютоновской механике закон сохранения энергии формулируется следующим образом:

Полная механическая энергия изолированной (замкнутой) системы тел остаётся постоянной.

Другими словами:

Энергия не возникает из ничего и не исчезает никуда, она может только переходить из одной формы в другую.

Классическими примерами этого утверждения являются: пружинный маятник и маятник на нити (с пренебрежимо малым затуханием). В случае пружинного маятника в процессе колебаний потенциальная энергия деформированной пружины (имеющая максимум в крайних положениях груза) переходит в кинетическую энергию груза (достигающую максимума в момент прохождения грузом положения равновесия) и обратно. В случае маятника на нити потенциальная энергия груза переходит в кинетическую энергию и обратно.

2 Оборудование

2.1 Динамометр.

2.2 Штатив лабораторный.

2.3 Груз массой 100 г – 2шт.

2.4 Линейка измерительная.

2.5 Кусочек мягкой ткани или войлока.

3 Теоретическое обоснование

Схема экспериментальной установки приведена на рисунке 1.

Динамометр укреплен вертикально в лапке штатива. На штатив по­мещают кусочек мягкой ткани или войлока. При подвешивании к ди­намометру грузов растяжение пружины динамометра определяется положением указателя. При этом максимальное удлинение (или стати­ческое смещение) пружины х 0 возникает тогда, когда сила упругости пружины с жесткостью k уравновешивает силу тяжести груза массой т:

kx 0 =mg, (1)

где g = 9,81- ускорение свободного падения.

Следовательно,

Статическое смещение характеризует новое положение равновесия О" нижнего конца пружины (рис. 2).

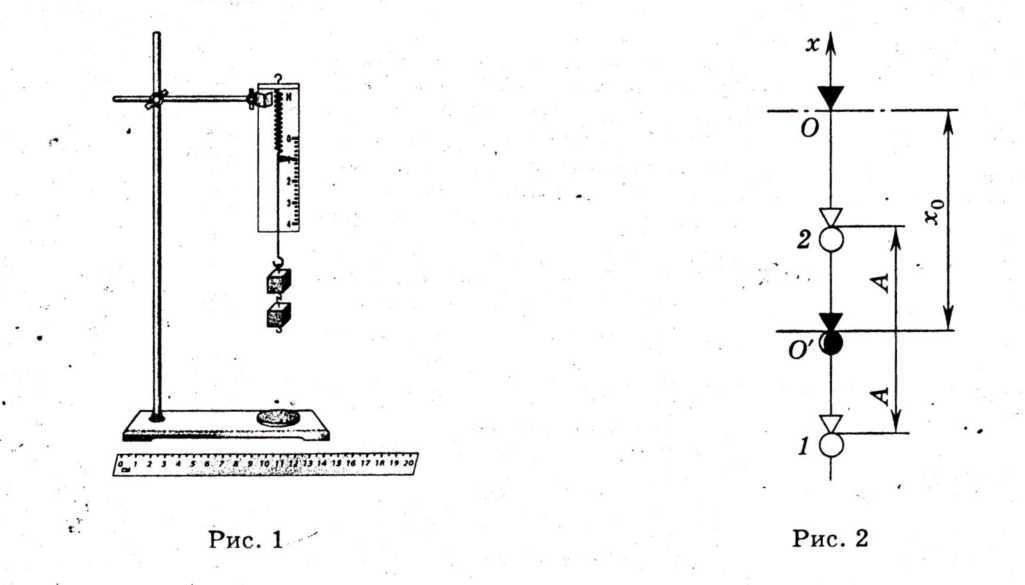
Если груз оттянуть вниз на расстояние А от точки О" и отпустить в точке 1, то возникают периодические колебания груза. В точках 1 и 2, называемых точками поворота, груз останавливается, изменяя на­правление движения на противоположное. Поэтому в этих точках ско­рость груза v = 0.

Максимальной скоростью v m ax груз будет обладать в средней точ­ке О". На колеблющийся груз действуют две силы: постоянная сила тяжести mg и переменная сила упругости kx. Потенциальная энергия тела в гравитационном поле в произвольной точке с координатой х равна mgx. Потенциальная энергия деформированного тела соответственно равна .

При этом за нуль отсчета потенциальной энергии для обеих сил принята точка х = 0, соответствующая положению указателя для не­растянутой пружины.

Полная механическая энергия груза в произвольной точке скла­дывается из его потенциальной и кинетической энергии. Пренебрегая силами трения, воспользуемся законом сохранения полной механиче­ской энергии.

Приравняем полную механическую энергию груза в точке 2 с коор­динатой -(х 0 -А) и в точке О" с координатой -х 0 :

Раскрывая скобки и проводя несложные преобразования, приведем формулу (3) к виду

Тогда модуль максимальной скорости грузов

Жесткость пружины можно найти, измерив статическое смещение х 0 . Как следует из формулы (1),

3.5. Законы сохранения и изменения энергии

3.5.1. Закон изменения полной механической энергии

Изменение полной механической энергии системы тел происходит при совершении работы силами, действующими как между телами системы, так и со стороны внешних тел.

Изменение механической энергии ∆E системы тел определяется законом изменения полной механической энергии :

∆E = E 2 − E 1 = A внеш + A тр(сопр) ,

где E 1 - полная механическая энергия начального состояния системы; E 2 - полная механическая энергия конечного состояния системы; A внеш - работа, совершаемая над телами системы внешними силами; A тр(сопр) - работа, совершаемая силами трения (сопротивления), действующими внутри системы.

Пример 30. На некоторой высоте покоящееся тело имеет потенциальную энергию, равную 56 Дж. К моменту падения на Землю тело имеет кинетическую энергию, равную 44 Дж. Определить работу сил сопротивления воздуха.

Решение. На рисунке показаны два положения тела: на некоторой высоте (первое) и к моменту падения на Землю (второе). Нулевой уровень потенциальной энергии выбран на поверхности Земли.

Полная механическая энергия тела относительно поверхности Земли определяется суммой потенциальной и кинетической энергии:

• на некоторой высоте

E 1 = W p 1 + W k 1 ;

• к моменту падения на Землю

E 2 = W p 2 + W k 2 ,

где W p 1 = 56 Дж - потенциальная энергия тела на некоторой высоте; W k 1 = 0 - кинетическая энергия покоящегося на некоторой высоте тела; W p 2 = 0 Дж - потенциальная энергия тела к моменту падения на Землю; W k 2 = 44 Дж - кинетическая энергия тела к моменту падения на Землю.

Работу сил сопротивления воздуха найдем из закона изменения полной механической энергии тела:

где E 1 = W p 1 - полная механическая энергия тела на некоторой высоте; E 2 = W k 2 - полная механическая энергия тела к моменту падения на Землю; A внеш = 0 - работа внешних сил (внешние силы отсутствуют); A сопр - работа сил сопротивления воздуха.

Искомая работа сил сопротивления воздуха, таким образом, определяется выражением

A сопр = W k 2 − W p 1 .

Произведем вычисление:

A сопр = 44 − 56 = −12 Дж.

Работа сил сопротивления воздуха является отрицательной величиной.

Пример 31. Две пружины с коэффициентами жесткости 1,0 кН/м и 2,0 кН/м соединены параллельно. Какую работу нужно совершить, чтобы растянуть систему пружин на 20 см?

Решение. На рисунке показаны две пружины с разными коэффициентами жесткости, соединенные параллельно.

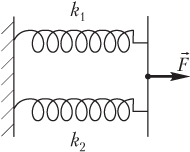
Внешняя сила F → , растягивающая пружины, зависит от величины деформации составной пружины, поэтому расчет работы указанной силы по формуле для вычисления работы постоянной силы неправомерен.

Для расчета работы воспользуемся законом изменения полной механической энергии системы:

E 2 − E 1 = A внеш + A сопр,

где E 1 - полная механическая энергия составной пружины в недеформированном состоянии; E 2 - полная механическая энергия деформированной пружины; A внеш - работа внешней силы (искомая величина); A сопр = 0 - работа сил сопротивления.

Полная механическая энергия составной пружины представляет собой потенциальную энергию ее деформации:

• для недеформированной пружины

E 1 = W p 1 = 0,

• для растянутой пружины

E 2 = W p 2 = k общ (Δ l) 2 2 ,

где k общ - общий коэффицент жесткости составной пружины; ∆l - величина растяжения пружины.

Общий коэффициент жесткости двух пружин, соединенных параллельно, есть сумма

k общ = k 1 + k 2 ,

где k 1 - коэффициент жесткости первой пружины; k 2 - коэффициент жесткости второй пружины.

Работу внешней силы найдем из закона изменения полной механической энергии тела:

A внеш = E 2 − E 1 ,

подставив в данное выражение формулы, определяющие E 1 и E 2 , а также выражение для общего коэффициента жесткости составной пружины:

A внеш = k общ (Δ l) 2 2 − 0 = (k 1 + k 2) (Δ l) 2 2 .

Выполним расчет:

A внеш = (1,0 + 2,0) ⋅ 10 3 ⋅ (20 ⋅ 10 − 2) 2 2 = 60 Дж.

Пример 32. Пуля массой 10,0 г, летящая со скоростью 800 м/с, попадает в стену. Модуль силы сопротивления движению пули в стене постоянен и составляет 8,00 кН. Определить, на какое расстояние пуля углубится в стену.

Решение. На рисунке показаны два положения пули: при ее подлете к стене (первое) и к моменту остановки (застревания) пули в стене (второе).

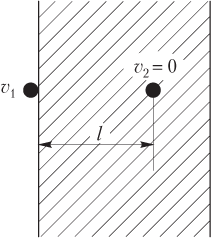
Полная механическая энергия пули яв­ляется кинетической энергией ее движения:

• при подлете пули к стене

E 1 = W k 1 = m v 1 2 2 ;

• к моменту остановки (застревания) пули в стене

E 2 = W k 2 = m v 2 2 2 ,

где W k 1 - кинетическая энергия пули при подлете к стене; W k 2 - кинетическая энергия пули к моменту ее остановки (застревания) в стене; m - масса пули; v 1 - модуль скорости пули при подлете к стене; v 2 = 0 - величина скорости пули к моменту остановки (застревания) в стене.

Расстояние, на которое пуля углубится в стену, найдем из закона изменения полной механической энергии пули:

E 2 − E 1 = A внеш + A сопр,

где E 1 = m v 1 2 2 - полная механическая энергия пули при подлете к стене; E 2 = 0 - полная механическая энергия пули к моменту ее остановки (застревания) в стене; A внеш = 0 - работа внешних сил (внешние силы отсутствуют); A сопр - работа сил сопротивления.

Работа сил сопротивления определяется произведением:

A сопр = F сопр l cos α ,

где F сопр - модуль силы сопротивления движению пули; l - расстояние, на которое углубится пуля в стену; α = 180° - угол между направлениями силы сопротивления и направлением движения пули.

Таким образом, закон изменения полной механической энергии пули в явном виде выглядит следующим образом:

− m v 1 2 2 = F сопр l cos 180 ° .

Искомое расстояние определяется отношением

l = − m v 1 2 2 F сопр cos 180 ° = m v 1 2 2 F сопр

l = 10,0 ⋅ 10 − 3 ⋅ 800 2 2 ⋅ 8,00 ⋅ 10 3 = 0,40 м = 400 мм.

Cтраница 1

Полная механическая энергия тела не изменяется. Энергия только превращается из одного вида в другой.  

Полная механическая энергия тела, на которое не действуют силы трения и сопротивления, в процессе его движения остается неизменной.  

Полной механической энергией тела называют сумму его кинетической и потенциальной энергий. Рассмотрим полную энергию свободно падающего тела в различные моменты времени.  

Изменяется ли полная механическая энергия тела при его падении.  

Что называют полной механической энергией тела.  

Таким образом, полная механическая энергия тела, совершающего гармонические колебания, пропорциональна квадрату амплитуды колебаний. Поэтому амплитуда А колебаний тоже не зависит от времени.  

Как видно из (44.13), полная механическая энергия тела при затухающих колебаниях уменьшается со временем по экспоненциальному закону.  

Сумма кинетической и потенциальной энергий образует полную механическую энергию тела.  

Абсолютно упругим называется такой удар, при котором полная механическая энергия тел сохраняется. Сначала кинетическая энергия частично или полностью переходит в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую и тела разлетаются со скоростями, определяемыми двумя - условиями - сохранением суммарной энергии и суммарного импульса тел.  

Абсолютно упругим называется такой удар, при котором полная механическая энергия тел сохраняется. Сначала кинетическая энергия частично или полностью переходит в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге Потенциальная энергия упругой деформации снова переходит в кинетическую и тела разлетаются со скоростями, определяемыми двумя условиями - сохранением суммарной энергии и суммарного импульса тел.  

Абсолютно упругим называется такой удар, при котором полная механическая энергия тел сохраняется. Сначала кинетическая энергия частично или полностью переходит в потенциальную энергию упру-i гой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую и тела разлетаются со скоростями, определяемыми двумя условиями - сохранением суммарной энергии и суммарного импульса тел.  

Эта работа расходуется на диссипацию энергии или изменение полной механической энергии тела.  

Согласно закону изменения энергии (см. § 28) работа силы сопротивления (сторонней силы) равна приращению полной механической энергии тела.  

Этот результат предсказуем, поскольку упругая сила, под действием которой движется тело, является консервативной, следовательно, выполняется за кон сохранения энергии - полная механическая энергия тела сохраняется.  

Механическая энергия характеризует способность тела совершать механическую работу. Полная механическая энергия тела складывается из кинетической и потенциальной энергии.