Конспект лекций по предмету

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

Для студентов специальности:

260501.65 Технология продуктов общественного питания,

форма обучения - очная

Конспект лекций составлен на основе:

1. Буторин Л.В., Бусыгина Е.Б. Теоретическая механика. Учебно-практическое пособие. – М., МГУ ТУ, 2004

2. Тарг С.М. Краткий курс теоретической механики. – М.: Высшая школа, 2001г. - с.

3. Яблонский А.А., Никифорова В.Н. Курс теоретической механики. М. “Лань”, 2000г.

Введение

Современные промышленные производства, в том числе пищевые, являются высокомеханизированными производствами. На технологическое оборудование возлагается решение все более сложных задач, что в свою очередь ведет к усложнению оборудования. Формирование современного инженера немыслимо без знания фундаментальных дисциплин. Одной из таких дисциплин является теоретическая механика .

Теоретическая механика – раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел.Механическим движением называется изменение с течением времени взаимного положения в пространстве материальных тел, механическим взаимодействием – такое взаимодействие, в результате которого изменяется механическое движение или изменяется взаимное положение частей тела.

Теоретическую механику принято делить на: статику, кинематику и динамику .

В статике изучаются условия равновесия материальных тел и методы тождественного преобразования системы сил. Равновесие – это состояние, при котором тело при действии сил остается неподвижным или движется равномерно прямолинейно.

В кинематике рассматриваются общие геометрические характеристики движения тел. Действующие на тело силы не рассматриваются. Закон движения задается. Закон движения тела – это зависимость положения тела в пространстве от времени.

В динамике изучают общие законы движения тел под действием сил.

1. C татика твердого тела

1.1 Основные понятия статики

Абсолютно твердое тело (твердое тело, тело) – материальное тело, расстояние между любыми точками в котором не изменяется. Следствие размеры и форма тела не изменяются.

Материальная точка – тело, размерами которого по условиям задачи можно пренебречь.

Свободное тело – тело, на перемещение которого не наложено никаких ограничений.

Несвободное (связанное) тело – тело, на перемещение которого наложены ограничения.

Связи – тела, препятствующие перемещению рассматриваемого объекта (тела или системы тел).

Механическая система – совокупность взаимосвязанных между собой тел или материальных точек.

Твердое тело можно рассматривать как механическую систему, положения и расстояние между точками которой не изменяются.

Сила – векторная величина, характеризующая механическое действие одного материального тела на другое.

Сила как вектор характеризуется точкой приложения, направлением действия и абсолютным значением (рис.1.1). Единица измерения модуля силы – Ньютон.

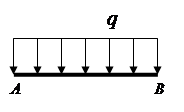Рис.1.1. Рис.1.2.

Линия действия силы – прямая, вдоль которой направлен вектор силы.

Сосредоточенная сила – сила, приложенная в одной точке.

Распределенные силы (распределенная нагрузка) – силы, действующие на все точки объема, поверхности или длины тела (рис.1.2).

Распределенная нагрузка задается силой, действующей на единицу объема (поверхности, длины).Размерность распределенной нагрузки – Н/м 3 (Н/м 2 , Н/м).

Внешняя сила – сила, действующая со стороны тела, не принадлежащего рассматриваемой механической системе.

Внутренняя сила – сила, действующая на материальную точку механической системы со стороны другой материальной точки, принадлежащей рассматриваемой системе.

Система сил – совокупность сил, действующих на механическую систему.

Плоская система сил – система сил, линии действия которых лежат в одной плоскости.

Пространственная система сил – система сил, линии действия которых не лежат в одной плоскости.

Система сходящихся сил – система сил, линии действия которых пересекаются в одной точке (рис.1.3).

Произвольная система сил – система сил, линии действия которых не пересекаются в одной точке.(рис.1.4)

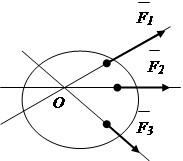Рис.1.3 Рис.1.4

Эквивалентные системы сил – такие системы сил, замена которых одна на другую не изменяет механического состояния тела. Принятое обозначение:

Уравновешенная система сил – система сил, которая будучи приложена к свободному твердому телу не изменяет его механического состояния (не выводит из равновесия).

Равнодействующая сила – сила, действие которой на тело эквивалентно действию системы сил.

Момент силы – величина, характеризующая вращающую способность силы.

Пара сил – система двух параллельных равных по модулю противоположно направленных сил. Принятое обозначение – ().Под действием пары сил тело будет совершать вращательное движение.

Проекция силы на ось – отрезок, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой оси (рис.1.5).

Проекция положительна, если направление отрезка совпадает с положительным направлением оси.

Проекция силы на плоскость – вектор на плоскости, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой плоскости (рис.1.6).

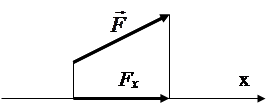
Рис.1.5 Рис.1.6

1.2. Аксиомы статики

В основе теоретических положений статики лежит ряд аксиом. Аксиома, это закон, сформулированный в результате обобщения результатов наблюдений.

1. Аксиома равновесия.

Две силы, действующие на твердое тело, уравновешиваются только в том случае, если они равны по модулю и действуют вдоль одной прямой в противоположные стороны (рис.1.7).

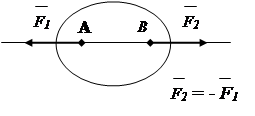
Рис.1.7 Рис.1.8

2. Аксиома присоединения (исключения) уравновешенной системы сил.

Действие системы сил на твердое тело не изменится, если к ней присоединить или исключить из нее уравновешенную систему сил (рис 1.8).

3. Аксиома о параллелограмме сил.

Система двух сил, приложенных в одной точке твердого тела, имеет равнодействующую, приложенную в той же точке. Вектор равнодействующей является диагональю параллелограмма, построенного на этих силах (рис.1.9).

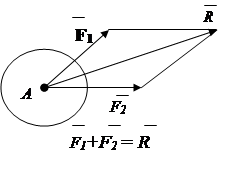
Рис. 1.9 Рис.1.10

4.Аксиома противодействия.

При действии одного твердого тела на другое возникает сила противодействия, равная по модулю, противоположно направленная действующей силе (рис.1.10).

Примечание. Силу, действие которой задано, называют активной силой , силу противодействия называют реакцией .

5.Аксиома связей.

Всякое несвободное тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие соответствующими реакциями.

1.3 Связи и их реакции

Тела, препятствующие перемещению рассматриваемого объекта, будем называть связями. Сила, с которой связь действует на рассматриваемый объект, называется реакцией связи . При определении возможных реакций связи следует исходить из того, что реакция это сила, препятствующая перемещению рассматриваемого тела. Реакция направлена в сторону, противоположную той, куда связь не позволяет перемещаться телу.

Рассмотрим некоторые часто встречающиеся связи.

Гладкая поверхность ограничивает перемещение по нормали к поверхности опоры. Реакция направлена перпендикулярно поверхности (рис.1.11).

Шарнирная подвижная опора ограничивает перемещение тела по нормали к опорной плоскости. Реакция направлена по нормали к поверхности опоры (рис.1.12)

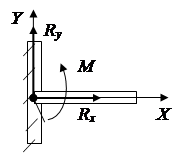
Шарнирная неподвижная опора противодействует любому перемещению в плоскости,перпендикулярной оси вращения. При расчетах реакцию Fr, как правило, представляют в виде двух составляющих по осям X и Y (рис.1.13).

Шарнирный невесомый стержень противодействует перемещению тела вдоль линии стержня. Реакция будет направлена вдоль линии стержня (рис.1.14).

Глухая заделка противодействует любому перемещению и вращению в плоскости (рис.1.15). Ее действие можно заменить силой, представленной в виде двух составляющих и парой сил с моментом.

Рис.1.11 Рис. 1.12 Рис.1.13 Рис.1.14 Рис.1.15

1.4 Момент силы относительно точки

Под действием силы твердое тело наряду с поступательным движением может совершать вращение вокруг того или иного центра. Вращательная способность силы характеризуется моментом силы. Вращательный эффект силы зависит от модуля силы, расстояния от центра до линии действия силы, направления поворота в плоскости вращения.

Абсолютное значение момента равно произведению модуля силы на кратчайшее расстояние h от центра вращения до линии действия силы. Расстояние h называют плечом силы (рис.1.16).

М 0 () = F×h , (1.1)

Момент считают положительным, если сила стремится вращать плечо h против хода часовой стрелки и отрицательным при вращении по ходу часовой стрелки.

Свойства момента силы относительно точки:

1. Момент силы не изменится при переносе точки приложения силы вдоль линии действия силы.

2. Момент силы равен нулю, если линия действия силы проходит через точку приложения силы.

3. Момент равнодействующей силы относительно точки равен сумме моментов слагаемых сил относительно этой точки.

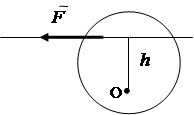Рис.1.16. Рис.1.17.

1.5. Момент силы относительно оси

Моментом силы относительно оси называется момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.

Момент считается положительным, если с положительного конца оси поворот, который сила стремится совершить, виден происходящим против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки.

. (1.3)

Чтобы найти момент силы относительно оси, нужно (рис 1.17);

1. Провести плоскость перпендикулярную оси z.

2. Спроецировать силу на эту плоскость и вычислить величину проекции .

3. Провести плечо h из точки пересечения оси с плоскостью на линию действия проекции силы и вычислить его длину.

4. Найти произведение этого плеча и проекции силы с соответствующим знаком /

Свойства момента силы относительно оси

Момент силы относительно оси равен нулю, если:

1. , т.е. сила параллельна оси.

2. h =0 , т.е. линия действия силы пересекает ось.

1.6. Момент пары сил

Пара сил оказывает на тело вращающее действие. Момент пары сил равен произведению одной силы на кратчайшее расстояние между линиями действия сил пары, которое называется плечом пары (рис.1.18)

, (1.4)

где: -силы, составляющие пару;

h - плечо пары

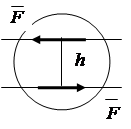Рис.1.18.

Момент пары считают положительным, если силы стремятся вращать плечо против хода часовой стрелки.

Свойства пары сил

1. Сумма проекций сил пары на любую ось равна нулю.

2. Не изменяя момента пары можно одновременно соответственно изменять значение сил и плечо пары.

3. Пару можно переносить в плоскости ее действия при этом действие пары на тело не изменится.

1.7. Тождественное преобразование систем сил

Преобразование может быть выполнено графическим или аналитическим способом.

1.7.1. Преобразование сходящейся системы сил

Равнодействующая R двух сходящихся сил находится на основании аксиомы о параллелограмме сил. (рис.1.9). Геометрическая сумма любого числа сходящихся сил может быть определена путем последовательного сложения двух сил (рис.1.19) – способ векторного многоугольника.

Вывод: система сходящихся сил ( n ) приводится к одной равнодействующей силе .

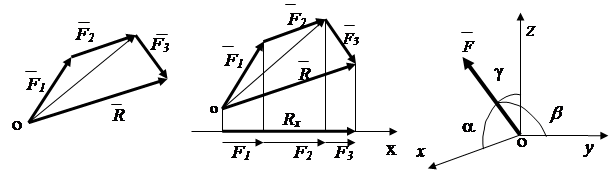
Рис.1.19 Рис.1.20. Рис.1.21.

Аналитически равнодействующая сила может быть определена через ее проекции на оси координат

, (1.5)

Согласно теореме: проекция равнодействующей на ось равна сумме проекций слагаемых сил на эту ось (рис.1.20). R x = F 1 x + F 2 x + F 3 x , или в общем виде

R x = åF kx (1.6)

С учетом (1.6) равнодействующая определяется выражением

Направление вектора равнодействующей определяется косинусами углов между вектором и осями x , y, z (рис.1.20)

1.7.2. Преобразование произвольной системы сил .

Применить правило параллелограмма сил непосредственно к произвольной системе сил нельзя, так как линии действия сил не пересекаются в одной точке. Предварительно систему сил приводят к одному центру на основании теоремы о параллельном переносе силы.

Теорема: силу, приложенную к твердому телу, можно, не изменяя оказываемого ею действия, перенести параллельно в другую точку тела, прибавляя при этом пару сил с моментом, равным моменту переносимой силы относительно точки, в которую она переносится (рис.1.22).

В результате указанного преобразования получается сходящаяся система сил и сумма моментов пар сил. Действие сходящейся системы сил заменяют действием суммарной силы, действие моментов - суммарным моментом. Суммарный вектор * называют главным вектором системы сил, суммарный момент * - главным моментом системы сил.

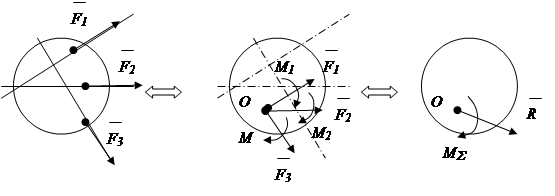
Рис.1.22

Вывод: произвольная система сил в результате тождественного преобразования приводится к главному вектору * и главному моменту * системы сил.

Аналитически главный вектор и главный момент системы сил могут быть определены через их проекции на оси координат

1.8 Условия равновесия систем сил

1.8.1. Равновесие системы сходящихся сил

По определению (см.п.1.1) действие системы сходящихся сил эквивалентно действию одной равнодействующей силы . Для равновесия тела необходимо и достаточно, чтобы равнодействующая равнялась нулю = 0.

Из формулы (1.7) следует, что для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Y,Zравнялась нулю

åF kx = 0

åF ky = 0 (1.10) åF k z = 0

Для равновесия плоской сходящейся системы сил необходимо и достаточно, чтобы сумма проекций всех сил на оси X,Yравнялась нулю

åF kx = 0

åF ky = 0 (1.11)

1.8.2. Равновесие произвольной системы сил.

Действие произвольной системы сил эквивалентно действию главного вектора и главного момента. Для равновесия необходимо и достаточно выполнения условия

Для равновесия произвольной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на оси X,Y,Z и суммы моментов всех сил относительно осей X,Y,Z равнялись нулю.

åF kx = 0

åF ky = 0

åF kz = 0 (1.13)

åМ х ( k) = 0

åМ y ( k) = 0

åМ z ( k) = 0

Для равновесия плоской произвольной системы сил необходимо и достаточно, чтобы сумма проекций главного вектора на оси X,Y, и алгебраическая сумма моментов сил относительно центра О были равны нулю.

åF ky = 0 (1.14)

åМ о ( k) = 0

1.9. Вопросы для самоконтроля по разделу

1. Дайте определение абсолютно твердого тела, материальной точки, силы, линии действия силы, системы сил (плоской, пространственной, сходящейся) произвольной систем сил.

2. Что называется проекцией силы на ось, на плоскость?

3. Что называется моментом силы, как определяется момент силы относительно точки?

4. Изменяется ли момент силы относительно данной точки при переносе силы вдоль линии ее действия?

5. В каком случае момент силы относительно данной точки равен нулю?

6. Какая система сил называется парой сил, чему равен момент пары сил?

7. Что называют связью? В чем заключается принцип освобождения от связей? Перечислите основные типы связей, покажите их реакции.

8. Каковы условия и уравнения равновесия системы сходящихся и произвольной систем сил, расположенных в пространстве и в плоскости?

9. Сформулируйте порядок решения задач статики.

2. Кинематика

Кинематика - раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела. Соответственно, изучение делят на кинематику точки и кинематику твердого тел

2.1 Основные понятия кинематики

Закон движения точки (тела) – зависимость положения точки (тела) в пространстве от времени.

Траектория точки – геометрическое место положений точки в пространстве при ее движении.

Скорость точки (тела) – характеристика изменения во времени положения точки (тела) в пространстве.

Ускорение точки (тела) – характеристика изменения во времени скорости точки (тела)

2.2. Кинематика точки

2.2.1 Способы задания движения точки

Задать движение точки - значит задать изменение ее положения по отношению к выбранной системе отсчета. Существует три основных систем отсчета: векторная, координатная, естественная . Соответственно возможны три способа задания движения точки.

В векторной системе положение точки относительно начала отсчета задается радиус-вектором (рис.2.1). Закон движения

Положение точки в системе координат OXYZ задается тремя координатами X,Y,Z (рис.2.2). Закон движения – x = x ( t ), y = y ( t ), z = z ( t ).

Положение точки в естественной системе отсчета задается расстоянием S от начала отсчета до этой точки вдоль траектории (рис.2.3). Закон движения – s = s ( t ).

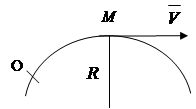
Рис.2.1 Рис. 2.2 Рис.2.3

Движение точки при естественном способе задания движения определено если известны:

1.Траектория движения.

2.Начало и направление отсчета дуговой координаты.

3.Уравнение движения.

При естественном способе задания движения, в отличии от других способов, используются подвижные координатные оси, движущиеся вместе с точкой по траектории. Такими осями являются (рис. 2.4).

Касательная () – направлена в сторону возрастания дуговой координаты по касательной к траектории.

Главная нормаль (п ) – направлена в сторону вогнутости кривой.

Бинормаль (в ) – направлена перпендикулярно к осям t , n.

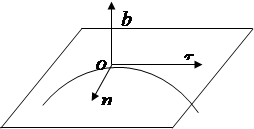Рис. 2.4

2.2.2 Определение кинематических характеристик точки

Траектория точки

В векторной системе отсчета траектория описывается выражением

В координатной системе отсчета траектория определяется по закону движения точки и описывается выражениями z = f ( x , y ) - в пространстве, или y = f(x) – в плоскости.

В естественной системе отсчета траектория задается заранее.

Скорость точки

Согласно определению (см. п. 2.1) скорость характеризует изменение во времени положения точки (тела) в пространстве.

Определение скорости точки в векторной системе координат

При задании движения точки в векторной системе координат отношение перемещения к интервалу времени называют средним значением скорости на этом интервале времени .

Принимая интервал времени бесконечно малой величиной, получают значение скорости в данный момент времени (мгновенное значение скорости)

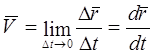(2.1)

Вектор средней скорости направлен вдоль вектора в сторону движения точки, вектор мгновенной скорости направлен по касательной к траектории в сторону движения точки (рис.2.5).

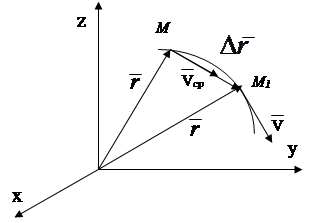Рис.2.5

Вывод: скорость точки – векторная величина, равная производной от закона движения по времени.

Отметим и используем в дальнейших рассуждениях следующее свойство производной: производная от какой либо величины по времени определяет скорость изменения этой величины.

Определение скорости точки в координатной системе отсчета

На основании свойства производной определим скорости изменения координат точки

Модуль полной скорости точки при прямоугольной системе координат будет равен

(2.3)

Направление вектора скорости определяется косинусами направляющих углов

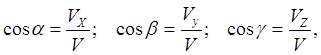
где - углы между вектором скорости и осями координат.

Определение скорости точки в естественной системе отсчета

Скорость точки в естественной системе отсчета определяется как производная от закона движения точки

V = (2.4)

Согласно предыдущим выводам вектор скорости направлен по касательной к траектории в сторону движения точки и в осях nb определяется только одной проекцией .

Ускорение точки

По определению ускорение характеризует изменение скорости, т.е. скорость изменения скорости.

Ускорения точки в векторной системе отсчета

На основании свойства производной

Вектор скорости может изменяться по модулю и направлению. Для определения приращения вектора совместим начала векторов (рис.2.6). Вектор ускорения направлен по линии приращения вектора скорости, т. е. В сторону искривления траектории.

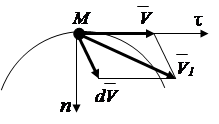
Рис.2.6

Ускорение точки в координатной системе отсчета

Ускорение изменения координат точки равно производной по времени от скоростей изменения этих координат

a x =; a y =; a z = .

Полное ускорение в прямоугольной системе координат будет определяться выражением

а = , (2.6)

Направляющие косинусы вектора ускорения

.

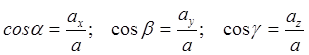Ускорение точки в естественной системе отсчета

Приращение вектора скорости (рис.2.7) можно разложить на составляющие, параллельные осям естественной системы координат

, (2.7)

Разделив левую и правую части равенства (2.7) на dt , получим,

, (2.8)

где: - тангенциальное ускорение, (2.9)

Нормальное ускорение, (вывод см., п.43)

где R - радиус кривизны траектории в окрестности точки

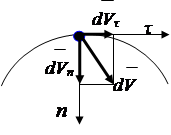Рис. 2.7

2.3. Кинематика твердого тела

В отличие от кинематики точки в кинематике твердых тел решаются две основные задачи:

Задание движения и определение кинематических характеристик тела в целом;

Определение кинематических характеристик точек тела.

Способы задания и определения кинематических характеристик зависят от типов движения тел.

В настоящем пособии рассматриваются три типа движения: поступательное, вращательное вокруг неподвижной оси и плоско-параллельное движение твердого тела

2.3.1. Поступательное движение твердого тела

Поступательным называют движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению (рис.2.8).

Доказана теорема: при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения (рис.2.8).

Вывод: Поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки.

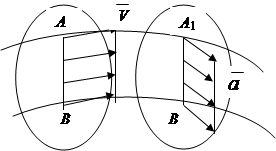Рис. 2.8 Рис. 2.9

2.3.2 Вращательное движение твердого тела вокруг неподвижной оси.

Вращательным вокруг неподвижной оси называют движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения.

Положение тела определяется углом поворота j (рис.2.9). Единица измерения угла – радиан. (Радиан - центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2p радиана.)

Закон вращательного движения тела вокруг неподвижной оси j = j(t). Угловую скорость и угловое ускорение тела определим методом дифференцирования

Угловая скорость, рад/с; (2.10)

Угловое ускорение, рад/с 2 (2.11)

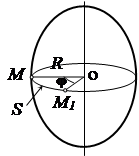
При вращательном движении тела вокруг неподвижной оси его точки, не лежащие на оси вращения, движутся по окружностям с центром на оси вращения.

Если рассечь тело плоскостью перпендикулярной оси, выбрать на оси вращения точку С и произвольную точка М, то точка М будет описывать вокруг точки С окружность радиуса R (рис. 2.9). За время dt происходит элементарный поворот на угол , при этом точка М совершит перемещение вдоль траектории на расстояние .Определим модуль линейной скорости:

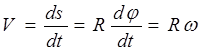(2.12)

Ускорение точки М при известной траектории определяется по его составляющим, см.(2.8)

,

Подставляя в формулы выражение (2.12) получим:

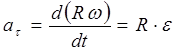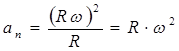, ., (2.13)

где: - тангенциальное ускорение,

Нормальное ускорение.

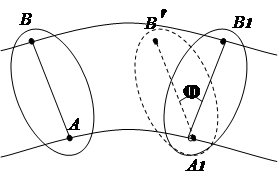
2.3.3. Плоско - параллельное движение твердого тела

Плоскопараллельным называется движение твердого тела, при котором все его точки перемещаются в плоскостях, параллельных одной неподвижной плоскости (рис.2.10). Для изучения движения тела достаточно изучить движение одного сечения S этого тела плоскостью, параллельной неподвижной плоскости. Движение сечения S в своей плоскости можно рассматривать как сложное, состоящее из двух элементарных движений: а) поступательного и вращательного; б) вращательного относительно подвижного (мгновенного) центра.

В первом варианте движение сечения может быть задано уравнениями движения одной его точки (полюса) и вращением сечения вокруг полюса (рис.2.11). В качестве полюса может быть принята любая точка сечения.

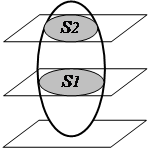Рис. 2.10 Рис. 2.11

Уравнения движения запишутся в виде:

Х А = Х А ( t )

Y А = Y А ( t ) (2.14)

j А = j А ( t )

Кинематические характеристики полюса определяют из уравнений его движения.

Скорость любой точки плоской фигуры, движущейся в своей плоскости слагается из скорости полюса (произвольно выбранной в сечении точки А ) и скорости вращательного движения вокруг полюса (вращение точки В вокруг точки А ).

Ускорение точки движущейся плоской фигуры складывается из ускорения полюса относительно неподвижной системы отсчета и ускорения за счет вращательного движения вокруг полюса.

(2.15)

(2.16)

Во втором варианте движение сечения рассматривается как вращательное вокруг подвижного (мгновенного) центра P (рис.1.12). В этом случае скорость любой точки В сечения будет определяться по формуле для вращательного движения

(2.17)

Угловая скорость вокруг мгновенного центра Р может быть определена если известна скорость какой либо точки сечения, например точки А.

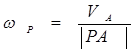(2.18)

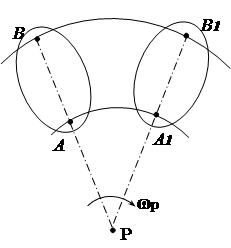
Рис.2.12

Положение мгновенного центра вращения может быть определено на основании следующих свойств:

Вектор скорости точки перпендикулярен радиусу;

Модуль скорости точки пропорционален расстоянию от точки до центра вращения (V = w ∙ R ) ;

Скорость в центре вращения равна нулю.

Рассмотрим некоторые случаи определения положения мгновенного центра.

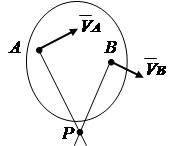
1. Известны направления скоростей двух точек плоской фигуры (рис.2.13). Проведем линии радиусов. Мгновенный центр вращения Р находится на пересечении перпендикуляров, проведенных к векторам скоростей.

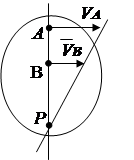
2. Скорости точек А и В известны, причем вектора и параллельны друг другу, а линия АВ перпендикулярна (рис. 2. 14). В этом случае мгновенный центр вращения лежит на линии АВ . Для его нахождения проведем линию пропорциональности скоростей на основании зависимости V = w R .

3. Тело катится без скольжения по неподвижной поверхности другого тела (рис.2.15). Точка касания тел в данный момент имеет нулевую скорость в то время, как скорости других точек тела не равны нулю. Точка касания Р будет мгновенным центром вращения.

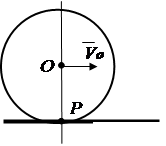Рис. 2.13 Рис. 2.14 Рис. 2.15

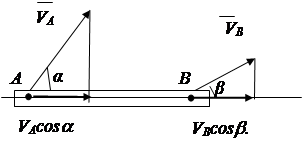
Кроме рассмотренных вариантов скорость точки сечения может быть определена на основании теоремы о проекциях скоростей двух точек твердого тела.

Теорема: проекции скоростей двух точек твердого тела на прямую, проведенную через эти точки, равны между собой и одинаково направлены .

Доказательство: расстояние АВ изменяться не может, следовательно,

V А cosa не может быть больше или меньше V В cosb (рис.2.16).

Рис. 2.16

Вывод: V А cosa=V В cosb. (2.19)

2.4. Сложное движение точки

В предыдущих параграфах рассматривалось движение точки относительно неподвижной системы отсчета, так называемое абсолютное движение. В практике встречаются задачи, в которых известно движение точки относительно системы координат, которая движется относительно неподвижной системы. При этом требуется определить кинематические характеристики точки относительно неподвижной системы.

Принято называть: движение точки относительно подвижной системы – относительным , движение точки вместе с подвижной системой – переносным , движение точки относительно неподвижной системы – абсолютным . Соответственно называют скорости и ускорения:

Относительные;- переносные; -абсолютные.

Согласно теореме о сложении скоростей абсолютная скорость точки равна векторной сумме относительной и переносной скоростей (рис.).

, (2.20)

Абсолютное значение скорости определяется по теореме косинусов

, (2.21)

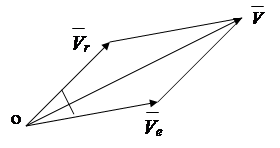
Рис.2.17

Ускорение по правилу параллелограмма определяется только при поступательном переносном движении

, (2.22)

При непоступательном переносном движении появляется третья составляющая ускорения, называемое поворотным или кориолисовым.

, (2.23)

где

Кориолисово ускорение численно равно

,

где a – угол между векторами и

Направление вектора кориолисова ускорения удобно определять по правилу Н.Е. Жуковского: вектор спроектировать на плоскость, перпендикулярную оси переносного вращения, проекцию повернуть на 90 градусов в сторону переносного вращения. Полученное направление будет соответствовать направлению кориолисова ускорения.

2.5 Вопросы для самоконтроля по разделу

1. В чем состоят основные задачи кинематики? Назовите кинематические характеристики.

2. Назовите способы задания движения точки и определение кинематических характеристик.

3. Дайте определение поступательного, вращательного вокруг неподвижной оси, плоскопараллельного движения тела.

4. Как задается движение твердого тела при поступательном, вращательном вокруг неподвижной оси и плоскопараллельном движении тела и как определяется скорость и ускорение точки при этих движениях тела?

3. Динамика

3.1 Задачи динамики

В динамике решаются два типа задач. Первая состоит в определении действующих сил при заданном законе движения материального объекта (точки или системы). Вторая задача обратная первой: определяется закон движения материального объекта при известных действующих на него силах.

3.2. Основные понятия динамики

Инерционность - свойство материальных тел сохранять состояние покоя или равномерного прямолинейного движения, пока внешние силы не изменят этого состояния.

Масса - количественная мера инерционности тела. Единица измерения массы - килограмм (кг).

Материальная точка - тело, обладающее массой, размерами которого при решении данной задачи пренебрегают.

Центр масс механической системы - геометрическая точка, координаты которой определяются формулами.

где m k , x k , y k , z k - масса и координаты k - той точки механической системы,

m - масса системы.

В однородном поле тяжести положение центра масс совпадает с положением центра тяжести.

Момент инерции материального тела относительно оси – количественная мера инертности при вращательном движении.

Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки от оси.

J Z = m × r 2 (3.2)

Момент инерции системы (тела) относительно оси равен арифметической сумме моментов инерции всех точек.

J Z = å m k × r k 2 (3.3)

Сила инерции материальной точки - векторная величина, равная по модулю произведению массы точки на модуль ускорения и направленная противоположно вектору ускорения

(3.4)

Сила инерции материального тела - векторная величина, равная по модулю произведению массы тела на модуль ускорения центра масс тела и направленная противоположно вектору ускорения центра масс

, (3.5)

где - ускорение центра масс тела.

Элементарный импульс силы - векторная величина , равная произведению вектора силы на бесконечно малый промежуток времени dt

, (3.6)

Полный импульс силы за D t равен интегралу от элементарных импульсов

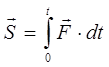(3.7)

Элементарная работа силы - скалярная величина dA , равная скалярному произведению вектора силы на бесконечно малое перемещение d .

Скалярное произведение векторов равно произведению их модулей на косинус угла между направлениями векторов.

dA = F × ds × cos a , (3.8)

где a - угол между направлениями векторов перемещения и силы.

Работа силы на конечном перемещении точки её приложения равна интегралу от элементарной работы, взятому по перемещению.

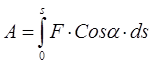(3.9)

Единица измерения работы - Джоуль (1 Дж=1 Н×м).

Количество движения материальной точки - векторная величина , равная произведению массы m на её скорость .

Количество движения механической системы равно векторной сумме количества движения её точек.

(3.11)

или с учетом формул (3.1).

где: m- масса механической системы,

Вектор скорости центра масс системы.

Кинетическая энергия материальной точки - скалярная величина Т, равная половине произведения массы точки на квадрат её скорости.

T = (3.13)

Кинетическая энергия механической системы равна сумме кинетических энергий всех её точек.

3.3. Аксиомы динамики

Первая аксиома - закон инерции .

Если на свободную материальную точку не действуют никакие силы или действует уравновешенная система сил, то точка будет находиться в состоянии покоя или равномерного прямолинейного движения.

Вторая аксиома- закон пропорциональности ускорения .

Ускорение, сообщаемое материальной точке действующей на неё силой, пропорционально этой силе и по направлению совпадает с направлением силы.

Выражение (3.15) называют основным законом динамики .

Третья аксиома - закон противодействия .

Силы, с которыми действуют друг на друга две материальные точки, равны по модулю и направлены вдоль прямой, соединяющей эти точки, в противоположные стороны

Четвертая аксиома - закон независимости действия сил .

При действии на материальную точку системы сил полное ускорение этой точки равно геометрической сумме ускорений от действия каждой силы

3.4. Дифференциальные уравнения динамики

Дифференциальные уравнения движения точки связывают ускорение точки с действующими на нее силами. Фактически дифференциальные уравнения являются записью основного закона динамики в явной дифференциальной форме.

Для абсолютного движения точки (движение в инерциальной системе отсчета) дифференциальное уравнение имеет вид

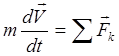, (3.18)

Векторное уравнение (3.17) может быть записано в проекциях на оси прямоугольной инерциальной системы координат

,

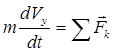, (3.19)

,

При известной траектория движения точки уравнение (3.18) может быть записано в проекциях на оси естественной системы координат

, (3.20)

C учетом (2.8) уравнения примут вид

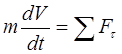(3.21)

3.5 Общие теоремы динамики

Общие теоремы динамики устанавливают зависимость между мерами механического движения и механического взаимодействия. Выводы теорем являются результатом тождественного преобразования основного закона динамики.

Теорема об изменении количества движения : изменение количества движения материальной точки (механической системы) за конечный промежуток времени равно сумме импульсов внешних сил за тот же промежуток времени

-для материальной точки; (3.22)

-для механической системы. (3.23)

Теорема об изменении кинетической энергии : изменение кинетической энергии точки (механической системы) при её перемещении равно сумме работ всех действующих внешних сил на этом перемещении

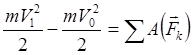- для материальной точки (3.24)

- для механической системы (3.25)

Кинетическая энергия механической системы определяется в соответствии с (3.14), при этом для твердых тел выведены следующие зависимости

При поступательном движении тела, (3.26)

При вращательном движении тела, (3.27)

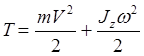- при плоско-параллельном движении тела. (3.28)

Моменты инерции некоторых однородных тел

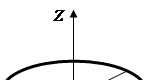Рис. 3.1 Рис.3.2. Рис.3.3.

Момент инерции цилиндра относительноего оси (рис. 3.1.)

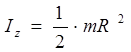
Момент инерции стержня относительно оси z (рис.3.2)

Момент инерции прямоугольной пластины относительно осей х и y (рис.3.3)

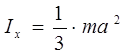
Момент инерции шара определяется по формуле:

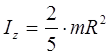
В общем случае работа сил определяется в соответствии с (3.8),(3.9).В ряде случаев действия сил работа может быть определена по частным зависимостям.

Работа силы тяжести

где: - сила тяжести,

Изменение положения тела по вертикали.

Работа силы при вращательном движении тела

, (3.30)

где: - момент силы,

Угловая скорость тела.

Следует иметь в виду, что работа, как скалярная величина, может быть положительной или отрицательной. Работа будет положительной если направление действия силы совпадает с направлением движения.

3.6 Принцип Даламбера

Изложенные выше методы исследования движения тел, базируются на законах Ньютона. Разработаны методы, в основу которых положены другие принципы. Одним из них является принцип Даламбера .Принцип формулируеся: если в любой момент времени к действующим на точку силам присоединить силы инерции, то полученная система сил будет уравновешенной

, (3.31)

или для механической системы

Принцип Даламбера позволяет применять к решению задач динамики более простые методы статики, поэтому он широко используется в инженерной практике.

3.7. Вопросы для самоконтроля по разделу

1. Сформулируйте основные задачи динамики.

2. Дайте определения массы, момента инерции, импульса силы, работы силы, количества движения, кинетической энергии.

3. Сформулируйте основные законы динамики.

4. Какое уравнение называется дифференциальным уравнением динамики? Какой алгоритм решения задач динамики с помощью дифференциальных уравнений?

5. Сформулируйте общие теоремы динамики.

6. Сформулируйте принцип Даламбера. Как определяются силы инерции?

7. Сформулируйте принцип возможных перемещений. Для каких условий применяется принцип возможных перемещений?

В этой главе рассмотрены задачи на определение работы, совершаемой постоянной силой, и развиваемой мощности при поступательном и вращательном движении тел (Е. М. Никитин , § 81-87).

§ 44. Работа и мощность при поступательном движении

Работа постоянной силы P на прямолинейном участке пути s, пройденном точкой приложения силы, определяется по формуле
(1) A = Ps cos α,
где α - угол между направлением действия силы и направлением перемещения.

При α = 90°
cos α = cos 90° = 0 и A = 0,
т. е. работа силы, действующей перпендикулярно к направлению перемещения, равна нулю.

Если направление действия силы совпадает с направлением перемещения, то α = 0, поэтому cos α = cos 0 = 1 и формула (1) упрощается:
(1") A = Ps.

На точку или на тело обычно действует не одна сила, а несколько, поэтому при решении задач целесообразно использовать теорему о работе равнодействующей системы сил (Е. М. Никитин , § 83):
(2) A R = ∑ A i ,
т. е. работа равнодействующей какой-либо системы сил на некотором пути равна алгебраической сумме работ всех сил этой системы на том же пути.

В частном случае, когда система сил уравновешена (тело движется равномерно и прямолинейно), равнодействующая системы сил равна нулю и, следовательно, A R =0. Поэтому при равномерном и прямолинейном движении точки или тела уравнение (2) принимает вид
(2") ∑ A i = 0,
т. е. алгебраическая сумма работ уравновешенной системы сил на некотором пути равна нулю.

При этом силы, работа которых положительна, называются движущими, а силы, работа которых отрицательна, называются силами сопротивления. Например, при движении тела вниз - сила тяжести - движущая сила и ее работа положительна, а при движении тела вверх его сила тяжести является силой сопротивления и работа силы тяжести при этом отрицательна.

При решении задач в случаях, когда неизвестна сила Р, работу которой нужно определить, можно рекомендовать два приема (метода).

1. При помощи сил, заданных в условии задачи, определить силу P, а затем по формуле (1) или (1") вычислить ее работу.

2. Не определяя непосредственно силы P, определить A p - работу требуемой силы при помощи формул (2) и (2"), выражающих теорему о работе равнодействующей.

Мощность, развиваемая при работе постоянной силы, определяется по формуле
(3) N = A/t или N = (Ps cos α)/t.

Если при определении работы силы Р скорость движения точки v=s/t остается постоянной, то
(3") N = Pv cos α.

Если же скорость движения точки изменяется, то s/t = v ср - средняя скорость и тогда формула (2") выпажает среднюю мощность
N ср = Pv ср cos α.

Коэффициент полезного действия (к. п. д.) при совершении работы можно определить как отношение работ
(4) η = A пол /A,
где A пол - полезная работа; A - вся произведенная работа, или как отношение соответствующих мощностей:
(4") η = N пол /N.

Единицей работы в СИ служит 1 джоуль (Дж) = 1 Н * 1 м.

Единицей мощности в СИ служит 1 ватт (Вт) = 1 Дж / 1 сек.

Популярной внесистемной единицей мощности является лошадиная сила (л. с.):
1000 Вт = 1,36 л. с. или 1 л. с. = 736 Вт.

Для перехода между ваттами и лошадиными силами следует пользоваться формулами
N (кВт) = 1,36 N (л. с.)
N (л. с.) = 0,736 N (кВт).

Лекция 2. Работа. Мощность. Теорема об изменении кинетической энергии точки.

В данной лекции рассматриваются следующие вопросы:

Работа силы.

Мощность.

Примеры вычисления работы.

Потенциальная энергия

Кинетическая энергия

Теорема об изменении кинетической энергии точки.

Теорема моментов.

Изучение данных вопросов необходимо для динамики движения центра масс механической системы, динамики вращательного движения твердого тела, кинетического момента механической системы, для решения задач в дисциплинах «Теория машин и механизмов» и «Детали машин».

Работа силы. Мощность.

Для характеристики действия, оказываемого силой на тело при некотором его перемещении, вводится понятие о работе силы.

Рис.16

При этом работа характеризует то действие силы, которым определяется изменение модуля скорости движущейся точки.

Введём сначала понятие об элементарной работе силы на бесконечно малом перемещении ds . Элементарной работой силы (рис.16) называется скалярная величина:

где - проекция силы на касательную к траектории, направленную в сторону перемещения точки, а -бесконечно малое перемещение точки, направленное вдоль этой касательной.

Данное определение соответствует понятию о работе, как о ха­рактеристике того действия силы, которое приводит к изменению модуля скорости точки. В самом деле, если разложить силу на составляющие и , то изменять модуль скорости точки будет только составляющая , сообщающая точке касательное ускорение Составляющая же или изменяет направление вектора скорости v (сообщает точке нормальное ускорение), или, при несвободном дви­жение изменяет давление на связь. На модуль скорости составляю­щая влиять не будет, т.е., как говорят, сила«не будет про­изводить работу».

Замечая, что , получаем:

. (1)

Таким образом, элементарная работа силы равна проекции силы на направление перемещения точки, умноженной на элементар­ное перемещениеили элементарная работа силы равна произведению модуля силы на элементарное перемещение и на косинус угла между направлением силы и направлением перемещения.

Если угол острый, то работа положительна. В частности, при элементарная работа .

Если угол тупой, то работа отрицательна. В частности, при элементарная работа .

Если угол , т.е. если сила направлена перпендикулярно перемещению, то элементарная работа силы равна нулю.

Найдем аналитическое выражение элементарной работы. Для этого разложим силу на составляющие , , по направлениям координатных осей (рис.17; сама сила на чертеже не показана).

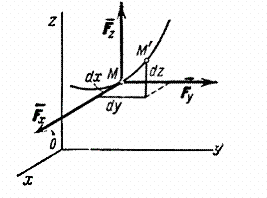
Рис.17

Элементарное перемещение слагается из перемещений , , вдоль координатных осей, где x , y , z - координаты точки М . Тогда работу силы на перемещении можно вычислить как сумму работ её составляющих , , на перемещениях , , .

Но на перемещении совершает работу только составляющая , причем её работа равна . Работа на перемещениях и вычисляется аналогично. Окончательно находим: .

Формула дает аналитическое выражение элементарной работы силы.

Работа силы на любом конечном перемещении М 0 М 1 вычисляется как интегральная сумма соответствующих элементарных работ и будет равна:

или

.

Следовательно, работа силы на любом перемещении М 0 М 1 равна взятому вдоль этого перемещения интегралу от элементарной работы. Пределы интеграла соответствуют значениям пере­менных интегрирования в точках М 0 и М 1 .

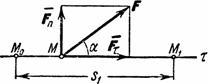
Рис.18

Если величина постоянна (= const), то и обозначая перемеще­ние М 0 М 1 через получим: .

Такой случай может иметь место, когда действующая сила постоянна по модулю и направлению (F = const), а точка, к ко­торой приложена сила, движется прямолинейно (рис.18}. В этом случае и работа силы .

Единицей измерения работы в системе СИ является джоуль (1 дж= 1 hm).

Мощность.

Мощностью называется величина, определяющая работу, совершаемую силой в единицу времени. Если работа совершается равномерно, то мощность

где t - время, в течение которого произведена работа A . В общем случае

.

Следовательно, мощность равна произведению касательной состав­ляющей силы на скорость движения.

Единицей измерения мощности в системе СИ является ватт (1 вт= 1 дж /сек). В технике за единицу мощности часто принимается 1 лошадиная сила, равная 75 кГм /сек или 736 вт .

Работу, произведенную машиной, можно измерять произведением ее мощности на время работы. Отсюда возникла употребительная в технике единица измерения работы киловатт-час (1 квт-ч = 3,6дж 367100 кГм ).

Из равенства видно, что у двигателя, имеющего дан­ную мощность W , сила тяги будет тем больше, чем меньше ско­рость движения V . Поэтому, например, на подъеме или на плохом участке дороги у автомобиля включают низшие передачи, позволяю­щие при полной мощности двигаться с меньшей скоростью и раз­вивать большую силу тяги.

Примеры вычисления работы.

Рассмотренные ниже при­меры дают результаты, которыми можно непосредственно пользо­ваться при решении задач.

1) Работа силы тяжести. Пусть точка М, на которую действует сила тяжести, перемещается из положения М ­ 0 (x ­ 0 , у 0 , z 0 ) в положениеM 1 (х 1 , у 1 , z 1 ). Выберем оси координат так, чтобы ось Oz была направлена вертикально вверх (рис.19).

Рис.19

Тогда Р x =0, Р y =0, P z = -Р . Подставляя эти значения и учитывая перемен­ную интегрирования z :

Если точка M 0 выше М 1 , то , где h -величина вер­тикального перемещения точки;

Если же точка M 0 ниже точки M 1 то .

Окончательно получаем: .

Следовательно, работа силы тяжести равна взятому со зна­ком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения. Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной. Из полученного результата следует, что работа силы тяжести не зависит от вида той траектории, по которой перемещается точка ее приложения.

Силы, обла­дающие таким свойством, назы­ваются потенциальными.

2) Работа силы упругости. Рассмотрим груз М , лежащий на горизонтальной плоскости и прикрепленный к свободному концу некоторой пружины (рис.20,а). Отметим на плоскости точкой О поло­жение, занимаемое концом пружины, когда она не напряже­на ( - длина ненапряженной пружины), и примем эту точку за начало координат. Если теперь оттянуть груз от равновесного положения О , удлинив пружину до величины , то на груз будет действовать сила упругости пружины F , направленная к точке О .

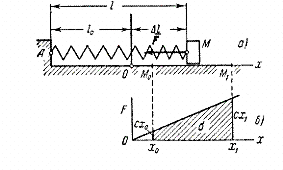
Рис.20

По закону Гука величина этой силы пропорциональна удлинению пружины . Так как в нашем случае , то по модулю .

Коэффициент с называется коэффициентом жесткости пружины. В технике обычно измеряют величину с в H/см, полагая коэф­фициент с численно равным силе, которую надо приложить к пру­жине, чтобы растянуть ее на 1 см.

Найдем работу, совершаемую силой упругости при перемещении груза из положения в положение . Так как в данном случае , , то получим:

(Этот же результат можно получить по графику зависимости F от х (рис.20, б), вычисляя площадь заштрихованной на чертеже тра­пеции и учитывая знак работы.) В полученной формуле представ­ляет собою начальное удлинение пружины , а конечное удлинение пружины . Следовательно,

,

т.е. работа силы упругости равна половине произведения коэффи­циента жесткости на разность квадратов начального и конеч­ного удлинений (или сжатий) пружины.

Работа будет положительной, когда , т. е. когда конец пружины перемещается к равновесному положению, и отрица­тельной, когда , т.е. конец пружины удаляется от равновесия положения. Можно доказать, что формула ос­тается справедливой и в случае, когда пе­ремещение точки М не является прямо­линейным.

Таким образом, оказывается, что работа силы F зависит только от значе­ний и и не зависит от вида траектории точки М . Следовательно, сила упругости также является потенциальной.

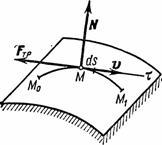
Рис.21

3) Работа силы трения. Рассмотрим точку, движущуюся по какой-нибудь шероховатой поверхности (рис. 21) или кривой. Действующая на точку сила трения равна по модулю fN , где f -коэффициент трения, а -нормальная реакция поверхности. Направлена сила трения противоположно перемещению точки. Следовательно, F тр = - fN и по формуле

.

Если величина силы трения постоянна, то , где s -длина дуги кривой М 0 М 1 по которой перемещается точка.

Таким образом, работа силы трения при скольжении всегда отрицательна. Величина этой работы зависит от длины дуги М 0 М 1 . Следовательно, сила трения является силой непотенциальной .

4) Работа силы, приложенной к телу, вращающемуся вокруг неподвижной оси.

В этом случае (рис.22) точка приложения силы движется по окружности радиуса r . Элементарная работа, по (1), , где .

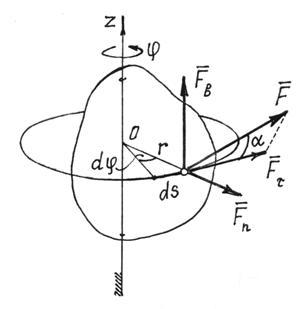
Рис.22

Поэтому .

Это нетрудно установить, разложив силу на три составляющие (рис. 22). (Моменты сил и равны нулю). Значит,

(2)

В частности, если момент силы относительно оси , работа силы при повороте тела на угол равна

. (3)

Знак работы определяется знаками момента силы и угла поворота. Если они одинаковы, работа положительная.

Из формулы (3) следует и правило определения работы пары сил. Если пара с моментом m расположена в плоскости перпендикулярной оси вращения тела, то ее работа при повороте тела на угол

Если же пара сил действует в плоскости не перпендикулярной оси вращения, то ее надо заменить двумя парами. Одну расположить в плоскости перпендикулярной оси, другую – в плоскости параллельной оси. Моменты их определяются разложением вектора момента по соответствующим направлениям: . Конечно работу будет совершать только первая пара с моментом , где – угол между вектором и осью вращения z ,

. (5)

Потенциальная энергия

Часть пространства, в которой на помещенную туда материальную точку действует сила, зависящая от места положения точки, называетсясиловым полем.

Причем, эта сила определяется с помощью силовой функции u = u(x, y, z). Если она не зависит от времени, то такое поле называетсястационарным. Если во всех точках она одинакова, то поле – однородное.

Если же проекции силы на декартовы оси есть частные производные от силовой функции по соответствующим координатам

то такое поле называется потенциальным.

Вычислим работу силы потенциального поля при перемещении точки из положения М 1 в положение М 2. (рис. 23).

Рис.23

Элементарная работа,

Это есть полный дифференциал силовой функции.

Работа на конечном перемещении

(7)

где u 2 и u 1 – значения силовой функции в точках М 2 и М 1 .

Следовательно, работа силы потенциального поля не зависит от траектории движения точки, а определяется лишь значениями силовой функции в начальном и конечном положениях точки.

Естественно, если точка вернется в начальное положение, работа силы будет равна нулю. Работа окажется равной нулю и при переходе в другую точку М 3 , если там значение силовой функции будет такое же, как и в начальном положении.

Нетрудно догадаться, что точки с одинаковыми значениями силовой функции будут образовывать целую поверхность. И что силовое поле – это слоеное пространство, состоящее из таких поверхностей (рис. 23). Эти поверхности называются поверхностями уровня или эквипотенциальными поверхностями . Уравнения их: u (x , y , z )= C (C – постоянная, равная значению u в точках этой поверхности). А силовую функцию называют, соответственно, потенциалом поля .

Конечно, эквипотенциальные поверхности не пересекаются. Иначе существовали бы точки поля с неопределенным потенциалом.

Поскольку, при перемещении точки по эквипотенциальной поверхности работа силы равна нулю, то вектор силы перпендикулярен поверхности.

Выберем среди этих поверхностей какую-нибудь одну и назовем ее нулевой поверхностью (положим у нее u = u 0 ).

Работа, которую совершит силапри переходе точки из определенного места М на нулевую поверхность, называют потенциальной энергией точки в этом определенном месте М:

. (8)

Заметим, что потенциальная энергия в одной и той же точке поля зависит от выбора нулевой поверхности.

По (8) силовая функция . Поэтому проекции силы на декартовы оси, по (6), так как ,

и вектор силы .

Рассмотрим несколько потенциальных полей.

1) Поле силы тяжести.

Вблизи поверхности Земли сила тяжести во всех точках одинакова , равна весу тела. Значит, это силовое поле однородное. Так как при перемещении точки в горизонтальной плоскости работа силы равна нулю, то эквипотенциальными поверхностями будут горизонтальные плоскости (рис. 24), а уравнения их: u = z = C .

Рис.24

Если нулевой поверхностью назначить плоскость xOy , то потенциальная энергия точки в положении М будет равна работе силы тяжести:

2) Поле упругой силы.

При деформации упругого тела, например пружины, появляется сила. То есть около этого тела возникает силовое поле, силы которого пропорциональны деформации тела и направлены в сторону недеформированного состояния. У пружины – в точку М 0 , где находится конец недеформированной пружины (рис. 25).

Рис.25

Если перемещать конец пружины так, чтобы длина ее не изменялась, то работа упругой силы будет равна нулю. Значит эквипотенциальными поверхностями являются сферические поверхности с центром в точке О.

Назначим нулевой поверхностью сферу, проходящую через точку М 0 , через конец недеформированной пружины. Тогда потенциальная энергия пружины в положении М : .

При таком выборе нулевой поверхности потенциальная энергия всегда будет положительной (П>0), и в растянутом, и в сжатом состоянии.

Теорема об изменении кинетической энергии точки.

Рассмотрим точку с массой т, перемещающуюся под действием при­ложенных к ней сил из положения M 0 , где она имеет скорость , в положение М 1 , где ее скорость равна .

Для получения искомой зависимости обратимся к уравнению выражающему основной закон динамики. Проектируя обе части этого равенства на касательную к траектории точ­ки М, направленную в сторону движения, получим:

Стоящую слева величину касательного ускорения можно пред­ставить в виде

.

В результате будем иметь:

.

Умножив обе части этого равенства на ds , внесем т под знак дифференциала. Тогда, замечая, что где - эле­ментарная работа силы F k получим выражение теоремы об изме­нении кинетической энергии в дифференциальной форме.

Работа силы тяжести. Силу тяжести Р материальной точки массой т вблизи поверхности Земли можно считать постоянной, равной mg

направленной по вертикали вниз.

Работа А силы Р на перемещении от точки М 0 до точки М

где h = z 0 - z x - высота опускания точки.

Работа силы тяжести равна произведению этой силы на высоту опус­кания (работа положительна) или высоту подъема (работа отрицатель­на). Работа силы тяжести не зависит от формы траектории между точками М 0 и М|, и если эти точки совпадают, то ра­бота силы тяжести равна нулю (случай замкнутого пути). Она равна нулю также, если точки М 0 и М лежат в одной и той же горизонтальной плос­кости.

Работа линейной силы упругости. Линейной силой упругости (или линейной восстанавливающей силой) называют силу, действую­щую по закону Гука (рис. 63):

F = - с r ,

где r - расстояние от точки статического равновесия, где сила равна нулю, до рассматриваемой точки М; с - постоянный коэффициент- коэффициент жесткости.

А=--().

По этой формуле и вычисляют работу линейной силы упругости. Если точка М 0 совпадает сточкой статического равновесия О, то тогда r 0 =0 и для работы силы на перемещении от точки О до точки М имеем

Величина r - кратчайшее расстояние между рассматриваемой точ­кой и точкой статического равновесия. Обозначим его λ и назовем де­формацией. Тогда

Работа линейной силы упругости на перемещении из состояния ста­тического равновесия всегда отрицательна и равна половине произве­дения коэффициента жесткости на квадрат деформации. Работа линейной силы упругости не зависит от формы перемещения и работа по любому замкнутому перемещению равна нулю. Она также равна нулю, если точки Мо и М лежат на одной сфере, описанной из точки статического равновесия.

Работа переменной силы при криволинейном движении.

Работа силы на криволинейном участке

Рассмотрим общий случай нахождения работы переменной силы, точка приложения которой движется по криволинейной траектории. Пусть точка М приложения переменной силы F движется по произвольной непрерывной кривой. Обозначим через вектор бесконечно малого перемещения точки М. Этот вектор направлен по касательной к кривой в ту же сторону, что и вектор скорости.

Элементарной работой переменной силы F на бесконечно малом перемещении

ds называется скалярное произведение векторов F и ds :

где а - угол между векторами F и ds

То есть элементарная работа силы равна произведению модулей векторов силы и бесконечно малого перемещения, умноженному на косинус угла между этими векторами.

Разложим вектор силы F на две составляющие: - направленную по касательной к траектории - и - направленную по нормали. Линия действия силы

перпендикулярна касательной к траектории, по которой движется точка, и ее работа равна нулю. Тогда:

dA = F t ds .

Для того, чтобы вычислить работу переменной силы F на конечном участке кривой от а до Ь, следует вычислить интеграл от элементарной работы:

Потенциальная и кинетическая энергии.

Потенциальной энергией П мат ериальной точки в рассматривае мой точке силового поля М называют работу , которую совершают силы по ля, действующие на материальную точку при перемещении ее из точки M в начальную точку M 0 , т. е.

П = Амм 0

П = =-U =- U

Постоянная С 0 одна и та же для всех точек поля, зависящая от того, какая точка поля выбрана за начальную. Очевидно, что потенциаль­ную энергию можно ввести только для потенциального силового поля, в котором работа не зависит от формы перемещения между точками М и М 0 . Непотенциальное силовое поле не имеет потенциальной энер­гии, для него не существует и силовой функции.

dA = dU = -dП; А = U - U 0 = П 0 - П

Из приведенных формул следует, что П определяется с точностью до произвольной постоянной, которая зависит от выбора начальной точки, но эта произвольная постоян­ная не влияет на вычисляемые через потенциальную энергию силы и рабо­ту этих сил. Учитывая это:

П = - U + const или П = - U .

Потенциальную энергию в какой- либо точке поля с точностью до произвольной постоянной можно оп­ределить как значение силовой функ­ции в этой же точке, взятое со зна­ком минус.

Кинетической энергией системы называется скалярная величина Т, равная сумме кинетических энергий всех точек системы:

Кинетическая энергия является характеристикой и поступатель­ного, и вращательного движений системы. Кинетическая энергия является величиной скалярной и притом су­щественно положительной. Поэтому она не зависит от направлений движения частей системы и не характеризует изменений этих на­правлений.

Отметим еще следующее важное обстоятельство. Внутренние силы действуют на части системы по взаимно противоположным на­правлениям. На изменения кинетической энергии влияет действие и внешних и внутренних сил

Равнопеременное движение точки.

Равнопеременное движение точки - движение, при к-ром касат. ускорение ω т точки (в случае прямолинейного движения полное ускорение ω )постоянно. Закон равнопеременного движения точки и закон изменения её скорости υ при этом движении даются равенствами:

где s - измеренное вдоль дуги траектории расстояние точки от выбранного на траектории начала отсчёта, t - время, s 0 - значение s в нач. момент времени t = = 0. - нач. скорость точки. Когда знакиυ и ω одинаковы, равнопеременное движение. является ускоренным, а когда разные - замедленным.

При поступат. равнопеременном движении твёрдого тела всё сказанное относится к каждой точке тела; при равномерном вращении вокруг неподвижной оси угл. ускорение e тела постоянно, а закон вращения и закон изменения угл. скорости ω тела даются равенствами

где φ - угол поворота тела, φ 0 - значение φ в нач. момент времени t = 0, ω 0 - нач. угл. скорость тела. Когда знаки ω и ε совпадают, вращение является ускоренным, а когда не совпадают - замедленным.

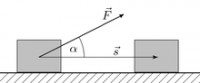
Работа постоянной силы при прямолинейном движени.

Определим работу для случая, когда действующая сила постоянна по величине и направлению, а точка ее приложения перемещается по прямолинейной траектории. Рассмотрим материальную точку С, к которой приложена постоянная по значению и направлению сила(рис. 134, а).

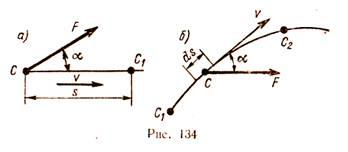
За некоторый промежуток времени t точка С переместилась в положение С1 по прямолинейной траектории на расстояние s.

Работа W постоянной силы при прямолинейном движении точки ее приложения равна произведению модуля силы F на рас­стояние s и на косинус угла между направлением силы и направле­нием перемещения, т. е.

Угол α между направлением силы и направлением движения может меняться в пределах от 0 до 180°. При α < 90° работа положительна, при α > 90° - отрицательна, при α = 90° работа равна нулю.

Если сила составляет с направлением движения острый угол, она называется движущей силой, работа силы всегда положительна. Если угол между направлениями силы и перемещения тупой, сила оказывает сопротивление движению, совершает отрицательную работу и носит название силы сопротивления. Примерами сил сопротивления могут служить силы резания, трения, сопротивле­ния воздуха и другие, которые всегда направлены в сторону, про­тивоположную движению.

Когда α = 0°, т. е. когда направление силы совпадает с направлением скорости, тогда W = F s, так как cos 0° = 1. Произведение F cos α есть проекция силы на направление движения материальной точки. Следовательно, работу силы можно определить как произведение перемещения s и проекции силына направление движения точки.

33. Силы инерции твердого тела

В классической механикепредставления осилахи их свойствах основываются назаконах Ньютонаи неразрывно связаны с понятиеминерциальная система отсчёта.

Действительно, физическая величина, называемая силой, вводится в рассмотрение вторым законом Ньютона, при этом сам закон формулируется только для инерциальных систем отсчёта. Соответственно, понятие силы первоначально оказывается определённым только для таких систем отсчёта.

Уравнение второго закона Ньютона, связывающее ускорениеимассуматериальной точкис действующей на неё силой, записывается в виде

Из уравнения непосредственно следует, что причиной ускорения тел являются только силы, и наоборот: действие на тело не скомпенсированных сил обязательно вызывает его ускорение.

Третий закон Ньютона дополняет и развивает сказанное о силах во втором законе.

сила есть мера механического действия на данное материальное тело других тел

в соответствии с третьим законом Ньютона силы способны существовать лишь попарно, при этом природа сил в каждой такой паре одинакова.

любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, силы обязательно представляют собой результат взаимодействия тел.

Никакие другие силы в механике в рассмотрение не вводятся и не используются. Возможность существования сил, возникших самостоятельно, без взаимодействующих тел, механикой не допускается.

Хотя в наименованиях эйлеровых и даламберовых сил инерции содержится слово сила , эти физические величины силами в смысле, принятом в механике, не являются.

34. Понятие о плоскопараллельном движении твердого тела

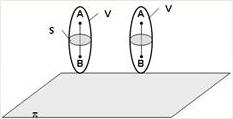
Движение твердого тела называется плоскопараллельным, если все точки тела перемещаются в плоскостях, параллельных некоторой фиксированной плоскости (основной плоскости). Пусть некоторое тело V совершает плоское движение, π - основная плоскость. Из определенияплоскопараллельного движения и свойств абсолютно твердого тела следует, что любой отрезок прямой АВ, перпендикулярный плоскости π, будет совершать поступательное движение. То есть траектории, скорости и ускорения всех точек отрезка АВ будут одинаковы. Таким образом, движение каждой точки сечения s параллельного плоскости π, определяет собой движение всех точек тела V, лежащих на отрезке перпендикулярном сечению в данной точке. Примерами плоскопараллельного движения являются: качение колеса по прямолинейному отрезку, так как все его точки перемещаются в плоскостях, параллельных плоскости, перпендикулярной оси колеса; частным случаем такого движения являетсявращение твердого тела вокруг неподвижной оси, в самом деле, все точки вращающегося тела движутся в плоскостях параллельных некоторой перпендикулярной оси вращения неподвижной плоскости.

35. Силы инерции при прямолинейном и криволинейном движении материальной точки

Сила, с которой точка сопротивляется изменению движения, называется силой инерции материальной точки. Сила инерции направлена противоположно ускорению точки и равна массе, умно­женной на ускорение.

При прямолинейном движении направление ускорения совпадает с траекторией. Сила инерции направлена в сторону, противоположную ускорению, и численное значение ее определяется по формуле:

При ускоренном движении направления ускорения и скорости совпадают и сила инерции направлена в сторону, противоположную движению. При замедленном движении, когда ускорение направлено в сторону, обратную скорости, сила инерции действует по направлению движения.

При криволинейном и неравномерном движении ускорение может быть разложено на нормальную аn и касательную at составляющие. Аналогично сила инерции точки также складывается из двух составляющих: нормальной и касательной.

Нормальная составляющая силы инерции равна произведению массы точки на нормальное ускорение и направлена противоположно этому ускорению:

Касательная составляющая силы инерции равна произведению массы точки на касательное ускорение и направлена противоположно этому ускорению:

Очевидно, что полная сила инерции точки М равна геометрической сумме нормальной и касательной составляющих, т. е.

Учитывая, что касательная и нормальная составляющие взаимно перпендикулярны, полная сила инерции:

36. Теоремы о сложении скоростей и ускорений точки при сложном движении

Теорема о сложении скоростей:

В механикеабсолютная скоростьточки равнавекторнойсумме еёотносительнойипереноснойскоростей:

Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчета, в которой находится тело.

при сложном движении абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей. Величина абсолютной скорости определяется где α – угол между векторам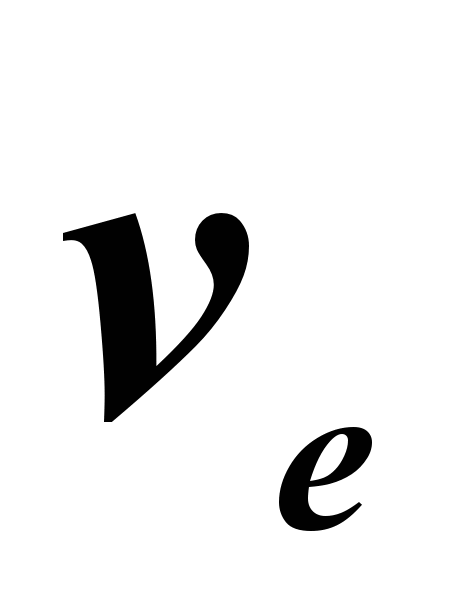и и.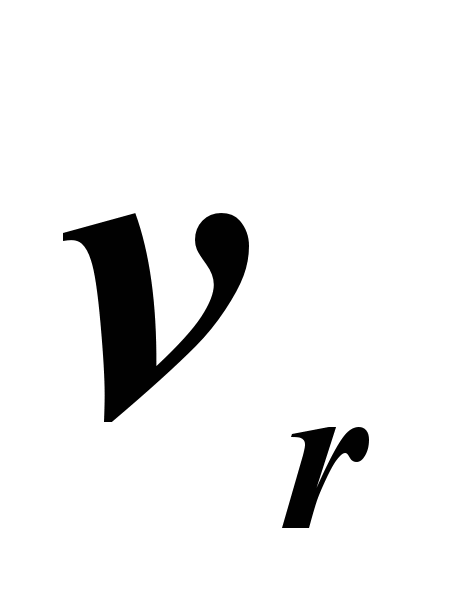

Теорема о сложении ускорений (ТЕОРЕМА КОРИОЛИСА)

aкор = aпер + aот + aкор

Формула выражает следующую теорему Кориолиса о сложении уско-

рений:1 при сложном движении ускорение точки равно геометрической

сумме трех ускорений: относительного, переносного и поворотного, или

кориолисова.

aкор = 2(ω × vот)

37.Принцип Даламбера

принцип Даламбера для материальной точки: в каждый момент движения материальной точки активные силы, реакции связей и сила инерции образуют уравновешенную систему сил.

Д’Аламбера принцип - в механике: один из основных принципов динамики, согласно которому, если к заданнымсилам, действующим на точки механической системы, и реакциям наложенных связей присоединитьсилы инерции, то получится уравновешенная система сил.

Согласно данному принципу, для каждой i-той точки системы верно равенство

где - действующая на эту точку активная сила,- реакция наложенной на точку связи,- сила инерции, численно равная произведению массыточки на её ускорениеи направленная противоположно этому ускорению ().

Фактически, речь идёт о выполняемом отдельно для каждой из рассматриваемых материальных точек переносе слагаемого ma справа налево во втором законе Ньютона() и нареканию этого слагаемого Д’Аламберовой силой инерции.

Принцип Д’Аламбера позволяет применить к решению задач динамики более простые методы статики, поэтому им широко пользуются в инженерной практике, т. н. метод кинетостатики. Особенно удобно им пользоваться для определения реакций связей в случаях, когда закон происходящего движения известен или найден из решения соответствующих уравнений.

Одно из важнейших понятий механики – работа силы .

Работа силы

Все физические тела в окружающем нас мире приводятся в движение с помощью силы. Если на движущееся тело в попутном или противоположном направлении действует сила или несколько сил со стороны одного или нескольких тел, то говорят, что совершается работа .

То есть, механическая работу совершает действующая на тело сила. Так, сила тяги электровоза приводит в движение весь поезд, тем самым совершая механическую работу. Велосипед приводится в движение мускульной силой ног велосипедиста. Следовательно, эта сила также совершает механическую работу.

В физике работой силы называют физическую величину, равную произведению модуля силы, модуля перемещения точки приложения силы и косинуса угла между векторами силы и перемещения.

A = F · s · cos (F, s) ,

где F модульсилы,

s – модуль перемещения.

Работа совершается всегда, если угол между ветрами силы и перемещения не равен нулю. Если сила действует в направлении, противоположном направлению движения, величина работы имеет отрицательное значение.

Работа не совершается, если на тело не действуют силы, или если угол между приложенной силой и направлением движения равен 90 о (cos 90 o = 0).

Если лошадь тянет телегу, то мускульная сила лошади, или сила тяги, направленная по ходу движения телеги, совершает работу. А сила тяжести, с которой извозчик давит на телегу, работы не совершает, так как она направлена вниз, перпендикулярно направлению перемещения.

Работа силы – величина скалярная.

Единица работы в системе измерений СИ - джоуль. 1 джоуль – это работа, которую совершает сила величиной в 1 ньютон на расстоянии 1 м, если направления силы и перемещения совпадают.

Если на тело или материальную точку действуют несколько сил, то говорят о работе, совершаемой их равнодействующей силой.

В случае, если приложенная сила непостоянна, то её работа вычисляется как интеграл:

Мощность

Сила, приводящая в движение тело, совершает механическую работу. Но как совершается эта работа, быстро или медленно, иногда очень важно знать на практике. Ведь одна и та же работа может быть совершена за разное время. Работу, которую выполняет большой электромотор, может выполнить и маленький моторчик. Но ему для этого понадобится гораздо больше времени.

В механике существует величина, характеризующая быстроту выполнения работы. Эта величина называется мощностью .

Мощность – это отношение работы, выполненной за определённый промежуток времени, к величине этого промежутка.

N = A /∆ t

По определению А = F · s · cos α , а s/∆ t = v , следовательно

N = F · v · cos α = F · v ,

где F – сила, v скорость, α – угол между направлением силы и направление скорости.

То есть мощность – это скалярное произведение вектора силы на вектор скорости движения тела .

В международной системе СИ мощность измеряется в ваттах (Вт).

Мощность в 1 ватт – это работа в 1 джоуль (Дж), совершаемая за 1 секунду (с).

Мощность можно увеличить, если увеличить силу, совершающую работу, или скорость, с которой эта работа совершается.