Velosiped g'ildiragi spikeriga o'rnatiladigan to'q sariq rangli plastik reflektorlarni eslaysizmi? Keling, reflektorni g'ildirak jantiga o'rnatamiz va uning traektoriyasini kuzatamiz. Olingan egri chiziqlar sikloidlar oilasiga tegishli. G'ildirak sikloidning hosil qiluvchi doirasi (yoki doirasi) deb ataladi. Ammo asrimizga qaytib, zamonaviyroq texnologiyaga o'tamiz. Velosiped yo'lida shinalar protektoriga tiqilib qolgan tosh bor edi.

G'ildirakni bir necha marta aylantirgandan so'ng, tosh protektordan chiqib ketganda qaerga uchadi? Mototsikl yo'nalishiga qarshimi yoki unga qarabmi? Ma'lumki, jismning erkin harakati u harakat qilgan traektoriyaga tangensial ravishda boshlanadi. Tsikloidga tegish har doim harakat yo'nalishi bo'yicha yo'naltiriladi va hosil qiluvchi doiraning yuqori nuqtasidan o'tadi. Bizning toshimiz harakat yo'nalishi bo'yicha uchadi. Bolaligingizda orqa qanotsiz velosipedda ko'lmaklardan qanday o'tganingizni eslaysizmi? Orqangizdagi ho'l chiziq hozirgina olingan natijani har kuni tasdiqlaydi.

17-asr sikloid asridir. Eng yaxshi olimlar uning ajoyib xususiyatlarini o'rganishdi. Jismni tortishish kuchi ta'sirida bir nuqtadan ikkinchi nuqtaga eng qisqa vaqt ichida qanday traektoriya olib boradi? Bu fanning birinchi muammolaridan biri bo'lib, hozirda o'zgaruvchanlik hisobi deb ataladi. Siz turli xil narsalarni - yo'l uzunligini, tezligini, vaqtini kamaytirishingiz (yoki maksimal darajaga ko'tarishingiz) mumkin. Brachistoxrone muammosida vaqt minimallashtiriladi (bu nomning o'zi tomonidan ta'kidlangan: yunoncha betosos - eng kichik, chrúnos - vaqt). Aqlga keladigan birinchi narsa - bu to'g'ri traektoriya. Shuningdek, berilgan nuqtalarning tepasida cho‘qqisi bo‘lgan teskari sikloidni ham ko‘rib chiqamiz. Va Galileo Galileydan keyin, bizning nuqtalarimizni bir-biriga bog'laydigan chorak doira. Keling, ko'rib chiqilgan profillar bilan bobsley treklarini yarataylik va qaysi bob birinchi bo'lib kelishini ko'raylik. Bobsley tarixi Shveytsariyada boshlangan. 1924 yilda birinchi qishki Olimpiya o'yinlari Frantsiyaning Shamonix shahrida bo'lib o'tdi. Ular allaqachon ikki va to'rt kishilik ekipajlar uchun bobsley musobaqalarini o'tkazishadi.

Olimpiada o'yinlarida besh kishidan iborat bobsley ekipaji bo'lgan yagona yil 1928 yil edi. O'shandan beri ikki va to'rt kishilik erkaklar ekipajlari doimo bobsleyda qatnashib kelishadi. Bobsley qoidalarida juda ko'p qiziqarli narsalar mavjud. Albatta, bob va jamoaning og'irligi bo'yicha cheklovlar mavjud, lekin hatto bob konkida ishlatilishi mumkin bo'lgan materiallarga ham cheklovlar mavjud (oldingi juftlik harakatlanuvchi va rulga ulangan, orqa juftlik qattiq mahkamlangan) . Masalan, konki ishlab chiqarishda radiumdan foydalanish mumkin emas.

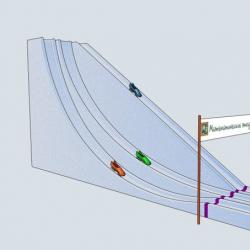
Keling, to'rt oyoqlarimizni boshlaymiz. Qaysi loviya marraga birinchi bo'lib yetib boradi? Yashil Bob, Matematik tadqiqotlar jamoasida o'ynab, sikloid slaydni pastga aylantirib, birinchi o'rinda turadi! Nima uchun Galiley Galiley aylananing to'rtdan bir qismini ko'rib chiqdi va bu vaqt nuqtai nazaridan eng yaxshi tushish traektoriyasi deb hisobladi? U singan chiziqlarni kiritdi va havolalar soni ortib borishi bilan tushish vaqti qisqarganini payqadi. Bu erdan Galiley tabiiy ravishda aylanaga o'tdi, lekin bu traektoriya barcha mumkin bo'lganlar orasida eng yaxshisi degan noto'g'ri xulosaga keldi. Ko'rib turganimizdek, eng yaxshi traektoriya sikloiddir. Bu ikki nuqta orqali sikloidning cho'qqisi yuqori nuqtada bo'lishi sharti bilan noyob sikloidni chizish mumkin. Va hatto sikloid ikkinchi nuqtadan o'tish uchun ko'tarilishi kerak bo'lsa ham, u baribir eng tik tushishning egri chizig'i bo'ladi! Tsikloid bilan bog'liq yana bir go'zal muammo - tautochrone muammosi. Yunon tilidan tarjima qilingan táōtís "xuddi shunday", chrōnos, biz allaqachon bilganimizdek - "vaqt" degan ma'noni anglatadi. Slaydlarning uchlari bir-biriga to'g'ri kelishi va sikloidning yuqori qismida joylashgan bo'lishi uchun sikloid ko'rinishidagi profilli uchta bir xil slaydni yasaymiz. Keling, uchta loviyani turli balandliklarga qo'yib, davom etaylik.

Eng hayratlanarli fakt shundaki, barcha loviya bir vaqtning o'zida tushadi! Qishda siz hovlingizda muzli slaydni qurishingiz va bu mulkni shaxsan sinab ko'rishingiz mumkin. Tavtoxron muammosi shunday egri chiziqni topishdan iboratki, har qanday boshlang'ich pozitsiyadan boshlab, berilgan nuqtaga tushish vaqti bir xil bo'ladi. Kristian Gyuygens yagona tautoxron sikloid ekanligini isbotladi. Albatta, Gyuygens muzli slaydlardan pastga tushishdan manfaatdor emas edi. O‘sha paytlarda olimlarning san’at ishqibozi uchun ilm-fanga intilish dabdabasi yo‘q edi. O‘rganilgan muammolar o‘sha davr texnikasining hayoti va talablaridan kelib chiqqan holda ishlab chiqilgan. 17-asrda uzoq dengiz sayohatlari allaqachon sodir bo'lgan. Dengizchilar allaqachon kenglikni aniq aniqlashga muvaffaq bo'lishgan, ammo ular uzunlikni umuman aniqlay olmaganlari ajablanarli. Kenglikni o'lchash uchun tavsiya etilgan usullardan biri aniq xronometrlarning mavjudligiga asoslangan edi. To'g'ri bo'lgan mayatnikli soatlar yasash haqida o'ylagan birinchi odam Galileo Galiley edi. Biroq, u ularni amalga oshirishni boshlagan paytda, u allaqachon qarib qolgan, u ko'r va umrining qolgan yilida olim soat yasashga ulgurmaydi. U buni o'g'liga vasiyat qiladi, lekin u ikkilanib, mayatnik ustida ishlashni faqat o'limidan oldin boshlaydi va rejani amalga oshirishga vaqt topolmaydi.

Keyingi taniqli shaxs Kristian Gyuygens edi. U Galiley tomonidan ko'rib chiqilgan oddiy mayatnikning tebranish davri boshlang'ich pozitsiyasiga bog'liqligini payqadi, ya'ni. amplitudadan. Yukning aylanish vaqti amplitudaga bog'liq bo'lmasligi uchun yukning traektoriyasi qanday bo'lishi kerakligi haqida o'ylab, u tautoxron muammosini hal qiladi. Ammo yukni sikloid bo'ylab qanday harakatlantirish kerak? Nazariy tadqiqotlarni amaliy tekislikka aylantirib, Gyuygens mayatnik arqon o'ralgan "yonoqlar" qiladi va yana bir nechta matematik muammolarni hal qiladi. U "yonoqlar" bir xil sikloid profiliga ega bo'lishi kerakligini isbotlaydi va shu bilan sikloidning evolyutsiyasi bir xil parametrlarga ega bo'lgan sikloid ekanligini ko'rsatadi. Bundan tashqari, Gyuygens tomonidan taklif qilingan sikloid mayatnikning dizayni sikloid uzunligini hisoblash imkonini beradi. Agar uzunligi ishlab chiqaruvchi doiraning to'rt radiusiga teng bo'lgan ko'k ip imkon qadar ko'proq burilsa, uning oxiri "yonoq" va sikloid-traektoriyaning kesishish nuqtasida bo'ladi, ya'ni. sikloidning tepasida - "yonoqlar". Bu sikloid yoy uzunligining yarmi bo'lgani uchun umumiy uzunlik hosil qiluvchi doiraning sakkiz radiusiga teng. Kristian Gyuygens sikloid mayatnik yasadi va u bilan soatlar dengiz sayohatlarida sinovdan o'tkazildi, ammo ildiz otmadi. Biroq, bu maqsadlar uchun muntazam sarkaçli soat bilan bir xil. Nima uchun oddiy mayatnikli soat mexanizmlari hali ham mavjud? Agar siz diqqat bilan qarasangiz, qizil sarkaç kabi kichik og'ishlar bilan, sikloid sarkaçning "yonoqlari" deyarli ta'sir qilmaydi. Shunga ko'ra, kichik og'ishlar uchun sikloid bo'ylab va aylana bo'ylab harakat deyarli mos keladi.

Adabiyot:
G. N. Berman. Tsikloid. M.: Nauka, 1980 yil.
S. G. Gindikin. Fiziklar va matematiklar haqida hikoyalar. M.: MTsNMO, 2006 yil.

Izohlar: 1

Vladimir Zaxarov

Rossiya Fanlar akademiyasining akademigi, fizika-matematika fanlari doktori, Rossiya Fanlar akademiyasining nochiziqli dinamika bo'yicha Ilmiy kengashi raisining ma'ruzasi. Rossiya Fanlar akademiyasining Fizika institutining matematik fizika bo'limi. Lebedev, Arizona universiteti professori (AQSh), ikki marta Davlat mukofoti sovrindori, Vladimir Evgenievich Zaxarov tomonidan Dirac medali sovrindori, 2010 yil 27 mayda Politexnika muzeyida "Siyosatga ommaviy ma'ruzalar" loyihasi doirasida o'tkazilgan. ru”.

Sergey Kuksin

“Klassik mexanika kunlari” xalqaro ilmiy konferensiyasi Moskva, Steklov nomidagi matematika instituti, st. Gubkina, 8, 2015 yil 26 yanvar

Xaos - har biri o'n uch daqiqadan iborat to'qqiz bobdan iborat matematik film. Bu dinamik tizimlar, kapalak effekti va xaos nazariyasiga bag'ishlangan keng omma uchun film.

Aleksandra Skripchenko

Matematik Aleksandra Skripchenko bilyard dinamik tizim sifatida, ratsional burchaklar va Puankare teoremasi haqida.

Yuliy Ilyashenko

Kolmogorov-Arnold-Mozer nazariyasi "Sayyoralar Quyoshga tushishi mumkinmi?" kabi savollarga javob beradi. Ha bo'lsa, qanday ehtimollik bilan? Va qancha vaqtdan keyin? ” Muammoning matematik formulasi: deylik, massalar shunchalik kichikki, ularning bir-biriga jalb etilishini e'tiborsiz qoldirish mumkin. Keyin sayyoralarning traektoriyalarini hisoblash mumkin; Nyuton buni qildi. Agar biz haqiqiy holatga o'tadigan bo'lsak, sayyoralarning o'zaro tortishishi ularning orbitalariga ta'sir qilganda, biz integral bo'lgan kichik buzilishni olamiz, ya'ni. aniq echiladigan tizim. Puankare differensial tenglamalar nazariyasining asosiy vazifasi klassik mexanikaning integral tizimlarining kichik tebranishlarini o'rganish deb hisobladi. Ma'ruzalar katta maktab o'quvchilari uchun ochiq bo'lgan darajada KAM nazariyasining asosiy g'oyalari haqida gapirib beradi. Biz n-tana masalasiga va klassik mexanikaga o'tmaymiz, lekin biz aylana diffeomorfizmlari va samoviy mexanika muammolari uchun Kolmogorov tomonidan taklif qilingan induksiya jarayonining asosiy bosqichini muhokama qilamiz.

Olga Romaskevich

Agar siz juda shafqatsiz harakat qilsangiz va matematikning qalam va qog'ozini olib qo'ysangiz, u yangi muammolarni qidirib osmonga qaraydi. Sayyoralar harakati haqidagi savol (matematik dunyoda "n-tana muammosi" deb nomlanadi) juda murakkab - shu qadar murakkabki, hatto n = 3 holatning maxsus kichik bo'limlari uchun ham har yili juda ko'p maqolalar nashr etiladi. Semestr kursida ham bu muammoning barcha jihatlarini tahlil qilib bo'lmaydi. Biroq, biz qo'rqmaymiz va bu erda paydo bo'lgan matematika bilan o'ynashga harakat qilamiz. Biz uchun asosiy turtki ikki jism muammosi bo'ladi: yaqin atrofda boshqa sayyoralar yo'q degan taxmin ostida bitta sayyoraning Quyosh atrofida harakati muammosi.

Dmitriy Anosov

Kitobda differentsial tenglamalar haqida gap boradi. Ayrim hollarda muallif differensial tenglamalar qanday yechilishini, boshqalarida esa geometrik mulohazalar ularning yechimlarining xossalarini tushunishga yordam beradi. (Kitob nomidagi “hal qilamiz, keyin chizamiz” so‘zlari shu bilan bog‘langan.) Bir nechta jismoniy misollar ko‘rib chiqiladi. Eng soddalashtirilgan darajada, 20-asrning ba'zi yutuqlari, shu jumladan deterministik ob'ektlarning xatti-harakatlarida "xaos" paydo bo'lish mexanizmini tushunish tasvirlangan. Kitob matematikaga qiziquvchi o'rta maktab o'quvchilari uchun mo'ljallangan. Ular qilishlari kerak bo'lgan narsa lotin ma'nosini bir lahzalik tezlik deb tushunishdir.

Aleksey Belov

Mashhur olimpiada muammosi bor: tekis stol ustida tangalar (qavariq shakllar) bor. Keyin ulardan biri boshqalarga ta'sir qilmasdan stoldan tortilishi mumkin. Uzoq vaqt davomida matematiklar ushbu bayonotning fazoviy o'xshashligini isbotlashga harakat qilishdi, toki qarshi misol tuzilmaguncha! Bir fikr paydo bo'ldi: mayda donalarda ko'pincha yoriq bo'lmaydi, yoriq don chegarasidan tashqariga chiqmaydi va yoriqlar bir-birini ushlab turadi. Ushbu g'oya nazariy jihatdan yoriqlar o'smaydigan kompozitsiyalarni, xususan, keramik zirhlarni yaratishga imkon beradi.

Aleksey Sosinskiy

Mexanika va nazariy fizikaning eng muhim tushunchalaridan biri - mexanik tizimning konfiguratsiya fazosi tushunchasi negadir nafaqat maktab o'quvchilariga, balki ko'pchilik matematika talabalariga ham noma'lum bo'lib qolmoqda. Ma'ruzada juda oddiy, ammo juda mazmunli mexanik tizimlar sinfi - ikki erkinlik darajasiga ega tekis menteşeli mexanizmlar muhokama qilinadi. Biz "umumiy holatda" ularning konfiguratsiya bo'shliqlari ikki o'lchovli yuzalar ekanligini aniqlaymiz va biz ularning qaysi biri ekanligini tushunishga harakat qilamiz. (Bu erda o'n yil oldin Dima Zvonkin tomonidan olingan yakuniy natijalar.) Keyinchalik, menteşe mexanizmlari bilan bog'liq hal qilinmagan matematik muammolar muhokama qilinadi. (Jumladan, amerikalik matematik Bill Tyurstonning ikkita gipotezasi, aniqrogʻi isbotlanmagan teoremalari.)

Vladimir Protasov

Variatsiyalar hisobi — cheksiz oʻlchamli fazoda funksiyaning minimalini topish haqidagi fan. Biz o‘rganib qolgan minimal masalalardan farqli o‘laroq, raqamni (parametrni) yoki, aytaylik, tekislikdagi nuqtani optimal tanlash kerak bo‘lganda, variatsion masalalarda biz optimal funksiyani topishimiz kerak. Shu bilan birga, kelib chiqishi juda xilma-xil bo'lgan muammolar bir xil vositalar to'plami yordamida hal qilinadi: klassik mexanikadan, geometriyadan, matematik iqtisodiyotdan va boshqalar. Biz 17-asrdan beri ma'lum bo'lgan eski muammolardan boshlaymiz va bir muammodan ikkinchisiga ko'prik qurib, biz tezda zamonaviy natijalarga va hal qilinmagan muammolarga erishamiz.

(yunon tilidan tarjima qilingan. dumaloq) – radiusli doiradagi nuqta bilan tasvirlangan tekis transsendental egri chiziq r toʻgʻri chiziq boʻylab sirgʻanmasdan dumalab yurish (transsendental egri chiziq toʻrtburchaklar koordinatalarida algebraik tenglama bilan tasvirlab boʻlmaydigan egri chiziq). Uning parametrik tenglamasi

x = rt – r gunoh t,
y= r - r cos t

Sikloidning aylana aylanayotgan toʻgʻri chiziq bilan kesishgan nuqtalari (bu aylana hosil qiluvchi aylana, u aylanib yuradigan toʻgʻri chiziq esa direktiv deb ataladi) choʻqqi nuqtalari, sikloiddagi eng yuqori nuqtalar deyiladi. , qo'shni cho'qqi nuqtalari orasidagi o'rtada joylashgan, sikloidning uchlari deyiladi.

Galileo Galiley sikloidni birinchi bo'lib o'rgangan. Bitta sikloid arkaning uzunligi 1658 yilda ingliz me'mori va matematigi, Londondagi Avliyo Pol sobori gumbazining loyihasi va quruvchisi Kristofer Ren tomonidan aniqlangan. Ma'lum bo'lishicha, sikloidning uzunligi hosil qiluvchi doiraning 8 radiusiga teng.
Unga o'z nomini bergan sikloidning ajoyib xususiyatlaridan biri - brachistochrone (yunoncha "eng qisqa" va "vaqt" so'zlaridan) eng keskin tushish muammosini hal qilish bilan bog'liq. Ikki nuqtani bir-biriga bog'lab turuvchi, yaxshi sayqallangan (ishqalanishni deyarli yo'q qilish uchun) trubaga qanday shakl berish kerakligi to'g'risida savol tug'ildi, shunda to'p bir nuqtadan ikkinchisiga qisqa vaqt ichida dumalab tushadi. Aka-uka Bernulli xandaq pastga siljoid shaklida bo'lishi kerakligini isbotladi.

Tsikloid bilan bog'liq egri chiziqlar hosil qiluvchi doirada joylashmagan nuqtalarning traektoriyalarini hisobga olgan holda olinishi mumkin.

Nuqtaga ruxsat bering 0 dan doira ichida joylashgan. O'tkazilsa 0 dan generatsiya aylanasi bilan bir xil markazga ega bo'lgan yordamchi doira, so'ngra hosil qiluvchi doira to'g'ri chiziq bo'ylab aylanganda AB kichik doira to'g'ri chiziqda aylanadi A´ IN´, lekin uning aylanishi sirpanish va davr bilan birga bo'ladi 0 dan qisqartirilgan sikloid deb ataladigan egri chiziqni tasvirlaydi.

Cho'zilgan sikloid shunga o'xshash tarzda aniqlanadi - bu hosil qiluvchi doira radiusining kengaytmasida joylashgan nuqtaning traektoriyasi, dumalash esa teskari yo'nalishda siljish bilan birga keladi.

Tsikloid egri chiziqlar ko'plab texnik hisob-kitoblarda qo'llaniladi va ularning xususiyatlari, masalan, tishli tish profillarini qurishda, sikloid mayatniklarda, optikada qo'llaniladi va shuning uchun bu egri chiziqlarni o'rganish amaliy nuqtai nazardan muhimdir. XVII asr olimlari ushbu egri chiziqlar va ularning xususiyatlarini o'rganishlari bir xil darajada muhimdir. differensial va integral hisoblarni yaratishga olib kelgan texnikani ishlab chiqdi va braxistoxron muammosi variatsiyalar hisobini ixtiro qilish uchun qadam bo'ldi.

Elena Malishevskaya

LEMNİKATLAR
Qutb koordinatalaridagi tenglama:
r 2 = a 2 cos2th

(x 2 + y 2) 2 = a 2 (x 2 - y 2)

AB" yoki A"B va x o'qi orasidagi burchak = 45 o

Bitta halqaning maydoni = 2/2

SIKLOID

Bir yoyning maydoni = 3pa 2

Bir kamarning yoy uzunligi = 8a

Bu x o'qi bo'ylab aylanadigan a radiusli doiradagi P nuqta bilan tasvirlangan egri chiziqdir.

TO'RT QO'LQALI GIPOTSIKLOIDLAR
To'rtburchaklar koordinatalaridagi tenglama:
x 2/3 + y 2/3 = a 2/3

Parametrik shakldagi tenglamalar:

Egri chiziq bilan o'ralgan maydon = 3pa 2 /8

Butun egri chiziqning yoy uzunligi = 6a

Bu radiusi a/4 bo'lgan doira ichida aylanib yuruvchi P nuqtasi bilan tasvirlangan egri chiziqdir.

KARDIOID
Tenglama: r = a(1 + costh)

Egri chiziq bilan o'ralgan maydon = 3pa 2 /2

Egri yoy uzunligi = 8a

Bu a radiusli doiradan tashqarida aylanib yuruvchi a radiusli aylana ustidagi P nuqta bilan tasvirlangan egri chiziqdir. Bu egri chiziq ham Paskal salyangozining alohida holatidir.

ZANJIRLI LINE
Tenglama:
y = a(e x/a + e -x/a)/2 = acosh(x/a)

Bu zanjir A nuqtadan B gacha vertikal ravishda osilgan bo'lgan egri chiziqdir.

UCH BERGAN Atirgul
Tenglama: r = acos3th

r = acos3th tenglamasi 30 o yoki p/6 radianli egri chiziq bo‘ylab soat miliga teskari aylanish natijasida olingan egri chiziqqa o‘xshaydi.

Umuman olganda, n toq bo'lsa, r = acosnth yoki r = asinnth n ta bo'lakka ega.

TO'RT PETALE ROSE
Tenglama: r = acos2th

r = asin2th tenglamasi 45 o yoki p/4 radian egri chizig'i bo'ylab soat miliga teskari aylanish natijasida olingan egri chiziqqa o'xshaydi.

Umuman olganda, r = acosnth yoki r = asinnth, agar n juft bo'lsa, 2n ta gulbargga ega.

EPICYCLOID
Parametrik tenglamalar:

Bu radiusi b bo'lgan aylanada P nuqta bilan tasvirlangan egri chiziq a radiusli aylananing tashqi tomoni bo'ylab aylanayotganda. Kardioid epitsikloidning alohida holatidir.

UMUMIY GIPOSİKLOID
Parametrik tenglamalar:

Bu radiusi b bo'lgan aylanada P nuqta bilan tasvirlangan egri chiziq a radiusli aylananing tashqi tomoni bo'ylab aylanayotganda.

Agar b = a/4 bo'lsa, egri chiziq to'rt nuqtadan iborat bo'lgan gipotsikloiddir.

TROXOID
Parametrik tenglamalar:

Bu x o'qi bo'ylab aylanayotganda a radiusli aylana markazidan b masofada P nuqta bilan tasvirlangan egri chiziqdir.
Agar b qisqargan sikloid bo'lsa.
Agar b > a bo'lsa, egri rasmda ko'rsatilgan shaklga ega. 11-11 va deyiladi yuruvchi.
Agar b = a bo'lsa, egri chiziq sikloiddir.

TRAKTRICE
Parametrik tenglamalar:

Bu PQ uzunlikdagi cho'zilgan ipning P nuqtasi bilan tasvirlangan egri chiziqning ikkinchi uchi Q x o'qi bo'ylab harakatlantirilganda.

VERZIERA (VERZIERA) AGNEZI (BA'ZAN CURL AGNEZI)
To'g'ri to'rtburchak koordinatadagi tenglama: y = 8a 3 /(x 2 + 4a 2)

Parametrik tenglamalar:

B. Rasmda OA oʻzgaruvchi chizigʻi y = 2a va radiusi a boʻlgan, mos ravishda A va B nuqtalarda (0,a) markazli aylana bilan kesishadi. "Kurilish" ning har qanday P nuqtasi x va y o'qlariga parallel ravishda va mos ravishda B va A orqali chiziqlar qurish va P ning kesishish nuqtasini aniqlash orqali aniqlanadi.

DESCARTES LEAF
To'rtburchaklar koordinatalaridagi tenglama:
x 3 + y 3 = 3 aks

Parametrik tenglamalar:

Loop maydoni 3a 2/2

Asimptot tenglamasi: x + y + a = 0.

DAVLAMA DARAJAT
Parametrik tenglamalar:

Bu radiusi a bo'lgan aylanadan yechilganida ipning oxirgi P nuqtasi tomonidan tasvirlangan egri chiziq.

ELLIPS INVOLVENT
To'rtburchaklar koordinatalaridagi tenglama:
(bolta) 2/3 + (tomonidan) 2/3 = (a 2 - b 2) 2/3

Parametrik tenglamalar:

Bu egri chiziq x 2 /a 2 + y 2 /b 2 = 1 ellipsga normal bo'lgan konvertdir.

CASSINI OVALS
Qutb tenglamasi: r 4 + a 4 - 2a 2 r 2 cos2th = b 4.

Bu P nuqta bilan tasvirlangan egri chiziq bo'lib, uning ikkita qo'zg'almas nuqtadan [tomongacha bo'lgan masofa 2a] masofasining mahsuloti doimiy b 2 bo'ladi.

Quyidagi rasmlardagi kabi egri chiziq b a bo'lganda.

Agar b = a bo'lsa, egri chiziq bo'ladi lemniskat

PASKAL SOLIGANI
Polar tenglama: r = b + acoth

O ning markazini O dan o tuvchi a diametrli aylanadagi istalgan Q nuqta bilan O q nuqta bilan bog lovchi chiziq bo lsin. U holda egri chiziq PQ = b bo ladigan barcha P nuqtalarning fokusi bo ladi.

b > a yoki b bo'lganda quyidagi rasmlarda ko'rsatilgan egri chiziq

DIOKLLARNING SİSSOIDI
To'g'ri to'rtburchak koordinatadagi tenglama: y 2 = x 3 /(2a - x)

Parametrik tenglamalar:

Bu masofa OP = masofa RS bo'lishi uchun P nuqta bilan tasvirlangan egri chiziqdir. Vazifada ishlatiladi kubni ikki barobarga oshirish, ya'ni. Berilgan kubning hajmi ikki barobar katta bo'lgan kubning tomonini topish

ARXIMED SPIRALI
Polar tenglama: r = ath

5. Parametrik sikloid tenglama va Dekart koordinatalaridagi tenglama

Faraz qilaylik, bizga markazi A nuqtada bo'lgan a radiusli aylana hosil qilgan sikloid berilgan.

Agar nuqta o'rnini belgilovchi parametr sifatida prokat boshida AO vertikal holatga ega bo'lgan radius aylana olgan t=∟NDM burchagini tanlasak, u holda M nuqtaning x va y koordinatalari bo'ladi. quyidagicha ifodalansin:

x= OF = ON - NF = NM - MG = at-a sin t,

y= FM = NG = ND – GD = a – a cos t

Shunday qilib, sikloidning parametrik tenglamalari quyidagi shaklga ega:

t -∞ dan +∞ ga o'zgarganda, bu rasmda ko'rsatilgandek cheksiz sonli novdalardan iborat egri chiziq olinadi.

Shuningdek, sikloidning parametrik tenglamasidan tashqari, uning Dekart koordinatalarida ham tenglamasi mavjud:

Bu yerda r sikloidni hosil qiluvchi aylana radiusi.

6. Sikloidning qismlari va sikloid hosil qilgan figuralarni topishga oid masalalar

Vazifa № 1. Tenglamasi parametrik berilgan sikloidning bir yoyi bilan chegaralangan figuraning maydonini toping.

va Ox o'qi.

Yechim. Ushbu muammoni hal qilish uchun biz integrallar nazariyasidan bilgan faktlardan foydalanamiz, xususan:

Egri sektorning maydoni.

[a, b] da aniqlangan ba'zi r = r(s) funksiyani ko'rib chiqaylik.

s 0 ∈ [a, b] r 0 = r(s 0) ga mos keladi va shuning uchun M 0 (s 0 , r 0) nuqtasi, bu erda s 0,

r 0 - nuqtaning qutb koordinatalari. Agar s butun [a, b] boʻylab “oʻtib” oʻzgarsa, M oʻzgaruvchan nuqta berilgan AB egri chizigʻini tasvirlaydi.

tenglama r = r(s).

Ta'rif 7.4. Egri sektor ikki nurlar s = a, s = b va qutbda aniqlangan AB egri chizig'i bilan chegaralangan shakldir.

koordinatalar r = r(s), a ≤ s ≤ b tenglama bo‘yicha.

Quyidagi gaplar haqiqat

Teorema. Agar funktsiya r(s) > 0 bo'lsa va [a, b] da uzluksiz bo'lsa, u holda maydon

egri chiziqli sektor quyidagi formula bo'yicha hisoblanadi:

Bu teorema avval aniq integral mavzusida isbotlangan.

Yuqoridagi teoremaga asoslanib, tenglamasi x= a (t – sin t), y= a (1) parametrik parametrlari bilan berilgan sikloidning bir yoyi bilan chegaralangan figuraning maydonini topish muammomiz. – cos t) va Ox o‘qi quyidagi yechimga keltiriladi.

Yechim. egri tenglamadan dx = a(1−cos t) dt. Tsikloidning birinchi yoyi t parametrining 0 dan 2p gacha o'zgarishiga mos keladi. Demak,

Vazifa № 2. Tsikloidning bir yoyi uzunligini toping

Quyidagi teorema va uning natijasi ham integral hisobda o‘rganilgan.

Teorema. Agar AB egri chizig'i y = f(x) tenglama bilan berilgan bo'lsa, bu erda f(x) va f ' (x) uzluksiz bo'lsa, AB to'g'rilanadigan va

Natija. AB parametrik ravishda berilgan bo'lsin

L AB = (1)

[a, b] da x(t), y(t) funksiyalar uzluksiz differentsiallansin. Keyin

(1) formulani quyidagicha yozish mumkin

Bu integralda o'zgaruvchilarni o'zgartirishni amalga oshiramiz x = x(t), keyin y’(x)= ;

dx= x’(t)dt va shuning uchun:

Endi muammomizni hal qilishga qaytaylik.

Yechim. Bizda bor va shuning uchun

Vazifa № 3. Tsikloidning bir yoyi aylanishidan hosil bo'lgan S sirt maydonini topishimiz kerak

L=((x,y): x=a(t – sin t), y=a(1 – xarajat), 0≤ t ≤ 2p)

Integral hisobda segmentda parametrik ravishda aniqlangan egri chiziqning x o'qi atrofida aylanish jismining sirt maydonini topish uchun quyidagi formula mavjud: x=ph(t), y=ps(t) (t) 0 ≤t ≤t 1)

Ushbu formulani sikloid tenglamamizga qo'llasak, biz quyidagilarni olamiz:

Vazifa № 4. Tsikloid yoyni aylantirish natijasida olingan jismning hajmini toping

Ox o'qi bo'ylab.

Integral hisoblashda hajmlarni o'rganishda quyidagi izoh mavjud:

Agar egri chiziqli trapetsiyani chegaralovchi egri chiziq parametrik tenglamalar bilan berilgan bo'lsa va bu tenglamalardagi funksiyalar o'zgaruvchining ma'lum bir integraldagi o'zgarishi haqidagi teorema shartlarini qanoatlantirsa, trapetsiyaning Ox o'qi atrofida aylanish tanasining hajmi bo'ladi. formula bo'yicha hisoblab chiqiladi

Keling, kerakli hajmni topish uchun ushbu formuladan foydalanamiz.

Muammo hal qilindi.

Xulosa

Shunday qilib, ushbu ish jarayonida sikloidning asosiy xususiyatlari aniqlandi. Shuningdek, biz sikloidni qurishni o'rgandik va sikloidning geometrik ma'nosini bilib oldik. Ma'lum bo'lishicha, sikloid nafaqat matematikada, balki texnologik hisoblar va fizikada ham juda katta amaliy qo'llanmalarga ega. Ammo sikloidning boshqa afzalliklari bor. U 17-asr olimlari tomonidan egri chiziqlarni o'rganish usullarini ishlab chiqishda qo'llanilgan - oxir-oqibat differentsial va integral hisoblar ixtirosiga olib kelgan usullar. Bu, shuningdek, Nyuton, Leybnits va ularning dastlabki tadqiqotchilari kuchli yangi matematik usullarning kuchini sinab ko'rgan "tegishli toshlardan" biri edi. Nihoyat, braxistoxron muammosi hozirgi fiziklar uchun juda zarur bo'lgan o'zgaruvchanlik hisobini ixtiro qilishga olib keldi. Shunday qilib, sikloid matematika tarixidagi eng qiziqarli davrlardan biri bilan uzviy bog'liq bo'lib chiqdi.

Adabiyot

1. Berman G.N. Tsikloid. – M., 1980 yil

2. Verov S.G. Brachistochrone yoki sikloidning boshqa siri // Kvant. – 1975. - 5-son

3. Verov S.G. Tsikloid sirlari // Kvant. – 1975. - 8-son.

4. Gavrilova R.M., Govoruxina A.A., Kartasheva L.V., Kostetskaya G.S., Radchenko T.N. Aniq integralning qo'llanilishi. Fizika fakulteti 1-kurs talabalari uchun uslubiy ko‘rsatmalar va individual topshiriqlar. - Rostov n/a: UPL RSU, 1994 yil.

5. Gindikin S.G. Tsikloidning yulduz yoshi // Kvant. – 1985. - 6-son.

6. Fikhtengolts G.M. Differensial va integral hisoblash kursi. T.1. – M., 1969 yil

Ushbu chiziq "konvert" deb ataladi. Har bir egri chiziq uning tangenslarining konvertidir.

Materiya va harakat va ular tashkil etuvchi usul har kimga haqiqatni bilishda o'z imkoniyatlarini ro'yobga chiqarish imkonini beradi. Tafakkurning dialektik-materialistik shaklini rivojlantirish metodologiyasini ishlab chiqish va shunga o'xshash bilish usulini o'zlashtirish inson qobiliyatlarini rivojlantirish va amalga oshirish muammosini hal qilish yo'lidagi ikkinchi qadamdir. Fragment XX Imkoniyatlar...

Bunday vaziyatda odamlar nevrasteniyani rivojlanishi mumkin - nevroz, klinik ko'rinishining asosi astenik holatdir. Nevrasteniya holatida ham, nevrastenik psixopatiyaning dekompensatsiyasi holatida ham aqliy (psixologik) himoyaning mohiyati qiyinchiliklardan vegetativ disfunktsiyalar bilan asabiy zaiflikka chekinishda namoyon bo'ladi: yoki odam ongsiz ravishda hujumga qarshi ko'proq "kurashadi". ..

Har xil faoliyat turlari; maktab o'quvchilarining fazoviy tasavvurini va fazoviy tushunchalarini, obrazli, fazoviy, mantiqiy, mavhum fikrlashni rivojlantirish; turli amaliy masalalarni yechish uchun geometrik va grafik bilim va ko'nikmalarni qo'llash qobiliyatini rivojlantirish; texnik va... sohasida loyiha faoliyati bosqichlarining mazmuni va ketma-ketligi bilan tanishish.

Yoylar. Spirallar, shuningdek, yopiq egri chiziqli evolventlardir, masalan, aylana involventi. Ayrim spirallarning nomlari qutb tenglamalarining dekart koordinatalaridagi egri chiziqlar tenglamalari bilan oʻxshashligi bilan beriladi, masalan: · parabolik spiral (a - r)2 = bj, · giperbolik spiral: r = a/j. · Rod: r2 = a/j · si-ci-spiral, parametrik tenglamalari quyidagi ko'rinishga ega: , )