Matris yönteminin belirlenmesi. Doğrusal denklem sistemlerinin matris yöntemini kullanarak çözülmesi. Matris yöntemini kullanarak bir doğrusal denklem sistemini çözme örnekleri
Hadi düşünelim doğrusal cebirsel denklem sistemi(SLAU) nispeten N Bilinmeyen X 1 , X 2 , ..., X N :
Bu sistem “daraltılmış” biçimde şu şekilde yazılabilir:
S N ben=1 A ben X J = b Ben , i=1,2, ..., n.
Matris çarpım kuralına uygun olarak, ele alınan doğrusal denklem sistemi şu şekilde yazılabilir: matris formu Balta=b, Nerede
Matris Aİlgili denklemde sütunları karşılık gelen bilinmeyenlerin katsayıları, satırları ise bilinmeyenlerin katsayıları olan denkleme denir. sistemin matrisi. Sütun matrisi B Elemanları sistem denklemlerinin sağ tarafları olan matrise sağ taraf matrisi veya basitçe denir. sistemin sağ tarafı. Sütun matrisi X Elemanları bilinmeyen bilinmeyenler olan şeye denir sistem çözümü.
şeklinde yazılmış bir doğrusal cebirsel denklem sistemi Balta=b, dır-dir matris denklemi.
Sistem matrisi ise dejenere olmayan, o zaman ters bir matrisi vardır ve sistemin çözümü Balta=b aşağıdaki formülle verilir:
x=A -1 B.
Örnek Sistemi çöz  matris yöntemi.
matris yöntemi.
Çözüm sistemin katsayı matrisinin ters matrisini bulalım

İlk satır boyunca genişleterek determinantı hesaplayalım:

Çünkü Δ ≠ 0 , O A -1 var.

Ters matris doğru bulundu.
Sisteme bir çözüm bulalım 
Buradan, X 1 = 1, x 2 = 2,x 3 = 3 .
Muayene: 
7. Bir doğrusal cebirsel denklem sisteminin uyumluluğuna ilişkin Kronecker-Capelli teoremi.
Doğrusal denklem sistemişu forma sahiptir:
a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2, (5.1)
a m1 x 1 + a m1 x 2 +... + a mn x n = b m.
Burada a i j ve b i (i = ; j = ) verilmiştir ve x j bilinmeyen gerçek sayılardır. Matrislerin çarpımı kavramını kullanarak sistemi (5.1) şu şekilde yeniden yazabiliriz:
burada A = (a i j), sistemin (5.1) bilinmeyenleri için katsayılardan oluşan bir matristir; buna denir sistemin matrisi, X = (x 1 , x 2 ,..., x n) T , B = (b 1 , b 2 ,..., b m) T sırasıyla bilinmeyenler x j ve serbest terimler b i'den oluşan sütun vektörleridir.
Sipariş edilen koleksiyon N reel sayılara (c 1, c 2,..., c n) denir sistem çözümü(5.1), eğer bu sayıların karşılık gelen x 1, x 2,..., xn değişkenleri yerine konulması sonucunda sistemin her denklemi bir aritmetik kimliğe dönüşürse; başka bir deyişle, AC B olacak şekilde bir C= (c 1 , c 2 ,..., c n) T vektörü varsa.
Sistem (5.1) çağrılır eklem yeri, veya çözülebilir, en az bir çözümü varsa. Sistem denir uyumsuz, veya çözülemez, eğer hiçbir çözümü yoksa.
 ,
,
A matrisinin sağ tarafına serbest terimlerden oluşan bir sütun atanarak oluşturulan matrise denir Sistemin genişletilmiş matrisi.
Sistemin (5.1) uyumluluğu sorunu aşağıdaki teorem ile çözülür.
Kronecker-Capelli teoremi . Bir doğrusal denklem sistemi ancak ve ancak A veA matrislerinin sıralarının çakışması durumunda tutarlıdır; r(A) = r(A) = r.
(5.1) sisteminin M çözüm kümesi için üç olasılık vardır:
1) M = (bu durumda sistem tutarsızdır);
2) M bir elementten oluşur, yani. sistemin benzersiz bir çözümü vardır (bu durumda sistem denir) kesin);
3) M birden fazla elemandan oluşur (bu durumda sistem denir) belirsiz). Üçüncü durumda (5.1) sisteminin sonsuz sayıda çözümü vardır.
Sistemin tek çözümü ancak r(A) = n ise vardır. Bu durumda denklem sayısı bilinmeyen sayısından (mn) az değildir; eğer m>n ise m-n denklemleri diğerlerinin sonuçlarıdır. 0 ise Rastgele bir doğrusal denklem sistemini çözmek için, denklem sayısının bilinmeyenlerin sayısına eşit olduğu sistemleri çözebilmeniz gerekir - buna sözde Kramer tipi sistemler: a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1, a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2, (5.3) ...
... ... ...
... ... a n1 x 1 + a n1 x 2 +... + a nn x n = b n . Sistemler (5.3) aşağıdaki yollardan biriyle çözülür: 1) Gauss yöntemi veya bilinmeyenleri ortadan kaldırma yöntemi; 2) Cramer'in formüllerine göre; 3) matris yöntemi. Örnek 2.12. Denklem sistemini inceleyin ve tutarlıysa çözün: 5x 1 - x 2 + 2x 3 + x 4 = 7, 2x 1 + x 2 + 4x 3 - 2x 4 = 1, x 1 - 3x 2 - 6x 3 + 5x 4 = 0. Çözüm. Sistemin genişletilmiş matrisini yazıyoruz:
Sistemin ana matrisinin rütbesini hesaplayalım. Örneğin sol üst köşedeki ikinci dereceden minörün = 7 0 olduğu açıktır; onu içeren üçüncü dereceden küçükler sıfıra eşittir: Sonuç olarak, sistemin ana matrisinin sıralaması 2'dir, yani. r(A) = 2. Genişletilmiş matris A'nın sırasını hesaplamak için sınırdaki küçük değeri dikkate alın bu, genişletilmiş matris r(A)'nın rütbesinin = 3 olduğu anlamına gelir. r(A) r(A) olduğundan sistem tutarsızdır. İlk bölümde bazı teorik materyallere, yerine koyma yöntemine ve sistem denklemlerinin terim terim eklenmesi yöntemine baktık. Bu sayfa aracılığıyla siteye erişen herkesin ilk bölümü okumasını tavsiye ederim. Belki bazı ziyaretçiler materyali çok basit bulacaktır, ancak doğrusal denklem sistemlerini çözme sürecinde genel olarak matematik problemlerinin çözümüne ilişkin çok önemli yorumlar ve sonuçlar çıkardım. Şimdi Cramer kuralını analiz etmenin yanı sıra ters matris (matris yöntemi) kullanarak bir doğrusal denklem sistemini çözeceğiz. Tüm materyaller basit, ayrıntılı ve net bir şekilde sunulmaktadır; neredeyse tüm okuyucular yukarıdaki yöntemleri kullanarak sistemlerin nasıl çözüleceğini öğrenebilecektir. İlk olarak, iki bilinmeyenli iki doğrusal denklem sistemi için Cramer kuralına daha yakından bakacağız. Ne için? – Sonuçta en basit sistem okul yöntemiyle, dönem dönem toplama yöntemiyle çözülebilir! Gerçek şu ki, bazen de olsa böyle bir görev ortaya çıkıyor - iki bilinmeyenli iki doğrusal denklem sistemini Cramer formüllerini kullanarak çözmek. İkinci olarak, daha basit bir örnek, Cramer kuralını daha karmaşık bir durum için (üç bilinmeyenli üç denklemden oluşan bir sistem) nasıl kullanacağınızı anlamanıza yardımcı olacaktır. Ek olarak, Cramer kuralı kullanılarak çözülmesi tavsiye edilen iki değişkenli doğrusal denklem sistemleri de vardır! Denklem sistemini düşünün İlk adımda determinantı hesaplıyoruz, buna denir sistemin ana belirleyicisi. Gauss yöntemi. Eğer ise sistemin tek bir çözümü vardır ve kökleri bulmak için iki determinantı daha hesaplamamız gerekir: Uygulamada yukarıdaki niteleyiciler Latin harfleriyle de gösterilebilir. Denklemin köklerini aşağıdaki formülleri kullanarak buluruz: Örnek 7 Doğrusal denklem sistemini çözme Çözüm: Denklemin katsayılarının oldukça büyük olduğunu görüyoruz, sağ tarafta virgüllü ondalık kesirler var. Virgül matematikteki pratik görevlerde oldukça nadir bir misafirdir; bu sistemi ekonometrik bir problemden aldım. Böyle bir sistem nasıl çözülür? Bir değişkeni diğerine göre ifade etmeye çalışabilirsiniz, ancak bu durumda muhtemelen üzerinde çalışılması son derece elverişsiz olan berbat süslü kesirlerle karşılaşacaksınız ve çözümün tasarımı tek kelimeyle berbat görünecektir. İkinci denklemi 6 ile çarpıp terim terim çıkarabilirsiniz ama burada da aynı kesirler ortaya çıkacaktır. Ne yapalım? Böyle durumlarda Cramer'in formülleri imdada yetişiyor. ; ; Cevap: , Her iki kökün de sonsuz kuyruğu vardır ve yaklaşık olarak bulunurlar; bu, ekonometri problemleri için oldukça kabul edilebilir (ve hatta sıradandır). Görev hazır formüller kullanılarak çözüldüğü için burada yorumlara gerek yok, ancak bir uyarı var. Bu yöntemi kullanırken, zorunlu Görev tasarımının bir parçası aşağıdaki parçadır: “Bu, sistemin benzersiz bir çözümü olduğu anlamına geliyor”. Aksi takdirde, incelemeyi yapan kişi sizi Cramer teoremine saygısızlıktan dolayı cezalandırabilir. Bir hesap makinesinde rahatlıkla yapılabilen kontrol etmek gereksiz olmayacaktır: yaklaşık değerleri sistemin her denkleminin sol tarafına koyarız. Sonuç olarak, küçük bir hatayla sağ taraftaki sayıları almalısınız. Örnek 8 Cevabı sıradan uygunsuz kesirlerle sunun. Bir kontrol yapın. Bu kendi başınıza çözebileceğiniz bir örnektir (son tasarım örneği ve dersin sonundaki cevap). Üç bilinmeyenli üç denklemden oluşan bir sistem için Cramer kuralını ele alalım: Sistemin ana belirleyicisini buluyoruz: Eğer ise, sistemin sonsuz sayıda çözümü vardır veya tutarsızdır (çözümleri yoktur). Bu durumda Cramer kuralı yardımcı olmayacaktır; Gauss yöntemini kullanmanız gerekir. Eğer ise sistemin tek bir çözümü vardır ve kökleri bulmak için üç belirleyiciyi daha hesaplamamız gerekir: Ve son olarak cevap şu formüller kullanılarak hesaplanır: Gördüğünüz gibi, "üçe üç" durumu temelde "ikiye iki" durumundan farklı değildir; serbest terimler sütunu, ana belirleyicinin sütunları boyunca sırayla soldan sağa "yürür". Örnek 9 Sistemi Cramer formüllerini kullanarak çözün. Çözüm: Sistemi Cramer formüllerini kullanarak çözelim. Cevap: Aslında burada da yine yorumlanacak özel bir şey yok, çünkü çözüm hazır formüllere dayanıyor. Ama birkaç yorum var. Hesaplamalar sonucunda "kötü" indirgenemez kesirler elde edilir, örneğin: . 1) Hesaplamalarda hata olabilir. “Kötü” bir kesirle karşılaştığınızda hemen kontrol etmeniz gerekir. Koşul doğru şekilde yeniden yazıldı mı?. Koşul hatasız olarak yeniden yazılırsa, başka bir satırdaki (sütun) genişletmeyi kullanarak belirleyicileri yeniden hesaplamanız gerekir. 2) Kontrol sonucunda herhangi bir hata tespit edilmezse, büyük olasılıkla görev koşullarında bir yazım hatası olmuştur. Bu durumda, görevin sonuna kadar sakin ve DİKKATLİ bir şekilde çalışın ve ardından kontrol ettiğinizden emin olun karar verdikten sonra temiz bir sayfaya çiziyoruz. Elbette kesirli bir cevabı kontrol etmek hoş olmayan bir iştir, ancak bu, gibi saçmalıklara eksi vermeyi gerçekten seven öğretmen için silahsızlandırıcı bir argüman olacaktır. Kesirlerin nasıl ele alınacağı Örnek 8'in yanıtında ayrıntılı olarak anlatılmıştır. Elinizde bir bilgisayarınız varsa, dersin başında ücretsiz olarak indirebileceğiniz otomatik bir kontrol programı kullanın. Bu arada, programı hemen kullanmak en karlısıdır (hatta çözüme başlamadan önce); hata yaptığınız ara adımı hemen göreceksiniz! Aynı hesap makinesi matris yöntemini kullanarak sistemin çözümünü otomatik olarak hesaplar. İkinci açıklama. Zaman zaman denklemlerde bazı değişkenlerin eksik olduğu sistemler de olabiliyor, örneğin: Örnek 10 Sistemi Cramer formüllerini kullanarak çözün. Bu, bağımsız bir çözüm örneğidir (son tasarımın bir örneği ve dersin sonundaki cevap). 4 bilinmeyenli 4 denklemden oluşan bir sistem için Cramer formülleri benzer prensiplere göre yazılır. Determinantların Özellikleri dersinde canlı bir örnek görebilirsiniz. Determinantın sırasını azaltmak - 4. dereceden beş determinant oldukça çözülebilir. Her ne kadar görev zaten şanslı bir öğrencinin göğsündeki profesör ayakkabısını andırıyor olsa da. Ters matris yöntemi aslında özel bir durumdur matris denklemi(Belirtilen dersin 3 numaralı örneğine bakınız). Bu bölümü incelemek için determinantları genişletebilmeniz, bir matrisin tersini bulabilmeniz ve matris çarpımını yapabilmeniz gerekir. Açıklamalar ilerledikçe ilgili bağlantılar verilecektir. Örnek 11 Sistemi matris yöntemini kullanarak çözün Çözüm: Sistemi matris formunda yazalım: Lütfen denklem ve matris sistemine bakın. Öğeleri matrislere yazma prensibimizi herkesin anladığını düşünüyorum. Tek yorum: Denklemlerde bazı değişkenler eksik olsaydı, matriste karşılık gelen yerlere sıfırların yerleştirilmesi gerekirdi. Ters matrisi aşağıdaki formülü kullanarak buluruz: Öncelikle determinantı inceleyelim: Burada determinant ilk satırda genişletilir. Dikkat! Eğer öyleyse, ters matris mevcut değildir ve sistemi matris yöntemini kullanarak çözmek imkansızdır. Bu durumda sistem bilinmeyenlerin ortadan kaldırılması yöntemi (Gauss yöntemi) ile çözülür. Şimdi 9 minör hesaplayıp bunları minör matrisine yazmamız gerekiyor Referans: Doğrusal cebirde çift indislerin anlamını bilmek faydalıdır. İlk hane, elemanın bulunduğu satırın numarasıdır. İkinci rakam, elemanın bulunduğu sütunun numarasıdır: Bize bir doğrusal denklem sistemi verilsin: Ana matrisin olduğunu varsayacağız. Yorum.
Doğrusal denklem sistemlerini çözmek için matris yönteminin, Gauss yönteminin aksine, sınırlı bir uygulamaya sahip olduğuna dikkat edin: bu yöntem yalnızca, öncelikle bilinmeyenlerin sayısının denklem sayısına eşit olduğu doğrusal denklem sistemlerini çözebilir ve ikincisi, ana matris tekil değildir. Örnek.
Matris yöntemini kullanarak bir doğrusal denklem sistemini çözün. Üç bilinmeyenli üç doğrusal denklem sistemi verilmiştir Denklem sisteminin ana matrisi tekil değildir çünkü determinantı sıfır değildir: Ters matris Doğrusal denklem sistemlerini çözmek için matris yönteminin formülünü kullanarak şunu elde ederiz: Bu yöntem, matris yöntemi gibi, yalnızca bilinmeyenlerin sayısının denklem sayısıyla çakıştığı doğrusal denklem sistemleri için geçerlidir. Cramer'in yöntemi aynı isimli teoreme dayanmaktadır: Teorem 5.2.
Sistem Ana matrisi tekil olmayan formüller kullanılarak elde edilebilecek benzersiz bir çözüme sahiptir. Nerede Örnek.
Önceki örnekte ele alınan doğrusal denklem sisteminin çözümünü Cramer yöntemini kullanarak bulalım. Denklem sisteminin ana matrisi dejenere değildir, çünkü Teorem 5.2'de sunulan formülleri kullanarak bilinmeyenlerin değerlerini hesaplıyoruz: Temel çözüm Bir doğrusal denklem sistemini incelemek, bu sistemin uyumlu olup olmadığını belirlemek, uyumlu ise bu sistemin belirli mi yoksa belirsiz mi olduğunu bulmak anlamına gelir. Bir doğrusal denklem sisteminin uyumluluk koşulu aşağıdaki teorem ile verilmektedir. Teorem 6.1 (Kronecker-Capelli).
Bir doğrusal denklem sistemi ancak ve ancak sistemin ana matrisinin derecesinin genişletilmiş matrisinin sırasına eşit olması durumunda tutarlıdır: Eş zamanlı bir doğrusal denklem sistemi için kesinliği veya belirsizliği sorunu aşağıdaki teoremler kullanılarak çözülür. Teorem 6.2.
Bir ortak sistemin ana matrisinin sıralaması bilinmeyenlerin sayısına eşitse sistem belirlidir Teorem 6.3.
Bir ortak sistemin ana matrisinin sıralaması bilinmeyenlerin sayısından azsa sistem belirsizdir. Böylece, formüle edilen teoremlerden doğrusal cebirsel denklem sistemlerini incelemek için bir yöntem izlenir. İzin vermek N– bilinmeyenlerin sayısı, Tanım 6.1.
Belirsiz bir doğrusal denklem sisteminin temel çözümü, tüm serbest bilinmeyenlerin sıfıra eşit olduğu bir çözümdür. Örnek.
Bir doğrusal denklem sistemini keşfedin. Sistem belirsizse temel çözümünü bulun. Ana rütbeleri hesaplayalım Matrisin ikinci satırını ilk satırına şununla çarparak ekleyin: Bu matrisin üçüncü satırına ikinci satırın çarpımını ekliyoruz adım matrisi aldığımız üçüncü ve dördüncü satırları kaldırmak Böylece, Bilinmeyen n'inci dereceden bir kare matris olsun Matris A-1 denir ters matris A matrisine göre, eğer A*A -1 = E ise, burada E, n'inci dereceden birim matristir. Kimlik matrisi- sol üst köşeden sağ alt köşeye geçen ana köşegen boyunca tüm elemanların bir olduğu ve geri kalanının sıfır olduğu böyle bir kare matris, örneğin: ters matris var olabilir yalnızca kare matrisler için onlar. satır ve sütun sayısının çakıştığı matrisler için. Bir matrisin ters matris olabilmesi için tekil olmaması gerekli ve yeterlidir. A = (A1, A2,...A n) matrisine denir dejenere olmayan Sütun vektörleri doğrusal olarak bağımsızsa. Bir matrisin doğrusal bağımsız sütun vektörlerinin sayısına matrisin rütbesi denir. Dolayısıyla ters bir matrisin var olabilmesi için matrisin rütbesinin boyutuna eşit olması gerekli ve yeterlidir diyebiliriz. r = n. A matrisi için ters A -1 matrisini bulun Çözüm: A matrisini yazıp E birim matrisini sağa atarız Jordan dönüşümlerini kullanarak A matrisini E birim matrisine indirgeriz. Hesaplamalar Tablo 31.1'de verilmiştir. Orijinal matris A ile ters matris A -1'i çarparak hesaplamaların doğruluğunu kontrol edelim. Matris çarpımı sonucunda birim matris elde edildi. Bu nedenle hesaplamalar doğru yapılmıştır. Cevap: Matris denklemleri şöyle görünebilir: AX = B, HA = B, AXB = C, burada A, B, C belirtilen matrislerdir, X istenen matristir. Matris denklemleri, denklemin ters matrislerle çarpılmasıyla çözülür.
Örneğin denklemden matrisi bulmak için bu denklemi soldaki ile çarpmanız gerekir. Bu nedenle denklemin çözümünü bulmak için ters matrisi bulup denklemin sağ tarafındaki matrisle çarpmanız gerekir. Diğer denklemler de benzer şekilde çözülür. AX = B denklemini çözün, eğer Çözüm: Ters matris eşit olduğundan (bkz. örnek 1) Diğerlerinin yanı sıra onlar da kullanılır matris yöntemleri. Bu yöntemler doğrusal ve vektör matris cebirine dayanmaktadır. Bu tür yöntemler, karmaşık ve çok boyutlu ekonomik olayların analiz edilmesi amacıyla kullanılmaktadır. Çoğu zaman bu yöntemler, kuruluşların işleyişinin ve yapısal bölümlerinin karşılaştırmalı bir değerlendirmesinin yapılması gerektiğinde kullanılır. Matris analiz yöntemlerinin uygulanması sürecinde birkaç aşama ayırt edilebilir. İlk aşamada bir ekonomik göstergeler sistemi oluşturuluyor ve buna dayanarak, sistem numaralarının ayrı satırlarda gösterildiği bir tablo olan bir ilk veri matrisi derleniyor (i = 1,2,....,n) ve dikey sütunlarda - göstergelerin sayısı (j = 1,2,....,m). İkinci aşamada Her dikey sütun için mevcut gösterge değerlerinden en büyüğü tanımlanır ve bu değer bir olarak alınır. Daha sonra bu sütuna yansıyan tüm tutarlar en büyük değere bölünerek standartlaştırılmış katsayılardan oluşan bir matris oluşturulur. Üçüncü aşamada matrisin tüm bileşenlerinin karesi alınır. Farklı önemleri varsa, her matris göstergesine belirli bir ağırlık katsayısı atanır. k. İkincisinin değeri uzman görüşüne göre belirlenir. Sonuncusunda, dördüncü aşama bulunan derecelendirme değerleri R j artış veya azalış sırasına göre gruplandırılmıştır. Ana hatlarıyla belirtilen matris yöntemleri, örneğin çeşitli yatırım projelerinin karşılaştırmalı analizinde ve kuruluşların faaliyetlerinin diğer ekonomik göstergelerinin değerlendirilmesinde kullanılmalıdır. Ters matris yöntemi Matris denklemleriyle çalışmanın genel ilkelerini biliyorsanız ve elbette temel cebirsel işlemleri nasıl gerçekleştireceğinizi biliyorsanız zor değildir. Ters matris yöntemini kullanarak bir denklem sistemini çözme. Örnek. Ters matris yöntemini anlamanın en uygun yolu açık bir örnek vermektir. Bir denklem sistemini ele alalım: Bu denklem sistemini çözmenin ilk adımı determinantı bulmaktır. Bu nedenle denklem sistemimizi aşağıdaki matrise dönüştürelim: Ve gerekli determinantı buluyoruz: Matris denklemlerini çözmek için kullanılan formül aşağıdaki gibidir: Bu nedenle X'i hesaplamak için A-1 matrisinin değerini belirleyip b ile çarpmamız gerekir. Başka bir formül bu konuda bize yardımcı olacaktır: Bu durumda olacak aktarılmış matris- yani aynı orijinal, ancak satırlar halinde değil sütunlar halinde yazılmıştır. Bunu unutmamalıyız ters matris yöntemi Cramer'in yöntemi gibi, yalnızca determinantının sıfırdan büyük veya küçük olduğu sistemler için uygundur. Determinant sıfıra eşitse Gauss yöntemini kullanmanız gerekir. Bir sonraki adım, aşağıdaki şemaya sahip bir küçükler matrisi derlemektir: Sonuç olarak, üç matris aldık - küçükler, cebirsel toplamalar ve aktarılmış bir cebirsel toplamalar matrisi. Artık ters matrisin gerçek derlemesine geçebilirsiniz. Formülü zaten biliyoruz. Örneğimiz için şöyle görünecek. .
.


Ve
, ![]()
![]()
![]()


 ,
,  ,
, 
![]()


Bu, sistemin benzersiz bir çözümü olduğu anlamına gelir.
![]()

![]()

![]()
![]() .
.
Aşağıdaki “tedavi” algoritmasını öneriyorum. Elinizde bir bilgisayar yoksa şunu yapın:
Burada ilk denklemde değişken yok, ikincisinde ise değişken yok. Bu gibi durumlarda ana belirleyiciyi doğru ve DİKKATLİ bir şekilde yazmak çok önemlidir:  – eksik değişkenlerin yerine sıfırlar konur.
– eksik değişkenlerin yerine sıfırlar konur.
Bu arada, gözle görülür derecede daha az hesaplama olduğundan, sıfırın bulunduğu satıra (sütun) göre determinantları sıfırlarla açmak mantıklıdır.
Ters matris kullanarak sistemi çözme

, Nerede 
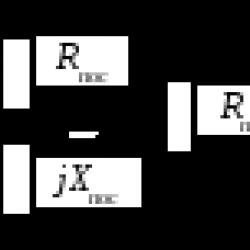
matrisin karşılık gelen elemanlarının cebirsel tamamlayıcılarının aktarılmış matrisi nerede.


Yani, çift alt simge, öğenin birinci satırda, üçüncü sütunda olduğunu ve örneğin öğenin 3 satır, 2 sütunda olduğunu gösterir. Bilinmeyen:
Bilinmeyen:



 dejenere olmayan. O halde Teorem 3.1'e göre ters bir matris vardır.
dejenere olmayan. O halde Teorem 3.1'e göre ters bir matris vardır.  Matris denkleminin çarpılması
Matris denkleminin çarpılması  matrise
matrise  solda, Teorem 1.1'in Tanım 3.2'sini ve 8) ifadesini kullanarak, doğrusal denklem sistemlerini çözmek için matris yönteminin dayandığı formülü elde ederiz:
solda, Teorem 1.1'in Tanım 3.2'sini ve 8) ifadesini kullanarak, doğrusal denklem sistemlerini çözmek için matris yönteminin dayandığı formülü elde ederiz:

 Nerede
Nerede



 3. paragrafta açıklanan yöntemlerden birini kullanarak yazalım.
3. paragrafta açıklanan yöntemlerden birini kullanarak yazalım.

5.3. Kramer yöntemi
 ile doğrusal denklemler
ile doğrusal denklemler  Bilinmeyen
Bilinmeyen

 taban matrisinden türetilen bir matrisin determinantı
taban matrisinden türetilen bir matrisin determinantı  denklem sistemini değiştirerek
denklem sistemini değiştirerek  ücretsiz üyelerden oluşan bir sütun içeren inci sütun.
ücretsiz üyelerden oluşan bir sütun içeren inci sütun. Belirleyicileri hesaplayalım
Belirleyicileri hesaplayalım 



6. Doğrusal denklem sistemlerinin incelenmesi.


 Daha sonra:
Daha sonra:

 ve genişletilmiş matrisler
ve genişletilmiş matrisler  Sistemin genişletilmiş (ve aynı zamanda ana) matrisini adım adım forma getirdiğimiz bu denklem sisteminin formülü:
Sistemin genişletilmiş (ve aynı zamanda ana) matrisini adım adım forma getirdiğimiz bu denklem sisteminin formülü:
 üçüncü satır - ilk satır çarpılarak
üçüncü satır - ilk satır çarpılarak  ve dördüncü satır - birinciyle çarpılır
ve dördüncü satır - birinciyle çarpılır  bir matris elde ederiz
bir matris elde ederiz
 ve dördüncü satıra – birincisi ile çarpılır
ve dördüncü satıra – birincisi ile çarpılır  Sonuç olarak matrisi elde ederiz.
Sonuç olarak matrisi elde ederiz.


 Sonuç olarak bu doğrusal denklem sistemi tutarlıdır ve sıra değeri bilinmeyen sayısından az olduğundan sistem belirsizdir.Temel dönüşümler sonucunda elde edilen adım matrisi denklem sistemine karşılık gelir.
Sonuç olarak bu doğrusal denklem sistemi tutarlıdır ve sıra değeri bilinmeyen sayısından az olduğundan sistem belirsizdir.Temel dönüşümler sonucunda elde edilen adım matrisi denklem sistemine karşılık gelir. Ve
Ve  başlıcaları ve bilinmeyenleri
başlıcaları ve bilinmeyenleri  Ve
Ve  özgür. Serbest bilinmeyenlere sıfır değer atayarak bu doğrusal denklem sistemine temel bir çözüm elde ederiz.
özgür. Serbest bilinmeyenlere sıfır değer atayarak bu doğrusal denklem sistemine temel bir çözüm elde ederiz.

Ters bir matrisin varoluş koşulu için teorem
Ters matrisi bulmak için algoritma
örnek 1 



Matris denklemlerini çözme


Ekonomik analizde matris yöntemi