1. Bir düzgün üçgeni ele alalım.
2. Ondan, köşeleri orijinal kenarların orta noktalarında bulunan bir üçgen kesiyoruz. Sonuç olarak, düzlemde her birinin alanı orijinalinin alanından dört kat daha az olan üç üçgen elde ediyoruz.
3. Ortaya çıkan üçgenlerle önceki manipülasyonları gerçekleştiriyoruz.

Süreç şöyle görünüyor:

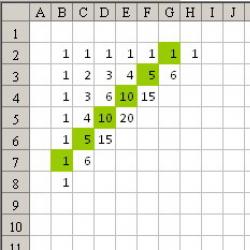
1. İlginç bir şekilde, Pascal üçgeninde tüm tek sayılar bir renkte ve çift sayılar başka bir renkteyse, o zaman bir Sierpinski üçgeni oluşur.

Bu gerçeğin avantajlarından yararlanalım. Yalnızca Excel'de Pascal üçgeninin klasik (satır satır) formunu değil, şunu kullanmak daha uygundur:

Burada binom katsayıları, birinci dolu satırda ve birinci dolu birlik sütununda çapraz olarak, geri kalanında ise üst ve sol elemanların toplamı olarak yazılır.

İnşaata geçelim. Bizim için katsayıları değil sadece paritelerini yazmak yeterlidir.

Öncelikle Excel'de hücrelerin boyutunu örneğin 7 x 7 piksel yapalım.

B2 hücresinde duralım, ardından B2:DY129 alanını seçelim - bunu yapmak için Ctrl + G tuşlarına basın ve bağlantı alanına B2:DY129 yazın.

Şimdi formül çubuğuna yazıyoruz =EĞER(VEYA(SATIR()=2,SÜTUN()=2),1,KALK(A2+B1,2))
ve seçilen alanın tamamını benzer bir formülle doldurmak için Ctrl + Enter tuşlarına basın.

Hadi gidelim Menü - Koşullu biçimlendirme ve değer 1 için hücrenin rengini belirtiyoruz.

Sonuç olarak şunu elde ederiz:

Sierpinski üçgeninin düzlem üzerinde bir tür rastgele yürüyüşle elde edildiğine dikkat edilmelidir. Yani:

1. Üçgenin 3 köşesini düzleme sabitleyelim ve başka bir nokta alalım.
2. İlk noktayı aradaki parçanın orta noktası olarak elde ederiz. kazara 1. adımdaki seçilen tepe noktası ve nokta.
3. İkinci noktayı aradaki segmentin orta noktası olarak elde ederiz. kazara seçilen tepe noktası ve ilk nokta.
4. İşlemi birçok kez tekrarlıyoruz.

Bu makroyu kullanabilirsiniz:

Genel Alt Makro()

Dim arRange(1 ila 3) Aralık Olarak
Tamsayı Olarak Dim tekRow
Dim tekColumn As Integer
Tam Sayı Olarak Dim i
iT'yi Tamsayı Olarak Dimle

tekRow = Int(1000 * Rnd) + 1
tekColumn = Int(200 * Rnd) + 1

arRange(1) = Hücreler(1, 1) değerini ayarlayın
arRange(2) = Hücreler(50, 250) olarak ayarlayın
arRange(3) = Hücreler(200, 20) olarak ayarlayın

Hücreler.Temizle

i = 1 ila 20000 için
iT = (Int(1000 * Rnd) Mod 3) + 1
tekRow = Int((tekRow + arRange(iT).Row) / 2)
tekColumn = Int((tekColumn + arRange(iT).Column) / 2)
Cells(tekRow, tekColumn).Interior.ColorIndex = 5
Sonraki

Son Alt

Sierpinski üçgeni- Polonyalı matematikçi Waclaw Sierpinski tarafından 1915'te önerilen Cantor kümesinin iki boyutlu analoglarından biri olan bir fraktal. Sierpinski'nin "peçetesi" olarak da bilinir.

Sierpinski üçgeni

Yapı

Yinelemeli yöntem

Sierpinski üçgeninin inşaatı

Eşkenar üçgenin kenarlarının orta noktaları doğru parçalarla birbirine bağlanır. 4 yeni üçgen elde edersiniz. Ortadaki üçgenin iç kısmı orijinal üçgenden çıkarılır. Çok şey ortaya çıkıyor T 1 (\displaystyle T_(1)) kalan 3 "birinci derece" üçgenden oluşur. Birinci derecedeki üçgenlerin her biri için tam olarak aynısını yaparak kümeyi elde ederiz. T 2 (\displaystyle T_(2)), ikinci dereceden 9 eşkenar üçgenden oluşur. Bu işlemi süresiz olarak sürdürürsek sonsuz bir dizi elde ederiz. T 0 ⊃ T 1 ⊃ ⋯ ⊃ T n ⊃ … (\displaystyle T_(0)\supset T_(1)\supset \dots \supset T_(n)\supset \dots )üyelerinin kesişimi bir Sierpinski üçgenidir.

Kaos yöntemi

1. Çekicilerin koordinatları belirtilmiştir - orijinal üçgenin köşeleri T 0 (\displaystyle T_(0)). 2. Olasılık uzayı (0 ; 1) (\displaystyle (0;1)) her biri bir çekiciye karşılık gelen 3 eşit parçaya bölünmüştür. 3. Belirli bir başlangıç ​​noktası belirlendi P 0 (\displaystyle P_(0)), üçgenin içinde yatıyor T 0 (\displaystyle T_(0)). 4. Sierpinski üçgeni kümesine ait noktaları oluşturma döngüsünün başlangıcı. 1. Rastgele bir sayı üretilir n ∈ (0 ; 1) (\displaystyle n\in (0;1)). 2. Aktif çekici, üretilen sayının olasılıksal alt uzayına düştüğü tepe noktası haline gelir. 3. Bir nokta inşa ediliyor P ben (\displaystyle P_(i)) yeni koordinatlarla: x ben = x ben - 1 + x A 2 ; y ben = y ben − 1 + y A 2 (\displaystyle x_(i)=(\frac (x_(i-1)+x_(A))(2));y_(i)=(\frac (y_(i) -1)+y_(A))(2))), Nerede: x ben − 1 , y ben − 1 (\displaystyle x_(i-1),y_(i-1))- önceki noktanın koordinatları P ben - 1 (\displaystyle P_(i-1)); x A , y A (\displaystyle x_(A),y_(A))- aktif çekici noktanın koordinatları. 5. Döngünün başlangıcına dönün.

Özellikler

Yinelemeli yöntemle inşaat

Kaos yöntemini kullanarak inşaat

Notlar

Bağlantılar

L sistemi

L sistemi veya Lindenmayer sistemi paralel bir yeniden yazma sistemi ve bir tür resmi dilbilgisidir. L-sistemi, diziler oluşturmak için kullanılabilecek bir sembol alfabesinden, her sembolün yerine geçme kurallarını belirleyen bir dizi kuraldan, yapının başlayacağı bir başlangıç ​​dizisinden (“aksiyom”) ve bu diziyi oluşturacak bir mekanizmadan oluşur. oluşturulan dizenin geometrik yapılara dönüştürülmesi. L sistemleri, 1968 yılında Utrecht Üniversitesi'nden Macar biyolog ve botanikçi Aristide Lindenmayer tarafından önerildi ve geliştirildi. Lindenmayer, bitki hücrelerinin davranışını tanımlamak ve bitki gelişim sürecini modellemek için L sistemlerini kullandı. L sistemleri ayrıca çeşitli organizmaların morfolojisini modellemek için de kullanılmıştır ve yinelenebilir fonksiyon sistemleri gibi kendine benzer fraktallar oluşturmak için kullanılabilir.

Raket (programlama dili)

Racket (eski adıyla PLTScheme), Lisp/Scheme ailesine ait çok paradigmalı, genel amaçlı bir programlama dilidir. Dil odaklı programlama için bir ortam sağlar; raketin amaçlarından biri programlama dillerinin oluşturulması, geliştirilmesi ve uygulanmasıdır. Dil çeşitli bağlamlarda kullanılır: bir kodlama dili olarak, genel amaçlı bir dil olarak, bilgisayar bilimleri öğretiminde, bilimsel araştırmalarda.

Platform, kullanıcıya gelişmiş bir çalışma zamanı sistemi, çeşitli kütüphaneler, bir JIT derleyicisi vb. dahil olmak üzere Racket dilinin bir uygulamasını ve ayrıca Racket'te yazılmış DrRacket geliştirme ortamını (eski adıyla DrScheme olarak biliniyordu) sağlar. Bu yazılım çerçevesi MIT'nin ProgramByDesign dersinde kullanılmaktadır. Temel Racket dili, gömülü ve alana özgü programlama dilleri, dil yapıları (örneğin sınıflar ve modüller) ve farklı anlamlara sahip Racket lehçeleri oluşturmanıza olanak tanıyan güçlü bir makro sisteme sahiptir.

Sistem, LGPL koşulları altında dağıtılan ücretsiz ve açık kaynaklı bir yazılımdır. Topluluk tarafından yazılan uzantılar ve paketler, sistemin web dağıtımı olan PLAneT'de mevcuttur.

Fraktal sıkıştırma algoritması

Fraktal görüntü sıkıştırma, yinelenen fonksiyon sistemlerinin (genellikle afin dönüşümler) görüntülere uygulanmasına dayanan kayıplı bir görüntü sıkıştırma algoritmasıdır. Bu algoritma, bazı durumlarda doğal nesnelerin gerçek fotoğrafları için kabul edilebilir görsel kalitede çok yüksek sıkıştırma oranları elde edilmesine olanak sağlamasıyla bilinir. Patent almanın zor durumu nedeniyle algoritma yaygın olarak kullanılamadı.

Bölme kiremit

Sürüngen döşemesi, şeklin kendisinin daha küçük kopyalarına kesilebilen bir şekil olan bir mozaik geometri konseptidir. 2012 yılında, İngiliz matematikçi Lee Salous tarafından Mathematics Magazine'de, kendinden döşemeli döşeme seti adı verilen bölme döşemelerinin bir genellemesi önerildi.

Nihai alt bölme kuralı

Matematikte alt bölmenin nihai kuralı, bir çokgeni ve diğer iki boyutlu şekilleri giderek daha küçük parçalara bölmenin yinelemeli bir yoludur. Bu anlamda alt bölme kuralları fraktalların bir genellemesidir. Aynı modeli defalarca tekrarlamak yerine, her adımda ince değişiklikler yapılarak daha zengin yapılara izin verilirken zarif fraktal stil korunur. Alt bölme kuralları mimari, biyoloji ve bilgisayar bilimlerinin yanı sıra hiperbolik manifoldların incelenmesinde de kullanılır. Döşeme ikameleri, iyi çalışılmış bir alt bölüm kuralı türüdür.

Peano eğrisi

Peano eğrisi, görüntüsü bir kare (veya daha genel olarak uzayın açık bölgeleri) içeren parametrik eğrilerin genel adıdır. Bir diğer adı ise boşluk doldurma eğrisidir.

Adını bu tür eğriyi keşfeden Giuseppe Peano'dan (1858-1932) alan Peano eğrisi, Peano'nun bulduğu spesifik eğriye verilen addır.

Sierpinski eğrisi

Sierpinski eğrileri Waclaw Sierpinski tarafından keşfedilen sürekli kapalı düzlemsel fraktal eğrilerin yinelemeli olarak tanımlanmış bir dizisidir. Limitteki eğri birim kareyi tamamen doldurur, dolayısıyla limit eğrisi de denir Sierpinski eğrisi, alanı dolduran eğrilerin bir örneğidir.

Sierpinski eğrisi uzayı doldurduğu için Hausdorff boyutu (limitte) n → ∞ (\displaystyle n\rightarrow \infty)) eşittir 2 (\displaystyle 2).
Öklid eğrisi uzunluğu

eşittir l n = 2 3 (1 + 2) 2 n − 1 3 (2 − 2) 1 2 n (\displaystyle l_(n)=(2 \over 3)(1+(\sqrt (2)))2^( n)-(1 \üzerinde 3)(2-(\sqrt (2))(1 \üzerinde 2^(n))),

yani büyüyor üstel olarakİle n (\displaystyle n) ve limit n → ∞ (\displaystyle n\rightarrow \infty) eğrinin çevrelediği bölgenin alanı Sn (\displaystyle S_(n)), dır-dir 5/12 (\displaystyle 5/12) kare (Öklid metriğinde).

Logaritma

Bir sayının logaritması b (\displaystyle b) dayalı a (\displaystyle a) (eski Yunanca'dan. λόγος "kelime; tavır" + ἀριθμός "sayı") tabanın yükseltilmesi gereken gücün bir göstergesi olarak tanımlanır a (\displaystyle a) numarayı almak için b (\displaystyle b). Tanım: log a ⁡ b (\displaystyle \log _(a)b), telaffuz edildi: " logaritma b (\displaystyle b) dayalı a (\displaystyle a) ».

Tanımdan şu sonuç çıkıyor: x = log a ⁡ b (\displaystyle x=\log _(a)b) denklemi çözmeye eşdeğerdir a x = b (\displaystyle a^(x)=b). Örneğin, günlük 2 ⁡ 8 = 3 (\displaystyle \log _(2)8=3), Çünkü 2 3 = 8 (\displaystyle 2^(3)=8).

Logaritmanın hesaplanmasına denir logaritmayla. Sayılar a , b (\displaystyle a,b)çoğu zaman gerçektir, ancak aynı zamanda karmaşık logaritma teorisi de vardır.

Logaritmalar, emek yoğun hesaplamaları önemli ölçüde basitleştirmek için yaygın kullanımlarını belirleyen benzersiz özelliklere sahiptir. Logaritma dünyasına geçerken çarpmanın yerini çok daha basit bir toplama işlemi alır, bölmenin yerini çıkarma alır ve üs alma ve kök çıkarma sırasıyla üsle çarpma ve bölmeye dönüştürülür. Laplace, logaritmanın icadının "gökbilimcinin işini kısaltarak ömrünü iki katına çıkardığını" söyledi.

Logaritmanın tanımı ve değerlerinin tablosu (trigonometrik fonksiyonlar için) ilk olarak 1614'te İskoç matematikçi John Napier tarafından yayınlandı. Diğer matematikçiler tarafından genişletilip geliştirilen logaritmik tablolar, elektronik hesap makineleri ve bilgisayarların ortaya çıkışına kadar üç yüzyıldan fazla bir süre boyunca bilimsel ve mühendislik hesaplamalarında yaygın olarak kullanıldı.

Zamanla logaritmik fonksiyonun olduğu anlaşıldı. y = log a ⁡ x (\displaystyle y=\log _(a)x) insan faaliyetinin diğer birçok alanında yeri doldurulamaz: diferansiyel denklemlerin çözülmesi, niceliklerin değerlerinin sınıflandırılması (örneğin, sesin frekansı ve yoğunluğu), çeşitli bağımlılıkların yaklaşımı, bilgi teorisi, olasılık teorisi vb. Bu fonksiyon aşağıdakilerden biridir: temel olanlar, üstel fonksiyonun tersidir. En sık kullanılanları tabanlı gerçek logaritmalardır. 2 (\displaystyle 2)(ikili), e (\displaystyle e) (doğal logaritma) ve 10 (\displaystyle 10)(ondalık).

DNA tabanlı nanoteknoloji

DNA nanoteknolojisi, teknolojik kullanım için nükleik asitlerden yapay yapıların geliştirilmesi ve üretilmesidir. Bu bilimsel alanda, nükleik asitler canlı hücrelerdeki genetik bilginin taşıyıcıları olarak değil, nanomalzemelerin biyolojik olmayan mühendisliğinin ihtiyaçlarına yönelik bir malzeme olarak kullanılmaktadır.

Teknoloji, nükleik asitlerin baz eşleşmesi için katı kurallar kullanır; bu kurallar, iplikçiklerin yalnızca tamamlayıcı baz dizilerine sahip kısımlarının güçlü, sert bir çift sarmal yapı oluşturmak üzere birbirine bağlanmasına izin verir. Bu kurallardan, hassas bir şekilde ayarlanmış nano ölçekli şekiller ve özelliklere sahip karmaşık hedef yapılar oluşturmak için seçici olarak bir araya getirilecek baz dizilerinin mühendisliğini yapmak mümkün hale gelir. Çoğu malzeme DNA kullanılarak yapılır, ancak RNA ve peptit nükleik asitleri (PNA) gibi diğer nükleik asitleri içeren yapılar da inşa edilerek teknoloji alanının "nükleotid bazlı nanoteknoloji" olarak adlandırılmasına olanak sağlanır.

DNA tabanlı nanoteknolojinin temel konsepti ilk olarak 1980'lerin başında Nadrian Seaman tarafından önerildi ve bu araştırma alanı 2000'li yılların ortalarında yaygın ilgi görmeye başladı. Gelişmekte olan bu teknoloji alanında çalışan araştırmacılar, iki ve üç boyutlu kristal kafesler, nanotüpler, çokyüzlüler ve diğer serbest biçimli şekiller gibi statik yapıların yanı sıra moleküler makineler ve DNA bilgisayarları gibi işlevsel yapılar oluşturdular.

Bu yapıları birleştirmek için, karoların daha küçük yapılardan bir araya getirildiği karo yapılanması, DNA origami tekniği kullanılarak oluşturulan katlama yapıları ve iplik yer değiştirme teknikleri kullanılarak oluşturulan dinamik olarak yeniden düzenlenen yapılar dahil olmak üzere çeşitli teknikler kullanılır. Araştırma alanı, protein yapısının belirlenmesine yönelik kristalografi ve spektroskopinin uygulamalı problemleri de dahil olmak üzere, yapısal biyoloji ve biyofizik alanlarındaki temel bilim problemlerinin çözümü için bir araç olarak kullanılmaya başlandı. Ölçeklenebilir moleküler elektronik ve nanotıp alanındaki potansiyel uygulamalara yönelik araştırmalar da devam etmektedir.

Doğal logaritma

Doğal logaritma tabanın logaritması e, Nerede e (\displaystyle e)- yaklaşık 2,72'ye eşit irrasyonel bir sabit. Olarak gösterilir ln ⁡ x (\displaystyle \ln x), log e ⁡ x (\displaystyle \log _(e)x) ya da bazen sadece günlük ⁡ x (\displaystyle \log x), eğer baz e (\displaystyle e) ima edildi. Genellikle sayı x (\displaystyle x) logaritmanın işareti altında gerçektir, ancak bu kavram karmaşık sayılara genişletilebilir.

Tanımdan logaritmik bağımlılığın üstel için ters fonksiyon olduğu sonucu çıkar. y = e x (\displaystyle y=e^(x)), dolayısıyla grafikleri birinci ve üçüncü çeyreğin açıortaylarına göre simetriktir (sağdaki şekle bakın). Üstel fonksiyon gibi logaritmik fonksiyon da aşkın fonksiyonlar kategorisine aittir.

Doğal logaritmalar, bilinmeyenin üs olarak mevcut olduğu cebirsel denklemlerin çözümünde faydalıdır ve matematiksel analizde vazgeçilmezdir. Örneğin, bilinen bir yarı ömür için bozunma sabitini bulmak veya radyoaktivite problemlerini çözerken bozunma süresini bulmak için logaritmalar kullanılır. Matematiğin ve uygulamalı bilimlerin pek çok alanında önemli bir rol oynarlar ve finansta bileşik faizin bulunması da dahil olmak üzere birçok problemi çözmek için kullanılırlar.

Lebesgue boyutu

Lebesgue boyutu veya topolojik boyut- topolojik uzayın en önemli değişmezi olan kaplamalarla tanımlanan boyut. Uzayın Lebesgue boyutu X (\displaystyle X) genellikle belirtilir sönük ⁡ X (\displaystyle \dim X).

Özyineleme

Özyineleme, bir nesnenin veya sürecin bu nesnenin veya sürecin kendi içindeki tanımı, açıklaması, görüntüsüdür, yani bir nesnenin kendisinin parçası olduğu durumdur. "Özineleme" terimi, dilbilimden mantığa kadar çeşitli özel bilgi alanlarında kullanılır, ancak en yaygın olarak matematik ve bilgisayar bilimlerinde kullanılır.

Sierpinski, Waclaw

Wacław Franciszek Sierpiński, başka bir transkripsiyonda - Sierpiński (Lehçe: Wacław Franciszek Sierpiński; 14 Mart 1882, Varşova - 21 Ekim 1969, age.) - Küme teorisi, seçim aksiyomu üzerine yaptığı çalışmalarla tanınan Polonyalı matematikçi ve öğretmen, süreklilik hipotezi, sayı teorisi, fonksiyon teorisi ve topoloji. 724 makale ve 50 kitabın yazarı.

Dört yüzlü (Bottrop)

Tetrahedron (Almanca: Tetraeder), Bottrop (Kuzey Ren-Vestfalya) şehrinde gözlem güvertesi olarak kullanılan, 9 metrelik dört beton destekle desteklenen, kenar uzunluğu 60 m olan tetrahedron şeklinde bir çelik yapıdır. . Dörtyüzlü, Prosper-Haniel madeninin (de: Bergwerk Prosper-Haniel) Beckstraße atık yığınının (Almanca: Beckstraße) tepesinde, deniz seviyesinden 105 m yükseklikte yer almaktadır. Üst gözlem güvertesinden Bottrop, Essen, Oberhausen, Gladbeck şehirlerinin manzaralarını görebilirsiniz. İyi görünürlükle görüş mesafesi 40 km'ye ulaşır ve hatta Düsseldorf'taki Rheinturm televizyon kulesini ayırt etmenize olanak tanır.

Bottrop Tetrahedron, Ruhr bölgesinin "Endüstriyel Kültür Yolu" bölgesel projesinin tematik noktasıdır.

Pascal üçgeni

Pascal üçgeni, üçgen şekle sahip sonsuz bir binom katsayıları tablosudur. Bu üçgende üstte ve yanlarda olanlar var. Her sayı, üstündeki iki sayının toplamına eşittir. Üçgenin çizgileri dikey eksene göre simetriktir. Adını Blaise Pascal'dan almıştır. Pascal üçgenini oluşturan sayılar cebirde, kombinatorikte, olasılık teorisinde, matematiksel analizde ve sayı teorisinde doğal olarak ortaya çıkar.

Fraktal

Fraktal (enlem. fractus - ezilmiş, kırılmış, kırılmış) kendine benzerlik özelliğine sahip bir kümedir (kendisinin bir parçasıyla tam olarak veya yaklaşık olarak çakışan, yani bütünün bir veya daha fazla ile aynı şekle sahip olduğu bir nesne) parçalar). Matematikte fraktallar, Öklid uzayında kesirli bir metrik boyuta (Minkowski veya Hausdorff anlamında) veya topolojik olandan farklı bir metrik boyuta sahip olan nokta kümeleri olarak anlaşılır; bu nedenle, aşağıdakilerle sınırlı olan diğer geometrik şekillerden ayırt edilmelidirler: sınırlı sayıda bağlantı. Kendilerini sonlu sayıda tekrarlayan kendine benzer şekillere prefraktallar denir.

Alışılmadık özelliklere sahip kendine benzer kümelerin ilk örnekleri, 19. yüzyılda sürekli türevlenemeyen fonksiyonların (örneğin Bolzano işlevi, Weierstrass işlevi, Cantor kümesi) incelenmesi sonucunda ortaya çıktı. “Fraktal” terimi, 1975 yılında Benoit Mandelbrot tarafından ortaya atılmış ve 1977 yılında “Doğanın Fraktal Geometrisi” adlı kitabının yayınlanmasıyla yaygın olarak tanınmıştır. Fraktallar, bu yapıların etkili bir şekilde görselleştirilmesini mümkün kılan bilgisayar teknolojilerinin gelişmesiyle özellikle popülerlik kazandı.

"Fraktal" kelimesi sadece matematiksel bir terim olarak kullanılmaz. Fraktal, aşağıdaki özelliklerden en az birine sahip olan bir nesne olarak adlandırılabilir:

Her ölçekte önemsiz olmayan bir yapıya sahiptir. Bu, normal şekillerin (daire, elips, pürüzsüz fonksiyonun grafiği gibi) tam tersidir: çok büyük ölçekte normal bir şeklin küçük bir parçasını düşünürseniz, düz bir çizginin parçası gibi görünecektir. Bir fraktal için ölçeğin arttırılması yapının basitleştirilmesine yol açmaz, yani tüm ölçeklerde eşit derecede karmaşık bir resim görebilirsiniz.

Kendine benzer veya yaklaşık olarak kendine benzer.

Kesirli bir metrik boyutu veya topolojik olanı aşan bir metrik boyutu vardır.Doğadaki birçok nesnenin fraktal özellikleri vardır, örneğin: kıyılar, bulutlar, ağaç taçları, kar taneleri, dolaşım sistemi, alveoller.

Fraktal boyut

Fraktal boyut(İngilizce fraktal boyut) - metrik uzayda bir kümenin boyutunu belirlemenin yollarından biri. Fraktal boyut N-boyutlu küme aşağıdaki formül kullanılarak tanımlanabilir:

D = − lim ε → 0 ln ⁡ (N ε) ln ⁡ (ε) (\displaystyle D=-\lim \limits _(\varepsilon \to 0)(\frac (\ln(N_(\varepsilon))) (\ln(\varepsilon)))), Nerede N ε (\ displaystyle N_(\ varepsilon ))- minimum sayı N yarıçaplı boyutlu “toplar” ε (\displaystyle \varepsilon), seti kaplamak için gereklidir.

Fraktal boyut tamsayı olmayan bir sayısal değer alabilir.

Kırık boyuta ilişkin temel fikrin matematik alanında uzun bir geçmişi vardır, ancak Benoit Mandelbrot'un 1967'de kesirli boyutu tanımladığı kendi kendine benzerlik hakkındaki makalesinde icat ettiği terim, terimin kendisidir. Bu makalede Mandelbrot, Lewis Fry Richardson'un, kıyı şeridinin ölçülen uzunluğunun bir ölçüm çubuğunun uzunluğuna bağlı olduğu şeklindeki mantık dışı fikri açıklayan önceki çalışmasına atıfta bulundu (bkz. Şekil 1). Bu fikri takiben, bir kıyı şeridinin fraktal boyutu, kıyı şeridinin uzunluğunu ölçmek için gereken kutup sayısının (belirli bir ölçekte) seçilen kutup ölçeğine oranına karşılık gelir. Ölçekte bir değişiklikle bir öğedeki değişime ilişkin bu temel kavram üzerine inşa edilen fraktal boyutun birkaç resmi matematiksel tanımı [⇨] vardır.

Temel bir örnek Koch kar tanesinin fraktal boyutudur. Topolojik boyutu 1'dir ancak Koch kar tanesinin herhangi iki noktası arasındaki eğrinin uzunluğu sonsuz olduğundan hiçbir şekilde düzeltilebilir bir eğri değildir. Ne kadar küçük olursa olsun bir eğrinin hiçbir kısmı düz bir çizgi parçası değildir. Aksine, Koch'un kar tanesi farklı açılarla birbirine bağlanan sonsuz sayıda parçadan oluşur. Bir eğrinin fraktal boyutu, bir fraktal çizginin tek boyutlu olamayacak kadar ayrıntılı (ayrıntılı), ancak iki boyutlu olamayacak kadar karmaşık olmayan bir nesne olduğu öne sürülerek sezgisel olarak açıklanabilir. Bu nedenle, boyutu olağan topolojik boyut 1 ile değil, bu durumda 1 ile 2 arasında yer alan bir sayıya eşit olan fraktal boyutuyla daha iyi tanımlanır.

Fraktal sanat

Fraktal sanat, fraktal nesnelerin hesaplanması ve hesaplamaların sonuçlarının durağan görüntüler, animasyonlar ve otomatik olarak oluşturulan medya dosyaları olarak sunulmasıyla oluşturulan bir algoritmik sanat biçimidir. Fraktal sanat 1980'lerin ortalarında başladı. Yeni medya sanatının bir parçası olan bir bilgisayar sanatı ve dijital sanat türüdür. Fraktal sanat aynı zamanda “bilimsel sanat” olarak adlandırılan alanlardan biridir.

Fraktal sanat nadiren elle yaratılır. Genellikle üç adım yoluyla fraktallar üreten yazılım tarafından dolaylı olarak oluşturulur: ilgili fraktal yazılımın parametrelerinin ayarlanması; muhtemelen uzun hesaplamalar yapmak; ve ürün değerlendirmeleri. Bazı durumlarda, oluşturulan görüntülerin daha da işlenmesi için başka grafik programları kullanılır. Fraktal olmayan görüntüler de bir sanat eserine dahil edilebilir. Julia Seti ve Mandelbrot Seti fraktal sanatın ikonları olarak kabul edilir.

Özellikler
En basit fraktallar

Bunu elde etmek için, iç kısmı olan (eşkenar) bir üçgen almanız, içine orta çizgiler çizmeniz ve oluşan dört küçük üçgenden ortadakini atmanız gerekir. Daha sonra aynı adımları kalan üç üçgenin vb. her biriyle tekrarlamanız gerekir. Resim ilk üç adımı gösterir ve flaş gösterisinde pratik yapabilir ve onuncu adıma kadar adımlar atabilirsiniz.

Ortadaki üçgenleri atmak, Sierpinski üçgenine ulaşmanın tek yolu değildir. "Ters yönde" hareket edebilirsiniz: başlangıçta "boş" bir üçgen alın, ardından içindeki orta çizgilerin oluşturduğu üçgeni tamamlayın, ardından aynısını üç köşe üçgenin her birinde yapın, vb. İlk başta şekiller çok farklı olacak, ancak yineleme sayısı arttıkça birbirlerine giderek daha fazla benzeyecekler ve limit dahilinde çakışacaklar.

Bir Sierpinski üçgeni elde etmenin bir sonraki yolu, bir sonraki yinelemenin parçalarını ölçekli bir parçayla değiştirerek geometrik fraktallar oluşturmaya yönelik olağan şemaya daha da benzer. Burada, her adımda, kesikli çizgiyi oluşturan bölümler, üç bağlantıdan oluşan kesikli bir çizgiyle değiştirilir (ilk yinelemede kendisi elde edilir). Bu kesikli çizgiyi dönüşümlü olarak sağa ve sonra sola yatırmanız gerekir. Zaten sekizinci yinelemenin fraktala çok yakın olduğu ve ne kadar ileri giderse çizginin ona o kadar yaklaşacağı görülüyor.

Ama hepsi bu değil. Sierpinski üçgeninin, düzlem üzerindeki bir noktanın rastgele yürüyüş çeşitlerinden birinin bir sonucu olarak elde edildiği ortaya çıktı. Bu yönteme "Kaos oyunu" denir. Onun yardımıyla başka fraktallar da oluşturabilirsiniz.

“Oyunun” özü budur. Bir düzleme düzenli bir üçgen sabitlenmiştir A 1 A 2 A 3. Herhangi bir başlangıç ​​noktasını işaretleyin B 0. Daha sonra üçgenin üç köşesinden birini rastgele seçin ve noktayı işaretleyin. B 1 - uçları bu tepe noktasında ve noktasında olan bir segmentin ortası B 0 (sağdaki şekilde köşe noktası rastgele seçilmiştir) A 1). Aynı şey bir nokta ile tekrarlanır B 1 almak B 2. Daha sonra puan alıyorlar B 3 , B 4, vb. Noktanın rastgele "atlaması" önemlidir, yani önceki adımlarda ne seçilmiş olursa olsun, üçgenin tepe noktasının her seferinde rastgele seçilmesi önemlidir. Bir dizideki noktaları işaretlerseniz şaşırtıcıdır B ben, o zaman Sierpinski üçgeni yakında ortaya çıkmaya başlayacak. 100, 500 ve 2500 puan işaretlendiğinde ne olacağı aşağıdadır.

Bazı özellikler

Seçenekler

Sierpinski'den halı (kare, peçete). Kare versiyon 1916'da Wacław Sierpinski tarafından tanımlandı. Kendisiyle kesişimleri olmayan bir düzlem üzerinde çizilebilecek herhangi bir eğrinin, bu delikli karenin bazı altkümelerine homeomorfik olduğunu kanıtlamayı başardı. Bir üçgen gibi bir kare de farklı tasarımlardan yapılabilir. Sağda klasik yöntem var: kareyi 9 parçaya bölüp orta kısmı atıyoruz. Daha sonra aynı şey kalan 8 kare için de tekrarlanır, vb.

Üçgen gibi karenin alanı da sıfırdır. Sierpinski halısının fraktal boyutu, üçgenin boyutuna benzer şekilde hesaplanan log 3 x 8'e eşittir.

Sierpinski Piramidi. Sierpinski üçgeninin üç boyutlu analoglarından biri. Olanların üç boyutluluğu dikkate alınarak benzer şekilde inşa edilmiştir: İlk piramidin 5 kopyası, iki kez sıkıştırılmış, ilk yinelemeyi oluşturur, 5 kopyası ikinci yinelemeyi oluşturur, vb. Fraktal boyut log 2 5'e eşittir. Şeklin hacmi sıfırdır (her adımda hacmin yarısı dışarı atılır), ancak aynı zamanda yüzey alanı yinelemeden yinelemeye korunur ve fraktal için bu, fraktal ile aynıdır. ilk piramit.

Menger süngeri. Sierpinski halısının üç boyutlu uzaya genelleştirilmesi. Bir sünger oluşturmak için, prosedürün sonsuz bir tekrarına ihtiyacınız vardır: yinelemeyi oluşturan küplerin her biri, merkezi olanın ve 6 komşusunun atıldığı 27 üç kat daha küçük küplere bölünür. Yani her küp üç kat daha küçük 20 yeni küp üretiyor. Bu nedenle fraktal boyut log 3 x 20'dir. Bu fraktal evrensel bir eğridir: üç boyutlu uzaydaki herhangi bir eğri süngerin bazı alt kümelerine homeomorfiktir. Süngerin hacmi sıfırdır (çünkü her adımda 20/27 ile çarpılır), ancak sonsuz geniş bir alana sahiptir.

L
Umman hattı:

N – segment sayısı, boyut A.

D – “bükülme derecesi”

N=(1/a)D; S=N*a ; S=(1/a)D-1

İLE
Riva Koç

2) N=4L=1/3S(4)=4/3

N=16 L=1/9S(16)=16/9

Fraktal boyut:

D=lg4 /lg3=1,26…

Bir kümenin fraktal boyutu

Fraktalın hacmi yerleştirme alanı her zaman sıfırdır. Ancak daha düşük boyutlu bir uzayda sıfırdan farklı olabilir. Bu alanın boyutunu belirlemek için D hadi her şeyi kıralım N kenar uzunluğuna sahip küçük küplere bölünmüş boyutlu uzay ε ve hacim ε N- Şekil 1. İzin vermek N(ε ) birlikte fraktal kümeyi tamamen kaplayan minimum küp sayısıdır, bu durumda tanım gereği

Bu sınırın varlığı fraktal hacmin sonlu olduğu anlamına gelir. D boyutlu uzay: küçük ε

ve alışılagelmiş boyuttan farklı olarak D fraktal kümeler için çoğunlukla olduğu gibi kesirli bir değer olabilir.

Açıkçası, sıradan kümeler için bu tanım iyi bilinen sonuçlara yol açmaktadır. Yani kalabalık için N sahip olduğumuz izole noktalar N(ε ) =N ve bu nedenle

Bir segment için düzgün bir uzunluk çizgisi yeterlidir L:N(ε ) =L/ε ve bu nedenle D= 1. Site için S iki boyutlu yüzey: N(ε ) =S/ε 2 ve D= 2 vb.

Yapıcı fraktallar oluşturmak için özyinelemeli algoritma.

1. Sierpinski üçgeni

Sierpinski üçgeni

Sierpinski üçgeni- Polonyalı matematikçi Sierpinski'nin 1915'te önerdiği Cantor kümesinin iki boyutlu analoglarından biri olan bir fraktal. Sierpinski "ızgara" veya "peçete" olarak da bilinir.

Yapı

Katı bir eşkenar üçgen alınır ve ilk adımda ortadaki üçgenin iç kısmı merkezden çıkarılır. İkinci adımda, kalan üç üçgenden ortadaki üç üçgen çıkarılır, vb. Bu prosedürün sonsuz tekrarından sonra, katı üçgenin bir alt kümesi kalır - Sierpinski üçgeni.

Sierpinski üçgeninin inşaatı

Sierpinski üçgeni aşağıdaki algoritma kullanılarak da elde edilebilir:

Düzlemde üç nokta alın ve bir üçgen çizin.

Üçgenin içindeki herhangi bir noktayı rastgele seçin ve bu noktadan üçgenin üç köşesinden herhangi birine olan mesafenin yarısını hareket ettirin.

Geçerli konumu işaretleyin.

2. adımdan itibaren tekrarlayın.

70'li yılların sonlarında ortaya çıkan fraktal ve fraktal geometri kavramları, 80'li yılların ortalarından itibaren matematikçiler ve programcılar arasında sağlam bir şekilde yerleşmiştir. Fraktal kelimesi Latince fraktus kelimesinden türemiştir ve parçalardan oluşan anlamına gelir. Benoit Mandelbrot tarafından 1975 yılında ilgilendiği düzensiz fakat kendine benzeyen yapılara atıfta bulunulması önerilmiştir. Fraktal geometrinin doğuşu genellikle Mandelbrot'un 1977'de "Doğanın Fraktal Geometrisi" kitabının yayınlanmasıyla ilişkilendirilir. Çalışmalarında 1875-1925 yılları arasında aynı alanda çalışan diğer bilim adamlarının bilimsel sonuçlarını kullanmıştır (Poincaré, Fatou, Julia, Cantor, Hausdorff Ancak onların çalışmalarını tek bir sistemde birleştirmek ancak bizim zamanımızda mümkün oldu.
Fraktalların günümüzde bilgisayar grafiklerindeki rolü oldukça büyüktür. Örneğin, çok karmaşık şekillerin çizgilerini ve yüzeylerini tanımlamak için birkaç katsayı kullanarak gerektiğinde kurtarmaya gelirler. Bilgisayar grafikleri açısından bakıldığında, yapay bulutlar, dağlar ve deniz yüzeyleri oluşturulurken fraktal geometri vazgeçilmezdir. Aslında görüntüleri doğal olanlara çok benzeyen, Öklidyen olmayan karmaşık nesneleri kolayca temsil etmenin bir yolu bulundu.
Fraktalların temel özelliklerinden biri kendine benzerliktir. En basit durumda, bir fraktalın küçük bir kısmı, tüm fraktal hakkında bilgi içerir. Mandelbrot'un fraktal tanımı şöyledir: "Fraktal, bir anlamda bütüne benzeyen parçalardan oluşan bir yapıdır."

Fraktallar adı verilen çok sayıda matematiksel nesne vardır (Sierpinski üçgeni, Koch kar tanesi, Peano eğrisi, Mandelbrot kümesi ve Lorentz çekicileri). Fraktallar, gerçek dünyanın birçok fiziksel olayını ve oluşumunu büyük bir doğrulukla tanımlar: dağlar, bulutlar, türbülanslı (girdap) akışlar, ağaçların kökleri, dalları ve yaprakları, basit geometrik şekillere karşılık gelmekten uzak kan damarları. Benoit Mandelbrot ilk kez çığır açan çalışması "Doğanın Fraktal Geometrisi"nde dünyamızın fraktal doğasından bahsetti.
Fraktal terimi, Benoit Mandelbrot tarafından 1977 yılında Fraktallar, Form, Kaos ve Boyut adlı temel çalışmasıyla tanıtıldı. Mandelbrot'a göre fraktal kelimesi, bir fraktalın özünü "kırık", düzensiz bir küme olarak yansıtan Latince fractus - kesirli ve frangere - kırılma kelimelerinden gelir.

Fraktalların sınıflandırılması.

Bunun için Fraktalların tüm çeşitliliğini sunmak için genel kabul görmüş sınıflandırmalarına başvurmak uygundur. Fraktalların üç sınıfı vardır.

1. Geometrik fraktallar.

Bu sınıfın fraktalları en görsel olanlardır. İki boyutlu durumda, jeneratör adı verilen kesikli bir çizgi (veya üç boyutlu durumda yüzey) kullanılarak elde edilirler. Algoritmanın bir adımında, kesikli çizgiyi oluşturan bölümlerin her biri şu şekilde değiştirilir: sürekli çizgi oluşturucu uygun bir ölçekte. Bu işlemin sonsuz tekrarı sonucunda geometrik bir fraktal elde edilir.

Bu fraktal nesnelerden birinin örneğine bakalım: Triadik Koch eğrisi.

Üçlü Koch eğrisinin yapısı.

Uzunluğu 1 olan bir doğru parçası alalım. Buna diyelim tohum. Çekirdeği 1/3 uzunluğunda üç eşit parçaya bölelim, orta kısmı atalım ve yerine 1/3 uzunluğunda iki bakladan oluşan kesikli bir çizgi koyalım.

Toplam uzunluğu 4/3 olan 4 bağlantıdan oluşan kesikli bir çizgi elde edeceğiz, bu yüzden diyoruz birinci nesil.

Koch eğrisinin bir sonraki nesline geçmek için her bağlantının orta kısmının atılıp değiştirilmesi gerekir. Buna göre ikinci neslin uzunluğu 16/9, üçüncü neslin uzunluğu ise 64/27 olacaktır. eğer bu süreci sonsuza kadar sürdürürsek sonuç üçlü bir Koch eğrisi olur.

Şimdi üçlü Koch eğrisinin özelliklerini ele alalım ve fraktallara neden “canavar” dendiğini öğrenelim.

Birincisi, bu eğrinin uzunluğu yoktur; gördüğümüz gibi, nesil sayısı arttıkça uzunluğu sonsuza doğru gider.

İkincisi, bu eğriye bir teğet oluşturmak imkansızdır - noktalarının her biri, türevin bulunmadığı bir bükülme noktasıdır - bu eğri düzgün değildir.

Uzunluk ve düzgünlük, hem Öklid geometrisi hem de Lobaçevski ve Riemann geometrisi tarafından incelenen eğrilerin temel özellikleridir. Geleneksel geometrik analiz yöntemlerinin üçlü Koch eğrisine uygulanamadığı ortaya çıktı, bu nedenle Koch eğrisinin bir canavar olduğu ortaya çıktı - geleneksel geometrilerin pürüzsüz sakinleri arasında bir "canavar".

Harter-Haithway "ejderhasının" inşası.

Başka bir fraktal nesne elde etmek için yapım kurallarını değiştirmeniz gerekir. Şekillendirme elemanının dik açılarla birbirine bağlanmış iki eşit parça olmasına izin verin. Sıfır nesilde birim segmentini şununla değiştirin: bu şekillendirme elemanı, köşe üstte olacak şekilde. Böyle bir değişiklikle bağlantının ortasının yer değiştirmesi olduğunu söyleyebiliriz. Sonraki nesilleri inşa ederken kural izlenir: soldaki ilk bağlantı, bağlantının ortası hareket yönünün soluna kaydırılacak şekilde bir şekillendirme elemanı ile değiştirilir ve sonraki bağlantıları değiştirirken, bağlantıların yönleri segmentlerin ortalarının yer değiştirmesi değişmeli. Şekil, yukarıda açıklanan prensibe göre oluşturulan eğrinin ilk birkaç neslini ve 11. neslini göstermektedir. N'nin sonsuza doğru yöneldiği bir eğriye Harter-Haithway ejderi denir.
Bilgisayar grafiklerinde ağaç ve çalı görüntüleri elde edilirken geometrik fraktalların kullanılması gereklidir. İki boyutlu geometrik fraktallar, üç boyutlu dokular (bir nesnenin yüzeyindeki desenler) oluşturmak için kullanılır.

2. Cebirsel fraktallar

Bu fraktalların en büyük grubudur. N boyutlu uzaylarda doğrusal olmayan işlemler kullanılarak elde edilirler. İki boyutlu süreçler en çok çalışılanlardır. Doğrusal olmayan yinelemeli bir süreci ayrı bir dinamik sistem olarak yorumlarken, bu sistemlerin teorisinin terminolojisi kullanılabilir: faz portresi, kararlı durum süreci, çekici vb.
Doğrusal olmayan dinamik sistemlerin birçok kararlı duruma sahip olduğu bilinmektedir. Belirli sayıda yinelemeden sonra dinamik sistemin kendini bulduğu durum, başlangıç ​​durumuna bağlıdır. Bu nedenle, her kararlı durum (veya dedikleri gibi çekici), sistemin mutlaka söz konusu son durumlara düşeceği belirli bir başlangıç ​​durumları bölgesine sahiptir. Böylece sistemin faz uzayı çekicilerin çekim alanlarına bölünmüş olur. Faz uzayı iki boyutlu bir uzay ise, çekim alanları farklı renklerle renklendirilerek bu sistemin renkli faz portresi elde edilebilir (yinelemeli süreç). Renk seçim algoritmasını değiştirerek tuhaf çok renkli desenlere sahip karmaşık fraktal desenler elde edebilirsiniz. Matematikçiler için bir sürpriz, ilkel algoritmalar kullanarak çok karmaşık, önemsiz olmayan yapılar üretme yeteneğiydi.

Mandelbrot kümesi.

Örnek olarak Mandelbrot kümesini ele alalım. Yapım algoritması oldukça basittir ve basit bir yinelemeli ifadeye dayanmaktadır: Z = Z * Z + C, Nerede Zi Ve C- karmaşık değişkenler. Karmaşık düzlemin bir alt kümesi olan dikdörtgen veya kare bölgeden her başlangıç ​​noktası için yinelemeler gerçekleştirilir. Yinelemeli süreç şu ana kadar devam eder: Z merkezi (0,0) noktasında bulunan 2 yarıçaplı dairenin ötesine geçmeyecek (bu, dinamik sistemin çekicisinin sonsuzda olduğu anlamına gelir) veya yeterince fazla sayıda yinelemeden sonra (örneğin, , 200-500) Zçember üzerinde bir noktada birleşecek. Tekrarlama sayısına bağlı olarak Z dairenin içinde kaldıysanız noktanın rengini ayarlayabilirsiniz C(Eğer Z yeterince fazla sayıda yineleme boyunca dairenin içinde kalırsa yineleme süreci durur ve bu tarama noktası siyaha boyanır).

3. Stokastik fraktallar

Fraktalların iyi bilinen bir başka sınıfı da stokastik fraktallardır; bunlar, bazı parametrelerinin yinelemeli bir süreçte rastgele değiştirilmesi durumunda elde edilir. Bu durumda, ortaya çıkan nesneler doğal olanlara çok benzer - asimetrik ağaçlar, engebeli kıyı şeritleri vb. Arazi ve deniz yüzeyi modellemesinde iki boyutlu stokastik fraktallar kullanılır.
Fraktalların başka sınıflandırmaları da vardır; örneğin, fraktalları deterministik (cebirsel ve geometrik) ve deterministik olmayan (stokastik) olarak ayırmak.

Fraktalların kullanımı hakkında

Her şeyden önce fraktallar, en basit formüller ve algoritmaların yardımıyla olağanüstü güzellikte ve karmaşıklıkta resimler elde edildiğinde inanılmaz bir matematik sanatı alanıdır! Oluşturulan görüntülerin dış hatlarında genellikle yapraklar, ağaçlar ve çiçekler görülmektedir.

Fraktalların en güçlü uygulamalarından bazıları bilgisayar grafiklerinde yatmaktadır. Birincisi, bu görüntülerin fraktal olarak sıkıştırılması ve ikincisi manzaraların, ağaçların, bitkilerin oluşturulması ve fraktal dokuların oluşturulmasıdır. Modern fizik ve mekanik, fraktal nesnelerin davranışını incelemeye yeni başlıyor. Ve elbette fraktallar doğrudan matematiğin kendisinde kullanılır.
Fraktal görüntü sıkıştırma algoritmalarının avantajları, paketlenmiş dosyanın çok küçük boyutu ve kısa görüntü kurtarma süresidir. Fraktal paketlenmiş görüntüler pikselleşmeye neden olmadan ölçeklenebilir. Ancak sıkıştırma işlemi uzun zaman alır ve bazen saatlerce sürer. Fraktal kayıplı paketleme algoritması, jpeg formatına benzer şekilde sıkıştırma oranını ayarlamanıza olanak tanır. Algoritma, görüntünün bazı küçük parçalara benzeyen büyük parçalarını aramaya dayanmaktadır. Ve çıktı dosyasına yalnızca hangi parçanın benzer olduğu yazılır. Sıkıştırma sırasında genellikle kare bir ızgara kullanılır (parçalar karedir), bu da görüntüyü geri yüklerken hafif bir açısallığa yol açar; altıgen ızgaranın bu dezavantajı yoktur.
Iterated, fraktal ve "dalga" (jpeg gibi) kayıpsız sıkıştırmayı birleştiren yeni bir görüntü formatı olan "Sting" geliştirdi. Yeni format, daha sonra yüksek kaliteli ölçeklendirme olanağı sunan görüntüler oluşturmanıza olanak tanır ve grafik dosyalarının hacmi, sıkıştırılmamış görüntülerin hacminin% 15-20'sidir.
Fraktalların dağlara, çiçeklere ve ağaçlara benzeme eğilimi bazı grafik editörleri tarafından istismar edilmektedir; örneğin, 3D studio MAX'tan fraktal bulutlar, World Builder'daki fraktal dağlar. Fraktal ağaçlar, dağlar ve tüm manzaralar basit formüllerle tanımlanır, programlanması kolaydır ve yaklaşıldığında ayrı üçgenlere ve küplere bölünmez.
Fraktalların matematikte kullanımı göz ardı edilemez. Küme teorisinde, Cantor kümesi hiçbir yerde yoğun olmayan mükemmel kümelerin varlığını kanıtlar; ölçü teorisinde, kendine afin fonksiyon "Cantor'un Merdiveni" tekil bir ölçünün dağılım fonksiyonuna iyi bir örnektir.
Mekanik ve fizikte fraktallar, birçok doğal nesnenin ana hatlarını tekrarlayan benzersiz özelliklerinden dolayı kullanılır. Fraktallar, segment veya çokgen kümelerini (aynı miktarda depolanan veriyle) kullanan yaklaşımlardan daha yüksek doğrulukla ağaçlara, dağ yüzeylerine ve çatlaklara yaklaşık olarak yaklaşmanıza olanak tanır. Fraktal modellerin de doğal nesneler gibi bir “pürüzlülüğü” vardır ve modelin büyütülmesi ne kadar büyük olursa olsun bu özellik korunur. Fraktallar üzerinde tekdüze bir ölçümün varlığı, entegrasyonun, potansiyel teorinin uygulanmasına ve önceden çalışılmış denklemlerde standart nesneler yerine bunların kullanılmasına olanak tanır.
Fraktal yaklaşımla kaos, mavi düzensizlik olmaktan çıkıp ince bir yapıya kavuşuyor. Fraktal bilimi hala çok genç ve önünde büyük bir gelecek var. Fraktalların güzelliği tükenmekten çok uzak ve bize hala birçok başyapıt verecek - hem göze hoş gelen hem de zihne gerçek zevk verenler.

Fraktalların oluşturulması hakkında

Ardışık yaklaşım yöntemi

Bu resme bakıldığında kendine benzeyen bir fraktalı (bu durumda Sierpinski piramidi) nasıl oluşturabileceğinizi anlamak zor değil. Düzenli bir piramit (tetrahedron) almalı, sonra ortasını (oktahedron) kesip dört küçük piramit elde etmeliyiz. Her biriyle aynı işlemi vb. gerçekleştiriyoruz. Bu biraz naif ama net bir açıklama.

Yöntemin özünü daha sıkı bir şekilde ele alalım. Bir miktar IFS sistemi olsun, yani. sıkıştırma haritalama sistemi S=(S 1 ,...,S m ) S i:R n ->R n (örneğin, piramidimiz için eşlemeler S i (x )=1/2*x+o i gibi görünür, burada o i tetrahedronun köşeleri, i=1,..,4). Daha sonra Rn'de bir A1 kompakt kümesi seçiyoruz (bizim durumumuzda bir tetrahedron seçiyoruz). Ve tümevarım yoluyla A k:A k+1 =S 1 (A k ) U...U S m (A k ) kümelerinin sırasını belirleriz. Artan k ile A k kümelerinin sistemin istenen çekicisine giderek daha iyi yaklaştığı bilinmektedir. S.

Bu yinelemelerin her birinin bir çekici olduğunu unutmayın. yinelenen yinelenen işlevler sistemi(İngilizce terim Digraf IFS, RIFS ve ayrıca Grafik odaklı IFS) ve bu nedenle programımızı kullanarak bunları oluşturmak kolaydır.

Noktadan noktaya veya olasılıksal yöntem

Bu, bilgisayarda uygulanması en kolay yöntemdir. Basit olması açısından düz kendine afin küme durumunu ele alıyoruz. O halde (S 1,..,S m) bir afin kasılma sistemi olsun. S i eşlemeleri şu biçimde temsil edilebilir: S i (x)=A i (x-o i)+o i, burada A i, 2x2 boyutunda sabit bir matristir ve o i, iki boyutlu bir sütun vektörüdür.

· İlk eşleme S 1'in sabit noktasını başlangıç ​​noktası olarak alalım:
x : = o1;
Burada S 1 ,..,Sm sıkıştırmasının tüm sabit noktalarının fraktala ait olması gerçeğinin avantajından yararlanıyoruz. Başlangıç ​​noktası olarak rastgele bir nokta seçebilirsiniz ve bu nokta tarafından oluşturulan noktaların sırası bir fraktal olarak çizilecektir, ancak daha sonra ekranda birkaç ekstra nokta görünecektir.

· Ekranda geçerli noktayı x= (x 1 ,x 2) olarak işaretleyelim:
putpixel(x 1 ,x 2 ,15);

· 1'den m'ye kadar rastgele bir j sayısı seçelim ve x noktasının koordinatlarını yeniden hesaplayalım:
j:=Rastgele (m)+1;
x:=Sj(x);

· 2. adıma geçiyoruz veya yeterince fazla sayıda yineleme yaptıysak duruyoruz.
Not. Si eşlemelerinin sıkıştırma oranları farklıysa, fraktal eşit olmayan noktalarla doldurulacaktır. Eğer eşlemeler Si benzerse, algoritmayı biraz karmaşıklaştırarak bu durum önlenebilir. Bunu yapmak için, algoritmanın 3. adımında, 1'den m'ye kadar j sayısı p 1 =r 1 s,..,p m =r m s olasılıklarıyla seçilmelidir; burada r i, Si eşlemelerinin sıkıştırma katsayılarını belirtir ve s sayısı (benzerlik boyutu olarak adlandırılır) r 1 s +...+r m s =1 denkleminden bulunur. Bu denklemin çözümü örneğin Newton yöntemiyle bulunabilir.

Fraktallar ve algoritmaları hakkında

Fraktal, Latince "fractus" sıfatından gelir ve çeviride parçalardan oluşan anlamına gelir ve buna karşılık gelen Latince "frangere" fiili, kırmak, yani düzensiz parçalar oluşturmak anlamına gelir. 70'li yılların sonlarında ortaya çıkan fraktal ve fraktal geometri kavramları, 80'li yılların ortalarından itibaren matematikçiler ve programcılar arasında sağlam bir şekilde yerleşmiştir. Bu terim 1975 yılında Benoit Mandelbrot tarafından ilgilendiği düzensiz fakat kendine benzeyen yapılara atıfta bulunmak için icat edildi. Fraktal geometrinin doğuşu genellikle Mandelbrot'un 1977'de "Doğanın Fraktal Geometrisi" kitabının yayınlanmasıyla ilişkilendirilir. Eserlerinde 1875-1925 yılları arasında aynı alanda çalışan diğer bilim adamlarının (Poincaré, Fatou, Julia, Cantor, Hausdorff) bilimsel sonuçlarından yararlanılmıştır.

Ayarlamalar

H.-O.'nun kitabında önerdiği algoritmalarda bazı ayarlamalar yapayım. Peitgen ve P.H. Richter "Fraktalların Güzelliği" M. 1993, tamamen yazım hatalarını ortadan kaldırmak ve süreçlerin anlaşılmasını kolaylaştırmak için, çünkü bunları inceledikten sonra çoğu şey benim için bir sır olarak kaldı. Ne yazık ki bu “anlaşılabilir” ve “basit” algoritmalar sallantılı bir yaşam tarzına öncülük ediyor.

Fraktalların yapısı, z = > z 2 +c geri beslemeli karmaşık bir sürecin belirli bir doğrusal olmayan fonksiyonuna dayanır, çünkü z ve c -k karmaşık sayılardır, bu durumda z = x + iy, c = p + iq gerekir Sıradan insan için daha gerçekçi bir düzleme gitmek amacıyla bunu x ve y'ye ayrıştırın:

x(k+1)=x(k) 2 -y(k) 2 + p,
y(k+1)=2*x(k)*y(k) + q.

Sabit değerler için tüm (x,y) çiftlerinden oluşan bir düzlem düşünülebilir. R ve q ve dinamik olanlarla. İlk durumda, tüm noktalardan geçerek (x ey) düzlemler ve yinelemeli süreçten çıkmak için gerekli fonksiyon tekrarı sayısına bağlı olarak bunları renklendirmek veya izin verilen maksimum tekrarlar aşıldığında onları renklendirmemek (siyah renk), Julia kümesinin bir haritasını elde ederiz. Aksine, başlangıç ​​​​değer çiftini (x, y) belirlersek ve p ve q parametrelerinin dinamik olarak değişen değerleriyle renksel kaderini izlersek, o zaman Mandelbrot kümeleri adı verilen görüntüler elde ederiz.

Fraktalların renklendirilmesine yönelik algoritmalar sorusu üzerine.

Genellikle setin gövdesi siyah bir alan olarak temsil edilir, ancak siyah rengin başka herhangi bir renkle değiştirilebileceği açıktır, ancak bu da biraz ilginç bir sonuçtur. Bir kümenin tüm renklerde renklendirilmiş görüntüsünü elde etmek döngüsel işlemler kullanılarak çözülemeyen bir görevdir çünkü gövdeyi oluşturan kümelerin yineleme sayısı mümkün olan maksimum sayıya eşittir ve her zaman aynıdır. Döngü çıkış koşulunun (z_magnitude) veya buna benzer bir şeyin kontrol edilmesi sonucunu, ancak diğer matematiksel işlemlerle renk numarası olarak kullanarak bir seti farklı renklerde renklendirmek mümkündür.

"Fraktal mikroskop" uygulaması

sınır olayını göstermek.

Çekiciler düzlemde hakimiyet mücadelesine öncülük eden merkezlerdir. Çekiciler arasında gösterişli bir modeli temsil eden bir sınır belirir. Kümenin sınırları içindeki değerlendirme ölçeğini artırarak, doğal dünyada yaygın bir fenomen olan deterministik kaos durumunu yansıtan önemsiz olmayan modeller elde edilebilir.

Coğrafyacılar tarafından incelenen nesneler, sınırları çok karmaşık bir şekilde düzenlenmiş bir sistem oluşturur ve bu nedenle bunların tanımlanması basit bir pratik iş haline gelmez. Doğal kompleksler, bölge uzaklaştıkça üzerindeki etkilerini kaybeden çekiciler olarak hareket eden tipiklik çekirdeklerine sahiptir.

Mandelbrot ve Julia kümeleri için bir fraktal mikroskop kullanılarak, değerlendirme ölçeğinden bağımsız olarak eşit derecede karmaşık olan sınır süreçleri ve fenomenler hakkında bir fikir oluşturulabilir ve böylece uzmanın algısı, dinamik ve görünüşte kaotik bir doğal nesneyle karşılaşmaya hazırlanabilir. Fraktal geometrinin doğasını anlamak için uzay ve zamanda. Rengarenk renkler ve fraktal müzik kesinlikle öğrencilerin zihninde derin bir iz bırakacaktır.

Fraktallara binlerce yayın ve geniş İnternet kaynağı ayrılmıştır, ancak bilgisayar biliminden uzak birçok uzman için bu terim tamamen yeni görünmektedir. Çeşitli bilgi alanlarındaki uzmanların ilgisini çeken fraktallar, bilgisayar bilimleri derslerinde uygun bir yer almalıdır.

Örnekler

SIEPINSKI IZGARA

Bu, Mandelbrot'un fraktal boyutlar ve yineleme kavramlarını geliştirirken denediği fraktallardan biridir. Daha büyük bir üçgenin orta noktaları birleştirilerek oluşturulan üçgenler kesiliyor ana üçgenden daha fazla deliğe sahip bir üçgen oluşturuyor. Bu durumda başlatıcı büyük üçgen, şablon ise büyük olana benzer üçgenlerin kesilmesi işlemidir. Sıradan bir tetrahedron kullanarak ve küçük tetrahedronları keserek de bir üçgenin üç boyutlu versiyonunu elde edebilirsiniz. Böyle bir fraktalın boyutu ln3/ln2 = 1,584962501'dir. Elde etmek üzere Sierpinski halısı, bir kare alın, onu dokuz kareye bölün ve ortadakini kesin. Geri kalan daha küçük kareler için de aynısını yapacağız. Sonunda alanı olmayan ancak sonsuz bağlantılara sahip düz bir fraktal ızgara oluşur. Sierpinski süngeri, mekânsal biçiminde, her bir uçtan uca öğenin sürekli olarak kendi türüyle değiştirildiği, uçtan uca formlardan oluşan bir sisteme dönüştürülür. Bu yapı kemik dokusunun bir bölümüne çok benzer. Bir gün bu tür tekrarlanan yapılar bina yapılarının bir unsuru haline gelecektir. Mandelbrot bunların statik ve dinamiklerinin yakından incelenmeyi hak ettiğine inanıyor.

SIERPINSKI FRAKTAL

Bu fraktalı Sierpinski kafesi ile karıştırmayın. Bunlar tamamen farklı iki nesnedir. Bu fraktalda başlatıcı ve üreteç aynıdır. Her yinelemede, başlatıcının daha küçük bir kopyası oluşturucunun her köşesine eklenir ve bu şekilde devam eder. Bu fraktal oluşturulurken sonsuz sayıda yineleme yapılsaydı, tek bir delik bile bırakmadan tüm düzlemi kaplardı. Dolayısıyla fraktal boyutu ln9/ln3 = 2,0'dır.

KOCH EĞRİSİ

Koch eğrisi en tipik deterministik fraktallardan biridir. On dokuzuncu yüzyılda, Georg Kontor ve Karl Weierstrasse'nin çalışmalarını incelerken alışılmadık davranışlara sahip bazı garip eğrilerin tanımlarıyla karşılaşan Helge von Koch adlı bir Alman matematikçi tarafından icat edildi. Başlatıcı düz bir çizgidir. Jeneratör, kenarları daha büyük bölümün uzunluğunun üçte birine eşit olan bir eşkenar üçgendir. Bu üçgenler her parçanın ortasına tekrar tekrar eklenir. Mandelbrot, araştırmasında Koch eğrileriyle kapsamlı deneyler yaptı ve bir tetrahedron kullanarak ve her bir yüzüne daha küçük tetrahedronlar ekleyerek Koch Adaları, Koch Haçları, Koch Kar Taneleri gibi şekiller ve hatta Koch eğrisinin üç boyutlu temsillerini üretti. Koch eğrisinin boyutu ln4/ln3 = 1,261859507'dir.

MANDELBROT FRAKTAL

Bu oldukça sık gördüğünüz Mandelbrot kümesi DEĞİLDİR. Mandelbrot kümesi doğrusal olmayan denklemlere dayanır ve karmaşık bir fraktaldır. Bu nesne ona benzemese de, bu aynı zamanda Koch eğrisinin bir çeşididir. Başlatıcı ve oluşturucu da Koch eğrisi ilkesine dayalı fraktallar oluşturmak için kullanılanlardan farklıdır, ancak fikir aynı kalır. Eşkenar üçgenleri bir eğri parçasına birleştirmek yerine kareler bir kareye birleştirilir. Bu fraktalın her yinelemede ayrılan alanın tam olarak yarısını kaplaması nedeniyle basit fraktal boyutu 3/2 = 1,5'tir.

FRAKTALLAR YILDIZ VE KAR TANESİ

Bu nesnelerin her ikisi de klasik fraktallar değildir ve Mandelbrot ya da başka bir ünlü matematikçi tarafından icat edilmemiştir. Bu fraktalları sadece ilgimden dolayı ve programlamayı denemek için yarattım. Buradaki hem başlatıcı hem de üreteç, düzgün bir altıgende kenarların orta noktalarının karşı kenarların orta noktalarıyla birleştirilmesiyle oluşturulan bir şekildir. Üstelik bu fraktalların yalnızca boyutundan şüpheleniyorum.

DARER PENTAGON

Bir fraktal, birbirine sıkıştırılmış bir grup beşgen gibi görünür. Aslında başlatıcı olarak bir beşgen ve jeneratör olarak büyük tarafın küçük tarafa oranının altın orana (1.618033989 veya 1/(2cos72)) tam olarak eşit olduğu ikizkenar üçgenler kullanılarak oluşturulur. . Bu üçgenler her bir beşgenin ortasından kesilerek, bir büyük beşgene yapıştırılmış 5 küçük beşgen gibi görünen bir şekil elde edilir. Bu fraktalın bir çeşidi, başlatıcı olarak bir altıgen kullanılarak elde edilebilir. Bu fraktal Davut Yıldızı olarak adlandırılıyor ve Koch Kar Tanesi'nin altıgen versiyonuna oldukça benziyor. Darer beşgeninin fraktal boyutu ln6/ln (1+g)'dir; burada g, üçgenin büyük kenarının uzunluğunun küçük kenarının uzunluğuna oranıdır. Bu durumda g Altın Oran olduğundan fraktal boyut yaklaşık 1,86171596 olur. Davut Yıldızı'nın fraktal boyutu ln6/ln3 veya 1.630929754.

HİLBERT EĞRİSİ

Bu fraktal, üreteç olan U harfinin genişliğinin her yinelemede değişmemesi dışında Labirent Fraktalına çok benzemektedir. Ancak Hilbert Oteli olarak da adlandırılan Hilbert eğrisi, Labirent Fraktalından farklı olarak tek bir fraktal boyuta sahiptir; bu tam olarak 2,0'dır, çünkü sonsuz sayıda yinelemeyle tüm düzlemi kaplayacaktır. fraktal ve daha sonra aynı işlemi o alanın küçük bir alanıyla yaparsanız, iki büyütme birbirinden önemli ölçüde farklı olacaktır. İki görüntü detay olarak birbirine çok benzeyecek ancak tamamen aynı olmayacak. Şekil 1. Mandelbrot kümesi yaklaşımı Örneğin burada gösterilen Mandelbrot kümesinin resimlerini karşılaştırın, bunlardan biri diğerinin belirli bir alanının büyütülmesiyle elde edilmiştir. Gördüğünüz gibi, kesinlikle aynı değiller, ancak her ikisinde de alevli dokunaçların farklı yönlere uzandığı siyah bir daire görüyoruz. Bu elemanlar Mandelbrot kümesinde azalan oranlarda süresiz olarak tekrarlanır. Deterministik fraktallar doğrusaldır, oysa karmaşık fraktallar doğrusal değildir. Doğrusal olmayan bu fraktallar, Mandelbrot'un doğrusal olmayan cebirsel denklemler dediği şey tarafından üretilir. Bunun iyi bir örneği, ikinci dereceden Mandelbrot ve Julia kümesini oluşturmak için kullanılan denklem olan Zn+1=ZnI + C sürecidir. Bu matematiksel denklemleri çözmek karmaşık ve sanal sayıları içerir. Denklem karmaşık düzlemde grafiksel olarak yorumlandığında, düz çizgilerin eğrilere dönüştüğü ve çeşitli ölçek düzeylerinde deformasyonsuz olmasa da kendine benzerlik etkilerinin ortaya çıktığı garip bir şekil ortaya çıkar. Aynı zamanda, bir bütün olarak resmin tamamı öngörülemez ve çok kaotik. Resimlere baktığınızda da görebileceğiniz gibi, karmaşık fraktallar gerçekten çok karmaşıktır ve bilgisayar yardımı olmadan oluşturulamaz. Renkli sonuçlar elde etmek için bu bilgisayarın güçlü bir matematiksel işlemciye ve yüksek çözünürlüklü bir monitöre sahip olması gerekir. Deterministik fraktalların aksine karmaşık fraktallar 5-10 tekrarda hesaplanmaz. Bilgisayar ekranındaki hemen hemen her nokta ayrı bir fraktal gibidir. Matematiksel işlem sırasında her nokta ayrı bir çizim olarak ele alınır. Her nokta belirli bir değere karşılık gelir. Denklem her nokta için yerleşiktir ve örneğin 1000 yinelemede gerçekleştirilir. Ev bilgisayarları için kabul edilebilir bir zaman diliminde nispeten bozulmamış bir görüntü elde etmek için bir nokta için 250 yinelemenin gerçekleştirilmesi mümkündür. Bugün gördüğümüz fraktalların çoğu güzel renklidir. Belki de fraktal görüntüler, tam da renk şemaları nedeniyle bu kadar büyük bir estetik önem kazanıyor. Denklem hesaplandıktan sonra bilgisayar sonuçları analiz eder. Sonuçlar sabit kalırsa veya belirli bir değer etrafında dalgalanırsa nokta genellikle siyaha döner. Bir adımdaki değer sonsuza doğru gidiyorsa nokta farklı bir renge, belki mavi veya kırmızıya boyanır. Bu işlem sırasında bilgisayar tüm hareket hızlarına renk atar. Tipik olarak hızlı hareket eden noktalar kırmızı renkte, daha yavaş olanlar ise sarı renktedir ve bu şekilde devam eder. Karanlık noktalar muhtemelen en kararlı olanlardır. Karmaşık fraktallar farklıdır deterministik Yani sonsuz derecede karmaşıktırlar ama aynı zamanda çok basit bir formülle de oluşturulabilirler. Deterministik fraktallar formül veya denklem gerektirmez. Sadece biraz çizim kağıdı alın ve herhangi bir zorluk yaşamadan 3 veya 4 tekrara kadar bir Sierpinski eleği oluşturabilirsiniz. Bunu bir sürü Julia ile deneyin! İngiltere'nin kıyı şeridinin uzunluğunu ölçmek artık daha kolay! MANDELBROT SETİ Şekil 2. Mandelbrot seti Mandelbrot ve Julia kümeleri muhtemelen karmaşık fraktallar arasında en yaygın olanlardır. Pek çok bilimsel dergide, kitap kapağında, kartpostalda ve bilgisayar ekran koruyucularında bulunabilirler. Benoit Mandelbrot tarafından oluşturulan Mandelbrot kümesi muhtemelen insanların fraktal kelimesini duyduklarında aklına gelen ilk çağrışımdır. Üzerinde yanan ağaç benzeri ve dairesel alanların eklendiği bir tarama makinesini andıran bu fraktal, Zn+1=Zna+C basit formülüyle üretiliyor; burada Z ve C karmaşık sayılar, a ise pozitif bir sayıdır. En sık görülen Mandelbrot kümesi 2. dereceden Mandelbrot kümesidir yani a = 2'dir. Mandelbrot kümesinin sadece Zn+1=ZnІ+C değil aynı zamanda formüldeki göstergesi herhangi bir pozitif sayı olabilen bir fraktal olması birçok kişiyi yanılttı. Bu sayfada a üssünün çeşitli değerleri için Mandelbrot kümesinin bir örneğini görüyorsunuz. Şekil 3. a=3.5 noktasında kabarcıkların görünümü Z=Z*tg (Z+C) süreci de popülerdir. Teğet fonksiyonu dahil edildiğinde sonuç, elmaya benzeyen bir alanla çevrelenmiş bir Mandelbrot kümesidir. Kosinüs fonksiyonu kullanıldığında hava kabarcığı etkileri elde edilir. Kısacası, Mandelbrot setini farklı güzel resimler üretecek şekilde yapılandırmanın sonsuz sayıda yolu vardır. BİR ÇOK JULIA Şaşırtıcı bir şekilde Julia kümeleri Mandelbrot kümesiyle aynı formüle göre oluşturulmuştur. Julia kümesi, Fransız matematikçi Gaston Julia tarafından icat edildi ve kümeye adı verildi. Mandelbrot ve Julia kümelerini görsel olarak tanıdıktan sonra ortaya çıkan ilk soru şudur: "Eğer her iki fraktal da aynı formüle göre üretiliyorsa, neden bu kadar farklılar?" İlk önce Julia setinin resimlerine bakın. İşin garibi, Julia setlerinin farklı türleri var. Farklı başlangıç ​​noktaları kullanarak bir fraktal çizerken (yineleme sürecini başlatmak için), farklı görüntüler oluşturulur. Bu yalnızca Julia seti için geçerlidir. Şekil 4. Julia seti Resimde görülmese de Mandelbrot fraktalı aslında birçok Julia fraktalının birbirine bağlanmasıdır. Mandelbrot kümesinin her noktası (veya koordinatı) bir Julia fraktalına karşılık gelir. Julia kümeleri, Z=ZI+C denkleminde bu noktalar başlangıç ​​değerleri olarak kullanılarak oluşturulabilir. Ancak bu, Mandelbrot fraktalında bir nokta seçip onu büyütürseniz Julia fraktalını elde edebileceğiniz anlamına gelmez. Bu iki nokta aynıdır, ancak yalnızca matematiksel anlamda. Bu noktayı alıp bu formülü kullanarak hesaplarsanız, Mandelbrot fraktalının belirli bir noktasına karşılık gelen Julia fraktalını elde edebilirsiniz.