1. Uzmimo pravilan trokut.
2. Iz njega smo izrezali trokut, čiji vrhovi leže na središtima stranica izvornog. Kao rezultat toga, na ravnini dobivamo tri trokuta, od kojih je površina svakog četiri puta manja od površine izvorne.
3. Izvodimo prethodne manipulacije s dobivenim trokutima.

Proces izgleda ovako:

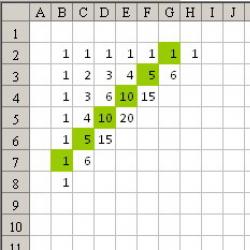
1. Zanimljivo je da ako su u Pascalovom trokutu svi neparni brojevi obojeni jednom bojom, a parni drugom bojom, tada nastaje trokut Sierpinskog.

Iskoristimo tu činjenicu. Samo u Excelu je prikladnije koristiti ne klasični (linija po red) oblik Pascalovog trokuta, već ovo:

Ovdje su dijagonalno ispisani binomni koeficijenti, u prvom popunjenom retku i prvom popunjenom stupcu jedinice, au ostalima zbroj gornjeg i lijevog elementa.

Prijeđimo na konstrukciju. Za nas je dovoljno zapisati ne koeficijente, već samo njihov paritet.

Prvo, napravimo veličinu ćelija u Excelu, na primjer 7 x 7 piksela.

Stanimo u ćeliju B2, zatim odaberite područje B2:DY129 - da biste to učinili, pritisnite Ctrl + G i napišite B2:DY129 u polje veze.

Sada u traci formule pišemo =IF(ILI(RED()=2,STUPAC()=2),1,REM(A2+B1,2))
i pritisnite Ctrl + Enter da ispunite cijelo odabrano područje sličnom formulom.

Idemo Jelovnik - Uvjetno oblikovanje a za vrijednost 1 označavamo boju ćelije.

Kao rezultat dobivamo:

Treba napomenuti da se trokut Sierpinskog dobiva nekom vrstom slučajnog hoda po ravnini. Naime:

1. Popravimo 3 vrha trokuta na ravnini i uzmimo drugu točku.
2. Dobivamo prvu točku kao središte segmenta između slučajno odabrani vrh i točku iz koraka 1.
3. Dobivamo drugu točku kao središte segmenta između slučajno odabrani vrh i prva točka.
4. Postupak ponavljamo mnogo puta.

Možete koristiti ovu makronaredbu:

Javni podmakro()

Dim arRange (1 do 3) kao raspon
Dim tekRow kao cijeli broj
Dim tekColumn Kao cijeli broj
Dim i kao cijeli broj
Dim it As Integer

tekRow = Int(1000 * Rnd) + 1
tekColumn = Int(200 * Rnd) + 1

Postavi arRange(1) = Cells(1, 1)
Postavi arRange(2) = Cells(50, 250)
Postavi arRange(3) = Cells(200, 20)

Ćelije.Jasno

Za i = 1 do 20000
iT = (Int(1000 * Rnd) Mod 3) + 1
tekRow = Int((tekRow + arRange(iT).Row) / 2)
tekColumn = Int((tekColumn + arRange(iT).Column) / 2)
Cells(tekRow, tekColumn).Interior.ColorIndex = 5
Sljedeći

End Sub

trokut Sierpinskog- fraktal, jedan od dvodimenzionalnih analoga Cantorovog skupa, kojeg je predložio poljski matematičar Waclaw Sierpinski 1915. godine. Također poznat kao Sierpinskijev "ubrus".

trokut Sierpinskog

Izgradnja

Iterativna metoda

Konstrukcija trokuta Sierpinskog

Središta stranica jednakostraničnog trokuta spojena su segmentima. Dobivate 4 nova trokuta. Unutrašnjost srednjeg trokuta uklonjena je iz izvornog trokuta. Ispada puno T 1 (\displaystyle T_(1)), koji se sastoji od 3 preostala trokuta "prvog reda". Čineći točno isto sa svakim od trokuta prvog ranga, dobivamo skup T 2 (\displaystyle T_(2)), koji se sastoji od 9 jednakostraničnog trokuta drugog reda. Nastavljajući ovaj proces unedogled, dobivamo beskonačan niz T 0 ⊃ T 1 ⊃ ⋯ ⊃ T n ⊃ … (\displaystyle T_(0)\supset T_(1)\supset \dots \supset T_(n)\supset \dots ), čije je sjecište članova trokut Sierpinskog.

Metoda kaosa

1. Zadane su koordinate atraktora - vrhova izvornog trokuta T 0 (\displaystyle T_(0)). 2. Prostor vjerojatnosti (0 ; 1) (\displaystyle (0;1)) podijeljen je na 3 jednaka dijela od kojih svaki odgovara jednom atraktoru. 3. Određena je početna točka P 0 (\displaystyle P_(0)), koji leži unutar trokuta T 0 (\displaystyle T_(0)). 4. Početak ciklusa konstruiranja točaka koje pripadaju skupu trokuta Sierpinskog. 1. Generira se nasumični broj n ∈ (0 ; 1) (\displaystyle n\in (0;1)). 2. Aktivni atraktor postaje vrh u čiji je probabilistički podprostor upao generirani broj. 3. Točka se konstruira P i (\displaystyle P_(i)) s novim koordinatama: x i = x i − 1 + x A 2 ; y i = y i − 1 + y A 2 (\displaystyle x_(i)=(\frac (x_(i-1)+x_(A))(2));y_(i)=(\frac (y_(i) -1)+y_(A))(2))), Gdje: x i − 1 , y i − 1 (\displaystyle x_(i-1),y_(i-1))- koordinate prethodne točke P i − 1 (\displaystyle P_(i-1)); x A , y A (\displaystyle x_(A),y_(A))- koordinate aktivne atraktorske točke. 5. Povratak na početak ciklusa.

Svojstva

Konstrukcija iterativnom metodom

Izgradnja metodom kaosa

Bilješke

Linkovi

L-sustav

L-sustav ili Lindenmayerov sustav je paralelni sustav prepisivanja i vrsta formalne gramatike. L-sustav sastoji se od abecede simbola koji se mogu koristiti za stvaranje nizova, skupa pravila za generiranje koja određuju pravila za zamjenu za svaki simbol, početnog niza ("aksioma") od kojeg počinje konstrukcija i mehanizma za prevođenje generiranog niza u geometrijske strukture. L-sustave je predložio i razvio 1968. Aristide Lindenmayer, mađarski biolog i botaničar sa Sveučilišta u Utrechtu. Lindenmayer je koristio L-sustave za opisivanje ponašanja biljnih stanica i modeliranje procesa razvoja biljaka. L-sustavi su također korišteni za modeliranje morfologije raznih organizama i mogu se koristiti za generiranje samosličnih fraktala kao što su sustavi funkcija koji se mogu ponavljati.

Reket (programski jezik)

Racket (ranije PLTScheme) je programski jezik opće namjene s više paradigmi koji pripada obitelji Lisp/Scheme. Pruža okruženje za jezično orijentirano programiranje - jedna od svrha reketa je stvaranje, razvoj i implementacija programskih jezika. Jezik se koristi u različitim kontekstima: kao skriptni jezik, kao jezik opće namjene, u nastavi informatike, u znanstvenom istraživanju.

Platforma korisniku pruža implementaciju jezika Racket, uključujući razvijeni sustav vremena izvođenja, razne biblioteke, JIT kompajler itd., kao i razvojno okruženje DrRacket (ranije poznato kao DrScheme) napisano u Racketu. Ovaj softverski okvir koristi se u tečaju ProgramByDesign na MIT-u. Temeljni jezik Racket ima snažan makro sustav koji vam omogućuje stvaranje ugrađenih i domenskih programskih jezika, jezičnih konstrukcija (na primjer, klasa i modula) i dijalekata Racket s različitom semantikom.

Sustav je besplatan softver otvorenog koda koji se distribuira pod uvjetima LGPL-a. Proširenja i paketi koje je napisala zajednica dostupni su na PLaneT-u, web distribuciji sustava.

Algoritam fraktalne kompresije

Fraktalna kompresija slike algoritam je kompresije slike s gubitkom koji se temelji na primjeni sustava iteriranih funkcija (obično afine transformacije) na slike. Ovaj je algoritam poznat po tome što u nekim slučajevima omogućuje postizanje vrlo visokih omjera kompresije uz prihvatljivu vizualnu kvalitetu za stvarne fotografije prirodnih objekata. Zbog teške situacije s patentiranjem, algoritam nije bio široko korišten.

Razdjelna pločica

Rep-tile je koncept geometrije mozaika, figura koja se može rezati na manje kopije same figure. U 2012., engleski matematičar Lee Salous u časopisu Mathematics Magazine predložio je generalizaciju razdjelnih pločica nazvanu samopopločavajući skup pločica.

Završno pravilo podjele

U matematici, krajnje pravilo podjele je rekurzivan način dijeljenja poligona i drugih dvodimenzionalnih oblika na sve manje dijelove. Pravila podjele u ovom smislu su generalizacija fraktala. Umjesto ponavljanja istog obrasca iznova i iznova, postoje suptilne promjene u svakom koraku, omogućujući bogatije strukture dok još uvijek održava elegantan fraktalni stil. Pravila podjele koriste se u arhitekturi, biologiji i informatici, kao iu proučavanju hiperboličkih mnogoznačnika. Zamjene pločica su dobro proučena vrsta pravila podjele.

Peano krivulja

Peano krivulja je opći naziv za parametarske krivulje čija slika sadrži kvadrat (ili, općenito, otvorene dijelove prostora). Drugi naziv je krivulja popunjavanja prostora.

Nazvana po Giuseppeu Peanu (1858.-1932.), pronalazaču ove vrste krivulje, Peanova krivulja je naziv dat specifičnoj krivulji koju je Peano pronašao.

Sierpinski krivulja

Sierpinskijevih krivulja je rekurzivno definiran niz kontinuiranih zatvorenih ravninskih fraktalnih krivulja koje je otkrio Waclaw Sierpinski. Krivulja u granici na potpuno ispunjava jedinični kvadrat, pa se granična krivulja, također naziva Sierpinski krivulja, je primjer krivulja koje ispunjavaju prostor.

Budući da krivulja Sierpinskog ispunjava prostor, njena Hausdorffova dimenzija (u granici pri n → ∞ (\displaystyle n\rightarrow \infty )) jednako je 2 (\displaystyle 2).
Duljina euklidske krivulje

jednak l n = 2 3 (1 + 2) 2 n − 1 3 (2 − 2) 1 2 n (\displaystyle l_(n)=(2 \preko 3)(1+(\sqrt (2)))2^( n)-(1 \preko 3)(2-(\sqrt (2)))(1 \preko 2^(n))),

tj. raste eksponencijalno Po n (\displaystyle n), a granica na n → ∞ (\displaystyle n\rightarrow \infty ) područje područja koje zatvara krivulja S n (\displaystyle S_(n)), je 5/12 (\displaystyle 5/12) kvadrat (u euklidskoj metrici).

Logaritam

Logaritam broja b (\displaystyle b) na temelju a (\displaystyle a) (iz starogrčkog. λόγος "riječ; stav" + ἀριθμός "broj") je definiran kao pokazatelj snage na koju se baza mora podići a (\displaystyle a) da dobijem broj b (\displaystyle b). Oznaka: log a ⁡ b (\displaystyle \log _(a)b), izgovara se: " logaritam b (\displaystyle b) na temelju a (\displaystyle a) ».

Iz definicije proizlazi da nalaz x = log a ⁡ b (\displaystyle x=\log _(a)b) je ekvivalentan rješavanju jednadžbe a x = b (\displaystyle a^(x)=b). Na primjer, log 2 ⁡ 8 = 3 (\displaystyle \log _(2)8=3), jer 2 3 = 8 (\displaystyle 2^(3)=8).

Izračunavanje logaritma naziva se logaritmom. Brojke a , b (\displaystyle a,b) najčešće pravi, ali postoji i teorija kompleksnih logaritama.

Logaritmi imaju jedinstvena svojstva koja su odredila njihovu široku upotrebu za značajno pojednostavljenje radno intenzivnih izračuna. Kad prijeđemo "u svijet logaritama", množenje se zamjenjuje mnogo jednostavnijim zbrajanjem, dijeljenje se zamjenjuje oduzimanjem, a potenciranje i vađenje korijena pretvaraju se u množenje i dijeljenje s eksponentom. Laplace je rekao da je izum logaritama, "skrativši astronomov rad, udvostručio njegov život."

Definiciju logaritama i tablicu njihovih vrijednosti (za trigonometrijske funkcije) prvi put je objavio 1614. škotski matematičar John Napier. Logaritamske tablice, koje su proširili i doradili drugi matematičari, naširoko su se koristile za znanstvene i inženjerske proračune više od tri stoljeća, sve do pojave elektroničkih kalkulatora i računala.

S vremenom je postalo jasno da logaritamska funkcija y = log a ⁡ x (\displaystyle y=\log _(a)x) je nezamjenjiv u mnogim drugim područjima ljudske djelatnosti: rješavanje diferencijalnih jednadžbi, klasifikacija vrijednosti veličina (primjerice, frekvencija i intenzitet zvuka), aproksimacija raznih ovisnosti, teorija informacija, teorija vjerojatnosti itd. Ova funkcija je jedna od one elementarne, to je inverzna eksponencijalnoj funkciji. Najčešće se koriste realni logaritmi s bazama 2 (\displaystyle 2)(binarni), e (\displaystyle e) (prirodni logaritam) i 10 (\displaystyle 10)(decimal).

Nanotehnologija temeljena na DNK

DNA nanotehnologija je razvoj i proizvodnja umjetnih struktura od nukleinskih kiselina za tehnološku uporabu. U ovom znanstvenom području nukleinske kiseline se koriste ne kao nositelji genetske informacije u živim stanicama, već kao materijal za potrebe nebiološkog inženjeringa nanomaterijala.

Tehnologija koristi stroga pravila za uparivanje baza nukleinskih kiselina, koja dopuštaju da se samo dijelovi lanaca s komplementarnim sekvencama baza međusobno povežu kako bi se stvorila snažna, kruta struktura dvostruke spirale. Iz ovih pravila postaje moguće konstruirati sekvence baza koje će se selektivno sastavljati da tvore složene ciljne strukture s precizno podešenim oblicima i svojstvima nanomjere. Većina materijala izrađena je korištenjem DNK, ali izgrađene su i strukture koje uključuju druge nukleinske kiseline kao što su RNK i peptidne nukleinske kiseline (PNA), što omogućuje da se tehnološko polje nazove "nanotehnologija na bazi nukleotida".

Osnovni koncept nanotehnologije koja se temelji na DNK prvi je predložio početkom 1980-ih Nadrian Seaman, a ovo istraživačko područje počelo je privlačiti veliki interes sredinom 2000-ih. Istraživači koji rade u ovom novom polju tehnologije stvorili su statične strukture kao što su dvodimenzionalne i trodimenzionalne kristalne rešetke, nanocijevi, poliedri i drugi slobodni oblici, kao i funkcionalne strukture kao što su molekularni strojevi i DNK računala.

Za sastavljanje ovih struktura koriste se različite tehnike, uključujući strukturiranje pločica, gdje se pločice sastavljaju od manjih struktura, sklopive strukture stvorene tehnikom DNK origamija i dinamički preuređene strukture stvorene tehnikama pomaka niti. Područje istraživanja počinje se koristiti kao alat za rješavanje osnovnih znanstvenih problema u poljima strukturne biologije i biofizike, uključujući primijenjene probleme kristalografije i spektroskopije za određivanje strukture proteina. Istraživanja su također u tijeku za potencijalne primjene u skalabilnoj molekularnoj elektronici i nanomedicini.

Prirodni logaritam

Prirodni logaritam je logaritam baze e, Gdje e (\displaystyle e)- iracionalna konstanta jednaka približno 2,72. Označava se kao ln ⁡ x (\displaystyle \ln x), log e ⁡ x (\displaystyle \log _(e)x) ili ponekad samo log ⁡ x (\displaystyle \log x), ako je baza e (\displaystyle e) podrazumijeva se. Obično broj x (\displaystyle x) pod znakom logaritma je realan, ali ovaj koncept se može proširiti na kompleksne brojeve.

Iz definicije proizlazi da je logaritamska ovisnost inverzna funkcija za eksponencijalnu y = e x (\displaystyle y=e^(x)), stoga su njihovi grafovi simetrični u odnosu na simetralu prvog i trećeg kvadranta (vidi sliku desno). Kao i eksponencijalna funkcija, logaritamska funkcija pripada kategoriji transcendentnih funkcija.

Prirodni logaritmi korisni su za rješavanje algebarskih jednadžbi u kojima je nepoznanica prisutna kao eksponent, a nezaobilazni su u matematičkoj analizi. Na primjer, logaritmi se koriste za pronalaženje konstante raspada za poznato vrijeme poluraspada ili za pronalaženje vremena raspada u rješavanju problema radioaktivnosti. Igraju važnu ulogu u mnogim područjima matematike i primijenjenih znanosti, a koriste se u financijama za rješavanje mnogih problema, uključujući pronalaženje složenih kamata.

Lebesgueova dimenzija

Lebesgueova dimenzija ili topološka dimenzija- dimenzija definirana pokrovima, najvažnija invarijanta topološkog prostora. Lebegova dimenzija prostora X (\displaystyle X) obično označeno dim ⁡ X (\displaystyle \dim X).

Rekurzija

Rekurzija je definicija, opis, slika objekta ili procesa unutar tog objekta ili samog procesa, odnosno situacija kada je objekt dio samog sebe. Pojam "rekurzija" koristi se u raznim specijaliziranim područjima znanja - od lingvistike do logike, ali se najviše koristi u matematici i informatici.

Sierpinski, Waclaw

Wacław Franciszek Sierpiński, u drugoj transkripciji - Sierpiński (polj. Wacław Franciszek Sierpiński; 14. ožujka 1882., Varšava - 21. listopada 1969., ibid.) - poljski matematičar i učitelj, poznat po svojim radovima o teoriji skupova, aksiomu izbora, hipoteza kontinuuma, teorija brojeva, teorija funkcija i topologija. Autor 724 članka i 50 knjiga.

Tetraedar (Bottrop)

Tetraedar (njemački: Tetraeder) je čelična konstrukcija u obliku tetraedra s rubom duljine 60 m, poduprta s četiri betonska nosača od 9 metara, koja se koristi kao osmatračnica, u gradu Bottropu (Sjeverna Rajna-Vestfalija) . Tetraedar se nalazi na vrhu gomile otpada Beckstraße (njemački: Beckstraße) rudnika Prosper-Haniel (de: Bergwerk Prosper-Haniel) na nadmorskoj visini od 105 m. S najvišeg vidikovca možete vidjeti pogled na gradove Bottrop, Essen, Oberhausen, Gladbeck. Uz dobru vidljivost, domet gledanja doseže 40 km i čak vam omogućuje razlikovanje televizijskog tornja Rheinturm u Düsseldorfu.

Bottrop Tetrahedron je tematska točka regionalnog projekta "Put industrijske kulture" regije Ruhr.

Pascalov trokut

Pascalov trokut je beskonačna tablica binomnih koeficijenata trokutastog oblika. U ovom trokutu postoje jedan na vrhu i na stranama. Svaki broj jednak je zbroju dvaju brojeva iznad njega. Crte trokuta su simetrične u odnosu na okomitu os. Ime je dobio po Blaiseu Pascalu. Brojevi koji čine Pascalov trokut prirodno se pojavljuju u algebri, kombinatorici, teoriji vjerojatnosti, matematičkoj analizi i teoriji brojeva.

Fraktal

Fraktal (lat. fractus - smrvljen, razbijen, razbijen) je skup koji ima svojstvo samosličnosti (objekt koji se točno ili približno poklapa s dijelom sebe, odnosno cjelina ima isti oblik kao jedan ili više dijelovi). Fraktali se u matematici shvaćaju kao skupovi točaka u euklidskom prostoru koji imaju frakcijsku metričku dimenziju (u smislu Minkowskog ili Hausdorffa), odnosno metričku dimenziju različitu od topološke, pa ih treba razlikovati od ostalih geometrijskih likova ograničenih konačan broj veza. Samoslični likovi koji se ponavljaju konačan broj puta nazivaju se prefraktali.

Prvi primjeri samosličnih skupova s ​​neobičnim svojstvima pojavili su se u 19. stoljeću kao rezultat proučavanja kontinuiranih nediferencijabilnih funkcija (na primjer, Bolzanova funkcija, Weierstrassova funkcija, Cantorov skup). Pojam "fraktal" uveo je Benoit Mandelbrot 1975. godine, a postao je široko poznat objavljivanjem njegove knjige "Fraktalna geometrija prirode" 1977. godine. Fraktali su posebnu popularnost stekli razvojem računalnih tehnologija koje su omogućile učinkovitu vizualizaciju ovih struktura.

Riječ "fraktal" ne koristi se samo kao matematički pojam. Fraktalom se može nazvati objekt koji ima barem jedno od sljedećih svojstava:

Ima netrivijalnu strukturu na svim razinama. Ovo je u suprotnosti s pravilnim figurama (kao što su krug, elipsa, graf glatke funkcije): ako uzmete u obzir mali fragment pravilne figure u vrlo velikom mjerilu, izgledat će kao fragment ravne linije. Za fraktal povećanje mjerila ne dovodi do pojednostavljenja strukture, odnosno na svim mjerilima možete vidjeti jednako složenu sliku.

Je sebi sličan ili približno sebi sličan.

Ima frakcijsku metričku dimenziju ili metričku dimenziju koja prelazi topološku Mnogi objekti u prirodi imaju fraktalna svojstva, npr.: obale, oblaci, krošnje drveća, snježne pahulje, krvožilni sustav, alveole.

Fraktalna dimenzija

Fraktalna dimenzija(engleski fractal dimension) - jedan od načina određivanja dimenzije skupa u metričkom prostoru. Fraktalna dimenzija n-dimenzionalni skup se može definirati pomoću formule:

D = − lim ε → 0 ln ⁡ (N ε) ln ⁡ (ε) (\displaystyle D=-\lim \limits _(\varepsilon \to 0)(\frac (\ln(N_(\varepsilon ))) (\ln(\varepsilon)))), Gdje N ε (\displaystyle N_(\varepsilon ))- minimalni broj n-dimenzionalne “lopte” radijusa ε (\displaystyle \varepsilon), potrebno za pokrivanje seta.

Fraktalna dimenzija može imati numeričku vrijednost koja nije cijeli broj.

Osnovna ideja razlomljene dimenzije ima dugu povijest u polju matematike, ali je sam pojam skovao Benoit Mandelbrot 1967. u svom članku o samosličnosti, u kojem je opisao frakcijsku dimenziju. U ovom se članku Mandelbrot osvrnuo na prethodni rad Lewisa Fryja Richardsona koji opisuje kontraintuitivnu ideju da izmjerena duljina obale ovisi o duljini mjernog štapa (vidi sliku 1). Slijedeći ovu ideju, fraktalna dimenzija obalne crte odgovara omjeru broja polova (u određenom mjerilu) potrebnih za mjerenje duljine obalne crte i odabranog mjerila pola. Postoji nekoliko formalnih matematičkih definicija [⇨] fraktalne dimenzije koje se grade na ovom osnovnom konceptu promjene elementa s promjenom razmjera.

Jedan elementarni primjer je fraktalna dimenzija Kochove pahulje. Njena topološka dimenzija je 1, ali nipošto nije ispravljajuća krivulja, budući da je duljina krivulje između bilo koje dvije točke Kochove pahulje beskonačna. Nijedan dio krivulje, koliko god malen bio, nije segment ravne linije. Umjesto toga, Kochova pahulja sastoji se od beskonačnog broja segmenata povezanih pod različitim kutovima. Fraktalna dimenzija krivulje može se intuitivno objasniti sugerirajući da je fraktalna linija objekt previše detaljan (detaljan) da bi bio jednodimenzionalan, ali nedovoljno složen da bi bio dvodimenzionalan. Stoga je njegovu dimenziju bolje opisati ne uobičajenom topološkom dimenzijom 1, već njegovom fraktalnom dimenzijom, koja je u ovom slučaju jednaka broju koji leži u intervalu između 1 i 2.

Fraktalna umjetnost

Fraktalna umjetnost oblik je algoritamske umjetnosti stvoren računanjem fraktalnih objekata i predstavljanjem rezultata izračuna kao nepokretnih slika, animacija i automatski generiranih medijskih datoteka. Fraktalna umjetnost započela je sredinom 1980-ih. To je žanr računalne umjetnosti i digitalne umjetnosti koji je dio novomedijske umjetnosti. Ujedno, fraktalna umjetnost jedno je od područja tzv. “znanstvene umjetnosti”.

Fraktalna umjetnost rijetko se stvara ručno. Obično se neizravno stvara softverom koji generira fraktale kroz tri koraka: postavljanje parametara odgovarajućeg fraktalnog softvera; izvođenje eventualno dugotrajnih izračuna; i ocjene proizvoda. U nekim se slučajevima za daljnju obradu generiranih slika koriste drugi grafički programi. U umjetničko djelo mogu se uključiti i nefraktalne slike. Julijin set i Mandelbrotov set smatraju se ikonama fraktalne umjetnosti.

Karakteristike
Najjednostavniji fraktali

Da biste ga dobili, trebate uzeti (jednakostranični) trokut s unutrašnjosti, nacrtati središnje linije u njemu i izbaciti središnji od četiri mala trokuta koja su nastala. Zatim iste korake treba ponoviti sa svakim od preostala tri trokuta itd. Na slici su prikazana prva tri koraka, a u flash demonstraciji možete vježbati i dobivati ​​korake do desetog.

Izbacivanje središnjih trokuta nije jedini način da se dobije trokut Sierpinskog. Možete se kretati "u suprotnom smjeru": uzmite inicijalno "prazan" trokut, zatim dovršite trokut koji čine srednje linije u njemu, zatim učinite isto u svakom od tri kutna trokuta, itd. U početku će figure biti vrlo različiti, ali s povećanjem broja iteracija, postajat će sve sličniji jedni drugima, au granici će se podudarati.

Sljedeći način dobivanja trokuta Sierpinskog još je sličniji uobičajenoj shemi za konstrukciju geometrijskih fraktala zamjenom dijelova sljedeće iteracije skaliranim fragmentom. Ovdje se u svakom koraku segmenti koji čine izlomljenu liniju zamjenjuju isprekidanom linijom od tri veze (ona se sama dobiva u prvoj iteraciji). Morate položiti ovu isprekidanu liniju naizmjenično udesno, a zatim ulijevo. Vidi se da je već osma iteracija vrlo blizu fraktalu, a što dalje odmiče, linija će mu se više približavati.

Ali to nije sve. Ispada da je trokut Sierpinskog dobiven kao rezultat jedne od varijanti slučajnog hoda točke na ravnini. Ova metoda se zove "Igra kaosa". Uz njegovu pomoć možete izgraditi neke druge fraktale.

Bit "igre" je ovo. Pravilni trokut je fiksiran na ravnini A 1 A 2 A 3. Označite bilo koju početnu točku B 0 . Zatim nasumično odaberite jedan od tri vrha trokuta i označite točku B 1 - sredina segmenta s krajevima na ovom vrhu i na B 0 (na slici desno, vrh je odabran nasumično A 1). Isto se ponavlja s točkom B 1 dobiti B 2. Tada dobivaju bodove B 3 , B 4 itd. Bitno je da točka slučajno “skače”, odnosno da se svaki put nasumično izabere vrh trokuta, neovisno o tome što je odabrano u prethodnim koracima. Nevjerojatno je da ako označite točke iz niza B i, tada će se uskoro početi pojavljivati ​​trokut Sierpinskog. Dolje je prikazano što se događa kada se označi 100, 500 i 2500 bodova.

Neka svojstva

Mogućnosti

Tepih (kvadrat, salveta) Sierpinski.Četvrtastu verziju opisao je Wacław Sierpinski 1916. Uspio je dokazati da je svaka krivulja koja se može nacrtati na ravnini bez samosjecišta homeomorfna nekom podskupu ovog rupičastog kvadrata. Kao i trokut, kvadrat se može napraviti od različitih dizajna. Desno je klasična metoda: podjela kvadrata na 9 dijelova i odbacivanje središnjeg dijela. Zatim se isto ponavlja za preostalih 8 kvadrata, itd.

Kao i trokut, kvadrat ima nultu površinu. Fraktalna dimenzija Sierpinski tepiha jednaka je log 3 8, izračunato slično dimenziji trokuta.

Piramida Sierpinski. Jedan od trodimenzionalnih analoga trokuta Sierpinskog. Konstruira se na sličan način, uzimajući u obzir trodimenzionalnost onoga što se događa: 5 kopija početne piramide, dva puta komprimirane, čine prvu iteraciju, njenih 5 kopija će činiti drugu iteraciju, itd. Fraktal dimenzija je jednaka log 2 5. Slika ima nula volumena (u svakom koraku se izbacuje polovica volumena), ali u isto vrijeme površina je očuvana iz iteracije u iteraciju, a za fraktal je ista kao za početna piramida.

Mengerova spužva. Generalizacija tepiha Sierpinskog u trodimenzionalni prostor. Za izgradnju spužve potrebno je beskrajno ponavljanje postupka: svaka od kockica koje čine iteraciju dijeli se na 27 tri puta manjih kockica, iz kojih se izbacuje središnja i njenih 6 susjednih. Odnosno, svaka kocka generira 20 novih, tri puta manjih. Stoga je fraktalna dimenzija log 3 20. Ovaj fraktal je univerzalna krivulja: svaka krivulja u trodimenzionalnom prostoru homeomorfna je nekom podskupu spužve. Spužva ima nula volumena (jer se u svakom koraku množi s 20/27), ali ima beskrajno veliku površinu.

L
Omanska linija:

N – broj segmenata, veličina A.

D – “stupanj savijanja”

N=(l/a)D; S=N*a; S=(1/a)D-1

DO
Riva Koch

2) N=4L=1/3S(4)=4/3

N=16 L=1/9S(16)=16/9

Fraktalna dimenzija:

D=lg4 /lg3=1,26…

Fraktalna dimenzija skupa

Volumen fraktala u svom prostor za ugradnju je uvijek nula. On, međutim, može biti različit od nule u prostoru niže dimenzije. Da bismo odredili dimenziju ovog prostora D, ajmo sve razbiti n-dimenzionalni prostor u male kocke s duljinom ruba ε i volumen ε n- Sl. 1. Neka N(ε ) je najmanji broj kockica koje zajedno potpuno pokrivaju fraktalni skup, tada po definiciji

Postojanje ove granice znači da je fraktalni volumen konačan D-dimenzionalni prostor: s malim ε

a za razliku od uobičajene dimenzije D može biti frakcijska vrijednost, što je najčešće za fraktalne skupove.

Očito, za obične skupove ova definicija dovodi do dobro poznatih rezultata. Dakle za mnoštvo N izolirane točke imamo N(ε ) =N i stoga

Za segment je dovoljna glatka linija dužine L:N(ε ) =L/ε i stoga D= 1. Za mjesto S dvodimenzionalna površina: N(ε ) =S/ε 2 i D= 2 itd.

Rekurzivni algoritam za konstruiranje konstruktivnih fraktala.

1. trokut Sierpinskog

trokut Sierpinskog

trokut Sierpinskog- fraktal, jedan od dvodimenzionalnih analoga Cantorovog skupa koji je predložio poljski matematičar Sierpinski 1915. godine. Poznata i kao "mreža" Sierpinskog ili "salveta".

Izgradnja

Uzima se puni jednakostranični trokut, au prvom koraku unutrašnjost srednjeg trokuta uklanja se iz središta. U drugom koraku, tri srednja trokuta se uklanjaju iz tri preostala trokuta, itd. Nakon beskonačnog ponavljanja ovog postupka, ostaje podskup punog trokuta - trokut Sierpinskog.

Konstrukcija trokuta Sierpinskog

Trokut Sierpinskog također se može dobiti pomoću sljedećeg algoritma:

Uzmite tri točke na ravnini i nacrtajte trokut.

Nasumično odaberite bilo koju točku unutar trokuta i pomaknite polovicu udaljenosti od te točke do bilo kojeg od tri vrha trokuta.

Označite trenutnu poziciju.

Ponovite od koraka 2.

Koncepti fraktala i fraktalne geometrije, koji su se pojavili u kasnim 70-ima, čvrsto su se ustalili među matematičarima i programerima od sredine 80-ih. Riječ fraktal izvedena je iz latinskog fractus i znači sastavljen od fragmenata. Predložio ju je Benoit Mandelbrot 1975. da se odnosi na nepravilne, ali sebi slične strukture kojima se on bavio. Rođenje fraktalne geometrije obično se povezuje s objavljivanjem Mandelbrotove knjige “Fraktalna geometrija prirode” 1977. Njegovi su radovi koristili znanstvene rezultate drugih znanstvenika koji su u razdoblju 1875.-1925. radili na istom području (Poincaré, Fatou, Julia, Cantor, Hausdorff Ali tek je u naše vrijeme bilo moguće kombinirati njihov rad u jedinstveni sustav.
Uloga fraktala u računalnoj grafici danas je prilično velika. Oni dolaze u pomoć, na primjer, kada je potrebno, koristeći nekoliko koeficijenata, definirati linije i površine vrlo složenih oblika. Sa stajališta računalne grafike, fraktalna geometrija je nezamjenjiva pri generiranju umjetnih oblaka, planina i morskih površina. Zapravo, pronađen je način za jednostavno predstavljanje složenih neeuklidskih objekata, čije su slike vrlo slične prirodnim.
Jedno od glavnih svojstava fraktala je samosličnost. U najjednostavnijem slučaju mali dio fraktala sadrži informacije o cijelom fraktalu. Mandelbrotova definicija fraktala je: "Fraktal je struktura koja se sastoji od dijelova koji su na neki način slični cjelini."

Postoji veliki broj matematičkih objekata koji se nazivaju fraktali (trokut Sierpinskog, Kochova pahulja, Peanova krivulja, Mandelbrotov skup i Lorentzovi atraktori). Fraktali s velikom točnošću opisuju mnoge fizičke pojave i formacije stvarnog svijeta: planine, oblake, turbulentne (vrtložne) tokove, korijenje, grane i lišće drveća, krvne žile, što je daleko od odgovaranja jednostavnim geometrijskim figurama. Benoit Mandelbrot prvi je put progovorio o fraktalnoj prirodi našeg svijeta u svom temeljnom djelu “Fraktalna geometrija prirode”.
Pojam fraktal uveo je Benoit Mandelbrot 1977. godine u svom temeljnom djelu Fraktali, oblik, kaos i dimenzija. Prema Mandelbrotu, riječ fraktal dolazi od latinskih riječi fractus - razlomak i frangere - razbiti, što odražava bit fraktala kao "izlomljenog", nepravilnog skupa.

Klasifikacija fraktala.

Za to Kako bismo predstavili čitavu raznolikost fraktala, zgodno je pribjeći njihovoj općeprihvaćenoj klasifikaciji. Postoje tri klase fraktala.

1. Geometrijski fraktali.

Fraktali ove klase su najvizualniji. U dvodimenzionalnom slučaju dobivaju se pomoću izlomljene linije (ili plohe u trodimenzionalnom slučaju), koja se naziva generator. U jednom koraku algoritma, svaki od segmenata koji čine isprekidanu liniju zamjenjuje se sa polilinija-generator u odgovarajućem mjerilu. Kao rezultat beskrajnog ponavljanja ovog postupka dobiva se geometrijski fraktal.

Pogledajmo primjer jednog od ovih fraktalnih objekata - trijadnu Kochovu krivulju.

Konstrukcija trijadne Kochove krivulje.

Uzmimo ravni isječak duljine 1. Nazovimo ga sjeme. Podijelimo sjeme na tri jednaka dijela duljine 1/3, odbacimo srednji dio i zamijenimo ga isprekidanom linijom od dvije karike duljine 1/3.

Dobit ćemo isprekidanu liniju koja se sastoji od 4 veze ukupne duljine 4/3, pa zovemo prva generacija.

Kako bi se prešlo na sljedeću generaciju Kochove krivulje, potrebno je odbaciti i zamijeniti srednji dio svake karike. Prema tome, duljina druge generacije bit će 16/9, treće - 64/27. nastavimo li ovaj proces ad infinitum, rezultat je trijadna Kochova krivulja.

Razmotrimo sada svojstva trijadičke Kochove krivulje i saznajmo zašto su fraktali nazvani "čudovištima".

Prvo, ova krivulja nema duljinu - kao što smo vidjeli, s brojem generacija njezina duljina teži beskonačnosti.

Drugo, nemoguće je konstruirati tangentu na ovu krivulju - svaka njena točka je točka infleksije u kojoj izvodnica ne postoji - ova krivulja nije glatka.

Duljina i glatkoća temeljna su svojstva krivulja, koja proučavaju i Euklidska geometrija i geometrija Lobačevskog i Riemanna. Pokazalo se da tradicionalne metode geometrijske analize nisu primjenjive na trijadnu Kochovu krivulju, pa se Kochova krivulja pokazala kao čudovište - "čudovište" među glatkim stanovnicima tradicionalnih geometrija.

Izgradnja Harter-Haithway "zmaja".

Da biste dobili još jedan fraktalni objekt, morate promijeniti pravila konstrukcije. Neka oblikovni element budu dva jednaka segmenta povezana pod pravim kutom. U nultoj generaciji zamijeni jedinični segment s ovaj element oblikovanja tako da je kut na vrhu. Možemo reći da takvom zamjenom dolazi do pomaka sredine veze. Pri izradi sljedećih generacija slijedi pravilo: prva karika s lijeve strane zamjenjuje se elementom za oblikovanje tako da se sredina karike pomakne ulijevo od smjera kretanja, a kod zamjene sljedećih karika smjerovi pomicanje sredina segmenata mora se izmjenjivati. Na slici je prikazano prvih nekoliko generacija i 11. generacija krivulje izgrađena prema gore opisanom principu. Krivulja s n koja teži beskonačnosti naziva se Harter-Haithawayev zmaj.
U računalnoj je grafici uporaba geometrijskih fraktala nužna pri dobivanju slika drveća i grmlja. Dvodimenzionalni geometrijski fraktali koriste se za stvaranje trodimenzionalnih tekstura (uzorci na površini predmeta).

2.Algebarski fraktali

Ovo je najveća skupina fraktala. Dobivaju se korištenjem nelinearnih procesa u n-dimenzionalnim prostorima. Najviše se proučavaju dvodimenzionalni procesi. Kada se nelinearni iterativni proces tumači kao diskretni dinamički sustav, može se koristiti terminologija teorije ovih sustava: fazni portret, stacionarni proces, atraktor itd.
Poznato je da nelinearni dinamički sustavi imaju nekoliko stabilnih stanja. Stanje u kojem se dinamički sustav nalazi nakon određenog broja ponavljanja ovisi o njegovom početnom stanju. Stoga svako stabilno stanje (ili, kako se kaže, atraktor) ima određeno područje početnih stanja, iz kojih će sustav nužno pasti u konačna stanja koja se razmatraju. Tako je fazni prostor sustava podijeljen na područja privlačenja atraktora. Ako je fazni prostor dvodimenzionalni prostor, tada se bojanjem područja privlačnosti različitim bojama može dobiti fazni portret u boji ovog sustava (iterativni proces). Promjenom algoritma odabira boja možete dobiti složene fraktalne uzorke s bizarnim višebojnim uzorcima. Iznenađenje za matematičare bila je sposobnost generiranja vrlo složenih netrivijalnih struktura korištenjem primitivnih algoritama.

Mandelbrotov set.

Kao primjer, razmotrite Mandelbrotov skup. Algoritam za njegovu konstrukciju prilično je jednostavan i temelji se na jednostavnom iterativnom izrazu: Z = Z * Z + C, Gdje Zi I C- složene varijable. Iteracije se izvode za svaku početnu točku iz pravokutnog ili kvadratnog područja - podskupa kompleksne ravnine. Iterativni proces se nastavlja sve dok Z neće izaći izvan kruga polumjera 2 čije središte leži u točki (0,0), (to znači da je atraktor dinamičkog sustava u beskonačnosti), ili nakon dovoljno velikog broja ponavljanja (npr. , 200-500) Zće konvergirati u neku točku na krugu. Ovisno o broju ponavljanja tijekom kojih Z ostane unutar kruga, možete postaviti boju točke C(Ako Z ostaje unutar kruga za dovoljno velik broj ponavljanja, proces ponavljanja se zaustavlja i ta rasterska točka se boji crno).

3. Stohastički fraktali

Još jedna dobro poznata klasa fraktala su stohastički fraktali, koji se dobivaju ako se neki od njegovih parametara nasumično mijenjaju u iterativnom procesu. U ovom slučaju, dobiveni objekti vrlo su slični prirodnim - asimetrična stabla, neravne obale itd. Dvodimenzionalni stohastički fraktali koriste se u modeliranju terena i površine mora.
Postoje i druge klasifikacije fraktala, na primjer, dijeljenje fraktala na determinističke (algebarske i geometrijske) i nedeterminističke (stohastičke).

O upotrebi fraktala

Prije svega, fraktali su područje nevjerojatne matematičke umjetnosti, kada se uz pomoć najjednostavnijih formula i algoritama dobivaju slike izuzetne ljepote i složenosti! Lišće, drveće i cvijeće često su vidljivi u konturama konstruiranih slika.

Neke od najmoćnijih primjena fraktala nalaze se u računalnoj grafici. Prvo, to je fraktalna kompresija slika, a drugo, konstrukcija krajolika, drveća, biljaka i stvaranje fraktalnih tekstura. Moderna fizika i mehanika tek počinju proučavati ponašanje fraktalnih objekata. I, naravno, fraktali se izravno koriste u samoj matematici.
Prednosti algoritama fraktalne kompresije slike su vrlo mala veličina zapakirane datoteke i kratko vrijeme oporavka slike. Fraktalno upakirane slike mogu se skalirati bez uzrokovanja pikselizacije. Ali proces kompresije traje dugo i ponekad traje satima. Algoritam fraktalnog pakiranja s gubitkom omogućuje vam postavljanje omjera kompresije, slično jpeg formatu. Algoritam se temelji na traženju velikih dijelova slike koji su slični nekim malim dijelovima. I samo koji je komad sličan kojem se upisuje u izlaznu datoteku. Prilikom sažimanja obično se koristi kvadratna mreža (komadi su kvadrati), što dovodi do blagog kuta pri vraćanju slike; šesterokutna mreža nema taj nedostatak.
Iterated je razvio novi format slike, "Sting", koji kombinira fraktalnu i "valnu" (kao što je jpeg) kompresiju bez gubitaka. Novi format omogućuje vam stvaranje slika s mogućnošću naknadnog visokokvalitetnog skaliranja, a volumen grafičkih datoteka iznosi 15-20% volumena nekomprimiranih slika.
Sklonost fraktala da nalikuju planinama, cvijeću i drveću iskorištavaju neki grafički urednici, na primjer, fraktalni oblaci iz 3D studija MAX, fraktalne planine u World Builderu. Fraktalna stabla, planine i cijeli krajolici definirani su jednostavnim formulama, lako ih je programirati i ne raspadaju se u zasebne trokute i kocke kada im se približi.
Ne može se zanemariti korištenje fraktala u samoj matematici. U teoriji skupova, Cantorov skup dokazuje postojanje savršenih nigdje gustih skupova; u teoriji mjere, samoafina funkcija "Cantorove ljestve" dobar je primjer distribucijske funkcije singularne mjere.
U mehanici i fizici fraktali se koriste zbog svog jedinstvenog svojstva ponavljanja obrisa mnogih prirodnih objekata. Fraktali vam omogućuju aproksimaciju drveća, planinskih površina i pukotina s većom točnošću nego aproksimacije pomoću skupova segmenata ili poligona (s istom količinom pohranjenih podataka). Fraktalni modeli, kao i prirodni objekti, imaju “hrapavost”, a to svojstvo je očuvano bez obzira koliko je veliko povećanje modela. Prisutnost jedinstvene mjere na fraktalima omogućuje primjenu integracije, teorije potencijala i njihovu upotrebu umjesto standardnih objekata u već proučavanim jednadžbama.
Fraktalnim pristupom kaos prestaje biti plavi nered i dobiva finu strukturu. Fraktalna znanost je još uvijek vrlo mlada i pred njom je velika budućnost. Ljepota fraktala ni izdaleka nije iscrpljena i tek će nam podariti mnoga remek-djela - ona koja oduševljavaju oko, i ona koja donose pravi užitak umu.

O konstruiranju fraktala

Metoda sukcesivne aproksimacije

Gledajući ovu sliku, nije teško razumjeti kako možete izgraditi sebi sličan fraktal (u ovom slučaju piramidu Sierpinskog). Trebamo uzeti pravilnu piramidu (tetraedar), zatim izrezati njenu sredinu (oktaedar), što rezultira četiri male piramide. Sa svakim od njih izvodimo istu operaciju itd. Ovo je pomalo naivno, ali jasno objašnjenje.

Razmotrimo strože suštinu metode. Neka postoji neki IFS sustav, t.j. sustav mapiranja kompresije S=(S 1 ,...,S m ) S i:R n ->R n (na primjer, za našu piramidu preslikavanja izgledaju kao S i (x )=1/2*x+o i , gdje su o i vrhovi tetraedra, i=1,..,4). Zatim izaberemo neki kompaktni skup A 1 u R n (u našem slučaju izaberemo tetraedar). I indukcijom odredimo niz skupova A k:A k+1 =S 1 (A k ) U...U S m (A k ). Poznato je da skupovi A k s porastom k sve bolje aproksimiraju željeni atraktor sustava S.

Imajte na umu da je svaka od ovih iteracija atraktor rekurentni sustav iteriranih funkcija(engleski izraz Digraf IFS, RIFS I također Grafom usmjereno IFS) i stoga ih je lako izgraditi pomoću našeg programa.

Točka po točka ili probabilistička metoda

Ovo je najlakši način za implementaciju na računalu. Radi jednostavnosti, razmatramo slučaj ravnog samoafinog skupa. Dakle, neka je (S 1,..,S m) neki sustav afinih kontrakcija. Preslikavanja S i mogu se predstaviti u obliku: S i (x)=A i (x-o i)+o i, gdje je A i fiksna matrica veličine 2x2, a o i je dvodimenzionalni vektor stupac.

· Uzmimo fiksnu točku prvog preslikavanja S 1 kao početnu točku:
x : = o1;
Ovdje koristimo činjenicu da sve fiksne točke kompresije S 1 ,..,S m pripadaju fraktalu. Možete odabrati proizvoljnu točku kao početnu točku i niz točaka koje ona generira bit će nacrtan u fraktal, ali tada će se na ekranu pojaviti nekoliko dodatnih točaka.

· Označimo trenutnu točku x= (x 1 ,x 2) na ekranu:
putpixel(x 1 ,x 2 ,15);

· Odaberimo nasumično broj j od 1 do m i preračunajmo koordinate točke x:
j:=Slučajni (m)+1;
x:=S j (x);

· Idemo na korak 2 ili, ako smo napravili dovoljno velik broj ponavljanja, zaustavljamo se.
Bilješka. Ako su omjeri kompresije preslikavanja S i različiti, tada će fraktal biti neravnomjerno ispunjen točkama. Ako su preslikavanja S i slična, to se može izbjeći laganim kompliciranjem algoritma. Da bi se to postiglo, u 3. koraku algoritma, broj j od 1 do m mora biti izabran s vjerojatnostima p 1 =r 1 s,..,p m =r m s, gdje r i označavaju koeficijente kompresije preslikavanja Si, i broj s (koji se naziva dimenzija sličnosti) nalazi se iz jednadžbe r 1 s +...+r m s =1. Rješenje ove jednadžbe može se pronaći, primjerice, Newtonovom metodom.

O fraktalima i njihovim algoritmima

Fraktal dolazi od latinskog pridjeva "fractus", au prijevodu znači koji se sastoji od fragmenata, a odgovarajući latinski glagol "frangere" znači lomiti, odnosno stvarati nepravilne fragmente. Koncepti fraktala i fraktalne geometrije, koji su se pojavili u kasnim 70-ima, čvrsto su se ustalili među matematičarima i programerima od sredine 80-ih. Izraz je skovao Benoit Mandelbrot 1975. kako bi se odnosio na nepravilne, ali sebi slične strukture kojima se bavio. Rođenje fraktalne geometrije obično se povezuje s objavljivanjem Mandelbrotove knjige “Fraktalna geometrija prirode” 1977. godine. U svojim radovima koristio je znanstvene rezultate drugih znanstvenika koji su u razdoblju 1875.-1925. djelovali na istom području (Poincaré, Fatou, Julia, Cantor, Hausdorff).

Prilagodbe

Dopustite mi da napravim neke prilagodbe algoritama predloženih u knjizi H.-O. Peitgen i P.H. Richter “Ljepota fraktala” M. 1993. čisto kako bi se iskorijenile greške pri upisu i olakšalo razumijevanje procesa budući da mi je nakon proučavanja mnogo toga ostalo misterij. Nažalost, ovi "razumljivi" i "jednostavni" algoritmi vode ljuljački način života.

Konstrukcija fraktala temelji se na određenoj nelinearnoj funkciji složenog procesa s povratnom spregom z = > z 2 +c budući da su z i c -k kompleksni brojevi, tada je z = x + iy , c = p + iq potrebno rastavite ga na x i y kako biste prešli na ravninu realniju za običnog čovjeka:

x(k+1)=x(k) 2 -y(k) 2 + p,
y(k+1)=2*x(k)*y(k) + q.

Ravnina koja se sastoji od svih parova (x,y) može se smatrati kao za fiksne vrijednosti R i q, i kod dinamičkih. U prvom slučaju prolaskom kroz sve točke (x ,y) ravnine i bojeći ih ovisno o broju ponavljanja funkcije potrebnih za izlazak iz iterativnog procesa ili ih ne bojeći (crna boja) kada se prekorači dopušteni maksimum ponavljanja, dobivamo preslikavanje Julijinog skupa. Ako, naprotiv, odredimo početni par vrijednosti (x,y) i pratimo njegovu kolorističku sudbinu s dinamički promjenjivim vrijednostima parametara p i q, tada dobivamo slike koje se nazivaju Mandelbrotovi skupovi.

O pitanju algoritama za bojanje fraktala.

Obično je tijelo skupa predstavljeno kao crno polje, iako je očito da se crna boja može zamijeniti bilo kojom drugom, ali ovo je također malo zanimljiv rezultat. Dobivanje slike skupa obojene u sve boje zadatak je koji se ne može riješiti pomoću cikličkih operacija jer broj ponavljanja skupova koji tvore tijelo jednak je najvećem mogućem i uvijek je isti. Moguće je obojiti skup u različite boje koristeći rezultat provjere izlaznog uvjeta iz petlje (z_magnitude) ili nešto slično, ali s drugim matematičkim operacijama, kao broj boje.

Primjena "fraktalnog mikroskopa"

demonstrirati granične pojave.

Atraktori su centri koji vode borbu za prevlast na planu. Između atraktora pojavljuje se granica koja predstavlja cvjetni uzorak. Povećanjem ljestvice razmatranja unutar granica skupa, mogu se dobiti netrivijalni obrasci koji odražavaju stanje determinističkog kaosa - uobičajene pojave u prirodnom svijetu.

Objekti koje proučavaju geografi tvore sustav s vrlo složeno organiziranim granicama, pa stoga njihova identifikacija postaje nimalo jednostavan praktični zadatak. Prirodni kompleksi imaju jezgre tipičnosti koje djeluju kao atraktori koji gube svoj utjecaj na teritorij kako se on udaljava.

Pomoću fraktalnog mikroskopa za Mandelbrotov i Julijin skup može se stvoriti predodžba o graničnim procesima i pojavama koji su jednako složeni bez obzira na mjerilo razmatranja i tako pripremiti percepciju stručnjaka za susret s dinamičnim i naizgled kaotičnim prirodnim objektom. u prostoru i vremenu, za razumijevanje prirode fraktalne geometrije. Raznobojnost boja i fraktalna glazba zasigurno će ostaviti dubok trag u svijesti učenika.

Tisuće publikacija i golemi internetski resursi posvećeni su fraktalima, ali za mnoge stručnjake koji su daleko od računalnih znanosti, ovaj se pojam čini potpuno novim. Fraktali, kao objekti interesa stručnjaka iz različitih područja znanja, trebali bi dobiti odgovarajuće mjesto u kolegijima informatike.

Primjeri

SIEPINSKI GRID

Ovo je jedan od fraktala s kojima je Mandelbrot eksperimentirao razvijajući koncepte fraktalnih dimenzija i ponavljanja. Izrezuju se trokutići nastali spajanjem središta većeg trokuta od glavnog trokuta, tvoreći trokut s više rupa. U ovom slučaju, inicijator je veliki trokut, a predložak je operacija izrezivanja trokuta sličnih većem. Također možete dobiti trodimenzionalnu verziju trokuta korištenjem običnog tetraedra i izrezivanja malih tetraedra. Dimenzija takvog fraktala je ln3/ln2 = 1,584962501. Dobiti Sierpinski tepih, uzmite kvadrat, podijelite ga na devet kvadrata i izrežite srednji. Isto ćemo učiniti i s ostalim, manjim kvadratima. Na kraju se formira ravna fraktalna mreža koja nema površinu, ali ima beskonačne veze. U svom prostornom obliku, spužva Sierpinski transformira se u sustav oblika od kraja do kraja, u kojem se svaki element od kraja do kraja neprestano zamjenjuje svojom vrstom. Ova je struktura vrlo slična dijelu koštanog tkiva. Jednog će dana takve strukture koje se ponavljaju postati element građevnih struktura. Njihova statika i dinamika, smatra Mandelbrot, zaslužuju pomno proučavanje.

FRAKTAL SIERPINSKOG

Nemojte brkati ovaj fraktal sa Sierpinskijevom rešetkom. To su dva potpuno različita objekta. U ovom fraktalu, inicijator i generator su isti. U svakoj iteraciji, manja kopija inicijatora se dodaje u svaki kut generatora, i tako dalje. Kada bi se napravio beskonačan broj ponavljanja pri stvaranju ovog fraktala, on bi zauzeo cijelu ravninu, ne ostavljajući niti jednu rupu. Stoga je njegova fraktalna dimenzija ln9/ln3 = 2,0.

KOCHOVA KRIVULJA

Kochova krivulja jedan je od najtipičnijih determinističkih fraktala. Izumio ju je u devetnaestom stoljeću njemački matematičar po imenu Helge von Koch, koji je, proučavajući radove Georga Kontora i Karla Weierstrassea, naišao na opise nekih čudnih krivulja neobičnog ponašanja. Inicijator je ravna linija. Generator je jednakostranični trokut čije su stranice jednake trećini duljine većeg segmenta. Ti se trokuti uvijek iznova dodaju u sredinu svakog segmenta. U svojim istraživanjima, Mandelbrot je opsežno eksperimentirao s Kochovim krivuljama i proizveo figure kao što su Kochovi otoci, Kochovi križevi, Kochove snježne pahuljice, pa čak i trodimenzionalne prikaze Kochove krivulje korištenjem tetraedra i dodavanjem manjih tetraedra na svako njegovo lice. Kochova krivulja ima dimenziju ln4/ln3 = 1,261859507.

MANDELBROT FRAKTAL

Ovo NIJE Mandelbrotov skup, koji često viđate. Mandelbrotov skup temelji se na nelinearnim jednadžbama i složen je fraktal. Ovo je također varijanta Kochove krivulje, iako joj ovaj objekt nije sličan. Inicijator i generator također se razlikuju od onih koji se koriste za stvaranje fraktala na principu Kochove krivulje, ali ideja ostaje ista. Umjesto spajanja jednakostraničnog trokuta s segmentom krivulje, kvadrati se spajaju s kvadratom. Zbog činjenice da ovaj fraktal zauzima točno polovicu dodijeljenog prostora u svakoj iteraciji, on ima jednostavnu fraktalnu dimenziju 3/2 = 1,5.

FRAKTALI ZVIJEZDA I PAHULJA

Oba ova objekta nisu klasični fraktali i nije ih izumio Mandelbrot ili bilo koji drugi poznati matematičar. Samo sam stvorio ove fraktale iz interesa i eksperimentiranja s programiranjem. I inicijator i generator ovdje su figura formirana spajanjem središta stranica sa središtima suprotnih stranica u pravilnom šesterokutu. Štoviše, mogu samo naslutiti dimenziju ovih fraktala.

SMELIJE PETOKUN

Fraktal izgleda kao hrpa peterokuta stisnutih zajedno. Zapravo, nastaje korištenjem peterokuta kao pokretača i jednakokračnih trokuta u kojima je omjer veće i manje stranice točno jednak tzv. zlatnom rezu (1,618033989 ili 1/(2cos72)) kao generatora . Ovi trokuti su izrezani iz sredine svakog peterokuta, što rezultira oblikom koji izgleda kao 5 malih peterokuta zalijepljenih na jedan veliki. Varijanta ovog fraktala može se dobiti korištenjem šesterokuta kao inicijatora. Ovaj fraktal se zove Davidova zvijezda i prilično je sličan heksagonalnoj verziji Kochove pahuljice. Fraktalna dimenzija Darerovog peterokuta je ln6/ln (1+g), gdje je g omjer duljine veće stranice trokuta i duljine manje. U ovom slučaju, g je zlatni rez, tako da je fraktalna dimenzija približno 1,86171596. Fraktalna dimenzija Davidove zvijezde ln6/ln3 ili 1.630929754.

HILBERTOVA KRIVULJA

Ovaj fraktal je vrlo sličan Fraktalu labirinta, osim što se širina slova U, koje je generator, ne mijenja sa svakom iteracijom. Međutim, za razliku od labirintskog fraktala, Hilbertova krivulja, koja se naziva i Hilbertov hotel, ima jednu jedinu fraktalnu dimenziju, a to je točno 2.0, budući da će s beskonačnim brojem ponavljanja zauzeti cijelu ravninu. fraktala, a zatim učinite isto s malim područjem tog područja, dva će se povećanja značajno razlikovati jedno od drugog. Dvije slike bit će vrlo slične u detaljima, ali neće biti potpuno identične. Slika 1. Aproksimacija Mandelbrotovog skupa Usporedite, na primjer, slike Mandelbrotovog skupa prikazane ovdje, od kojih je jedna dobivena povećanjem određenog područja druge. Kao što vidite, oni apsolutno nisu identični, iako na oba vidimo crni krug, iz kojeg se plameni pipci protežu u različitim smjerovima. Ovi se elementi ponavljaju unedogled u Mandelbrotovom skupu u opadajućim omjerima. Deterministički fraktali su linearni, dok složeni fraktali nisu. Budući da su nelinearni, ti su fraktali generirani pomoću onoga što je Mandelbrot nazvao nelinearnim algebarskim jednadžbama. Dobar primjer je proces Zn+1=ZnI + C, što je jednadžba korištena za konstrukciju Mandelbrot-ovog i Julijinog skupa drugog stupnja. Rješavanje ovih matematičkih jednadžbi uključuje kompleksne i imaginarne brojeve. Kada se jednadžba grafički interpretira u kompleksnoj ravnini, rezultat je čudan lik u kojem se ravne linije pretvaraju u krivulje i pojavljuju se učinci samosličnosti, iako ne bez deformacija, na različitim razinama mjerila. Pritom je cijela slika u cjelini nepredvidiva i vrlo kaotična. Kao što možete vidjeti gledajući slike, složeni fraktali su zaista vrlo složeni i ne mogu se stvoriti bez pomoći računala. Za dobivanje živopisnih rezultata ovo računalo mora imati snažan matematički koprocesor i monitor visoke rezolucije. Za razliku od determinističkih fraktala, složeni fraktali se ne izračunavaju u 5-10 iteracija. Gotovo svaka točka na zaslonu računala je poput zasebnog fraktala. Prilikom matematičke obrade svaka točka se tretira kao zaseban crtež. Svaka točka odgovara određenoj vrijednosti. Jednadžba je ugrađena za svaku točku i izvodi se npr. 1000 ponavljanja. Za dobivanje relativno neiskrivljene slike u vremenskom razdoblju prihvatljivom za kućna računala, moguće je izvršiti 250 ponavljanja za jednu točku. Većina fraktala koje danas vidimo lijepo su obojeni. Možda fraktalne slike dobivaju tako veliki estetski značaj upravo zbog svojih shema boja. Nakon što se jednadžba izračuna, računalo analizira rezultate. Ako rezultati ostanu stabilni ili variraju oko određene vrijednosti, točka obično postaje crna. Ako vrijednost na jednom ili drugom koraku teži beskonačnosti, točka se boji u drugu boju, možda plavu ili crvenu. Tijekom ovog procesa, računalo dodjeljuje boje svim brzinama kretanja. Obično su točkice koje se brzo kreću obojene crvenom bojom, dok su one sporije obojene žutom bojom i tako dalje. Tamne mrlje vjerojatno su najstabilnije. Složeni fraktali razlikuju se od deterministički u smislu da su beskonačno složeni, ali se u isto vrijeme mogu generirati vrlo jednostavnom formulom. Deterministički fraktali ne zahtijevaju formule ili jednadžbe. Samo uzmite malo papira za crtanje i možete bez ikakvih poteškoća izgraditi sito Sierpinskog do 3 ili 4 ponavljanja. Pokušajte ovo s puno Julije! Lakše je otići izmjeriti duljinu engleske obale! MANDELBROT SET Slika 2. Mandelbrotov skup Mandelbrotov i Julijin skup vjerojatno su dva najčešća među složenim fraktalima. Mogu se pronaći u mnogim znanstvenim časopisima, na naslovnicama knjiga, razglednicama i čuvarima zaslona računala. Mandelbrotov skup, koji je konstruirao Benoit Mandelbrot, vjerojatno je prva asocijacija koja se ljudima pojavi kad čuju riječ fraktal. Ovaj fraktal, koji nalikuje stroju za kartanje s gorućim stablom i kružnim područjima pričvršćenim na njega, generira se jednostavnom formulom Zn+1=Zna+C, gdje su Z i C kompleksni brojevi, a a pozitivan broj. Mandelbrotov skup, koji se najčešće može vidjeti, je Mandelbrotov skup 2. stupnja, odnosno a = 2. Činjenica da Mandelbrotov skup nije samo Zn+1=ZnÍ+C, već fraktal, čiji indikator u formuli može biti bilo koji pozitivan broj, dovela je mnoge u zabludu. Na ovoj stranici vidite primjer Mandelbrotovog skupa za različite vrijednosti eksponenta a. Slika 3. Pojava mjehurića na a=3,5 Popularan je i postupak Z=Z*tg (Z+C). Uključivanjem funkcije tangente rezultat je Mandelbrotov skup okružen područjem nalik jabuci. Pri korištenju kosinusne funkcije dobivaju se efekti mjehurića zraka. Ukratko, postoji beskonačan broj načina za konfiguriranje Mandelbrot skupa za proizvodnju različitih lijepih slika. PUNO JULIJA Iznenađujuće, Julijini skupovi formirani su prema istoj formuli kao i Mandelbrotov skup. Julijin skup je izumio francuski matematičar Gaston Julia, po kojem je skup i dobio ime. Prvo pitanje koje se postavlja nakon vizualnog upoznavanja s Mandelbrotovim i Julijinim skupovima je "ako su oba fraktala generirana prema istoj formuli, zašto su toliko različiti?" Prvo pogledajte slike seta Julia. Čudno je da postoje različite vrste Julia kompleta. Prilikom crtanja fraktala koristeći različite početne točke (za početak procesa ponavljanja), generiraju se različite slike. Ovo se odnosi samo na set Julia. Slika 4. Julijin set Iako se ne vidi na slici, Mandelbrotov fraktal je zapravo mnogo Julijinih fraktala povezanih zajedno. Svaka točka (ili koordinata) Mandelbrotovog skupa odgovara Julijinom fraktalu. Julia skupovi se mogu generirati korištenjem ovih točaka kao početnih vrijednosti u jednadžbi Z=ZI+C. Ali to ne znači da ako odaberete točku na Mandelbrotovom fraktalu i povećate je, možete dobiti Julijin fraktal. Ove dvije točke su identične, ali samo u matematičkom smislu. Ako uzmete ovu točku i izračunate je pomoću ove formule, možete dobiti Julijin fraktal, koji odgovara određenoj točki Mandelbrotovog fraktala.