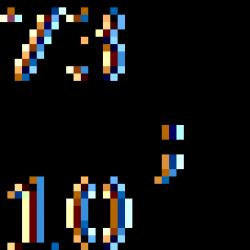Of the many fractions found in arithmetic, those with 10, 100, 1000 in the denominator deserve special attention - in general, any power of ten. These fractions have a special name and notation.

A decimal is any number whose denominator is a power of ten.

Decimal examples:

Why was it necessary to isolate such fractions at all? Why do they need their own entry form? There are at least three reasons for this:

1. Decimals are much easier to compare. Remember: to compare ordinary fractions, you need to subtract them from each other and, in particular, bring the fractions to a common denominator. In decimal fractions, none of this is required;
2. Reduction of calculations. Decimals add and multiply according to their own rules, and with a little practice you will be able to work with them much faster than with ordinary ones;
3. Ease of recording. Unlike ordinary fractions, decimals are written in one line without loss of clarity.

Most calculators also give answers in decimals. In some cases, a different recording format may cause problems. For example, what if you demand change in the amount of 2/3 rubles in a store :)

Rules for writing decimal fractions

The main advantage of decimal fractions is a convenient and visual notation. Namely:

Decimal notation is a form of decimal notation where the integer part is separated from the fractional part using a regular dot or comma. In this case, the separator itself (dot or comma) is called the decimal point.

For example, 0.3 (read: “zero integer, 3 tenths”); 7.25 (7 integers, 25 hundredths); 3.049 (3 integers, 49 thousandths). All examples are taken from the previous definition.

In writing, a comma is usually used as a decimal point. Here and below, the comma will also be used throughout the site.

To write an arbitrary decimal fraction in the specified form, you need to follow three simple steps:

1. Write out the numerator separately;
2. Shift the decimal point to the left by as many places as there are zeros in the denominator. Assume that initially the decimal point is to the right of all digits;
3. If the decimal point has shifted, and after it there are zeros at the end of the record, they must be crossed out.

It happens that in the second step the numerator does not have enough digits to complete the shift. In this case, the missing positions are filled with zeros. And in general, any number of zeros can be assigned to the left of any number without harm to health. It's ugly, but sometimes useful.

At first glance, this algorithm may seem rather complicated. In fact, everything is very, very simple - you just need to practice a little. Take a look at the examples:

Task. For each fraction, indicate its decimal notation:

The numerator of the first fraction: 73. We shift the decimal point by one sign (because the denominator is 10) - we get 7.3.

The numerator of the second fraction: 9. We shift the decimal point by two digits (because the denominator is 100) - we get 0.09. I had to add one zero after the decimal point and one more before it, so as not to leave a strange notation like “.09”.

The numerator of the third fraction: 10029. We shift the decimal point by three digits (because the denominator is 1000) - we get 10.029.

The numerator of the last fraction: 10500. Again we shift the point by three digits - we get 10.500. There are extra zeros at the end of the number. We cross them out - we get 10.5.

Pay attention to the last two examples: the numbers 10.029 and 10.5. According to the rules, the zeros on the right must be crossed out, as is done in the last example. However, in no case should you do this with zeros that are inside the number (which are surrounded by other digits). That is why we got 10.029 and 10.5, and not 1.29 and 1.5.

So, we figured out the definition and form of recording decimal fractions. Now let's find out how to convert ordinary fractions to decimals - and vice versa.

Change from fractions to decimals

Consider a simple numerical fraction of the form a / b . You can use the basic property of a fraction and multiply the numerator and denominator by such a number that you get a power of ten below. But before doing so, please read the following:

There are denominators that are not reduced to the power of ten. Learn to recognize such fractions, because they cannot be worked with according to the algorithm described below.

That's it. Well, how to understand whether the denominator is reduced to the power of ten or not?

The answer is simple: factorize the denominator into prime factors. If only factors 2 and 5 are present in the expansion, this number can be reduced to the power of ten. If there are other numbers (3, 7, 11 - whatever), you can forget about the degree of ten.

Task. Check if the specified fractions can be represented as decimals:

We write out and factorize the denominators of these fractions:

20 \u003d 4 5 \u003d 2 2 5 - only the numbers 2 and 5 are present. Therefore, the fraction can be represented as a decimal.

12 \u003d 4 3 \u003d 2 2 3 - there is a "forbidden" factor 3. The fraction cannot be represented as a decimal.

640 \u003d 8 8 10 \u003d 2 3 2 3 2 5 \u003d 2 7 5. Everything is in order: there is nothing except the numbers 2 and 5. A fraction is represented as a decimal.

48 \u003d 6 8 \u003d 2 3 2 3 \u003d 2 4 3. The factor 3 “surfaced” again. It cannot be represented as a decimal fraction.

So, we figured out the denominator - now we will consider the entire algorithm for switching to decimal fractions:

1. Factorize the denominator of the original fraction and make sure that it is generally representable as a decimal. Those. check that only factors 2 and 5 are present in the expansion. Otherwise, the algorithm does not work;
2. Count how many twos and fives are present in the decomposition (there will be no other numbers there, remember?). Choose such an additional multiplier so that the number of twos and fives is equal.
3. Actually, multiply the numerator and denominator of the original fraction by this factor - we get the desired representation, i.e. the denominator will be a power of ten.

Of course, the additional factor will also be decomposed only into twos and fives. At the same time, in order not to complicate your life, you should choose the smallest such factor from all possible ones.

And one more thing: if there is an integer part in the original fraction, be sure to convert this fraction to an improper one - and only then apply the described algorithm.

Task. Convert these numbers to decimals:

Let's factorize the denominator of the first fraction: 4 = 2 · 2 = 2 2 . Therefore, a fraction can be represented as a decimal. There are two twos and no fives in the expansion, so the additional factor is 5 2 = 25. The number of twos and fives will be equal to it. We have:

Now let's deal with the second fraction. To do this, note that 24 \u003d 3 8 \u003d 3 2 3 - there is a triple in the expansion, so the fraction cannot be represented as a decimal.

The last two fractions have denominators 5 (a prime number) and 20 = 4 5 = 2 2 5 respectively - only twos and fives are present everywhere. At the same time, in the first case, “for complete happiness”, there is not enough multiplier 2, and in the second - 5. We get:

Switching from decimals to ordinary

The reverse conversion - from decimal notation to normal - is much easier. There are no restrictions and special checks, so you can always convert a decimal fraction into a classic "two-story" one.

The translation algorithm is as follows:

1. Cross out all the zeros on the left side of the decimal, as well as the decimal point. This will be the numerator of the desired fraction. The main thing - do not overdo it and do not cross out the internal zeros surrounded by other numbers;
2. Calculate how many digits are in the original decimal fraction after the decimal point. Take the number 1 and add as many zeros to the right as you counted the characters. This will be the denominator;
3. Actually, write down the fraction whose numerator and denominator we just found. Reduce if possible. If there was an integer part in the original fraction, now we will get an improper fraction, which is very convenient for further calculations.

Task. Convert decimals to ordinary: 0.008; 3.107; 2.25; 7,2008.

We cross out the zeros on the left and the commas - we get the following numbers (these will be numerators): 8; 3107; 225; 72008.

In the first and second fractions after the decimal point there are 3 decimal places, in the second - 2, and in the third - as many as 4 decimal places. We get the denominators: 1000; 1000; 100; 10000.

Finally, let's combine the numerators and denominators into ordinary fractions:

As can be seen from the examples, the resulting fraction can very often be reduced. Once again, I note that any decimal fraction can be represented as an ordinary one. The reverse transformation is not always possible.

We have already said that fractions are ordinary And decimal. At the moment, we have studied ordinary fractions a little. We learned that there are regular fractions and improper fractions. We also learned that ordinary fractions can be reduced, added, subtracted, multiplied and divided. And we also learned that there are so-called mixed numbers, which consist of an integer and a fractional part.

We have not yet fully studied ordinary fractions. There are many subtleties and details that should be discussed, but today we will begin to study decimal fractions, since ordinary and decimal fractions quite often have to be combined. That is, when solving problems, you have to work with both types of fractions.

This lesson may seem complicated and incomprehensible. It's quite normal. These kinds of lessons require that they be studied and not skimmed over.

Expressing quantities in fractional form

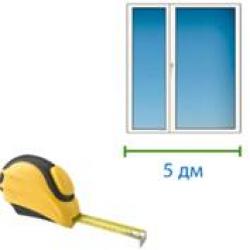
Sometimes it is convenient to show something in fractional form. For example, one tenth of a decimeter is written like this:

This expression means that one decimeter was divided into ten equal parts, and one part was taken from these ten parts. And one part out of ten in this case is equal to one centimeter:

Consider the following example. Show 6 cm and another 3 mm in centimeters in fractional form.

So, you want to show 6 cm and 3 mm in centimeters, but in fractional form. We already have 6 whole centimeters:

But there are still 3 millimeters left. How to show these 3 millimeters, while in centimeters? Fractions come to the rescue. One centimeter is ten millimeters. Three millimeters is three parts out of ten. And three parts out of ten are written as cm

The expression cm means that one centimeter was divided into ten equal parts, and three parts were taken from these ten parts.

As a result, we have six whole centimeters and three tenths of a centimeter:

In this case, 6 shows the number of whole centimeters, and the fraction shows the number of fractional. This fraction is read as "six point and three tenths of a centimeter".

Fractions, in the denominator of which there are numbers 10, 100, 1000, can be written without a denominator. First write the integer part, and then the numerator of the fractional part. The integer part is separated from the numerator of the fractional part by a comma.

For example, let's write without a denominator. First write down the whole part. The whole part is 6

The whole part is recorded. Immediately after writing the whole part, put a comma:

And now we write down the numerator of the fractional part. In a mixed number, the numerator of the fractional part is the number 3. We write the three after the decimal point:

Any number that is represented in this form is called decimal.

Therefore, you can show 6 cm and another 3 mm in centimeters using a decimal fraction:

6.3 cm

It will look like this:

In fact, decimals are the same common fractions and mixed numbers. The peculiarity of such fractions is that the denominator of their fractional part contains the numbers 10, 100, 1000 or 10000.

Like a mixed number, a decimal has an integer part and a fractional part. For example, in a mixed number, the integer part is 6 and the fractional part is .

In the decimal fraction 6.3, the integer part is the number 6, and the fractional part is the numerator of the fraction, that is, the number 3.

It also happens that ordinary fractions in the denominator of which the numbers 10, 100, 1000 are given without an integer part. For example, a fraction is given without an integer part. To write such a fraction as a decimal, first write down 0, then put a comma and write down the numerator of the fractional part. A fraction without a denominator would be written like this:

Reads like "zero point five tenths".

Convert mixed numbers to decimals

When we write mixed numbers without a denominator, we are converting them to decimals. When converting ordinary fractions to decimal fractions, there are a few things you need to know, which we'll talk about now.

After the integer part is written, it is imperative to count the number of zeros in the denominator of the fractional part, since the number of zeros in the fractional part and the number of digits after the decimal point in the decimal fraction must be the same. What does it mean? Consider the following example:

At first

And you could immediately write down the numerator of the fractional part and the decimal fraction is ready, but you must definitely count the number of zeros in the denominator of the fractional part.

So, we count the number of zeros in the fractional part of the mixed number. The denominator of the fractional part has one zero. So in the decimal fraction after the decimal point there will be one digit and this figure will be the numerator of the fractional part of the mixed number, that is, the number 2

Thus, the mixed number, when translated into a decimal fraction, becomes 3.2.

This decimal is read like this:

"Three whole two tenths"

"Tenths" because the fractional part of the mixed number contains the number 10.

Example 2 Convert mixed number to decimal.

We write down the whole part and put a comma:

And you could immediately write down the numerator of the fractional part and get the decimal fraction 5.3, but the rule says that after the decimal point there should be as many digits as there are zeros in the denominator of the fractional part of the mixed number. And we see that there are two zeros in the denominator of the fractional part. So in our decimal fraction after the decimal point there should be two digits, not one.

In such cases, the numerator of the fractional part needs to be slightly modified: add a zero before the numerator, that is, before the number 3

Now you can convert this mixed number to a decimal. We write down the whole part and put a comma:

And write the numerator of the fractional part:

The decimal fraction 5.03 reads like this:

"Five point three hundredths"

"Hundredths" because the denominator of the fractional part of the mixed number is the number 100.

Example 3 Convert mixed number to decimal.

From the previous examples, we learned that in order to successfully convert a mixed number to a decimal, the number of digits in the numerator of the fractional part and the number of zeros in the denominator of the fractional part must be the same.

Before converting a mixed number into a decimal fraction, its fractional part needs to be slightly modified, namely, to make sure that the number of digits in the numerator of the fractional part and the number of zeros in the denominator of the fractional part are the same.

First of all, we look at the number of zeros in the denominator of the fractional part. We see that there are three zeros:

Our task is to organize three digits in the numerator of the fractional part. We already have one digit - this is the number 2. It remains to add two more digits. They will be two zeros. Add them before the number 2. As a result, the number of zeros in the denominator and the number of digits in the numerator will become the same:

Now we can turn this mixed number into a decimal. We write down the whole part first and put a comma:

and immediately write down the numerator of the fractional part

3,002

We see that the number of digits after the decimal point and the number of zeros in the denominator of the fractional part of the mixed number are the same.

The decimal 3.002 reads like this:

"Three whole, two thousandths"

"Thousandths" because the denominator of the fractional part of the mixed number is the number 1000.

Converting common fractions to decimals

Ordinary fractions, in which the denominator is 10, 100, 1000 or 10000, can also be converted to decimal fractions. Since an ordinary fraction does not have an integer part, first write down 0, then put a comma and write down the numerator of the fractional part.

Here, too, the number of zeros in the denominator and the number of digits in the numerator must be the same. Therefore, you should be careful.

Example 1

The integer part is missing, so first we write 0 and put a comma:

Now look at the number of zeros in the denominator. We see that there is one zero. And the numerator has one digit. So you can safely continue the decimal fraction by writing the number 5 after the decimal point

In the resulting decimal fraction 0.5, the number of digits after the decimal point and the number of zeros in the denominator of the fraction are the same. So the fraction is correct.

The decimal fraction 0.5 reads like this:

"Zero point, five tenths"

Example 2 Convert common fraction to decimal.

The whole part is missing. We write 0 first and put a comma:

Now look at the number of zeros in the denominator. We see that there are two zeros. And the numerator has only one digit. To make the number of digits and the number of zeros the same, add one zero in the numerator before the number 2. Then the fraction will take the form . Now the number of zeros in the denominator and the number of digits in the numerator are the same. So you can continue the decimal:

In the resulting decimal fraction 0.02, the number of digits after the decimal point and the number of zeros in the denominator of the fraction are the same. So the fraction is correct.

The decimal fraction 0.02 reads like this:

"Zero point, two hundredths."

Example 3 Convert common fraction to decimal.

We write 0 and put a comma:

Now we count the number of zeros in the denominator of the fraction. We see that there are five zeros, and there is only one digit in the numerator. To make the number of zeros in the denominator and the number of digits in the numerator the same, you need to add four zeros in the numerator before the number 5:

Now the number of zeros in the denominator and the number of digits in the numerator are the same. So you can continue the decimal. We write down the numerator of the fraction after the decimal point

In the resulting decimal fraction 0.00005, the number of digits after the decimal point and the number of zeros in the denominator of the fraction are the same. So the fraction is correct.

The decimal fraction 0.00005 reads like this:

"Zero point, five hundred-thousandths."

Convert improper fractions to decimals

An improper fraction is a fraction whose numerator is greater than the denominator. There are improper fractions that have the numbers 10, 100, 1000 or 10000 in the denominator. Such fractions can be converted to decimal fractions. But before converting to a decimal fraction, such fractions must have an integer part.

Example 1

The fraction is an improper fraction. To convert such a fraction to a decimal fraction, you must first select its integer part. We recall how to select the whole part of improper fractions. If you forgot, we advise you to return to and study it.

So, let's select the integer part in the improper fraction. Recall that a fraction means division - in this case, dividing the number 112 by the number 10

Let's look at this picture and assemble a new mixed number, like a children's construction set. The number 11 will be the integer part, the number 2 will be the numerator of the fractional part, the number 10 will be the denominator of the fractional part.

We got a mixed number. Let's convert it to a decimal. And we already know how to translate such numbers into decimal fractions. First we write down the whole part and put a comma:

Now we count the number of zeros in the denominator of the fractional part. We see that there is one zero. And the numerator of the fractional part has one digit. This means that the number of zeros in the denominator of the fractional part and the number of digits in the numerator of the fractional part are the same. This gives us the opportunity to immediately write the numerator of the fractional part after the decimal point:

In the resulting decimal fraction 11.2, the number of digits after the decimal point and the number of zeros in the denominator of the fraction are the same. So the fraction is correct.

This means that an improper fraction, when converted to a decimal fraction, turns into 11.2

Decimal 11.2 reads like this:

"Eleven whole, two tenths."

Example 2 Convert improper fraction to decimal.

This is an improper fraction because the numerator is greater than the denominator. But it can be converted to a decimal fraction, since the denominator is the number 100.

First of all, we select the integer part of this fraction. To do this, divide 450 by 100 by a corner:

Let's collect a new mixed number - we get . And we already know how to translate mixed numbers into decimal fractions.

We write down the whole part and put a comma:

Now we count the number of zeros in the denominator of the fractional part and the number of digits in the numerator of the fractional part. We see that the number of zeros in the denominator and the number of digits in the numerator are the same. This gives us the opportunity to immediately write the numerator of the fractional part after the decimal point:

In the resulting decimal fraction 4.50, the number of digits after the decimal point and the number of zeros in the denominator of the fraction are the same. So the fraction is translated correctly.

So the improper fraction, when translated into a decimal fraction, turns into 4.50

When solving problems, if there are zeros at the end of the decimal fraction, they can be discarded. Let's drop the zero in our answer. Then we get 4.5

This is one of the interesting features of decimals. It lies in the fact that the zeros that are at the end of the fraction do not give this fraction any weight. In other words, the decimals 4.50 and 4.5 are equal. Let's put an equal sign between them:

4,50 = 4,5

The question arises: why is this happening? After all, 4.50 and 4.5 look like different fractions. The whole secret lies in the basic property of the fraction, which we studied earlier. We will try to prove why the decimal fractions 4.50 and 4.5 are equal, but after studying the next topic, which is called "converting a decimal fraction to a mixed number."

Decimal to mixed number conversion

Any decimal fraction can be converted back to a mixed number. To do this, it is enough to be able to read decimal fractions. For example, let's convert 6.3 to a mixed number. 6.3 is six whole points and three tenths. We write down six integers first:

and next three tenths:

Example 2 Convert decimal 3.002 to mixed number

3.002 is three integers and two thousandths. Write down three integers first.

and next we write two thousandths:

Example 3 Convert decimal 4.50 to mixed number

4.50 is four point and fifty hundredths. Write down four integers

and next fifty hundredths:

By the way, let's remember the last example from the previous topic. We said that the decimals 4.50 and 4.5 are equal. We also said that zero can be discarded. Let's try to prove that decimal 4.50 and 4.5 are equal. To do this, we convert both decimal fractions to mixed numbers.

After converting to a mixed number, the decimal 4.50 becomes , and the decimal 4.5 becomes

We have two mixed numbers and . Convert these mixed numbers to improper fractions:

Now we have two fractions and . It is time to remember the basic property of a fraction, which says that when multiplying (or dividing) the numerator and denominator of a fraction by the same number, the value of the fraction does not change.

Let's divide the first fraction by 10

Received, and this is the second fraction. So and are equal to each other and equal to the same value:

Try dividing 450 by 100 first on a calculator, and then 45 by 10. A funny thing will work out.

Convert decimal to common fraction

Any decimal fraction can be converted back to a common fraction. To do this, again, it is enough to be able to read decimal fractions. For example, let's convert 0.3 to an ordinary fraction. 0.3 is zero and three tenths. We write zero integers first:

and next to three tenths 0 . Zero is traditionally not written down, so the final answer will not be 0, but simply.

Example 2 Convert decimal 0.02 to common fraction.

0.02 is zero and two hundredths. We don’t write down zero, so we immediately write down two hundredths

Example 3 Convert 0.00005 to fraction

0.00005 is zero and five hundred thousandths. Zero is not written down, so we immediately write down five hundred thousandths

Did you like the lesson?
Join our new Vkontakte group and start receiving notifications of new lessons

In this tutorial, we'll look at each of these operations one by one.

Adding decimals

As we know, a decimal has an integer part and a fractional part. When adding decimals, the integer and fractional parts are added separately.

For example, let's add the decimals 3.2 and 5.3. It is more convenient to add decimal fractions in a column.

First, we write these two fractions in a column, while the integer parts must be under the integer parts, and the fractional ones under the fractional parts. In school, this requirement is called "comma under comma".

Let's write the fractions in a column so that the comma is under the comma:

We begin to add the fractional parts: 2 + 3 \u003d 5. We write down the five in the fractional part of our answer:

Now we add up the integer parts: 3 + 5 = 8. We write the eight in the integer part of our answer:

Now we separate the integer part from the fractional part with a comma. To do this, we again follow the rule "comma under comma":

Got the answer 8.5. So the expression 3.2 + 5.3 is equal to 8.5

In fact, not everything is as simple as it seems at first glance. Here, too, there are pitfalls, which we will now talk about.

Places in decimals

Decimals, like ordinary numbers, have their own digits. These are tenth places, hundredth places, thousandth places. In this case, the digits begin after the decimal point.

The first digit after the decimal point is responsible for the tenths place, the second digit after the decimal point for the hundredths place, the third digit after the decimal point for the thousandths place.

Decimal digits store some useful information. In particular, they report how many tenths, hundredths, and thousandths are in a decimal.

For example, consider the decimal 0.345

The position where the triple is located is called tenth place

The position where the four is located is called hundredths place

The position where the five is located is called thousandths

Let's look at this figure. We see that in the category of tenths there is a three. This suggests that there are three tenths in the decimal fraction 0.345.

If we add the fractions, and then we get the original decimal fraction 0.345

It can be seen that at first we got the answer, but converted it to a decimal fraction and got 0.345.

When adding decimal fractions, the same principles and rules are followed as when adding ordinary numbers. The addition of decimal fractions occurs by digits: tenths are added to tenths, hundredths to hundredths, thousandths to thousandths.

Therefore, when adding decimal fractions, it is required to follow the rule "comma under comma". A comma under a comma provides the same order in which tenths are added to tenths, hundredths to hundredths, thousandths to thousandths.

Example 1 Find the value of the expression 1.5 + 3.4

First of all, we add the fractional parts 5 + 4 = 9. We write the nine in the fractional part of our answer:

Now we add up the integer parts 1 + 3 = 4. We write down the four in the integer part of our answer:

Now we separate the integer part from the fractional part with a comma. To do this, we again observe the rule "comma under a comma":

Got the answer 4.9. So the value of the expression 1.5 + 3.4 is 4.9

Example 2 Find the value of the expression: 3.51 + 1.22

We write this expression in a column, observing the rule "comma under a comma"

First of all, add the fractional part, namely the hundredths 1+2=3. We write the triple in the hundredth part of our answer:

Now add tenths of 5+2=7. We write down the seven in the tenth part of our answer:

Now add the whole parts 3+1=4. We write down the four in the whole part of our answer:

We separate the integer part from the fractional part with a comma, observing the “comma under the comma” rule:

Got the answer 4.73. So the value of the expression 3.51 + 1.22 is 4.73

3,51 + 1,22 = 4,73

As with ordinary numbers, when adding decimal fractions, . In this case, one digit is written in the answer, and the rest are transferred to the next digit.

Example 3 Find the value of the expression 2.65 + 3.27

We write this expression in a column:

Add hundredths of 5+7=12. The number 12 will not fit in the hundredth part of our answer. Therefore, in the hundredth part, we write the number 2, and transfer the unit to the next bit:

Now we add the tenths of 6+2=8 plus the unit that we got from the previous operation, we get 9. We write the number 9 in the tenth of our answer:

Now add the whole parts 2+3=5. We write the number 5 in the integer part of our answer:

Got the answer 5.92. So the value of the expression 2.65 + 3.27 is 5.92

2,65 + 3,27 = 5,92

Example 4 Find the value of the expression 9.5 + 2.8

Write this expression in a column

We add the fractional parts 5 + 8 = 13. The number 13 will not fit in the fractional part of our answer, so we first write down the number 3, and transfer the unit to the next digit, or rather transfer it to the integer part:

Now we add the integer parts 9+2=11 plus the unit that we got from the previous operation, we get 12. We write the number 12 in the integer part of our answer:

Separate the integer part from the fractional part with a comma:

Got the answer 12.3. So the value of the expression 9.5 + 2.8 is 12.3

9,5 + 2,8 = 12,3

When adding decimal fractions, the number of digits after the decimal point in both fractions must be the same. If there are not enough digits, then these places in the fractional part are filled with zeros.

Example 5. Find the value of the expression: 12.725 + 1.7

Before writing this expression in a column, let's make the number of digits after the decimal point in both fractions the same. The decimal fraction 12.725 has three digits after the decimal point, while the fraction 1.7 has only one. So in the fraction 1.7 at the end you need to add two zeros. Then we get the fraction 1,700. Now you can write this expression in a column and start calculating:

Add thousandths of 5+0=5. We write the number 5 in the thousandth part of our answer:

Add hundredths of 2+0=2. We write the number 2 in the hundredth part of our answer:

Add tenths of 7+7=14. The number 14 will not fit in a tenth of our answer. Therefore, we first write down the number 4, and transfer the unit to the next bit:

Now we add the integer parts 12+1=13 plus the unit that we got from the previous operation, we get 14. We write the number 14 in the integer part of our answer:

Separate the integer part from the fractional part with a comma:

Got the answer 14,425. So the value of the expression 12.725+1.700 is 14.425

12,725+ 1,700 = 14,425

Subtraction of decimals

When subtracting decimal fractions, you must follow the same rules as when adding: “a comma under a comma” and “an equal number of digits after a decimal point”.

Example 1 Find the value of the expression 2.5 − 2.2

We write this expression in a column, observing the “comma under comma” rule:

We calculate the fractional part 5−2=3. We write the number 3 in the tenth part of our answer:

Calculate the integer part 2−2=0. We write zero in the integer part of our answer:

Separate the integer part from the fractional part with a comma:

We got the answer 0.3. So the value of the expression 2.5 − 2.2 is equal to 0.3

2,5 − 2,2 = 0,3

Example 2 Find the value of the expression 7.353 - 3.1

This expression has a different number of digits after the decimal point. In the fraction 7.353 there are three digits after the decimal point, and in the fraction 3.1 there is only one. This means that in the fraction 3.1, two zeros must be added at the end to make the number of digits in both fractions the same. Then we get 3,100.

Now you can write this expression in a column and calculate it:

Got the answer 4,253. So the value of the expression 7.353 − 3.1 is 4.253

7,353 — 3,1 = 4,253

As with ordinary numbers, sometimes you will have to borrow one from the adjacent bit if subtraction becomes impossible.

Example 3 Find the value of the expression 3.46 − 2.39

Subtract hundredths of 6−9. From the number 6 do not subtract the number 9. Therefore, you need to take a unit from the adjacent digit. Having borrowed one from the neighboring digit, the number 6 turns into the number 16. Now we can calculate the hundredths of 16−9=7. We write down the seven in the hundredth part of our answer:

Now subtract tenths. Since we took one unit in the category of tenths, the figure that was located there decreased by one unit. In other words, the tenth place is now not the number 4, but the number 3. Let's calculate the tenths of 3−3=0. We write zero in the tenth part of our answer:

Now subtract the integer parts 3−2=1. We write the unit in the integer part of our answer:

Separate the integer part from the fractional part with a comma:

Got the answer 1.07. So the value of the expression 3.46−2.39 is equal to 1.07

3,46−2,39=1,07

Example 4. Find the value of the expression 3−1.2

This example subtracts a decimal from an integer. Let's write this expression in a column so that the integer part of the decimal fraction 1.23 is under the number 3

Now let's make the number of digits after the decimal point the same. To do this, after the number 3, put a comma and add one zero:

Now subtract tenths: 0−2. Do not subtract the number 2 from zero. Therefore, you need to take a unit from the adjacent digit. By borrowing one from the adjacent digit, 0 turns into the number 10. Now you can calculate the tenths of 10−2=8. We write down the eight in the tenth part of our answer:

Now subtract the whole parts. Previously, the number 3 was located in the integer, but we borrowed one unit from it. As a result, it turned into the number 2. Therefore, we subtract 1 from 2. 2−1=1. We write the unit in the integer part of our answer:

Separate the integer part from the fractional part with a comma:

Got the answer 1.8. So the value of the expression 3−1.2 is 1.8

Decimal multiplication

Multiplying decimals is easy and even fun. To multiply decimals, you need to multiply them like regular numbers, ignoring the commas.

Having received the answer, it is necessary to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in both fractions, then count the same number of digits on the right in the answer and put a comma.

Example 1 Find the value of the expression 2.5 × 1.5

We multiply these decimal fractions as ordinary numbers, ignoring the commas. To ignore the commas, you can temporarily imagine that they are absent altogether:

We got 375. In this number, it is necessary to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in fractions of 2.5 and 1.5. In the first fraction there is one digit after the decimal point, in the second fraction there is also one. A total of two numbers.

We return to the number 375 and begin to move from right to left. We need to count two digits from the right and put a comma:

Got the answer 3.75. So the value of the expression 2.5 × 1.5 is 3.75

2.5 x 1.5 = 3.75

Example 2 Find the value of the expression 12.85 × 2.7

Let's multiply these decimals, ignoring the commas:

We got 34695. In this number, you need to separate the whole part from the fractional part with a comma. To do this, you need to calculate the number of digits after the decimal point in fractions of 12.85 and 2.7. In the fraction 12.85 there are two digits after the decimal point, in the fraction 2.7 there is one digit - a total of three digits.

We return to the number 34695 and begin to move from right to left. We need to count three digits from the right and put a comma:

Got the answer 34,695. So the value of the expression 12.85 × 2.7 is 34.695

12.85 x 2.7 = 34.695

Multiplying a decimal by a regular number

Sometimes there are situations when you need to multiply a decimal fraction by a regular number.

To multiply a decimal and an ordinary number, you need to multiply them, regardless of the comma in the decimal. Having received the answer, it is necessary to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the decimal fraction, then in the answer, count the same number of digits to the right and put a comma.

For example, multiply 2.54 by 2

We multiply the decimal fraction 2.54 by the usual number 2, ignoring the comma:

We got the number 508. In this number, you need to separate the integer part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fraction 2.54. The fraction 2.54 has two digits after the decimal point.

We return to the number 508 and begin to move from right to left. We need to count two digits from the right and put a comma:

Got the answer 5.08. So the value of the expression 2.54 × 2 is 5.08

2.54 x 2 = 5.08

Multiplying decimals by 10, 100, 1000

Multiplying decimals by 10, 100, or 1000 is done in the same way as multiplying decimals by regular numbers. It is necessary to perform the multiplication, ignoring the comma in the decimal fraction, then in the answer, separate the integer part from the fractional part, counting the same number of digits on the right as there were digits after the decimal point in the decimal fraction.

For example, multiply 2.88 by 10

Let's multiply the decimal fraction 2.88 by 10, ignoring the comma in the decimal fraction:

We got 2880. In this number, you need to separate the whole part from the fractional part with a comma. To do this, you need to count the number of digits after the decimal point in the fraction 2.88. We see that in the fraction 2.88 there are two digits after the decimal point.

We return to the number 2880 and begin to move from right to left. We need to count two digits from the right and put a comma:

Got the answer 28.80. We discard the last zero - we get 28.8. So the value of the expression 2.88 × 10 is 28.8

2.88 x 10 = 28.8

There is a second way to multiply decimal fractions by 10, 100, 1000. This method is much simpler and more convenient. It consists in the fact that the comma in the decimal fraction moves to the right by as many digits as there are zeros in the multiplier.

For example, let's solve the previous example 2.88×10 in this way. Without giving any calculations, we immediately look at the factor 10. We are interested in how many zeros are in it. We see that it has one zero. Now in the fraction 2.88 we move the decimal point to the right by one digit, we get 28.8.

2.88 x 10 = 28.8

Let's try to multiply 2.88 by 100. We immediately look at the factor 100. We are interested in how many zeros are in it. We see that it has two zeros. Now in the fraction 2.88 we move the decimal point to the right by two digits, we get 288

2.88 x 100 = 288

Let's try to multiply 2.88 by 1000. We immediately look at the factor 1000. We are interested in how many zeros are in it. We see that it has three zeros. Now in the fraction 2.88 we move the decimal point to the right by three digits. The third digit is not there, so we add another zero. As a result, we get 2880.

2.88 x 1000 = 2880

Multiplying decimals by 0.1 0.01 and 0.001

Multiplying decimals by 0.1, 0.01, and 0.001 works in the same way as multiplying a decimal by a decimal. It is necessary to multiply fractions like ordinary numbers, and put a comma in the answer, counting as many digits on the right as there are digits after the decimal point in both fractions.

For example, multiply 3.25 by 0.1

We multiply these fractions like ordinary numbers, ignoring the commas:

We got 325. In this number, you need to separate the whole part from the fractional part with a comma. To do this, you need to calculate the number of digits after the decimal point in fractions of 3.25 and 0.1. In the fraction 3.25 there are two digits after the decimal point, in the fraction 0.1 there is one digit. A total of three numbers.

We return to the number 325 and begin to move from right to left. We need to count three digits on the right and put a comma. After counting three digits, we find that the numbers are over. In this case, you need to add one zero and put a comma:

We got the answer 0.325. So the value of the expression 3.25 × 0.1 is 0.325

3.25 x 0.1 = 0.325

There is a second way to multiply decimals by 0.1, 0.01 and 0.001. This method is much easier and more convenient. It consists in the fact that the comma in the decimal fraction moves to the left by as many digits as there are zeros in the multiplier.

For example, let's solve the previous example 3.25 × 0.1 in this way. Without giving any calculations, we immediately look at the factor 0.1. We are interested in how many zeros are in it. We see that it has one zero. Now in the fraction 3.25 we move the decimal point to the left by one digit. Moving the comma one digit to the left, we see that there are no more digits before the three. In this case, add one zero and put a comma. As a result, we get 0.325

3.25 x 0.1 = 0.325

Let's try multiplying 3.25 by 0.01. Immediately look at the multiplier of 0.01. We are interested in how many zeros are in it. We see that it has two zeros. Now in the fraction 3.25 we move the comma to the left by two digits, we get 0.0325

3.25 x 0.01 = 0.0325

Let's try multiplying 3.25 by 0.001. Immediately look at the multiplier of 0.001. We are interested in how many zeros are in it. We see that it has three zeros. Now in the fraction 3.25 we move the decimal point to the left by three digits, we get 0.00325

3.25 × 0.001 = 0.00325

Do not confuse multiplying decimals by 0.1, 0.001 and 0.001 with multiplying by 10, 100, 1000. A common mistake most people make.

When multiplying by 10, 100, 1000, the comma is moved to the right by as many digits as there are zeros in the multiplier.

And when multiplying by 0.1, 0.01 and 0.001, the comma is moved to the left by as many digits as there are zeros in the multiplier.

If at first it is difficult to remember, you can use the first method, in which the multiplication is performed as with ordinary numbers. In the answer, you will need to separate the integer part from the fractional part by counting as many digits on the right as there are digits after the decimal point in both fractions.

Dividing a smaller number by a larger one. Advanced level.

In one of the previous lessons, we said that when dividing a smaller number by a larger one, a fraction is obtained, in the numerator of which is the dividend, and in the denominator is the divisor.

For example, to divide one apple into two, you need to write 1 (one apple) in the numerator, and write 2 (two friends) in the denominator. The result is a fraction. So each friend will get an apple. In other words, half an apple. A fraction is the answer to a problem how to split one apple between two

It turns out that you can solve this problem further if you divide 1 by 2. After all, a fractional bar in any fraction means division, which means that this division is also allowed in a fraction. But how? We are used to the fact that the dividend is always greater than the divisor. And here, on the contrary, the dividend is less than the divisor.

Everything will become clear if we remember that a fraction means crushing, dividing, dividing. This means that the unit can be split into as many parts as you like, and not just into two parts.

When dividing a smaller number by a larger one, a decimal fraction is obtained, in which the integer part will be 0 (zero). The fractional part can be anything.

So, let's divide 1 by 2. Let's solve this example with a corner:

One cannot be divided into two just like that. If you ask a question "how many twos are in one" , then the answer will be 0. Therefore, in private we write 0 and put a comma:

Now, as usual, we multiply the quotient by the divisor to pull out the remainder:

The moment has come when the unit can be split into two parts. To do this, add another zero to the right of the received one:

We got 10. We divide 10 by 2, we get 5. We write down the five in the fractional part of our answer:

Now we take out the last remainder to complete the calculation. Multiply 5 by 2, we get 10

We got the answer 0.5. So the fraction is 0.5

Half an apple can also be written using the decimal fraction 0.5. If we add these two halves (0.5 and 0.5), we again get the original one whole apple:

This point can also be understood if we imagine how 1 cm is divided into two parts. If you divide 1 centimeter into 2 parts, you get 0.5 cm

Example 2 Find the value of expression 4:5

How many fives are in four? Not at all. We write in private 0 and put a comma:

We multiply 0 by 5, we get 0. We write zero under the four. Immediately subtract this zero from the dividend:

Now let's start splitting (dividing) the four into 5 parts. To do this, to the right of 4, we add zero and divide 40 by 5, we get 8. We write the eight in private.

We complete the example by multiplying 8 by 5, and get 40:

We got the answer 0.8. So the value of the expression 4: 5 is 0.8

Example 3 Find the value of expression 5: 125

How many numbers 125 are in five? Not at all. We write 0 in private and put a comma:

We multiply 0 by 5, we get 0. We write 0 under the five. Immediately subtract from the five 0

Now let's start splitting (dividing) the five into 125 parts. To do this, to the right of this five, we write zero:

Divide 50 by 125. How many numbers 125 are in 50? Not at all. So in the quotient we again write 0

We multiply 0 by 125, we get 0. We write this zero under 50. Immediately subtract 0 from 50

Now we divide the number 50 into 125 parts. To do this, to the right of 50, we write another zero:

Divide 500 by 125. How many numbers are 125 in the number 500. In the number 500 there are four numbers 125. We write the four in private:

We complete the example by multiplying 4 by 125, and get 500

We got the answer 0.04. So the value of the expression 5: 125 is 0.04

Division of numbers without a remainder

So, let's put a comma in the quotient after the unit, thereby indicating that the division of integer parts is over and we proceed to the fractional part:

Add zero to the remainder 4

Now we divide 40 by 5, we get 8. We write the eight in private:

40−40=0. Received 0 in the remainder. So the division is completely completed. Dividing 9 by 5 results in a decimal of 1.8:

9: 5 = 1,8

Example 2. Divide 84 by 5 without a remainder

First we divide 84 by 5 as usual with a remainder:

Received in private 16 and 4 more in the balance. Now we divide this remainder by 5. We put a comma in the private, and add 0 to the remainder 4

Now we divide 40 by 5, we get 8. We write the figure eight in the quotient after the decimal point:

and complete the example by checking if there is still a remainder:

Dividing a decimal by a regular number

A decimal fraction, as we know, consists of an integer and a fractional part. When dividing a decimal fraction by a regular number, first of all you need:

• divide the integer part of the decimal fraction by this number;
• after the integer part is divided, you need to immediately put a comma in the private part and continue the calculation, as in ordinary division.

For example, let's divide 4.8 by 2

Let's write this example as a corner:

Now let's divide the whole part by 2. Four divided by two is two. We write the deuce in private and immediately put a comma:

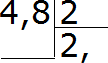
Now we multiply the quotient by the divisor and see if there is a remainder from the division:

4−4=0. The remainder is zero. We do not write zero yet, since the solution is not completed. Then we continue to calculate, as in ordinary division. Take down 8 and divide it by 2

8: 2 = 4. We write the four in the quotient and immediately multiply it by the divisor:

Got the answer 2.4. Expression value 4.8: 2 equals 2.4

Example 2 Find the value of the expression 8.43:3

We divide 8 by 3, we get 2. Immediately put a comma after the two:

Now we multiply the quotient by the divisor 2 × 3 = 6. We write the six under the eight and find the remainder:

We divide 24 by 3, we get 8. We write the eight in private. We immediately multiply it by the divisor to find the remainder of the division:

24−24=0. The remainder is zero. Zero is not recorded yet. Take the last three of the dividend and divide by 3, we get 1. Immediately multiply 1 by 3 to complete this example:

Got the answer 2.81. So the value of the expression 8.43: 3 is equal to 2.81

Dividing a decimal by a decimal

To divide a decimal fraction into a decimal fraction, in the dividend and in the divisor, move the comma to the right by the same number of digits as there are after the decimal point in the divisor, and then divide by a regular number.

For example, divide 5.95 by 1.7

Let's write this expression as a corner

Now, in the dividend and in the divisor, we move the comma to the right by the same number of digits as there are after the decimal point in the divisor. The divisor has one digit after the decimal point. So we must move the comma to the right by one digit in the dividend and in the divisor. Transferring:

After moving the decimal point to the right by one digit, the decimal fraction 5.95 turned into a fraction 59.5. And the decimal fraction 1.7, after moving the decimal point to the right by one digit, turned into the usual number 17. And we already know how to divide the decimal fraction by the usual number. Further calculation is not difficult:

The comma is moved to the right to facilitate division. This is allowed due to the fact that when multiplying or dividing the dividend and the divisor by the same number, the quotient does not change. What does it mean?

This is one of the interesting features of division. It is called the private property. Consider expression 9: 3 = 3. If in this expression the dividend and the divisor are multiplied or divided by the same number, then the quotient 3 will not change.

Let's multiply the dividend and divisor by 2 and see what happens:

(9 × 2) : (3 × 2) = 18: 6 = 3

As can be seen from the example, the quotient has not changed.

The same thing happens when we carry a comma in the dividend and in the divisor. In the previous example, where we divided 5.91 by 1.7, we moved the comma one digit to the right in the dividend and divisor. After moving the comma, the fraction 5.91 was converted to the fraction 59.1 and the fraction 1.7 was converted to the usual number 17.

In fact, inside this process, multiplication by 10 took place. Here's what it looked like:

5.91 × 10 = 59.1

Therefore, the number of digits after the decimal point in the divisor depends on what the dividend and divisor will be multiplied by. In other words, the number of digits after the decimal point in the divisor will determine how many digits in the dividend and in the divisor the comma will be moved to the right.

Decimal division by 10, 100, 1000

Dividing a decimal by 10, 100, or 1000 is done in the same way as . For example, let's divide 2.1 by 10. Let's solve this example with a corner:

But there is also a second way. It's lighter. The essence of this method is that the comma in the dividend is moved to the left by as many digits as there are zeros in the divisor.

Let's solve the previous example in this way. 2.1: 10. We look at the divider. We are interested in how many zeros are in it. We see that there is one zero. So in the divisible 2.1, you need to move the comma to the left by one digit. We move the comma to the left by one digit and see that there are no more digits left. In this case, we add one more zero before the number. As a result, we get 0.21

Let's try to divide 2.1 by 100. There are two zeros in the number 100. So in the divisible 2.1, you need to move the comma to the left by two digits:

2,1: 100 = 0,021

Let's try to divide 2.1 by 1000. There are three zeros in the number 1000. So in the divisible 2.1, you need to move the comma to the left by three digits:

2,1: 1000 = 0,0021

Decimal division by 0.1, 0.01 and 0.001

Dividing a decimal by 0.1, 0.01, and 0.001 is done in the same way as . In the dividend and in the divisor, you need to move the comma to the right by as many digits as there are after the decimal point in the divisor.

For example, let's divide 6.3 by 0.1. First of all, we move the commas in the dividend and in the divisor to the right by the same number of digits as there are after the decimal point in the divisor. The divisor has one digit after the decimal point. So we move the commas in the dividend and in the divisor to the right by one digit.

After moving the decimal point to the right by one digit, the decimal fraction 6.3 turns into the usual number 63, and the decimal fraction 0.1, after moving the decimal point to the right by one digit, turns into one. And dividing 63 by 1 is very simple:

So the value of the expression 6.3: 0.1 is equal to 63

But there is also a second way. It's lighter. The essence of this method is that the comma in the dividend is transferred to the right by as many digits as there are zeros in the divisor.

Let's solve the previous example in this way. 6.3:0.1. Let's look at the divider. We are interested in how many zeros are in it. We see that there is one zero. So in the divisible 6.3, you need to move the comma to the right by one digit. We move the comma to the right by one digit and get 63

Let's try to divide 6.3 by 0.01. Divisor 0.01 has two zeros. So in the divisible 6.3, you need to move the comma to the right by two digits. But in the dividend there is only one digit after the decimal point. In this case, one more zero must be added at the end. As a result, we get 630

Let's try dividing 6.3 by 0.001. The divisor of 0.001 has three zeros. So in the divisible 6.3, you need to move the comma to the right by three digits:

6,3: 0,001 = 6300

Tasks for independent solution

Did you like the lesson?
Join our new Vkontakte group and start receiving notifications of new lessons

Subject: Decimals. Adding and subtracting decimals

Lesson: Decimal notation of fractional numbers

The denominator of a fraction can be expressed as any natural number. Fractional numbers in which the denominator is expressed by the number 10; 100; 1000;…, where n , agreed to write without a denominator. Any fractional number whose denominator is 10; 100; 1000 etc. (that is, a one with several zeros) can be represented as a decimal notation (as a decimal fraction). First, write the integer part, then the numerator of the fractional part, and separate the integer part from the fractional part with a comma.

For example,

If the whole part is missing, i.e. the fraction is correct, then the integer part is written as 0.

To write a decimal correctly, the numerator of the fractional part must have as many digits as there are zeros in the fractional part.

1. Write as a decimal.

2. Represent the decimal as a fraction or mixed number.

3. Read the decimals.

12.4 - 12 whole 4 tenths;

0.3 - 0 whole 3 tenths;

1.14 - 1 whole 14 hundredths;

2.07 - 2 whole 7 hundredths;

0.06 - 0 point 6;

0.25 - 0 whole 25 hundredths;

1.234 - 1 whole 234 thousandths;

1.230 - 1 whole 230 thousandths;

1.034 - 1 whole 34 thousandths;

1.004 - 1 whole 4 thousandths;

1.030 - 1 whole 30 thousandths;

0.010101 - 0 point 10101 ppm.

4. Move the comma in each digit 1 digit to the left and read the numbers.

34,1; 310,2; 11,01; 10,507; 2,7; 3,41; 31,02; 1,101; 1,0507; 0,27.

5. Move the comma in each of the numbers 1 digit to the right and read the resulting number.

1,37; 0,1401; 3,017; 1,7; 350,4; 13,7; 1,401; 30,17; 17; 3504.

6. Express in meters and centimeters.

3.28 m = 3 m + .

7. Express in tons and kilograms.

24.030 t = 24 t.

8. Write down the quotient as a decimal fraction.

1710: 100 = ;

64: 10000 =

803: 100 =

407: 10 =

9. Express in dm.

5 dm 6 cm = 5 dm + ;

9 mm =

fractional number.

Decimal notation of a fractional number is a set of two or more digits from $0$ to $9$, between which is the so-called \textit (decimal point).

Example 1

For example, $35.02; $100.7; $123 \ $456.5; $54.89.

The leftmost digit in the decimal representation of a number cannot be zero, except when the decimal point is immediately after the first digit $0$.

Example 2

For example, $0.357; $0.064.

Often the decimal point is replaced by a decimal point. For example, $35.02$; $100.7$; $123 \ $456.5; $54.89.

Decimal definition

Definition 1

Decimals are fractional numbers that are represented in decimal notation.

For example, $121.05; $67.9; $345.6700.

Decimals are used for a more compact representation of regular fractions whose denominators are the numbers $10$, $100$, $1\000$, etc. and mixed numbers whose denominators are $10$, $100$, $1\000$, etc.

For example, the common fraction $\frac(8)(10)$ can be written as the decimal $0.8$, and the mixed number $405\frac(8)(100)$ as the decimal $405.08$.

Reading decimals

Decimals that correspond to regular fractions are read the same as ordinary fractions, only the phrase "zero integers" is added in front. For example, the common fraction $\frac(25)(100)$ (read "twenty-five hundredths") corresponds to the decimal fraction $0.25$ (read "zero point twenty-five hundredths").

Decimals that correspond to mixed numbers are read the same way as mixed numbers. For example, the mixed number $43\frac(15)(1000)$ corresponds to the decimal fraction $43.015$ (read "forty-three point fifteen thousandths").

Places in decimals

In decimal notation, the value of each digit depends on its position. Those. in decimal fractions, the concept also takes place discharge.

The digits in decimal fractions up to the decimal point are called the same as the digits in natural numbers. The digits in decimal fractions after the decimal point are listed in the table:

Picture 1.

Example 3

For example, in the decimal fraction $56,328$, $5$ is in the tens place, $6$ is in the units place, $3$ is in the tenth place, $2$ is in the hundredth place, $8$ is in the thousandth place.

The digits in decimal fractions are distinguished by seniority. When reading a decimal fraction, they move from left to right - from senior discharge to junior.

Example 4

For example, in decimal $56.328$, the most significant (highest) digit is the tens digit, and the least significant (lowest) digit is the thousandths digit.

A decimal fraction can be expanded into digits in the same way as expansion into digits of a natural number.

Example 5

For example, let's expand the decimal fraction $37,851$ into digits:

$37,851=30+7+0,8+0,05+0,001$

End decimals

Definition 2

End decimals are called decimal fractions, the records of which contain a finite number of characters (digits).

For example, $0.138; $5.34; $56.123456; $350,972.54.

Any final decimal fraction can be converted to a common fraction or a mixed number.

Example 6

For example, the final decimal fraction $7.39$ corresponds to the fractional number $7\frac(39)(100)$, and the final decimal fraction $0.5$ corresponds to the proper fraction $\frac(5)(10)$ (or any fraction, which is equal to it, for example, $\frac(1)(2)$ or $\frac(10)(20)$.

Converting an ordinary fraction to a decimal fraction

Convert common fractions with denominators $10, 100, \dots$ to decimals

Before converting some proper ordinary fractions to decimals, they must first be “prepared”. The result of such preparation should be the same number of digits in the numerator and the number of zeros in the denominator.

The essence of the “preliminary preparation” of correct ordinary fractions for conversion to decimal fractions is to add on the left in the numerator such a number of zeros that the total number of digits becomes equal to the number of zeros in the denominator.

Example 7

For example, let's prepare the common fraction $\frac(43)(1000)$ for conversion to decimal and get $\frac(043)(1000)$. And the ordinary fraction $\frac(83)(100)$ does not need to be prepared.

Let's formulate rule for converting a proper common fraction with denominator $10$, or $100$, or $1\000$, $\dots$ to a decimal fraction:

write $0$;

put a decimal point after it;

write down the number from the numerator (together with added zeros after preparation, if necessary).

Example 8

Convert proper fraction $\frac(23)(100)$ to decimal.

Solution.

The denominator is the number $100$, which contains $2$ two zeros. The numerator contains the number $23$, which contains $2$.digits. this means that preparation for this fraction for conversion to decimal is not necessary.

Let's write $0$, put a decimal point and write the number $23$ from the numerator. We get the decimal fraction $0.23$.

Answer: $0,23$.

Example 9

Write the proper fraction $\frac(351)(100000)$ as a decimal.

Solution.

The numerator of this fraction has $3$ digits, and the number of zeros in the denominator is $5$, so this ordinary fraction needs to be prepared for conversion to decimal. To do this, add $5-3=2$ zeros to the left in the numerator: $\frac(00351)(100000)$.

Now we can form the desired decimal fraction. To do this, write $0$, then put a comma and write the number from the numerator. We get the decimal fraction $0.00351$.

Answer: $0,00351$.

Let's formulate rule for converting improper common fractions with denominators $10$, $100$, $\dots$ to decimals:

write a number from the numerator;

separate with a decimal point as many digits on the right as there are zeros in the denominator of the original fraction.

Example 10

Convert improper common fraction $\frac(12756)(100)$ to decimal.

Solution.

Let's write the number from the numerator $12756$, then separate the digits on the right with a decimal point $2$, because the denominator of the original fraction $2$ is zero. We get the decimal fraction $127.56$.