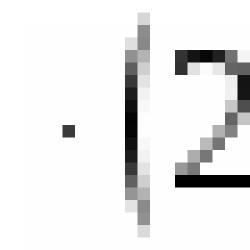"Natural logarithm" - 0.1. natural logarithms. 4. "Logarithmic darts". 0.04. 7.121.

"Power function grade 9" - U. Cubic parabola. Y = x3. Grade 9 teacher Ladoshkina I.A. Y = x2. Hyperbola. 0. Y \u003d xn, y \u003d x-n where n is a given natural number. X. The exponent is an even natural number (2n).

"Quadratic function" - 1 Quadratic function definition 2 Function properties 3 Function graphs 4 Quadratic inequalities 5 Conclusion. Properties: Inequalities: Prepared by Andrey Gerlitz, a student of grade 8A. Plan: Graph: -Intervals of monotonicity at a > 0 at a< 0. Квадратичная функция. Квадратичные функции используются уже много лет.

"Quadratic function and its graph" - Decision. y \u003d 4x A (0.5: 1) 1 \u003d 1 A-belongs. When a=1, the formula y=ax takes the form.

"Class 8 quadratic function" - 1) Construct the top of the parabola. Plotting a quadratic function. x. -7. Plot the function. Algebra Grade 8 Teacher 496 school Bovina TV -1. Construction plan. 2) Construct the axis of symmetry x=-1. y.

Build a function

We bring to your attention a service for plotting function graphs online, all rights to which belong to the company Desmos. Use the left column to enter functions. You can enter manually or using the virtual keyboard at the bottom of the window. To enlarge the chart window, you can hide both the left column and the virtual keyboard.

Benefits of online charting

• Visual display of introduced functions
• Building very complex graphs
• Plotting implicitly defined graphs (e.g. ellipse x^2/9+y^2/16=1)
• The ability to save charts and get a link to them, which becomes available to everyone on the Internet
• Scale control, line color
• The ability to plot graphs by points, the use of constants
• Construction of several graphs of functions at the same time
• Plotting in polar coordinates (use r and θ(\theta))

With us it is easy to build graphs of varying complexity online. The construction is done instantly. The service is in demand for finding intersection points of functions, for displaying graphs for their further transfer to a Word document as illustrations for solving problems, for analyzing the behavioral features of function graphs. The best browser for working with charts on this page of the site is Google Chrome. When using other browsers, correct operation is not guaranteed.

Lesson: how to build a parabola or a quadratic function?

THEORETICAL PART

A parabola is a graph of a function described by the formula ax 2 +bx+c=0.
To build a parabola, you need to follow a simple algorithm of actions:

1) Parabola formula y=ax 2 +bx+c,
If a>0 then the branches of the parabola are directed up,
and then the branches of the parabola are directed down.
free member c this point intersects the parabola with the OY axis;

2) , it is found by the formula x=(-b)/2a, we substitute the found x into the parabola equation and find y;

3)Function zeros or in other words, the points of intersection of the parabola with the OX axis, they are also called the roots of the equation. To find the roots, we equate the equation to 0 ax2+bx+c=0;

Types of equations:

a) The complete quadratic equation is ax2+bx+c=0 and is solved by the discriminant;
b) Incomplete quadratic equation of the form ax2+bx=0. To solve it, you need to take x out of brackets, then equate each factor to 0:
ax2+bx=0,
x(ax+b)=0,
x=0 and ax+b=0;
c) Incomplete quadratic equation of the form ax2+c=0. To solve it, you need to move the unknown to one side, and the known to the other. x =±√(c/a);

4) Find some additional points to build the function.

PRACTICAL PART

And so now, with an example, we will analyze everything by actions:
Example #1:
y=x 2 +4x+3
c=3 means the parabola intersects OY at the point x=0 y=3. The branches of the parabola look up because a=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4- 8+3=-1 vertex is at point (-2;-1)
Find the roots of the equation x 2 +4x+3=0
We find the roots by the discriminant
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x1=(-4+2)/2=-1
x2=(-4-2)/2=-3

Let's take some arbitrary points that are near the top x=-2

x -4 -3 -1 0
y 3 0 0 3

We substitute instead of x in the equation y \u003d x 2 + 4x + 3 values
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
It can be seen from the values ​​​​of the function that the parabola is symmetrical about the straight line x \u003d -2

Example #2:
y=-x 2 +4x
c=0 means the parabola intersects OY at the point x=0 y=0. The branches of the parabola look down because a=-1 -1 Find the roots of the equation -x 2 +4x=0
An incomplete quadratic equation of the form ax 2 +bx=0. To solve it, you need to take x out of brackets, then equate each factor to 0.
x(-x+4)=0, x=0 and x=4.

Let's take some arbitrary points that are near the vertex x=2
x 0 1 3 4
y 0 3 3 0
We substitute instead of x in the equation y \u003d -x 2 +4x values
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
It can be seen from the values ​​​​of the function that the parabola is symmetrical about the straight line x \u003d 2

Example #3
y=x 2 -4
c=4 means the parabola intersects OY at the point x=0 y=4. The branches of the parabola look up because a=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 vertex is at point (0;-4 )
Find the roots of the equation x 2 -4=0
An incomplete quadratic equation of the form ax 2 +c=0. To solve it, you need to move the unknown to one side, and the known to the other. x =±√(c/a)
x2=4
x1=2
x 2 \u003d -2

Let's take some arbitrary points that are near the top x=0
x -2 -1 1 2
y 0 -3 -3 0
We substitute instead of x in the equation y \u003d x 2 -4 values
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
It can be seen from the values ​​of the function that the parabola is symmetrical about the straight line x=0

Subscribe to the channel on YOUTUBE to keep abreast of all the news and prepare with us for exams.

The form y = kx + m with two variables x, y. True, the variables x, y appearing in this equation (in this mathematical model) were considered unequal: x is an independent variable (argument), to which we could attach any values, regardless of anything; y is the dependent variable because its value depended on which value of x was chosen. But then a natural question arises: are there any mathematical models of the same plan, but those in which y is expressed through x not according to the formula y \u003d kx + m, but in some other way? The answer is clear: of course they do. If, for example, x is the side of a square and y is its
area, then y - x 2 . If x is the side of the cube and y is its volume, then y is x 3 . If x is one side of a rectangle whose area is 100 cm 2, and y is its other side, then. Therefore, it is natural that in mathematics they are not limited to studying the model y-kx + m, one has to study the model y \u003d x 2, and the model y \u003d x 3, and the model, and many other models that have the same structure: on the left side of the equality is the variable y, and in the right - some expression with the variable x. For such models, the term "function" is retained, omitting the adjective "linear".

In this section, we consider the function y = x 2 and construct it schedule.

Let's give the independent variable x several specific values ​​​​and calculate the corresponding values ​​​​of the dependent variable y (using the formula y \u003d x 2):

if x \u003d 0, then y \u003d O 2 \u003d 0;
if x \u003d 1, then y \u003d I 2 \u003d 1;
if x = 2, then y = 2 2 = 4;
if x \u003d 3, then y \u003d Z 2 \u003d 9;
if x \u003d - 1, then y \u003d (- I 2) - 1;
if x \u003d - 2, then y \u003d (- 2) 2 \u003d 4;
if x \u003d - 3, then y \u003d (- Z) 2 \u003d 9;
In short, we have compiled the following table:

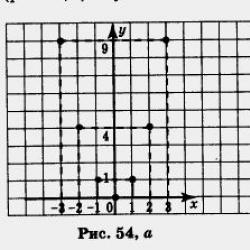
Let's construct the found points (0; 0), (1; 1), (2; 4), 93; 9), (-1; 1), (- 2; 4), (- 3; 9), on the xOy coordinate plane (Fig. 54, a).

These points are located on a certain line, let's draw it (Fig. 54, b). This line is called a parabola.

Of course, ideally, one would have to give the argument x all possible values, calculate the corresponding values ​​of the variable y, and plot the resulting points (x; y). Then the schedule would be absolutely accurate, flawless. However, this is unrealistic, because there are infinitely many such points. Therefore, mathematicians do this: they take a finite set of points, build them on coordinate plane and see which line is drawn by these points. If the contours of this line appear quite clearly (as we did, say, in example 1 from § 28), then this line is drawn. Are mistakes possible? Not without it. Therefore, it is necessary to study mathematics deeper and deeper so that there are means to avoid mistakes.

Let's try, looking at Figure 54, to describe the geometric properties of a parabola.

Firstly, we note that the parabola looks quite beautiful, because it has symmetry. Indeed, if any line parallel to the x-axis is drawn above the x-axis, then this line will intersect the parabola at two points located at equal distances from the y-axis, but on opposite sides of it (Fig. 55). By the way, the same can be said about the points marked in Figure 54, but:

(1; 1) and (- 1; 1); (2; 4) and (-2; 4); C; 9) and (-3; 9).

It is said that the y-axis is the axis of symmetry of the parabola y=x2 or that the parabola is symmetrical about the y-axis.

Secondly, we notice that the axis of symmetry, as it were, cuts the parabola into two parts, which are usually called the branches of the parabola.

Third, we note that the parabola has a singular point at which both branches meet and which lies on the axis of symmetry of the parabola - the point (0; 0). Given its peculiarity, it was given a special name - the top of the parabola.

Fourth when one branch of the parabola connects at the top with another branch, this happens smoothly, without a break; the parabola, as it were, "presses" against the abscissa axis. Usually they say: the parabola touches the x-axis.

Now let's try, looking at Figure 54, to describe some properties of the function y \u003d x 2.

Firstly, we notice that y - 0 for x = 0, y > 0 for x > 0 and for x< 0.

Secondly, note that y nam. = 0, while naib does not exist.

Third, we notice that the function y \u003d x 2 decreases on the beam (-° °, 0] - for these values ​​of x, moving along the parabola from left to right, we “go down the hill” (see Fig. 55). Function y \u003d x 2 increases on the beam ;
b) on the segment [- 3, - 1.5];
c) on the segment [- 3, 2].

Solution,

a) Let's build a parabola y \u003d x 2 and select that part of it that corresponds to the values ​​​​of the variable x from the segment (Fig. 56). For the selected part of the graph, we find at naim. = 1 (for x = 1), y max. = 9 (for x = 3).

b) Let's build a parabola y \u003d x 2 and select that part of it that corresponds to the values ​​​​of the variable x from the segment [-3, -1.5] (Fig. 57). For the selected part of the graph, we find y name. \u003d 2.25 (at x \u003d - 1.5), y max. = 9 (at x = - 3).

c) Let's build a parabola y \u003d x 2 and select that part of it that corresponds to the values ​​​​of the variable x from the segment [-3, 2] (Fig. 58). For the selected part of the graph, we find y max = 0 (at x = 0), y max. = 9 (at x = - 3).

Advice. In order not to plot the function y - x 2 point by point each time, cut out a parabola template from thick paper. With it, you will be able to draw a parabola very quickly.

Comment. Offering you to prepare a parabola template, we, as it were, equalize the rights of the function y \u003d x 2 and linear function y = kx + m. After all, the graph of a linear function is a straight line, and an ordinary ruler is used to depict a straight line - this is the template of the graph of the function y \u003d kx + m. So let you also have a graph template for the function y \u003d x 2.

Example 2 Find the intersection points of the parabola y \u003d x 2 and the line y - x + 2.

Solution. Let us construct a parabola y \u003d x 2 in one coordinate system, a straight line y \u003d x + 2 (Fig. 59). They intersect at points A and B, and according to the drawing it is not difficult to find the coordinates of these points A and B: for point A we have: x \u003d - 1, y \u003d 1, and for point B we have: x - 2, y \u003d 4.

Answer: the parabola y \u003d x 2 and the straight line y \u003d x + 2 intersect at two points: A (-1; 1) and B (2; 4).

Important note. Until now, we have rather boldly drawn conclusions with the help of a drawing. However, mathematicians do not trust drawings too much. Having found in figure 59 two points of intersection of a parabola and a line and having determined the coordinates of these points using the figure, a mathematician usually checks himself: does the point (-1; 1) actually lie both on the line and on the parabola; does the point (2; 4) really lie on both the line and the parabola?

To do this, you need to substitute the coordinates of points A and B in the equation of a straight line and in the equation of a parabola, and then make sure that in both cases the correct equality will be obtained. In example 2, in both cases, the correct equalities will be obtained. Such a check is especially often made when the accuracy of the drawing is in doubt.

In conclusion, we note one curious property of the parabola, discovered and proved jointly by physicists and mathematicians.

If we consider the parabola y \u003d x 2 as a screen, as a reflective surface, and place a light source at a point, then the rays, reflected from the parabola of the screen, form a parallel beam of light (Fig. 60). The point is called the focus of the parabola. This idea is used in automobiles: the reflective surface of the headlight is parabolic, and the light bulb is placed at a focal point - then the light from the headlight travels far enough.

Calendar-thematic planning in mathematics, video in mathematics online, Math at school download

A. V. Pogorelov, Geometry for grades 7-11, Textbook for educational institutions

The construction of graphs of functions containing modules usually causes considerable difficulties for schoolchildren. However, everything is not so bad. It is enough to remember several algorithms for solving such problems, and you can easily plot even the most seemingly complex function. Let's see what these algorithms are.

1. Plotting the function y = |f(x)|

Note that the set of function values ​​y = |f(x)| : y ≥ 0. Thus, the graphs of such functions are always located completely in the upper half-plane.

Plotting the function y = |f(x)| consists of the following simple four steps.

1) Construct carefully and carefully the graph of the function y = f(x).

2) Leave unchanged all points of the graph that are above or on the 0x axis.

3) The part of the graph that lies below the 0x axis, display symmetrically about the 0x axis.

Example 1. Draw a graph of the function y = |x 2 - 4x + 3|

1) We build a graph of the function y \u003d x 2 - 4x + 3. It is obvious that the graph of this function is a parabola. Let's find the coordinates of all points of intersection of the parabola with the coordinate axes and the coordinates of the vertex of the parabola.

x 2 - 4x + 3 = 0.

x 1 = 3, x 2 = 1.

Therefore, the parabola intersects the 0x axis at points (3, 0) and (1, 0).

y \u003d 0 2 - 4 0 + 3 \u003d 3.

Therefore, the parabola intersects the 0y axis at the point (0, 3).

Parabola vertex coordinates:

x in \u003d - (-4/2) \u003d 2, y in \u003d 2 2 - 4 2 + 3 \u003d -1.

Therefore, the point (2, -1) is the vertex of this parabola.

Draw a parabola using the received data (Fig. 1)

2) The part of the graph lying below the 0x axis is displayed symmetrically with respect to the 0x axis.

3) We get the graph of the original function ( rice. 2, shown by dotted line).

2. Plotting the function y = f(|x|)

Note that functions of the form y = f(|x|) are even:

y(-x) = f(|-x|) = f(|x|) = y(x). This means that the graphs of such functions are symmetrical about the 0y axis.

Plotting the function y = f(|x|) consists of the following simple chain of actions.

1) Plot the function y = f(x).

2) Leave that part of the graph for which x ≥ 0, that is, the part of the graph located in the right half-plane.

3) Display the part of the graph specified in paragraph (2) symmetrically to the 0y axis.

4) As the final graph, select the union of the curves obtained in paragraphs (2) and (3).

Example 2. Draw a graph of the function y = x 2 – 4 · |x| + 3

Since x 2 = |x| 2 , then the original function can be rewritten as follows: y = |x| 2 – 4 · |x| + 3. And now we can apply the algorithm proposed above.

1) We build carefully and carefully the graph of the function y \u003d x 2 - 4 x + 3 (see also rice. 1).

2) We leave that part of the graph for which x ≥ 0, that is, the part of the graph located in the right half-plane.

3) Display the right side of the graph symmetrically to the 0y axis.

(Fig. 3).

Example 3. Draw a graph of the function y = log 2 |x|

We apply the scheme given above.

1) We plot the function y = log 2 x (Fig. 4).

3. Plotting the function y = |f(|x|)|

Note that functions of the form y = |f(|x|)| are also even. Indeed, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), and therefore, their graphs are symmetrical about the 0y axis. The set of values ​​of such functions: y ≥ 0. Hence, the graphs of such functions are located completely in the upper half-plane.

To plot the function y = |f(|x|)|, you need to:

1) Construct a neat graph of the function y = f(|x|).

2) Leave unchanged the part of the graph that is above or on the 0x axis.

3) The part of the graph located below the 0x axis should be displayed symmetrically with respect to the 0x axis.

4) As the final graph, select the union of the curves obtained in paragraphs (2) and (3).

Example 4. Draw a graph of the function y = |-x 2 + 2|x| – 1|.

1) Note that x 2 = |x| 2. Hence, instead of the original function y = -x 2 + 2|x| - 1

you can use the function y = -|x| 2 + 2|x| – 1, since their graphs are the same.

We build a graph y = -|x| 2 + 2|x| – 1. For this, we use algorithm 2.

a) We plot the function y \u003d -x 2 + 2x - 1 (Fig. 6).

b) We leave that part of the graph, which is located in the right half-plane.

c) Display the resulting part of the graph symmetrically to the 0y axis.

d) The resulting graph is shown in the figure with a dotted line (Fig. 7).

2) There are no points above the 0x axis, we leave the points on the 0x axis unchanged.

3) The part of the graph located below the 0x axis is displayed symmetrically with respect to 0x.

4) The resulting graph is shown in the figure by a dotted line (Fig. 8).

Example 5. Plot the function y = |(2|x| – 4) / (|x| + 3)|

1) First you need to plot the function y = (2|x| – 4) / (|x| + 3). To do this, we return to algorithm 2.

a) Carefully plot the function y = (2x – 4) / (x + 3) (Fig. 9).

Note that this function is linear-fractional and its graph is a hyperbola. To build a curve, you first need to find the asymptotes of the graph. Horizontal - y \u003d 2/1 (the ratio of the coefficients at x in the numerator and denominator of a fraction), vertical - x \u003d -3.

2) The part of the chart that is above or on the 0x axis will be left unchanged.

3) The part of the chart located below the 0x axis will be displayed symmetrically with respect to 0x.

4) The final graph is shown in the figure (Fig. 11).

site, with full or partial copying of the material, a link to the source is required.