Energy transitions in the atom
As a manuscript
Physics
Lecture notes
(Part 7. Atomic physics. lasers)
For students of direction 230400
« Information Systems and technologies"
Electronic educational resource
Compiled by: Candidate of Physical and Mathematical Sciences, Associate Professor V.V. Konovalenko
Minutes No. 1 dated 04.09.2013
Atomic physics
Hydrogen atom.
Recall that a system consisting of a fixed nucleus and an electron moving around it is called a hydrogen-like atom or a hydrogen-like ion.
The field in which the electron moves is centrally symmetric. Therefore, when solving the Schrödingenr equation in this case, a spherical coordinate system is used: The Schrödingenr equation for an electron in the central field of a nucleus with a charge has the form:
 (35.1)
(35.1)
Substituting the Laplace operator in spherical coordinates into this equation, we get:
Solutions (35.2) satisfying standard conditions, are obtained for any positive E and for discrete negative values:
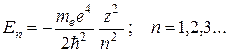 (35.3)
(35.3)
Positive energy values correspond to an electron flying near the nucleus and receding to infinity. Such an electron is not bound to the nucleus, does not form an atom (or ion), and is of no interest.
An electron bound to a nucleus corresponds to negative values of energy (35.3). It must be emphasized that these values correspond to the values obtained in the Bohr theory, but in quantum mechanics they are a consequence of the Schrödinger equation, and additional assumptions in the form of postulates are not required.
The eigenfunctions of the Schrödinger equation contain three integer parameters: n,l,m:
![]()
n- is called principal quantum number and coincides with the energy level number in (35.3).
l and m – azimuth and magnetic quantum numbers , which determine the module and the projection of the angular momentum on a certain direction.
Solutions satisfying the standard conditions are obtained only for the values l not exceeding . Therefore, for a given n, azimuthal quantum number l may matter
![]() (35.4)
(35.4)
For a given l magnetic quantum number m can take on different values:
(35.5)
The electron energy of an electron in a hydrogen atom depends only on n main quantum number(see (35.3)), therefore, each energy level corresponds to several eigenfunctions that differ in values l and m. In this way, a hydrogen atom can have the same energy, being in states described by different wave functions. The energy states in this case are called degenerate , and the number of different states corresponding to a given energy is the multiplicity of the degeneracy of the corresponding energy level.
Degeneracy multiplicity energy levels hydrogen is easy to calculate. Each of n number values l corresponds to 2 l+ 1 value m. Thus, the degeneracy multiplicity can be calculated by the formula:
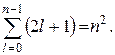
Recall that the azimuthal quantum number determines the value of the angular momentum, and the states of an electron in a hydrogen atom with different values of the azimuthal quantum number l differ in the magnitude of the angular momentum. An electron in a state with
l= 0 – calleds -electron ( s condition);
l= 1 - calledp -electron (p state)
l= 2– calledd -electron (d state)
l= 3 - calledf -electron (f state), etc.
When designating the state in which the electron is located, the value of the main quantum number is taken n indicate before the symbol of the quantum number l. Therefore, an electron n= 3 at l = 1 is denoted by symbols 3 p.
Because the l< n the following states are possible:
2s 2p
3s 3p 3d
4s 4p 4d 4f etc.
As in Bohr's theory, quantum mechanics assumes that light is emitted and absorbed when an electron moves from one level to another. However, the photon has own angular momentum equal approximately Therefore, when a photon is emitted or absorbed, the angular momentum of an atom must change by selection rule for the azimuthal quantum number:
Obviously, this rule is simply a consequence of the law of conservation of angular momentum.
Diagram of the energy levels of the hydrogen atom.
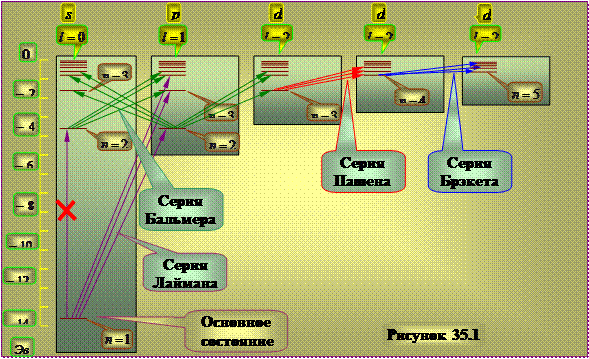 |
Selection rule effect(35.6) leads to the fact that not all transitions between energy levels can actually be realized. For example transition from state 2 s in 1s cannot happen because it contradicts the selection rule. In this regard, the scheme of energy levels of an electron in a hydrogen atom can be represented as shown in Figure 35.1
The 1s state is the ground state of the hydrogen atom where the hydrogen atom has the lowest energy. When absorbed by an atom, a photon disappears completely, transferring its energy to the atom, since it is indivisible. The absorbing atom is usually in the ground state, so the absorption spectrum of a hydrogen atom should consist of lines corresponding to transitions 1 s-np, which is in complete agreement with the experimental results.
Electron in a hydrogen atom
The eigenfunctions of the Schrödinger equation for the hydrogen atom split into two factors, one of which depends only on r, and the other from the corners J and j.
The multiplier is real, - imaginary. The function is an eigenfunction of the angular momentum squared operator. For s-states of an electron (i.e. with an angular momentum equal to zero), this function is a constant, and -functions of the form depend only on r.
volume element dV spherical coordinate system can be represented as
![]()
where d W = is the element of the solid angle.
Probability dP finding an electron in an element dV
Taking the integral of (35.7) over the solid angle 4 p, we find the probability of finding an electron in a thin spherical layer of radius r and thickness dr:.
![]() (35.9)
(35.9)
Since Y is assumed to be normalized, the integral in (35.9) is equal to one, and
![]() (35.10)
(35.10)
From (35.9) it follows that is the probability density of finding an electron at a distance r from the nucleus ,
The long vertical lines show the radii of the corresponding Bohr orbits.
Figure 35.1
Spectra alkali metals
These spectra are similar to the emission spectrum of the hydrogen atom, but only qualitatively. Several series of lines are observed, and the most intense of them are named based on experimentally observed features:
sharp(sharp) - The lines of this series looked very clear and narrow.
home(principal) - the lines of this series were also observed in the absorption and emission spectra, which indicated that they correspond to the transition of atoms to the ground state;
blurry(diffuse) - the lines of this series looked blurry, fuzzy;
main(fundamental) - the lines of this series resembled a series of lines of the hydrogen atom.
It was found that the considered series of lines are associated with transitions of the outer (valence) or optical electron .
The system of energy levels corresponding to the emission of the indicated lines for the sodium atom has the form approximately shown in figure 35.3.
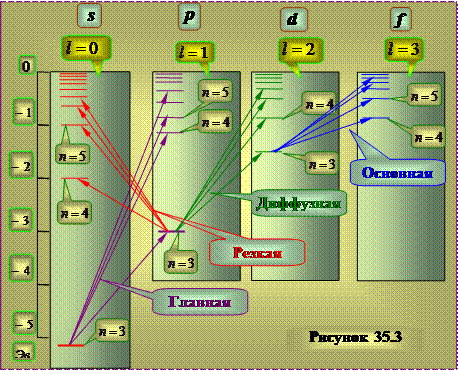 Unlike the hydrogen atom, the energy of the state turns out to depend not only on the value of the quantum number n, but also on the number of the series of terms.
The series of terms, as in the hydrogen atom, correspond to different values of the azimuthal quantum number l.
Unlike the hydrogen atom, the energy of the state turns out to depend not only on the value of the quantum number n, but also on the number of the series of terms.
The series of terms, as in the hydrogen atom, correspond to different values of the azimuthal quantum number l.
These conclusions correspond to the results of quantum mechanical calculations - the solution of the Schrödinger equation for an electron moving in centrally symmetric non-Coulomb field. The field of the nucleus in alkali metal atoms is partially screened by the electrons of the inner electron shells of the atoms. In this case, the field retains spherical symmetry, but varies from the distance to the nucleus according to a law different from the Coulomb law. In such a field, the energy of an electron turns out to depend on the quantum number: It is customary to say that the degeneracy is lifted azimuthal quantum number . However, Basically, the energy depends on principal quantum number n.
Determined that the angular momentum of the atomic residue of alkali atoms after the removal of an optical electron is zero . Therefore, the azimuthal quantum number L of the resulting angular momentum atom coincides with azimuthal quantum number valence electron. When an atom is excited (i.e., when it is transferred by some action from a state with a minimum energy to a state with a higher energy) and when it emits light state only changes valence electron , therefore the scheme of levels of an atom is identical to the scheme of the equation of a valence electron.
The terms corresponding to the columns of levels can be denoted on the energy level diagram by the symbols nS, nP, nD and nF. Then the frequencies spectral lines, equal to the difference between the terms of the final and initial states, can be represented in the following form: excited states cannot be considered strictly stationary. Due to the fact that time and energy are canonically conjugate quantities, the uncertainty relation determines the finite width Г of the energy levels:
Only the ground state does not allow spontaneous transitions and its energy has a strictly defined value.
In accordance with finite Г, the frequency range of emitted photons
For visible light with corresponding ![]() it the so-called natural linewidth
.
it the so-called natural linewidth
.
Thermal motion of atoms leads to Doppler broadening of spectral lines. In this case, for radiation with a wavelength at a temperature T\u003d 1000 K, the value is obtained ![]() , which is many times greater than the natural width of the spectral lines.
, which is many times greater than the natural width of the spectral lines.
The energy of the hydrogen atom, as follows from (6), is determined only by the main quantum number n. lowest energy level E 1 , corresponding n \u003d 1, corresponds to the minimum possible energy of an atom and is called the main one. All other energy levels E n (E n > E 1 , n= 2,3,..) are called excited. The diagram of the energy levels of the hydrogen atom with a graph of the dependence of the potential energy U(r) on the distance to the nucleus is shown in fig. 2. For negative values of energy (E<0) движение электрона является связанным. По мере роста главного квантового числа n уровни располагаются теснее и при n→ ∞ E ∞ =0.
For positive energy values, the motion of an electron is free, the region of the continuous spectrum E> 0 (shaded in Fig. 2) corresponds to an ionized atom. Ionization energy of a hydrogen atom

Scheme of the energy levels of the hydrogen atom (Fig. 2a) and transitions
between them (Fig. 2b). [E] - eV.
Energy set point, except E 1 , corresponds to several different states of the atom, differing in the values of quantum numbers l and m. Conditionally values with l= 0, 1, 2,… are denoted by Latin letters s, p, d, f,… The value of the main quantum number is indicated by a number before the designation of the orbital quantum number. For example, electrons in the state n= 1 and l= 0 are denoted by 1s, in the state n= 2 and l\u003d 0, 1 - respectively 2s and 2p; With n=3 - 3s, 3p, 3d, etc.
Taking into account different values of quantum numbers n and l generally accepted is the diagram of the image of energy levels, shown in fig. 3.

Scheme of the energy levels of the hydrogen atom and transitions between them, taking into account the orbital quantum number l.
Emission and absorption of light by an atom occurs when an electron passes from one energy level to any other, and the energy of the emitted (absorbed) quantum is equal to:
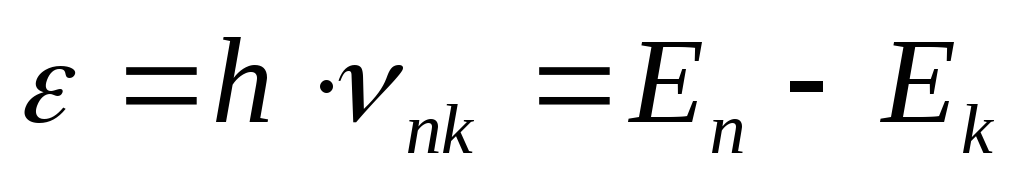 (18) where n,
k
are the numbers of energy levels (states), respectively, ν is the frequency of the electromagnetic radiation of the transition n→
k.
In the process of emission (absorption) of light, only such transitions can occur, as a result of which changes in the orbital and magnetic quantum numbers are determined by the conditions:
(18) where n,
k
are the numbers of energy levels (states), respectively, ν is the frequency of the electromagnetic radiation of the transition n→
k.
In the process of emission (absorption) of light, only such transitions can occur, as a result of which changes in the orbital and magnetic quantum numbers are determined by the conditions:
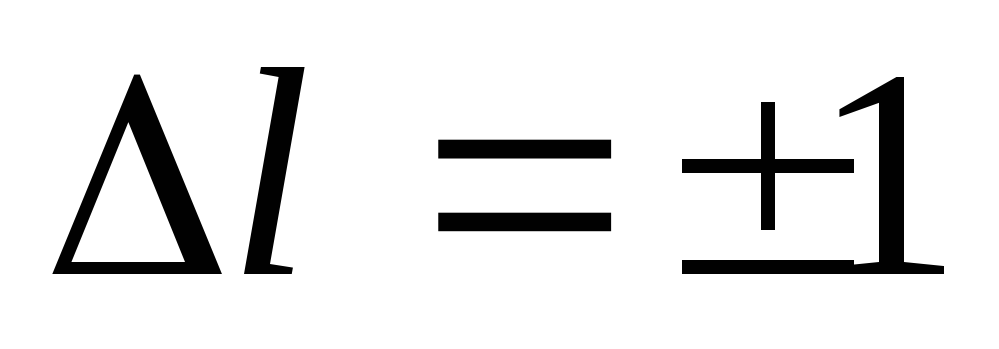 (19)
(19)
 (20)
(20)
Formulas (19) and (20) are called selection rules, which limit the number of possible electron transitions in an atom.
Taking into account (6), the radiation frequency during the transition of the hydrogen atom (Z = 1) from the stationary state n to a steady state k with less energy is:
 (21)
(21)
Where k, n-whole numbers; k < n.
Because  , then formula (21), by determining the wavelengths of the corresponding transitions, takes the form:
, then formula (21), by determining the wavelengths of the corresponding transitions, takes the form:
 (22)
(22)
Where R is the Rydberg constant equal to
 (23)
(23)
From expressions (21) and (22) it follows that for given k and changing values n (n >k) spectral lines form groups or series. In the emission spectrum of the hydrogen atom, as follows from (22), the following series are distinguished, the wavelengths of which are found by the formulas:
Lyman series (ultraviolet region of the spectrum):
 , where n=2,3,4,…
(24)
, where n=2,3,4,…
(24)
 (24a)
(24a)
Balmer series (visible spectrum):
 , where n=
3,4,5,…
(25)
, where n=
3,4,5,…
(25)
Paschen series (infrared spectrum):
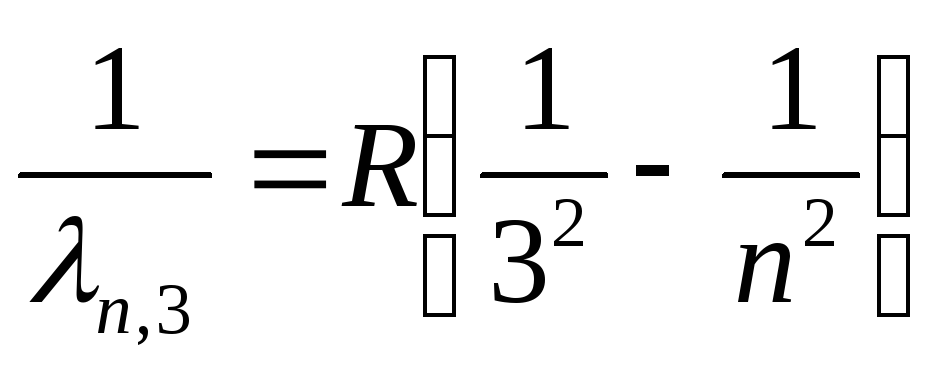 , where n=
4,5,6,…
(26)
, where n=
4,5,6,…
(26)
Bracket Series (Far Infrared):
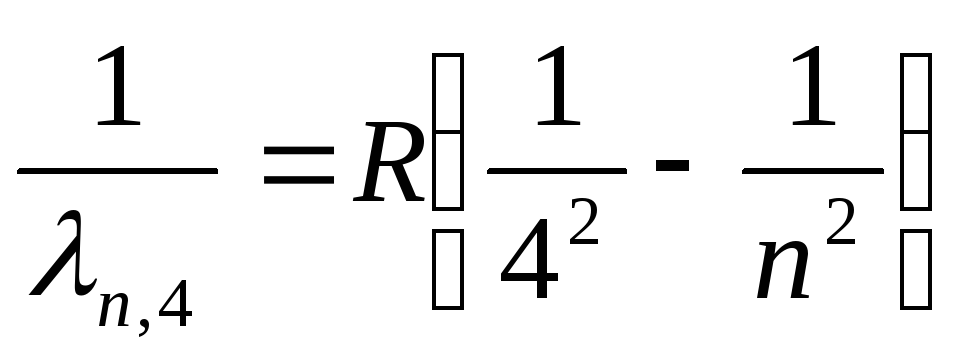 , where n=5,6,7,…
(27)
, where n=5,6,7,…
(27)
Formulas (24a)-(27a), in accordance with the selection rules (19), determine the states of the electron, during the transition between which the spectral lines of the reduced series in the hydrogen atom are emitted. For the Lyman and Balmer series, they are shown in Fig. 3 completely.
It should be noted that formulas (21)-(22), obtained theoretically in quantum mechanics for calculating the wavelengths (frequencies) of the spectral lines of the hydrogen atom, coincide with the generalized Balmer formula (1), previously obtained empirically by generalizing experimental data.
hydrogen atom
Hydrogen Atom
hydrogen atom- a bound system consisting of a positively charged nucleus - a proton and a negatively charged electron.
The size of an atom is determined by its size electron shell≈ 10 -8 cm.
The energies of the bound states of an electron are obtained by solving the Schrödinger equation with the potential V(r) = -e 2 /r and are determined by the relation
where n is the main quantum number that determines the energies of various states of an electron in a hydrogen atom (n = 1, 2, 3…), R is the Rydberg constant
(R = 1.0974 10 5 cm -1).
Each level with the main quantum number n corresponds to n states differing in quantum numbers l = 0, 1, 2, ..., (n-1). Such a degeneracy of levels in energy is typical only for the Coulomb field. In addition, each of these l-degenerate states is (2l + 1)-fold degenerate in the magnetic number
m = ±l, ±(l-1),...±1, 0. Thus, the total multiplicity of the degeneracy of the stationary quantum state with principal quantum number n is given by .
This consideration is valid provided that the spin of the electron is zero. Since the electron has spin s = 1/2, the total angular momentum of the electron will be determined by vector sum its orbital and spin moments
=
+
.
Since the spin of an electron is s = 1/2, its total angular momentum J can only be half-integer.
For a given value of the orbital momentum l, two states are possible in the hydrogen atom, differing in the values of the total momentum = + = l + 1/2 and
j = l - s = l - 1/2. These two values differ in the mutual orientations of the orbital and spin vectors. The energies of an electron in the states l + 1/2 and l - 1/2 in the Coulomb field of a proton differ somewhat, and the degeneracy in the energy of the states is lifted. This additional interaction is called the spin-orbit interaction. Taking into account the removal of degeneracy, the spectrum of low-lying states of the hydrogen atom is enriched, and a fine splitting of energy levels occurs. Instead of two lower levels of hydrogen without taking into account the spin-orbit splitting (the main 1s and the first excited 2s2p (Fig. 1a)) with allowance for the spin-orbit splitting, there are four of them (Fig. 1b). The quantum characteristics of these levels are given in the table. The level with a large value j = l + 1/2 is located higher in energy than the level with j = l - 1/2. States with different values of l but the same value of nj are still degenerate. For example, 2s 1/2 and 2p 1/2 .
Quantum characteristics of an electron in the lowest
states of the hydrogen atom
| n | l | s | j = l ± s | level designation |
| 1 | 0 | 1/2 | 1/2 | 1s 1/2 |
| 2 | 0 1 |
1/2 1/2 |
1/2 1/2, 3/2 |
2s 1/2 2p 1/2, 2p 3/2 |
| 3 | 0 1 2 |
1/2 1/2 1/2 |
1/2 1/2, 3/2 3/2, 5/2 |
3s 1/2 3p 1/2 , 3p 3/2 3d 1/2 , 3d 3/2 |
From the exact solution relativistic equation Dirac for an electron with spin s = 1/2 follows the dependence of the energy of the levels of the hydrogen atom on the quantum numbers n and j
 ,
,
where α = 1/137 is the fine structure constant. The correction in E nj does not depend on the quantum number l. Therefore, the energies of states with the same j and different l must be equal. The fine splitting of levels δE j+1,j for a given n is determined by the relation
The splitting of the level with n = 2 is ≈ 4.5·10 -5 eV.
The nucleus of the hydrogen atom - the proton - also has its own moment - the spin s = 1/2. This also slightly changes the interaction of the electron with the proton, since there is an additional interaction of the magnetic moment of the proton, caused by the presence of its spin, with magnetic field electron. The value of this interaction depends on the mutual orientation of the spin moment of the proton and the total moment of the electron. Thus, another type of splitting of atomic levels arises, called hyperfine, since its value is much smaller than the fine splitting. Hyperfine splitting will be observed already for the ground state
(n = 1, l = 0). The transition between two sublevels of the hyperfine splitting of the ground state of hydrogen leads to radiation with a wavelength λ = 21 cm (radiation frequency 1420 MHz). With the help of this radiation, interstellar hydrogen in the Universe is usually registered.
The states from n = 2 to n = ∞ are called excited states. The excitation energy E ex (the energy that must be reported to the system so that it passes from the initial state n i to the final state n f) is determined from the relation

All states from n = 1 to n = ∞ are bound states because they have negative energies. As n approaches infinity, the energies of the states approach each other, and the difference in the energies of neighboring states becomes so small that the split levels merge, and the discrete spectrum of levels transforms into a continuous (continuous) one. When the energy of an electron becomes positive (E > 0), the system becomes unbound and the electron becomes free. The energy spectrum of a free electron is continuous.
Transitions from the states n = 2, 3, … ∞ to the state n = 1 form the Lyman series. Transitions from the state n = 3, 4, … ∞ to the state n = 2 are the Balmer series. Transitions between states with negative energy (E< 0) приводят
к образованию дискретного спектра переходов, в то время как переходы между
состояниями с E >0 and states with E< 0 дают непрерывный спектр переходов.
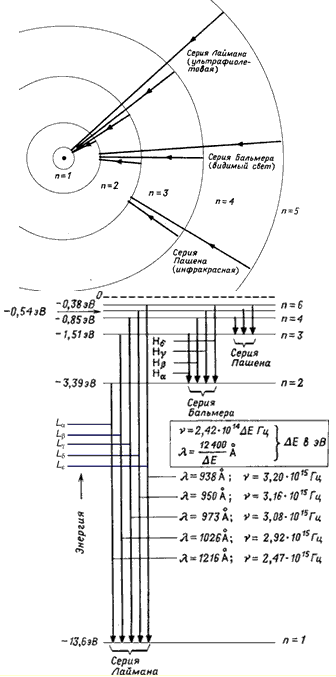
Rice. 2. Scheme of levels of the hydrogen atom.
According to the exact solution of the Dirac equation, energy levels with the same value of the quantum number n = 1, 2, 3,... and the same value of the total momentum
j = 1/2, 3/2,... must match in energy regardless of the value of the quantum number l. In 1947, W. Lamb and R. Riserford discovered a shift in the 2s 1/2 and 2p 1/2 levels in the hydrogen atom. This level shift is called Lamb shift
. The main reason for the Lamb shift is due to radiative corrections:
- Emission of virtual photons by a bound electron.
- Vacuum polarization - the birth of electron-positron pairs in vacuum.
These two corrections fully explain the observed Lamb shift of the 2s 1/2 and 2p 1/2 levels (ΔE = 4.5·10 -6 eV).
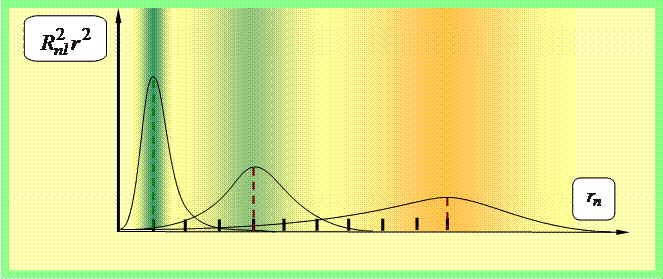
The probability dw of finding an electron in a volume dV at a certain point in space is given by
dw = |ψ(x, y, z)|2 dV = |R nl (r)Y lm (θ,φ)| 2 r 2 sinθdθdφdr =
= |R nl (r)| 2 r 2 |Y lm (θ,φ)| 2 sinθdθdφdr,
decomposes into the radial probability ||R nl (r)| 2 r 2 | 2 r 2 dr and angular - |Y lm (θ,φ)| 2 dΩ. The distributions of these probabilities are given in Figs. 3–5.
Suppose that the scheme of the lower energy levels of atoms of a certain element has the form shown in the figure, and the atoms are in a state with energy. An electron, having collided with one of such resting atoms, received some additional energy as a result of the collision. The momentum of the electron after the collision with the atom turned out to be equal Determine the kinetic energy of the electron before the collision. The possibility of emission of light by an atom in a collision with an electron is neglected. Ignore the recoil effect.
Solution.
p electron is related to its kinetic energy by the relation or where m is the mass of the electron.
Consequently,
Guest 18.05.2012 17:00
Please explain why the electron went into the state E(0) and why we add this energy (3.5 eV) to the energy of the electron?
Guest
Good afternoon!
According to Bohr's postulates, an atom can exist only in strictly defined states. When an atom and an electron collide, the law of conservation of energy is fulfilled. According to the condition, the energy of the electron increased, which means that the energy of the atom had to decrease. Since the atom is at the first energy level, the only way for it to decrease its energy is to go to the zero level. In this case, its energy decreases by Since the probability of radiation can be neglected, according to the condition, and the value of the kinetic energy of the recoil of the nucleus can be neglected due to its smallness, we conclude that all this energy is transferred to the electron.
Vitaly 22.03.2016 07:54
Hello!
There are several questions in problem 3045 in physics:
1) Do I understand correctly that the system indirectly refers to 2 electrons? One is in the field of the central forces of the nucleus. The second - a free electron flying past the atom and conditionally never interacting with the nucleus, but with the "atomic" electron - only at the moment of momentum transfer?
2) If the answer to the first question is "yes", then the scheme of "energy levels of the atom" - are these the permissible energy levels of the bound, "atomic" electron?
3) Is it correct that the incoming electron is at the level E (infinity) or higher?
4) A passing electron having interacted with email. in the atom was not captured? Does he fly away with even more energy?
5) What type of energy can be attributed to the energy of a passing electron (kinetic, etc.) at the moment of its approach to the atom?
After answering these questions, I will be able to decide whether there is an error in the task or not. Sorry for writing here, in China there are problems with access to VK.
Anton
1) No, the problem is about an atom and a free electron.
2) In this problem, it is not necessary to consider the contributions of the electrons of the atom and its nucleus to the energy levels of the atom. An atom is considered as a single object with a given energy spectrum.
3) A free electron is not part of an atom, it is not correct to place its energy on the diagram of the energy levels of an atom (its energy can be depicted side by side). If we talk about the possible spectrum of kinetic energies of a free electron, then it is continual (not discrete): In this problem kinetic energy free electron before the collision was 1.45 eV, and 4.95 eV after.
4) The electron interacted with the atom as a whole and received a portion of energy from it.
5) Kinetic.
Suppose that the scheme of the lower energy levels of atoms of a certain element has the form shown in the figure, and the atoms are in a state with energy. An electron, colliding with one of these atoms, received some additional energy as a result of the collision. The kinetic energy of the electron before the collision was equal to Determine the momentum of the electron after the collision with the atom. The possibility of emission of light by an atom during a collision with an electron is neglected; before the collision, the atom is considered immobile.
Solution.
If, upon collision with an atom, the electron acquired energy, then the atom passed into the state. Consequently, after the collision, the kinetic energy of the electron became equal to where is the energy of the electron before the collision; from here: Impulse p electron is related to its kinetic energy by the relation where m is the mass of the electron.
Consequently,
Answer:
The figure shows the energy levels of an atom and indicates the wavelengths of photons emitted and absorbed during transitions from one level to another. What is the wavelength of photons emitted during the transition from level to level if ?
Solution.
The frequency of a photon emitted or absorbed by an atom during the transition from one energy level to another is proportional to the energy difference between these levels. Therefore we have:
From here (because):
The figure shows the energy levels of the electron shell of an atom and indicates the frequencies of photons emitted and absorbed during transitions from one level to another. What is the wavelength of photons absorbed during the transition from level to level if
Solution.
The frequency of a photon emitted or absorbed by an atom during the transition from one energy level to another is proportional to the energy difference between these levels:
Therefore, we write: From here:
Answer:
The figure shows several energy levels of an atom and indicates the wavelengths of photons emitted and absorbed during transitions from one level to another.
It has been experimentally established that the minimum wavelength for photons emitted during transitions between these levels is What is the value of if ?
Solution.
The minimum wavelength corresponds to the maximum frequency and energy of the photon. That is, and
The frequency of a photon emitted or absorbed by an atom during the transition from one energy level to another is proportional to the energy difference between these two levels. That's why
The energy levels of an electron in a hydrogen atom are given by the formula where . When an atom passes from state to state, the atom emits a photon. Once on the surface of the photocathode, a photon knocks out a photoelectron. The wavelength of light corresponding to the red border of the photoelectric effect for the surface material of the photocathode, What is the maximum possible kinetic energy of the photoelectron?
Solution.
According to Bohr's postulates, light is emitted when an atom passes to lower energy levels, while photons carry an energy equal to the difference between the energies of the initial and final states. Thus, the emitted photon had an energy
Source: Unified State Examination in Physics 06/06/2013. main wave. Siberia. Option 1.
EV where . When an atom passes from state to state, the atom emits a photon. Once on the surface of the photocathode, this photon knocks out a photoelectron. Light frequency corresponding to the red border of the photoelectric effect for the material of the photocathode surface, Hz. What is the maximum possible momentum of a photoelectron?
Solution.
According to the photoelectric effect equation, the maximum kinetic energy of the emitted photoelectrons is related to the photon energy and the work function by the relation
Source: Unified State Examination in Physics 06/06/2013. main wave. Siberia. Option 2.
The energy levels of an electron in a hydrogen atom are given by the formula eV, where . When an atom passes from state to state, the atom emits a photon. Once on the surface of the photocathode, this photon knocks out a photoelectron. The wavelength of light corresponding to the red border of the photoelectric effect for the surface material of the photocathode, What is the maximum possible modulus of the photoelectron momentum?
Solution.
According to Bohr's postulates, light is emitted when an atom passes to lower energy levels, while photons carry an energy equal to the difference between the energies of the initial and final states. Thus, the emitted photon had an energy
According to the photoelectric effect equation, the maximum kinetic energy of the emitted photoelectrons is related to the photon energy and the work function by the relation
The work function is related to the wavelength of the red boundary by the relation:
Thus, the maximum possible momentum of a photoelectron is
Source: Unified State Examination in Physics 06/06/2013. main wave. Siberia. Option 3.
Energy levels of terms of of terms are given by the formula
where . When an atom passes from state to state, the atom emits a photon. Once on the surface of the photocathode, this photon knocks out a photoelectron. Light frequency corresponding to the red border of the photoelectric effect for the material of the photocathode surface, Hz. What is the maximum possible kinetic energy of a photoelectron?
Solution.
According to Bohr's postulates, light is emitted when an atom passes to lower energy levels, while photons carry an energy equal to the difference between the energies of the initial and final states. Thus, the emitted photon had an energy
According to the photoelectric effect equation, the maximum kinetic energy of the emitted photoelectrons is related to the photon energy and the work function by the relation
The work function is related to the frequency of the red border by the relation:
Thus, the maximum possible kinetic energy of a photoelectron is






