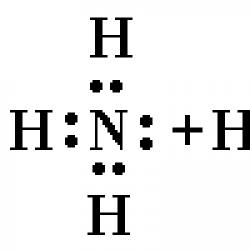Bisiklet tekerleğinin jant tellerine takılan turuncu plastik reflektörleri hatırlıyor musunuz? Reflektörü jantın kendisine bağlayalım ve yörüngesini takip edelim. Ortaya çıkan eğriler sikloid ailesine aittir. Tekerleğe sikloidin üreten dairesi (veya dairesi) denir. Ama yüzyılımıza geri dönelim ve daha modern teknolojiye geçelim. Bisikletin yolu üzerinde lastik sırtına çakıl taşı sıkıştı.

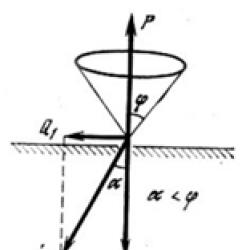
Tekerleği birkaç kez çevirdikten sonra lastik sırtından fırlayan taş nereye uçacak? Motosikletin yönüne karşı mı yoksa ona doğru mu? Bilindiği gibi bir cismin serbest hareketi, hareket ettiği yörüngeye teğet olarak başlar. Sikloide teğet her zaman hareket yönündedir ve üreten dairenin en üst noktasından geçer. Çakıl taşımız hareket yönünde uçacak. Çocukken arka kanadı olmayan bir bisikletle su birikintilerinden nasıl geçtiğinizi hatırlıyor musunuz? Sırtınızdaki ıslak şerit, yeni elde ettiğiniz sonucun günlük onayıdır.

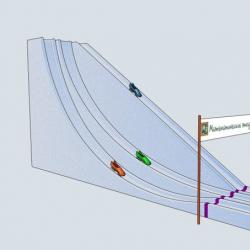
17. yüzyıl sikloidin yüzyılıdır. En iyi bilim adamları onun şaşırtıcı özelliklerini incelediler. Yer çekimi etkisi altında hareket eden bir cismi en kısa sürede bir noktadan diğerine hangi yörünge yönlendirir? Bu, günümüzde varyasyonlar hesabı olarak adlandırılan bilimin ilk problemlerinden biriydi. Yol uzunluğu, hız, zaman gibi farklı şeyleri en aza indirebilir (veya en üst düzeye çıkarabilirsiniz). Brachistochrone probleminde en aza indirilen zamandır (bu, ismin kendisi tarafından vurgulanmaktadır: Yunanca βράχιστος - en küçük, χρόνος - zaman). Akla gelen ilk şey düz bir yörüngedir. Ayrıca verilen noktaların tepesinde sivri ucu olan ters çevrilmiş bir sikloidi de düşünelim. Ve Galileo Galilei'yi takip ederek, noktalarımızı birleştiren dairenin çeyreği. Dikkate alınan profillerle yarış kızağı parkurları yapalım ve hangi bob'un önce geldiğini görelim. Yarış kızağının tarihi İsviçre'den geliyor. 1924'te ilk Kış Olimpiyat Oyunları Fransa'nın Chamonix şehrinde düzenlendi. Zaten ikişerli ve dörtlü takımlar için yarış kızağı yarışmalarına ev sahipliği yapıyorlar.

Olimpiyat Oyunlarında yarış kızağı ekibinin beş kişiden oluştuğu tek yıl 1928'di. O zamandan beri yarış kızağında her zaman iki ve dört kişilik erkek takımlar yarıştı. Yarış kızağı kurallarında pek çok ilginç şey var. Elbette bob ve takımın ağırlığında kısıtlamalar var, ancak bob patenlerinde kullanılabilecek malzemeler konusunda bile kısıtlamalar var (ön çift hareketli ve gidona bağlı, arka çift sağlam bir şekilde sabitleniyor) . Örneğin radyum paten yapımında kullanılamaz.

Dörtlülerimize bir başlangıç ​​yapalım. Bitiş çizgisine ilk ulaşan fasulye hangisi olacak? Matematiksel Çalışmalar takımında oynayan ve sikloid kaydıraktan aşağı yuvarlanan Yeşil Bob birinci oluyor! Galileo Galilei neden dairenin çeyreğini düşündü ve bunun zaman açısından en iyi iniş yolu olduğuna inandı? İçine kesikli çizgiler girdi ve bağlantı sayısı arttıkça iniş süresinin azaldığını fark etti. Galileo buradan doğal olarak bir daireye geçti, ancak bu yörüngenin mümkün olan tüm yörüngeler arasında en iyisi olduğu yönünde yanlış bir sonuca vardı. Gördüğümüz gibi en iyi yörünge sikloiddir. Bu iki nokta aracılığıyla, sikloidin tepe noktasının en üst noktada olması koşuluyla benzersiz bir sikloid çizilebilir. Ve sikloid ikinci noktadan geçmek için yükselmek zorunda kalsa bile, yine de en dik iniş eğrisi olacaktır! Sikloid ile ilgili bir diğer güzel problem ise tautokron problemidir. Yunancadan tercüme edilen ταύτίς, "aynı" anlamına gelir, χρόνος, zaten bildiğimiz gibi - "zaman". Sikloid şeklinde bir profile sahip üç özdeş slayt yapalım, böylece slaytların uçları çakışacak ve sikloidin tepesinde yer alacaktır. Üç tane fasulyeyi farklı yüksekliklere koyalım ve devam edelim.

En şaşırtıcı gerçek ise tüm fasulyelerin aynı anda aşağıya inmesidir! Kışın bahçenize bir buz kaydırağı inşa edebilir ve bu özelliği bizzat test edebilirsiniz. Tautokron problemi, herhangi bir başlangıç ​​konumundan başlayarak, belirli bir noktaya iniş zamanının aynı olacağı bir eğri bulmaktır. Christiaan Huygens tek tautokron'un sikloid olduğunu kanıtladı. Elbette Huygens buz kaydıraklarından aşağı inmekle ilgilenmiyordu. O dönemde bilim adamlarının sanat aşkıyla bilim peşinde koşma lüksleri yoktu. İncelenen problemler o zamanın teknolojisinin yaşamına ve taleplerine dayanıyordu. 17. yüzyılda zaten uzun deniz yolculukları yapılıyordu. Denizciler zaten enlemi oldukça doğru bir şekilde belirleyebiliyorlardı, ancak boylamı hiç belirleyememeleri şaşırtıcı. Enlemi ölçmek için önerilen yöntemlerden biri de hassas kronometrelerin varlığına dayanıyordu. Sarkaçlı saatleri doğru yapmayı düşünen ilk kişi Galileo Galilei'ydi. Ancak bunları uygulamaya başladığı anda zaten yaşlanmıştır, kördür ve bilim adamının ömrünün geri kalan yılında saat yapacak vakti yoktur. Bunu oğluna miras bırakır, ancak tereddüt eder ve ancak ölmeden önce sarkaç üzerinde çalışmaya başlar ve planı gerçekleştirecek zamanı yoktur.

Bir sonraki ikonik figür Christiaan Huygens'ti. Galileo tarafından düşünülen sıradan bir sarkacın salınım periyodunun başlangıç ​​​​konumuna bağlı olduğunu fark etti; genlikten. Yükün yörüngesinin ne olması gerektiğini düşünerek, yuvarlanma süresinin genliğe bağlı olmaması için tautokron problemini çözer. Peki bir yükün sikloid boyunca hareket etmesi nasıl sağlanır? Teorik araştırmayı pratik bir düzleme dönüştüren Huygens, sarkaç ipinin sarıldığı "yanaklar" yapıyor ve birkaç matematik problemini daha çözüyor. "Yanaklar"ın aynı sikloidin profiline sahip olması gerektiğini kanıtlıyor, böylece bir sikloidin evriminin aynı parametrelere sahip bir sikloid olduğunu gösteriyor. Ayrıca Huygens tarafından önerilen sikloidal sarkacın tasarımı, sikloidin uzunluğunu hesaplamayı mümkün kılmaktadır. Uzunluğu, üreten dairenin dört yarıçapına eşit olan mavi iplik mümkün olduğu kadar saptırılırsa, sonu "yanak" ile sikloid yörüngenin kesişme noktasında olacaktır, yani. sikloidin tepesinde - “yanaklar”. Bu, sikloid yayın uzunluğunun yarısı olduğundan, toplam uzunluk, üreten dairenin sekiz yarıçapına eşittir. Christiaan Huygens sikloidal bir sarkaç yaptı ve onunla birlikte saatler deniz yolculuklarında test edildi, ancak kök salmadı. Ancak bu amaçlar için normal sarkaçlı bir saatle aynıdır. Peki neden sıradan sarkaçlı saat mekanizmaları hala var? Kırmızı sarkaç gibi küçük sapmalarla yakından bakarsanız, sikloidal sarkacın "yanaklarının" neredeyse hiçbir etkisi yoktur. Buna göre, küçük sapmalar için sikloid ve daire boyunca hareket neredeyse çakışmaktadır.

Edebiyat:
G. N. Berman. Sikloid. M.: Nauka, 1980.
S. G. Gindikin. Fizikçiler ve matematikçiler hakkında hikayeler. M.: MTsNMO, 2006.

Yorumlar: 1

Vladimir Zakharov

Rusya Bilimler Akademisi Akademisyeni, Fiziksel ve Matematik Bilimleri Doktoru, Rusya Bilimler Akademisi Doğrusal Olmayan Dinamikler Bilimsel Konseyi Başkanı, Başkan tarafından verilen konferans. Rusya Bilimler Akademisi Fizik Enstitüsü Matematiksel Fizik Bölümü. Arizona Üniversitesi'nde (ABD) profesör, iki kez Devlet Ödülü'nü kazanan, Vladimir Evgenievich Zakharov'un Dirac madalyasını kazanan Lebedev, 27 Mayıs 2010'da Politeknik Müzesi'nde “Politikaya Halk Dersleri” projesi kapsamında verildi. ru”.

Sergey Kuksin

Uluslararası bilimsel konferans “Klasik mekaniğin günleri” Moskova, Steklov Matematik Enstitüsü, st. Gubkina, 8 Ocak 26, 2015

Kaos, her biri on üç dakika süren dokuz bölümden oluşan bir matematik filmidir. Bu, dinamik sistemlere, kelebek etkisine ve kaos teorisine adanmış, halka yönelik bir film.

Alexandra Skripçenko

Matematikçi Alexandra Skripchenko dinamik bir sistem olarak bilardo, rasyonel açılar ve Poincaré teoremi hakkında.

Yuliy İlyaşenko

Kolmogorov-Arnold-Moser teorisi “Gezegenler Güneş'in içine düşebilir mi? Eğer evet ise, o zaman hangi olasılıkla? Peki ne kadar sonra?" Problemin matematiksel formülasyonu: Kütlelerin çok küçük olduğunu ve birbirlerine olan çekimlerinin ihmal edilebileceğini varsayalım. Daha sonra gezegenlerin yörüngeleri hesaplanabilir; Newton bunu yaptı. Gerçek duruma geçersek, gezegenlerin karşılıklı çekiciliği yörüngelerini etkilediğinde, integrallenebilirlikte küçük bir tedirginlik elde ederiz, yani. tam olarak çözülebilir sistem. Poincaré, klasik mekaniğin integrallenebilir sistemlerinin küçük tedirginliklerinin incelenmesini diferansiyel denklemler teorisinin ana görevi olarak görüyordu. Dersler, daha büyük okul çocuklarının erişebileceği bir düzeyde, KAM teorisinin ana fikirlerini anlatacaktır. N-cisim problemine ve klasik mekaniğe girmeyeceğiz, ancak dairenin difeomorfizmalarını ve Kolmogorov'un gök mekaniği problemleri için önerdiği tümevarım sürecinin temel adımını tartışacağız.

Olga Romaskeviç

Eğer çok zalimce davranıp bir matematikçinin kalemini ve kağıdını elinizden alırsanız, o da yeni problemler aramak için gökyüzüne bakacaktır. Gezegensel hareket sorunu (matematik dünyasında "n-cisim problemi" olarak adlandırılan kod adı) son derece karmaşıktır; o kadar karmaşıktır ki, n=3 durumunun özel alt durumları için bile her yıl çok sayıda makale yayınlanmaktadır. Bir dönemlik derste dahi bu sorunun tüm boyutlarıyla analiz edilmesi mümkün değildir. Ancak biz korkmayacağız ve burada ortaya çıkan matematikle oynamaya çalışacağız. Bizim için temel motivasyon iki cisim problemi olacaktır: Yakınlarda başka gezegen olmadığı varsayımıyla bir gezegenin Güneş etrafında hareketi problemi.

Dmitry Anosov

Kitap diferansiyel denklemlerden bahsediyor. Bazı durumlarda yazar diferansiyel denklemlerin nasıl çözüldüğünü, diğerlerinde ise geometrik değerlendirmelerin çözümlerin özelliklerini anlamaya nasıl yardımcı olduğunu açıklıyor. (Kitabın başlığındaki “çözüyoruz, sonra çiziyoruz” ifadesi bununla bağlantılı.) Çeşitli fiziksel örnekler ele alınıyor. En basitleştirilmiş düzeyde, deterministik nesnelerin davranışında "kaos" un ortaya çıkma mekanizmasının anlaşılması da dahil olmak üzere 20. yüzyılın bazı başarıları anlatılmaktadır. Kitap matematiğe ilgi duyan lise öğrencilerine yöneliktir. Tek yapmaları gereken anlık hız olarak türevin anlamını anlamaktır.

Alexey Belov

Olimpiyatların çok iyi bilinen bir problemi var: Düz bir masanın üzerinde madeni paralar (dışbükey şekiller) var. Daha sonra bunlardan biri diğerlerini etkilemeden masadan çekilebilir. Uzun bir süre matematikçiler, bir karşı örnek oluşturulana kadar bu ifadenin uzaysal benzerini kanıtlamaya çalıştılar! Bir fikir ortaya çıktı: Küçük tanelerde genellikle çatlak olmaz, çatlak tane sınırının ötesine geçmez ve çatlaklar birbirini tutar. Bu fikir teorik olarak çatlakların büyümediği kompozitlerin, özellikle seramik zırhın oluşturulmasını mümkün kılar.

Alexey Sosinsky

Mekaniğin ve teorik fiziğin en önemli kavramlarından biri - mekanik bir sistemin konfigürasyon alanı kavramı - bazı nedenlerden dolayı sadece okul çocukları için değil, aynı zamanda çoğu matematik öğrencisi için de bilinmemektedir. Ders çok basit ama çok anlamlı bir mekanik sistem sınıfını tartışıyor - iki serbestlik derecesine sahip düz menteşeli mekanizmalar. “Genel durumda” konfigürasyon uzaylarının iki boyutlu yüzeyler olduğunu keşfedeceğiz ve bunların hangileri olduğunu anlamaya çalışacağız. (İşte Dima Zvonkin'in on yıl öncesine ait nihai sonuçları.) Daha sonra menteşe mekanizmalarıyla ilgili çözülmemiş matematik problemleri tartışılıyor. (Amerikalı matematikçi Bill Thurston'un iki hipotezi, daha doğrusu kanıtlanmamış teoremleri de dahil.)

Vladimir Protasov

Varyasyon hesabı, sonsuz boyutlu uzayda bir fonksiyonun minimumunu bulma bilimidir. Alıştığımız minimum problemlerden farklı olarak, bir sayıyı (parametreyi) veya örneğin düzlemdeki bir noktayı optimal olarak seçmemiz gerektiğinde, varyasyonel problemlerde optimal fonksiyonu bulmamız gerekir. Aynı zamanda, çok farklı kökenlere sahip problemler aynı araç seti kullanılarak çözülür: klasik mekanik, geometri, matematiksel ekonomi vb. 17. yüzyıldan beri bilinen eski problemlerle başlayacağız ve bir problemden diğerine köprüler kurarak hızla modern sonuçlara ve çözülmemiş problemlere ulaşacağız.

(Yunancadan tercüme edilmiştir. dairesel) - yarıçaplı bir daire üzerindeki bir nokta ile tanımlanan düz bir aşkın eğri R kaymadan düz bir çizgi boyunca yuvarlanma (aşkın bir eğri, dikdörtgen koordinatlardaki cebirsel bir denklemle tanımlanamayan bir eğridir). Parametrik denklemi

X = rt – günah,
sen= r – r maliyet t

Sikloidin, dairenin yuvarlandığı düz çizgiyle kesişme noktalarına (bu daireye üreten daire denir ve boyunca yuvarlandığı düz çizgiye direktif denir) doruk noktaları ve sikloid üzerindeki en yüksek noktalar denir. Bitişik doruk noktaları arasında ortada bulunanlara sikloidin köşeleri denir.

Sikloidi inceleyen ilk kişi Galileo Galilei'dir. Bir sikloid kemerin uzunluğu, 1658 yılında Londra'daki St. Paul Katedrali'nin kubbesinin tasarımının ve kurucusu olan İngiliz mimar ve matematikçi Christopher Wren tarafından belirlendi. Sikloidin uzunluğunun, üreten dairenin 8 yarıçapına eşit olduğu ortaya çıktı.
Ona adını veren sikloidin dikkat çekici özelliklerinden biri olan brachistochrone (Yunanca "en kısa" ve "zaman" kelimelerinden) en dik iniş probleminin çözümüyle ilişkilidir. Topun mümkün olan en kısa sürede bir noktadan diğerine yuvarlanması için iki noktayı birbirine bağlayan iyi cilalanmış (sürtünmeyi neredeyse tamamen ortadan kaldırmak için) bir oluğa hangi şeklin verilmesi gerektiği sorusu ortaya çıktı. Bernoulli kardeşler hendeğin aşağı doğru sikloid şeklinde olması gerektiğini kanıtladılar.

Sikloide ilişkin eğriler, üreten çember üzerinde yer almayan noktaların yörüngeleri dikkate alınarak elde edilebilir.

Bırakın nokta 0'dan itibarençemberin içindedir. Eğer yürütülürse 0'dan itibarenüreten daire ile aynı merkeze sahip yardımcı daire, daha sonra üreten daire düz bir çizgi boyunca yuvarlandığında AB küçük bir daire düz bir çizgide yuvarlanacak A´ İÇİNDE`, ancak yuvarlanmasına kayma eşlik edecek ve nokta 0'dan itibaren kısaltılmış sikloid adı verilen bir eğriyi tanımlar.

Uzatılmış bir sikloid de benzer şekilde tanımlanır - bu, yuvarlanmaya ters yönde kayma eşlik ederken, üreten dairenin yarıçapının bir uzantısı üzerinde bulunan bir noktanın yörüngesidir.

Sikloidal eğriler birçok teknik hesaplamada kullanılır ve özellikleri örneğin dişli diş profillerinin yapımında, sikloidal sarkaçlarda, optikte kullanılır ve bu nedenle bu eğrilerin incelenmesi uygulamalı bir bakış açısıyla önemlidir. 17. yüzyıl bilim adamlarının bu eğrileri ve özelliklerini incelemesi de aynı derecede önemlidir. diferansiyel ve integral hesabının yaratılmasına yol açan teknikler geliştirdi ve brakistokron problemi, varyasyon hesabının icadına doğru bir adımdı.

Elena Malishevskaya

LEMNİKATLAR
Kutupsal koordinatlarda denklem:
r 2 = a 2 cos2θ

(x 2 + y 2) 2 = a 2 (x 2 - y 2)

AB" veya A"B ile x ekseni arasındaki açı = 45 o

Bir döngünün alanı = a 2/2

SİKLOİD

Bir yayın alanı = 3πa 2

Bir yayın yay uzunluğu = 8a

Bu, x ekseni boyunca yuvarlanan a yarıçaplı bir daire üzerindeki bir P noktasıyla tanımlanan bir eğridir.

DÖRT ÇUBUKLU HİPOSİKLOİDLER
Dikdörtgen koordinatlarda denklem:
x 2/3 + y 2/3 = a 2/3

Parametrik formdaki denklemler:

Eğrinin çevrelediği alan = 3πa 2 /8

Tüm eğrinin yay uzunluğu = 6a

Bu, a yarıçaplı bir dairenin içinde dönen, a/4 yarıçaplı bir daire üzerindeki bir P noktasıyla tanımlanan bir eğridir.

KARDİYOD
Denklem: r = a(1 + cosθ)

Eğrinin çevrelediği alan = 3πa 2 /2

Eğri yay uzunluğu = 8a

Bu, a yarıçaplı bir çember üzerinde, a yarıçaplı çemberin dışında dönen bir P noktasıyla tanımlanan bir eğridir. Bu eğri aynı zamanda Pascal salyangozunun özel bir durumudur.

ZİNCİR HATTI
Denklem:
y = a(e x/a + e -x/a)/2 = acosh(x/a)

Bu, bir zincirin A noktasından B noktasına dikey olarak asıldığında asılı kalacağı eğridir.

ÜÇ YAPRAKLI GÜL
Denklem: r = acos3θ

r = acos3θ denklemi, 30 o veya π/6 radyanlık bir eğri boyunca saat yönünün tersine döndürülerek elde edilen eğriye benzer.

Genel olarak r = acosnθ veya r = asinnθ, eğer n tek ise n loba sahiptir.

DÖRT TAÇLI GÜL
Denklem: r = acos2θ

r = asin2θ denklemi, 45 o veya π/4 radyan eğrisi boyunca saat yönünün tersine döndürülerek elde edilen eğriye benzer.

Genel olarak r = acosnθ veya r = asinnθ, eğer n çift ise 2n yaprağa sahiptir.

episikloid
Parametrik denklemler:

Bu, b yarıçaplı bir çember üzerinde, a yarıçaplı çemberin dış tarafı boyunca yuvarlanırken P noktasıyla tanımlanan eğridir. Kardioid, episikloidin özel bir durumudur.

GENEL HİPOSİKLOİD
Parametrik denklemler:

Bu, b yarıçaplı bir çember üzerinde, a yarıçaplı çemberin dış tarafı boyunca yuvarlanırken P noktasıyla tanımlanan eğridir.

Eğer b = a/4 ise eğri dört noktalı bir hiposikloiddir.

TROKOİD
Parametrik denklemler:

Bu, x ekseni boyunca yuvarlanırken yarıçapı a olan bir dairenin merkezinden b mesafesindeki P noktası tarafından tanımlanan eğridir.
Eğer b kısaltılmış bir sikloid ise.
Eğer b > a ise eğri Şekil 2'de gösterilen şekle sahiptir. 11-11 ve denir yürüteç.
Eğer b = a ise eğri sikloittir.

TRAKTRICE
Parametrik denklemler:

Bu, PQ uzunluğundaki uzatılmış bir ipin diğer Q ucu x ekseni boyunca hareket ettirildiğinde uç noktası P tarafından tanımlanan eğridir.

VERZIERA (VERZIERA) AGNEZI (BAZEN CURL AGNEZI)
Dikdörtgen koordinatlarda denklem: y = 8a 3 /(x 2 + 4a 2)

Parametrik denklemler:

B. Şekilde OA değişken doğrusu y = 2a ve merkezi (0,a) olan a yarıçaplı bir çemberle sırasıyla A ve B'de kesişiyor. "Rotasyon" üzerindeki herhangi bir P noktası, sırasıyla B ve A boyunca x ve y eksenlerine paralel çizgiler oluşturularak ve P'nin kesişme noktası tanımlanarak belirlenir.

DESCARTES YAPRAĞI
Dikdörtgen koordinatlarda denklem:
x 3 + y 3 = 3 eksen

Parametrik denklemler:

Döngü alanı 3a 2 /2

Asimptot denklemi: x + y + a = 0.

ÇEVRE KATILIMCISI
Parametrik denklemler:

Bu, a yarıçaplı bir çemberden çözülen ipin P uç noktası tarafından tanımlanan eğridir.

ELİPSE TUTULAN
Dikdörtgen koordinatlarda denklem:
(ax) 2/3 + (by) 2/3 = (a 2 - b 2) 2/3

Parametrik denklemler:

Bu eğri, x 2 /a 2 + y 2 /b 2 = 1 elipsine normal olan zarftır.

CASSINI OVALLERİ
Kutupsal denklem: r 4 + a 4 - 2a 2 r 2 cos2θ = b 4.

Bu, iki sabit noktaya olan uzaklığının çarpımı [kenardan 2a uzaklığı] sabit bir b2 olacak şekilde bir P noktası tarafından tanımlanan bir eğridir.

Sırasıyla b a iken aşağıdaki şekillerdeki gibi eğri.

Eğer b = a ise eğri Sonsuzluk işareti

PASCAL'IN SALYANGANI
Kutupsal denklem: r = b + acosθ

OQ, O'nun merkezini O'dan geçen a çaplı bir daire üzerinde herhangi bir Q noktasına bağlayan çizgi olsun. Bu durumda eğri, PQ = b olacak şekilde tüm P noktalarının odak noktasıdır.

b > a veya b olduğunda aşağıdaki şekillerde gösterilen eğri

DİOKLESİN CİSSOİDİ
Dikdörtgen koordinatlarda denklem: y 2 = x 3 /(2a - x)

Parametrik denklemler:

Bu, OP mesafesi = RS mesafesi olacak şekilde bir P noktası tarafından tanımlanan bir eğridir. Görevde kullanıldı küpü ikiye katlamak yani Belirli bir küpün hacminin iki katı olan bir küpün kenarını bulma

ARŞİMEDES SARMALI
Kutupsal denklem: r = aθ

5. Kartezyen koordinatlarda parametrik sikloid denklem ve denklem

Bize, merkezi A noktasında olan, yarıçapı a olan bir çemberin oluşturduğu bir sikloid verildiğini varsayalım.

Yuvarlanmanın başlangıcında dikey konumu AO olan yarıçapın dönmeyi başardığı t=∟NDM açısını noktanın konumunu belirleyen parametre olarak seçersek, M noktasının x ve y koordinatları şu şekilde olacaktır: şu şekilde ifade edilebilir:

x= OF = ON - NF = NM - MG = at-a sin t,

y= FM = NG = ND – GD = a – a cos t

Yani sikloidin parametrik denklemleri şu şekildedir:

t -∞'dan +∞'a değiştiğinde, bu şekilde gösterilenler gibi sonsuz sayıda daldan oluşan bir eğri elde edilecektir.

Ayrıca sikloidin parametrik denklemine ek olarak Kartezyen koordinatlarda denklemi de vardır:

Burada r, sikloidi oluşturan dairenin yarıçapıdır.

6. Sikloidin parçalarını ve sikloidin oluşturduğu şekilleri bulma problemleri

Görev No.1. Denklemi parametrik olarak verilen bir sikloidin bir yayı ile sınırlanan bir şeklin alanını bulun

ve Öküz ekseni.

Çözüm. Bu sorunu çözmek için integral teorisinden bildiğimiz gerçekleri kullanacağız:

Kavisli bir sektörün alanı.

[α, β] üzerinde tanımlanan r = r(ϕ) fonksiyonunu düşünün.

ϕ 0 ∈ [α, β] r 0 = r(ϕ 0)'a karşılık gelir ve dolayısıyla M 0 noktası (ϕ 0 , r 0), burada ϕ 0,

r 0 - noktanın kutupsal koordinatları. Eğer ϕ değişirse, tüm [α, β] boyunca “geçerek”, o zaman M değişken noktası verilen bir AB eğrisini tanımlayacaktır.

denklem r = r(ϕ).

Tanım 7.4. Eğrisel bir sektör, iki ışın ϕ = α, ϕ = β ve kutupsal olarak tanımlanan bir AB eğrisi ile sınırlanan bir şekildir.

r = r(ϕ), α ≤ ϕ ≤ β denklemiyle koordinatlar.

Aşağıdaki doğrudur

Teorem. Eğer fonksiyon r(ϕ) > 0 ve [α, β] üzerinde sürekli ise, o zaman alan

eğrisel sektör aşağıdaki formülle hesaplanır:

Bu teorem daha önce belirli integral konusunda kanıtlanmıştı.

Yukarıdaki teoreme dayanarak, denklemi x= a (t – sin t), y= a (1) parametrik parametreleriyle verilen bir sikloidin bir yayı ile sınırlı bir şeklin alanını bulma problemimiz – cos t) ve Ox ekseni aşağıdaki çözüme indirgenir.

Çözüm. Eğri denkleminden dx = a(1−cos t) dt. Sikloidin ilk yayı, t parametresinin 0'dan 2π'ye değişmesine karşılık gelir. Buradan,

Görev No.2. Sikloidin bir yayının uzunluğunu bulun

Aşağıdaki teorem ve onun sonucu da integral hesabında incelenmiştir.

Teorem. AB eğrisi y = f(x) denklemiyle veriliyorsa, burada f(x) ve f '(x) üzerinde süreklidir, o zaman AB düzeltilebilir ve

Sonuçlar. AB parametrik olarak verilsin

LAB = (1)

x(t), y(t) fonksiyonlarının [α, β] üzerinde sürekli türevlenebilir olmasına izin verin. Daha sonra

formül (1) aşağıdaki gibi yazılabilir

Bu integralde değişkenleri değiştirelim x = x(t), sonra y'(x)=;

dx= x’(t)dt ve dolayısıyla:

Şimdi sorunumuzu çözmeye geri dönelim.

Çözüm. Bizde var ve bu nedenle

Görev No.3. Sikloidin bir yayının dönmesinden oluşan S yüzey alanını bulmamız gerekiyor.

L=((x,y): x=a(t – sin t), y=a(1 – maliyet), 0≤ t ≤ 2π)

İntegral hesabında, bir parça üzerinde parametrik olarak tanımlanan bir eğrinin x ekseni etrafındaki bir devrim cismin yüzey alanını bulmak için aşağıdaki formül vardır: x=φ(t), y=ψ(t) (t 0 ≤t ≤t 1)

Bu formülü sikloid denklemimize uyguladığımızda şunu elde ederiz:

Görev No.4. Sikloid yayın döndürülmesiyle elde edilen cismin hacmini bulun

Öküz ekseni boyunca.

İntegral hesabında hacimleri incelerken aşağıdaki açıklama vardır:

Eğrisel bir yamuğu sınırlayan eğri parametrik denklemlerle veriliyorsa ve bu denklemlerdeki fonksiyonlar belirli bir integraldeki değişkenin değişimine ilişkin teoremin koşullarını sağlıyorsa, o zaman yamuğun Ox ekseni etrafında dönme gövdesinin hacmi şu şekilde olacaktır: formülle hesaplanır

İhtiyacımız olan hacmi bulmak için bu formülü kullanalım.

Problem çözüldü.

Çözüm

Böylece bu çalışma sırasında sikloidin temel özellikleri açıklığa kavuşturuldu. Ayrıca bir sikloidin nasıl inşa edileceğini öğrendik ve bir sikloidin geometrik anlamını öğrendik. Anlaşıldığı üzere sikloidin sadece matematikte değil, aynı zamanda teknolojik hesaplamalar ve fizikte de muazzam pratik uygulamaları var. Ancak sikloidin başka yararları da var. 17. yüzyılda bilim adamları tarafından eğri çizgileri incelemek için teknikler geliştirirken kullanıldı; bu teknikler sonuçta diferansiyel ve integral hesabın icadına yol açtı. Aynı zamanda Newton, Leibniz ve onların ilk araştırmacılarının güçlü yeni matematiksel yöntemlerin gücünü test ettiği "mihenk taşlarından" biriydi. Son olarak brakistokron sorunu, günümüz fizikçileri için çok gerekli olan varyasyon hesabının bulunmasına yol açtı. Böylece sikloidin matematik tarihinin en ilginç dönemlerinden biriyle ayrılmaz bir şekilde bağlantılı olduğu ortaya çıktı.

Edebiyat

1. Berman G.N. Sikloid. – M., 1980

2.Verov S.G. Brachistochrone veya sikloidin başka bir sırrı // Kuantum. – 1975. - No.5

3. Verov S.G. Sikloidin sırları // Kuantum. – 1975. - Sayı 8.

4. Gavrilova R.M., Govorukhina A.A., Kartasheva L.V., Kostetskaya G.S., Radchenko T.N. Belirli bir integralin uygulamaları. Fizik Fakültesi 1. sınıf öğrencileri için metodolojik talimatlar ve bireysel ödevler. - Rostov yok: UPL RSU, 1994.

5. Gindikin S.G. Sikloidin yıldız yaşı // Kuantum. – 1985. - Sayı 6.

6. Fikhtengolts G.M. Diferansiyel ve integral hesabının seyri. T.1. – M., 1969

Bu çizgiye “zarf” denir. Her eğri çizgi, teğetlerinin bir zarfıdır.

Madde ve hareket ve bunların oluşturduğu yöntem, herkesin hakikat bilgisindeki potansiyelinin farkına varmasını sağlar. Diyalektik-materyalist bir düşünme biçiminin geliştirilmesi ve benzer bir biliş yöntemine hakim olmak için bir metodoloji geliştirmek, İnsan yeteneklerinin geliştirilmesi ve gerçekleştirilmesi sorununu çözmeye yönelik ikinci adımdır. XX. Parça Fırsatları...

Bu durumda, insanlar nevrasteni geliştirebilir - klinik tablonun temeli astenik bir durum olan bir nevroz. Hem nevrasteni durumunda hem de nevrastenik psikopatinin dekompansasyonu durumunda, zihinsel (psikolojik) savunmanın özü, zorluklardan vejetatif işlev bozuklukları ile sinirli zayıflığa çekilmeye yansır: ya kişi bilinçsizce saldırıyla daha fazla "savaşır". ..

Çeşitli faaliyet türleri; okul çocuklarının mekansal hayal gücü ve mekansal kavramlarının gelişimi, mecazi, mekansal, mantıksal, soyut düşünme; çeşitli uygulamalı problemleri çözmek için geometrik ve grafik bilgi ve becerilerini uygulama yeteneğini geliştirmek; teknik ve proje alanındaki proje faaliyetlerinin aşamalarının içeriği ve sırasına aşinalık...

Yaylar. Spiraller aynı zamanda kapalı eğrilerin de kıvrımlarıdır, örneğin bir dairenin kıvrımları. Bazı spirallerin isimleri kutupsal denklemlerinin Kartezyen koordinatlardaki eğri denklemleriyle benzerliğine göre verilmektedir, örneğin: · parabolik spiral (a - r)2 = bj, · hiperbolik spiral: r = a/j. · Çubuk: r2 = a/j · si-ci-spiral, parametrik denklemleri şu şekildedir: , )