Up an inclined plane. Movement of a body on an inclined plane
case of accelerated downward movement
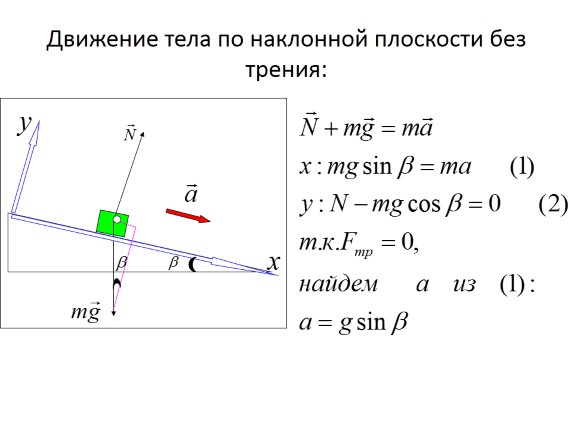
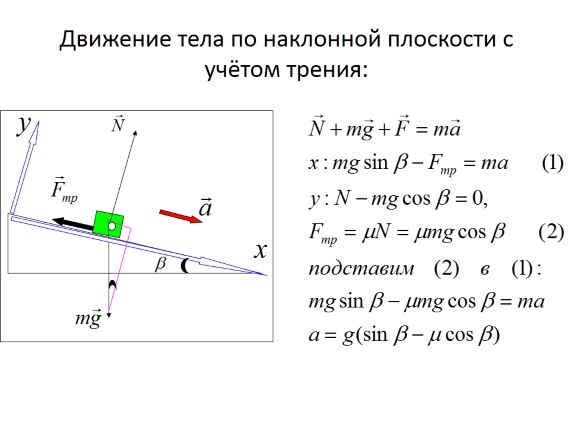
Body movement along inclined plane
The motion of a body along an inclined plane is a classic example of the motion of a body under the action of several non-co-directional forces. The standard method for solving problems of this kind of motion is to expand the vectors of all forces into components directed along the coordinate axes. Such components are linearly independent. This allows one to write down Newton's second law for the components along each axis separately. So Newton's second law, which is vector equation, turns into a system of two (three for the three-dimensional case) algebraic equations.
Consider a body that is sliding down an inclined plane. In this case, the following forces act on it:
- Gravity m g , directed vertically down;
- Support reaction force N , directed perpendicular to the plane;
- sliding friction force F tr, directed opposite to the speed (up along the inclined plane when the body slips)
sliding friction force F tr = µN proportional to the reaction force of the support. This allows you to get following expression for friction force: F tr = mmg cos( α ) . This force is opposite to the "pulling" component of gravity. Therefore, for body sliding down , we obtain the expressions for the total resultant force and acceleration:
F x= mg(sin( α
) – µ
cos( α
));
a x= g(sin( α
) – µ
cos( α
)).
It is not difficult to see that if µ α) , then the expression has a positive sign and we are dealing with a uniformly accelerated movement down the inclined plane. If µ >tg( α ), then the acceleration will have a negative sign and the motion will be equally slow. Such movement is possible only if the body is given an initial velocity down the slope. In this case, the body will gradually stop. If, subject to µ >tg( α ) the object is initially at rest, then it will not begin to slide down. Here, the static friction force will fully compensate for the "pulling" component of gravity.
When the coefficient of friction is exactly equal to the tangent of the angle of inclination of the plane: µ
= tg( α
) , we are dealing with a mutual compensation of all three forces. In this case, according to Newton's first law, the body can either be at rest or move at a constant speed (In this case, uniform motion is only possible downwards).
The forces acting on the block
sliding on an inclined plane:
up slow motion case
However, the body can also drive up the inclined plane. An example of such a movement is the movement of a hockey puck up an ice slide. When a body moves upward, both the friction force and the "pulling" component of gravity are directed downward along an inclined plane. In this case, we are always dealing with uniformly slow motion, since the total force is directed in the direction opposite to the speed. The expression for the acceleration for this situation is obtained in a similar way and differs only in sign. So for body sliding up an inclined plane , we have:
a x= g(sin( α
) + µ
cos( α
)).
id="tabs-1">
This model is an animated diagram of a classic school laboratory work in physics, to study the accelerated motion of a body under the action of several forces along an inclined plane.
In this model, you can set the following values:
- Height / angle of the inclined plane (red dot);
- Coefficient of sliding friction of the bar on the surface (upper slider);
- Initial position of the body (blue dot M);
- The position of the stopwatch sensors (red triangles S 1 and S 1);
- Flag for displaying force vectors acting on the body.
- The angle of inclination of the inclined plane;
- Time of body movement from the first stopwatch sensor to the second:
- When calculating the time, it is artificially introduced time measurement error, distributed according to the normal law!
- Sensor coordinates;
- The coordinates of the initial position of the bar;
- The vectors of forces acting on the body are constructed.
Managing the Interactive Model
- Change scale: "CTRL + mouse wheel" or "CTRL + "+""–"CTRL + "-""
- Change position: drag while holding "CTRL + left mouse button"
- Erase all "traces": CTRL+F»
Download model
Models marked with © CC-BY-SA are authored by the individuals listed on the site. Interactive models distributed under license Creative Commons Attribution-Share Like 3.0
Attribution-ShareAlike (by-sa)- License "With indication of authorship - Copyleft". This license allows others to rework, correct, and develop the work, even for commercial purposes, provided that attribution is given and derivative works are licensed under similar terms. This license is a copyleft license. All new works based on those licensed under it will have the same license, so all derivative works will be allowed to be modified and used for commercial purposes. When reproducing works distributed under this license, a link to the site is required!
Download model
id="tabs-2">
Questions for self-examination on the topic "Inclined plane"
- When is motion on an inclined plane uniformly slow?
- When does a body slide uniformly down an inclined plane?
- At what values of the angle of inclination can the bar rest on an inclined plane?
- Why is it convenient to choose an oblique coordinate system for an inclined plane?
- What is the force of friction holding the block at rest?
- What happens to the reaction force of the support when the angle of inclination increases?
- Can a body move uniformly up an inclined plane?
          |
Slides and text of this presentation
slide 1
slide 2
Plan for solving problems in dynamics
1. Make a drawing on which to indicate the direction of the coordinate axes, acceleration and all forces applied to the body.
2. For each body, write down in vector form the equation of Newton's second law, listing on its right side in any order all the forces applied to the body
3. Write down the equations obtained in paragraph 2 in projection onto the coordinate axes.
5. Find the numerical value of the unknown quantity, if required by the condition of the problem.
4. From the resulting equation (system of equations) express unknown quantity.
slide 3
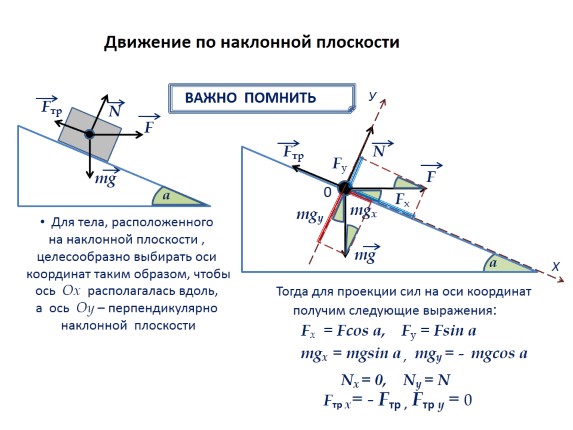
Movement on an inclined plane
IMPORTANT TO REMEMBER
mg
N
F
Ftr.
For a body located on an inclined plane, it is advisable to choose the coordinate axes in such a way that the Ox axis is located along, and the Oy axis is perpendicular to the inclined plane.
a
Then for the projection of forces on the coordinate axes we obtain the following expressions:
Fx. = Fcos a, Fu = Fsin a
mgx. = mgsin a, mgy = - mgcos a
Nx = 0,
Ny=N
Ftr x= - Ftr., Ftr y = 0 .
slide 4
Motion of a body on an inclined plane without friction:
slide 5
The motion of a body along an inclined plane, taking into account friction:
slide 6
a
β
m1g
m2g
N1
N2
T
T
At
At
X
X
a
a
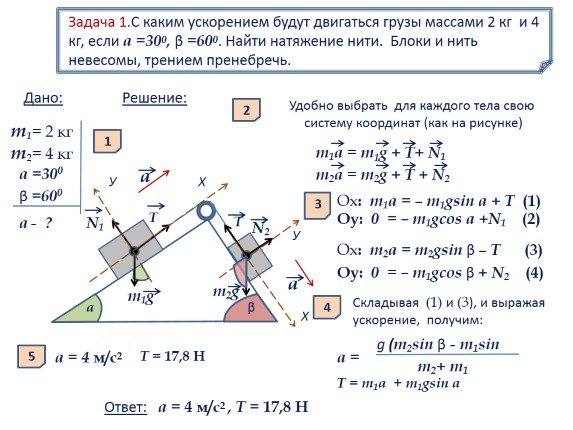
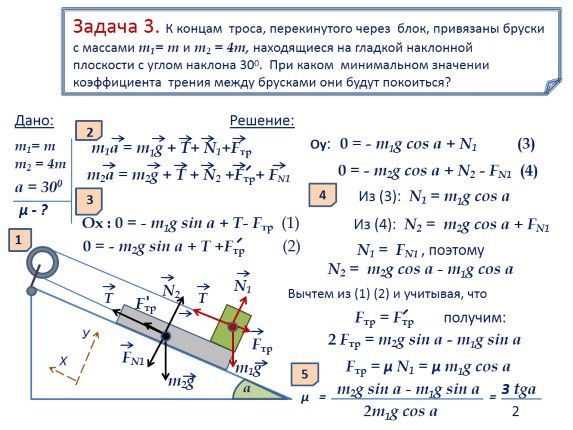
Task 1. With what acceleration will the loads of masses 2 kg and 4 kg move, if a = 300, β = 600. Find the thread tension. Blocks and thread are weightless, friction is neglected.
m1= 2 kg
m2= 4 kg
Given:
a = 300
β=600
a - ?
Solution:
1
2
It is convenient to choose for each body its own coordinate system (as in the figure)
m1a = m1g + T + N1
m2a = m2g + T + N2
3
Ox: m1a \u003d - m1gsin a + T (1)
Oy: 0 = - m1gcos a + N1 (2)
Оx: m2a = m2gsin β – T (3)
Oy: 0 = – m1gcos β + N2 (4)
4
Adding (1) and (3), and expressing the acceleration, we get:
g (m2sin β - m1sin
a =
m2+ m1
T = 17.8 H
T = m1a + m1gsin a
5
a = 4 m/s2
Answer: a \u003d 4 m / s2, T \u003d 17.8 H
Slide 7
Problem 2. A man of mass m1, resting his feet on a box of mass m2, pulls it up with a rope thrown over a block along an inclined plane with an angle of inclination a. What is the minimum force required to pull the rope to pull the box to the block? Coefficient of friction between the core and the inclined plane μ
So, I will try to describe in detail the course of my reasoning on this issue. At the first lesson, I put the question to the students: how can a body move along an inclined plane? Together we answer: roll evenly, with acceleration; rest on an inclined plane; stay on it; move out under the action of traction force evenly, with acceleration; drive under the action of the traction force evenly, with acceleration. In the figures, in two or three examples, we show what forces act on the body in this case. Along the way, I introduce the concept of a rolling resultant. We write the equation of motion in vector form, then we replace the sum of the rolling resultant in it (denote it as you like). We do this for two reasons: firstly, there is no need to project the force vectors onto the axis and solve two equations; secondly, the balance of forces will be shown correctly, based on the conditions of the problem.
I will show you with specific examples. Example 1: the body under the action of the traction force moves out uniformly (Figure 1).
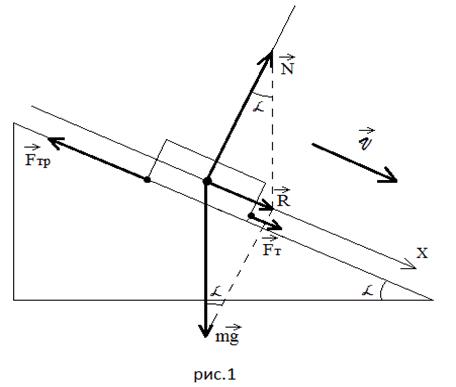
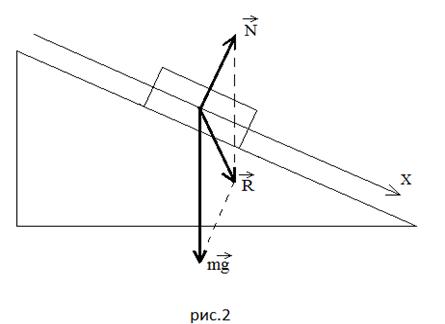
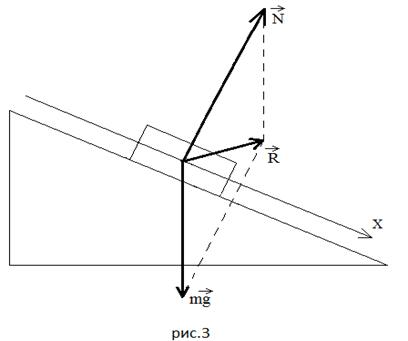
First of all, students must learn the algorithm for constructing a drawing. We depict an inclined plane, in the middle of it - a body in the form of a rectangle, draw an axis through the middle of the body parallel to the inclined plane. The direction of the axis is not essential, but in the case of uniformly accelerated motion, it is better to show in the direction of the vector, so that in algebraic form in the equation of motion on the right side in front there is a plus sign. Next, we build strength. We draw the force of gravity vertically downwards of arbitrary length (I demand to make the drawings large so that everything is clear to everyone). Then from the point of application of the force of gravity - perpendicular to the axis, along which the reaction force of the support will go. Draw a dashed line parallel to this perpendicular from the end of the vector until it intersects with the axis. From this point - a dotted line parallel to the intersection with the perpendicular - we get a vector of the correct length. Thus, we built a parallelogram on the vectors and , automatically indicating the correct value of the support reaction force and constructing, according to all the rules of vector geometry, the resultant of these forces, which I call the rolling resultant (the diagonal coinciding with the axis). At this point, using the method from the textbook, in a separate figure I show the reaction force of a support of arbitrary length: first, shorter than necessary, and then longer than necessary. I show the resultant force of gravity and the reaction force of the support: in the first case, it is directed downward at an angle to the inclined plane (Figure 2), in the second case, upwards at an angle to the inclined plane (Figure 3).
We draw a very important conclusion: the ratio between the force of gravity and the reaction force of the support must be such that the body under their action (or under the action of a rolling resultant) in the absence of other forces moves down along inclined plane. Next, I ask: what other forces act on the body? The guys answer: traction force and friction force. I ask the following question: what force will we show first, and what then? I strive for a correct and justified answer: first, in this case, it is necessary to show the traction force, and then the friction force, the module of which will be is equal to the sum modules of traction force and rolling resultant: , because according to the condition of the problem, the body moves uniformly, therefore, the resultant of all forces acting on the body must be equal to zero according to Newton's first law. For control, I ask a provocative question: so how many forces act on the body? The guys must answer - four (not five!): gravity, support reaction force, traction force and friction force. Now we write the equation of motion in vector form according to Newton's first law:
We replace the sum of vectors with a rolling resultant:
We get an equation in which all vectors are parallel to the axis. Now we write this equation in terms of the projections of the vectors onto the axis:
This entry can be skipped in the future. Let us replace in the equation the projections of vectors on their modules, taking into account the directions:
Example 2: the body under the action of the traction force drives onto an inclined plane with acceleration (Figure 4).
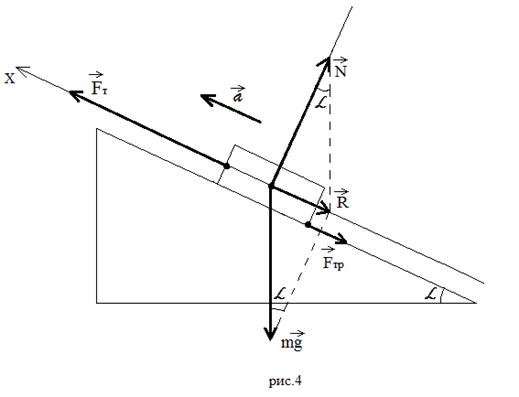
In this example, students should say that after constructing the force of gravity, the reaction force of the support and the rolling resultant of the next one, it is necessary to show the friction force, the last one is the traction force vector, which must be greater than the sum of the vectors, because the resultant of all forces must be directed in the same direction as the acceleration vector according to Newton's second law. The equation of motion of the body must be written according to Newton's second law:
If there is an opportunity to consider other cases in the lesson, then we do not neglect this opportunity. If not, then I give this task home. Someone can consider all the remaining cases, someone some - the right to choose students. In the next lesson, we check, correct errors and proceed to solving specific problems, having previously expressed from vector triangles and :
Equality (2) is desirable to analyze for various angles . At 
we have: as when moving horizontally under the action of a horizontal thrust force. As the angle increases, its cosine decreases, therefore, the reaction force of the support also decreases and becomes less and less than the force of gravity. At an angle 
it is equal to zero, i.e. the body does not act on the support and the support, accordingly, "does not react".
I foresee the question of opponents: how to apply this technique for cases when the thrust force is horizontal or directed at an angle to an inclined plane? I will answer with specific examples.
a) The body is dragged with acceleration onto an inclined plane, applying a traction force horizontally (Figure 5).
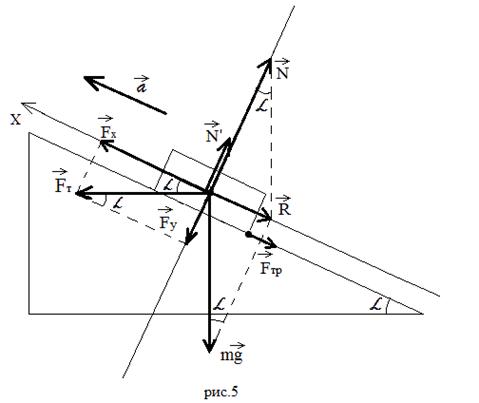
We decompose the horizontal traction force into two components: along the axis - and perpendicular to the axis - (the operation is the opposite of constructing the resultant of perpendicular forces). We write the equation of motion:
We replace the rolling resultant, and instead we write:
From vector triangles we express: 
and : 
.
Under the action of a horizontal force, the body not only rises up the inclined plane, but also additionally presses against it. Therefore, an additional pressure force arises equal to the modulus of the vector and, according to Newton's third law, an additional support reaction force: 
. Then the friction force will be: 
.
The equation of motion will take the form:
Here we have completely deciphered the equation of motion. Now it remains to express the desired value from it. Try to solve this problem in the traditional way and you will get the same equation, only the solution will be more cumbersome.
b) The body is pulled evenly from the inclined plane, applying the traction force horizontally (Figure 6).
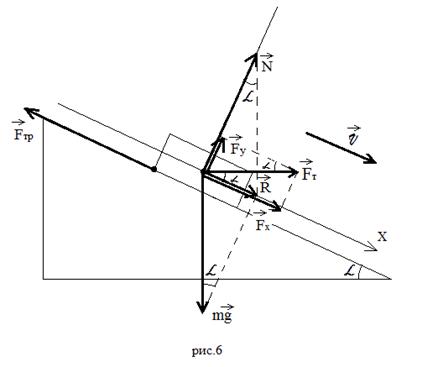
In this case, the traction force, in addition to pulling the body down along the inclined plane, also separates it from the inclined plane. So the final equation looks like:
c) The body is dragged evenly onto an inclined plane, applying a pulling force at an angle to the inclined plane (Figure 7).
I propose to consider specific tasks in order to advertise my methodical approach to solving such problems even more convincingly. But first, I draw attention to the solution algorithm (I think all physics teachers draw the attention of students to it, and my whole story was subordinated to this algorithm):
1) after carefully reading the problem, find out how the body moves;
2) make a drawing with the correct image of forces, based on the conditions of the problem;
3) write the equation of motion in vector form according to Newton's first or second law;
4) write this equation in terms of the projections of the force vectors on the x axis (this step can be omitted later, when the ability to solve problems in dynamics is brought to automatism);
5) express the projections of the vectors in terms of their modules, taking into account the directions and write the equation in algebraic form;
6) express the modules of forces by formulas (if necessary);
7) express the desired value.
Task 1. How long does it take for a mass of a body to slide off an inclined plane with a height and an angle of inclination if it moves uniformly along an inclined plane with an angle of inclination?
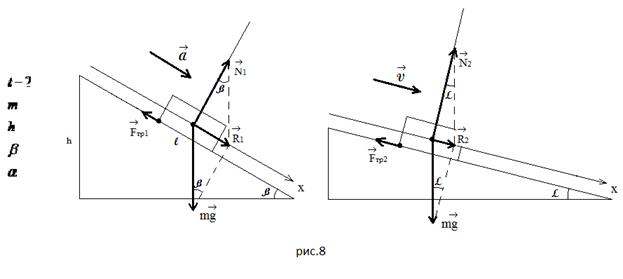
What would it be like to solve this problem in the usual way!
Task 2. Which is easier: to keep the body on an inclined plane or to move it uniformly upwards along it?
Here, when explaining, one cannot do without a rolling resultant, in my opinion.
As can be seen from the figures, in the first case, the friction force helps to hold the body (it is directed in the same direction as the holding force), in the second case, it, together with the rolling resultant, is directed against the movement. In the first case, in the second case.
