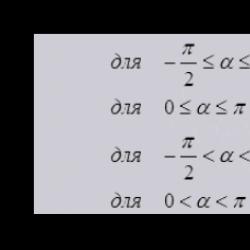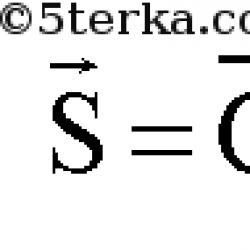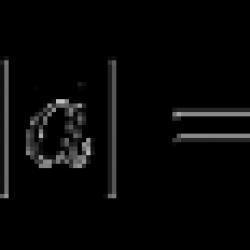Bu sayfada bir şeyler okudum (http://gamedeveloperjourney.blogspot.com/2009/04/point-plane-collision-detection.html)

D = - D3DXVec3Dot(&vP1, &vNormal);

burada vP1 düzlem üzerinde bir noktadır ve vNormal düzlemin normalidir. Sonuç her zaman 0 olacağından, bunun size dünyanın başlangıcından olan mesafeyi nasıl verdiğini merak ediyorum. Ayrıca, açık olmak gerekirse (2 boyutlu denklemin D kısmında hala biraz bulanık olduğum için), 2 boyutlu denklemde d, düzlemin başlangıcından önce dünyanın başlangıcına kadar olan çizgiden olan mesafedir?

3 Yanıt

6

Genel olarak, bir p noktası ile bir düzlem arasındaki mesafe aşağıdaki formül kullanılarak hesaplanabilir:

Nerede -nokta çarpım işlemi

= ax*bx + ay*by + az*bz

ve burada p0 düzlemde bir noktadır.

Eğer n birim uzunluğa sahipse, o zaman vektör ile arasındaki iç çarpım, vektörün Normal'e izdüşümünün (işaretli) uzunluğudur.

Bildirdiğiniz formül, p noktasının başlangıç ​​noktası olduğu özel bir durumdur. Bu durumda

Mesafe = = -

Bu eşitlik teknik olarak yanlıştır çünkü nokta çarpım noktalarla değil vektörlerle ilgilidir... ama yine de sayısal olarak geçerlidir. Açık bir formül yazarak bunu elde edersiniz

(0 - p0.x)*n.x + (0 - p0.y)*n.y + (0 - p0.z)*n.z

aynısı

- (p0.x*n.x + p0.y*n.y + p0.z*n.z)

2

Sonuç her zaman sıfır değildir. Sonuç yalnızca düzlemin orijinden geçmesi durumunda sıfır olacaktır. (Burada uçağın orijinden geçmediğini varsayalım.)

Temel olarak, size başlangıç ​​noktasından düzlemdeki bir noktaya kadar bir çizgi verilir. (Yani başlangıç ​​noktasından vP1'e kadar bir vektörünüz var). Bu vektörle ilgili sorun, büyük olasılıkla çarpık olması ve düzlemdeki en yakın nokta yerine, düzlem üzerinde uzak bir yere doğru gitmesidir. Yani eğer vP1 uzunluğunu yeni aldıysanız, çok fazla mesafe kat etmiş olursunuz.

Yapmanız gereken, vP1'in izdüşümü düzleme dik olduğunu bildiğiniz bir vektör üzerine almaktır. Elbette vNormaldir. Yani vP1 ve vNormal'in iç çarpımını alın ve bunu vNormal'in uzunluğuna bölün; cevabınızı bulun. (Eğer size zaten bir büyüklük olan bir vNormal verecek kadar nezaket gösterirlerse, o zaman bölmeye gerek yoktur.)

1

Bu sorunu Lagrange çarpanlarıyla çözebilirsiniz:

Uçaktaki en yakın noktanın şöyle görünmesi gerektiğini biliyorsunuz:

C=p+v

Burada c en yakın noktadır ve v düzlem boyunca bir vektördür (bu nedenle n'nin normaline diktir). En küçük normlu (veya kareli normlu) c'yi bulmaya çalışıyorsunuz. Yani v n'ye dik olduğu sürece nokta(c,c)'yi en aza indirmeye çalışıyorsunuz (böylece nokta(v,n) = 0).

Böylece Lagrangian'ı ayarlayın:

L = nokta(c,c) + lambda * (nokta(v,n)) L = nokta(p+v,p+v) + lambda * (nokta(v,n)) L = nokta(p,p) + 2*nokta(p,v) + nokta(v,v) * lambda * (nokta(v,n))

Ve v'ye göre türevi alın (ve 0'a ayarlayın):

2 * p + 2 * v + lambda * n = 0

Yukarıdaki denklemde lambda'yı noktalı olarak çözebilir ve her iki tarafı da n üzerinde üreterek elde edebilirsiniz.

2 * nokta(p,n) + 2 * nokta(v,n) + lambda * nokta(n,n) = 0 2 * nokta(p,n) + lambda = 0 lambda = - 2 * nokta(p,n) ))

nokta(n,n) = 1 ve nokta(v,n) = 0 olduğuna tekrar dikkat edin (çünkü v düzlemdedir ve n ona diktir). Yedek lambda daha sonra şunu elde etmek için geri döner:

2 * p + 2 * v - 2 * nokta(p,n) * n = 0

ve şunu elde etmek için v'yi çözün:

V = nokta(p,n) * n - p

Daha sonra şunu elde etmek için bunu tekrar c = p + v'ye takın:

C = nokta(p,n) * n

Bu vektörün uzunluğu |nokta(p,n)| işareti size noktanın orijinden normal vektör yönünde mi, yoksa orijinden ters yönde mi olduğunu söyler.

Diyelim ki ax+by+cz=d şeklinde bir düzlem denklemim var, düzlemden orijine olan en kısa mesafeyi nasıl bulabilirim? Bu yazıdan geriye doğru gidiyorum. Bu yazıda onlar...

Diyelim ki Kinect (0,0,0) konumunda duruyor ve +Z yönüne bakıyor. (1, 1, 1)'de bir nesne olduğunu ve Kinect derinlik görüntüsündeki piksellerden birinin bu nesneyi temsil ettiğini varsayalım.

Noktaların iki koordinatlı bir veri çerçevesi tarafından verildiği tüm noktalara olan mesafeyi orijinden eşitlemek istiyorum. Tüm noktalarım şöyle: x y 1 0,0 0,0 2 -4,0 -2,8 3 -7,0 -6,5 4 -9,0 -11,1...

Arka Plan Bilgisi Burada gösterilene benzer bir küresel koordinat sistemi düşünün: Koordinat Sistemi http://www.shokhirev.com/nikolai/projects/global/image013.gif Belirli bir nokta için...

3 boyutlu bir sahnem ve gluPerspective ile tanımlanmış bir kameram var. Sabit bir görüş alanım var ve herhangi bir geometrinin kameradan minimum mesafesini biliyorum (bu birinci şahıs görüşü, yani...

A, B, C noktaları ve uzayda bir nokta (P) olan bir üçgenim var. Bir noktadan uçağa olan mesafeyi nasıl alabilirim? P'den uçağa olan mesafeyi hesaplamam gerekiyor, buna rağmen...

Bir CGPoint'i (kırmızı dikdörtgen) başka bir CGPoint'in (mavi dikdörtgen) etrafında döndürmek istiyorum ancak orijinden (mavi dikdörtgen) olan mesafeyi değiştiriyor... köşede 270 verdiğimde oluşturduğu...

X, Y, Z düzlem merkezini, Kartezyen koordinatlarını almam gerekiyor. Düzlemin Normali ve merkez noktasından orijine olan mesafeye sahibim. Noktaları herhangi bir yere yerleştirebilirim ve...

Verilen: (x1, y1, z1) noktası yön vektörü (a1, b1, c1) düzlem ax + by + cz + d = 0 Bu vektör boyunca D noktasından düzleme olan mesafeyi nasıl bulabilirim? Teşekkür ederim

Döndürme matrisi R ve dünya koordinat sistemine göre bir çeviri T ile tanımlanan bir kamera koordinat sistemim var. Bir düzlem, kamera koordinatlarında normal bir N ve üzerindeki bir P noktası ile tanımlanır.

Bu yazıda, bir noktadan bir düzleme olan mesafeyi tanımlayacağız ve üç boyutlu uzayda belirli bir noktadan belirli bir düzleme olan mesafeyi bulmanızı sağlayan koordinat yöntemini analiz edeceğiz. Teorinin sunumundan sonra, birkaç tipik örnek ve problemin çözümlerini ayrıntılı olarak analiz edeceğiz.

Sayfada gezinme.

Bir noktadan bir düzleme olan mesafe bir tanımdır.

Bir noktadan bir düzleme olan uzaklık, biri belirli bir nokta, diğeri ise belirli bir noktanın belirli bir düzleme izdüşümü ile belirlenir.

Üç boyutlu uzayda bir M 1 noktası ve bir düzlem verilsin. M 1 noktasından geçen, düzleme dik bir düz çizgi a çizelim. a doğrusu ile düzlemin kesişme noktasını H 1 olarak gösterelim. M 1 H 1 segmentine denir dik, M 1 noktasından düzleme indirildi ve H 1 noktası - dik tabanı.

Tanım.

belirli bir noktadan belirli bir düzleme çizilen dikmenin tabanına kadar olan mesafedir.

Bir noktadan bir düzleme olan mesafenin tanımı aşağıdaki biçimde daha yaygındır.

Tanım.

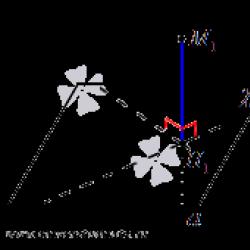
Noktadan düzleme uzaklık belirli bir noktadan belirli bir düzleme bırakılan dikmenin uzunluğudur.

Bu şekilde belirlenen M1 noktasından düzleme olan mesafenin, verilen M1 noktasından düzlemin herhangi bir noktasına olan mesafelerin en küçüğü olduğuna dikkat edilmelidir. Aslında H 2 noktasının düzlemde olmasına ve H 1 noktasından farklı olmasına izin verin. Açıkçası, M 2 H 1 H 2 üçgeni dikdörtgendir, içinde M 1 H 1 bir bacaktır ve M 1 H 2 hipotenüstür, bu nedenle, . Bu arada, M 1 H 2 segmentine denir eğik M1 noktasından düzleme çizilir. Dolayısıyla, belirli bir noktadan belirli bir düzleme çizilen dikme, aynı noktadan belirli bir düzleme çizilen eğik noktadan her zaman daha küçüktür.

Bir noktadan düzleme olan mesafe - teori, örnekler, çözümler.

Bazı geometrik problemler çözümün bir aşamasında bir noktadan bir düzleme olan mesafenin bulunmasını gerektirir. Bunun yöntemi kaynak verilere bağlı olarak seçilir. Genellikle sonuç, Pisagor teoreminin veya üçgenlerin eşitlik ve benzerlik işaretlerinin kullanılmasıdır. Üç boyutlu uzayda verilen bir noktadan düzleme olan mesafeyi bulmanız gerekiyorsa, koordinat yöntemi kurtarmaya gelir. Makalenin bu paragrafında sadece analiz edeceğiz.

Öncelikle problemin durumunu formüle ediyoruz.

Üç boyutlu uzayda Oxyz dikdörtgen koordinat sisteminde bir nokta verilir , düzlem ve M 1 noktasından düzleme olan mesafeyi bulmak gerekir.

Bu sorunu çözmenin iki yoluna bakalım. Bir noktadan düzleme olan mesafeyi hesaplamanıza izin veren ilk yöntem, M1 noktasından düzleme bırakılan dikin tabanı olan H1 noktasının koordinatlarını bulmaya ve ardından mesafeyi hesaplamaya dayanır. M 1 ve H 1 noktaları arasında. Belirli bir noktadan belirli bir düzleme olan mesafeyi bulmanın ikinci yolu, belirli bir düzlem için normal denklemin kullanılmasını içerir.

Bir noktaya olan mesafeyi hesaplamanın ilk yolu uçağa.

M1 noktasından düzleme çizilen dikmenin tabanı H1 olsun. H 1 noktasının koordinatlarını belirlersek, M 1 noktasından düzleme gerekli mesafe, noktalar arasındaki mesafe olarak hesaplanabilir. Ve formüle göre. Böylece geriye H1 noktasının koordinatlarını bulmak kalıyor.

Bu yüzden, Bir noktadan mesafeyi bulmak için algoritma uçağa kadar Sonraki:

Bir noktaya olan mesafeyi bulmak için uygun olan ikinci yöntem uçağa.

Bize Oxyz dikdörtgen koordinat sisteminde bir düzlem verildiği için düzlemin normal denklemini şeklinde elde edebiliriz. Daha sonra noktaya olan mesafe düzleme oranı formülle hesaplanır. Bir noktadan bir düzleme olan mesafeyi bulmak için bu formülün geçerliliği aşağıdaki teorem ile belirlenir.

teorem.

Dikdörtgen bir koordinat sistemi olan Oxyz'in üç boyutlu uzayda bir nokta olarak sabitlenmesine izin verin. ve form düzleminin normal denklemi. M 1 noktasından düzleme olan mesafe, düzlemin normal denkleminin sol tarafındaki ifadenin değerinin mutlak değerine eşittir, yani .

Kanıt.

Bu teoremin ispatı, Bir noktadan bir çizgiye olan mesafenin bulunması bölümünde verilen benzer bir teoremin ispatına tamamen benzerdir.

M1 noktasından düzleme olan mesafenin, M1 sayısal projeksiyonu ile orijinden düzleme olan mesafe arasındaki farkın modülüne eşit olduğunu göstermek kolaydır; , Nerede - Düzlemin normal vektörü bire eşittir, - vektör tarafından belirlenen yöne.

Ve tanımı gereği öyledir, ancak koordinat biçimindedir. Bu nedenle ve kanıtlanması gerektiği gibi.

Böylece, noktadan uzaklık Düzlemin normal denkleminin sol tarafına M1 noktasının x, y ve z yerine x 1 , y 1 ve z 1 koordinatları yerleştirilip elde edilen değerin mutlak değeri alınarak düzleme göre hesaplanabilir. .

Bir noktadan mesafeyi bulma örnekleri uçağa.

Örnek.

Noktaya olan mesafeyi bulun uçağa.

Çözüm.

İlk yol.

Problemin durumunda bize formun düzleminin genel bir denklemi veriliyor, buradan da görülebiliyor: bu düzlemin normal vektörüdür. Bu vektör, verilen düzleme dik olan düz çizginin yönlendirici vektörü olarak alınabilir. O zaman uzaydaki noktadan geçen bir doğrunun kanonik denklemlerini yazabiliriz. ve koordinatları olan bir yön vektörü var, benziyorlar.

Doğrunun kesişme noktasının koordinatlarını bulmaya başlayalım ve uçaklar. H 1 olarak gösterelim. Bunu yapmak için önce düz çizginin kanonik denklemlerinden kesişen iki düzlemin denklemlerine geçişi gerçekleştiriyoruz:

Şimdi denklem sistemini çözelim (gerekirse makaleye bakın). Kullanırız:

Böylece, .

Belirli bir noktadan belirli bir düzleme gerekli mesafeyi, noktalar arasındaki mesafe olarak hesaplamak kalır. Ve :
.

İkinci çözüm.

Verilen düzlemin normal denklemini alalım. Bunu yapabilmek için düzlemin genel denklemini normal forma getirmemiz gerekiyor. Normalleştirme faktörünü belirledikten sonra düzlemin normal denklemini elde ederiz . Ortaya çıkan denklemin sol tarafının değerini hesaplamak için kalır. ve elde edilen değerin modülünü alın - bu noktadan istenen mesafeyi verecektir uçağa:

Bu makale bir noktadan bir düzleme olan mesafenin belirlenmesinden bahsediyor. üç boyutlu uzayda belirli bir noktaya olan mesafeyi bulmamızı sağlayacak koordinat yöntemini analiz edelim. Birleştirmek için çeşitli görev örneklerini göz önünde bulundurun.

Bir noktadan bir düzleme olan mesafe, bir noktadan bir noktaya bilinen bir mesafe aracılığıyla bulunur; bunlardan biri verilir, diğeri ise belirli bir düzleme izdüşümdür.

Uzayda χ düzlemli bir M1 noktası verildiğinde, bu noktadan düzleme dik bir düz çizgi çizilebilir. H 1 bunların kesişimlerinin ortak noktasıdır. Buradan, M 1 H 1 segmentinin, M 1 noktasından χ düzlemine çizilen bir dik olduğunu anlıyoruz; burada H 1 noktası, dikin tabanıdır.

tanım 1

Belirli bir noktadan belirli bir düzleme çizilen dikmenin tabanına kadar olan mesafeye denir.

Tanım farklı formülasyonlarla yazılabilir.

Tanım 2

Noktadan düzleme uzaklık Belirli bir noktadan belirli bir düzleme çizilen dikmenin uzunluğuna denir.

M1 noktasından χ düzlemine olan mesafe şu şekilde tanımlanır: M1 noktasından χ düzlemine olan mesafe, belirli bir noktadan düzlemdeki herhangi bir noktaya kadar en küçük olacaktır. H 2 noktası χ düzleminde bulunuyorsa ve H 2 noktasına eşit değilse, M 2 H 1 H 2 formunda bir dik üçgen elde ederiz. M 2 H 1, M 2 H 2 bacağının bulunduğu dikdörtgen olan - hipotenüs. Dolayısıyla bu şu anlama gelir: M 1 H 1< M 1 H 2 . Тогда отрезок М 2 H 1 M1 noktasından χ düzlemine çizilen eğimli kabul edilir. Belirli bir noktadan bir düzleme çizilen dikmenin, belirli bir noktadan belirli bir düzleme çizilen eğik çizgiden küçük olduğunu biliyoruz. Aşağıdaki şekilde bu durumu düşünün.

Bir noktadan düzleme olan mesafe - teori, örnekler, çözümler

Çözümleri bir noktadan düzleme olan mesafeyi içermesi gereken bir takım geometrik problemler vardır. Bunu tespit etmenin yolları farklı olabilir. Çözüm için Pisagor teoremini veya üçgenlerin benzerliğini kullanın. Koşula göre, üç boyutlu uzayın dikdörtgen koordinat sisteminde verilen bir noktadan düzleme olan mesafeyi hesaplamak gerektiğinde, koordinat yöntemini kullanarak çözerler. Bu paragraf bu yöntemle ilgilidir.

Problemin durumuna göre, üç boyutlu uzayda χ düzlemi ile M 1 (x 1, y 1, z 1) koordinatlarına sahip bir nokta verilmiştir, M 1'den uzaklığı belirlemek gerekir. düzlem χ. Çözmek için çeşitli çözümler kullanılır.

ilk yol

Bu yöntem, M1 noktasından χ düzlemine dik olanın tabanı olan H1 noktasının koordinatlarını kullanarak bir noktadan düzleme olan mesafeyi bulmaya dayanır. Daha sonra M 1 ile H 1 arasındaki mesafeyi hesaplamanız gerekir.

Sorunu ikinci şekilde çözmek için belirli bir düzlemin normal denklemi kullanılır.

İkinci yol

Koşul olarak, H1'in, M1 noktasından χ düzlemine indirilen dikin tabanı olduğunu biliyoruz. Daha sonra H 1 noktasının koordinatlarını (x 2, y 2, z 2) belirleriz. M1'den χ düzlemine istenen mesafe M 1 H 1 \u003d (x 2 - x 1) 2 + (y 2 - y 1) 2 + (z 2 - z 1) 2 formülü ile bulunur, burada M 1 (x 1, y 1 , z 1) ve H 1 (x 2 , y 2 , z 2) . Çözmek için H 1 noktasının koordinatlarını bilmeniz gerekir.

H1'in, χ düzleminin, χ düzlemine dik olarak yerleştirilmiş M1 noktasından geçen a çizgisi ile kesişme noktası olduğunu biliyoruz. Belirli bir düzleme dik olarak belirli bir noktadan geçen düz bir çizginin denklemini formüle etmenin gerekli olduğu sonucu çıkar. İşte o zaman H 1 noktasının koordinatlarını belirleyebiliriz. Doğrunun ve düzlemin kesişme noktasının koordinatlarını hesaplamak gerekir.

M 1 (x 1, y 1, z 1) koordinatlarına sahip bir noktadan χ düzlemine olan mesafeyi bulma algoritması:

Tanım 3

• M 1 noktasından geçen ve aynı zamanda bir düz çizginin denklemini oluşturun
• χ düzlemine dik;
• H 1 noktasının nokta olan koordinatlarını (x 2, y 2, z 2) bulun ve hesaplayın
• a çizgisinin χ düzlemiyle kesişimi;
• M 1 H 1 = (x 2 - x 1) 2 + (y 2 - y 1) 2 + z 2 - z 1 2 formülünü kullanarak M 1 ile χ arasındaki mesafeyi hesaplayın.

üçüncü yol

Belirli bir dikdörtgen koordinat sisteminde O x y z bir χ düzlemi vardır, o zaman cos α · x + cos β · y + cos γ · z - p = 0 formundaki düzlemin normal bir denklemini elde ederiz. Buradan, M 1 H 1 = cos α x + cos β y + cos formülüyle hesaplanan, χ düzlemine çizilen M 1 (x 1 , y 1 , z 1) noktasıyla M 1 H 1 mesafesinin elde edildiğini görüyoruz. γ z-p. Bu formül teorem sayesinde oluşturulduğu için geçerlidir.

teorem

Üç boyutlu uzayda bir M 1 (x 1 , y 1 , z 1) noktası verilmişse, cos α x + cos β y + cos γ z - p = 0 formundaki χ düzleminin normal denklemine sahip olan, daha sonra noktadan M 1 H 1 düzlemine olan mesafenin hesaplanması, M 1 H 1 = cos α · x + cos β · y + cos γ · z - p formülünden türetilir, çünkü x = x 1 , y = y 1 , z = z1 .

Kanıt

Teoremin kanıtı bir noktadan bir çizgiye olan mesafeyi bulmaya indirgenmiştir. Buradan, M 1'den χ düzlemine olan mesafenin, M 1 yarıçap vektörünün sayısal izdüşümü ile orijinden χ düzlemine olan mesafe arasındaki farkın modülü olduğunu anlıyoruz. Daha sonra M 1 H 1 = n p n → O M → - p ifadesini elde ederiz. χ düzleminin normal vektörü şu şekle sahiptir: n → = cos α , cos β , cos γ ve uzunluğu bire eşittir, n p n → Ö M → O M → = (x 1 , y 1 vektörünün sayısal izdüşümüdür) , z 1) n → vektörünün belirlediği yönde.

Skaler vektörleri hesaplamak için formülü uygulayalım. Daha sonra n → , O M → = n → n p n → O M → = 1 n p n → Ö M → = n p n → O M → formunda bir vektör bulmak için bir ifade elde ederiz, çünkü n → = cos α , cos β , cos γ z ve Ö M → = (x 1 , y 1 , z 1) . Gösterimin koordinat biçimi şu şekilde olacaktır: n →, O M → = cos α x 1 + cos β y 1 + cos γ z 1, sonra M 1 H 1 = n p n → O M → - p = cos α x 1 + cos β · y 1 + çünkü γ · z 1 - p . Teorem kanıtlandı.

Buradan, M 1 (x 1, y 1, z 1) noktasından χ düzlemine olan mesafenin, cos α x + cos β y + cos düzleminin normal denkleminin sol tarafına ikame edilerek hesaplandığını anlıyoruz. x, y, z koordinatları yerine γ z - p = 0 x 1 , y 1 ve z1 M 1 noktasına ilişkin olarak elde edilen değerin mutlak değeri alınır.

Koordinatları olan bir noktadan belirli bir düzleme olan mesafeyi bulma örneklerini düşünün.

örnek 1

M 1 (5 , - 3 , 10) koordinatlı noktadan 2 x - y + 5 z - 3 = 0 düzlemine olan mesafeyi hesaplayın.

Çözüm

Sorunu iki şekilde çözelim.

İlk yöntem a doğrusunun yön vektörünün hesaplanmasıyla başlayacaktır. Koşul gereği, verilen 2 x - y + 5 z - 3 = 0 denkleminin genel bir düzlem denklemi olduğu ve n → = (2 , - 1 , 5)'in verilen düzlemin normal vektörü olduğu elimizdedir. Verilen düzleme dik olan a düz çizgisi için yönlendirici vektör olarak kullanılır. Uzayda M 1 (5, - 3, 10) içinden geçen bir düz çizginin kanonik denklemini koordinatları 2, - 1, 5 olan bir yön vektörüyle yazmalısınız.

Denklem şu şekilde görünecektir: x - 5 2 = y - (- 3) - 1 = z - 10 5 ⇔ x - 5 2 = y + 3 - 1 = z - 10 5 .

Kesişme noktaları tanımlanmalıdır. Bunu yapmak için, kanonikten kesişen iki çizginin denklemlerine geçiş için denklemleri yavaşça bir sistemde birleştirin. Bu noktayı H 1 olarak alalım. Bunu anlıyoruz

x - 5 2 = y + 3 - 1 = z - 10 5 ⇔ - 1 (x - 5) = 2 (y + 3) 5 (x - 5) = 2 (z - 10) 5 ( y + 3) = - 1 (z - 10) ⇔ ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0

Daha sonra sistemi etkinleştirmeniz gerekir

x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 2 x - y + 5 z - 3 = 0 ⇔ x + 2 y = 1 5 x - 2 z = 5 2 x - y + 5 z = 3

Sistemi Gauss'a göre çözme kuralına dönelim:

1 2 0 - 1 5 0 - 2 5 2 - 1 5 3 ~ 1 2 0 - 1 0 - 10 - 2 10 0 - 5 5 5 ~ 1 2 0 - 1 0 - 10 - 2 10 0 0 6 0 ⇒ ⇒ z = 0 6 = 0 , y = - 1 10 10 + 2 z = - 1 , x = - 1 - 2 y = 1

Bunu H 1 (1, - 1, 0) olarak elde ederiz.

Belirli bir noktadan bir düzleme olan mesafeyi hesaplıyoruz. M 1 (5, - 3, 10) ve H 1 (1, - 1, 0) noktalarını alıyoruz ve şunu elde ediyoruz:

M 1 H 1 \u003d (1 - 5) 2 + (- 1 - (- 3)) 2 + (0 - 10) 2 \u003d 2 30

İkinci çözüm ise öncelikle verilen 2 x - y + 5 z - 3 = 0 denklemini normal forma getirmektir. Normalleştirme faktörünü belirliyoruz ve 1 2 2 + (- 1) 2 + 5 2 = 1 30 elde ediyoruz. Buradan 2 30 · x - 1 30 · y + 5 30 · z - 3 30 = 0 düzleminin denklemini türetiyoruz. Denklemin sol tarafı x \u003d 5, y \u003d - 3, z \u003d 10 değiştirilerek hesaplanır ve M 1 (5, - 3, 10) ile 2 x - y + arasındaki mesafeyi almanız gerekir. 5 z - 3 = 0 modülo. Şu ifadeyi elde ederiz:

M 1 H 1 \u003d 2 30 5 - 1 30 - 3 + 5 30 10 - 3 30 \u003d 60 30 \u003d 2 30

Cevap: 2 30 .

χ düzlemi, düzlemi belirlemeye yönelik kesit yöntemleri yöntemlerinden biriyle belirtildiğinde, önce χ düzleminin denklemini elde etmeniz ve herhangi bir yöntemi kullanarak gerekli mesafeyi hesaplamanız gerekir.

Örnek 2

Üç boyutlu uzayda M 1 (5 , - 3 , 10) , A (0 , 2 , 1) , B (2 , 6 , 1) , C (4 , 0 , - 1) koordinatlarına sahip noktalar ayarlanır. M 1'den A B C düzlemine olan mesafeyi hesaplayın.

Çözüm

Öncelikle M 1 (5, - 3, 10) , A (0 , 2 , 1) , B (2 , 6 , 1) , C ( koordinatlarına sahip verilen üç noktadan geçen düzlemin denklemini yazmanız gerekir. 4 , 0 , - 1) .

x - 0 y - 2 z - 1 2 - 0 6 - 2 1 - 1 4 - 0 0 - 2 - 1 - 1 = 0 ⇔ x y - 2 z - 1 2 4 0 4 - 2 - 2 = 0 ⇔ ⇔ - 8x + 4y - 20z + 12 = 0 ⇔ 2x - y + 5z - 3 = 0

Sorunun öncekine benzer bir çözümü olduğu sonucu çıkıyor. Dolayısıyla M 1 noktasından A B C düzlemine olan uzaklık 2 30'dur.

Cevap: 2 30 .

Bir düzlemdeki belirli bir noktadan veya paralel oldukları bir düzleme olan mesafeyi bulmak, M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 - p formülünü uygulayarak daha uygundur. . Buradan düzlemlerin normal denklemlerinin birkaç adımda elde edildiğini anlıyoruz.

Örnek 3

M 1 (- 3 , 2 , - 7) koordinatlarına sahip belirli bir noktadan O x y z koordinat düzlemine ve 2 y - 5 = 0 denklemiyle verilen düzleme olan mesafeyi bulun.

Çözüm

O y z koordinat düzlemi x = 0 formundaki bir denkleme karşılık gelir. O y z düzlemi için bu normaldir. Bu nedenle, x \u003d - 3 değerlerini ifadenin sol tarafına koymak ve M 1 (- 3, 2, - 7) koordinatlı noktadan düzleme olan mesafenin mutlak değerini almak gerekir. . -3 = 3 değerine eşit bir değer elde ederiz.

Dönüşüm sonrasında 2 y - 5 = 0 düzleminin normal denklemi y - 5 2 = 0 formunu alacaktır. Daha sonra M 1 (- 3 , 2 , - 7) koordinatlı noktadan 2 y - 5 = 0 düzlemine kadar gerekli mesafeyi bulabilirsiniz. Yerine koyup hesapladığımızda 2 - 5 2 = 5 2 - 2 elde ederiz.

Cevap: M 1 (- 3 , 2 , - 7)'den O y z'ye istenilen mesafe 3 değerine, 2 y - 5 = 0'a ise 5 2 - 2 değerine sahiptir.

Metinde bir hata fark ederseniz, lütfen onu vurgulayın ve Ctrl+Enter tuşlarına basın.