Trigonometrik fonksiyonların integralleri.
Çözüm örnekleri

Bu dersimizde trigonometrik fonksiyonların integrallerini ele alacağız, yani integrallerin doldurulması çeşitli kombinasyonlarda sinüs, kosinüs, teğet ve kotanjant olacaktır. Tüm örnekler detaylı bir şekilde analiz edilecek, bir çaydanlık için bile erişilebilir ve anlaşılır olacaktır.

Trigonometrik fonksiyonların integrallerini başarılı bir şekilde incelemek için, en basit integraller konusunda bilgili olmanızın yanı sıra bazı integral tekniklerinde uzman olmanız gerekir. Derslerde bu materyallerle tanışabilirsiniz. Belirsiz integral. Çözüm örnekleri Ve .

Ve şimdi ihtiyacımız var: İntegral tablosu, Türev tablosu Ve Trigonometrik formüllerin referans kitabı. Tüm kılavuzları sayfada bulabilirsiniz Matematiksel formüller ve tablolar. Her şeyi yazdırmanızı öneririm. Özellikle trigonometrik formüllere odaklanıyorum, gözlerinin önünde olmalılar– onsuz işin verimliliği gözle görülür şekilde azalacaktır.

Ama önce bu makaledeki hangi integraller hakkında HAYIR. Burada formun integrali yoktur, - kosinüs, sinüsün bir polinomla çarpılması (daha az sıklıkla, teğet veya kotanjantlı bir şey). Bu tür integraller parçalara göre integral alınır ve yöntemi öğrenmek için Parçalara göre integral alma dersini ziyaret edin. Çözüm örnekleri Ayrıca, "kemerler" - ark teğet, ark sinüs vb. ile integraller yoktur, bunlar çoğunlukla parçalar halinde entegre edilir.

Trigonometrik fonksiyonların integrallerini bulurken bir dizi yöntem kullanılır:

(4) Tablo formülünü kullanın tek fark, "x" yerine karmaşık bir ifadeye sahip olmamızdır.

Örnek 2

Örnek 3

Belirsiz integrali bulun.

Sıralamalarda boğulanlar için türün bir klasiği. Muhtemelen fark ettiğiniz gibi, integral tablosunda teğet ve kotanjantın integrali yoktur, ancak yine de bu tür integraller bulunabilir.

(1) Trigonometrik formülü kullanıyoruz

(2) Fonksiyonu diferansiyelin işareti altına getiriyoruz.

(3) Tablo integralini kullanın .

Örnek 4

Belirsiz integrali bulun.

Bu kendi kendine çözmeye bir örnektir, tam çözüm ve cevap dersin sonundadır.

Örnek 5

Belirsiz integrali bulun.

Seviyelerimiz yavaş yavaş artacak =).
Önce çözüm:

(1) Formülü kullanıyoruz

(2) Temel trigonometrik özdeşliği kullanıyoruz , bundan şu sonuç çıkıyor .

(3) Payı payda terimine ve terime bölün.

(4) Belirsiz integralin doğrusallık özelliğini kullanıyoruz.

(5) Tabloyu kullanarak integral alıyoruz.

Örnek 6

Belirsiz integrali bulun.

Bu kendi kendine çözmeye bir örnektir, tam çözüm ve cevap dersin sonundadır.

Ayrıca daha yüksek kuvvetlerde olan teğet ve kotanjantların integralleri de vardır. Küpteki tanjantın integrali derste ele alınmaktadır. Düzlem figürünün alanı nasıl hesaplanır? Tanjantın (kotanjant) dördüncü ve beşinci kuvvetlerdeki integralleri sayfada elde edilebilir. Karmaşık integraller.

İntegral derecesinin azaltılması

Bu teknik, integraller sinüs ve kosinüslerle doldurulduğunda işe yarar. eşit derece. Dereceyi azaltmak için trigonometrik formüller kullanılır. , ve ve son formül daha çok ters yönde kullanılır: .

Örnek 7

Belirsiz integrali bulun.

Çözüm:

Prensip olarak burada formülü uygulamamız dışında yeni bir şey yok. (integrandın derecesi düşürülür). Lütfen çözümü kısalttığımı unutmayın. Tecrübe kazanıldıkça integral sözlü olarak bulunabilir, bu zaman kazandırır ve ödevleri bitirirken oldukça kabul edilebilirdir. Bu durumda kuralın yazılmaması tavsiye edilir. önce sözel olarak 1'in, sonra da -'nin integralini alıyoruz.

Örnek 8

Belirsiz integrali bulun.

Bu kendi kendine çözmeye bir örnektir, tam çözüm ve cevap dersin sonundadır.

Vaat edilen derece artışı şöyledir:

Örnek 9

Belirsiz integrali bulun.

Önce çözüm, sonra yorum:

(1) Formülü uygulamak için integrali hazırlayın .

(2) Aslında formülü uyguluyoruz.

(3) Paydanın karesini alırız ve integral işaretinden sabiti çıkarırız. Biraz farklı yapılabilirdi ama bence daha uygun.

(4) Formülü kullanıyoruz

(5) Üçüncü dönemde yine dereceyi düşürüyoruz ancak formülü kullanarak .

(6) Benzer terimler veriyoruz (burada terimi terime böldüm) ve eklemeyi yaptım).

(7) Aslında integrali alıyoruz, doğrusallık kuralını ve fonksiyonu diferansiyelin işareti altına getirme yöntemi sözlü olarak gerçekleştirilir.

(8) Cevabı tarıyoruz.

! Belirsiz integralde cevap genellikle birkaç şekilde yazılabilir.

Az önce ele alınan örnekte, son cevap farklı şekilde yazılabilir - parantezleri açın ve hatta bunu ifadeyi entegre etmeden önce yapın, yani örneğin aşağıdaki sonu oldukça kabul edilebilir:

Bu seçeneğin daha da uygun olması mümkündür, bunu kendi kendime karar verdiğim şekilde açıkladım). Bağımsız bir çözüm için başka bir tipik örnek:

Örnek 10

Belirsiz integrali bulun.

Bu örnek iki şekilde çözülür ve şunları elde edebilirsiniz: tamamen farklı iki cevap.(daha doğrusu, tamamen farklı görünecekler, ancak matematiksel açıdan eşdeğer olacaklar). Büyük olasılıkla, en rasyonel yolu göremeyeceksiniz ve diğer trigonometrik formülleri kullanarak parantezleri açmaktan sıkıntı çekeceksiniz. En etkili çözüm dersin sonunda verilir.

Paragrafı özetlersek, formun herhangi bir integralinin olduğu sonucuna varıyoruz. , Nerede ve - eşit sayısı, integralin derecesi düşürülerek çözülür.
Uygulamada 8 ve 10 derecelik integrallerle karşılaştım, dereceyi birkaç kez düşürerek korkunç hemoroitlerini çözmek zorunda kaldım, sonuçta uzun, uzun cevaplar ortaya çıktı.

Değişken değiştirme yöntemi

Makalede belirtildiği gibi Belirsiz integralde değişken değişim yöntemi yerine koyma yöntemini kullanmanın temel ön koşulu, integralin bir fonksiyon ve onun türevini içermesidir:
(fonksiyonların mutlaka üründe olması gerekmez)

Örnek 11

Belirsiz integrali bulun.

Türev tablosuna bakıyoruz ve formüllere dikkat ediyoruz, yani integralimizde bir fonksiyon ve onun türevi var. Bununla birlikte, farklılaşırken kosinüs ve sinüsün karşılıklı olarak birbirine dönüştüğünü görüyoruz ve şu soru ortaya çıkıyor: değişkende nasıl değişiklik yapılır ve sinüs veya kosinüs için ne belirlenmeli?! Soru, bilimsel dürtme yöntemiyle çözülebilir: Değiştirmeyi yanlış yaparsak, bundan iyi bir şey çıkmaz.

Genel kural: Benzer durumlarda paydadaki fonksiyonu belirtmeniz gerekir.

Çözümü kesiyoruz ve değiştirme işlemini gerçekleştiriyoruz

Paydada bizim için her şey yolunda, her şey sadece bağlı , şimdi neye dönüşeceğini bulmak kalıyor.
Bunu yapmak için diferansiyeli buluyoruz:

Veya kısaca:
Ortaya çıkan eşitlikten orantı kuralına göre ihtiyacımız olan ifadeyi ifade ediyoruz:

Bu yüzden:

Artık tüm integrand yalnızca buna bağlı ve çözüme devam edebiliriz

Hazır. Değiştirmenin amacının integrali basitleştirmek olduğunu size hatırlatırım, bu durumda her şey güç fonksiyonunun masa üzerinden entegrasyonuna indirgenir.

Bu örneği bu kadar detaylı boyamam tesadüf değildi, ders materyallerini tekrarlamak ve pekiştirmek için yapıldı. Belirsiz integralde değişken değişim yöntemi.

Ve şimdi bağımsız bir çözüm için iki örnek:

Örnek 12

Belirsiz integrali bulun.

Örnek 13

Belirsiz integrali bulun.

Dersin sonunda çözümleri ve cevapları tamamlayın.

Örnek 14

Belirsiz integrali bulun.

Burada yine integralde, kosinüslü bir sinüs (türevli bir fonksiyon) var, ancak zaten çarpımda ve bir ikilem ortaya çıkıyor - sinüs mü yoksa kosinüs mü?

Bilimsel dürtme yöntemini kullanarak değiştirmeyi deneyebilirsiniz ve hiçbir şey işe yaramazsa, onu başka bir işlev olarak atayabilirsiniz, ancak şu var:

Genel kural: Mecazi anlamda "rahatsız edici bir konumda" olan işlevi belirlemeniz gerekir..

Bu örnekte öğrenci kosinüsünün dereceden "zarar gördüğünü" ve sinüsün kendi başına bu şekilde serbestçe oturduğunu görüyoruz.

O halde bir değişiklik yapalım:

Eğer değişken değiştirme algoritması ve diferansiyeli bulma konusunda hala zorluk yaşayan varsa derse dönmelidir. Belirsiz integralde değişken değişim yöntemi.

Örnek 15

Belirsiz integrali bulun.

İntegrali analiz ediyoruz, ne ile gösterilmeli?
Şimdi yönergelerimize bir göz atalım:
1) Fonksiyon büyük olasılıkla paydadadır;
2) Fonksiyon "rahatsız edici bir konumdadır".

Bu arada, bu kurallar yalnızca trigonometrik fonksiyonlar için geçerli değildir.

Her iki kritere göre (özellikle ikincisine göre) sinüs uyuyor, dolayısıyla bir değişim kendini gösteriyor. Prensip olarak, değiştirme zaten gerçekleştirilebilir, ancak önce ne yapacağınızı bulmak güzel olur mu? Öncelikle bir kosinüsü “sabitliyoruz”:

"Gelecekteki" farkımız için ayırıyoruz

Ve temel trigonometrik özdeşliği kullanarak sinüs aracılığıyla şunu ifade ederiz:

Şimdi değiştirme şu:

Genel kural: İntegralde trigonometrik fonksiyonlardan biri (sinüs veya kosinüs) varsa garip derece, o zaman tek dereceden bir işlevi "ısırmanız" ve arkasında başka bir işlev belirlemeniz gerekir. Sadece kosinüs ve sinüslerin olduğu integrallerden bahsediyoruz.

Ele alınan örnekte, tek dereceli bir kosinüsümüz vardı, bu yüzden dereceden bir kosinüsü ayırdık ve sinüsü gösterdik.

Örnek 16

Belirsiz integrali bulun.

Seviyeler artıyor =).
Bu kendin yap örneğidir. Dersin sonunda tam çözüm ve cevap.

Evrensel trigonometrik ikame

Evrensel trigonometrik ikame, değişken yönteminin değiştirilmesinin yaygın bir durumudur. "Ne yapacağınızı bilemediğinizde" uygulamayı deneyebilirsiniz. Ama aslında uygulanması için bazı kurallar var. Evrensel trigonometrik ikamenin uygulanması gereken tipik integraller aşağıdaki integrallerdir: , , , vesaire.

Örnek 17

Belirsiz integrali bulun.

Bu durumda evrensel trigonometrik ikame şu şekilde uygulanır. Değiştirelim: . Harfi kullanmıyorum ama harf, bu bir tür kural değil, yine de karar vermeye o kadar alıştım ki.

Burada ifade ettiğim eşitlikten bunun için diferansiyeli bulmak daha uygundur:
Ark teğetinin her iki kısmına da asılıyorum:

Arktanjant ve teğet birbirini iptal eder:

Böylece:

Uygulamada, bu kadar ayrıntılı bir şekilde boyayamazsınız, ancak yalnızca bitmiş sonucu kullanabilirsiniz:

! İfade yalnızca sinüs ve kosinüslerin altında integral için sadece "x'ler" varsa geçerlidir (buna daha sonra değineceğiz) her şey biraz farklı olacak!

Sinüsleri ve kosinüsleri değiştirirken aşağıdaki kesirlere dönüşürüz:
, , bu eşitlikler iyi bilinen trigonometrik formüllere dayanmaktadır: ,

Yani temizlik şöyle görünebilir:

Evrensel bir trigonometrik değişiklik yapalım:

Yanıtlarını görebileceğiniz bağımsız bir çözüme yönelik görevler de olacaktır.

İntegral, trigonometrik fonksiyonların çarpımından toplama dönüştürülebilir

İntegralin, birinci derece x'in sinüs ve kosinüslerinin farklı faktörlerle çarpımının ürünü olduğu integralleri, yani formun integrallerini düşünün.

İyi bilinen trigonometrik formüllerin kullanılması

(2)
(3)
(4)
(31) formundaki integrallerin her bir ürünü cebirsel toplama dönüştürülebilir ve formüllerle entegre edilebilir

(5)

(6)

örnek 1 Bulmak

Çözüm. Formül (2)'ye göre

Örnek 2 Bulmak trigonometrik fonksiyonun integrali

Çözüm. Formül (3)'e göre

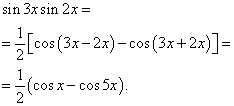
Örnek 3 Bulmak trigonometrik fonksiyonun integrali

Çözüm. Formül (4)'e göre integralin aşağıdaki dönüşümünü elde ederiz:

Formül (6)'yı uygulayarak şunu elde ederiz:

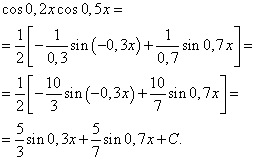
Aynı argümanın sinüs ve kosinüs kuvvetlerinin çarpımının integrali

Şimdi aynı argümanın sinüs ve kosinüs kuvvetlerinin çarpımı olan fonksiyonların integrallerini ele alalım;

(7)

Belirli durumlarda, göstergelerden biri ( M veya N) sıfır olabilir.

Bu tür fonksiyonları entegre ederken, kosinüsün eşit gücünün sinüs cinsinden ifade edilebileceği ve sinüs diferansiyelinin cos'a eşit olduğu kullanılır. x dx(veya sinüsün çift kuvveti kosinüs cinsinden ifade edilebilir ve kosinüs diferansiyeli - günah x dx ) .

İki durum birbirinden ayrılmalıdır: 1) göstergelerden en az biri M Ve N garip; 2) her iki gösterge de eşit.

İlk durum, yani üs gerçekleşsin N = 2k+ 1 - tek. Sonra bunu göz önünde bulundurarak

İntegral, bir kısmı yalnızca sinüsün bir fonksiyonu, diğeri ise sinüsün diferansiyeli olacak şekilde sunulur. Şimdi değişken değişikliğiyle T= günah Xçözüm, polinomun şuna göre entegrasyonuna indirgenir: T. Eğer sadece derece M tek ise aynısını yapın ve günah faktörünü ayırın X, integralin geri kalanını cos cinsinden ifade etmek X ve varsayıyorum T= çünkü X. Bu yaklaşım şu durumlarda da kullanılabilir: sinüs ve kosinüsün kısmi kuvvetlerinin entegrasyonu , Ne zaman göstergelerden en az biri tuhaf . Bütün mesele şu ki sinüs ve kosinüsün kuvvetlerinin bölümü, bunların çarpımının özel bir durumudur : Trigonometrik fonksiyon integralin paydasında olduğunda derecesi negatiftir. Ancak dereceleri yalnızca çift olan kısmi trigonometrik fonksiyonlar da vardır. Onlar hakkında - sonraki paragraf.

Her iki gösterge de M Ve N eşitse trigonometrik formüller kullanılıyor

sinüs ve kosinüs üslerini düşürün, bundan sonra yukarıdakiyle aynı türde bir integral elde edilecektir. Bu nedenle entegrasyonun aynı şekilde sürdürülmesi gerekmektedir. Çift göstergelerden biri negatifse, yani sinüs ve kosinüsün çift güçlerinin bölümü dikkate alınırsa, bu şema uygun değildir. . Daha sonra integralin nasıl dönüştürülebileceğine bağlı olarak bir değişken değişikliği kullanılır. Böyle bir durum bir sonraki bölümde ele alınacaktır.

Örnek 4 Bulmak trigonometrik fonksiyonun integrali

Çözüm. Kosinüsün üssü tektir. Bu nedenle hayal edin

T= günah X(Daha sonra dt= çünkü X dx ). Sonra alırız

Eski değişkene dönersek sonunda şunu bulduk:

Örnek 5 Bulmak trigonometrik fonksiyonun integrali

.

Çözüm. Kosinüsün üssü, önceki örnekte olduğu gibi tektir, ancak daha fazladır. Hayal etmek

ve değişken değişikliğini yapın T= günah X(Daha sonra dt= çünkü X dx ). Sonra alırız

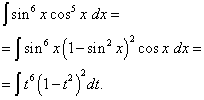
Parantezleri açalım

ve Al

Eski değişkene dönersek çözümü elde ederiz

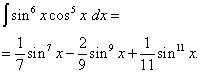
Örnek 6 Bulmak trigonometrik fonksiyonun integrali

Çözüm. Sinüs ve kosinüs üsleri çifttir. Bu nedenle integrali şu şekilde dönüştürüyoruz:

Sonra alırız

İkinci integralde değişken değişikliği yapıyoruz, ayarlıyoruz T= günah2 X. Daha sonra (1/2)dt= cos2 X dx . Buradan,

Sonunda alırız

Değişken Değiştirme Yöntemini Kullanma

Değişken değiştirme yöntemi Trigonometrik fonksiyonları entegre ederken, sinüs ve kosinüsün çarpımı olan ve sinüs veya kosinüsün birinci derecede, teğet veya kotanjant olduğu integralde yalnızca bir sinüs veya yalnızca bir kosinüsün mevcut olduğu durumlarda kullanılabilir. bir ve aynı argümanın sinüs ve kosinüsünün çift kuvvetlerinin bölümü olarak. Bu durumda sadece günah işlemekle kalmayıp permütasyon da yapmak mümkündür. X = T ve günah X = T, ama aynı zamanda tg X = T ve ctg X = T .

Örnek 8 Bulmak trigonometrik fonksiyonun integrali

.

Çözüm. Değişkeni değiştirelim: , sonra . Ortaya çıkan integral, integral tablosu üzerinde kolayca entegre edilir:

.

Örnek 9 Bulmak trigonometrik fonksiyonun integrali

Çözüm. Tanjantı sinüs ve kosinüs oranına dönüştürelim:

Değişkeni değiştirelim: , sonra . Ortaya çıkan integral: masa integrali eksi işaretiyle:

.

Orijinal değişkene dönersek sonunda şunu elde ederiz:

.

Örnek 10 Bulmak trigonometrik fonksiyonun integrali

Çözüm. Değişkeni değiştirelim: , sonra .

Trigonometrik özdeşliği uygulamak için integrali dönüştürüyoruz :

İntegralin önüne eksi işareti koymayı unutmadan değişken değişikliği yapıyoruz (yukarıya bakın, neye eşittir) dt). Daha sonra integrali faktörlere ayırıyoruz ve tabloya göre entegre ediyoruz:

Orijinal değişkene dönersek sonunda şunu elde ederiz:

.

Trigonometrik fonksiyonun integralini kendiniz bulun ve ardından çözüme bakın

Evrensel trigonometrik ikame

Evrensel trigonometrik ikame İntegralin önceki paragraflarda tartışılan durumların kapsamına girmediği durumlarda kullanılabilir. Temel olarak sinüs veya kosinüs (veya her ikisi de) bir kesirin paydasında olduğunda. Sinüs ve kosinüsün, orijinal açının yarısının tanjantını içeren başka bir ifadeyle değiştirilebileceği aşağıdaki gibi kanıtlanmıştır:

Ancak evrensel trigonometrik ikamenin genellikle oldukça karmaşık cebirsel dönüşümler gerektirdiğini unutmayın; bu nedenle, başka hiçbir yöntemin işe yaramadığı durumlarda kullanılması en iyisidir. Evrensel trigonometrik ikame ile birlikte diferansiyel işareti altında ikame ve belirsiz katsayılar yönteminin kullanıldığı örneklere bakalım.

Örnek 12. Bulmak trigonometrik fonksiyonun integrali

.

Çözüm. Çözüm. hadi kullanalım evrensel trigonometrik ikame. Daha sonra
.

Pay ve paydadaki kesirleri ile çarpıyoruz ve ikiliyi çıkarıp integral işaretinin önüne koyuyoruz. Daha sonra

Antiderivatifler tablosu ("integraller"). İntegral tablosu. Tablosal belirsiz integraller. (Basit integraller ve parametreli integraller). Parçalara göre entegrasyon formülleri. Newton-Leibniz formülü.

Parçalara göre entegrasyon formülleri. Entegrasyon kuralları.

Türev tablosu. Tablo türevleri. Ürünün türevi. Özelin türevi. Karmaşık bir fonksiyonun türevi.

Eğer x bağımsız bir değişken ise:

Logaritmanın özellikleri. Logaritmanın temel formülleri. Ondalık sayı (lg) ve doğal logaritmalar (ln).

Doğal logaritma ln (logaritma tabanı e = 2,718281828459045…) ln(e)=1; günlük(1)=0

Taylor serisi. Bir fonksiyonun Taylor serisinde açılımı.

Görünüşe göre çoğu pratikte karşılaşılan Matematiksel fonksiyonlar, değişkenin kuvvetlerini artan sırada içeren güç serileri şeklinde belirli bir nokta civarında herhangi bir doğrulukla temsil edilebilir. Örneğin x=1 noktasının yakınında:

Çağrılan satırları kullanırken Taylor satırları, Cebirsel, trigonometrik ve üstel fonksiyonları içeren karma fonksiyonlar tamamen cebirsel fonksiyonlar olarak ifade edilebilir. Serilerin yardımıyla farklılaştırma ve entegrasyon çoğu zaman hızlı bir şekilde gerçekleştirilebilir.

a noktası civarındaki Taylor serisi aşağıdaki formlara sahiptir:

1) burada f(x), x=a noktasında tüm mertebelerden türevleri olan bir fonksiyondur. R n - Taylor serisindeki kalan terim şu ifadeyle belirlenir:

2)

Serinin k-inci katsayısı (x k'de) formülle belirlenir

3) Taylor serisinin özel bir durumu Maclaurin serisidir (=McLaren) (ayrışma a=0 noktası etrafında gerçekleşir)

a=0 için

serinin üyeleri formülle belirlenir

Taylor serilerinin uygulanma koşulları.

1. f(x) fonksiyonunun (-R;R) aralığında Taylor serisine genişletilebilmesi için, bunun için Taylor formülündeki (Maclaurin (=McLaren)) kalan terimin olması gerekli ve yeterlidir. fonksiyon belirtilen aralıkta (-R;R) k →∞'da sıfıra yönelir.

2. Taylor serisini kuracağımız yakın çevrede bu fonksiyonun türevlerinin olması gerekmektedir.

Taylor serisinin özellikleri.

Eğer f analitik bir fonksiyon ise, bu durumda f'nin tanım kümesinin herhangi bir a noktasındaki Taylor serisi, a'nın bir komşuluğunda f'ye yakınsar.

Taylor serileri yakınsak olan ancak a'nın herhangi bir komşuluğundaki fonksiyondan farklı olan sonsuz türevlenebilir fonksiyonlar vardır. Örneğin:

Taylor serileri, polinomlarla yaklaşıklık (bir yaklaşım, bazı nesnelerin bir anlamda orijinaline yakın, ancak daha basit olan diğerleriyle değiştirilmesinden oluşan bilimsel bir yöntemdir) fonksiyonları için kullanılır. Özellikle, doğrusallaştırma ((doğrusallıktan - doğrusal), doğrusal olmayan bir sistemin çalışmasının, orijinaline eşdeğer bir anlamda doğrusal bir sistemin analizi ile değiştirildiği, kapalı doğrusal olmayan sistemlerin yaklaşık temsil yöntemlerinden biri. Denklemlerin .) Taylor serisine genişletilmesi ve birinci derecenin üzerindeki tüm terimlerin kesilmesiyle oluşur.

Böylece hemen hemen her fonksiyon belirli bir doğrulukla bir polinom olarak temsil edilebilir.

Maclaurin serisindeki (=McLaren, Taylor 0 noktası civarında) ve Taylor 1 noktası civarındaki güç fonksiyonlarının bazı ortak açılımlarına örnekler. Taylor ve MacLaren serilerinde ana fonksiyonların açılımlarının ilk terimleri.

Maclaurin serisindeki güç fonksiyonlarının bazı yaygın açılımlarına örnekler (= MacLaren, Taylor 0 noktası civarında)

1. nokta etrafındaki bazı yaygın Taylor serisi açılımlarına örnekler

İntegrallerin parçalara göre çözüm örnekleri ayrıntılı olarak ele alınır; bunların integrali bir polinomun ve bir üssün (e üzeri x) veya bir sinüs (sinüs x) veya bir kosinüs (cos x) ürünüdür.

Ayrıca bakınız: Parçalara göre entegrasyon yöntemi
Belirsiz integral tablosu
Belirsiz integralleri hesaplama yöntemleri
Temel temel fonksiyonlar ve özellikleri

Parça formülüne göre entegrasyon

Bu bölümdeki örnekleri çözerken parçalara göre entegrasyon formülü kullanılır:
;
.

Bir polinom ile sin x, cos x veya e x'in çarpımını içeren integral örnekleri

İşte bu tür integrallerin örnekleri:
, , .

Bu tür integrallerin integralini almak için polinom u ile, geri kalan ise v dx ile gösterilir. Daha sonra parçalara göre entegrasyon formülünü uyguluyoruz.

Aşağıda bu örneklerin ayrıntılı bir çözümü bulunmaktadır.

İntegral çözme örnekleri

Üslü örnek, e üzeri x'in kuvveti

İntegrali tanımlayın:
.

Üssü diferansiyel işaretin altına tanıtıyoruz:
e - x dx = - e - x d(-x) = - d(e - x).

Parçalara göre entegre oluyoruz.

Burada
.
Kalan integral de parçalar halinde integrallenebilir.
.
.
.
Sonunda elimizde:
.

Bir integralin sinüsle tanımlanmasına bir örnek

İntegrali hesaplayın:
.

Sinüs'ü diferansiyelin işareti altında tanıtıyoruz:

Parçalara göre entegre oluyoruz.

burada u = x 2 , v = çünkü(2x+3), du = ( x2 )′ dx

Kalan integral de parçalar halinde integrallenebilir. Bunu yapmak için kosinüsü diferansiyelin işareti altına dahil ediyoruz.


burada u = x, v = günah(2x+3), du = dx

Sonunda elimizde:

Bir polinom ve kosinüsün çarpımına bir örnek

İntegrali hesaplayın:
.

Kosinüsü diferansiyelin işareti altında tanıtıyoruz:

Parçalara göre entegre oluyoruz.

burada u = x 2+3x+5, v = günah2x, du = ( x 2 + 3 x + 5 )′ dx