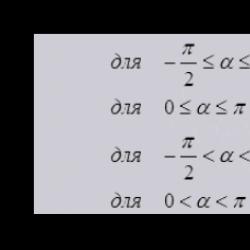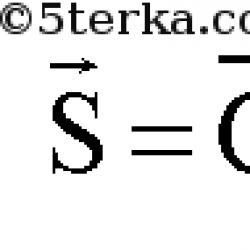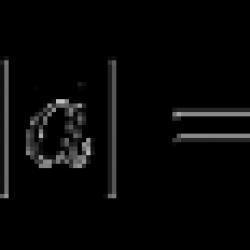Vektörlerin koordinatları ve modülleri nasıl belirlenir. Bir vektörün uzunluğunu bulma, örnekler ve çözümler. Hangi vektörler eşittir
Vektörün uzunluğunu koordinatlarına (dikdörtgen bir koordinat sisteminde), vektörün başlangıç ve bitiş noktalarının koordinatlarına ve kosinüs teoremine (2 vektör ve aralarındaki açı verilmiştir) göre bulalım.
Vektör yönlendirilmiş bir doğru parçasıdır. Bu parçanın uzunluğu vektörün sayısal değerini belirler ve denir. vektör uzunluğu veya vektör modülü.
1. Bir vektörün uzunluğunun koordinatlarından hesaplanması
Vektör koordinatları düz (iki boyutlu) dikdörtgen bir koordinat sisteminde verilmişse; a x ve a y biliniyorsa vektörün uzunluğu formülle bulunabilir
Uzayda bir vektör olması durumunda üçüncü bir koordinat eklenir

MS EXCEL ifadesinde =KÖK(TOPLA(B8:B9)) vektörün modülünü hesaplamanıza izin verir (vektör koordinatörlerinin hücrelere girildiği varsayılır) B8:B9, örnek dosyaya bakın).

SUMSQ() işlevi, bağımsız değişkenlerin karelerinin toplamını döndürür; bu durumda =B8*B8+B9*B9 formülüne eşdeğerdir.
Örnek dosya aynı zamanda vektörün uzaydaki uzunluğunu da hesaplar.
Alternatif bir formül ifadedir =KÖK(TOPLAM(B8:B9,B8:B9)).
2. Bir vektörün uzunluğunu noktaların koordinatlarından bulma
eğer vektör başlangıç ve bitiş noktalarının koordinatları aracılığıyla verilirse formül farklı olacaktır =KÖK(TOPLAMDIFF(C28:C29;B28:B29))
Formül, başlangıç ve bitiş noktalarının koordinatlarının aralıklara girildiğini varsayar C28:C29 Ve B28:B29 sırasıyla.

İşlev SUMMQVAR() içindeİki dizideki karşılık gelen değerlerin kare farklarının toplamını döndürür.
Aslında formül önce vektörün koordinatlarını (noktaların karşılık gelen koordinatları arasındaki fark) hesaplar, ardından bunların karelerinin toplamını hesaplar.
![]()
3. Kosinüs teoremini kullanarak bir vektörün uzunluğunu bulma
Kosinüs teoremini kullanarak bir vektörün uzunluğunu bulmak istiyorsanız genellikle 2 vektör verilir (modülleri ve aralarındaki açı).

Formülü kullanarak vektörün uzunluğunu bulun =KÖK(TOPLA(B43:C43)-2*B43*C43*COS(B45))
Hücrelerde B43:B43 a ve b vektörlerinin uzunluklarını ve hücreyi içerir B45 - radyan cinsinden aralarındaki açı (PI() sayısının kesirleri cinsinden).
Açı derece olarak verilirse formül biraz farklı olacaktır. =KÖK(B43*B43+C43*C43-2*B43*C43*COS(B46*PI()/180))

Not: netlik sağlamak için, açı değeri derece cinsinden olan bir hücrede kullanabilirsiniz, örneğin makaleye bakın
vektör modülü- vektörün büyüklüğü - [L.G. Sumenko. İngilizce Rusça Bilgi Teknolojileri Sözlüğü. M .: GP TsNIIS, 2003.] Genel olarak bilgi teknolojisi konuları Eş anlamlılar vektör değeri EN bir vektörün mutlak değeri ...
vektör modülü- vektoriaus modulis statusas T sritis fizika atitikmenys: angl. vok vektörünün mutlak değeri. Vectorbetrag, m rus. vektör uzunluğu, f; vektör modülü, m pranc. bir vektör modülü, m … Fizikos terminų žodynas
- (Latince modül "küçük ölçü"den): Vikisözlük'te "modülüs" başlıklı bir makale var Mo ... Vikipedi
Modül (Latince modül "küçük ölçü"den gelir), genelden ayrılabilir veya en azından zihinsel olarak ayrılmış bir bileşendir. Modüler bir şeye genellikle açıkça tanımlanmış parçalardan oluşan ve çoğu zaman bir şeyi yok etmeden çıkarılabilen veya eklenebilen bir şey denir ... ... Vikipedi
Gerçek veya karmaşık bir sayı x'in mutlak değeri veya modülü, x'ten orijine olan mesafedir. Daha doğrusu: Bir x gerçek sayısının mutlak değeri, |x| ile gösterilen, negatif olmayan bir sayıdır. ve şu şekilde tanımlanmıştır: ... ... Vikipedi
dalga vektör modülü- - [L.G. Sumenko. İngilizce Rusça Bilgi Teknolojileri Sözlüğü. M .: GP TsNIIS, 2003.] Genel olarak bilgi teknolojisi konuları EN yayılma vektörünün büyüklüğü ... Teknik Çevirmen El Kitabı
zarf kodu vektör konvolver modülü- - [L.G. Sumenko. İngilizce Rusça Bilgi Teknolojileri Sözlüğü. M.: GP TsNIIS, 2003.] Genel olarak bilgi teknolojisi konuları TR şekil kod vektörü evrişim modülü ... Teknik Çevirmen El Kitabı
Karmaşık bir sayının modülü, bu sayıya karşılık gelen vektörün uzunluğudur: . Bir z karmaşık sayısının modülü genellikle | z | veya r. Ve karmaşık bir sayı olacak şekilde gerçek sayılar olsun (normal gösterim). Sonra Sayılar ... Vikipedi
Matematikte modül, 1) M. (veya mutlak değeri) z = x + iy karmaşık sayısının ═ sayısıdır (kökü artı işaretiyle alınır). Karmaşık bir z sayısını trigonometrik formda z \u003d r (cos j + i sin j) olarak temsil ederken, gerçek sayı r ... ... Büyük Sovyet Ansiklopedisi
Operatör halkalı değişmeli grup. M., K'nın bir halka ile değiştirildiği durum için bir K alanı üzerindeki (doğrusal) vektör uzayının genelleştirilmesidir. Bir A halkası verilsin, toplamsal Abel grubu Mnas. sol A modülü, eğer tanımlanmışsa... ... Matematik Ansiklopedisi
Büyüklük ve yön ile karakterize edilir. Örneğin geometride ve doğa bilimlerinde bir vektör, Öklid uzayında (veya bir düzlemde) yönlendirilmiş bir çizgi parçasıdır.
Lineer cebirin temel kavramlarından biridir. En genel tanım kullanıldığında, vektörlerin matrisler ve tensörler de dahil olmak üzere doğrusal cebirde incelenen hemen hemen tüm nesneler olduğu ortaya çıkar, ancak bu nesneler çevredeki bağlamda mevcutsa, bir vektör sırasıyla bir satır vektörü veya bir vektör olarak anlaşılır. sütun vektörü, birinci dereceden bir tensör. Vektörler üzerindeki işlemlerin özellikleri vektör hesabında incelenir.
Gösterim [ | ]
Kümenin temsil ettiği vektör n (\displaystyle n) elemanlar (bileşen) a 1 , a 2 , … , a n (\displaystyle a_(1),a_(2),\ldots ,a_(n)) aşağıdaki şekillerde belirtilir:
⟨ a 1 , a 2 , … , a n ⟩ , (a 1 , a 2 , … , a n) , ( a 1 , a 2 , … , a n ) (\displaystyle \langle a_(1),a_(2), \ldots ,a_(n)\,\rangle ,\ \left(a_(1),a_(2),\ldots ,a_(n)\,\right),\(a_(1),a_(2) ,\ldots ,a_(n)\,\)).Bunun bir vektör olduğunu (skaler değil) vurgulamak için üst çizgi, üst ok, kalın veya gotik yazı tipi kullanın:
bir ¯ , bir → , bir , bir , bir . (\displaystyle (\bar (a)),\ (\vec (a)),\mathbf (a) ,(\mathfrak (A)),\ (\mathfrak (a))).)Vektörlerin eklenmesi neredeyse her zaman artı işaretiyle gösterilir:
a → + b → (\displaystyle (\vec (a))+(\vec (b))).Bir sayıyla çarpma işlemi, özel bir işaret olmadan yanına basitçe yazılır, örneğin:
k b → (\displaystyle k(\vec (b))),ve sayı genellikle solda yazılır.
Genel olarak kabul edilen bir vektör tanımı yoktur; kalın yazı tipi, bir harfin üzerinde çizgi veya ok, Gotik alfabe vb. kullanılır.
Geometride [ | ]
Geometride vektörler yönlendirilmiş bölümler olarak anlaşılır. Bu yorum genellikle bilgisayar grafiklerinde yüzey normallerini kullanarak ışık haritaları oluştururken kullanılır. Vektörleri, üçgenler ve paralelkenarlar gibi çeşitli şekillerin alanlarının yanı sıra dört yüzlü ve paralel yüzlü cisimlerin hacimlerini bulmak için de kullanabilirsiniz.
Bazen bir yön bir vektörle tanımlanır.
Geometride bir vektör doğal olarak transfer (paralel transfer) ile ilişkilendirilir ve bu da açıkça adının kökenini açıklığa kavuşturur (enlem. vektör, taşıyıcı). Aslında, herhangi bir yönlendirilmiş parça, bir düzlemin veya uzayın bir tür paralel ötelenmesini benzersiz bir şekilde tanımlar ve bunun tersi de geçerlidir; paralel öteleme, tek bir yönlendirilmiş parçayı benzersiz bir şekilde tanımlar (açıkça - eğer aynı yön ve uzunluktaki tüm yönlendirilmiş parçaların eşit olduğunu düşünürsek - yani bunları ücretsiz vektörler olarak düşünün).
Bir vektörün çeviri olarak yorumlanması, vektör toplama işlemini doğal ve sezgisel olarak açık bir şekilde - iki (veya daha fazla) çevirinin bir bileşimi (ardışık uygulama) olarak - sunmamıza olanak tanır; aynı durum bir vektörü bir sayıyla çarpma işlemi için de geçerlidir.
Doğrusal cebirde[ | ]
Genel tanım[ | ]
Bir vektörün en genel tanımı genel cebir yoluyla verilir:
- belirtmek F (\ displaystyle (\ mathfrak (F)))(Gotik F) birçok unsurun bulunduğu bir alan F (\displaystyleF), eklemeli işlem + (\displaystyle +), çarpımsal işlem ∗ (\displaystyle*) ve karşılık gelen nötr öğeler: toplamsal birim ve çarpımsal birim 1 (\displaystyle 1).
- belirtmek V (\ displaystyle (\ mathfrak (V)))(Gotik V) bir dizi öğeye sahip bazı Abel grubu V (\görüntü stili V), eklemeli işlem + (\displaystyle +) ve buna göre katkı ünitesi ile 0 (\displaystyle\mathbf(0)).
Başka bir deyişle, izin ver F = ⟨F; + , ∗ ⟩ (\displaystyle (\mathfrak (F))=\langle F;+,*\rangle ) Ve V = ⟨V; + ⟩ (\displaystyle (\mathfrak (V))=\langle V;+\rangle ).
Bir operasyon varsa F × V → V (\displaystyle F\times V\to V), öyle ki herhangi biri için a , b ∈ F (\displaystyle a,b\F'de) ve herhangi biri için x , y ∈ V (\displaystyle \mathbf (x) ,\mathbf (y) \in V) aşağıdaki ilişkiler yerine getirilir:
Dizi olarak vektör[ | ]
Vektör- (sıra, demet) homojen elemanlar. Bu, hiçbir geleneksel vektör işleminin verilmeyebileceği, bunlardan daha az olabileceği veya olağan doğrusal uzay aksiyomlarını karşılamayabilecekleri anlamında en genel tanımdır. Programlamada bir vektör bu biçimde anlaşılır; burada kural olarak köşeli parantez içeren bir tanımlayıcı adla gösterilir (örneğin, nesne). Kabul edilen özellik modellerinin listesi
a → vektörünün uzunluğu a → ile gösterilecektir. Bu gösterim bir sayının modülüne benzer, dolayısıyla bir vektörün uzunluğu aynı zamanda bir vektörün modülü olarak da adlandırılır.
Düzlemdeki bir vektörün uzunluğunu koordinatlarına göre bulmak için dikdörtgen Kartezyen koordinat sistemi O x y'nin dikkate alınması gerekir. Koordinatları a x olan bir a → vektörünü içersin; evet. a → vektörünün uzunluğunu (modülünü) a x ve a y koordinatları cinsinden bulmak için bir formül sunuyoruz.
O A → = a → vektörünü orijinden ayırın. A noktasının koordinat eksenlerine karşılık gelen izdüşümlerini A x ve A y olarak tanımlayalım. Şimdi O A köşegenine sahip bir O A x A A y dikdörtgenini düşünün.
Pisagor teoreminden şu eşitlik çıkar: O A 2 = O A x 2 + O A y 2, dolayısıyla O A = O A x 2 + O A y 2. Dikdörtgen Kartezyen koordinat sistemindeki bir vektörün koordinatlarının halihazırda bilinen tanımından, O A x 2 = a x 2 ve O A y 2 = a y 2 olduğunu ve yapı gereği O A'nın uzunluğunun uzunluğuna eşit olduğunu elde ederiz. vektör O A → dolayısıyla O A → = O A x 2 + O A y 2.
Dolayısıyla ortaya çıkıyor ki Bir vektörün uzunluğunu bulma formülü bir → = bir x; a y karşılık gelen forma sahiptir: a → = a x 2 + a y 2 .
a → vektörü, a → = a x i → + a y j → koordinat vektörlerinde bir genişleme olarak verilirse, uzunluğu aynı formül kullanılarak hesaplanabilir a → = a x 2 + a y 2, bu durumda a x ve a y katsayıları şöyledir: verilen koordinat sistemindeki a → vektörünün koordinatları olarak.
örnek 1
a → = 7 vektörünün uzunluğunu hesaplayın; e , dikdörtgen koordinat sisteminde verilmiştir.
Çözüm
Bir vektörün uzunluğunu bulmak için, bir vektörün uzunluğunu a → = a x 2 + a y 2 koordinatlarına göre bulma formülünü kullanacağız: a → = 7 2 + e 2 = 49 + e
Cevap: a → = 49 + e .
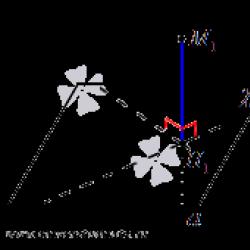
Bir vektörün uzunluğunu bulma formülü a → = a x ; evet; a z, uzaydaki Kartezyen koordinat sistemi Oxyz'deki koordinatlarıyla, düzlemdeki durum için formüle benzer şekilde türetilir (aşağıdaki şekle bakın)

Bu durumda, O A 2 \u003d O A x 2 + O A y 2 + O A z 2 (OA dikdörtgen bir paralel borunun köşegeni olduğundan), dolayısıyla O A \u003d O A x 2 + O A y 2 + O A z 2. Vektörün koordinatlarının tanımından aşağıdaki eşitlikleri yazabiliriz: O A x = a x; O Bir y = bir y; Ö A z = a z; ve OA'nın uzunluğu aradığımız vektörün uzunluğuna eşittir, dolayısıyla O A → = O A x 2 + O A y 2 + O A z 2 .
Bundan, vektörün uzunluğunun a → = a x olduğu sonucu çıkar; evet; a z eşittir a → = a x 2 + a y 2 + a z 2 .
Örnek 2
a → = 4 i → - 3 j → + 5 k → vektörünün uzunluğunu hesaplayın; burada i → , j → , k → dikdörtgen koordinat sisteminin birim vektörleridir.
Çözüm
a → = 4 · i → - 3 · j → + 5 · k → vektörünün ayrıştırılması verildiğinde, koordinatları a → = 4, - 3, 5'tir. Yukarıdaki formülü kullanarak a → = a x 2 + a y 2 + a z 2 = 4 2 + (- 3) 2 + 5 2 = 5 2 elde ederiz.
Cevap: bir → = 5 2 .
Bir vektörün başlangıç ve bitiş noktalarının koordinatları cinsinden uzunluğu
Yukarıda, bir vektörün uzunluğunu koordinatlarına göre bulmanızı sağlayan formüller türetilmiştir. Düzlemdeki ve üç boyutlu uzaydaki durumları ele aldık. Bunları vektörün koordinatlarını başlangıç ve bitiş noktalarının koordinatlarına göre bulmak için kullanalım.
Dolayısıyla, A (a x; a y) ve B (b x; b y) koordinatlarına sahip noktalar verildiğinde, A B → vektörünün koordinatları vardır (b x - a x; b y - a y), bu da uzunluğunun aşağıdaki formülle belirlenebileceği anlamına gelir: Bir B → = ( b x - a x) 2 + (b y - a y) 2
Ve üç boyutlu uzayda A (a x; a y; a z) ve B (b x; b y; b z) koordinatları verilen noktalar verilirse, A B → vektörünün uzunluğu formülle hesaplanabilir.
Bir B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2
Örnek 3
A B → dikdörtgen koordinat sistemindeyse A 1, 3, B - 3, 1 vektörünün uzunluğunu bulun.
Çözüm
Düzlemdeki başlangıç ve bitiş noktalarının koordinatlarından vektör uzunluğunu bulma formülünü kullanarak A B → = (b x - a x) 2 + (b y - a y) 2: A B → = (- 3 - 1) 2 elde ederiz. + (1 - 3) 2 = 20 - 2 3 .
İkinci çözüm şu formüllerin uygulanmasını içerir: A B → = (- 3 - 1; 1 - 3) = (- 4; 1 - 3) ; Bir B → = (- 4) 2 + (1 - 3) 2 = 20 - 2 3 . -
Cevap: Bir B → = 20 - 2 3 .
Örnek 4
A B → vektörünün uzunluğunun hangi değerler için A (0 , 1 , 2) ise 30'a eşit olduğunu belirleyin; B(5,2,λ2) .
Çözüm
Öncelikle A B → vektörünün uzunluğunu aşağıdaki formüle göre yazalım: A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2 = (5 - 0) 2 + (2 - 1) 2 + (λ 2 - 2) 2 = 26 + (λ 2 - 2) 2
Daha sonra ortaya çıkan ifadeyi 30'a eşitliyoruz, buradan istenilen λ'yı buluyoruz:
26 + (λ 2 - 2) 2 = 30 26 + (λ 2 - 2) 2 = 30 (λ 2 - 2) 2 = 4 λ 2 - 2 = 2 ve l ve λ 2 - 2 = - 2 λ 1 = - 2 , λ2 = 2 , λ3 = 0 .
Cevap: λ 1 \u003d - 2, λ 2 \u003d 2, λ 3 \u003d 0.
Kosinüs yasasını kullanarak bir vektörün uzunluğunu bulma
Ne yazık ki, bir vektörün koordinatları görevlerde her zaman bilinmez, bu yüzden bir vektörün uzunluğunu bulmanın diğer yollarını düşünelim.
A B → , A C → iki vektörünün uzunlukları ve aralarındaki açı (veya açının kosinüsü) verilse, B C → veya C B → vektörünün uzunluğunu bulmak gerekir. Bu durumda, △ A B C üçgeninde kosinüs teoremini kullanmalı, vektörün istenen uzunluğuna eşit olan B C tarafının uzunluğunu hesaplamalısınız.
Aşağıdaki örnekte böyle bir durumu ele alalım.
Örnek 5
A B → ve A C → vektörlerinin uzunlukları sırasıyla 3 ve 7'ye eşittir ve aralarındaki açı π 3'e eşittir. B C → vektörünün uzunluğunu hesaplayın.
Çözüm
B C → vektörünün uzunluğu bu durumda △ A B C üçgeninin B C tarafının uzunluğuna eşittir. Üçgenin A B ve A C kenarlarının uzunlukları koşuldan bilinir (karşılık gelen vektörlerin uzunluklarına eşittirler), aralarındaki açı da bilinir, dolayısıyla kosinüs teoremini kullanabiliriz: B C 2 = A B 2 + A C 2 - 2 A B A C çünkü ∠ (A B , → A C →) = 3 2 + 7 2 - 2 3 7 çünkü π 3 = 37 ⇒ B C = 37 Böylece, B C → = 37 .
Cevap: BC → = 37 .
Dolayısıyla, bir vektörün uzunluğunu koordinatlara göre bulmak için, başlangıç ve bitiş noktalarının koordinatlarına göre a → = a x 2 + a y 2 veya a → = a x 2 + a y 2 + a z 2 formülleri vardır. A B → = (b x - a x) 2 + ( b y - a y) 2 veya A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2 vektörünün, bazı durumlarda kosinüs teoremi kullanılmalıdır.
Metinde bir hata fark ederseniz, lütfen onu vurgulayın ve Ctrl+Enter tuşlarına basın.