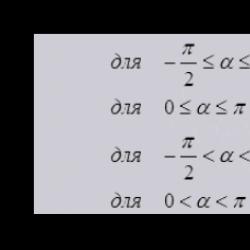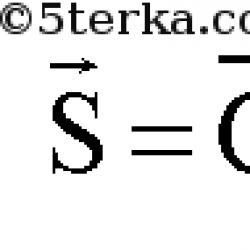Yay teğetleri ve yay teğetleri tablosu. Arksinüs, arkkosinüs, arktanjant ve arkkotanjant değerlerinin bulunması. Arcsin değerini arccos, arctg, arcctg, vb. aracılığıyla bulma.

Sin, cos, tg ve ctg fonksiyonlarına her zaman bir arksinüs, arkkosinüs, arktanjant ve arkkotanjant eşlik eder. Biri diğerinin sonucudur ve fonksiyon çiftleri trigonometrik ifadelerle çalışırken eşit derecede önemlidir.

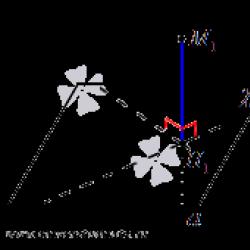
Trigonometrik fonksiyonların değerlerini grafiksel olarak gösteren bir birim daire çizimini düşünün.

OA, arcos OC, arctg DE ve arcctg MK yaylarını hesaplarsanız, bunların hepsi α açısının değerine eşit olacaktır. Aşağıdaki formüller, ana trigonometrik fonksiyonlar ve bunlara karşılık gelen yaylar arasındaki ilişkiyi yansıtmaktadır.

Arsinüsün özelliklerini daha iyi anlamak için fonksiyonunu dikkate almak gerekir. Takvim koordinatların merkezinden geçen asimetrik bir eğri formuna sahiptir.

Arcsine özellikleri:

Grafikleri karşılaştırırsak günah Ve ark günahı, iki trigonometrik fonksiyon ortak kalıplar bulabilir.

Ark kosinüs

A sayısının Arcco'su, kosinüsü a'ya eşit olan α açısının değeridir.

eğri y = arcosx arcsin x'in grafiğini yansıtır, tek fark OY ekseni üzerindeki π/2 noktasından geçmesidir.

Arkosinüs fonksiyonunu daha ayrıntılı olarak düşünün:

Fonksiyon [-1; 1].
Arccos için ODZ - .
Grafiğin tamamı I ve II bölgelerinde yer alır ve fonksiyonun kendisi ne çift ne de tektir.
x = 1 için Y = 0.
Eğri tüm uzunluğu boyunca azalır. Ark kosinüsün bazı özellikleri kosinüs fonksiyonuyla aynıdır.

Ark kosinüsün bazı özellikleri kosinüs fonksiyonuyla aynıdır.

“Kemerler” hakkında böylesine “ayrıntılı” bir çalışmanın okul çocukları için gereksiz görünmesi mümkündür. Ancak aksi takdirde bazı temel düzeydeki tipik USE görevleri öğrencileri çıkmaz sokağa sürükleyebilir.

1. Egzersiz.Şekilde gösterilen fonksiyonları belirtin.

Cevap: pirinç. 1 - 4, şekil 2 - 1.

Bu örnekte vurgu küçük şeylere yapılmıştır. Genellikle öğrenciler grafiklerin oluşturulması ve fonksiyonların görünümü konusunda çok dikkatsizdirler. Aslında, her zaman hesaplanan noktalardan oluşturulabiliyorsa neden eğrinin şeklini ezberleyesiniz ki? Test koşullarında, basit bir görev için çizim yapmak için harcanan zamanın daha karmaşık görevleri çözmek için gerekli olacağını unutmayın.

arktanjant

Arctg a sayısı, α açısının tanjantı a'ya eşit olacak şekilde bir değeridir.

Ark teğetinin grafiğini dikkate alırsak, aşağıdaki özellikleri ayırt edebiliriz:

Grafik sonsuzdur ve (- ∞; + ∞) aralığında tanımlanır.
Arktanjant tek bir fonksiyondur, dolayısıyla arktan (- x) = - arktan x.
x = 0 için Y = 0.
Eğri tüm tanım alanı boyunca artar.

Tg x ve arctg x'in kısa bir karşılaştırmalı analizini tablo halinde verelim.

Ark tanjantı

a - sayısının arkctg'si (0; π) aralığından öyle bir α değeri alır ki kotanjantı a'ya eşit olur.

Yay kotanjant fonksiyonunun özellikleri:

Fonksiyon tanımı aralığı sonsuzdur.
Kabul edilebilir değerlerin aralığı (0; π) aralığıdır.
F(x) ne çift ne de tektir.
Fonksiyonun grafiği uzunluğu boyunca azalır.

Ctg x ve arctg x'i karşılaştırmak çok basittir; sadece iki çizim çizmeniz ve eğrilerin davranışını tanımlamanız yeterlidir.

Görev 2. Grafiği ve fonksiyonun formunu ilişkilendirin.

Mantıksal olarak grafikler her iki fonksiyonun da arttığını göstermektedir. Bu nedenle, her iki şekil de bazı arktg fonksiyonlarını göstermektedir. Ark tanjantının özelliklerinden x = 0 için y=0 olduğu bilinmektedir,

Cevap: pirinç. 1 - 1, şek. 2-4.

Trigonometrik kimlikler arcsin, arcos, arctg ve arcctg

Daha önce kemerler ile trigonometrinin ana işlevleri arasındaki ilişkiyi zaten tanımlamıştık. Bu bağımlılık, örneğin bir argümanın sinüsünü arksinüsü, arkkosinüsü veya tam tersi aracılığıyla ifade etmeye izin veren bir dizi formülle ifade edilebilir. Bu tür kimliklerin bilgisi belirli örneklerin çözümünde faydalı olabilir.

Arctg ve arcctg için de oranlar vardır:

Başka bir kullanışlı formül çifti, aynı açının arcsin ve arcos ve arcctg ve arcctg değerlerinin toplamının değerini ayarlar.

Problem çözme örnekleri

Trigonometri görevleri koşullu olarak dört gruba ayrılabilir: belirli bir ifadenin sayısal değerini hesaplamak, belirli bir fonksiyonu çizmek, tanım alanını veya ODZ'yi bulmak ve örneği çözmek için analitik dönüşümler gerçekleştirmek.

İlk tür görevleri çözerken aşağıdaki eylem planına uymak gerekir:

Fonksiyon grafikleriyle çalışırken asıl önemli olan, özelliklerinin bilgisi ve eğrinin görünümüdür. Trigonometrik denklemleri ve eşitsizlikleri çözmek için kimlik tablolarına ihtiyaç vardır. Öğrenci ne kadar çok formülü hatırlarsa, görevin cevabını bulmak o kadar kolay olur.

Sınavda aşağıdaki türden bir denklemin cevabını bulmanın gerekli olduğunu varsayalım:

İfadeyi doğru şekilde dönüştürüp istediğiniz forma getirirseniz çözümü çok basit ve hızlı olur. Öncelikle arcsin x'i denklemin sağ tarafına taşıyalım.

Formülü hatırlarsak arksin (sinα) = α, o zaman cevap arayışını iki denklemden oluşan bir sistemin çözümüne indirgeyebiliriz:

X modeli üzerindeki kısıtlama yine arcsin'in özelliklerinden ortaya çıkmıştır: x için ODZ [-1; 1]. a ≠ 0 olduğunda sistemin bir kısmı kökleri x1 = 1 ve x2 = - 1/a olan ikinci dereceden bir denklemdir. a = 0 olduğunda x 1'e eşit olacaktır.

Bu makale hakkındadır arksinüs, arkkosinüs, arktanjant ve arkkotanjant değerlerini bulma verilen numara. Öncelikle arksinüs, arkkosinüs, arktanjant ve arkkotanjantın değeri olarak adlandırılan değeri açıklığa kavuşturacağız. Daha sonra, bu yay fonksiyonlarının ana değerlerini alıyoruz, ardından ark sinüs, ark kosinüs, ark tanjant ve ark tanjant değerlerinin sinüs tablolarından nasıl bulunduğunu anlayacağız. Bradys'in kosinüsleri, teğetleri ve kotanjantları. Son olarak, bir sayının arkkosinüsü, arktanjantı veya arkkotanjantı vb. bilindiğinde arksinüsünü bulma hakkında konuşalım.

Sayfada gezinme.

Arsinüs, arkkosinüs, arktanjant ve arkkotanjant değerleri

İlk önce ne olduğunu bulmanız gerekiyor arksinüs, arkkosinüs, arktanjant ve arkkotanjantın değeri».

Sinüs ve kosinüs tablolarının yanı sıra Bradys'in teğetleri ve kotanjantları, pozitif bir sayının arksinüs, arkkosinüs, arktanjant ve arkkotanjant değerini bir dakikalık doğrulukla derece cinsinden bulmanızı sağlar. Negatif sayıların arksinüs, arkkosinüs, arktanjant ve arkkotanjant değerlerini bulmanın, pozitif sayıların karşılık gelen arkfonksiyonlarının değerlerini arcsin, arccos, arctg ve formüllerine başvurarak bulmaya indirgenebileceğini burada belirtmekte fayda var. arcsin(−a)=−arcsin a, arccos (−a)=π−arccos a, arctg(−a)=−arctg a ve arcctg(−a)=π−arcctg a formundaki zıt sayıların arcctg'si.

Bradis tablolarını kullanarak arksinüs, arkkosinüs, arktanjant ve arkkotanjant değerlerini bulmayla ilgilenelim. Bunu örneklerle yapacağız.

Arsinüs 0,2857'nin değerini bulmamız gerektiğini varsayalım. Bu değeri sinüs tablosunda buluyoruz (bu değerin tabloda olmadığı durumları aşağıda analiz edeceğiz). 16 derece 36 dakikanın sinüsüne karşılık gelir. Dolayısıyla 0,2857 sayısının arksinüsünün istenilen değeri 16 derece 36 dakikalık bir açıdır.

Genellikle tablonun sağındaki üç sütundaki düzeltmelerin dikkate alınması gerekir. Örneğin 0,2863'ün ark sinüsünü bulmamız gerekiyorsa. Sinüs tablosuna göre bu değer 0,2857 artı 0,0006 düzeltme olarak elde edilir, yani 0,2863 değeri 16 derece 38 dakikalık sinüse (16 derece 36 dakika artı 2 dakika düzeltme) karşılık gelir.

Ark sinüsü bizi ilgilendiren sayı tabloda değilse ve düzeltmeler dikkate alınarak elde edilemiyorsa, o zaman tabloda ona en yakın sinüslerin iki değerini bulmanız gerekir, bu sayının arasına eklenmiştir. Örneğin 0,2861573 sayısının ark sinüsünün değerini arıyoruz. Bu sayı tabloda yok, yapılan değişikliklerle bu sayıya da ulaşılamıyor. Daha sonra orijinal sayının dahil edildiği 0,2860 ve 0,2863'ün en yakın iki değerini buluyoruz, bu sayılar 16 derece 37 dakika ve 16 derece 38 dakika sinüslere karşılık geliyor. Arsinüsün istenen değeri 0,2861573 bunların arasında yer alır, yani bu açı değerlerinden herhangi biri 1 dakikalık bir doğrulukla arksinüsün yaklaşık değeri olarak alınabilir.

Ark kosinüs değerleri ve ark tanjant değerleri ve ark kotanjant değerleri kesinlikle benzerdir (bu durumda elbette sırasıyla kosinüs, teğet ve kotanjant tabloları kullanılır) .

Arcsin değerini arccos, arctg, arcctg, vb. aracılığıyla bulma.

Örneğin, diyelim ki arcsin a=−π/12'yi bildiğimizi ancak arccos a'nın değerini bulmamız gerektiğini varsayalım. İhtiyacımız olan arkkosinüsün değerini hesaplıyoruz: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12.

A sayısının arksinüsü veya arkkosinüsünün bilinen değerinden, bu a sayısının arktanjantının veya arkkotanjantının değerinin bulunması veya bunun tersinin bulunması gerektiğinde durum çok daha ilginçtir. Ne yazık ki bu tür ilişkileri tanımlayan formülleri bilmiyoruz. Nasıl olunur? Bunu bir örnekle ele alalım.

A sayısının ark kosinüsünün π/10'a eşit olduğunu ve bu a sayısının ark tanjantının değerini hesaplamamız gerektiğini bilelim. Sorunu şu şekilde çözebilirsiniz: Ark kosinüsün bilinen değerinden a sayısını bulun ve ardından bu sayının ark tanjantını bulun. Bunu yapmak için önce bir kosinüs tablosuna, sonra da teğet tablosuna ihtiyacımız var.

π / 10 radyan açısı 18 derecelik bir açıdır, kosinüs tablosuna göre 18 derecelik kosinüsün yaklaşık olarak 0,9511'e eşit olduğunu buluruz, bu durumda örneğimizdeki a sayısı 0,9511'dir.

Teğet tablosuna dönmeye devam ediyor ve onun yardımıyla ihtiyacımız olan yay tanjantının değerini 0,9511 buluyor, yaklaşık 43 derece 34 dakikaya eşit.

Bu konu makalenin materyali tarafından mantıksal olarak devam ettirilmektedir. arcsin, arccos, arctg ve arcctg içeren ifadeleri değerlendirin.

Kaynakça.

Cebir: Proc. 9 hücre için. ortalama okul / Y. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky.- M.: Aydınlanma, 1990.- 272 s.: Ill.- ISBN 5-09-002727-7
Bashmakov M.I. Cebir ve analizin başlangıcı: Proc. 10-11 hücre için. ortalama okul - 3. baskı. - M .: Aydınlanma, 1993. - 351 s .: hasta. - ISBN 5-09-004617-4.
Cebir ve analizin başlangıcı: Proc. 10-11 hücre için. Genel Eğitim kurumlar / A.N. Kolmogorov, A.M. Abramov, Yu.P. Dudnitsyn ve diğerleri; Ed. A. N. Kolmogorova.- 14. baskı.- M.: Aydınlanma, 2004.- 384 s.: ill.- ISBN 5-09-013651-3.
I. V. Boikov, L. D. Romanova. Sınava hazırlanmak için görevlerin toplanması, bölüm 1, Penza 2003.
Bradis V.M. Dört basamaklı matematik tablolar: Genel eğitim için. ders kitabı kuruluşlar. - 2. baskı. - M.: Bustard, 1999.- 96 s.: hasta. ISBN 5-7107-2667-2

Konuyla ilgili ders ve sunum: "Ark tanjantı. Ark tanjantı. Ark tanjantı ve ark tanjantı tabloları"

Ek materyaller
Sevgili kullanıcılar, yorumlarınızı, geri bildirimlerinizi, önerilerinizi bırakmayı unutmayın! Tüm materyaller bir antivirüs programı tarafından kontrol edilir.

1C şirketinden "Integral" çevrimiçi mağazasındaki kılavuzlar ve simülatörler
Geometri problemlerini çözüyoruz. 7-10. Sınıflar için etkileşimli inşaat görevleri
Geometri problemlerini çözüyoruz. Uzayda inşa etmek için etkileşimli görevler

Neyi inceleyeceğiz:
1. Ark tanjantı nedir?
2. Ark tanjantının tanımı.
3. Ark tanjantı nedir?
4. Ark tanjantının tanımı.
5. Değer tabloları.
6. Örnekler.

arktanjant nedir?

Arkadaşlar, kosinüs ve sinüs denklemlerini nasıl çözeceğimizi zaten öğrendik. Şimdi benzer denklemleri teğet ve kotanjant için nasıl çözeceğimizi öğrenelim. tg(x)= 1 denklemini düşünün. Bu denklemi çözmek için iki grafik oluşturuyoruz: y= 1 ve y= tg(x). Fonksiyonlarımızın grafikleri sonsuz sayıda kesişim noktasına sahiptir. Bu noktaların apsisleri şuna benzer: x= x1 + πk, x1, y= 1 doğrusu ile y= tg(x), (-π/2 <x1> π) fonksiyonunun ana dalının kesişme noktasının apsisidir. /2). X1 sayısı için gösterim yay tanjantı olarak tanıtıldı. O zaman denklemimizin çözümü şu şekilde yazılacaktır: x= arctg(1) + πk.

Ark tanjantının tanımı

arctg(a), [-π/2; π/2], tanjantı a'dır.

tg(x)= a denkleminin bir çözümü vardır: x= arctg(a) + πk, burada k bir tamsayıdır.

Ayrıca şunu da unutmayın: arctg(-a)= -arctg(a).

Yay tanjantı nedir?

сtg(x)=1 denklemini çözelim.Bunu yapmak için iki grafik oluşturacağız: y=1 ve y=сtg(x). Fonksiyonlarımızın grafikleri sonsuz sayıda kesişim noktasına sahiptir. Bu noktaların apsisleri şöyle görünür: x= x1 + πk. x1, y= 1 doğrusu ile y= сtg(x), (0 <x1> π) fonksiyonunun ana dalının kesişme noktasının apsisidir.
X1 sayısı için gösterim yay tanjantı olarak tanıtıldı. Daha sonra denklemimizin çözümü şöyle yazılacaktır: x= arcсtg(1) + πk.

Ark tanjantının tanımı

arcctg(a), kotanjantı a'ya eşit olan parçadan bir sayıdır.

ctg(x)= a denkleminin bir çözümü vardır: x= arcctg(a) + πk, burada k bir tamsayıdır.

Ayrıca şunu da unutmayın: arcctg(-a)= π - arcctg(a).

Ark tanjantı ve ark tanjantı değer tabloları

Teğet ve kotanjant değerleri tablosu

Arktanjant ve arkkotanjant değerleri tablosu

Örnekler

1. Hesaplayın: arctg(-√3/3).
Çözüm: arctg(-√3/3)= x olsun, sonra tg(x)= -√3/3 olsun. Tanım gereği –π/2 ≤x≤ π/2. Tablodaki teğetin değerlerine bakalım: x= -π/6, çünkü tg(-π/6)= -√3/3 ve – π/2 ≤ -π/6 ≤ π/2.
Cevap: arctg(-√3/3)= -π/6.

2. Hesaplayın: arctg(1).
Çözüm: arctg(1)= x olsun, sonra tg(x)= 1 olsun. Tanım gereği –π/2 ≤ x ≤ π/2. Tablodaki teğetin değerlerine bakalım: x= π/4, çünkü tg(π/4)= 1 ve – π/2 ≤ π/4 ≤ π/2.
Cevap: arctg(1)= π/4.

3. Hesaplayın: arcctg(√3/3).
Çözüm: arcctg(√3/3)= x olsun, sonra ctg(x)= √3/3 olsun. Tanım gereği 0 ≤ x ≤ π. Tablodaki kotanjant değerlerine bakalım: x= π/3, çünkü ctg(π/3)= √3/3 ve 0 ≤ π/3 ≤ π.
Cevap: arcctg(√3/3) = π/3.

4. Hesaplayın: arcctg(0).
Çözüm: arcctg(0)= x olsun, sonra ctg(x) = 0 olsun. Tanım gereği 0 ≤ x ≤ π. Tablodaki kotanjant değerlerine bakalım: x= π/2, çünkü ctg(π/2)= 0 ve 0 ≤ π/2 ≤ π.
Cevap: arcctg(0) = π/2.

5. Denklemi çözün: tg(x)= -√3/3.
Çözüm: Tanımı kullanıp şunu elde edelim: x= arctg(-√3/3) + πk. Arctg(-a)= -arctg(a) formülünü kullanalım: arctg(-√3/3)= – arctg(√3/3)= – π/6; o zaman x= – π/6 + πk.
Cevap: x= = - π/6 + πk.

6. Denklemi çözün: tg(x)= 0.
Çözüm: Tanımı kullanıp şunu elde edelim: x= arctg(0) + πk. arctan(0)= 0 ise çözümü şu formülde değiştiririz: x= 0 + πk.
Cevap: x= πk.

7. Denklemi çözün: tg(x) = 1,5.
Çözüm: Tanımı kullanıp şunu elde edelim: x= arctg(1.5) + πk. Tabloda bu değere ait bir arktanjant değeri yok, o zaman cevabı bu formda bırakacağız.
Cevap: x= arctg(1,5) + πk.

8. Denklemi çözün: ctg(x)= -√3/3.
Çözüm: Şu formülü kullanalım: ctg(x)= 1/tg(x); ctg(x)= -√3/3 =1/tg(x) => tg(x)= -√3. Tanımı kullanıp şunu elde edelim: x= arctg (-√3) + πk. arctg(-√3)= –arctg(√3)= –π/3, sonra x= -π/3 + πk.
Cevap: x= - π/3 + πk.

9. Denklemi çözün: ctg(x)= 0.
Çözüm: Şu formülü kullanalım: ctg(x)= cos(x)/sin(x). Daha sonra cos(x)=0 olan x değerlerini bulmamız gerekir, x= π/2+ πk sonucunu elde ederiz.
Cevap: x= π/2 + πk.

10. Denklemi çözün: ctg(x)= 2.
Çözüm: Tanımı kullanıp şunu elde edelim: x= arcсtg(2) + πk. Tabloda bu değere ait ark tanjant değeri yok o zaman cevabı bu formda bırakacağız. Cevap: x= arctg(2) + πk.

Bağımsız çözüm için görevler

1) Hesaplayın: a) arctg(√3), b) arctg(-1), c) arcctg(-√3), d) arcctg(-1).
2) Denklemi çözün: a) tg(x)= -√3, b) tg(x)= 1, c) tg(x)= 2,5, d) ctg(x)= √3, e) ctg(x ) = 1,85.

Ark sinüs, ark kosinüs nedir? Yay tanjantı, yay tanjantı nedir?

Dikkat!
Ek var
Özel Bölüm 555'teki materyal.
Kesinlikle "pek değil..." diyenler için
Ve "çok..." diyenler için)

Kavramlara arksinüs, arkkosinüs, arktanjant, arkkotanjant öğrenci nüfusu temkinli. Bu şartları anlamıyor ve dolayısıyla bu şanlı aileye güvenmiyor.) Ama boşuna. Bunlar çok basit kavramlar. Bu arada, trigonometrik denklemleri çözerken bilgili bir kişinin hayatı çok daha kolay hale geliyor!

Basitlik konusunda kafanız mı karıştı? Boşuna.) Tam burada ve şimdi buna ikna olacaksınız.

Elbette anlamak için sinüs, kosinüs, tanjant ve kotanjantın ne olduğunu bilmek güzel olurdu. Evet, bazı açılar için tablo değerleri... En azından en genel anlamda. O zaman burada da hiçbir sorun olmayacak.

Biz de şaşırdık ama unutmayın: arksinüs, arkkosinüs, arktanjant ve arktanjant sadece bazı açılardır. Ne fazla ne az. 30° gibi bir açı var. Ve bir açı var arcsin0.4. Veya arctg(-1,3). Her türlü açı vardır.) Açıları farklı şekillerde yazabilirsiniz. Açıyı derece veya radyan cinsinden yazabilirsiniz. Veya sinüs, kosinüs, teğet ve kotanjant aracılığıyla ...

İfade ne anlama geliyor?

arcsin 0.4?

Bu sinüsü 0,4 olan açıdır! Evet evet. Bu arksinüsün anlamıdır. Özellikle tekrar ediyorum: arcsin 0,4, sinüsü 0,4 olan bir açıdır.

Ve bu kadar.

Bu basit düşünceyi uzun süre kafamda tutmak için, bu korkunç terimin - arksinüsün - bir dökümünü bile vereceğim:

yay günah 0,4
köşe, kimin sinüsü 0,4'e eşittir

Nasıl yazılırsa öyle duyulur.) Neredeyse. Konsol yay araç yay(kelime kemer biliyor musun?), çünkü eski insanlar köşeler yerine yaylar kullanıyorlardı ama bu, konunun özünü değiştirmiyor. Matematiksel bir terimin bu temel kod çözümünü hatırlayın! Ayrıca ark kosinüs, ark tanjant ve ark tanjant için kod çözme yalnızca fonksiyonun adında farklılık gösterir.

Arccos 0.8 nedir?
Bu, kosinüsü 0,8 olan bir açıdır.

Arctan(-1,3) nedir?
Bu, tanjantı -1,3 olan bir açıdır.

Arcctg 12 nedir?
Bu, kotanjantı 12 olan bir açıdır.

Böyle bir temel kod çözme, bu arada, epik hatalardan kaçınmaya da olanak tanır.) Örneğin, arccos1,8 ifadesi oldukça sağlam görünüyor. Kod çözmeye başlayalım: arccos1,8 kosinüsü 1,8'e eşit olan bir açıdır... Hop-hop!? 1.8!? Kosinüs birden büyük olamaz!

Sağ. Arccos1,8 ifadesi mantıklı değil. Ve bir yanıtta böyle bir ifadenin yazılması, doğrulayıcıyı oldukça eğlendirecektir.)

Gördüğünüz gibi temel.) Her açının kendi kişisel sinüsü ve kosinüsü vardır. Ve neredeyse herkesin kendi teğet ve kotanjantı vardır. Bu nedenle trigonometrik fonksiyonu bilerek açının kendisini yazabilirsiniz. Bunun için arksinüsler, arkkosinüsler, arktanjantlar ve arkkotanjantlar amaçlanmıştır. Ayrıca, tüm bu aileye küçültme diyeceğim - kemerler. daha az yazmak için.)

Dikkat! Temel sözlü ve bilinçli kemerlerin şifresini çözmek, çeşitli görevleri sakin ve güvenli bir şekilde çözmenize olanak tanır. Ve olağan dışı yalnızca kendisinin kaydettiği görevler.

Kemerlerden normal derecelere veya radyanlara geçiş mümkün müdür?- Dikkatli bir soru duyuyorum.)

Neden!? Kolayca. Oraya gidip dönebilirsin. Üstelik bazen bunu yapmak da gerekli olabiliyor. Kemerler basit bir şeydir, ancak onlar olmadan bir şekilde daha sakin olur, değil mi?)

Örneğin: arcsin 0.5 nedir?

Şifre çözme işlemine bakalım: arcsin 0,5 sinüsü 0,5 olan açıdır.Şimdi başınızı (veya Google'ı) açın ve hangi açının sinüsü 0,5 olduğunu hatırlıyor musunuz? Sinüs 0,5 y 30 derecelik açı. Hepsi bu kadar: arcsin 0,5 30°'lik bir açıdır. Güvenle yazabilirsiniz:

arksin 0,5 = 30°

Veya daha kesin olarak radyan cinsinden:

İşte bu kadar, ark sinüsünü unutabilir ve normal derece veya radyanlarla çalışabilirsiniz.

Eğer fark ettiysen arksinüs nedir, arkkosinüs ... Arktanjant, arkkotanjant nedir ... O zaman örneğin böyle bir canavarla kolayca başa çıkabilirsiniz.)

Cahil bir kişi dehşet içinde geri çekilecektir, evet ...) Ve bilgili bir kişi şifre çözmeyi hatırla: ark sinüs, sinüsü ... Peki, vb. olan açıdır. Bilgili bir kişi sinüs tablosunu da biliyorsa... Kosinüs tablosu. Teğet ve kotanjantlardan oluşan bir tablo, o zaman hiçbir sorun kalmaz!

Şunu düşünmek yeterlidir:

Şifresini çözeceğim, yani. formülü kelimelere çevirin: tanjantı 1 olan açı (arctg1) 45°'lik bir açıdır. Veya aynısı olan Pi/4. Benzer şekilde:

hepsi bu... Tüm kemerleri radyan cinsinden değerlerle değiştiriyoruz, her şey azaltılıyor, geriye 1 + 1'in ne kadar olacağını hesaplamak kalıyor. 2 olacaktır.) Hangisi doğru cevaptır.

Arksinüslerden, arkkosinüslerden, arktanjantlardan ve arktanjantlardan sıradan derece ve radyanlara bu şekilde geçiş yapabilirsiniz (ve yapmalısınız). Bu, korkutucu örnekleri büyük ölçüde basitleştirir!

Çoğu zaman bu tür örneklerde kemerlerin içi olumsuz değerler. Arctg(-1.3) veya örneğin arccos(-0.8) gibi... Bu sorun değil. Negatiften pozitife geçiş için bazı basit formüller şunlardır:

Bir ifadenin değerini belirlemek için örneğin şunları yapmanız gerekir:

Bunu trigonometrik bir daire kullanarak çözebilirsiniz, ancak onu çizmek istemezsiniz. İyi tamam. Giden olumsuz ark kosinüs içindeki değerler pozitif ikinci formüle göre:

Sağdaki arkkosinüsün içinde zaten pozitif Anlam. Ne

sadece bilmen gerekiyor. Ark kosinüs yerine radyanları değiştirmek ve cevabı hesaplamak kalır:

Bu kadar.

Arksinüs, arkkosinüs, arktanjant, arkkotanjant ile ilgili kısıtlamalar.

Örnek 7 - 9'da bir sorun mu var? Evet, burada bir hile var.)

1'den 9'a kadar tüm bu örnekler 555. Bölüm'deki raflarda özenle sıralanıyor. Ne, nasıl ve neden. Tüm gizli tuzaklar ve hilelerle. Ayrıca çözümü önemli ölçüde basitleştirmenin yolları. Bu arada, bu bölüm genel olarak trigonometri hakkında pek çok faydalı bilgi ve pratik ipucu içeriyor. Ve sadece trigonometride değil. Çok yardımcı oluyor.