I mbani mend reflektorët e plastikës portokalli që ngjiten në foletë e një rrote biçiklete? Le të lidhim reflektorin në buzën e rrotës dhe të ndjekim trajektoren e tij. Kurbat që rezultojnë i përkasin familjes cikloide. Rrota quhet rrethi (ose rrethi) gjenerues i cikloidit. Por le të kthehemi në shekullin tonë dhe të kalojmë në teknologjinë më moderne. Rrugës së biçikletës ka pasur një guralec që ka ngecur në shkallën e gomës.

Pasi ta ktheni timonin disa herë, ku do të fluturojë guri kur të dalë nga shkelja? Kundër drejtimit të motoçikletës apo drejt saj? Siç dihet, lëvizja e lirë e një trupi fillon në mënyrë tangjenciale me trajektoren përgjatë së cilës ai lëvizi. Tangjenti i cikloidit është gjithmonë i drejtuar në drejtimin e lëvizjes dhe kalon nëpër pikën e sipërme të rrethit gjenerues. Guralecët tanë do të fluturojnë në drejtim të lëvizjes. A ju kujtohet se si keni hipur nëpër pellgje me një biçikletë pa krahun e pasmë si fëmijë? Një shirit i lagësht në shpinë është konfirmimi i përditshëm i rezultatit që sapo keni marrë.

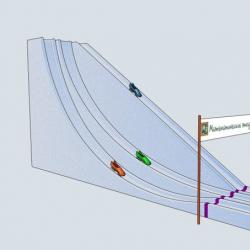
Shekulli i 17-të është shekulli i cikloidit. Shkencëtarët më të mirë kanë studiuar vetitë e tij mahnitëse. Cila trajektore do të çojë një trup që lëviz nën ndikimin e gravitetit nga një pikë në tjetrën në kohën më të shkurtër? Ky ishte një nga problemet e para të shkencës që tani quhet llogaritja e variacioneve. Ju mund të minimizoni (ose maksimizoni) gjëra të ndryshme - gjatësinë e rrugës, shpejtësinë, kohën. Në problemin brakistokron është koha që minimizohet (që theksohet nga vetë emri: greq. βράχιστος - më i vogli, χρόνος - kohë). Gjëja e parë që të vjen në mendje është një trajektore e drejtë. Le të shqyrtojmë gjithashtu një cikloide të përmbysur me një majë në krye të pikave të dhëna. Dhe, duke ndjekur Galileo Galilein, një çerek rrethi që lidh pikat tona. Le të bëjmë pista bobsleigh me profilet e konsideruara dhe të shohim se cili bob vjen i pari. Historia e bobsleigh e ka origjinën në Zvicër. Në vitin 1924, Lojërat e para Olimpike Dimërore u mbajtën në qytetin francez të Chamonix. Ata tashmë presin gara bobsleigh për ekuipazhet me dy dhe katër veta.

I vetmi vit kur një ekuipazh me bobslei përbëhej nga pesë persona në Lojërat Olimpike ishte viti 1928. Që atëherë, ekuipazhet e meshkujve prej dy dhe katër personash kanë garuar gjithmonë në bobsleigh. Ka shumë gjëra interesante në rregullat e bobsleigh. Natyrisht, ka kufizime në peshën e bobit dhe ekipit, por ka edhe kufizime për materialet që mund të përdoren në patina (çifti i përparmë është i lëvizshëm dhe i lidhur me timonin, çifti i pasmë është i fiksuar në mënyrë të ngurtë) . Për shembull, radiumi nuk mund të përdoret në prodhimin e patinave.

Le t'i japim të katërt një fillim. Cila fasule do të jetë e para që do të arrijë në vijën e finishit? Green Bob, duke luajtur për ekipin e Studimeve Matematikore dhe duke hedhur poshtë rrëshqitjen cikloide, vjen i pari! Pse Galileo Galilei konsideroi një të katërtën e një rrethi dhe besonte se kjo ishte trajektorja më e mirë e zbritjes për sa i përket kohës? Ai futi vija të thyera në të dhe vuri re se me rritjen e numrit të lidhjeve, koha e zbritjes zvogëlohej. Nga këtu Galileo u zhvendos natyrshëm në një rreth, por bëri përfundimin e gabuar se kjo trajektore ishte më e mira nga të gjitha të mundshmet. Siç e kemi parë, trajektorja më e mirë është një cikloide. Nëpërmjet këtyre dy pikave mund të vizatohet një cikloid unik me kushtin që maja e cikloidit të jetë në pikën e sipërme. Dhe edhe kur cikloidi duhet të ngrihet për të kaluar nëpër pikën e dytë, ajo do të jetë prapë kurba e zbritjes më të pjerrët! Një tjetër problem i bukur që lidhet me cikloidin është problemi i tautokronit. Përkthyer nga greqishtja, ταύτίς do të thotë "i njëjtë", χρόνος, siç e dimë tashmë - "kohë". Le të bëjmë tre rrëshqitje identike me një profil në formën e një cikloidi, në mënyrë që skajet e rrëshqitjeve të përkojnë dhe të vendosen në majë të cikloidit. Le të vendosim tre fasule në lartësi të ndryshme dhe të japim miratimin.

Fakti më mahnitës është se të gjitha fasulet do të zbresin në të njëjtën kohë! Në dimër, ju mund të ndërtoni një rrëshqitje akulli në oborrin tuaj dhe ta provoni këtë pronë personalisht. Problemi i tautokronit është të gjesh një kurbë të tillë që, duke filluar nga çdo pozicion fillestar, koha e zbritjes në një pikë të caktuar do të jetë e njëjtë. Christiaan Huygens vërtetoi se i vetmi tautokron është cikloidi. Sigurisht, Huygens nuk ishte i interesuar të zbriste rrëshqitjet e akullit. Në atë kohë, shkencëtarët nuk kishin luksin për të ndjekur shkencën për dashurinë ndaj artit. Problemet që u studiuan bazoheshin në jetën dhe kërkesat e teknologjisë së asaj kohe. Në shekullin e 17-të, tashmë po zhvilloheshin udhëtime të gjata detare. Detarët tashmë ishin në gjendje të përcaktonin gjerësinë gjeografike mjaft të saktë, por është për t'u habitur që ata nuk ishin në gjendje të përcaktonin fare gjatësinë. Dhe një nga metodat e propozuara për matjen e gjerësisë gjeografike bazohej në disponueshmërinë e kronometrit të saktë. Personi i parë që mendoi të bënte orë lavjerrës që ishin të sakta ishte Galileo Galilei. Sidoqoftë, në momentin kur fillon t'i zbatojë ato, ai tashmë është i moshuar, është i verbër dhe në vitin e mbetur të jetës së tij shkencëtari nuk ka kohë të bëjë një orë. Ai ia lë trashëgim djalit të tij, por ai heziton dhe fillon të punojë në lavjerrës vetëm para vdekjes së tij dhe nuk ka kohë për të realizuar planin.

Figura tjetër ikonë ishte Christiaan Huygens. Ai vuri re se periudha e lëkundjes së një lavjerrës të zakonshëm, e konsideruar nga Galileo, varet nga pozicioni fillestar, d.m.th. nga amplituda. Duke menduar se cila duhet të jetë trajektorja e ngarkesës në mënyrë që koha e rrotullimit përgjatë saj të mos varet nga amplituda, ai zgjidh problemin tautokron. Por si të bëni një lëvizje të ngarkesës përgjatë një cikloide? Duke përkthyer kërkimin teorik në një plan praktik, Huygens bën "faqe" në të cilat është mbështjellë litari i lavjerrësit dhe zgjidh disa probleme të tjera matematikore. Ai vërteton se "mollëzat" duhet të kenë profilin e të njëjtit cikloide, duke treguar kështu se evolucioni i një cikloidi është një cikloide me të njëjtat parametra. Për më tepër, dizajni i një lavjerrës cikloide të propozuar nga Huygens bën të mundur llogaritjen e gjatësisë së cikloidit. Nëse një fije blu, gjatësia e së cilës është e barabartë me katër rreze të rrethit gjenerues, devijohet sa më shumë që të jetë e mundur, atëherë fundi i saj do të jetë në pikën e kryqëzimit të "faqes" dhe trajektores cikloide, d.m.th. në kulmin e cikloidit - "faqet". Meqenëse kjo është gjysma e gjatësisë së harkut cikloid, gjatësia totale është e barabartë me tetë rreze të rrethit gjenerues. Christiaan Huygens bëri një lavjerrës cikloide, dhe orët me të u testuan në udhëtimet detare, por nuk zunë rrënjë. Sidoqoftë, njësoj si një orë me një lavjerrës të rregullt për këto qëllime. Pse, megjithatë, ekzistojnë ende mekanizmat e orës me një lavjerrës të zakonshëm? Nëse shikoni nga afër, me devijime të vogla, si lavjerrësi i kuq, "faqet" e lavjerrësit cikloide nuk kanë pothuajse asnjë efekt. Prandaj, lëvizja përgjatë cikloidit dhe përgjatë rrethit për devijime të vogla pothuajse përkojnë.

Literatura:
G. N. Berman. Cikloide. M.: Nauka, 1980.
S. G. Gindikin. Tregime rreth fizikanëve dhe matematikanëve. M.: MTsNMO, 2006.

Komentet: 1

Vladimir Zakharov

Ligjëratë nga Akademiku i Akademisë së Shkencave Ruse, Doktor i Shkencave Fizikore dhe Matematikore, Kryetar i Këshillit Shkencor të Akademisë së Shkencave Ruse mbi Dinamikën Jolineare, Drejtor. Departamenti i Fizikës Matematikore në Institutin Fizik të Akademisë së Shkencave Ruse. Lebedev, profesor në Universitetin e Arizonës (SHBA), dy herë fitues i Çmimit Shtetëror, fitues i medaljes Dirac nga Vladimir Evgenievich Zakharov, dhënë më 27 maj 2010 në Muzeun Politeknik si pjesë e projektit "Leksione publike për Polit. ru”.

Sergej Kuksin

Konferenca shkencore ndërkombëtare "Ditët e mekanikës klasike" Moskë, Instituti Matematikor Steklov, rr. Gubkina, 8 janar 26, 2015

Kaosi është një film matematikor i përbërë nga nëntë kapituj, secili prej trembëdhjetë minutash. Ky është një film për publikun e gjerë, kushtuar sistemeve dinamike, efektit të fluturës dhe teorisë së kaosit.

Alexandra Skripchenko

Matematikanja Alexandra Skripchenko rreth bilardos si një sistem dinamik, këndeve racionale dhe teoremës së Poincare-së.

Yuliy Ilyashenko

Teoria Kolmogorov–Arnold–Moser u përgjigjet pyetjeve si “A mund të bien planetët në Diell? Nëse po, atëherë me çfarë probabiliteti? Dhe pas sa kohësh?” Formulimi matematikor i problemit: supozoni se masat janë aq të vogla saqë tërheqja e tyre ndaj njëra-tjetrës mund të neglizhohet. Pastaj mund të llogariten trajektoret e planetëve; Njutoni e bëri këtë. Nëse kalojmë në rastin real, kur tërheqja reciproke e planetëve ndikon në orbitat e tyre, marrim një shqetësim të vogël të integrueshëm, d.m.th. sistem saktësisht i zgjidhshëm. Poincaré e konsideroi studimin e perturbimeve të vogla të sistemeve të integrueshme të mekanikës klasike si detyrën kryesore të teorisë së ekuacioneve diferenciale. Leksionet do të tregojnë, në një nivel të arritshëm për nxënësit e moshuar, për idetë kryesore të teorisë KAM. Ne nuk do të shkojmë te problemi n-trup dhe mekanika klasike, por do të diskutojmë difeomorfizmat e rrethit dhe hapin bazë të procesit të induksionit të propozuar nga Kolmogorov për problemet e mekanikës qiellore.

Olga Romaskevich

Nëse veproni shumë mizorisht dhe hiqni lapsin dhe letrën e një matematikani, ai do të shikojë drejt qiellit në kërkim të problemeve të reja. Çështja e lëvizjes planetare (në botën matematikore të koduar "problemi i trupave n") është jashtëzakonisht komplekse - aq komplekse sa që edhe për nënrastet e veçanta të rastit n=3, një numër i madh punimesh publikohen çdo vit. Është e pamundur të analizohen të gjitha aspektet e këtij problemi edhe në një kurs semestral. Ne, megjithatë, nuk do të kemi frikë dhe do të përpiqemi të luajmë me matematikën që lind këtu. Motivimi kryesor për ne do të jetë problemi i dy trupave: problemi i lëvizjes së një planeti rreth Diellit nën supozimin se duket se nuk ka planetë të tjerë në afërsi.

Dmitry Anosov

Libri flet për ekuacionet diferenciale. Në disa raste, autori shpjegon se si zgjidhen ekuacionet diferenciale, dhe në të tjera, se si konsideratat gjeometrike ndihmojnë për të kuptuar vetitë e zgjidhjeve të tyre. (Me këtë lidhen fjalët "zgjidhim, pastaj vizatojmë" në titullin e librit.) Janë marrë në konsideratë disa shembuj fizikë. Në nivelin më të thjeshtuar, përshkruhen disa arritje të shekullit të 20-të, duke përfshirë një kuptim të mekanizmit të shfaqjes së "kaosit" në sjelljen e objekteve deterministe. Libri u dedikohet nxënësve të shkollave të mesme të interesuara në matematikë. Gjithçka që duhet të bëjnë është të kuptojnë kuptimin e derivatit si shpejtësi e menjëhershme.

Alexey Belov

Ekziston një problem i njohur i Olimpiadës: Ka monedha (figura konvekse) në një tryezë të sheshtë. Pastaj njëri prej tyre mund të tërhiqet nga tavolina pa ndikuar tek të tjerët. Për një kohë të gjatë, matematikanët u përpoqën të vërtetonin analogun hapësinor të kësaj deklarate, derisa u ndërtua një kundërshembull! Lindi një ide: në kokrra të vogla shpesh nuk ka çarje, plasaritja nuk rritet përtej kufirit të kokrrës dhe çarjet mbajnë njëra-tjetrën. Kjo ide teorikisht bën të mundur krijimin e përbërjeve në të cilat nuk rriten çarjet, në veçanti, forca të blinduara qeramike.

Alexey Sosinsky

Një nga konceptet më të rëndësishme të mekanikës dhe fizikës teorike - koncepti i hapësirës së konfigurimit të një sistemi mekanik - për disa arsye mbetet i panjohur jo vetëm për nxënësit e shkollës, por edhe për shumicën e studentëve të matematikës. Leksioni diskuton një klasë shumë të thjeshtë, por shumë kuptimplote të sistemeve mekanike - mekanizmat me varëse të sheshta me dy shkallë lirie. Ne do të zbulojmë se në "rastin e përgjithshëm" hapësirat e konfigurimit të tyre janë sipërfaqe dydimensionale dhe do të përpiqemi të kuptojmë se cilat janë ato. (Këtu janë rezultatet përfundimtare të dhjetë viteve më parë nga Dima Zvonkin.) Më pas, diskutohen probleme matematikore të pazgjidhura që lidhen me mekanizmat e menteshës. (Përfshirë dy hipoteza, ose më mirë teorema të paprovuara, të matematikanit amerikan Bill Thurston.)

Vladimir Protasov

Llogaritja e variacioneve është shkenca e gjetjes së minimumit të një funksioni në një hapësirë ​​me dimensione të pafundme. Ndryshe nga problemet minimale me të cilat jemi mësuar, kur duhet të zgjedhim në mënyrë optimale një numër (parametër), ose, të themi, një pikë në një rrafsh, në problemet variacionale duhet të gjejmë funksionin optimal. Në të njëjtën kohë, problemet me origjinë shumë të ndryshme zgjidhen duke përdorur të njëjtin grup mjetesh: nga mekanika klasike, gjeometria, ekonomia matematikore, etj. Ne do të fillojmë me problemet e vjetra, të njohura që nga shekulli i 17-të dhe, duke ndërtuar ura nga një problem në tjetrin, do të arrijmë shpejt te rezultatet moderne dhe problemet e pazgjidhura.

(përkthyer nga greqishtja. rrethore) - një kurbë e sheshtë transcendentale, e cila përshkruhet nga një pikë në një rreth me rreze r rrotullimi përgjatë një vije të drejtë pa rrëshqitje (një kurbë transcendentale është një kurbë që nuk mund të përshkruhet nga një ekuacion algjebrik në koordinata drejtkëndore). Ekuacioni parametrik i tij

x = rt – r mëkat t,
y= r - r cos t

Pikat e prerjes së cikloidit me vijën e drejtë përgjatë së cilës rrotullohet rrethi (ky rreth quhet rrethi gjenerues, dhe vija e drejtë përgjatë së cilës rrotullohet quhet direktivë) quhen pika kufitare dhe pikat më të larta në cikloide. , të vendosura në mes midis pikave ngjitur të skajit, quhen kulme të cikloidit.

Galileo Galilei ishte i pari që studioi cikloidin. Gjatësia e një harku cikloide u përcaktua në vitin 1658 nga arkitekti dhe matematikani anglez Christopher Wren, autori i projektimit dhe ndërtuesit të kupolës së Katedrales së Shën Palit në Londër. Doli se gjatësia e cikloidit është e barabartë me 8 rreze të rrethit gjenerues.
Një nga vetitë e jashtëzakonshme të cikloidit, i cili i dha emrin e tij - brachistochrone (nga fjalët greke "më i shkurtër" dhe "kohë") lidhet me zgjidhjen e problemit të prejardhjes më të pjerrët. U ngrit pyetja se çfarë forme duhet t'i jepet një brazdë të lëmuar mirë (për të eliminuar praktikisht fërkimin) që lidh dy pika në mënyrë që topi të rrokulliset nga një pikë në tjetrën në kohën më të shkurtër të mundshme. Vëllezërit Bernoulli vërtetuan se hendeku duhet të kishte formën e një cikloidi në rënie.

Lakoret e lidhura me cikloidin mund të merren duke marrë parasysh trajektoret e pikave që nuk ndodhen në rrethin gjenerues.

Lëreni pikën Nga 0është brenda rrethit. Nëse kryhet Nga 0 rrethi ndihmës me të njëjtën qendër si rrethi gjenerues, atëherë kur rrethi gjenerues rrotullohet përgjatë një vije të drejtë AB një rreth i vogël do të rrokulliset në një vijë të drejtë A´ NË’, por rrotullimi i tij do të shoqërohet me rrëshqitje dhe pikë Nga 0 përshkruan një kurbë të quajtur cikloide e shkurtuar.

Një cikloide e zgjatur përcaktohet në mënyrë të ngjashme - kjo është trajektorja e një pike të vendosur në një shtrirje të rrezes së rrethit gjenerues, ndërsa rrotullimi shoqërohet me rrëshqitje në drejtim të kundërt.

Kurbat cikloide përdoren në shumë llogaritje teknike dhe vetitë e tyre përdoren, për shembull, në ndërtimin e profileve të dhëmbëve të ingranazheve, në lavjerrës cikloide, në optikë dhe, për rrjedhojë, studimi i këtyre kthesave është i rëndësishëm nga pikëpamja aplikative. Është po aq e rëndësishme që, duke studiuar këto kthesa dhe vetitë e tyre, shkencëtarët e shek. zhvilloi teknika që çuan në krijimin e llogaritjeve diferenciale dhe integrale, dhe problemi brakistokron ishte një hap drejt shpikjes së llogaritjes së variacioneve.

Elena Malishevskaya

LEMNIKATËS
Ekuacioni në koordinatat polare:
r 2 = a 2 cos2θ

(x 2 + y 2) 2 = a 2 (x 2 - y 2)

Këndi ndërmjet AB" ose A"B dhe boshtit x = 45 o

Sipërfaqja e një lak = a 2/2

CIKLOID

Sipërfaqja e një harku = 3πa 2

Gjatësia e harkut të një harku = 8a

Kjo është një kurbë e përshkruar nga një pikë P në një rreth me rreze a, e cila rrotullohet përgjatë boshtit x.

HIPOCIKLOIDË ME KATËR GJALLA
Ekuacioni në koordinata drejtkëndore:
x 2/3 + y 2/3 = a 2/3

Ekuacionet në formë parametrike:

Sipërfaqja e mbyllur nga kurba = 3πa 2 /8

Gjatësia e harkut të të gjithë lakores = 6a

Kjo është një kurbë e përshkruar nga një pikë P në një rreth me rreze a/4, e cila rrotullohet brenda një rrethi me rreze a.

KARDIOID
Ekuacioni: r = a (1 + cosθ)

Sipërfaqja e mbyllur nga kurba = 3πa 2 /2

Gjatësia e harkut të kurbës = 8a

Është një kurbë e përshkruar nga një pikë P në një rreth me rreze a, e cila rrotullohet jashtë rrethit të rrezes a. Kjo kurbë është gjithashtu një rast i veçantë i kërmillit të Paskalit.

LINJA ZINXHIRE
Ekuacioni:
y = a(e x/a + e -x/a)/2 = acosh(x/a)

Kjo është kurba përgjatë së cilës do të varej një zinxhir kur varej vertikalisht nga pika A në B.

Trëndafili me tre petale
Ekuacioni: r = acos3θ

Ekuacioni r = acos3θ është i ngjashëm me lakoren e përftuar duke rrotulluar në drejtim të kundërt të akrepave të orës përgjatë një lakore prej 30 o ose π/6 radian.

Në përgjithësi, r = acosnθ ose r = asinnθ ka n lobe nëse n është tek.

KATËR TRENDAMBIL PETALE
Ekuacioni: r = acos2θ

Ekuacioni r = asin2θ është i ngjashëm me lakoren e përftuar duke rrotulluar në drejtim të kundërt të akrepave të orës përgjatë një kurbë radian 45 o ose π/4.

Në përgjithësi r = acosnθ ose r = asinnθ ka 2n petale nëse n është çift.

EPICIKLOID
Ekuacionet parametrike:

Është kurba e përshkruar nga pika P në një rreth me rreze b ndërsa rrotullohet përgjatë pjesës së jashtme të rrethit me rreze a. Kardioidi është një rast i veçantë i epicikloidit.

HIPOCIKLOID I PËRGJITHSHËM
Ekuacionet parametrike:

Është kurba e përshkruar nga pika P në një rreth me rreze b ndërsa rrotullohet përgjatë pjesës së jashtme të rrethit me rreze a.

Nëse b = a/4, kurba është një hipocikloid me katër pika.

TROHOIDA
Ekuacionet parametrike:

Kjo është kurba e përshkruar nga pika P në një distancë b nga qendra e një rrethi me rreze a ndërsa rrotullohet përgjatë boshtit x.
Nëse b është një cikloid i shkurtuar.
Nëse b > a, kurba ka formën e treguar në Fig. 11-11 dhe quhet këmbësor.
Nëse b = a, kurba është një cikloide.

TRAKTRICE
Ekuacionet parametrike:

Është kurba e përshkruar nga pika fundore P e një vargu të shtrirë me gjatësi PQ kur skaji tjetër Q lëviz përgjatë boshtit x.

VERZIERA (VERZIERA) AGNEZI (NDONJË HERË KURRO AGNEZIN)
Ekuacioni në koordinatat drejtkëndore: y = 8a 3 /(x 2 + 4a 2)

Ekuacionet parametrike:

B. Në figurë, drejtëza e ndryshueshme OA pret y = 2a dhe një rreth me rreze a me qendër (0,a) përkatësisht në A dhe B. Çdo pikë P në "curl" përcaktohet duke ndërtuar vija paralele me boshtet x dhe y, dhe përmes B dhe A respektivisht, dhe duke përcaktuar pikën e kryqëzimit të P.

DESCARTES LEAF
Ekuacioni në koordinata drejtkëndore:
x 3 + y 3 = 3 bosht

Ekuacionet parametrike:

Zona e lakut 3a 2/2

Ekuacioni asimptotik: x + y + a = 0.

RRETHONI I PËRFSHIRË
Ekuacionet parametrike:

Kjo është lakorja e përshkruar nga pika fundore P e vargut ndërsa ai zbërthehet nga një rreth me rreze a.

ELIPS E PËRFSHIRË
Ekuacioni në koordinata drejtkëndore:
(sëpatë) 2/3 + (nga) 2/3 = (a 2 - b 2) 2/3

Ekuacionet parametrike:

Kjo kurbë është mbështjellja normale me elipsin x 2 /a 2 + y 2 /b 2 = 1.

OVALE KASINI
Ekuacioni polar: r 4 + a 4 - 2a 2 r 2 cos2θ = b 4.

Është një kurbë e përshkruar nga një pikë P e tillë që produkti i distancës së saj nga dy pika fikse [distanca 2a në anën] është një konstante b2.

Lakorja si në figurat e mëposhtme kur b a përkatësisht.

Nëse b = a, kurba është lemniskat

Kërmilli i PASCALIT
Ekuacioni polar: r = b + acosθ

Le të jetë OQ vija që lidh qendrën e O me çdo pikë Q në një rreth me diametër a që kalon nëpër O. Atëherë kurba është fokusi i të gjitha pikave P e tillë që PQ = b.

Lakorja e treguar në figurat e mëposhtme kur b > a ose b

CISSOID E DIOCLES
Ekuacioni në koordinatat drejtkëndore: y 2 = x 3 /(2a - x)

Ekuacionet parametrike:

Kjo është një kurbë e përshkruar nga një pikë P e tillë që distanca OP = distanca RS. Përdoret në detyrë duke dyfishuar kubin, d.m.th. gjetja e anës së një kubi që ka dyfishin e vëllimit të një kubi të caktuar

SPIRALJA E ARKIMEDIT
Ekuacioni polar: r = aθ

5. Ekuacioni parametrik cikloide dhe ekuacioni në koordinatat karteziane

Le të supozojmë se na është dhënë një cikloid i formuar nga një rreth me rreze a me qendër në pikën A.

Nëse zgjedhim si parametër që përcakton pozicionin e pikës këndin t=∟NDM nëpër të cilin rrezja, e cila kishte pozicion vertikal AO në fillim të rrotullimit, arriti të rrotullohej, atëherë koordinatat x dhe y të pikës M do të të shprehet si më poshtë:

x= OF = ON - NF = NM - MG = at-a sin t,

y= FM = NG = ND – GD = a – a cos t

Pra, ekuacionet parametrike të cikloidit kanë formën:

Kur t ndryshon nga -∞ në +∞, do të fitohet një kurbë, e përbërë nga një numër i pafund degësh si ato të paraqitura në këtë figurë.

Gjithashtu, përveç ekuacionit parametrik të cikloidit, ekziston edhe ekuacioni i tij në koordinatat karteziane:

Ku r është rrezja e rrethit që formon cikloidin.

6. Probleme për gjetjen e pjesëve të një ciklodi dhe figurave të formuara nga një cikloide

Detyra nr. 1. Gjeni sipërfaqen e një figure të kufizuar nga një hark i një cikloidi, ekuacioni i të cilit është dhënë në mënyrë parametrike

dhe boshti Ox.

Zgjidhje. Për të zgjidhur këtë problem, ne do të përdorim faktet që dimë nga teoria e integraleve, përkatësisht:

Zona e një sektori të lakuar.

Konsideroni një funksion r = r(φ) të përcaktuar në [α, β].

ϕ 0 ∈ [α, β] korrespondon me r 0 = r(ϕ 0) dhe, për rrjedhojë, pikën M 0 (ϕ 0 , r 0), ku ϕ 0,

r 0 - koordinatat polare të pikës. Nëse ϕ ndryshon, duke "përshkuar" të gjithë [α, β], atëherë pika e ndryshueshme M do të përshkruajë një kurbë AB, të dhënë

ekuacioni r = r(ϕ).

Përkufizimi 7.4. Një sektor lakor është një figurë e kufizuar nga dy rreze ϕ = α, ϕ = β dhe një kurbë AB e përcaktuar në polare

koordinatat nga ekuacioni r = r(ϕ), α ≤ ϕ ≤ β.

Sa më poshtë është e vërtetë

Teorema. Nëse funksioni r(ϕ) > 0 dhe është i vazhdueshëm në [α, β], atëherë zona

Sektori curvilinear llogaritet me formulën:

Kjo teoremë është vërtetuar më herët në temën e integralit të caktuar.

Bazuar në teoremën e mësipërme, problemi ynë i gjetjes së sipërfaqes së një figure të kufizuar nga një hark i një cikloidi, ekuacioni i së cilës jepet nga parametrat parametrikë x= a (t – sin t), y= a (1 – cos t), dhe boshti Ox, reduktohet në zgjidhjen e mëposhtme.

Zgjidhje. Nga ekuacioni i kurbës dx = a(1−cos t) dt. Harku i parë i cikloidit korrespondon me një ndryshim në parametrin t nga 0 në 2π. Prandaj,

Detyra nr. 2. Gjeni gjatësinë e një harku të cikloidit

Teorema e mëposhtme dhe rrjedha e saj u studiuan gjithashtu në llogaritjen integrale.

Teorema. Nëse kurba AB jepet nga ekuacioni y = f(x), ku f(x) dhe f ’ (x) janë të vazhdueshme në , atëherë AB është e ndreqshme dhe

Pasoja. Le të jepet AB në mënyrë parametrike

L AB = (1)

Le të jenë funksionet x(t), y(t) të diferencueshëm vazhdimisht në [α, β]. Pastaj

formula (1) mund të shkruhet si më poshtë

Le të bëjmë një ndryshim të ndryshoreve në këtë integral x = x(t), pastaj y’(x)= ;

dx= x’(t)dt dhe prandaj:

Tani le të kthehemi te zgjidhja e problemit tonë.

Zgjidhje. Ne kemi, dhe për këtë arsye

Detyra nr. 3. Duhet të gjejmë sipërfaqen S të formuar nga rrotullimi i një harku të cikloidit

L=((x,y): x=a(t – sin t), y=a(1 – kosto), 0≤ t ≤ 2π)

Në llogaritjen integrale, ekziston formula e mëposhtme për gjetjen e sipërfaqes së një trupi rrotullues rreth boshtit x të një lakore të përcaktuar parametrikisht në një segment: x=φ(t), y=ψ(t) (t 0 ≤t ≤t 1)

Duke zbatuar këtë formulë në ekuacionin tonë cikloid, marrim:

Detyra nr 4. Gjeni vëllimin e trupit të marrë nga rrotullimi i harkut cikloid

Përgjatë boshtit Ox.

Në llogaritjen integrale, kur studioni vëllimet, ekziston vërejtja e mëposhtme:

Nëse kurba që kufizon një trapez lakor jepet me ekuacione parametrike dhe funksionet në këto ekuacione plotësojnë kushtet e teoremës për ndryshimin e ndryshores në një integral të caktuar, atëherë vëllimi i trupit të rrotullimit të trapezit rreth boshtit Ox do të të llogaritet me formulë

Le të përdorim këtë formulë për të gjetur vëllimin që na nevojitet.

Problemi është zgjidhur.

konkluzioni

Pra, gjatë kësaj pune, u sqaruan vetitë themelore të cikloidit. Ne gjithashtu mësuam se si të ndërtonim një cikloide dhe zbuluam kuptimin gjeometrik të një cikloide. Siç doli, cikloidi ka aplikime të mëdha praktike jo vetëm në matematikë, por edhe në llogaritjet teknologjike dhe fizikë. Por cikloidi ka merita të tjera. Ajo u përdor nga shkencëtarët e shekullit të 17-të kur zhvillonin teknika për studimin e linjave të lakuara - ato teknika që përfundimisht çuan në shpikjen e llogaritjeve diferenciale dhe integrale. Ishte gjithashtu një nga "gurët e prekjes" mbi të cilin Njutoni, Leibniz dhe studiuesit e tyre të hershëm testuan fuqinë e metodave të reja të fuqishme matematikore. Më në fund, problemi i brakistokronës çoi në shpikjen e llogaritjes së variacioneve, e cila është aq e nevojshme për fizikantët e sotëm. Kështu, cikloidi doli të ishte i lidhur pazgjidhshmërisht me një nga periudhat më interesante në historinë e matematikës.

Letërsia

1. Berman G.N. Cikloide. - M., 1980

2. Verov S.G. Brachistochrone, ose një sekret tjetër i cikloidit // Kuantike. – 1975. - Nr.5

3. Verov S.G. Sekretet e cikloidit // Kuantike. – 1975. - Nr.8.

4. Gavrilova R.M., Govorukhina A.A., Kartasheva L.V., Kostetskaya G.S., Radchenko T.N. Zbatimet e një integrali të caktuar. Udhëzime metodologjike dhe detyra individuale për studentët e vitit 1 të Fakultetit të Fizikës. - Rostov n/a: UPL RSU, 1994.

5. Gindikin S.G. Mosha yjore e cikloidit // Kuantike. – 1985. - Nr.6.

6. Fikhtengolts G.M. Kursi i njehsimit diferencial dhe integral. T.1. - M., 1969

Kjo linjë quhet "zarf". Çdo vijë e lakuar është një mbështjellje e tangjentave të saj.

Lënda dhe lëvizja dhe metoda që ato përbëjnë, i mundësojnë secilit të realizojë potencialin e tij në njohjen e së vërtetës. Zhvillimi i një metodologjie për zhvillimin e një forme dialektike-materialiste të të menduarit dhe zotërimi i një metode të ngjashme të njohjes është hapi i dytë drejt zgjidhjes së problemit të zhvillimit dhe realizimit të aftësive njerëzore. Fragmenti XX Mundësitë...

Në këtë situatë, njerëzit mund të zhvillojnë neurasteni - një neurozë, baza e pamjes klinike të së cilës është një gjendje asthenike. Si në rastin e neurastenisë ashtu edhe në rastin e dekompensimit të psikopatisë neurastenike, thelbi i mbrojtjes mendore (psikologjike) reflektohet në tërheqjen nga vështirësitë në dobësi nervoze me disfunksione vegjetative: ose personi në mënyrë të pandërgjegjshme "lufton" më shumë sulmin. ..

Lloje të ndryshme aktivitetesh; zhvillimi i imagjinatës hapësinore dhe koncepteve hapësinore, të menduarit figurativ, hapësinor, logjik, abstrakt i nxënësve të shkollës; zhvillimi i aftësisë për të zbatuar njohuritë dhe aftësitë gjeometrike dhe grafike për zgjidhjen e problemeve të ndryshme të aplikuara; njohja me përmbajtjen dhe sekuencën e fazave të aktiviteteve të projektit në fushën teknike dhe...

harqe. Spiralet janë gjithashtu involuta të kthesave të mbyllura, për shembull involuti i një rrethi. Emrat e disa spiraleve jepen nga ngjashmëria e ekuacioneve të tyre polare me ekuacionet e kurbave në koordinatat karteziane, p.sh.: · spirale parabolike (a - r)2 = bj, · spirale hiperbolike: r = a/j. · Shufra: r2 = a/j · si-ci-spiral, ekuacionet parametrike të së cilës kanë formën: , )