Uzdužni valovi. Uzdužne vibracije homogenog štapa Matematički model, Korteweg-de Vriesova jednadžba
Predlaže se frekvencijska metoda za rješavanje problema uzdužnih vibracija šipki stepenasto promjenjivog presjeka sa ili bez uzimanja u obzir rasipanja energije pri udaru o krutu prepreku. Jednadžba uzdužnih vibracija štapa se transformira prema Laplaceu u prisutnosti početnih uvjeta različitih od nule. Rješava se rubni problem koji se sastoji u pronalaženju Laplace-transformiranih rubnih uzdužnih sila kao funkcija rubnih pomaka. Zatim se sastavlja sustav jednadžbi ravnoteže za čvorove, čijim se rješavanjem konstruiraju amplitudno-fazno-frekvencijske karakteristike (APFC) za dijelove štapa od interesa. Izvođenjem inverzne Laplaceove transformacije konstruira se prijelazni proces. Kao ispitni primjer razmatra se štap konstantnog presjeka konačne duljine. Dana je usporedba s poznatim valnim rješenjem. Predložena metoda za dinamički proračun štapa u sudaru s krutom preprekom omogućuje generalizaciju na proizvoljan sustav štapa u prisutnosti neograničenog broja elastično vezanih masa, s proizvoljnom silom primijenjenom na krajevima i duž duljine štapa. štap.
Frekvencijska metoda
uzdužne vibracije štapa
1. Biderman, V.L. Primijenjena teorija mehaničkih vibracija / V.L. Biderman. – M.: Viša škola, 1972. – 416 str.
2. Lavrentiev, M.A. Metode teorije funkcija kompleksne varijable / M.A. Lavrentiev, B.V. Šabat. – M.: Nauka, 1973. – 736 str.
3. Sankin, Yu.N. Dinamičke karakteristike viskoelastičnih sustava s raspodijeljenim parametrima / Yu.N. Sankin. – Saratov: Izdavačka kuća Sarat. sveučilište, 1977. – 312 str.
4. Sankin, Yu.N. Nestacionarne vibracije štapnih sustava pri sudaru s preprekom / Yu.N. Sankin, N.A. Yuganova; pod općim izd. Yu.N. Sankina. – Uljanovsk: Uljanovsko državno tehničko sveučilište, 2010. – 174 str.
5. Sankin, Y.N. Uzdužne vibracije elastičnih šipki stepenasto promjenjivog presjeka pri sudaru s krutom preprekom \ Yu. N. Sankin i N.A. Yuganova, J. Appl. Matematički strojevi, sv. 65, br. 3, str. 427–433, 2001.
Razmotrimo frekvencijsku metodu za rješavanje problema uzdužnih vibracija štapova stepenasto promjenjivog presjeka sa ili bez uzimanja u obzir rasipanja energije pri udaru o krutu prepreku, koju ćemo usporediti s poznatim valnim rješenjem i rješenjem u oblik niza načina vibracija (14).
Diferencijalna jednadžba za uzdužne vibracije štapa, uzimajući u obzir sile unutarnjeg otpora, ima oblik:
Postavimo sljedeće granične i početne uvjete:

 . (2)
. (2)
Transformirajmo jednadžbu (1) i rubne uvjete (2) prema Laplaceu za zadane početne uvjete (2). Tada će jednadžba (2) i rubni uvjeti (2) biti napisani na sljedeći način:
![]() ; (3)
; (3)
 ,
,
gdje su Laplace-transformirani pomaci točaka štapa; p je parametar Laplaceove transformacije.
Jednadžba (3) bez uzimanja u obzir disipacije energije (pri = 0) poprimit će oblik:
![]() . (4)
. (4)
Za rezultirajuću nehomogenu diferencijalnu jednadžbu rješava se rubni problem koji se sastoji u pronalaženju Laplace-transformiranih rubnih uzdužnih sila kao funkcija rubnih pomaka.
Da biste to učinili, razmotrite homogenu jednadžbu uzdužnih vibracija štapa uzimajući u obzir rasipanje energije
![]() (5)
(5)
Određivanje
![]()
i prelazeći na novu varijablu, dobivamo umjesto (5)
![]() (6)
(6)
Ako, gdje je tada parametar frekvencije
![]() .
.
Rješenje homogene jednadžbe (6) ima oblik:
Integracijske konstante c1 i c2 nalazimo iz početnih uvjeta:
u = u0; N = N0,

Oni. ![]() ;
;
Ovo rješenje odgovara sljedećoj matrici prijenosa:
 . (7)
. (7)
Zamjenom dobivenih izraza za elemente matrice prijenosa u formule metode pomaka dobivamo:
![]() ;
;![]() (8)
(8)
 ;
;


Indeksi n i k označavaju početak odnosno kraj dijela šipke. A geometrijske i fizikalne konstante s indeksima nk i kn odnose se na određeni presjek štapa.
Dijeleći štap na elemente, pomoću formula (8), sastaviti ćemo jednadžbe za dinamičku ravnotežu čvorova. Ove jednadžbe predstavljaju sustav jednadžbi za nepoznate čvorne pomake. Budući da se odgovarajući koeficijenti dobivaju točnom integracijom, duljina dijelova štapa nije ograničena.
Rješavanjem dobivenog sustava jednadžbi za konstruiramo amplitudno-fazno-frekvencijske karakteristike za presjeke štapa koji nas zanimaju. Ovi AFC-ovi se mogu smatrati grafičkom slikom jednosmjerne Fourierove transformacije, koja se podudara s Laplaceovom transformacijom pod pulsnim utjecajima. Budući da sve singularne točke odgovarajućih izraza leže lijevo od imaginarne osi, inverzna transformacija se može izvesti uz pretpostavku , tj. pomoću konstruiranih AFC-ova. Zadatak konstruiranja AFC-a, gdje se polje početnih brzina pomnoženo s gustoćom štapa pojavljuje kao djelovanje sile, je pomoćni. Tipično, AFC-ovi se konstruiraju iz utjecaja ometajućih sila, zatim se inverzna Laplaceova transformacija provodi numeričkom integracijom ili nekom drugom metodom.
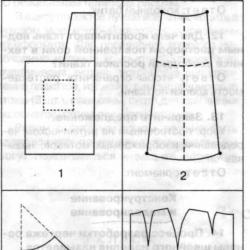
Kao jednostavan primjer, razmotrimo ravni štap duljine l, koji se uzdužno sudara s krutom preprekom brzinom V0 (slika 1).

Odredimo pomak točaka štapa nakon udarca. Pretpostavit ćemo da nakon udarca ostaje kontakt između prepreke i šipke, tj. nema odskoka štapa. Ako je veza nesadržajna, tada se problem može smatrati komadno linearnim. Kriterij za prijelaz na drugu opciju rješenja je promjena predznaka brzine u točki kontakta.
U monografiji Lavrentyev M.A., Shabat B.V. valno rješenje jednadžbe (4) je dano:

i pronađen je njegov original
 , (9)
, (9)
gdje je funkcija jediničnog koraka.
Drugi pristup rješavanju ovog problema može se provesti metodom frekvencije opisanom u. U odnosu na ovaj problem imat ćemo:
![]() ;
; ![]() ;
;
![]() ; ;
; ;
; ![]() ;
;
 . (10)
. (10)
Pronađimo original (11)


Riješimo isti problem metodom učestalosti. Iz jednadžbe ravnoteže 1. čvora:
![]() (12)
(12)
dobivamo formulu za pomicanje kraja štapa.
Sada, ako se ispitna šipka konstantnog poprečnog presjeka podijeli na dva proizvoljna dijela duljine l1 i l2 (vidi sliku 1), tada će uvjeti ravnoteže za čvorove biti sljedeći:
 (13)
(13)
Kao rezultat rješavanja sustava (13) dobivamo grafove fazno-frekvencijskog odziva za pomake u 1. i 2. presjeku (U1 odnosno U2). Dakle, slika za pomak ruba u zatvorenom obliku, uzimajući u obzir disipaciju energije, u slučaju (12) i (13) podudara se i ima oblik:
![]() . (14)
. (14)
Provjerimo podudarnost rezultata na kraju štapa. Na sl. Na slici 2 prikazani su grafovi rješenja (10) pri x = l0,1 i kao rezultat rješavanja sustava (13). Potpuno su isti.

Diskretna Fourierova transformacija može se koristiti za dobivanje prijelaznog procesa. Rezultat se može dobiti izvođenjem numeričke integracije pri t=0... pomoću formule
 . (15)
. (15)
U AFC-u (vidi sliku 2) samo se jedan vidljivi zaokret značajno manifestira. Stoga treba uzeti jedan član serije (15). Grafikoni na slici 3 pokazuju koliko se točno rješenje (9) i rješenje za vibracijske modove (11) podudaraju s predloženim frekvencijskim rješenjem. Greška ne prelazi 18%. Nastala razlika se objašnjava činjenicom da rješenja (9) i (11) ne uzimaju u obzir disipaciju energije u materijalu štapa.

Riža. 3. Prijelazni proces za kraj štapa; 1, 2, 3 - grafikoni konstruirani prema formulama (9), (11), (15).
Kao složeniji primjer razmotrimo problem uzdužnih vibracija stepenastog štapa (sl. 4) s teretom na kraju, koji se sudara s krutom preprekom brzinom V0, a neka je masa tereta jednaka masi susjednog dijela štapa:.

Riža. 4. Proračunski dijagram uzdužnih vibracija stepenastog štapa s teretom na kraju
Uvedimo karakteristične presjeke 1,2,3 štapa u kojima ćemo izračunati pomake. Kreirajmo sustav rješavanja jednadžbi:
 (16)
(16)
Kao rezultat rješavanja sustava (16) dobivamo grafove fazno-frekvencijskog odziva (slika 5) za pomake u drugom i trećem presjeku (U2() odnosno U3(). Proračuni su provedeni sa sljedećim konstantnim vrijednostima: l = 2 m; E = 2,1×1011 Pa; F = 0,06 m2; = 7850 kg/m3; V = 10 m/s. U dobivenim AFC-ima značajno se manifestiraju samo dva vidljiva zavoja. Stoga pri konstrukciji prijelaznog procesa u odabranim presjecima uzimamo dva člana serije (16). Da biste to učinili, prvo morate odrediti

Riža. 5. AFC pomaka u drugom i trećem dijelu stepenaste šipke (vidi sl. 4)
Prijelazni proces se konstruira na sličan način pomoću formule (15).
Zaključak: razvijena je metoda za proračun uzdužnih vibracija štapova pri udaru o prepreku.
Recenzenti:
Lebedev A.M., doktor tehničkih znanosti, izvanredni profesor, profesor Uljanovske više zrakoplovne škole (Institut), Uljanovsk.
Antonets I.V., doktor tehničkih znanosti, profesor Uljanovskog državnog tehničkog sveučilišta, Uljanovsk.
Bibliografska poveznica
Yuganova N.A. UZDUŽNE VIBRACIJE ŠTAPOVA U SUDARU S TVRDOM PREPREKOM // Suvremeni problemi znanosti i obrazovanja. – 2014. – br. 2.;URL: http://science-education.ru/ru/article/view?id=12054 (datum pristupa: 15.01.2020.). Predstavljamo vam časopise izdavačke kuće "Akademija prirodnih znanosti"
Slobodne oscilacije sustava s raspodijeljenim parametrima
Glavna značajka procesa slobodnih titraja sustava s beskonačnim brojem stupnjeva slobode izražava se u beskonačnosti broja vlastitih frekvencija i oblika modova. To je povezano i s matematičkim značajkama: umjesto običnih diferencijalnih jednadžbi koje opisuju oscilacije sustava s konačnim brojem stupnjeva slobode, ovdje imamo posla s parcijalnim diferencijalnim jednadžbama. Osim početnih uvjeta koji određuju početne pomake i brzine, potrebno je uzeti u obzir i rubne uvjete koji karakteriziraju fiksaciju sustava.
6.1. Uzdužne vibracije štapova
Pri analizi uzdužnih vibracija ravnog štapa (slika 67, a), pretpostavit ćemo da presjeci ostaju ravni i da čestice štapa ne izvode poprečna kretanja, već se kreću samo u uzdužnom smjeru.
Neka u - uzdužno kretanje trenutnog presjeka štapa tijekom vibracija; ovo kretanje ovisi o mjestu presjeka (koordinate x) i o vremenu t. Dakle, postoji funkcija dviju varijabli; njegova definicija predstavlja glavni zadatak. Pomak beskonačno bliskog dijela jednak je , dakle, apsolutno produljenje beskonačno malog elementa je jednako (slika 67, b), a njegovo relativno produljenje je .
Prema tome, uzdužna sila u presjeku s koordinat x može se napisati kao
![]() ,(173)
,(173)
gdje je krutost štapa u napetosti (stisku). Sila N također je funkcija dvaju argumenata – koordinata x i vrijeme t.
Razmotrimo štapni element koji se nalazi između dva beskonačno bliska dijela (slika 67, c). Sila N djeluje na lijevu stranu elementa, a sila na desnu stranu. Ako označimo gustoću materijala štapa, tada je masa predmetnog elementa . Dakle, jednadžba gibanja u projekciji na os x
![]() ,
,
Uzimajući u obzir(173)i prihvaćajući A= const, dobivamo
Slijedeći Fourierovu metodu, tražimo posebno rješenje diferencijalne jednadžbe (175) u obliku
,(177)
oni. pretpostavimo da pokret u može se prikazati kao proizvod dviju funkcija, od kojih jedna ovisi samo o argumentu x, a drugi samo iz argumenta t. Tada je umjesto definiranja funkcije dviju varijabli u (x, t) potrebno definirati dvije funkcije X(x) i T(t), od kojih svaka ovisi samo o jednoj varijabli.
Zamjenom (177) u (174) dobivamo
gdje prosti brojevi označavaju operaciju diferencijacije u odnosu na x, i po točkama t. Prepišimo ovu jednadžbu na sljedeći način:
Ovdje lijeva strana ovisi samo o x, a desna samo o t. Da bi ova jednakost vrijedila identično (za bilo koji x i t) potrebno je da svaki njegov dio bude jednak konstanti koju označavamo sa:
; .(178)
To dovodi do dvije jednadžbe:
;![]() .(179)
.(179)
Prva jednadžba ima rješenje:
![]() ,(180)
,(180)
što ukazuje na oscilatornu prirodu, a iz (180) je jasno da nepoznata veličina ima značenje frekvencije slobodnih oscilacija.
Druga od jednadžbi (179) ima rješenje:
![]() ,(181)
,(181)
određivanje oblika vibracija.
Frekvencijska jednadžba koja određuje vrijednost sastavlja se korištenjem rubnih uvjeta. Ova jednadžba je uvijek transcendentalna i ima beskonačan broj korijena. Dakle, broj vlastitih frekvencija je beskonačan, a svaka vrijednost frekvencije odgovara vlastitoj funkciji T n (t), određenoj ovisnošću (180), i vlastitoj funkciji Xn (x), određenoj ovisnošću (181). Rješenje (177) je samo djelomično i ne daje potpuni opis gibanja. Potpuno rješenje dobiva se superponiranjem svih parcijalnih rješenja:
![]() .
.
Funkcije X n (x) nazivaju se vlastite funkcije probleme i opisuju vlastite načine vibracije. Ne ovise o početnim uvjetima i zadovoljavaju uvjet ortogonalnosti, koji za A = const ima oblik
![]() , Ako .
, Ako .
Razmotrimo neke opcije za rubne uvjete.
Fiksni kraj šipke(Slika 68, a). Na krajnjem presjeku, pomak u mora biti jednak nuli; proizlazi da u ovom odjeljku
X=0(182)
Slobodni kraj šipke(Slika 68, b). Na krajnjem presjeku, uzdužna sila
(183)
mora biti identički jednak nuli, što je moguće ako je na kraju odsječka X"=0.
Otporan kraj šipke(Slika 68, c).
Prilikom kretanja u krajnje šipke, dolazi do reakcije elastične potpore ![]() , gdje je C o krutost oslonca. Uzimajući u obzir (183) za uzdužnu silu, dobivamo rubni uvjet
, gdje je C o krutost oslonca. Uzimajući u obzir (183) za uzdužnu silu, dobivamo rubni uvjet
ako se nosač nalazi na lijevom kraju šipke (slika 68, c), i
ako se nosač nalazi na desnom kraju šipke (slika 68, d).

Koncentrirana masa na kraju šipke.
Sila inercije koju razvija masa:
![]() .
.
Budući da se, prema prvoj od jednadžbi (179), , sila tromosti može napisati u obliku . Dobivamo rubni uvjet
![]() ,
,
ako je masa na lijevom kraju (slika 68, d), i
![]() , (184)
, (184)
ako je masa spojena na desni kraj (slika 68, e).
Odredimo vlastite frekvencije konzolnog štapa (sl. 68,a").
Prema (182) i (183), rubni uvjeti
X=0 na x=0;
X"=0 pri x= .
Zamjenjujući ove uvjete jedan po jedan u rješenje (181), dobivamo
Uvjet C0 dovodi do frekvencijske jednadžbe:
Korijeni ove jednadžbe
![]() (n=1,2,…)
(n=1,2,…)
odrediti vlastite frekvencije:
![]() (n=1,2,…).(185)
(n=1,2,…).(185)
Prva (najniža) frekvencija pri n=1:
![]() .
.
Druga frekvencija (pri n=2):
Odredimo vlastite frekvencije štapa s masom na kraju (slika 68, f).
Prema (182) i (184) imamo
X=0 kod x=0;
![]() pri x= .
pri x= .
Zamjenom ovih uvjeta u rješenje (181) dobivamo:
D=0; ![]() .
.
Prema tome, jednadžba frekvencije kada se uzme u obzir (176) ima oblik
![]() .
.
Ovdje desna strana predstavlja omjer mase štapa i mase krajnjeg opterećenja.
Za rješavanje dobivene transcendentne jednadžbe potrebno je upotrijebiti neku približnu metodu.
At i vrijednosti najvažnijeg najnižeg korijena bit će 0,32 odnosno 0,65.
Kod malog omjera opterećenje ima odlučujući utjecaj i približno rješenje daje dobre rezultate
 .
.
Za šipke promjenjivog presjeka, tj. za Aconst, iz (173) i (174) dobiva se jednadžba gibanja u obliku
![]() .
.
Ova se diferencijalna jednadžba ne može riješiti u zatvorenom obliku. Stoga je u takvim slučajevima potrebno pribjeći približnim metodama određivanja vlastitih frekvencija.
6.2. Torzijske vibracije vratila
Torzijske vibracije osovina s kontinuirano raspoređenom masom (slika 69, a) opisuju se jednadžbama koje se po strukturi potpuno podudaraju s gornjim jednadžbama za uzdužne vibracije šipki.

Moment M u presjeku s apscisom x povezan je s kutom rotacije diferencijalnom ovisnošću sličnom (173):
Gdje Jp-polarni moment tromosti presjeka.
U dijelu koji se nalazi na udaljenosti dx, moment je jednak (Sl. 69, b):
Označavajući kroz (gdje je gustoća materijala osovine) intenzitet momenta tromosti mase osovine u odnosu na njezinu os (tj. moment tromosti po jedinici duljine), jednadžba gibanja elementarnog presjeka osovine može se napisati na sljedeći način:
![]() ,
,
ili slično (174):
![]() .
.
Zamjena izraza (186) ovdje, sa Jp=const dobivamo, slično (175):
![]() , (187)
, (187)
Opće rješenje jednadžbe (187), kao i jednadžba (175), ima oblik
![]() ,
,
![]() (188)
(188)
Vlastite frekvencije i vlastite funkcije određene su posebnim rubnim uvjetima.
U glavnim slučajevima učvršćivanja krajeva, slično kao i kod uzdužnih vibracija, dobivamo
a) fiksni kraj (=0): X=0;
b) slobodni kraj (M=0): X"=0;
V) otporan lijevi kraj: CoH=GJpX "(Koeficijent krutosti);
G) otporan desni kraj: -CoX=GJpX ";
e) disk na lijevom kraju: ![]() (Jo je moment tromosti diska u odnosu na os stapa);
(Jo je moment tromosti diska u odnosu na os stapa);
e) disk na desnom kraju: ![]() .
.
Ako je osovina fiksirana na lijevom kraju (x=0), a desni kraj (x=) je slobodan, tada je X=0 na x=0 i X"=0 na x=; prirodne frekvencije se određuju slično kao ( 185):
![]() (n=1,2,…).
(n=1,2,…).
Ako je lijevi kraj fiksiran, a na desnom kraju je disk, dobivamo transcendentalnu jednadžbu:
![]() .
.
Ako su oba kraja osovine fiksirana, tada će rubni uvjeti biti X=0 za x=0 i x=. U ovom slučaju iz (188) dobivamo
oni.
(n=1,2,…),
odavde nalazimo prirodne frekvencije:
Ako je lijevi kraj osovine slobodan, a na desnom kraju postoji disk, tada je X"=0 za x=0;Jo X=GJpX "za x=.
Pomoću (188) nalazimo
C=0; ![]() ,
,
ili transcendentna frekvencijska jednadžba:
 .
.
6.3.Savojne vibracije greda
6.3.1 Osnovna jednadžba
Iz kolegija o čvrstoći materijala poznate su diferencijalne ovisnosti za savijanje greda:
gdje je EJ krutost na savijanje; y=y (x, t) - otklon; M=M(x, t) - moment savijanja; q je intenzitet raspodijeljenog opterećenja.
Kombinirajući (189) i (190), dobivamo
 .(191)
.(191)
U problemu slobodnih vibracija, opterećenje za elastični skelet su raspoređene inercijske sile:
gdje je m intenzitet mase grede (masa po jedinici duljine), a jednadžba (191) ima oblik
 .
.
U posebnom slučaju konstantnog presjeka, kada je EJ = const, m = const, imamo:
![]() .(192)
.(192)
Za rješavanje jednadžbe (192), pretpostavljamo, kao gore,
g= X ( x)× T ( t ).(193)
Zamjenom (193) u (192) dolazimo do jednadžbe:
![]() .
.
Da bi ova jednakost bila identično ispunjena, potrebno je da svaki od dijelova jednakosti bude konstantan. Označavajući ovu konstantu s , dobivamo dvije jednadžbe:
![]() .(195)
.(195)
Prva jednadžba pokazuje da je kretanje oscilatorno s frekvencijom.
Druga jednadžba određuje oblik vibracija. Rješenje jednadžbe (195) sadrži četiri konstante i ima oblik
Prikladno je koristiti varijantu pisanja općeg rješenja koje je predložio A.N. Krylov:
 (198)
(198)
predstavljaju funkcije A.N.Krylova.
Obratimo pozornost na činjenicu da je S=1, T=U=V=0 pri x=0. Funkcije S,T,U,V međusobno su povezane na sljedeći način:
Stoga se izvodni izrazi (197) pišu u obliku
 (200)
(200)
U problemima klase koja se razmatra, broj vlastitih frekvencija je beskonačno velik; svaki od njih ima svoju vremensku funkciju T n i svoju temeljnu funkciju X n . Opće rješenje se dobiva nametanjem parcijalnih rješenja oblika (193)
![]() .(201)
.(201)
Za određivanje vlastitih frekvencija i formula potrebno je uzeti u obzir rubne uvjete.
6.3.2. Granični uvjeti
Za svaki kraj šipke možete odrediti dva rubna uvjeta .
Slobodni kraj šipke(Slika 70, a). Poprečna sila Q=EJX""T i moment savijanja M=EJX""T jednaki su nuli. Stoga rubni uvjeti imaju oblik
X""=0; X"""=0 .(202)

Zglobno oslonjeni kraj šipke(Slika 70, b). Progib y=XT i moment savijanja M=EJX""T jednaki su nuli. Prema tome, rubni uvjeti su:
X=0; X""=0 .(203)
Stegnut kraj(Slika 70, c). Otklon y=XT i kut zakreta jednaki su nuli. Granični uvjeti:
X=0; X"=0 . (204)
Na kraju štapa nalazi se točkasta masa(Slika 70, d). Njegova inercijalna sila ![]() može se napisati pomoću jednadžbe (194) na sljedeći način: ; mora biti jednaka posmičnoj sili Q=EJX"""T, pa rubni uvjeti imaju oblik
može se napisati pomoću jednadžbe (194) na sljedeći način: ; mora biti jednaka posmičnoj sili Q=EJX"""T, pa rubni uvjeti imaju oblik
![]() ; X""=0 .(205)
; X""=0 .(205)
U prvom uvjetu, znak plus se uzima kada je točkasto opterećenje spojeno na lijevi kraj štapa, a znak minus kada je spojeno na desni kraj štapa. Drugi uvjet proizlazi iz nepostojanja momenta savijanja.
Elastično poduprti kraj šipke(Slika 70, d). Ovdje je moment savijanja jednak nuli, a poprečna sila Q=EJX"""T jednaka je reakciji oslonca ![]() (C o - koeficijent krutosti nosača).
(C o - koeficijent krutosti nosača).
Granični uvjeti:
X""=0 ; (206)
(predznak minus se uzima kada je elastična potpora lijevo, a znak plus kada je desna).
6.3.3. Frekvencijska jednadžba i svojstveni oblici
Prošireni zapis rubnih uvjeta dovodi do homogenih jednadžbi s obzirom na konstante C 1, C 2, C 3, C 4.
Da te konstante ne bi bile jednake nuli, determinanta koju čine koeficijenti sustava mora biti jednaka nuli; to dovodi do frekvencijske jednadžbe. Tijekom ovih operacija pojašnjavaju se odnosi između C1, C2, C3, C4, tj. određeni su prirodni načini vibracija (do konstantnog faktora).
Pratimo sastav frekvencijskih jednadžbi koristeći primjere.
Za gredu sa zglobnim krajevima, prema (203), imamo sljedeće rubne uvjete: X=0; X""=0 za x=0 i x= . Koristeći (197)-(200) iz prva dva uvjeta dobivamo: C 1 =C 3 =0. Dva preostala uvjeta mogu se napisati kao

Da C 2 i C 4 ne bi bili jednaki nuli, determinanta mora biti jednaka nuli:
![]() .
.
Dakle, frekvencijska jednadžba ima oblik
![]() .
.
Zamjenom izraza T i U dobivamo
Budući da je konačna frekvencijska jednadžba napisana na sljedeći način:
. (207)
Korijeni ove jednadžbe su:
,(n =1,2,3,...).
Uzimajući u obzir (196), dobivamo
![]() .(208)
.(208)
Prijeđimo na definiranje vlastitih oblika. Iz gore napisanih homogenih jednadžbi slijedi sljedeći odnos između konstanti C 2 i C 4 :
![]() .
.
Posljedično, (197) poprima oblik

Prema (207), imamo
![]() ,(209)
,(209)
gdje je nova konstanta, čija vrijednost ostaje neizvjesna dok se početni uvjeti ne uvedu u razmatranje.
6.3.4. Određivanje gibanja na temelju početnih uvjeta
Ako je potrebno odrediti kretanje nakon početnog poremećaja, tada je potrebno navesti i početne pomake i početne brzine za sve točke grede:
 (210)
(210)
i koristiti svojstvo ortogonalnosti svojstvenih oblika:
![]() .
.
Opće rješenje (201) pišemo na sljedeći način:
![]() .(211)
.(211)
Brzina je dana sa
![]() .(212)
.(212)
Zamjenom početnih pomaka i brzina za koje se pretpostavlja da su poznati u desne strane jednadžbi (211) i (212), te u lijeve strane, dobivamo
![]()
![]() .
.
Množenjem ovih izraza i integriranjem po cijeloj dužini, imamo
 (213)
(213)
Beskonačni zbrojevi na desnim stranama su nestali zbog svojstva ortogonalnosti. Iz (213) slijede formule za konstante i
 (214)
(214)
Sada te rezultate treba zamijeniti u rješenje (211).
Naglasimo ponovno da je izbor ljestvice svojstvenih oblika nevažan. Ako, na primjer, u izrazu svojstvenog oblika (209) umjesto toga uzmemo vrijednost koja je puta veća, tada će (214) dati rezultate koji su puta manji; nakon supstitucije u otopinu (211), te se razlike međusobno kompenziraju. Unatoč tome, oni često koriste normalizirane svojstvene funkcije, odabirući njihovu skalu tako da su nazivnici izraza (214) jednaki jedinici, što pojednostavljuje izraze i .
6.3.5. Učinak konstantne uzdužne sile
Razmotrimo slučaj kada na oscilirajuću gredu djeluje uzdužna sila N, čija se veličina ne mijenja tijekom procesa osciliranja. U tom slučaju, statička jednadžba savijanja postaje kompliciranija i poprima oblik (pod uvjetom da se tlačna sila smatra pozitivnom)
![]() .
.
Uzimajući i uzimajući u obzir konstantu krutosti, dobivamo jednadžbu slobodnih vibracija
![]() .(215)
.(215)
I dalje prihvaćamo određeno rješenje u obrascu.
Tada se jednadžba (215) dijeli na dvije jednadžbe:

Prva jednadžba izražava oscilatornu prirodu rješenja, druga određuje oblik oscilacija, a također vam omogućuje pronalaženje frekvencija. Prepišimo to ovako:
(216)
Gdje K određuje se formulom (196), i
Rješenje jednadžbe (216) ima oblik


Razmotrimo slučaj kada oba kraja šipke imaju zglobne nosače. Uvjeti na lijevom kraju ![]() dati . Zadovoljavajući iste uvjete na desnom kraju, dobivamo
dati . Zadovoljavajući iste uvjete na desnom kraju, dobivamo

Izjednačujući s nulom determinantu sastavljenu od koeficijenata za veličine i , dolazimo do jednadžbe
Korijeni ove frekvencijske jednadžbe su:
Stoga se vlastita frekvencija određuje iz jednadžbe
 .
.
Odavde, uzimajući u obzir (217), nalazimo
 .(219)
.(219)
Kada se rasteže, frekvencija se povećava, kada se stisne smanjuje. Kada se sila pritiska N približi kritičnoj vrijednosti, korijen teži nuli.
6.3.6. Učinak lančanih sila
Prethodno se uzdužna sila smatrala zadanom i neovisnom o pomacima sustava. U nekim praktičnim problemima, uzdužna sila koja prati proces transverzalnih vibracija nastaje zbog savijanja grede i ima karakter reakcije oslonca. Razmotrimo, na primjer, gredu na dva zglobna i fiksna nosača. Kada se savija, dolazi do vodoravnih reakcija nosača, zbog čega se greda rasteže; obično se naziva odgovarajuća horizontalna sila sila lanca. Ako greda oscilira poprečno, sila lanca će se mijenjati tijekom vremena.
Ako su u trenutku t progibi grede određeni funkcijom, tada se produljenje osi može pronaći pomoću formule
![]() .
.
Odgovarajuću lančanu silu nalazimo koristeći Hookeov zakon
![]() .
.
Zamijenimo ovaj rezultat u (215) umjesto uzdužne sile N (uzimajući u obzir predznak)
![]() .(220)
.(220)
Rezultirajući nelinearni integrodiferencijalni jednadžba je pojednostavljena korištenjem supstitucije
![]() ,(221)
,(221)
gdje je bezdimenzionalna funkcija vremena, čija se najveća vrijednost može postaviti jednakom bilo kojem broju, na primjer, jedinici; amplituda oscilacija.
Zamjenom (221) u (220) dobivamo običnu diferencijalnu jednadžbu
![]() ,(222)
,(222)
čiji koeficijenti imaju sljedeće vrijednosti:
![]() ;.
;.
Diferencijalna jednadžba (222) je nelinearna, stoga frekvencija slobodnih oscilacija ovisi o njihovoj amplitudi.
Točno rješenje za frekvenciju transverzalnih vibracija ima oblik
gdje je frekvencija poprečnih vibracija, izračunata bez uzimanja u obzir lančanih sila; korekcijski faktor koji ovisi o omjeru amplitude titranja i polumjera vrtnje poprečnog presjeka; vrijednost je navedena u referentnoj literaturi.
Kada su amplituda i radijus vrtnje poprečnog presjeka razmjerni, korekcija frekvencije postaje značajna. Ako je npr. amplituda titranja okruglog štapa jednaka njegovom promjeru, tada je , a frekvencija je gotovo dvostruko veća nego u slučaju slobodnog pomaka oslonaca.
Slučaj odgovara nultoj vrijednosti polumjera tromosti, kada je krutost grede na savijanje nestajuće mala - struna. U isto vrijeme, formula za daje nesigurnost. Otkrivajući tu nesigurnost, dobivamo formulu za frekvenciju titranja žice
![]() .
.
Ova formula vrijedi za slučaj kada je napetost nula u ravnotežnom položaju. Često se problem oscilacija strune postavlja pod drugim pretpostavkama: smatra se da su pomaci mali, a vlačna sila zadana i ostaje nepromijenjena tijekom procesa osciliranja.
U ovom slučaju formula za frekvenciju ima oblik
gdje je N konstantna vlačna sila.
6.4. Učinak viskoznog trenja
Prethodno se pretpostavljalo da je materijal šipki savršeno elastičan i da nema trenja. Razmotrimo utjecaj unutarnjeg trenja, pod pretpostavkom da je viskozno; tada se odnos između naprezanja i deformacije opisuje odnosima
![]() ;
;![]() .(223)
.(223)
Neka štap s raspodijeljenim parametrima izvodi slobodne uzdužne vibracije. U ovom slučaju, uzdužna sila će biti zapisana u obliku
Iz jednadžbe gibanja štapnog elementa dobivena je relacija (174).
Zamjenom (224) ovdje dolazimo do glavne diferencijalne jednadžbe
![]() ,(225)
,(225)
koji se od (175) razlikuje po drugom članu koji izražava utjecaj sila viskoznog trenja.
Slijedeći Fourierovu metodu, rješenje jednadžbe (225) tražimo u obliku
![]() ,(226)
,(226)
gdje je funkcija samo koordinate x, a funkcija samo vrijeme t.
U tom slučaju svaki član niza mora zadovoljiti rubne uvjete problema, a cijeli zbroj također mora zadovoljiti početne uvjete. Zamjena (226) u (225) i zahtijevanje da jednakost bude zadovoljena za bilo koji broj r, dobivamo
![]() ,(227)
,(227)
gdje prosti brojevi označavaju diferencijaciju s obzirom na koordinatu x, a točke su diferencijacija s obzirom na vrijeme t.
Dijeljenje (227) umnoškom ![]() , dolazimo do jednakosti
, dolazimo do jednakosti
 ,(228)
,(228)
lijeva strana, koja može ovisiti samo o koordinati x, a desna - samo od vremena t. Da bi jednakost (228) bila identično ispunjena, potrebno je da oba dijela budu jednaka istoj konstanti koju označavamo s .
Iz ovoga slijede jednadžbe
![]() (229)
(229)
![]() .(230)
.(230)
Jednadžba (229) ne ovisi o koeficijentu viskoznosti K, a posebno ostaje ista u slučaju savršeno elastičnog sustava, kada je . Dakle, brojevi se potpuno podudaraju s onima koji su ranije pronađeni; međutim, kao što će biti prikazano u nastavku, vrijednost daje samo približnu vrijednost prirodne frekvencije. Imajte na umu da su svojstveni oblici potpuno neovisni o viskoznim svojstvima štapa, tj. oblici slobodnih prigušenih oscilacija podudaraju se s oblicima slobodnih neprigušenih oscilacija.
Prijeđimo sada na jednadžbu (230), koja opisuje proces prigušenih oscilacija; njegovo rješenje ima oblik
 .(233)
.(233)
Izraz (232) određuje brzinu opadanja, a (233) određuje frekvenciju osciliranja.
Dakle, potpuno rješenje jednadžbe problema
![]() .(234)
.(234)
Konstanta i uvijek se može pronaći na temelju zadanih početnih uvjeta. Neka su početni pomaci i početne brzine svih dijelova štapa određeni na sljedeći način:
;![]() ,(235)
,(235)
gdje su i poznate funkcije.
Tada za , prema (211) i (212), imamo

množenjem obje strane ovih jednakosti i integracijom po cijeloj dužini štapa, dobivamo
 (236)
(236)
Prema uvjetu ortogonalnosti svojstvenih oblika, svi ostali članovi uključeni u desne strane ovih jednakosti postaju nula. Sada je iz jednakosti (236) lako pronaći za bilo koji broj r.
Uzimajući u obzir (232) i (234), primjećujemo da što je veći broj moda vibracije, to je njeno prigušenje brže. Osim toga, izrazi uključeni u (234) opisuju prigušene oscilacije ako postoji realan broj. Iz (233) je jasno da se to događa samo za nekoliko početnih vrijednosti r sve dok je nejednakost zadovoljena
Za dovoljno velike vrijednosti r nejednakost (237) je narušena i količina postaje imaginarna. U tom slučaju odgovarajući članovi općeg rješenja (234) više neće opisivati prigušene oscilacije, već će predstavljati aperiodično prigušeno gibanje. Drugim riječima, vibracije, u uobičajenom smislu riječi, izražavaju se samo određenim konačnim dijelom zbroja (234).
Svi ovi kvalitativni zaključci vrijede ne samo za slučaj uzdužnih vibracija, već i za slučajeve torzijskih i savojnih vibracija.
6.5. Vibracije šipki promjenjivog presjeka
U slučajevima kada su raspodijeljena masa i presjek štapa promjenjivi duž njegove duljine, umjesto jednadžbe uzdužnih vibracija (175), treba poći od jednadžbe
![]() .(238)
.(238)
Jednadžba torzijskih vibracija (187) mora se zamijeniti jednadžbom
![]() ,(239)
,(239)
a jednadžba poprečnih vibracija (192) je jednadžba
 .(240)
.(240)
Jednadžbe (238)-(240) uz pomoć sličnih supstitucija ;;mogu se svesti na obične diferencijalne jednadžbe za funkciju
DEFINICIJA
Uzdužni val– ovo je val, tijekom čijeg širenja se čestice medija pomiču u smjeru širenja vala (slika 1, a).
Uzrok longitudinalnog vala je kompresija/ekstenzija, tj. otpornost medija na promjene njegovog volumena. U tekućinama ili plinovima takva je deformacija popraćena razrjeđivanjem ili zbijanjem čestica medija. Longitudinalni valovi mogu se širiti u svim medijima - krutim, tekućim i plinovitim.
Primjeri longitudinalnih valova su valovi u elastičnom štapu ili zvučni valovi u plinovima.
Transverzalni valovi
DEFINICIJA
Transverzalni val– ovo je val, tijekom čijeg širenja se čestice medija pomiču u smjeru okomitom na širenje vala (slika 1, b).
Uzrok transverzalnog vala je posmična deformacija jednog sloja medija u odnosu na drugi. Kada se transverzalni val širi kroz medij, formiraju se grebeni i udubljenja. Tekućine i plinovi, za razliku od čvrstih tijela, nemaju elastičnost u odnosu na smicanje slojeva, tj. ne opirite se promjeni oblika. Stoga se transverzalni valovi mogu širiti samo u čvrstim tijelima.
Primjeri transverzalnih valova su valovi koji putuju duž rastegnutog užeta ili niti.
Valovi na površini tekućine nisu ni uzdužni ni poprečni. Ako bacite plovak na površinu vode, možete vidjeti da se kreće, njišući se na valovima, u kružnom uzorku. Dakle, val na površini tekućine ima i poprečnu i uzdužnu komponentu. Na površini tekućine mogu se pojaviti i valovi posebne vrste - tzv površinski valovi. Nastaju kao posljedica djelovanja i sile površinske napetosti.
Primjeri rješavanja problema
PRIMJER 1
| Vježbajte | Odredite smjer širenja transverzalnog vala ako plovak u nekom trenutku ima smjer brzine označen na slici. |
| Riješenje | Napravimo crtež. Nacrtajmo površinu vala u blizini plovka nakon određenog vremena, vodeći računa da je za to vrijeme plovak tonuo, budući da je u trenutku bio usmjeren prema dolje. Nastavljajući liniju desno i lijevo, prikazujemo položaj vala u trenutku . Usporedivši položaj vala u početnom trenutku vremena (puna linija) iu trenutku vremena (isprekidana linija), zaključujemo da se val širi ulijevo. |
MEHANIKA
UDK 531.01/534.112
UZDUŽNE VIBRACIJE PAKETA ŠTAPOVA
prije podne Pavlov, A.N. Temnov
MSTU im. N.E. Bauman, Moskva, Ruska Federacija e-mail: [e-mail zaštićen]; [e-mail zaštićen]
U pitanjima dinamike raketa na tekuće gorivo važnu ulogu igra problem stabilnosti gibanja rakete kada se pojave uzdužne elastične oscilacije. Pojava takvih oscilacija može dovesti do uspostavljanja autooscilacija, što, ako je raketa nestabilna u uzdužnom smjeru, može dovesti do njezinog brzog uništenja. Formuliran je problem uzdužnih oscilacija paketne rakete, a kao proračunski model korišten je paket šipki. Prihvaćeno je da je tekućina u spremnicima raketa "zamrznuta", tj. ne uzimaju se u obzir vlastita gibanja tekućine. Formuliran je zakon bilance ukupne energije za razmatrani problem i dana je njegova operatorska formulacija. Dan je numerički primjer za koji su određene frekvencije, te konstruirani i analizirani oblici vlastitih oscilacija.
Ključne riječi: uzdužne vibracije, frekvencija i oblik vibracija, paket štapova, zakon ravnoteže ukupne energije, samopridruženi operator, spektar vibracija, POGO.
SUSTAV ŠIPKI UZDUŽNE VIBRACIJE A.M. Pavlov, AL. Temnov
Moskovsko državno tehničko sveučilište Bauman, Moskva, Ruska Federacija e-pošta: [e-mail zaštićen]; [e-mail zaštićen]
U pitanjima dinamike raketa na tekuće gorivo važnu ulogu ima problem stabilnosti gibanja ove rakete s pojavom uzdužnih elastičnih vibracija. Pojava takve vrste vibracija može izazvati samovibracije koje mogu izazvati brzo uništenje rakete u slučaju nestabilnosti rakete u uzdužnom smjeru. Problem uzdužnih vibracija rakete na tekuće gorivo temeljen na paketnoj shemi formuliran je korištenjem paketnih šipki kao računskog modela. Pretpostavlja se da je tekućina u spremnicima rakete "smrznuta", tj. pravilna gibanja tekućine nisu uključena. Za ovaj problem formuliran je princip očuvanja energije i dan je njegov operatorski stupanj. Postoji numerički primjer za koji su određene frekvencije, izgrađeni i analizirani oblici Eigenovih vibracija.
Ključne riječi: longitudinalne vibracije, svojstveni modovi i frekvencije, štapni model, princip očuvanja energije, samopridruženi operator, spektar vibracija, POGO.
Uvod. Trenutačno se u Rusiji i inozemstvu za lansiranje korisnog tereta u potrebnu orbitu često koriste lansirna vozila paketnog izgleda s identičnim bočnim blokovima ravnomjerno raspoređenim oko središnjeg bloka.
Studije vibracija paketnih struktura nailaze na određene poteškoće povezane s dinamičkim učinkom bočnih i središnjih blokova. U slučaju simetrije rasporeda rakete-nosača, složena, prostorna interakcija blokova konstrukcije paketa može se podijeliti na konačan broj vrsta vibracija, od kojih su jedna uzdužne vibracije središnjeg i bočnih blokova. U radu je detaljno razmotren matematički model uzdužnih vibracija takve strukture u obliku paketa šipki tankih stijenki. Riža. 1. Shema središnjeg- Ovaj članak prikazuje teoretski štap i računske rezultate longitudinalnog
vibracije paketa šipki, nadopunjujući studiju koju je proveo A.A. Šteta.
Formulacija problema. Razmotrimo druge uzdužne vibracije paketa šipki koji se sastoji od središnje šipke duljine l0 i N bočnih šipki iste duljine j = l, (l0 > lj), j = 1, 2,..., N, pričvršćenih u točki A (xA = l) (slika 1) sa središnjim opružnim elementima krutosti k.
Uvedimo fiksni referentni okvir OX i pretpostavimo da su krutost štapova EFj (x), raspodijeljena masa mj (x) i poremećaj q (x,t) ograničene funkcije koordinate x:
0 0 < mj < mj (x) < Mj; (1) 0 Neka tijekom uzdužnih vibracija nastaju pomaci Uj (x, t) u presjecima štapova s koordinatom x, određenim jednadžbama mj (x) ^ - ¿(eFj (x) ^ = qj (x,t), j = 0,1, 2,..., N, (2) rubni uvjeti za nepostojanje normalnih sila na krajevima štapova 3 =0, x = 0, ^ = 1, 2, 0, x = 0, x = l0; uvjeti jednakosti normalnih sila koje nastaju u štapovima, EF-3 = F x = l elastične sile opružnih elemenata FpPJ = k (š (ha) - u (¡,)); (4) EUodX (xa - 0) - EFodX (xa + 0) = , x = xa; uvjet jednakosti pomaka u točki xa središnjeg štapa Shch (ha-o) = Shch (xa+o) i početni uvjeti Shch y (x, 0) - Shch (x); , _ u(x, 0) = u(x), gdje je u(x, 0) = "d^1(x, 0). Zakon ukupne energetske bilance. Pomnožimo jednadžbu (2) s u(x,ξ), integrirajmo po duljini svakog štapa i zbrojimo rezultate koristeći rubne uvjete (3) i uvjet podudaranja (4). Kao rezultat dobivamo (( 1 ^ [ (diL 2 TZ (x) "BT" (x+ dt | 2 ^ J 3 w V dt N x „ h 2 .. N „ i. 1 ^ G „„ , f dp3\ , 1 ^ Gj 1 N /* i dpl 2 1 N fl j EF3 dx +2^Uo I (x - -)(no - Uj)2 dx = / ^ (x, £) njih y (x, £) (x, (6) gdje je 8 (x - ¡y) Diracova delta funkcija. U jednadžbi (6) prvi član u vitičastim zagradama predstavlja kinetičku energiju T (¿) sustava, drugi je potencijalna energija Pr (£), uzrokovana deformacijom šipki, a treći je potencijalna energija Pk (£) opružnih elemenata, koji se u prisutnosti elastičnih deformacija šipki mogu napisati u obliku Pk (*) = 2 £ / Cy (¡y) 8 (x - ¡1) E^ (¡y) (ddit (¡1)) 2 (x, Cy = Eu. Jednadžba (6) pokazuje da je promjena ukupne energije po jedinici vremena mehaničkog sustava koji se razmatra jednaka snazi vanjski utjecaj. U nedostatku vanjskih smetnji q (x,t), dobivamo zakon održanja ukupne energije: T (t) + Pr (t) + Pk (t) = T (0) + Pr (0) + Pk (0). Kinematografija. Zakon ravnoteže energije pokazuje da se za bilo koje vrijeme t funkcije Uj (x, t) mogu smatrati elementima Hilbertovog prostora L2j(; m3 (x)), definiranog na duljini ¡i skalarnim umnoškom (us,Vk)j = J mj (x) usVkdx 0 i odgovarajuću normu. Uvedimo Hilbertov prostor H jednak ortogonalnom zbroju L2j, H = L20 F L21 F... F L2N, vektorsku funkciju U = (uo, Ui,..., uN)t i operator A koji djeluje u prostor H prema relaciji AU = dijagnoza (A00U0, A11U1,..., Annun). mj(x)dx\jdx" operatori definirani na skup B (A33) S N funkcija koje zadovoljavaju uvjete (3) i (4). Izvorni problem (1)-(5) zajedno s početnim uvjetima bit će napisan u obrascu Au = f (*), u (0) = u0, 17(0) = u1, (7) gdje je f (*) = (to (*),51 (*),..., Yam (¿))t. Lema. 1. Ako su prva dva uvjeta (1) zadovoljena, tada je operator A u problemu evolucije (7) neograničen, samo-adjungiran, pozitivno određen operator u prostoru H (Au,K)n = (u,AK)n, (Au, u)i > c2 (i, u)i. 2. Operator A generira energetski prostor NA s normom dvostrukom potencijalnom energijom oscilacija paketa štapića 3\^I h)2 = 2P > 0. (8) IIUIIA = £/ EF^^J dx + k £ (uo - U)2 = 2P > 0. < Оператор А неограничен в пространстве Н, поскольку неограничен каждый диагональный элемент А33. Самосопряженность и положительная определенность оператора А проверяются непосредственно: (AU, v)h =/m (x) (-^| (EFo (x) ^j) Vo (x) dx+ +£ jm(x) (- jx) | (ef- (x) dndxa))v-(x) dx=... = EFo (x) uo (x) vo (x) dx - EFo (x) U) (x) vo (x) J EFo (x) uo (x) vo (x) dx - EFo (x) uo (x) ?o (x) + ^^ / EF- (x) u- (x) vo (x) dx - ^^ EF- (x) u- (x) v- (x) J EFo (x) uo (x) v" (x) dx - EFo (xa - 0) uo (xa - 0) vo (xa) + 0 EFo (xa + 0) uo (xa + 0) vo (xa) - £ EF- (/-) u- (/-) v- (/-) + J EF- (x) u- (x) v- (x) dx = J EFo (x) uo (x) vo (x) dx+ -=100 + £ / EF.,- (x) u- (x) g?- (x) dx+ o O(xa)- £ EF- (/-) u- (/-) v?"- (/-) = EFo (x) uo (x) v?"o (x) dx+ -=10 + £ / EF- (x) u- (x) v- (x) dx+ -=1 0 - + £ k (uo (xa) - u- (/-)) (vo (xa) - v- (/-)) = (U, A?)H (AU, U)H = ... = I EF0 (x) u"2 (x) dx - EF0 (x) u0 (x) u0 (x) J EF0 (x) u"0 (x) dx - EF0 (x) u0 (x) u0 (x) + ^^ / EFj (x) u"2 (x) dx - ^^ EFj (x) uj (x) u3 (x) "J EF°(x) u"2 (x) dx 4EF0 (x) u"2 (x) dx+£ JEFj (x) u"2 (x) dx U^ k (u0 (l) uj (l) - u2 (/)) + u0 (l) ^ k (u0 (l) - uj (l)) = EF0 (x) u"2 (x) dx + / EF0 (x) u"0 (x) dx + S / EFj (x) u"2 (x) dx + k ^ (u0 (l) - uj (l))2 > c2 (U, U)H Iz gornjih rezultata proizlazi da je norma energije operatora A izražena formulom (8). Rješivost evolucijskog problema. Formulirajmo sljedeći teorem. Teorem 1. Neka su uvjeti zadovoljeni U0 £ D (A1/2) , U0 £ H, f (t) £ C (; H), tada problem (7) ima jedinstveno slabo rješenje U (t) na intervalu definiranom formulom U (t) = U0 cos (tA1/2) +U1 sin (tA1/2) +/sin ((t - s) A1/2) A-1/2f (s) ds. 5 u odsutnosti vanjskih smetnji f (£), zakon održanja energije je zadovoljen 1 II A 1/2UI2 = 1 1 II A1/2U 0|H. < Эволюционная задача (7) - это стандартная задача Коши для дифференциального операторного уравнения гиперболического типа, для которого выполнены все условия теоремы о разрешимости . Prirodne vibracije paketa šipki. Pretpostavimo da na sustav štapova ne djeluje polje vanjskih sila: f (t) = 0. U tom slučaju kretanja štapova nazivamo slobodnima. Slobodna gibanja štapova, ovisno o vremenu t prema zakonu exp (iwt), nazvat ćemo prirodnim titrajima. Uzimajući U (x, t) = U (x) eiWÍ u jednadžbi (7), dobivamo spektralni problem za operator A: AU - AEU = 0, L = w2. (9) Svojstva operatora A omogućuju nam da formuliramo teorem o spektru i svojstvima svojstvenih funkcija. Teorem 2. Spektralni problem (9) o prirodnim vibracijama paketa štapova ima diskretni pozitivni spektar 0 < Ai < Л2 < ... < Ak < ..., Ak ^ то i sustav svojstvenih funkcija (Uk (x))^=0, potpun i ortogonalan u prostorima H i HA, te su zadovoljene sljedeće formule ortogonalnosti: (Ufe, Us)H = £ m (xj UfejMSjdx = j=0 0 (Uk= £/T^) d*+ K (“feo - Mfej) (uso -) = Afeífes. j=i Proučavanje spektralnog problema u slučaju homogenog paketa štapića. Prikazujući funkciju pomaka m- (x, £) u obliku m- (x, £) = m- (x), nakon odvajanja varijabli dobivamo spektralne probleme za svaki štap: ^Ou + Lm = 0, ^ = 0,1,2,..., N (10) koju zapisujemo u matričnom obliku 4 £ + Li = 0, A = -,-,-,...,- \ t0 t1 t2 t « u = (u0, u1, u2,..., u«)t. Rješenje i analiza dobivenih rezultata. Označimo funkcije pomaka za središnji štap u presjeku s u01, a na presjeku s u02 (g). U ovom slučaju za funkciju u02 pomičemo ishodište koordinata u točku s koordinatom /. Za svaki štap prikazujemo rješenje jednadžbe (10) u obliku Da bismo pronašli nepoznate konstante u (11), koristimo rubne uvjete formulirane gore. Iz homogenih rubnih uvjeta moguće je odrediti neke konstante, i to: C02 = C12 = C22 = C32 = C42 = ... = CN 2 = 0. Kao rezultat, ostaje pronaći N + 3 konstante: C01, C03, C04, C11, C21, C31, C41,..., CN1. Da bismo to učinili, rješavamo N + 3 jednadžbe za N + 3 nepoznanice. Zapišimo dobiveni sustav u matričnom obliku: (A) (C) = (0) . Ovdje je (C) = (C01, C03, C04, C11, C21, C31, C41,..., Cn 1)t vektor nepoznanica; (A) - karakteristična matrica, cos (A1) EF0 A sin (A1) + L sin (L (Zo - 1)) L cos (L (Zo - 1)) 0 00 0 \ -1 0 0000 0 g. 00 00 0 000 g a = k soe ^ ^A-L^ ; u = -k co8((.40-01L)1/2 ^ ; 7 = (A4"-1 l) 1/2 ap ((A"1l) 1/2 + k sov ((A"1l) 1/2; (~ \ 1/2 ~ L= ^L] ; A--: 3 = 0. Da bismo pronašli netrivijalno rješenje, kao varijablu uzimamo konstantu C01 € M. Imamo dvije mogućnosti: C01 = 0; C01 = 0. Neka je C01 = 0, tada je C03 = C04 = 0. U ovom slučaju može se dobiti netrivijalno rješenje ako je 7 = 0 iz (12) kada je ispunjen dodatni uvjet £ s-1 = 0, (13) koja se može dobiti iz treće jednadžbe sustava (12). Kao rezultat, dobivamo jednostavnu frekvencijsku jednadžbu EP (A"1 L)1/2 W ((A"1^1/2 P + zz \V zz K cos ^ (A-/a) 1/2 ^ = 0, j G , koja se podudara s frekvencijskom jednadžbom za štap elastično fiksiran na jednom kraju, koji se može smatrati prvim parcijalnim sustavom. U ovom slučaju, sve moguće kombinacije kretanja bočnih šipki koje zadovoljavaju uvjet (13) mogu se uvjetno podijeliti u skupine koje odgovaraju različitim kombinacijama faza (u razmatranom slučaju faza je određena znakom C.d). Ako pretpostavimo da su bočne šipke identične, tada imamo dvije mogućnosti: 1) Sd = 0, tada se broj takvih kombinacija n za različite N može izračunati pomoću formule n = N 2, gdje je funkcija dijeljenja bez ostatka; 2) bilo koja (ili bilo koja) od konstanti C- jednaka je 0, tada se broj mogućih kombinacija povećava i može se odrediti formulom £ [(N - m) div 2]. Neka je Coi = 0, tada je Cn = C21 = C31 = C41 = ... = CN1 = = C01 (-v/t), gdje su in i y kompleksi uključeni u (12). Iz sustava (12) također imamo: C03 = C01 cos (A/); C04=C03 tg (L (/0 - /)) = C01 cos (A/) x x tg (L (/0 - /)), tj. sve konstante su izražene kroz C01. Frekvencijska jednadžba ima oblik EFo U-o1 L tg A-1 L) " (lo - l)) - K2 cos | í a!-,1 L Kao primjer, razmotrite sustav s četiri bočne šipke. Uz gore opisanu metodu, za ovaj primjer, možete napisati jednadžbu frekvencije za cijeli sustav izračunavanjem determinante matrice A i izjednačavanjem s nulom. Pogledajmo to Y4 (L sin (L (/o - /)) cos (L/) EFoL+ L cos (L (/o - /)) (EFoL sin (L/) + 4v)) - 4av3L cos (L(/0 - /)) = 0. Grafikoni transcendentalnih frekvencijskih jednadžbi za gore razmatrane slučajeve prikazani su na slici. 2. Kao početni podaci uzeti su: EF = 2,109 N; EF0 = 2,2 109 N; k = 7 107 N/m; m = 5900 kg/m; mo = 6000 kg/m; / = 23; /o = 33 m. Vrijednosti prve tri frekvencije oscilacija razmatranog kruga dane su u nastavku: n.................................. i, drago mi je ............................. 1 2 3 20,08 31,53 63,50 Riža. 2. Grafovi transcendentalnih frekvencijskih jednadžbi za Coi = 0 (i) i Coi = 0 (2) Navedimo modove vibracija koji odgovaraju dobivenim rješenjima (u općem slučaju, modovi vibracija nisu normalizirani). Oblici vibracija koji odgovaraju prvoj, drugoj, trećoj, četvrtoj, 13 i 14 frekvenciji prikazani su na slici. 3. Na prvoj frekvenciji titranja, bočne šipke vibriraju istim oblikom, ali u parovima u protufazi sl.3. Oblici vibracija bočnih (1) i središnjih (2) štapova, koji odgovaraju prvom V = 3,20 Hz (a), drugom V = 5,02 Hz (b), trećem V = 10,11 Hz (c), četvrtom V = 13,60 Hz (d), 13. V = 45,90 Hz (d) i 14. V = 50,88 Hz (f) frekvencije (Sl. 3, a), s drugom, središnja šipka oscilira, a bočne osciliraju u istom obliku u fazi (Sl. 3, b). Treba napomenuti da prva i druga frekvencija vibracija razmatranog štapnog sustava odgovaraju vibracijama sustava koji se sastoji od čvrstih tijela. Kada sustav oscilira s trećom vlastitom frekvencijom, čvorovi se pojavljuju po prvi put (slika 3c). Treća i sljedeće frekvencije (slika 3d) odgovaraju elastičnim vibracijama sustava. S povećanjem frekvencije vibracija, povezanih sa smanjenjem utjecaja elastičnih elemenata, frekvencije i oblici vibracija imaju tendenciju da budu djelomični (slika 3, e, f). Krivulje funkcija čije su sjecišne točke s osi apscisa rješenja transcendentalnih jednadžbi prikazane su na slici. 4. Prema slici vlastite frekvencije oscilacija sustava nalaze se u blizini parcijalnih frekvencija. Kao što je gore navedeno, s povećanjem frekvencije povećava se konvergencija vlastitih frekvencija s parcijalnim. Kao rezultat toga, frekvencije na kojima cijeli sustav oscilira konvencionalno se dijele u dvije skupine: one koje su blizu parcijalnih frekvencija bočnog štapa i frekvencije koje su blizu parcijalnih frekvencija središnjeg štapa. Zaključci. Razmatran je problem uzdužnih vibracija paketa šipki. Opisuju se svojstva postavljenog rubnog problema i spektar njegovih svojstvenih vrijednosti. Predlaže se rješenje spektralnog problema za proizvoljan broj homogenih bočnih štapova. Za numerički primjer, nalaze se vrijednosti prvih frekvencija oscilacija i konstruiraju se odgovarajući oblici. Identificirana su i neka karakteristična svojstva konstruiranih modova vibracija. Riža. 4. Krivulje funkcija čije su sjecišne točke s osi apscisa rješenja transcendentnih jednadžbi, za CoX = 0 (1), Cox = 0 (2) podudaraju se s prvim parcijalnim sustavom (bočna šipka pričvršćena na elastičnu element u točki x = I) i drugi djelomični sustav (5) (središnja šipka pričvršćena na četiri elastična elementa u točki A) KNJIŽEVNOST 1. Kolesnikov K.S. Dinamika raketa. M.: Strojarstvo, 2003. 520 str. 2. Balističke rakete i lansirna vozila / O.M. Alifanov, A.N. Andreev, V.N. Gushchin i dr. M.: Bustard, 2004. 511 str. 3. Rabinovich B.I. Uvod u dinamiku raketa-nosača svemirskih letjelica. M.: Strojarstvo, 1974. 396 str. 4. Studija parametara o POGO stabilnosti tekućih raketa / Z. Zhao, G. Ren, Z. Yu, B. Tang, Q. Zhang // J. of Spacecraft and Rockets. 2011. Vol. 48. Jest. 3. Str. 537-541. 5. Balakirev Yu.G. Metode za analizu uzdužnih vibracija lansirnih vozila na tekući pogon // Cosmonautics and Rocket Science. 1995. br. 5. str. 50-58. 6. Balakirev Yu.G. Značajke matematičkog modela tekuće rakete šaržnog rasporeda kao upravljačkog objekta // Odabrani problemi čvrstoće suvremenog strojarstva. 2008. str. 43-55. 7. Dokuchaev L.V. Poboljšanje metoda za proučavanje dinamike paketnog lansirnog vozila, uzimajući u obzir njihovu simetriju // Kozmonautika i raketna znanost. 2005. br. 2. str. 112-121. 8. Pozhalostin A.A. Razvoj približnih analitičkih metoda za proračun vlastitih i prisilnih vibracija elastičnih ljuski s tekućinom: dis. ... dr. tehn. Sci. M., 2005. 220 str. 9. Ždral S.G. Linearne diferencijalne jednadžbe u Banachovim prostorima. M.: Nauka, 1967. 464 str. 10. Kopachevsky I.D. Operatorske metode matematičke fizike. Simferopol: LLC "Forma", 2008. 140 str. Kolesnikov K.S. Dinamika raketa. Moskva, Mašinostroenie Publ., 2003. 520 str. Alifanov O.N., Andreev A.N., Gushchin V.N., ur. Balisticheskie rakety i rakety-nositeli. Moskva, Drofa Publ., 2003. 511 str. Rabinovich B.I. Vvedenie v dinamiku raket-nositeley kosmicheskikh apparatov. Moskva, Mašinostroenie Publ., 1974. 396 str. Zhao Z., Ren G., Yu Z., Tang B., Zhang Q. Studija parametara POGO stabilnosti rakete na tekuće gorivo. J. Svemirske letjelice i rakete, 2011., sv. 48, br. 3, str. 537-541 (prikaz, ostalo). Balakirev Yu.G. Metode analize uzdužnih vibracija raketa-nosača s motorom na tekuće gorivo. Kozm. i raketostr. , 1995., br. 5, str. 50-58 (na ruskom). Balakirev Yu.G. Osobennosti matematicheskoy modeli zhidkostnoy rakety paketnoy komponovki kak ob"ekta upravlenii. Sb. "Izbrannye problemy prochnosti sovremennogo mashinostroeniya". Moskva, Fizmatlit Publ., 2008. 204 str. (citirano str. 4355). Dokuchaev L.V. Usavršavanje metoda proučavanja dinamike klasteriranih lansirnih vozila s obzirom na njihovu simetriju. Kozm. i raketostr. , 2005., br. 2, str. 112-121 (na ruskom). Pozhalostin A.A. Razrabotka priblizhennykh analiticheskikh metodov rascheta sobstvennykh i vynuzhdennykh kolebaniy uprugikh obolochek s zhidkost"yu. Diss. doct. tekhn. nauk . Kreyn S.G. Lineynye differentsial"nye uravneniya v Banakhovykh prostranstvakh. Moskva, Nauka Publ., 1967. 464 str. Kopachevskiy I.D. Operatornye metody matematicheskoy fiziki. Simferopol", Forma Publ., 2008. 140 str. Članak je u uredništvo zaprimljen 28.04.2014 Pavlov Arsenij Mihajlovič - student Odsjeka za svemirske letjelice i lansirna vozila na Moskovskom državnom tehničkom sveučilištu. N.E. Bauman. Specijalizirao se u području raketne i svemirske tehnologije. MSTU im. N.E. Baumash, Ruska Federacija, 105005, Moskva, 2. Baumanskaja, 5. Pavlov A.M. - student odjela "Svemirske letjelice i lansirna vozila" Moskovskog državnog tehničkog sveučilišta Bauman. Specijalist u području raketno-svemirske tehnologije. Moskovsko državno tehničko sveučilište Bauman, 2-ya Baumanskaya st. 5, Moskva, 105005 Ruska Federacija. Temnov Alexander Nikolaevich - Ph.D. fizike i matematike znanosti, izvanredni profesor Odsjeka za svemirske letjelice i lansirna vozila, Moskovsko državno tehničko sveučilište. N.E. Bauman. Autor više od 20 znanstvenih radova iz područja mehanike fluida i plina te raketne i svemirske tehnike. MSTU im. N.E. Baumash, Ruska Federacija, 105005, Moskva, 2. Baumanskaja, 5. Temnov A.N. - Cand. Sci. (fiz.-matem.), izv. prof. profesor na odjelu "Svemirske letjelice i lansirna vozila" Moskovskog državnog tehničkog sveučilišta Bauman. Autor više od 20 radova iz područja mehanike fluida i plina te raketno-svemirske tehnike. Moskovsko državno tehničko sveučilište Bauman, 2-ya Baumanskaya st. 5, Moskva, 105005 Ruska Federacija.