Remember the orange plastic reflectors that attach to the spokes of a bicycle wheel? Let's attach the reflector to the wheel rim itself and follow its trajectory. The resulting curves belong to the cycloid family. The wheel is called the generating circle (or circle) of the cycloid. But let's go back to our century and switch to more modern technology. On the way of the bike there was a pebble that got stuck in the tire tread.

After turning the wheel a few times, where will the stone fly when it pops out of the tread? Against the direction of the motorcycle or towards it? As is known, the free movement of a body begins tangentially to the trajectory along which it moved. The tangent to the cycloid is always directed in the direction of motion and passes through the top point of the generating circle. Our pebble will fly in the direction of movement. Do you remember how you rode through puddles on a bicycle without a rear wing as a child? A wet stripe on your back is everyday confirmation of the result you have just obtained.

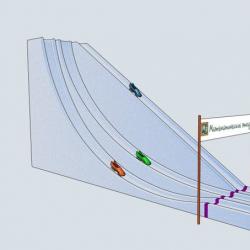
The 17th century is the century of the cycloid. The best scientists have studied its amazing properties. What trajectory will lead a body moving under the influence of gravity from one point to another in the shortest time? This was one of the first problems of the science that is now called the calculus of variations. You can minimize (or maximize) different things - path length, speed, time. In the brachistochrone problem, it is time that is minimized (which is emphasized by the name itself: Greek βράχιστος - smallest, χρόνος - time). The first thing that comes to mind is a straight trajectory. Let's also consider an inverted cycloid with a cusp at the top of the given points. And, following Galileo Galilei, a quarter of a circle connecting our points. Let's make bobsleigh tracks with the considered profiles and see which bob comes first. The history of bobsleigh originates in Switzerland. In 1924, the first Winter Olympic Games were held in the French city of Chamonix. They already host bobsleigh competitions for crews of twos and fours.

The only year when a bobsled crew consisted of five people at the Olympic Games was 1928. Since then, men's crews of two and four have always competed in bobsleigh. There are a lot of interesting things in the rules of bobsleigh. Of course, there are restrictions on the weight of the bob and team, but there are even restrictions on the materials that can be used in the bob skates (the front pair is movable and connected to the handlebars, the back pair is rigidly fixed). For example, radium cannot be used in the manufacture of skates.

Let's give our fours a start. Which bean will be the first to reach the finish line? Green Bob, playing for the Mathematical Studies team and rolling down the cycloidal slide, comes first! Why did Galileo Galilei consider a quarter of a circle and believe that this was the best descent trajectory in terms of time? He entered broken lines into it and noticed that as the number of links increased, the descent time decreased. From here Galileo naturally moved to a circle, but made the incorrect conclusion that this trajectory was the best among all possible ones. As we have seen, the best trajectory is a cycloid. Through these two points a unique cycloid can be drawn with the condition that the cusp of the cycloid is at the top point. And even when the cycloid has to rise to pass through the second point, it will still be the curve of steepest descent! Another beautiful problem related to the cycloid is the tautochrone problem. Translated from Greek, ταύτίς means “the same”, χρόνος, as we already know - “time”. Let's make three identical slides with a profile in the form of a cycloid, so that the ends of the slides coincide and are located at the top of the cycloid. Let's put three beans at different heights and give the go-ahead.

The most amazing fact is that all the beans will come down at the same time! In winter, you can build an ice slide in your yard and test this property in person. The tautochrone problem is to find a curve such that, starting from any initial position, the time of descent to a given point will be the same. Christiaan Huygens proved that the only tautochrone is the cycloid. Of course, Huygens was not interested in going down the ice slides. At that time, scientists did not have the luxury of pursuing science for the love of art. The problems that were studied were based on the life and demands of technology of that time. In the 17th century, long sea voyages were already taking place. The sailors were already able to determine latitude quite accurately, but it is surprising that they were not able to determine longitude at all. And one of the proposed methods for measuring latitude was based on the availability of precise chronometers. The first person to think of making pendulum clocks that were accurate was Galileo Galilei. However, at the moment when he begins to implement them, he is already old, he is blind, and in the remaining year of his life the scientist does not have time to make a clock. He bequeaths this to his son, but he hesitates and begins to work on the pendulum only before his death and does not have time to realize the plan.

The next iconic figure was Christiaan Huygens. He noticed that the period of oscillation of an ordinary pendulum, considered by Galileo, depends on the initial position, i.e. from amplitude. Thinking about what the trajectory of the load should be so that the time of rolling along it does not depend on the amplitude, he solves the tautochrone problem. But how to make a load move along a cycloid? Translating theoretical research into a practical plane, Huygens makes “cheeks” on which the pendulum rope is wound, and solves several more mathematical problems. He proves that the “cheeks” must have the profile of the same cycloid, thereby showing that the evolute of a cycloid is a cycloid with the same parameters. In addition, the design of a cycloidal pendulum proposed by Huygens makes it possible to calculate the length of the cycloid. If a blue thread, the length of which is equal to four radii of the generating circle, is deflected as much as possible, then its end will be at the point of intersection of the “cheek” and the cycloid-trajectory, i.e. at the apex of the cycloid - “cheeks”. Since this is half the length of the cycloid arc, the total length is equal to eight radii of the generating circle. Christiaan Huygens made a cycloidal pendulum, and clocks with it were tested on sea voyages, but did not take root. However, the same as a clock with a regular pendulum for these purposes. Why, however, do clock mechanisms with an ordinary pendulum still exist? If you look closely, with small deviations, like the red pendulum, the “cheeks” of the cycloidal pendulum have almost no effect. Accordingly, the movement along the cycloid and along the circle for small deviations almost coincide.

Literature:
G. N. Berman. Cycloid. M.: Nauka, 1980.
S. G. Gindikin. Stories about physicists and mathematicians. M.: MTsNMO, 2006.

Comments: 1

Vladimir Zakharov

Lecture by Academician of the Russian Academy of Sciences, Doctor of Physical and Mathematical Sciences, Chairman of the Scientific Council of the Russian Academy of Sciences on Nonlinear Dynamics, Head. Department of Mathematical Physics at the Physical Institute of the Russian Academy of Sciences. Lebedev, professor at the University of Arizona (USA), twice winner of the State Prize, winner of the Dirac medal by Vladimir Evgenievich Zakharov, given on May 27, 2010 at the Polytechnic Museum as part of the project “Public Lectures to Polit.ru”.

Sergey Kuksin

International scientific conference “Days of classical mechanics” Moscow, Steklov Mathematical Institute, st. Gubkina, 8 January 26, 2015

Chaos is a mathematical film consisting of nine chapters, each thirteen minutes long. This is a film for the general public, dedicated to dynamical systems, the butterfly effect and chaos theory.

Alexandra Skripchenko

Mathematician Alexandra Skripchenko about billiards as a dynamic system, rational angles and Poincaré's theorem.

Yuliy Ilyashenko

The Kolmogorov–Arnold–Moser theory answers questions like “Can planets fall into the Sun? If yes, then with what probability? And after how long?” Mathematical formulation of the problem: suppose that the masses are so small that their attraction to each other can be neglected. Then the trajectories of the planets can be calculated; Newton did this. If we move on to the real case, when the mutual attraction of the planets affects their orbits, we get a small perturbation of the integrable, i.e. exactly solvable system. Poincaré considered the study of small perturbations of integrable systems of classical mechanics to be the main task of the theory of differential equations. The lectures will tell, at a level accessible to older schoolchildren, about the main ideas of the KAM theory. We will not go up to the n-body problem and classical mechanics, but we will discuss diffeomorphisms of the circle and the basic step of the induction process proposed by Kolmogorov for problems of celestial mechanics.

Olga Romaskevich

If you act very cruelly and take away a mathematician’s pencil and paper, he will look to the sky in search of new problems. The question of planetary motion (in the mathematical world codenamed the "n-body problem") is extremely complex - so complex that even for special subcases of the n=3 case, a huge number of papers are published every year. It is impossible to analyze all aspects of this problem even in a semester course. We, however, will not be afraid, and will try to play with the mathematics that arises here. The main motivation for us will be the two-body problem: the problem of the motion of one planet around the Sun under the assumption that there seem to be no other planets in the vicinity.

Dmitry Anosov

The book talks about differential equations. In some cases, the author explains how differential equations are solved, and in others, how geometric considerations help to understand the properties of their solutions. (The words “we solve, then we draw” in the title of the book are connected with this.) Several physical examples are considered. At the most simplified level, some achievements of the 20th century are described, including an understanding of the mechanism of the emergence of “chaos” in the behavior of deterministic objects. The book is intended for high school students interested in mathematics. All they need to do is understand the meaning of the derivative as instantaneous speed.

Alexey Belov

There is a well-known Olympiad problem: There are coins (convex figures) on a flat table. Then one of them can be pulled off the table without affecting the others. For a long time, mathematicians tried to prove the spatial analogue of this statement, until a counterexample was constructed! An idea arose: in small grains there is often no crack, the crack does not grow beyond the grain boundary, and the cracks hold each other. This idea theoretically makes it possible to create composites in which cracks do not grow, in particular, ceramic armor.

Alexey Sosinsky

One of the most important concepts of mechanics and theoretical physics - the concept of configuration space of a mechanical system - for some reason remains unknown not only to schoolchildren, but also to most mathematics students. The lecture discusses a very simple, but very meaningful class of mechanical systems - flat hinged mechanisms with two degrees of freedom. We will discover that in the “general case” their configuration spaces are two-dimensional surfaces, and we will try to understand which ones they are. (Here are the final results from ten years ago by Dima Zvonkin.) Next, unsolved mathematical problems associated with hinge mechanisms are discussed. (Including two hypotheses, or rather unproven theorems, of the American mathematician Bill Thurston.)

Vladimir Protasov

Calculus of variations is the science of finding the minimum of a function in an infinite-dimensional space. Unlike the minimum problems we are used to, when we need to optimally choose a number (parameter), or, say, a point on a plane, in variational problems we need to find the optimal function. At the same time, problems of very different origins are solved using the same set of tools: from classical mechanics, geometry, mathematical economics, etc. We will start with old problems, known since the 17th century, and, building bridges from one problem to another, we will quickly get to modern results and unsolved problems.

(translated from Greek. circular) – a flat transcendental curve, which is described by a point on a circle of radius r rolling along a straight line without sliding (a transcendental curve is a curve that cannot be described by an algebraic equation in rectangular coordinates). Its parametric equation

x = rt – r sin t,
y= r – r cos t

The points of intersection of the cycloid with the straight line along which the circle rolls (this circle is called the generating circle, and the straight line along which it rolls is called the directive) are called cusp points, and the highest points on the cycloid, located in the middle between adjacent cusp points, are called the vertices of the cycloid.

Galileo Galilei was the first to study the cycloid. The length of one cycloid arch was determined in 1658 by the English architect and mathematician Christopher Wren, the author of the design and builder of the dome of St. Paul's Cathedral in London. It turned out that the length of the cycloid is equal to 8 radii of the generating circle.
One of the remarkable properties of the cycloid, which gave it its name - brachistochrone (from the Greek words “shortest” and “time”) is associated with solving the problem of steepest descent. The question arose of what shape should be given to a well-polished (to virtually eliminate friction) groove connecting two points so that the ball would roll down from one point to another in the shortest possible time. The Bernoulli brothers proved that the trench should have the shape of a downward cycloid.

Curves related to the cycloid can be obtained by considering the trajectories of points not located on the generating circle.

Let the point From 0 is inside the circle. If carried through From 0 auxiliary circle with the same center as the generating circle, then when the generating circle rolls along a straight line AB a small circle will roll in a straight line A´ IN´, but its rolling will be accompanied by sliding, and period From 0 describes a curve called a shortened cycloid.

An elongated cycloid is defined in a similar way - this is the trajectory of a point located on an extension of the radius of the generating circle, while rolling is accompanied by sliding in the opposite direction.

Cycloidal curves are used in many technical calculations and their properties are used, for example, in constructing gear tooth profiles, in cycloidal pendulums, in optics and, thus, the study of these curves is important from an applied point of view. It is equally important that, studying these curves and their properties, scientists of the 17th century. developed techniques that led to the creation of differential and integral calculus, and the brachistochrone problem was a step towards the invention of the calculus of variations.

Elena Malishevskaya

LEMNICATES
Equation in polar coordinates:
r 2 = a 2 cos2θ

(x 2 + y 2) 2 = a 2 (x 2 - y 2)

Angle between AB" or A"B and x-axis = 45 o

Area of ​​one loop = a 2 /2

CYCLOID

Area of ​​one arc = 3πa 2

Arc length of one arch = 8a

This is a curve described by a point P on a circle of radius a, which rolls along the x axis.

HYPOCYCLOIDS WITH FOUR SPOKES
Equation in rectangular coordinates:
x 2/3 + y 2/3 = a 2/3

Equations in parametric form:

Area enclosed by curve = 3πa 2 /8

Arc length of the whole curve = 6a

This is a curve described by a point P on a circle of radius a/4, which rolls inside a circle of radius a.

CARDIOID
Equation: r = a(1 + cosθ)

Area enclosed by curve = 3πa 2 /2

Curve arc length = 8a

It is a curve described by a point P on a circle of radius a, which rolls outside the circle of radius a. This curve is also a special case of Pascal's snail.

CHAIN ​​LINE
The equation:
y = a(e x/a + e -x/a)/2 = acosh(x/a)

This is the curve along which a chain would hang when suspended vertically from point A to B.

THREE PETAL ROSE
Equation: r = acos3θ

The equation r = acos3θ is similar to the curve obtained by rotating counterclockwise along a curve of 30 o or π/6 radians.

In general, r = acosnθ or r = asinnθ has n lobes if n is odd.

FOUR PETALE ROSE
Equation: r = acos2θ

The equation r = asin2θ is similar to the curve obtained by rotating counterclockwise along a 45 o or π/4 radian curve.

In general, r = acosnθ or r = asinnθ has 2n petals if n is even.

EPICYCLOID
Parametric equations:

It is the curve described by point P on a circle of radius b as it rolls along the outside of the circle of radius a. Cardioid is a special case of epicycloid.

GENERAL HYPOCYCLOID
Parametric equations:

It is the curve described by point P on a circle of radius b as it rolls along the outside of the circle of radius a.

If b = a/4, the curve is a hypocycloid with four points.

TROCHOID
Parametric equations:

This is the curve described by point P at a distance b from the center of a circle of radius a as it rolls along the x axis.
If b is a shortened cycloid.
If b > a, the curve has the shape shown in Fig. 11-11 and is called walker.
If b = a, the curve is a cycloid.

TRAKTRICE
Parametric equations:

It is the curve described by the end point P of a stretched string of length PQ when the other end Q is moved along the x axis.

VERZIERA (VERZIERA) AGNEZI (SOMETIMES CURL AGNEZI)
Equation in rectangular coordinates: y = 8a 3 /(x 2 + 4a 2)

Parametric equations:

B. In the figure, the variable line OA intersects y = 2a and a circle with radius a with center (0,a) at A and B, respectively. Any point P on the "curl" is determined by constructing lines parallel to the x and y axes, through B and A respectively, and defining the intersection point of P.

DESCARTES LEAF
Equation in rectangular coordinates:
x 3 + y 3 = 3axy

Parametric equations:

Loop area 3a 2 /2

Asymptote equation: x + y + a = 0.

CIRCLE INVOLVENT
Parametric equations:

This is the curve described by the end point P of the string as it unwinds from a circle of radius a.

ELLIPSE INVOLVENT
Equation in rectangular coordinates:
(ax) 2/3 + (by) 2/3 = (a 2 - b 2) 2/3

Parametric equations:

This curve is the envelope normal to the ellipse x 2 /a 2 + y 2 /b 2 = 1.

CASSINI OVALS
Polar equation: r 4 + a 4 - 2a 2 r 2 cos2θ = b 4.

It is a curve described by a point P such that the product of its distance from two fixed points [distance 2a to the side] is a constant b 2 .

Curve as in the figures below when b a respectively.

If b = a, the curve is lemniscate

PASCAL'S SNAIL
Polar equation: r = b + acosθ

Let OQ be the line connecting the center of O with any point Q on a circle of diameter a passing through O. Then the curve is the focus of all points P such that PQ = b.

The curve shown in the figures below when b > a or b

CISSOID OF DIOCLES
Equation in rectangular coordinates: y 2 = x 3 /(2a - x)

Parametric equations:

This is a curve described by a point P such that distance OP = distance RS. Used in the task doubling the cube, i.e. finding the side of a cube that has twice the volume of a given cube

ARCHIMEDES' SPIRAL
Polar equation: r = aθ

5. Parametric cycloid equation and equation in Cartesian coordinates

Let us assume that we are given a cycloid formed by a circle of radius a with a center at point A.

If we choose as a parameter that determines the position of the point the angle t=∟NDM through which the radius, which had a vertical position AO at the beginning of rolling, managed to rotate, then the x and y coordinates of point M will be expressed as follows:

x= OF = ON - NF = NM - MG = at-a sin t,

y= FM = NG = ND – GD = a – a cos t

So the parametric equations of the cycloid have the form:

When t changes from -∞ to +∞, a curve will be obtained, consisting of an infinite number of branches such as those shown in this figure.

Also, in addition to the parametric equation of the cycloid, there is also its equation in Cartesian coordinates:

Where r is the radius of the circle forming the cycloid.

6. Problems on finding parts of a cycloid and figures formed by a cycloid

Task No. 1. Find the area of ​​a figure bounded by one arc of a cycloid whose equation is given parametrically

and the Ox axis.

Solution. To solve this problem, we will use the facts we know from the theory of integrals, namely:

Area of ​​a curved sector.

Consider some function r = r(ϕ) defined on [α, β].

ϕ 0 ∈ [α, β] corresponds to r 0 = r(ϕ 0) and, therefore, the point M 0 (ϕ 0 , r 0), where ϕ 0,

r 0 - polar coordinates of the point. If ϕ changes, “running through” the entire [α, β], then the variable point M will describe some curve AB, given

equation r = r(ϕ).

Definition 7.4. A curvilinear sector is a figure bounded by two rays ϕ = α, ϕ = β and a curve AB defined in polar

coordinates by the equation r = r(ϕ), α ≤ ϕ ≤ β.

The following is true

Theorem. If the function r(ϕ) > 0 and is continuous on [α, β], then the area

curvilinear sector is calculated by the formula:

This theorem was proven earlier in the topic of definite integral.

Based on the above theorem, our problem of finding the area of ​​a figure limited by one arc of a cycloid, the equation of which is given by the parametric parameters x= a (t – sin t), y= a (1 – cos t), and the Ox axis, is reduced to the following solution .

Solution. From the curve equation dx = a(1−cos t) dt. The first arc of the cycloid corresponds to a change in the parameter t from 0 to 2π. Hence,

Task No. 2. Find the length of one arc of the cycloid

The following theorem and its corollary were also studied in integral calculus.

Theorem. If the curve AB is given by the equation y = f(x), where f(x) and f ’ (x) are continuous on , then AB is rectifiable and

Consequence. Let AB be given parametrically

L AB = (1)

Let the functions x(t), y(t) be continuously differentiable on [α, β]. Then

formula (1) can be written as follows

Let’s make a change of variables in this integral x = x(t), then y’(x)= ;

dx= x’(t)dt and therefore:

Now let's get back to solving our problem.

Solution. We have, and therefore

Task No. 3. We need to find the surface area S formed from the rotation of one arc of the cycloid

L=((x,y): x=a(t – sin t), y=a(1 – cost), 0≤ t ≤ 2π)

In integral calculus, there is the following formula for finding the surface area of ​​a body of revolution around the x-axis of a curve defined parametrically on a segment: x=φ(t), y=ψ(t) (t 0 ≤t ≤t 1)

Applying this formula to our cycloid equation we get:

Task No. 4. Find the volume of the body obtained by rotating the cycloid arch

Along the Ox axis.

In integral calculus, when studying volumes, there is the following remark:

If the curve bounding a curvilinear trapezoid is given by parametric equations and the functions in these equations satisfy the conditions of the theorem on the change of variable in a certain integral, then the volume of the body of revolution of the trapezoid around the Ox axis will be calculated by the formula

Let's use this formula to find the volume we need.

The problem is solved.

Conclusion

So, in the course of this work, the basic properties of the cycloid were clarified. We also learned how to build a cycloid and found out the geometric meaning of a cycloid. As it turned out, the cycloid has enormous practical applications not only in mathematics, but also in technological calculations and physics. But the cycloid has other merits. It was used by scientists of the 17th century when developing techniques for studying curved lines - those techniques that ultimately led to the invention of differential and integral calculus. It was also one of the “touchstones” on which Newton, Leibniz and their early researchers tested the power of powerful new mathematical methods. Finally, the problem of the brachistochrone led to the invention of the calculus of variations, which is so necessary for physicists of today. Thus, the cycloid turned out to be inextricably linked with one of the most interesting periods in the history of mathematics.

Literature

1. Berman G.N. Cycloid. – M., 1980

2. Verov S.G. Brachistochrone, or another secret of the cycloid // Quantum. – 1975. - No. 5

3. Verov S.G. Secrets of the cycloid // Quantum. – 1975. - No. 8.

4. Gavrilova R.M., Govorukhina A.A., Kartasheva L.V., Kostetskaya G.S., Radchenko T.N. Applications of a definite integral. Methodological instructions and individual assignments for 1st year students of the Faculty of Physics. - Rostov n/a: UPL RSU, 1994.

5. Gindikin S.G. The stellar age of the cycloid // Quantum. – 1985. - No. 6.

6. Fikhtengolts G.M. Course of differential and integral calculus. T.1. – M., 1969

This line is called the “envelope”. Every curved line is an envelope of its tangents.

Matter and motion, and the method that they constitute, enable everyone to realize their potential in the knowledge of truth. Developing a methodology for the development of a dialectical-materialistic form of thinking and mastering a similar method of cognition is the second step towards solving the problem of development and realization of Human capabilities. Fragment XX Opportunities...

In this situation, people can develop neurasthenia - a neurosis, the basis of the clinical picture of which is an asthenic state. Both in the case of neurasthenia and in the case of decompensation of neurasthenic psychopathy, the essence of mental (psychological) defense is reflected in the withdrawal from difficulties into irritable weakness with vegetative dysfunctions: either the person unconsciously “fights off” the attack more...

Various types of activities; development of spatial imagination and spatial concepts, figurative, spatial, logical, abstract thinking of schoolchildren; developing the ability to apply geometric and graphic knowledge and skills to solve various applied problems; familiarization with the content and sequence of stages of project activities in the field of technical and...

Arcs. Spirals are also involutes of closed curves, for example the involute of a circle. The names of some spirals are given by the similarity of their polar equations with the equations of curves in Cartesian coordinates, for example: · parabolic spiral (a - r)2 = bj, · hyperbolic spiral: r = a/j. · Rod: r2 = a/j · si-ci-spiral, the parametric equations of which have the form: , )