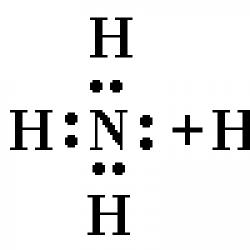Let a body of weight P move under the action of force T along a rough surface. On the one hand, the surface does not allow the body to fall down under the influence of gravity P. On the other hand, the surface prevents the free movement of the body under the influence of force T. Thus, the friction force F also , like a normal reaction, is brought to life by the surface, i.e. the friction force is also a reaction. The normal reaction and the friction force add up to the total reaction R, which is deviated from the normal by an angle c. This angle is called the friction angle. Using Fig. It is easy to calculate what the tangent of the friction angle is equal to tgts=F/N=µN/N=µ, i.e. the tangent of the friction angle is numerically equal to the friction coefficient.

Now imagine that you rotate the total reaction around the surface normal. In this case, the force R describes a cone, which is called the cone of friction. It is interesting in that the area limited by the friction cone determines the equilibrium region for the body: if a force acts on the body inside the friction cone, it will not move the body, no matter how great it is; if a force acts on a body outside the friction cone, it moves the body, no matter how small it is (Fig. 19).

Rice. 19.

Let's see why this happens (Fig. 20).

Rice. 20.

If the force Q acts inside the friction cone, then the shear force Q 1 = Qsinb. Let's calculate the friction force:

F=µN=µQcosб=Qcosбtgс.

Safety factor F-Q 1 =Q(cosb tgts-sin b) = Qsin(ts-b)/costs. Thus, the safety margin is proportional to Q, since sin(c-b)/cosс is a constant value. The greater the force Q, the greater the holding force F-Q 1.

This is why you need to be able to build a friction cone.

Once a bridge collapsed in Munich, and the fault was not a hurricane wind, not a regiment of soldiers marching in step, but... a friction cone.

This bridge was secured at one end with a hinge, and at the other end it was placed on rollers (Fig. 21). The bridge is always secured in such a way that it does not become warped due to temperature fluctuations. The hinge was filled with paste, which protected it from corrosion. On a hot summer day, the paste melted and its viscosity became less. The nature of friction has changed - it has also decreased. The friction cone narrowed, and the pressure force on the support went beyond the cone.

Rice. 21.

The balance was broken and the bridge collapsed. Engineers often have to construct a cone of friction to determine whether a given structure will be in equilibrium or not. But engineers are not the only ones who deal with the friction cone. Each of us encounters this physical phenomenon every day.

To get to the exit on a crowded bus or trolleybus, you have to squirm like a snake. We do this unconsciously, without thinking that in this way we get out of the friction cones at the points of contact with other passengers.

Whether we are skating, going to work, or turning a page in a book, everywhere we encounter friction and, in particular, the cone of friction.

Lecture 3. Calculation of trusses. Sliding and rolling friction.

This lecture covers the following issues

1. Calculation of trusses.

2. The concept of a farm.

3. Analytical calculation of flat trusses.

4. Graphic calculation of flat trusses.

5. Friction.

6. Laws of sliding friction.

7. Reactions of rough bonds.

8. Friction angle.

9. Equilibrium in the presence of friction.

10. Rolling and spinning friction.

11. The moment of force relative to the center as a vector.

12. Moment of a couple of forces as a vector.

13. Moment of force about the axis.

14. The relationship between the moments of force relative to the center and relative to the axis.

15. Bringing the spatial system of forces to a given center.

16. Conditions for equilibrium of an arbitrary spatial system of forces.

17. Problems on body balance under the influence of a spatial system of forces.

The study of these issues is necessary in the future to study the dynamics of the movement of bodies taking into account sliding and rolling friction, the dynamics of the movement of the center of mass of a mechanical system, kinetic moments, to solve problems in the discipline “Strength of Materials”.

Calculation of farms. Farm concept. Analytical calculation of flat trusses.

Fermoy called a rigid structure of straight rods connected at the ends by hinges. If all the bars of a truss lie in the same plane, the truss is called flat. The connection points of the truss rods are called nodes. All external loads on the truss are applied only at the nodes. When calculating a truss, friction at the nodes and the weight of the rods (compared to external loads) are neglected or the weights of the rods are distributed among the nodes. Then each of the truss rods will be acted upon by two forces applied to its ends, which, in equilibrium, can only be directed along the rod. Therefore, we can assume that the truss rods work only in tension or compression. We will limit ourselves to considering rigid flat trusses, without extra rods formed from triangles. In such trusses, the number of rods k and the number of nodes n are related by the relation

The calculation of a truss comes down to determining the support reactions and forces in its rods.

Support reactions can be found using conventional statics methods, considering the truss as a whole as a rigid body. Let's move on to determining the forces in the rods.

Knot cutting method. This method is convenient to use when you need to find the forces in all the rods of the truss. It comes down to a sequential consideration of the conditions of equilibrium of forces converging at each of the nodes of the truss. We will explain the calculation process using a specific example.

Fig.23

Let's consider the one shown in Fig. 23,a a truss formed from identical isosceles right triangles; forces acting on the truss are parallel to the axis X and are equal: F 1 = F 2 = F 3 = F = 2.

The number of nodes in this farm is n= 6, and the number of rods k= 9. Consequently, the relation is satisfied and the truss is rigid, without extra rods.

Compiling the equilibrium equations for the farm as a whole, we find that the reactions of the supports are directed as shown in the figure and are numerically equal;

Let's move on to determining the forces in the rods.

Let's number the truss nodes with Roman numerals, and the rods with Arabic numerals. We will denote the required efforts S 1 (in rod 1), S 2 (in rod 2), etc. Let us mentally cut off all the nodes together with the rods converging in them from the rest of the truss. We will replace the action of the discarded parts of the rods with forces that will be directed along the corresponding rods and are numerically equal to the required forces S 1 , S 2, ... We depict all these forces at once in the figure, directing them from the nodes, i.e., considering all the rods to be stretched (Fig. 23, a; the picture shown should be imagined for each node as shown in Fig. 23, b for node III). If, as a result of the calculation, the magnitude of the force in any rod turns out to be negative, this will mean that this rod is not stretched, but compressed. There are no letter designations for the forces acting along the rods in Fig. 23 not inputs, since it is clear that the forces acting along rod 1 are numerically equal S 1, along the rod 2 - equal S 2, etc.

Now for the forces converging at each node, we compose sequentially the equilibrium equations

We start from node 1, where two rods meet, since only two unknown forces can be determined from the two equilibrium equations.

Compiling the equilibrium equations for node 1, we obtain

F 1 +S 2 cos45 0 =0, N+S 1 +S 2 sin45 0 =0.

From here we find

Now knowing S 1, go to node II. For it the equilibrium equations give

S 3 +F 2 =0, S 4 -S 1 =0,

S 3 =-F=-2H, S 4 =S 1 =-1H.

Having determined S 4, we compose in a similar way the equilibrium equations, first for node III, and then for node IV. From these equations we find:

Finally, to calculate S 9 we compose an equilibrium equation for the forces converging at node V, projecting them onto the By axis. We get Y A +S 9 cos45 0 =0 from where

The second equilibrium equation for node V and two equations for node VI can be compiled as verification equations. To find the forces in the rods, these equations were not needed, since instead of them, three equilibrium equations for the entire truss as a whole were used to determine N, X A, and Y A.

The final calculation results can be summarized in a table:

As the signs of effort show, rod 5 is stretched, the remaining rods are compressed; rod 7 is not loaded (zero rod).

The presence of zero rods in the truss, similar to rod 7, is immediately detected, since if three rods converge in a node not loaded by external forces, two of which are directed along the same straight line, then the force in the third rod is zero. This result is obtained from the equilibrium equation in projection onto the axis perpendicular to the two rods mentioned.

If during the calculation you encounter a node for which the number of unknowns is more than two, then you can use the section method.

Method of sections (Ritter method). This method is convenient to use to determine the forces in individual truss rods, in particular, for verification calculations. The idea of ​​the method is that the truss is divided into two parts with a section passing through three rods in which (or in one of which) the force is required to be determined, and the equilibrium of one of these parts is considered. The action of the discarded part is replaced by corresponding forces, directing them along the cut rods from the nodes, i.e., considering the rods to be stretched (as in the method of cutting nodes). Then the equilibrium equations are constructed, taking the centers of the moments (or the axis of projections) so that each equation includes only one unknown force.

Graphic calculation of flat trusses.

Calculation of a truss by cutting out nodes can be done graphically. To do this, first determine the support reactions. Then, sequentially cutting off each of its nodes from the truss, they find the forces in the rods converging at these nodes, constructing the corresponding closed force polygons. All constructions are carried out on a scale that must be selected in advance. The calculation begins with the node at which two rods meet (otherwise it will not be possible to determine the unknown forces).

Fig.24

As an example, consider the farm shown in Fig. 24, a. The number of nodes in this farm is n= 6, and the number of rods k= 9. Consequently, the relation is satisfied and the truss is rigid, without extra rods. The support reactions and for the truss under consideration are depicted along with the forces and as known.

We begin determining the forces in the rods by considering the rods converging at node I (we number the nodes with Roman numerals, and the rods with Arabic numerals). Having mentally cut off the rest of the truss from these rods, we discard its action and mentally replace the discarded part with forces and , which should be directed along rods 1 and 2. From the forces converging at node I, we build a closed triangle (Fig. 24, b). To do this, we first depict a known force on a selected scale, and then draw straight lines through its beginning and end, parallel to rods 1 and 2. In this way, the forces and acting on rods 1 and 2 will be found. Then we consider the equilibrium of the rods converging at node II. We mentally replace the action on these rods of the discarded part of the truss with the forces , , and , directed along the corresponding rods; Moreover, the force is known to us, since by the equality of action and reaction. By constructing a closed triangle from the forces converging at node II (starting with the force ), we find the values ​​S 3 and S 4 (in this case S 4 = 0). The forces in the remaining rods are found similarly. The corresponding force polygons for all nodes are shown in Fig. 24, b. The last polygon (for node VI) is constructed for verification, since all the forces included in it have already been found.

From the constructed polygons, knowing the scale, we find the magnitude of all efforts. The sign of the force in each rod is determined as follows. Having mentally cut out a node along the rods converging in it (for example, node III), we apply the found forces to the edges of the rods (Fig. 25); the force directed from the node (in Fig. 25) stretches the rod, and the force directed towards the node (and in Fig. 25) compresses it.

Fig.25

According to the accepted condition, we assign the sign “+” to tensile forces, and the sign “-” to compressive forces. In the example considered (Fig. 25), rods 1, 2, 3, 6, 7, 9 are compressed, and rods 5, 8 are stretched.

Friction.

Why does a violin string sound when a bow is played across it? After all, the bow moves, and the string vibrations are periodic. How does a car accelerate, and what force slows it down when braking? Why does a car skid on a slippery road? The answers to all these and many other important questions related to the movement of bodies are provided by the laws of friction.

You see how friction manifests itself in various and sometimes unexpected ways in the environment around us. Friction takes part, and a very significant one at that, where we don’t even suspect it. If friction suddenly disappeared from the world, many ordinary phenomena would proceed in a completely different way.

The French physicist Guillaume writes very colorfully about the role of friction:

“We’ve all had to go out in icy conditions; how much effort it took us to keep ourselves from falling, how many funny movements we had to do in order to stand! This forces us to recognize that usually the ground we walk on has a precious quality that allows us to maintain our balance without much effort. The same thought occurs to us when we ride a bicycle on a slippery pavement or when a horse slips on the asphalt and falls. By studying such phenomena, we come to the discovery of the consequences that friction leads to. Engineers strive to eliminate it in cars as much as possible - and do a good job. In applied mechanics, friction is spoken of as an extremely undesirable phenomenon, and this is correct, but only in a narrow, specialized area. In all other cases, we should be grateful to friction: it gives us the opportunity to walk, sit and work without fear that books and inkwell will fall to the floor, that the table will slide until it hits a corner, and the pen will slip out of our fingers.

Friction is such a common phenomenon that, with rare exceptions, we do not have to call on it for help: it comes to us on its own.

Friction promotes stability. Carpenters level the floor so that the tables and chairs remain where they were placed. Saucers, plates, glasses placed on the table remain motionless without any special worries on our part, unless it happens on a steamboat during rocking.

Let us imagine that friction can be completely eliminated. Then no bodies, be they the size of a block of stone or small as grains of sand, will ever be able to rest on one another: everything will slide and roll until it ends up on the same level. If there were no friction, the Earth would be a sphere without irregularities, like a liquid.”

To this we can add that in the absence of friction, nails and screws would slip out of the walls, not a single thing could be held in the hands, no whirlwind would ever stop, no sound would cease, but would echo endlessly, reverberating incessantly, for example , from the walls of the room.

An object lesson that convinces us of the enormous importance of friction is given to us every time by black ice. Caught by her on the street, we find ourselves helpless and always at risk of falling. Here is an instructive excerpt from the newspaper (December 1927):

“London 21. Due to heavy ice, street and tram traffic in London is very difficult. About 1,400 people were admitted to hospitals with broken arms, legs, etc.”

“In a collision near Hyde Park, three cars and two tram cars were destroyed by a gasoline explosion...”

"Paris 21. Ice in Paris and its suburbs caused numerous accidents..."

However, the negligible friction on ice can be successfully exploited technically. Already ordinary sleds serve as an example of this. This is even better evidenced by the so-called ice roads, which were arranged for transporting timber from the cutting site to the railway or to rafting points. On such a road, which has smooth ice rails, two horses pull a sleigh loaded with 70 tons of logs.

Rest friction, sliding friction.

Previously, it was thought that the mechanism of friction was not complicated: the surface was covered with irregularities and friction was the result of the lifting of the sliding parts on these irregularities; but this is wrong, because then there would be no loss of energy, but in fact energy is wasted on friction.

The mechanism of losses is different. And here it turns out to be extremely unexpected that empirically this friction can be approximately described by a simple law. The force required to overcome friction and drag one object along the surface of another depends on the force directed normal to the contact surfaces.

The surface of a solid body usually has irregularities. For example, even with very well polished metals, “mountains” and “valleys” measuring 100-1000A in size are visible under an electron microscope. When bodies are compressed, contact occurs only in the highest places and the area of ​​actual contact is significantly less than the total area of ​​the contacting surfaces. The pressure at the contact points can be very high, and plastic deformation occurs there. In this case, the contact area increases and the pressure drops. This continues until the pressure reaches a certain value at which the deformation stops. Therefore, the actual contact area turns out to be proportional to the compressive force.

At the point of contact, molecular adhesion forces act (for example, very clean and smooth metal surfaces are known to stick to each other).

This model of dry friction forces (the so-called friction between solid bodies) is apparently close to the real situation in metals.

If a body, for example, simply lies on a horizontal surface, then the friction force does not act on it. Friction occurs if you try to move a body or apply force to it. As long as the magnitude of this force does not exceed a certain value, the body remains at rest and the friction force is equal in magnitude and opposite in direction to the applied force. Then the movement begins.

It may seem surprising, but it is the static friction force that accelerates the car. After all, when the car moves, the wheels do not slip relative to the road, and a static friction force arises between the tires and the road surface. As is easy to see, it is directed in the direction the car is moving. The magnitude of this force cannot exceed the maximum value of static friction. Therefore, if you sharply press the gas on a slippery road, the car will begin to slip. But if you press the brakes, the rotation of the wheels will stop and the car will slide along the road. The friction force will change its direction and begin to slow down the car.

The friction force during sliding of solid bodies depends not only on the properties of the surfaces and the pressure force (this dependence is qualitatively the same as for static friction), but also on the speed of movement. Often, as speed increases, the friction force first drops sharply and then begins to increase again.

This important feature of the sliding friction force explains why a violin string sounds. Initially, there is no slippage between the bow and the string, and the string is grabbed by the bow. When the static friction force reaches its maximum value, the string breaks, and then it vibrates almost as if it were free, then it is again captured by the bow, etc.

Similar, but already harmful vibrations can occur when processing metal on a lathe due to friction between the removed chips and the cutter. And if the bow is rubbed with rosin to make the dependence of the friction force on speed sharper, then when processing metal you have to do the opposite (choose a special cutter shape, lubricant, etc.). So it is important to know the laws of friction and be able to use them.

In addition to dry friction, there is also the so-called liquid friction, which occurs during the movement of solid bodies in liquids and gases and is associated with their viscosity. The forces of fluid friction are proportional to the speed of movement and vanish when the body stops. Therefore, in a liquid, you can make a body move by applying even a very small force. For example, a person can set a heavy barge in motion on the water by pushing off the bottom with a pole, but on land, of course, he cannot move such a load. This important feature of liquid friction forces explains, for example, the fact why a car “skids” on a wet road. Friction becomes liquid, and even small road irregularities that create lateral forces lead to a “skid” of the car.

Summarizing the above, we can conclude that the occurrence of friction is due, first of all, to the roughness of surfaces, which creates resistance to movement, and the presence of adhesion between bodies pressed against each other. The study of all the features of the phenomenon of friction is a rather complex physical and mechanical problem, the consideration of which goes beyond the scope of the course of theoretical mechanics.

In engineering calculations, they usually proceed from a number of general principles established experimentally, which reflect the main features of the friction phenomenon with sufficient accuracy for practice. These laws, called the laws of sliding friction at rest (Coulomb's laws), can be formulated as follows:

1. When trying to move one body along the surface of another in the plane of contact of the bodies, a friction force (or adhesion force) arises, the magnitude of which can take any value from zero to the value F pr, called the ultimate friction force.

Sliding friction force (or simply by friction) is the component of the coupling reaction force that lies in the tangent plane to the surfaces of the contacting bodies.

The friction force is directed in the direction opposite to that in which the acting forces tend to move the body.

In theoretical mechanics, it is assumed that there is no lubricant between the surfaces of contacting bodies.

Dry friction called friction when there is no lubricant between the surfaces of contacting bodies.

We will consider two cases: friction when a body is at rest or in equilibrium, and sliding friction when one body moves along the surface of another with a certain relative speed.

At rest, the friction force depends only on the active forces. With the chosen direction of the tangent at the point of contact of the surfaces of the bodies, the friction force is calculated by the formula:

Similarly, with the chosen direction of the normal, the normal reaction is expressed in terms of the given forces:

When one body moves on the surface of another, the friction force is a constant value.

2. The magnitude of the ultimate friction force is equal to the product of the static coefficient of friction and normal pressure or normal reaction:

Static coefficient of friction - abstract number 0< <1; он опре­деляется опытным путем и зависит от материала соприкасающихся тел и состояния поверхностей (характер обработки, температура, влажность, смазка и т. п.). Считается, что коэффициент трения не зависит от скорости движения.

3. The maximum sliding friction force, all other things being equal, does not depend on the contact area of ​​the rubbing surfaces. From this law it follows that in order to move, for example, a brick, it is necessary to apply the same force, regardless of which face it is placed on the surface, wide or narrow.

Combining the first and second laws together, we obtain that at equilibrium the static friction force (adhesion force)

Reactions of rough bonds. Friction angle.

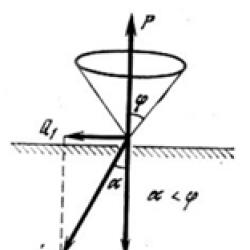
Until now, when solving problems of statics, we have neglected friction and considered the bond surfaces to be smooth and their reactions to be directed along the normals to these surfaces. The reaction of a real (rough) connection will consist of two components: the normal reaction and the friction force perpendicular to it. Consequently, the total reaction will be deviated from the normal to the surface by some angle. When the friction force changes from zero to F, the force R will change from N to R, and its angle with the normal will increase from zero to a certain limiting value (Fig. 26).

Fig.26

The largest angle that the total reaction of a rough bond makes with the normal to the surface is called friction angle. From the drawing it is clear that

Since , from here we find the following relationship between the friction angle and the friction coefficient:

At equilibrium the complete reaction is R, depending on the shear forces, can pass anywhere within the friction angle. When equilibrium becomes limiting, the reaction will be deviated from the normal by an angle .

Friction cone called a cone described by the maximum reaction force of a rough bond around the direction of the normal reaction.

If a force is applied to a body lying on a rough surface R, forming an angle with the normal (Fig. 27), then the body will move only when the shear force Psin is greater (we consider N=Pcos, neglecting the weight of the body). But inequality , in which , is executed only when , i.e. at . Consequently, no force forming an angle with the normal that is smaller than the friction angle can move the body along a given surface. This explains the well-known phenomena of jamming or self-braking of bodies.

Fig.27

For the equilibrium of a solid body on a rough surface, it is necessary and sufficient that the line of action of the resultant active forces acting on the solid body pass inside the friction cone or along its generatrix through its apex.

A body cannot be thrown out of balance by any modulus active force if its line of action passes inside the friction cone.

The phenomena of sliding friction were first experimentally studied at the end of the 17th century. French physicist Amonton (1663-1705), the laws of friction were formulated almost a hundred years later by Coulomb (1736-1806).

1. The friction force lies in the plane tangent to the contacting surfaces of the rubbing bodies.

2. The friction force does not depend on the area of ​​contact between the bodies.

3. The maximum value of the friction force is proportional to the normal pressure N body onto a plane (in the case under consideration N=P):

F max= fN

To body weight P lying on a horizontal table (Fig. 13), we will apply a horizontal force S. We neglect the dimensions of the body, considering it as a material point (the case of a body of finite dimensions is discussed below). If S =0, the body will be in balance (in this case, at rest relative to the table); if force S if we start to increase, the body will still remain at rest; therefore, the horizontal component of the table reaction, called the friction force Ftr balances the applied force S and grows with it until the balance is disrupted. This will happen at the moment when the friction force reaches its maximum value.

F max= fN(1.17)

and the proportionality coefficient f, called the sliding friction coefficient, is determined experimentally and turns out to depend on the material and state (roughness) of the surfaces of the rubbing bodies. The numerical value of the sliding friction coefficient for various materials can be found in reference books. Along with the friction coefficient f Let us introduce the friction angle φ into consideration, defining it by the relation . The origin of this equation and the name “angle of friction” will be explained below. When R will reach the value Fmax, a critical (trigger) moment of equilibrium will come; If S will remain equal Fmax, then the balance will not be disturbed, but the most insignificant increment of effort is enough S so that the body moves. You can notice that as soon as the body moves, the friction force immediately decreases somewhat; experiments have shown that friction during mutual motion of bodies is somewhat less than friction during mutual rest. It is important to note that before the critical moment, i.e. while the body is at rest, the friction force is equal to the applied force and one can only say that F≤ N. The equal sign refers to the critical moment of equilibrium. The direction of the friction force at rest is opposite to the direction of the force S and changes with a change in the direction of this force.

Friction coefficient f depends on the speed of the body, decreasing for most materials as the speed increases. (As an exception, we can point out the case of skin rubbing against metal; here f increases with increasing relative speed.). Relation (17) corresponds quite well to observations during friction of dry or weakly lubricated bodies; the theory of friction in the presence of a lubricant layer, created by N.P. Petrov and O. Reynolds, represents a special section of the hydrodynamics of a viscous fluid.

Friction angle, friction cone.

Considering static friction, let us assume that a force is applied to a body resting on a horizontal rough plane Q, making an angle α with a normal to the plane (Fig. 14). Let's create equilibrium equations. For a convergent system of forces, it is enough to write two equations

.

The written equations determine the friction force and normal reaction. In order for a body to not be moved from its place under the influence of an applied force, it is necessary that or . Dividing the resulting inequality by , we have , or introducing the friction angle, we get α ≤φ . Consequently, depending on the material and the nature of the surface of the rubbing bodies, it is possible to determine such an angle from a given friction coefficient φ , what if the force applied to the body is inclined to the normal by an angle less than the angle φ, then no matter how great this force is, the body will remain in balance. This explains the name of the angle φ friction angle. Area inside segments with an angle 2φ(“friction region”) represents a region with a remarkable property: no matter how great the intensity of the force, the line of action of which is located inside this region, this force will not move a body resting on a plane.

If we consider a body that has the ability to move in any direction along the plane, then the friction area will be limited by the surface of the cone with a dissolution angle equal to 2φ(the so-called friction cone). The presence of a friction area explains the phenomenon of jamming or, as they say, “jamming” of machine parts, when no force applied inside the cone is able to move the corresponding part of the machine. The friction coefficient can have different values ​​for different directions on the plane (for example, when rubbing on wood along and across the fibers, when rubbing on rolled iron along and perpendicular to the rolling direction). Therefore, the friction cone does not always represent a straight round cone.

Varlamov A.A. Friction cone // Quantum. - 1986. - No. 1. - P. 24-25.

By special agreement with the editorial board and editors of the journal "Kvant"

If we consider the conditions of equilibrium of a body on an inclined plane, the angle of inclination of which can be changed, then it is easy to obtain (do it yourself) that the body will begin to slide off the plane at an angle φ such that

\(~\operatorname(tg) \varphi = \mu\) ,

Where μ - coefficient of friction of the body on the plane. Don't you find it surprising that this angle does not depend on body weight?

The same expression for the angle φ can be obtained in another, perhaps simpler way. But to do this, you must first become familiar with the concept of “friction cone”.

Let the body, which can be considered a material point, be located on a rough horizontal plane. The force of gravity \(~m \vec g\) presses the body to the surface, and the surface “responds”, acting on the body with a force of normal pressure \(~\vec N\). If some horizontal force is also applied to the body, then another force appears from the surface - the force of friction. As long as the magnitude of the horizontal force does not exceed the maximum value of the static friction force F tr.p. max = μN, the body is at rest. When this value is reached, the body begins to move, and the surface acts on it with a sliding friction force that prevents movement

\(~F_(tr.sk.) = F_(tr.p.max) = \mu N\) .

Both the normal reaction force and the friction force are generated by the surface, so we can talk about the total reaction force of the surface. In the case when a body, under the influence of an external force (of course, including the force of gravity) moves along the surface (Fig. 1), the total reaction force is

\(~\vec R = \vec N + \vec F_(tr.sk)\) .

This force is directed at an angle φ to the normal, which is easy to determine:

\(~\operatorname(tg) \varphi = \frac(F_(tr.sk))(N) = \mu ; \varphi = \operatorname(arctg) \mu\) .

Corner φ called the friction angle.

We will now mentally rotate the vector \(~\vec R\) around the normal to the surface without changing the angle φ between them. In this case, the vector will describe a cone (with an angle of 2 φ at the top), called friction cone. It has the following remarkable property. No matter how large the external force is applied to the body, if it lies inside the friction cone, the body remains at rest. If this force goes beyond the cone of friction, then no matter how small it is, the body begins to move.

It is not difficult to verify the validity of this statement. Indeed, let the external force \(~\vec F\) (see Fig. 1) be applied to the body so that its line of action makes an angle α with the normal to the surface. Then the force “shifting” the body along the surface is equal to F sin α , and the normal reaction force is equal to F cos α . Thus, the maximum possible static friction force holding the body in place is

\(~F_(tr.p.max) = \mu N = \mu F \cos \alpha = F \operatorname(tg) \varphi \cos \alpha\) .

While the force \(~\vec F\) lies inside the friction cone, α < φ and therefore F sin α < F tg φ cos α . The body is at rest. However, as soon as the angle α the friction angle becomes larger φ , the last inequality is violated. Now friction is no longer able to hold the body in place, and it begins to slide. Let's return to the body left at the beginning of the article on an inclined plane and construct a friction cone for it (Fig. 2).

The external force here is the force of gravity \(~m \vec g\) directed vertically downwards. Bye α < φ , according to what was said above, the body will be at rest. But as soon as the corner α exceeds the angle φ - the movement will begin. Therefore, we immediately obtain the condition for the body to begin sliding from the inclined plane:

\(~\operatorname(tg) \alpha > \mu ; \alpha > \operatorname(arctg) \mu\) .

Note that the concept of a friction cone is used by engineers when calculating a particular structure. For example, even when designing a stool, you should keep the cone of friction in mind.

Imagine a stool whose legs are connected to the seat by hinges (Fig. 3). Of course, in reality no one would do this, but such a fastening system will allow us to more easily understand the role of the friction cone. Let's place such a stool on the floor so that the corner α , which the legs make with the normal to the floor, was less than the angle of friction φ . In this case, no matter how we load the stool, its legs will not move apart - the force with which each leg acts on the floor lies within the corresponding cone of friction. If the angle α make more angle φ , then the force with which the leg acts on the floor will go beyond the limits of the friction cone, the legs will move apart and the stool will fall.

In a real stool, the legs are not connected to the seat using hinges, but are glued or screwed into it.

However, if you make the angle α exceeded the friction angle φ , then at the junction of the legs of the stool with the seat, significant stress may arise and the stool will break.

In reality, there are no absolutely smooth surfaces. All surfaces of bodies are rough to one degree or another. Therefore, the reaction force of a rough surface when the body is in equilibrium depends on the active forces not only in numerical value, but also in direction.

Let us decompose the reaction force of a rough surface into components: one of which we will direct along the common normal to the contact surface, and the other we will direct in the tangent plane to these surfaces.

Friction force sliding (or simply friction force) is the component of the bond reaction force that lies in the tangent plane to the surfaces of the contacting bodies.

By force of normal reaction bond is the component of the bond reaction force, which is directed along the common normal to the surfaces of the contacting bodies.

The nature of the friction force is very complex and We do not touch upon it. In theoretical mechanics, it is assumed that there is no lubricant between the surfaces of contacting bodies.

Dry friction called friction when there is no lubricant between the surfaces of contacting bodies.

We will consider two cases: friction when a body is at rest or in equilibrium, and sliding friction when one body moves along the surface of another with a certain relative speed.

At rest, the friction force depends only on the active forces. With the chosen direction of the tangent at the point of contact of the surfaces of the bodies, the friction force is calculated by the formula:

Similarly, with the chosen direction of the normal, the normal reaction is expressed in terms of the given forces:

When one body moves on the surface of another, the friction force is a constant value.

Engineering calculations are usually based on a number of experimentally established patterns that reflect the main features of the dry friction phenomenon with sufficient accuracy for practice. These laws are called the laws of sliding friction or Coulomb's laws.

Coulomb's Laws

1. The sliding friction force is located in the common tangent plane of the contacting surfaces of the bodies and is directed in the direction opposite to the direction of possible sliding of the body under the action of active forces. The friction force depends on the active forces, and its module is between zero and the maximum value, which is achieved at the moment the body leaves the equilibrium position, that is:

Called ultimate friction force .

2. The maximum sliding friction force, all other things being equal, does not depend on the area of ​​contact of the rubbing surfaces. From this law it follows that in order to move, for example, a brick, it is necessary to apply the same force, regardless of which face it is placed on the surface, wide or narrow.

3. The limiting sliding friction force is proportional to the normal reaction (normal pressure), that is

where the dimensionless coefficient is called the sliding friction coefficient; it is independent of the normal reaction.

4. The coefficient of sliding friction depends on the material and physical state of the rubbing surfaces, that is, on the size and nature of roughness, humidity, temperature and other conditions. The friction coefficient is determined experimentally.

It is believed that the friction coefficient does not depend on the speed of movement.

Friction angle. Equilibrium conditions.

Many problems involve balancing a body on a rough surface, i.e. in the presence of friction, it is convenient to solve geometrically. To do this, we introduce the concept of angle and cone of friction.

The reaction of a real (rough) connection consists of two components: the normal reaction and the friction force perpendicular to it. Consequently, the bond reaction deviates from the normal to the surface by a certain angle. When the friction force changes from zero to maximum, the reaction force changes from zero to , and its angle with the normal increases from zero to a certain limiting value j.

Friction angle is called the largest angle between the maximum reaction force of a rough bond and the normal reaction.

The angle of friction depends on the coefficient of friction.

Friction cone called a cone described by the maximum reaction force of a rough bond around the direction of the normal reaction.

Example.

If a force P is applied to a body lying on a rough surface, forming an angle with the normal, then the body will move only when the shear force  is greater than the limiting friction force  (if we neglect the weight of the body, then but the inequality

Executed only when , i.e. at ,

Consequently, no force that forms an angle with the normal that is smaller than the angle of friction  cannot move the body along a given surface.

For the equilibrium of a solid body on a rough surface, it is necessary and sufficient that the line of action of the resultant active forces acting on the solid body pass inside the friction cone or along its generatrix through its apex.

A body cannot be thrown out of balance by any modulus active force if its line of action passes inside the friction cone.

Example.

Let's consider a body that has a vertical plane of symmetry. The cross-section of the body of this plane has the shape of a rectangle. Body width is 2a.

A vertical force is applied to the body at point C, lying on the axis of symmetry, and at point A, lying at a distance h from the base, a horizontal force is applied. The reaction of the base plane (bond reaction) is reduced to the normal reaction and friction force. The line of action of the force is unknown. Let us denote the distance from point C to the line of action of the force as x. (). Let's create three equilibrium equations:

According to Coulomb's law, i.e. . (1)

Since , then (2)

Let's analyze the results:

We will increase our strength.

1) If , then equilibrium will take place until the friction force reaches its limiting value, condition (1) will turn into equality. A further increase in force will cause the body to slide along the surface.

2) If , then equilibrium will take place until the friction force reaches the value , condition (2) will turn into equality. The value of x will be equal to h. A further increase in force will cause the body to tip around point B (there will be no sliding).

Rolling friction

Rolling friction is the resistance that occurs when one body rolls over the surface of another.

Consider a cylindrical roller of radius r on a horizontal plane. Reactions may occur under the roller and the plane at the point of contact that prevent the roller from rolling along the plane through the action of active forces. Due to the deformation of surfaces, not only sliding, but also rolling.

The active forces acting on rollers in the form of wheels usually consist of gravity, a horizontal force applied to the center of the roller, and a couple of forces with a moment tending to roll the wheel. The wheel in this case is called follower-leader. If , a , then the wheel is called slave. If , a , then the wheel is called leading.