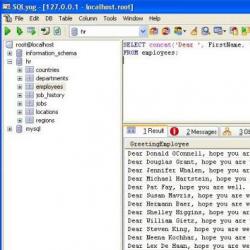
Gibbs energy table of standard values. Standard enthalpies of formation of substances, standard entropies and standard Gibbs energies of formation of substances
The standard molar enthalpy of formation of a substance ΔH o6p, m (298 K) is the change in enthalpy during the formation of one mole of a given substance from its constituent elements in their standard states at a temperature of 298 K and a pressure of one atmosphere.
Let's compare this definition with the examples given above. We made sure
that the oxidation of hydrogen can be represented by at least three different stoichiometric equations. Thus, we know at least three different standard molar enthalpies:
a) ΔH°t (298 K, 2H20(l.)) = - 571.6 kJ/mol
b) ΔH°t (298 K, H20(l.)) = - 285.8 kJ/mol
c) ΔH°t (298 K, H2O(T.)) = - 241.8 kJ/mol
Which of these values corresponds to the standard molar enthalpy of formation of water? The value (c) cannot correspond to it, since the standard state of water at 298 K is not a vaporous (gaseous) state, corresponding to the designation H20(g). The standard molar enthalpy of formation of water can have one of two remaining values, the difference between which is determined by how the reaction equation is written. However, since the above definition of the standard molar enthalpy of formation indicates that it corresponds to the change in enthalpy per mole of the formed substance, option (b) should be chosen. In this way, standard molar enthalpy of formation of water\u003d - 285.8 kJ / mol.
In table. Table 5.1 lists the standard molar enthalpies of formation of some common substances in their standard states. Note that the table includes not only substances, but also some ions. Ions and many compounds cannot be obtained by direct synthesis from the elements that form them. However, their standard enthalpies of formation can be calculated using Hess's law (which we will learn about in Section 5.3).
Most compounds are characterized by negative enthalpies of formation. Therefore, they are called exothermic compounds. Only a few compounds have a positive enthalpy of formation. They are called endothermic compounds. An example of an endothermic compound is benzene.
Attention should be paid to the fact that the enthalpies of formation of solid compounds, as a rule, have larger (in absolute value) negative values than the enthalpies of formation of gases. The standard molar enthalpy of formation of a substance or ion is a measure of its stability compared to the elements that form a given compound. The more (in absolute value) the negative value of the enthalpy of formation of a compound, the more stable this compound is.
By definition, the standard molar enthalpy of formation of any element in its standard state at 298 K is zero. For example, ΔH (298 K, 02(g)) = 0.
Table 5.1. Standard molar enthalpies of formation
Substance |
ΔН(298 K), kJ/mol |
Substance |
D298 K), kJ/mol |
Group components for calculating ideal gas properties according to Benson
Cycloalkanes
Acetylene hydrocarbons
aromatic hydrocarbons
Enthalpy of formation
Forecasting the enthalpy of formation
Prediction of organic compounds by the Benson method for atoms with their first environment
Some multivalent groups of the Benson method for the ideal gas state
INTRODUCTION
The best solution to the development of chemical technology processes and equipment for their implementation is possible only with reliable information on the physicochemical and thermodynamic properties of chemical compounds. Such information often makes up 50 to 90% of the design input.
For practice, experimental data are preferable. Over the years, a huge amount of such data has been collected and processed. This information is available in numerous compilations and reference books. In some of them, all currently known values of thermodynamic and physicochemical characteristics are given and their critical analysis is given. Others contain only values recommended by the authors, often being either average values or the result of statistical processing of the entire array of accumulated information. However, the rapid progress of technology and the introduction of more and more new substances and materials into the field cause a significant gap between the need for data and their availability. Determining the experimental values in broad parameters of the state and compositions is often difficult, and sometimes simply impossible.
For this reason, the engineer is often forced to rely on a variety of methods for calculating and predicting the properties of substances. It should be borne in mind that the terms "calculation" and "forecast" are often used interchangeably, although the second of them carries an honest recognition of the fact that the result can only be partially correct. Calculations can be based on theory, on the correlation of experimental values, or on a combination of both.
Enthalpy of formation
The enthalpy of formation is the main property used in solving many theoretical and practical problems. Knowing the enthalpies of formation of reactants makes it possible to calculate the thermal effects of the reactions of interest, which is necessary when estimating the adiabatic temperature difference in the reaction zone, forming requirements for the reactor design and technological features of the chemical process. The enthalpies of formation of substances are necessary when performing a quantitative thermodynamic analysis of processes, determining the theoretical degree of conversion of reagents, choosing the conditions for conducting chemical transformation etc. The quality of the performed thermodynamic analysis largely depends on the reliability of information on the enthalpies of formation of substances.
The units of enthalpy are kJ/mol and J/mol. In the reference literature of previous years, the enthalpies of formation are often presented in kcal/mol (1 cal = 4.184 J, 1 kcal = 4.184 kJ).
The enthalpy of formation () of the connection in the narrow sense is standard enthalpy change in the reaction of formation of a given substance from elements or simple substances. Simple substances are chemical elements that are at the considered temperature in their natural phase and chemical states.
As the standard state of a substance, such a state is chosen in which this substance is stable at a standard pressure of 1 atm (101325 Pa). The condensed state of a substance is standard up to those temperatures at which its pressure saturated steam reaches 1 atm. Above these temperatures, the ideal gas state is chosen as the standard.
For simple substances involved in the formation of the molecules of most organic compounds, the standard state at 298.15 K is:
for carbon - graphite;
for hydrogen, oxygen, nitrogen, fluorine and chlorine - an ideal diatomic gas;
for bromine, a diatomic liquid;
for iodine and sulfur - a crystalline state, diatomic and monatomic, respectively.
Absolute enthalpy values cannot be determined as they include absolute values internal energy. The need to determine the enthalpies of formation of compounds required the achievement of an international agreement, according to which the values of elements and simple substances in the standard state were taken equal to zero.
The magnitude and sign of substances with a complex molecular structure can be different. This is explained as follows. The formation of matter from free atoms is always accompanied by the release of energy, the resulting substances are negative. However, when a substance is formed from simple substances consisting of diatomic molecules (H 2, O 2, N 2, Cl 2, etc.) or in a condensed state (carbon, bromine, etc.), a certain amount of energy is required to break bonds in the molecules of these simple substances or to transfer them to a gaseous state. As a result, the enthalpy of formation can be both positive and negative, and equal to zero.
In the general case, the value and sign do not give grounds for any statements regarding the thermodynamic stability of a substance, since it depends not only on the enthalpy, but also on the entropy component of the change in free energy during the formation of this substance. Nevertheless, to compare the thermodynamic stability of representatives of the same homologous group or compounds with a similar molecular structure, it can be quite informative, in the first approximation, to analyze their enthalpies of formation. In this case, a substance with a lower enthalpy of formation has a greater thermodynamic stability.
For most compounds, the reactions of their formation from simple substances cannot be carried out in practice. The main source of factual information about the enthalpies of formation of organic compounds are experimental data on the enthalpies of their combustion (), obtained by the calorimetric method. Accumulated to date and recommended values and are contained in the compilations. So far, reference information about has been provided exclusively by calorimetric data. Modern empirical forecasting methods are also based only on calorimetric data. At the same time, it should be noted that information unique in terms of the range of substances involved, the volume of studies performed and the accuracy of the obtained thermodynamic characteristics is contained in the results of the study of chemical equilibrium. In our opinion, the effective use of this information will significantly expand the prognostic capabilities of methods for mass calculations of organic substances.
FORECASTING THE ENTHALPIES OF FORMATION
The main methods for predicting the enthalpies of formation of organic compounds refer to, that is, they characterize the property of a substance in the state of an ideal gas at a pressure of 1 atm. and a temperature of 298.15 K, which is often called the standard. Among the methods of mass calculations, special attention should be paid to the methods of molecular mechanics and additive methods (lat. additio- addition). Most semi-empirical methods do not provide the required forecast quality. Non-empirical methods do not give direct access to the enthalpies of formation of substances and, moreover, are still inaccessible for calculating the properties of organic substances with a complex molecular structure.
In the group of methods of molecular mechanics, we have accumulated considerable experience in using the MMX method (based on force field Ellinger). The method has proven itself well in application to alkanes. However, even for aromatic compounds, it is advisable to use it not for calculating the enthalpies of formation, but for evaluating the effects of the interaction of substituents in the molecule, i.e. for differences in the enthalpies of formation of isomers. For most organohalogen, oxygen-, nitrogen- and sulfur-containing compounds, the method gives biased estimates. However, this method should be used in all cases for express evaluation of a property. Like any other method, it requires the results to be supported by information obtained by another forecasting method. The molecular mechanics method has an excellent interface and is extremely effective as a source of information about the structure of molecules and their geometric parameters.
In the absence of reference data for forecasting, various additive methods are currently widely used. Since the creation of the main additive methods for predicting the properties of organic substances in the state of an ideal gas, a significant period of time has passed, but they retain their importance, despite the increasingly accessible methods of molecular modeling. These methods are effective in those cases when the property changes linearly with a change in the number of fragments of the same type in the molecule. Strictly additive is, for example, the molecular weight of a substance. For the enthalpies of formation of organic compounds, the additive approach is in many cases only some approximation in the calculation. The fact is that even in a homologous group it changes non-linearly with a change in the number of carbon atoms in the molecule (Fig. 1.1).
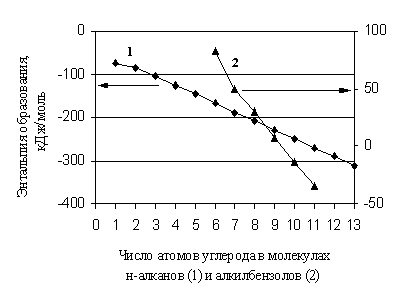
Rice. 1.1. Dependence of the enthalpy of formation of n-alkanes and alkyl benzenes on the number of carbon atoms in their molecules
Thus, the homologous difference is not a constant value, especially for the first members of homologous groups. In the same way, with an increase in the number of substituents of the same type in the molecules of organic substances, it is very often necessary to speak of a deviation from additivity in . However, when corrections for nonadditivity are introduced, the methods of this group work quite satisfactorily if the degree and depth of their detailing are sufficient and correspond to the accuracy of modern experiment.
Depending on the ideology adopted, the structural and quantitative information carriers in additive methods can be the atoms, groups of atoms, or bonds that make up a molecule. Most forecasting methods are constructed in such a way that, as the database on the enthalpies of formation expands, it is relatively easy to refine the values of partial contributions or introduce new corrections.
The general approach to predicting the enthalpies of formation of substances involves the calculation with subsequent, if necessary, transition to ideal gas enthalpies of formation at other temperatures or k , i.e. to a property of matter in a real state.
Of the variety of additive calculation methods, we consider two; Benson's group method for atoms with their first environment and Tatevskii's method for bonds.
Prediction of organic compounds by the Benson method for atoms with their first environment
It should be recognized that of all the variety of additive schemes for predicting the enthalpies of formation of organic substances, the Benson method is most widely used over a long period. This is probably explained by the fact that this method covers the widest range of compounds. For the rapid assessment of the vast majority of compounds without the involvement of any technical means, the method, perhaps, has no equal. It is quite obvious that the price of its universality is the accuracy of the forecast. Therefore, when using the method, it is necessary to be aware of its inevitable limitations. We will try to draw the attention of potential users to the main ones, which are the result of our extensive testing of the method.
The Benson method is usually called the group method, although atom with his first entourage. The method was developed by the author to calculate the following ideal gas properties of substances: heat capacity at temperatures that are multiples of 100 degrees, the enthalpy of formation and entropy.
The enthalpy of the system. standard conditions. Enthalpy of formation of a substance. Enthalpy of reaction. Endothermic and exothermic reactions.
The enthalpy of the system (from the Greek enthalpo I heat) is ϶ᴛᴏ a single-valued function H of the state of a thermodynamic system with independent entropy parameters S and pressure P, which is related to the internal energy U by the relation H=U+PV, where V is the volume of the system. In chemistry, more often than not it is considered isobaric processes (P = const), and the thermal effect in this case is called the change in the enthalpy of the system or the enthalpy of the process: Qp = ∆H; ∆H=∆U+P∆V. Enthalpy has the dimension of energy (kJ). Its value is proportional to the amount of substance; the enthalpy of a unit amount of a substance (mol) is measured in kJ∙mol–1. In a thermodynamic system, the released heat of a chemical process is considered to be negative (exothermic process, ΔH< 0), а поглощение системой теплоты соответствует эндотермическому процессу, ΔH >0. Equations of chemical reactions indicating the enthalpy of the process are called thermochemical. The numerical values of the enthalpy ΔH are indicated with a comma in kJ and refer to the entire reaction, taking into account stoichiometric coefficients all reactants. Since the reactants can be in different states of aggregation, then it is indicated by the lower right index in brackets: (t) - solid, (k) - crystalline, (g) - liquid, (d) - gaseous, (p) - dissolved. For example, the interaction of gaseous H2 and Cl2 produces two moles of gaseous HCl. The thermochemical equation is written as follows: When gaseous H2 and O2 interact, the formed H2O can be in three states of aggregation, which will affect the change in enthalpy: 298 K. The standard state of a thermodynamic function, for example, enthalpy, is indicated by subscripts and superscripts: the subscript is usually omitted: Δ .
Enthalpy of formation (heat of formation), the enthalpy of the reaction of formation of a given substance (or solution) from given initial substances. The enthalpy of formation of a chemical compound is called the enthalpy of the reaction of formation of a given compound from simple substances. As simple substances choose chemical elements in their natural phase and chemical state at a given temperature. So, at 298 K, for chlorine, gaseous chlorine, consisting of C12 molecules, is a simple substance, and for potassium, metallic potassium. The enthalpy of formation of solid KCl at 298 K is the enthalpy of the reaction: K(solid) + 1/2Cl2= KCl(solid). The enthalpy of formation of KCl(solid) at 500 K corresponds to the reaction: K(liquid) + 1/2Cl2 = KCl (solid), since the natural phase state (simple substance) for potassium is no longer a crystal, but a liquid (melting temperature K 336.66 K).
The enthalpy of formation must be determined at any temperature. The standard enthalpies of formation correspond to reactions of formation in which both the simple substances and the resulting compound are under pressure of 1 atm (1.01 x 105 Pa). By definition, for all simple substances at any temperature = 0. For most chemical. conn. enthalpy of formation - negative. quantities.
The units of measurement of the enthalpy of formation are J / g, J / mol. In the thermodynamics of solutions (melts), the enthalpy of formation is understood as the change in enthalpy during the isothermal-isobaric formation of 1 mol (1 g) of a solution (melt) of a given composition from pure components. So, in the two-component system KF-A1F3, the enthalpy of formation of a melt of 50% molar composition corresponds to the process: 1/2KF (liquid) + 1/2A1F3 (liquid) = KF-A1F3 (melt, 50 mol.%).
Endothermic reactions (from other Greek ἔνδον - inside and θέρμη - heat) - chemical reactions accompanied by the absorption of heat. For endothermic reactions, the change in enthalpy and internal energy are positive (ΔH > 0, ΔU > 0), thus, the reaction products contain more energy than the original components. Endothermic reactions include: reactions of reduction of metals from oxides, electrolysis (electrical energy is absorbed ), electrolytic dissociation (for example, the dissolution of salts in water), ionization, photosynthesis. Endothermic reactions are the opposite of exothermic reactions.
An exothermic reaction is a chemical reaction accompanied by the release of heat. The opposite of an endothermic reaction. The total amount of energy in a chemical system is extremely difficult to measure or calculate. On the other hand, the change in enthalpy ΔH in chemical reaction much easier to measure or count. For these purposes, calorimeters are used. The measured value of ∆H is related to the binding energy of the molecules as follows: ∆H = the energy expended in breaking bonds - the energy released when the bonds of the reaction products are formed. For exothermic reactions, this formula gives a negative value for ∆H, since the larger value is subtracted from the smaller value . During the combustion of hydrogen, for example: 2H2 + O2 → 2 H2O, the enthalpy change is ΔH = −483.6 kJ per one mole of O2.
Combustion of fuel in atmospheric oxygen.
Gunpowder burning.
Adding concentrated sulfuric acid to water.
Oxidation of fats and carbohydrates in living organisms.
Adiabatic combustion
The enthalpy of the system. standard conditions. Enthalpy of formation of a substance. Enthalpy of reaction. Endothermic and exothermic reactions. - concept and types. Classification and features of the category "Enthalpy of the system. Standard conditions. Enthalpy of formation of matter. Enthalpy of reaction. Endothermic and exothermic reactions." 2014, 2015.
Basic equations of chemical thermodynamics and chemical equilibrium
1.Q=DE+W-equation of the first law of thermodynamics
2.W=PDV
3. Q v = DE v -heat of isochoric process
4. Q p = DH p -heat of isobaric process
5. DH p = DE + PDV -equation of the first law of thermodynamics for isobaric processes
6. DH = å n DH 0 298 arr. prod. react. - å n DH 0 298 arr. ref. substances - P First corollary of Hess' law
7. DH = å n DH 0 298 combust. Exodus. in. - å n DH 0 298 burned out prod. reactions - insecond corollary of Hess' law
8.Q=W-equation of the first law of thermodynamics for biosystems
9.DS = ¾¾ -entropy as a function of the state of the system
10.DS ³ 0 -equation of the second law of thermodynamics
11 S = å n S 0 298 cont. R. - å n S 0 298 ref. in. -reaction entropy calculation
12. DG 0 = DH 0 - TDS 0 -equations for calculating the Gibbs energy
13. DG 0 = å n DG 0 298 prod. R. - å n DG 0 298 ref. in.(x)
14. DG 0 \u003d - 2.3RT lg Ks - chemical reaction isotherm equation at standard conditions
15. - chemical reaction isotherm equation
16. - chemical equilibrium constant expressed in terms of equilibrium concentrations of a substance
17. - chemical equilibrium constant expressed in terms of equilibrium partial pressures substances
18. - isobar equation
19. - calculation of the thermal effect from the values of the constants
Table 1
| Substance | Standard enthalpy of formation kJ/mol | Standard entropy J/mol×K | Standard Gibbs energy of formation kJ/mol |
| inorganic substances | |||
| C (graphite) | +6 | ||
| CO (g) | -110 | +198 | -137 |
| CO 2 (g) | -393,5 | +214 | -394 |
| Cl 2 (g) | +223 | ||
| Cl 2 O (g) | +76 | +266 | +94 |
| FeСО 3 (tv) | -753 | +96 | -680 |
| H 2 (g) | +131 | ||
| HCl (g) | -92 | +187 | -95 |
| HI (g) | +24 | +206 | -1 |
| HNO 2 (solution) | -119 | +153 | -56 |
| HNO 3 (l) | -174 | +156 | -81 |
| H 2 O (l) | -286 | +70 | -237 |
| H 2 O 2 (l) | -187 | +110 | -120 |
| H 2 S (g) | -21 | +206 | -34 |
| H 2 SO 4 (l) | -814 | +157 | -690 |
| KNO 3 (TV) | -495 | +133 | -395 |
| KOH(solution) | -477 | +92 | -441 |
| N 2 (g) | +192 | ||
| NH 3 (g) | -46 | +192 | -16 |
| H 2 O (g) | +82 | +220 | +104 |
| NO (g) | +91 | +211 | +87 |
| NO 2 (g) | +33 | +240 | +51 |
| N 2 O 3 (g) | +11 | +356 | +115 |
| Na 2 O 2 (TV) | -510 | +95 | -447 |
| Na 2 S 2 O 3 (TV) | -1117 | +225 | -1043 |
| O 2 (g) | +205 | ||
| SO 2 (g) | -297 | +248 | -300 |
| SO 3 (g) | -396 | +257 | -371 |
| organic matter | |||
| Methane (g) | -75 | +186 | -51 |
| Ethane (g) | -85 | +229 | -33 |
| Ethylene (g) | +52 | +219 | +68 |
| Acetylene (g) | +227 | +201 | +209 |
| Benzene (w) | +49 | +173 | +125 |
| Cyclohexane (l) | -156 | +204 | +27 |
| Chloromethane (g) | -86 | +234 | -63 |
| Dichloromethane (g) | -95 | +270 | -69 |
| Trichloromethane (g) | -101 | +296 | -69 |
| Carbon tetrachloride (g) | -100 | +310 | -58 |
| Methanol (w) | -239 | +127 | -166 |
| Ethanol (w) | -277 | +161 | -174 |
| Diethyl ether (l) | -279 | +253 | -123 |
| Acetaldehyde (g) | -166 | +264 | -133 |
| Acetone (w) | -247 | +199 | -154 |
| Pyruvate ion (solution) | + | -559 | |
| L-lactic acid (solution) | -686 | +222 | -539 |
| Sucrose (TV) | -2222 | +360 | -1545 |
| D-glucose (solution) | -1264 | +269 | -917 |
| Nitrobenzene (w) | +16 | +224 | +146 |
| Aniline (w) | +31 | +191 | +149 |
| L-leucine (solution) | -643 | +208 | -362 |
| Glycine (solution) | -523 | +159 | -380 |
| D,L-leucylglycine (solution) | + | -464 | |
| Glycylglycine (solution) | -734 | +231 | -492 |
Standard enthalpies of combustion of organic substances, kJ/mol
Specific heat complete oxidation of substances in the body, kJ/g.
Learning tasks:
Task 1 In the human body, the oxidation reaction of ethyl alcohol proceeds in two stages. The first is the oxidation of ethyl alcohol to acetaldehyde with the participation of the enzyme alcohol dehydrogenase proceeds according to the equation: C 2 H 5 OH + ½ O 2 \u003d CH 3 COH + H 2 O.
Calculate the DH 0 of the reaction using the first corollary of Hess' law if
DН 0 arr. (C 2 H 5 OH) \u003d - 278 kJ / mol;
DН 0 arr. (CH 3 COH) \u003d - 166 kJ / mol;
DН 0 arr. (H 2 O) \u003d - 286 kJ / mol.
Decision: DH 0 = å n DH 0 - å n DН 0 inverse ref.in.in; DH = (-166+ (-286)-(-278)) = - 174 kJ/mol
Answer: thermal effect of the reaction DH = -174 kJ/mol, i.e. exothermic process.
Task 2. The heat of combustion of glucose is -2810 kJ/mol, the heat of combustion of ethyl alcohol is -1366 kJ/mol. Based on these data, calculate the thermal effect of the biochemical process of glucose fermentation:
C 6 H 12 O 6 \u003d 2C 2 H 5 OH + 2CO 2
Decision: The thermal effect of this reaction can be calculated by applying the second corollary of Hess's law:
DH = ån DH 0 burn. Exodus. substances - å n DH 0 combust. prod. reactions
DH \u003d -2810 - 2 ∙ (-1366) \u003d - 78 kJ / mol
Answer: the thermal effect of the fermentation process is - 78 kJ / mol.
Task 3. Calculate the standard entropy of the reaction:
NH 2 - CH 2 - COOH + NH 2 - CH 2 - COOH → NH 2 - CH 2 - CO - NH - CH 2 - COOH + H 2 O
glycine glycine glycylglycine
If S 0 (glycylglycine) = 231 J / mol × K;
S 0 (glycine) \u003d 159 J / mol × K;
S 0 (H 2 O) \u003d 70 J / mol × K;
Decision:
DS \u003d S 0 298 (hl-hl) + S 0 298 (H 2 O) - 2 S 0 298 (glycine) \u003d (231 + 70) - (159 + 159) \u003d -17 J / mol × K
Answer: DS 0 298 \u003d - 17 J / mol × K, i.e. entropy will decrease.
Task 4. The heat of combustion of carbohydrates, proteins and fats is 17, 17 and 39 kJ
respectively. The average daily requirement for proteins, fats and carbohydrates for male students is 113, 106 and 451g. What is the daily requirement of male students for energy?
Decision: Calculate how much energy is released during the oxidation of carbohydrates, proteins and fats
DH = (451×17) + (113×17) + (106×39) = 13722 kJ.
Answer: The daily energy requirement is 13722 kJ.
Task 5. Why is the process of protein denaturation at 40 0 C spontaneous if the reaction is endothermic and the thermal effect is 2830 J/mol? The DS value for this reaction is 288 J/mol∙K
Decision: To determine the direction of the process, it is necessary to know the magnitude of the change in the Gibbs energy, calculated by the equation: DG 0 = DH 0 - TDS 0 . The calculation shows that DG< 0 (DG 0 = 2830 Дж/моль - (313К × 288 Дж/моль∙К) = - 87314 Дж/моль или - 87,3 кДж/моль).
Answer: Because DG< 0, то процесс денатурации белка при 40 0 С протекает самопроизвольно, повышение температуры тела может представлять опасность для жизнедеятельности организма.
Task 6. Calculate the Gibbs energy, which is a criterion for the spontaneity of processes, for the glycolysis reaction under standard conditions: C 6 H 12 O 6 (solution) ® 2C 3 H 6 O 3 (solution) (lactic acid).
Decision:
From the table of thermodynamic values, we write the standard Gibbs energy for the participants in the chemical process: ∆G 0 (C 6 H 12 O 6) = -917 kJ / mol; ∆G 0 (C 3 H 6 O 3) = -539 kJ / mol. Using 1 corollary from the Hess law, we calculate the Gibbs energy:
ΔG 0 = 2×ΔG 0 (C 3 H 6 O 3) - ΔG 0 (C 6 H 12 O 6)
ΔG 0 \u003d 2 (-539) - (-917) \u003d -161 kJ / mol
Answer: because ∆G0< 0, то реакция протекает самопроизвольно в forward direction.
Task 7. Calculate the change in the Gibbs energy at 25 0 C using the standard values of the enthalpies of formation and absolute entropies for this reaction: CO + 2H 2 = CH 3 OH
DН 0 arr CH 3 OH \u003d -293 kJ / mol S 0 (CH 3 OH) \u003d 127 J / mol × K
DH 0 arr CO \u003d - 110 kJ / mol. S 0 (CO) \u003d 198 J / mol × K
S 0 (H 2) \u003d 131 J / mol × K
Decision: DG 0 = DH 0 - TDS 0
DH 0 = ånDH 0 arr. pr. reak. - ånDH 0 arr. ref. substances
DH 0 \u003d - 293 - (-110) \u003d - 183 kJ / mol
DS 0 = å n S 0 cont. p - å n S 0 outcome. substances
DS 0 \u003d 127 - (198 + 2 (131) \u003d - 333 J / mol × K
DG 0 \u003d - 183.5 kJ / mol - (298K × 0.333 kJ / mol × K) \u003d - 83.8 kJ / mol
Answer: DG 0 \u003d - 83.8 kJ / mol
Task 8. Calculate the equilibrium constant at 310 K for the reaction ATP + AMP ↔ 2ADP if free energy Gibbs reaction ΔG°=-2.10kJ/mol.
Decision: in equilibrium DG 0 = - 2.3RT log Ks
K c \u003d 10 0.354 \u003d 2.26
Answer: Kc = 2.26
Task 9. The equilibrium constant of the reaction: PCl 5 (g) "PCl 3 (g) + Cl 2 (g) at 250 0 C is 2. In which direction does the reaction proceed at the following concentrations: C (PCl 5) \u003d C (PCl 3) \u003d 2 mol/l; C (Cl 2) \u003d 4 mol / l?
Decision: To determine the direction of the reaction, we use the isotherm equation
Calculate Ps
Because P s > K s, then DG > 0
Conclusion: the reaction cannot proceed spontaneously in the forward direction, because DG>0.
Task 10. The equilibrium constant of the reaction 2SO 2 (g) + O 2 (g) Û 2SO 3 (g) at a temperature of 627 0 C is 2.3 ∙ 10 -7, DH 0 = 376.5 kJ / mol. Calculate the equilibrium constant at 727 0 С.
Decision: we use the equation of the isobar of a chemical reaction:
T 1 \u003d 273 + 627 \u003d 900 K
T2 = 273 + 727 = 1000K
Answer: The equilibrium constant at 727 0 C is 3.56 × 10 -5.
Task 11. For the reaction H 2 O (g) + CO (g) ® CO 2 (g) + H 2 (g), the chemical equilibrium constants are: at 800 0 C Kp = 2.87, at 1000 0 C Kp = 1.39. Calculate the thermal effect of this reaction.
Decision: Applying the equation of the isobar of a chemical reaction, we calculate DH
Let's take T 1 = 800 + 273 = 1073 K
T 2 \u003d 1000 + 273 \u003d 1273 K
Answer: DH = -39.16 kJ/mol.
Tasks for independent solution:
Task 1. It takes 40 kJ to evaporate 1 mole of water. How much heat will be lost per day when 720 g of water is released through the skin?
Answer: 1600 kJ
Task 2. Hydrogen peroxide (H 2 O 2) in the form of a solution with a mass fraction of 3%. used in medicine for the treatment of wounds. Prove that the process of decomposition of hydrogen peroxide in the presence of the catalase enzyme is spontaneous, using the values of the standard entropy of formation of the initial substances and reaction products to calculate:
S 0 298 (H 2 O 2) =110 J/mol×K; S 0 298 (H 2 O) \u003d 70 J / mol × K; S 0 298 (O 2) = 205 J / mol × K.
Answer: Δ S = 62.5 J/mol × K
Task 3. When burning methane with a volume of 2 m 3, 79600 kJ of heat is released. Calculate the standard heat of combustion of methane.
Answer: 891.52 kJ/mol
Task 4. Calculate the standard Gibbs energy for the process of glucose oxidation according to the following data: DH 0 arr (C 6 H 12 O 6) \u003d - 1264.4 kJ / mol; DH 0 arr (CO 2) \u003d - 393 kJ / mol;
DH 0 arr (H 2 O) \u003d - 286 kJ / mol. The change in the entropy of the entire reacting system is 0.259 kJ/mol×K
Answer: DG \u003d - 2886.8 kJ / mol.
Task5. Calculate the standard enthalpy of formation of ethanol using the required standard enthalpies of combustion.
Answer: DН 0 arr. = -273 kJ/mol
Task 6. The equilibrium constant of the reaction N 2 0 4 (g) ↔ 2N0 2 (g) at 25°C is 0.1. In which direction will the reaction proceed at the following concentrations of substances:
a) C (N0 2) \u003d C (N 2 0 4) \u003d 0.1 mol / l;
b) C (N0 2) \u003d 0.01 mol / l; C (N 2 0 4) \u003d 0.02 mol / l?
Task 7. For the reaction H 2 + I 2 ® 2HI at 444 0 C, the equilibrium constant is 50. Determine the direction of the process if the initial mixture has the following composition: C (H 2) \u003d 2 mol / l, C (HI) \u003d 10 mol / l.
Answer: The state of equilibrium, because ∆G=0.
Task 8 . Calculate the equilibrium constant if DG 0 298 for this reaction is 4.478 kJ/mol.
Answer: 6,1
Task 9. The equilibrium constant of the decomposition of a medicinal substance in an autoclave at 413K is 0.396∙10 5 Pa, and at 443K it is 1.286∙10 5 Pa. Calculate the thermal effect of the reaction.
Answer: 59.6 kJ/mol.
Task 10. Using the ΔG° value, determine whether there is a threat of patient poisoning when used as a drug nitric oxide (I), Toxic nitric oxide (II) can be formed by the reaction: 2N 2 O + O 2 = 4NO. All substances are in gaseous state. See the table for reference data.