Task 1

Find the cosine of the angle between the lines $\frac(x+3)(5) =\frac(y-2)(-3) =\frac(z-1)(4) $ and $\left\(\begin(array )(c) (x=2\cdot t-3) \\ (y=-t+1) \\ (z=3\cdot t+5) \end(array)\right.$.

Let two lines be given in space: $\frac(x-x_(1) )(m_(1) ) =\frac(y-y_(1) )(n_(1) ) =\frac(z-z_(1 ) )(p_(1) ) $ and $\frac(x-x_(2) )(m_(2) ) =\frac(y-y_(2) )(n_(2) ) =\frac(z- z_(2) )(p_(2) ) $. We choose an arbitrary point in space and draw two auxiliary lines through it, parallel to the data. The angle between the given lines is any of the two adjacent corners formed by auxiliary lines. The cosine of one of the angles between the lines can be found using the well-known formula $\cos \phi =\frac(m_(1) \cdot m_(2) +n_(1) \cdot n_(2) +p_(1) \cdot p_( 2) )(\sqrt(m_(1)^(2) +n_(1)^(2) +p_(1)^(2) ) \cdot \sqrt(m_(2)^(2) +n_( 2)^(2) +p_(2)^(2) ) ) $. If the value $\cos \phi >0$, then sharp corner between lines if $\cos \phi

Canonical equations of the first line: $\frac(x+3)(5) =\frac(y-2)(-3) =\frac(z-1)(4) $.

The canonical equations of the second straight line can be obtained from the parametric ones:

\ \ \

Thus, the canonical equations of this line are: $\frac(x+3)(2) =\frac(y-1)(-1) =\frac(z-5)(3) $.

We calculate:

\[\cos \phi =\frac(5\cdot 2+\left(-3\right)\cdot \left(-1\right)+4\cdot 3)(\sqrt(5^(2) +\ left(-3\right)^(2) +4^(2) ) \cdot \sqrt(2^(2) +\left(-1\right)^(2) +3^(2) ) ) = \frac(25)(\sqrt(50) \cdot \sqrt(14) ) \approx 0.9449.\]

Task 2

The first line passes through the given points $A\left(2,-4,-1\right)$ and $B\left(-3,5,6\right)$, the second line passes through the given points $C\left (1,-2,8\right)$ and $D\left(6,7,-2\right)$. Find the distance between these lines.

Let some line be perpendicular to lines $AB$ and $CD$ and intersect them at points $M$ and $N$, respectively. Under these conditions, the length of the segment $MN$ is equal to the distance between the lines $AB$ and $CD$.

We build the vector $\overline(AB)$:

\[\overline(AB)=\left(-3-2\right)\cdot \bar(i)+\left(5-\left(-4\right)\right)\cdot \bar(j)+ \left(6-\left(-1\right)\right)\cdot \bar(k)=-5\cdot \bar(i)+9\cdot \bar(j)+7\cdot \bar(k ).\]

Let the segment representing the distance between the lines pass through the point $M\left(x_(M) ,y_(M) ,z_(M) \right)$ on the line $AB$.

We build the vector $\overline(AM)$:

\[\overline(AM)=\left(x_(M) -2\right)\cdot \bar(i)+\left(y_(M) -\left(-4\right)\right)\cdot \ bar(j)+\left(z_(M) -\left(-1\right)\right)\cdot \bar(k)=\] \[=\left(x_(M) -2\right)\ cdot \bar(i)+\left(y_(M) +4\right)\cdot \bar(j)+\left(z_(M) +1\right)\cdot \bar(k).\]

The vectors $\overline(AB)$ and $\overline(AM)$ are the same, hence they are collinear.

It is known that if the vectors $\overline(a)=x_(1) \cdot \overline(i)+y_(1) \cdot \overline(j)+z_(1) \cdot \overline(k)$ and $ \overline(b)=x_(2) \cdot \overline(i)+y_(2) \cdot \overline(j)+z_(2) \cdot \overline(k)$ are collinear, then their coordinates are proportional, then is $\frac(x_((\it 2)) )((\it x)_((\it 1)) ) =\frac(y_((\it 2)) )((\it y)_( (\it 1)) ) =\frac(z_((\it 2)) )((\it z)_((\it 1)) ) $.

$\frac(x_(M) -2)(-5) =\frac(y_(M) +4)(9) =\frac(z_(M) +1)(7) =m$, where $m $ is the result of the division.

From here we get: $x_(M) -2=-5\cdot m$; $y_(M) +4=9\cdot m$; $z_(M) +1=7\cdot m$.

Finally, we obtain expressions for the coordinates of the point $M$:

We build the $\overline(CD)$ vector:

\[\overline(CD)=\left(6-1\right)\cdot \bar(i)+\left(7-\left(-2\right)\right)\cdot \bar(j)+\ left(-2-8\right)\cdot \bar(k)=5\cdot \bar(i)+9\cdot \bar(j)-10\cdot \bar(k).\]

Let the segment representing the distance between the lines pass through the point $N\left(x_(N) ,y_(N) ,z_(N) \right)$ on the line $CD$.

We construct the vector $\overline(CN)$:

\[\overline(CN)=\left(x_(N) -1\right)\cdot \bar(i)+\left(y_(N) -\left(-2\right)\right)\cdot \ bar(j)+\left(z_(N) -8\right)\cdot \bar(k)=\] \[=\left(x_(N) -1\right)\cdot \bar(i)+ \left(y_(N) +2\right)\cdot \bar(j)+\left(z_(N) -8\right)\cdot \bar(k).\]

The vectors $\overline(CD)$ and $\overline(CN)$ are the same, hence they are collinear. We apply the condition of collinear vectors:

$\frac(x_(N) -1)(5) =\frac(y_(N) +2)(9) =\frac(z_(N) -8)(-10) =n$ where $n $ is the result of the division.

From here we get: $x_(N) -1=5\cdot n$; $y_(N) +2=9\cdot n$; $z_(N) -8=-10\cdot n$.

Finally, we obtain expressions for the coordinates of point $N$:

We build the $\overline(MN)$ vector:

\[\overline(MN)=\left(x_(N) -x_(M) \right)\cdot \bar(i)+\left(y_(N) -y_(M) \right)\cdot \bar (j)+\left(z_(N) -z_(M) \right)\cdot \bar(k).\]

We substitute the expressions for the coordinates of the points $M$ and $N$:

\[\overline(MN)=\left(1+5\cdot n-\left(2-5\cdot m\right)\right)\cdot \bar(i)+\] \[+\left(- 2+9\cdot n-\left(-4+9\cdot m\right)\right)\cdot \bar(j)+\left(8-10\cdot n-\left(-1+7\cdot m\right)\right)\cdot \bar(k).\]

After completing the steps, we get:

\[\overline(MN)=\left(-1+5\cdot n+5\cdot m\right)\cdot \bar(i)+\left(2+9\cdot n-9\cdot m\right )\cdot \bar(j)+\left(9-10\cdot n-7\cdot m\right)\cdot \bar(k).\]

Since the lines $AB$ and $MN$ are perpendicular, the scalar product of the corresponding vectors is equal to zero, i.e. $\overline(AB)\cdot \overline(MN)=0$:

\[-5\cdot \left(-1+5\cdot n+5\cdot m\right)+9\cdot \left(2+9\cdot n-9\cdot m\right)+7\cdot \ left(9-10\cdot n-7\cdot m\right)=0;\] \

After completing the steps, we get the first equation for determining $m$ and $n$: $155\cdot m+14\cdot n=86$.

Since the lines $CD$ and $MN$ are perpendicular, the scalar product of the corresponding vectors is equal to zero, i.e. $\overline(CD)\cdot \overline(MN)=0$:

\ \[-5+25\cdot n+25\cdot m+18+81\cdot n-81\cdot m-90+100\cdot n+70\cdot m=0.\]

After completing the steps, we obtain the second equation for determining $m$ and $n$: $14\cdot m+206\cdot n=77$.

Find $m$ and $n$ by solving the system of equations $\left\(\begin(array)(c) (155\cdot m+14\cdot n=86) \\ (14\cdot m+206\cdot n =77) \end(array)\right.$.

We apply the Cramer method:

\[\Delta =\left|\begin(array)(cc) (155) & (14) \\ (14) & (206) \end(array)\right|=31734; \] \[\Delta _(m) =\left|\begin(array)(cc) (86) & (14) \\ (77) & (206) \end(array)\right|=16638; \] \[\Delta _(n) =\left|\begin(array)(cc) (155) & (86) \\ (14) & (77) \end(array)\right|=10731;\ ]\

Find the coordinates of points $M$ and $N$:

\ \

Finally:

Finally, we write the vector $\overline(MN)$:

$\overline(MN)=\left(2.691-\left(-0.6215\right)\right)\cdot \bar(i)+\left(1.0438-0.7187\right)\cdot \bar (j)+\left(4,618-2,6701\right)\cdot \bar(k)$ or $\overline(MN)=3,3125\cdot \bar(i)+0,3251\cdot \bar( j)+1.9479\cdot\bar(k)$.

The distance between lines $AB$ and $CD$ is the length of the vector $\overline(MN)$:$d=\sqrt(3.3125^(2) +0.3251^(2) +1.9479^( 2) ) \approx 3.8565$ lin. units

a. Let two lines be given. These lines, as was indicated in Chapter 1, form various positive and negative angles which can be either sharp or blunt. Knowing one of these angles, we can easily find any other.

By the way, for all these angles, the numerical value of the tangent is the same, the difference can only be in the sign

Equations of lines. The numbers are the projections of the directing vectors of the first and second lines. The angle between these vectors is equal to one of the angles formed by straight lines. Therefore, the problem is reduced to determining the angle between the vectors, We get

For simplicity, we can agree on an angle between two straight lines to understand an acute positive angle (as, for example, in Fig. 53).

Then the tangent of this angle will always be positive. Thus, if a minus sign is obtained on the right side of formula (1), then we must discard it, i.e., keep only the absolute value.

Example. Determine the angle between lines

By formula (1) we have

With. If it is indicated which of the sides of the angle is its beginning and which is its end, then, counting always the direction of the angle counterclockwise, we can extract something more from formulas (1). As is easy to see from Fig. 53 the sign obtained on the right side of the formula (1) will indicate which one - acute or obtuse - the angle forms the second line with the first.

(Indeed, from Fig. 53 we see that the angle between the first and second direction vectors is either equal to the desired angle between the lines, or differs from it by ±180°.)

d. If the lines are parallel, then their direction vectors are also parallel. Applying the condition of parallelism of two vectors, we get!

This is a necessary and sufficient condition for two lines to be parallel.

Example. Direct

are parallel because

e. If the lines are perpendicular, then their direction vectors are also perpendicular. Applying the condition of perpendicularity of two vectors, we obtain the condition of perpendicularity of two lines, namely

Example. Direct

perpendicular because

In connection with the conditions of parallelism and perpendicularity, we will solve the following two problems.

f. Draw a line parallel to a given line through a point

The decision is made like this. Since the desired line is parallel to the given one, then for its directing vector we can take the same one as that of the given line, i.e., a vector with projections A and B. And then the equation of the desired line will be written in the form (§ 1)

Example. Equation of a straight line passing through a point (1; 3) parallel to a straight line

will be next!

g. Draw a line through a point perpendicular to the given line

Here, it is no longer suitable to take a vector with projections A and as a directing vector, but it is necessary to win a vector perpendicular to it. The projections of this vector must therefore be chosen according to the condition that both vectors are perpendicular, i.e., according to the condition

This condition can be fulfilled in an infinite number of ways, since here there is one equation with two unknowns. But the easiest way is to take it. Then the equation of the desired line will be written in the form

Example. Equation of a line passing through a point (-7; 2) in a perpendicular line

will be the following (according to the second formula)!

h. In the case when the lines are given by equations of the form

rewriting these equations differently, we have

Corner φ general equations A 1 x + B 1 y + C 1 = 0 and A 2 x + B 2 y + C 2 = 0, is calculated by the formula:

Corner φ between two straight lines canonical equations(x-x 1) / m 1 \u003d (y-y 1) / n 1 and (x-x 2) / m 2 \u003d (y-y 2) / n 2, is calculated by the formula:

Distance from point to line

Each plane in space can be represented as linear equation called general equation plane

Special cases.

o If in equation (8), then the plane passes through the origin.

o With (,) the plane is parallel to the axis(axis, axis), respectively.

o When (,) the plane is parallel to the plane(plane, plane).

Solution: use (7)

Answer: the general equation of the plane.

Example.

The plane in the rectangular coordinate system Oxyz is given by the general equation of the plane . Write down the coordinates of all normal vectors in this plane.

We know that the coefficients of the variables x, y, and z in the general equation of the plane are the corresponding coordinates of the normal vector of that plane. Therefore, the normal vector of the given plane has coordinates. The set of all normal vectors can be given as.

Write the equation of a plane if in a rectangular coordinate system Oxyz in space it passes through a point , a is the normal vector of this plane.

We present two solutions to this problem.

From the condition we have . We substitute these data into the general equation of the plane passing through the point:

Write the general equation for a plane parallel to the coordinate plane Oyz and passing through the point .

A plane that is parallel to the coordinate plane Oyz can be given by a general incomplete equation of the plane of the form . Since the point belongs to the plane by condition, then the coordinates of this point must satisfy the equation of the plane, that is, equality must be true. From here we find. Thus, the desired equation has the form.

Solution. The vector product, by definition 10.26, is orthogonal to the vectors p and q. Therefore, it is orthogonal to the desired plane and the vector can be taken as its normal vector. Find the coordinates of the vector n:

that is . Using formula (11.1), we obtain

Opening the brackets in this equation, we arrive at the final answer.

Answer: .

Let's rewrite the normal vector in the form and find its length:

According to the above:

Answer:

Parallel planes have the same normal vector. 1) From the equation we find the normal vector of the plane:.

2) We compose the equation of the plane according to the point and the normal vector:

Answer:

Vector equation of a plane in space

Parametric equation of a plane in space

Equation of a plane passing through a given point perpendicular to a given vector

Let a rectangular Cartesian coordinate system be given in three-dimensional space. Let's formulate the following problem:

Write an equation for a plane passing through given point M(x 0, y 0, z 0) perpendicular to the given vector n = ( A, B, C} .

Solution. Let P(x, y, z) is an arbitrary point in space. Dot P belongs to the plane if and only if the vector MP = {x − x 0, y − y 0, z − z 0) orthogonal to vector n = {A, B, C) (Fig. 1).

Having written the orthogonality condition for these vectors (n, MP) = 0 in coordinate form, we get:

Equation of a plane by three points

In vector form

In coordinates

Mutual arrangement of planes in space

– general equations two planes. Then:

1) if , then the planes coincide;

2) if , then the planes are parallel;

3) if or , then the planes intersect and the system of equations

(6)

are the equations of the line of intersection of the given planes.

Write parametric equations for the following lines:

Solution: The lines are given by canonical equations and at the first stage one should find some point belonging to the line and its direction vector.

a) From the equations remove the point and the direction vector: . You can choose another point (how to do this is described above), but it is better to take the most obvious one. By the way, to avoid mistakes, always substitute its coordinates into the equations.

Let us compose the parametric equations of this straight line:

The convenience of parametric equations is that with their help it is very easy to find other points of the line. For example, let's find a point whose coordinates, say, correspond to the value of the parameter :

Thus: b) Consider the canonical equations . The choice of a point here is simple, but insidious: (be careful not to mix up the coordinates!!!). How to pull out a guide vector? You can argue what this straight line is parallel to, or you can use a simple formal trick: the proportion is “y” and “z”, so we write the direction vector , and put zero in the remaining space: .

We compose the parametric equations of the straight line:

c) Let's rewrite the equations in the form , that is, "Z" can be anything. And if any, then let, for example, . Thus, the point belongs to this line. To find the direction vector, we use the following formal technique: in the initial equations there are "x" and "y", and in the direction vector at these places we write zeros: . In the remaining place we put unit: . Instead of one, any number, except zero, will do.

We write the parametric equations of the straight line:

Definition. If two lines are given y = k 1 x + b 1 , y = k 2 x + b 2 , then the acute angle between these lines will be defined as

Two lines are parallel if k 1 = k 2 . Two lines are perpendicular if k 1 = -1/ k 2 .

Theorem. The straight lines Ax + Vy + C \u003d 0 and A 1 x + B 1 y + C 1 \u003d 0 are parallel when the coefficients A 1 \u003d λA, B 1 \u003d λB are proportional. If also С 1 = λС, then the lines coincide. The coordinates of the point of intersection of two lines are found as a solution to the system of equations of these lines.

Equation of a line passing through a given point

Perpendicular to this line

Definition. The line passing through the point M 1 (x 1, y 1) and perpendicular to the line y \u003d kx + b is represented by the equation:

Distance from point to line

Theorem. If a point M(x 0, y 0) is given, then the distance to the line Ax + Vy + C \u003d 0 is defined as

.

Proof. Let the point M 1 (x 1, y 1) be the base of the perpendicular dropped from the point M to the given line. Then the distance between points M and M 1:

(1)

The x 1 and y 1 coordinates can be found as a solution to the system of equations:

The second equation of the system is the equation of a straight line passing through given point M 0 is perpendicular to a given line. If we transform the first equation of the system to the form:

A(x - x 0) + B(y - y 0) + Ax 0 + By 0 + C = 0,

then, solving, we get:

Substituting these expressions into equation (1), we find:

The theorem has been proven.

Example. Determine the angle between the lines: y = -3 x + 7; y = 2 x + 1.

k 1 \u003d -3; k2 = 2; tgφ = ; φ= p /4.

Example. Show that the lines 3x - 5y + 7 = 0 and 10x + 6y - 3 = 0 are perpendicular.

Solution. We find: k 1 \u003d 3/5, k 2 \u003d -5/3, k 1 * k 2 \u003d -1, therefore, the lines are perpendicular.

Example. The vertices of the triangle A(0; 1), B (6; 5), C (12; -1) are given. Find the equation for the height drawn from vertex C.

Solution. We find the equation of the side AB: ; 4 x = 6 y - 6;

2x – 3y + 3 = 0;

The desired height equation is: Ax + By + C = 0 or y = kx + b. k = . Then y = . Because the height passes through point C, then its coordinates satisfy this equation: whence b = 17. Total: .

Answer: 3x + 2y - 34 = 0.

Equation of a line passing through a given point in a given direction. Equation of a straight line passing through two given points. Angle between two lines. Condition of parallelism and perpendicularity of two lines. Determining the point of intersection of two lines

1. Equation of a line passing through a given point A(x 1 , y 1) in a given direction, determined by the slope k,

y - y 1 = k(x - x 1). (1)

This equation defines a pencil of lines passing through a point A(x 1 , y 1), which is called the center of the beam.

2. Equation of a straight line passing through two points: A(x 1 , y 1) and B(x 2 , y 2) is written like this:

The slope of a straight line passing through two given points is determined by the formula

3. Angle between straight lines A and B is the angle by which the first straight line must be rotated A around the point of intersection of these lines counterclockwise until it coincides with the second line B. If two lines are given by slope equations

y = k 1 x + B 1 ,

y = k 2 x + B 2 , (4)

then the angle between them is determined by the formula

It should be noted that in the numerator of the fraction, the slope of the first straight line is subtracted from the slope of the second straight line.

If the equations of a straight line are given in general view

A 1 x + B 1 y + C 1 = 0,

A 2 x + B 2 y + C 2 = 0, (6)

the angle between them is determined by the formula

4. Conditions for parallelism of two lines:

a) If the lines are given by equations (4) with a slope, then the necessary and sufficient condition for their parallelism is the equality of their slopes:

k 1 = k 2 . (8)

b) For the case when the lines are given by equations in general form (6), the necessary and sufficient condition for their parallelism is that the coefficients at the corresponding current coordinates in their equations are proportional, i.e.

5. Conditions for perpendicularity of two lines:

a) In the case when the lines are given by equations (4) with a slope, the necessary and sufficient condition for their perpendicularity is that they slope factors are reciprocal in magnitude and opposite in sign, i.e.

This condition can also be written in the form

k 1 k 2 = -1. (11)

b) If the equations of straight lines are given in general form (6), then the condition for their perpendicularity (necessary and sufficient) is to fulfill the equality

A 1 A 2 + B 1 B 2 = 0. (12)

6. The coordinates of the point of intersection of two lines are found by solving the system of equations (6). Lines (6) intersect if and only if

1. Write the equations of the lines passing through the point M, one of which is parallel and the other is perpendicular to the given line l.

ANGLE BETWEEN PLANES

Let's consider two planes α 1 and α 2 given respectively by the equations:

Under angle between two planes we mean one of the dihedral angles formed by these planes. It is obvious that the angle between the normal vectors and the planes α 1 and α 2 is equal to one of the indicated adjacent dihedral angles or . That's why . Because and , then

.

Example. Determine the angle between planes x+2y-3z+4=0 and 2 x+3y+z+8=0.

Condition of parallelism of two planes.

Two planes α 1 and α 2 are parallel if and only if their normal vectors and are parallel, and hence .

So, two planes are parallel to each other if and only if the coefficients at the corresponding coordinates are proportional:

or

Condition of perpendicularity of planes.

It is clear that two planes are perpendicular if and only if their normal vectors are perpendicular, and therefore, or .

In this way, .

Examples.

DIRECT IN SPACE.

VECTOR EQUATION DIRECT.

PARAMETRIC EQUATIONS DIRECT

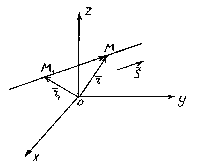
The position of a straight line in space is completely determined by specifying any of its fixed points M 1 and a vector parallel to this line.

A vector parallel to a straight line is called guiding the vector of this line.

So let the straight l passes through a point M 1 (x 1 , y 1 , z 1) lying on a straight line parallel to the vector .

Consider an arbitrary point M(x,y,z) on a straight line. It can be seen from the figure that .

The vectors and are collinear, so there is such a number t, what , where is the multiplier t can take any numeric value depending on the position of the point M on a straight line. Factor t is called a parameter. Denoting the radius vectors of points M 1 and M respectively, through and , we obtain . This equation is called vector straight line equation. It shows that each parameter value t corresponds to the radius vector of some point M lying on a straight line.

We write this equation in coordinate form. Notice, that , and from here

The resulting equations are called parametric straight line equations.

When changing the parameter t coordinates change x, y and z and dot M moves in a straight line.

CANONICAL EQUATIONS DIRECT

Let M 1 (x 1 , y 1 , z 1) - a point lying on a straight line l, and is its direction vector. Again, take an arbitrary point on a straight line M(x,y,z) and consider the vector .

It is clear that the vectors and are collinear, so their respective coordinates must be proportional, hence

– canonical straight line equations.

Remark 1. Note that the canonical equations of the line could be obtained from the parametric equations by eliminating the parameter t. Indeed, from the parametric equations we obtain or .

Example. Write the equation of a straight line in a parametric way.

Denote , hence x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Remark 2. Let the line be perpendicular to one of the coordinate axes, for example, the axis Ox. Then the direction vector of the line is perpendicular Ox, Consequently, m=0. Consequently, the parametric equations of the straight line take the form

Eliminating the parameter from the equations t, we obtain the equations of the straight line in the form

However, in this case too, we agree to formally write the canonical equations of the straight line in the form . Thus, if the denominator of one of the fractions is zero, then this means that the line is perpendicular to the corresponding coordinate axis.

Similarly, the canonical equations corresponds to a straight line perpendicular to the axes Ox and Oy or parallel axis Oz.

Examples.

GENERAL EQUATIONS A DIRECT LINE AS A LINE OF INTERCEPTION OF TWO PLANES

Through each straight line in space passes an infinite number of planes. Any two of them, intersecting, define it in space. Therefore, the equations of any two such planes, considered together, are the equations of this line.

In general, any two non-parallel planes given by the general equations

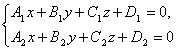
determine their line of intersection. These equations are called general equations straight.

Examples.

Construct a straight line given by equations

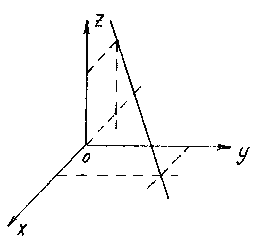
To construct a line, it is enough to find any two of its points. The easiest way is to choose the points of intersection of the line with the coordinate planes. For example, the point of intersection with the plane xOy we obtain from the equations of a straight line, assuming z= 0:

Solving this system, we find the point M 1 (1;2;0).

Similarly, assuming y= 0, we get the point of intersection of the line with the plane xOz:

From the general equations of a straight line, one can proceed to its canonical or parametric equations. To do this, you need to find some point M 1 on the line and the direction vector of the line.

Point coordinates M 1 we obtain from this system of equations, giving one of the coordinates an arbitrary value. To find the direction vector, note that this vector must be perpendicular to both normal vectors and . Therefore, for the direction vector of the straight line l you can take vector product normal vectors:

.

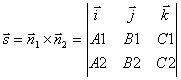Example. Give the general equations of the straight line to the canonical form.

Find a point on a straight line. To do this, we choose arbitrarily one of the coordinates, for example, y= 0 and solve the system of equations:

The normal vectors of the planes defining the line have coordinates Therefore, the direction vector will be straight

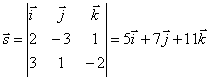. Consequently, l: .

ANGLE BETWEEN RIGHTS

corner between straight lines in space we will call any of the adjacent angles formed by two straight lines drawn through an arbitrary point parallel to the data.

Let two straight lines be given in space:

Obviously, the angle φ between the lines can be taken as the angle between their direction vectors and . Since , then according to the formula for the cosine of the angle between the vectors we get