Distribute silicon electrons among quantum cells. Distribution of vanadium electrons over quantum cells
Tasks for section 1
Sample execution homework
The structure of the atom
Task 1. a) Indicate the numerical values of the main and orbital quantum numbers of these sublevels, calculate the sequence of their filling: 5 p, 7p, 7s.
Solution. 5p 7p 7s
Meaning n 5 7 7
Meaning l 1 1 0
Sum ( n +l ) 6 8 7
Filling sequence (based on Klechkovsky's rules):
1 – 5p; 2 – 7s; 3 – 7p.
b) Distribute over quantum cells valence electrons 2s 2 2p 4, determine the chemical element and its position in the D.I. Mendeleev (period number, group, subgroup).
Solution. Valence electrons in quantum cells are distributed as follows: 2 s 2 2p 4
The proposed element oxygen is located in the second period, the sixth group, the main subgroup of the Periodic Table of D.I. Mendeleev.
in) Write the electronic formulas of atoms and ions, indicate their position in the D.I. Mendeleev (period number, group, subgroup): K, Zn 2+ .
Solution. The electronic formula of the chemical element potassium is as follows: 1 s 2 2s 2 2p 6 3s 2 3p 6 4s one . It is located in the fourth period, the first group, the main subgroup of the Periodic Table of D.I. Mendeleev. Electronic formula of the Zn 2+ cation: 1 s 2 2s 2 2p 6 3s 2 3p 6 3d 10 . Chemical element zinc is located in the fourth period, the second group, a side subgroup.
Do the same for all assignments.
STRUCTURE OF THE ATOM
In the Periodic system of D. I. Mendeleev (Table P.4) all known elements. It consists of seven periods (1-3 - small, 4-7 - large), 8 groups. Each group is divided into main and secondary subgroups. The main subgroup contains elements of small and large periods, and the side group contains only large ones.
Example 1 Specify in the Periodic system D.I. Mendeleev position (period number, group number, main or secondary subgroup) of an atom of an element with a nuclear charge of 85.
Solution. Element (85 At) is in the 6th period, 7th group, main subgroup.
Atoms of elements consist of a positively charged nucleus (protons and neutrons) and electrons. The number of electrons is equal to the atomic number of the element. The state of an electron in an atom is characterized by quantum numbers n,l, m l and m s, which are named respectively most importantly, orbital, magnetic and spin.
The order of filling the orbitals with electrons is determined by the following rules of V. Klechkovsky:
filling occurs in ascending order of the amount ( n + l);
At the same values of this sum, the sublevel with the lower value of the main value is filled first quantum number n.
Electron filling sequence energy levels and sublevels in multielectron atoms has the form
1s<2s<2p<3s<3p<4s<3d <4p<5s<4d <5p<6s<5d 4f<6p <7s<6d 5f<7p.
Example 2. Using the Klechkovsky rules, calculate which sublevel is filled with electrons first 4 R or 5 s.
Solution. For 4 R-sublevel sn + l= 4 + 1 = 5; for 5 s-sublevel Sn+l= 5 + 0 = 5. Since the sum is the same, the sublevel with the lower value is filled first n, i.e. 4 R.
Example 3 According to the distribution of valence electrons - 3d 5 4s 2 Determine what element it is, indicate its symbol and write the complete electronic formula.
Solution. The value of the principal quantum number of the last energy level corresponds to room period, so the element is in 4th period. The sum of valence electrons shows room the group in which the element is located, in this case the number groups 7. Since the valence electrons are on d-sublevel, then this is an element side subgroup: 25 Mn 1 s 2 2s 2 2p 6 3s 2 3p 6 3d 5 4s 2 .
Example 4. Write the complete electronic formula of an atom of an element with a nuclear charge of 22.
Solution. 22 Ti 1 s 2 2s 2 2p 6 3s 2 3p 6 3d 2 4s 2 .
Example 5. Write the complete electronic formulas of the Fq, Sn 2+ ions.
Solution. When a negatively charged ion is formed, the neutral atom of the element accepts electrons: F 0 + 1 ē = Fq; electronic formula of the ion 9 Fq1 s 2 2s 2 2p 6. A positively charged ion is obtained when a neutral atom of an element gives up electrons: Sn 0 - 2 ē = Sn 2+ ; electronic formula of the ion 50 Sn 2+ 1 s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 6 4d 10 5s 2 5p 0 .
Tasks for section 1
Each task contains three questions(a B C).
| Job number | a) Indicate the numerical values of the main and orbital quantum numbers of these sublevels, calculate the sequence of their filling | b) Distribute the valence electrons among the quantum cells, determine the chemical element and its position in the D.I. Mendeleev system (period number, group, sub-group) | c) Write the electronic formulas of the proposed atoms and ions, indicate their position in the system of D.I. Mendeleev (period number, group, subgroup) |
| 3p; 4s; 2p | 3d 1 4s 2 | Fe, Na+ | |
| 3d; 4p; 3p | 3d 2 4s 2 | Co, Cl- | |
| 5d; 4p; 4d | 3d 3 4s 2 | Ni, Ba2+ | |
| 3d; 4f; 5s | 3d 5 4s 1 | Zn, Ca2+ | |
| 4d; 4s; 5s | 4d 5 5s 2 | Sn, S 2- | |
| 6s; 4p; 4f | 3d 6 4s 2 | W, In 3+ | |
| 3d; 5s; 7p | 3d 7 4s 2 | S, La 3+ | |
| 4d; 6s; 5d | 3d 8 4s 2 | F, Tl 3+ | |
| 4p; 5p; 4f | 3d 10 4s 1 | Br, Zr 4+ | |
| 3d; 3p; 2s | 3d 10 4s 2 | Al, Hg2+ | |
| 5d; 3s; 6s | 4s 2 4p 1 | Pb, Au 3+ | |
| 6d; 4f; 5p | 4s 2 4p 2 | Ge, Ag+ | |
| 5d; 3p; 4d | 4 s 2 4p 3 | Ga, Sb 3+ | |
| 7s; 6p; 4d | 4s 2 4p 4 | N, Bi 3+ | |
| 5d; 4p; 3d | 4s 2 4p 5 | Cl, Pb 2+ | |
| 5s; 6s; 4p | 4s 2 4p 6 | Y, Hf 4+ | |
| 6p; 5f; 6d | 5d 7 6 s 2 | Zr, At- | |
| 5d; 5s; 4f | 5d 10 6 s 2 | Ta, Ga 3+ | |
| 3s; 4d; 3p | 5d 3 6 s 2 | Cr, Se 2- | |
| 5f; 4d; 4s | 5d 5 6 s 2 | Mo, Cu 2+ |
Lecture 5. MAIN QUANTUM NUMBER (n) The number (n) characterizes the total energy of an electron in an atom. It can take the values of integers: 1, 2, 3 ... n Each value of the quantum number n has its own energy level. The number of energy levels in an atom populated by electrons is equal to the number of the period in which the element is located in the periodic table.

PRINCIPAL QUANTUM NUMBER (n) For example, electrons in an atom of any element belonging to the third period are located on three energy levels. Electrons located at the energy level closest to the series (n=1) have the lowest energy. When absorbing quantum energy (E=hν), the electron goes to a higher energy level. When moving to a lower level, an electron emits a quantum of energy. (continuation)

ORBITAL QUANTUM NUMBER (ɭ) The number ɭ determines the shape of the orbital, and hence the electron cloud. It can take a value from zero to n-1: ɭ = 0, 1, 2, 3 … n-1 For example, if the main quantum number is four (n=4), then ɭ takes the values 0, 1, 2, 3.

Electrons with the same values of the number n, but different (ɭ), differ somewhat in energy. Therefore, the electrons of a given energy level are said to group into energy sublevels. ORBITAL QUANTUM NUMBER (ɭ) These sublevels are assigned the following letter designations: Orbital quantum number (l) Energy sublevel designation s p d f (continued)

The number of sublevels in each energy level is equal to its quantum number, i.e. number of this level. The first energy level (n=1) consists of one s - sublevel; the second (n=2) - from two (s; p) sublevels; the third (n=3) - from three (s; p; d) sublevels; fourth (n=4) – from four (s; p; d; f) sublevels: Principal quantum number (n) (level number) Types of sublevels s s, p s, p, d s, p, d, f ORBITAL QUANTUM NUMBER (ɭ ) (continuation)

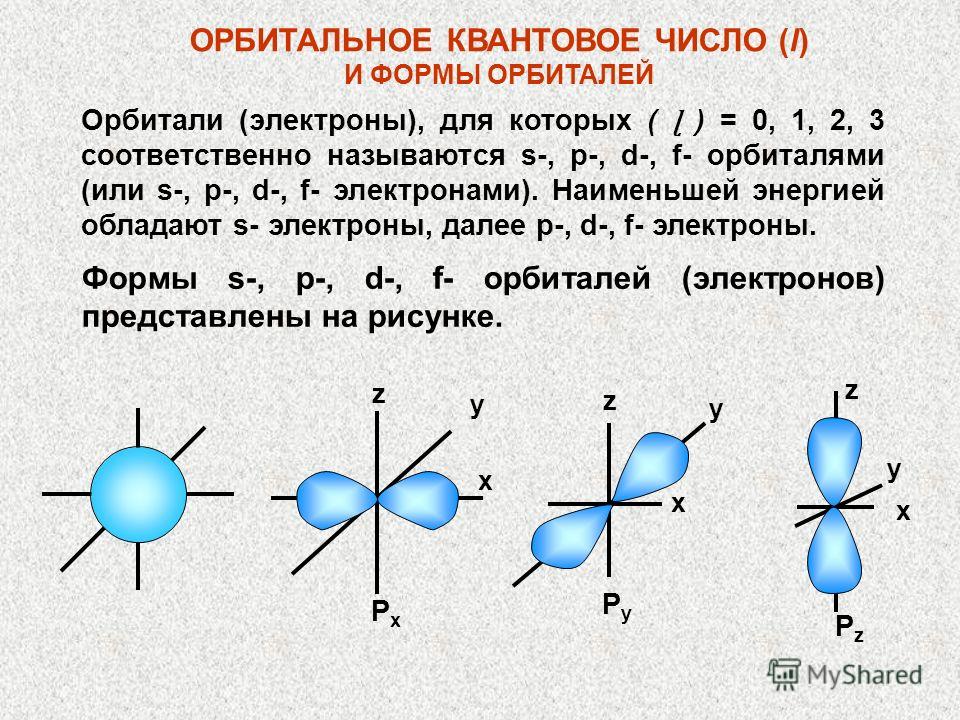
ORBITAL QUANTUM NUMBER (l) AND ORBITAL SHAPES Orbitals (electrons) for which (ɭ) = 0, 1, 2, 3 respectively are called s-, p-, d-, f-orbitals (or -, f- electrons). S-electrons have the lowest energy, then p-, d-, f-electrons. The shapes of s-, p-, d-, f-orbitals (electrons) are shown in the figure. x x x z PyPy PzPz y y y z z PxPx
The number m characterizes the spatial arrangement of the orbitals (clouds). It can take all integer values from – ɭ to + ɭ, including zero: m = – l … 0 … + l For example: with ɭ = 2 we have m = – 2, – 1, 0, + 1, + 2 m depends on the orbital quantum number and indicates the number of energy states (orbitals) in which an electron of a given sublevel can be (with a given value of ɭ). The number of orbitals with a given value (ɭ) is 2 ɭ + 1 MAGNETIC QUANTUM NUMBER (m)

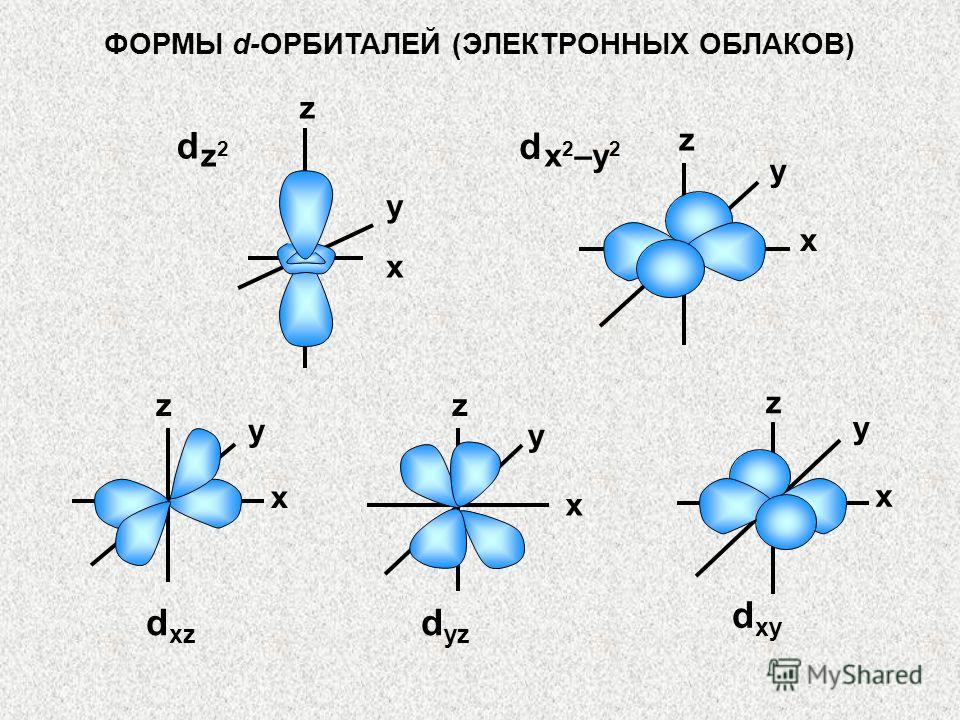
RELATIONSHIP OF MAGNETIC AND ORBITAL QUANTUM NUMBERS Orbital quantum number (ɭ) Magnetic quantum number (m) Number of orbitals (clouds) – 1, 0, + 1 – 2, – 1, 0, + 1, + 2 –3, – 2, – 1, 0, +1, +2,

QUANTUM CELLS (ORBITALS) Each orbital is usually represented by a rectangle, which is also called a quantum cell. s - sublevel consists of 1 cell p - sublevel consists of 3 cells d - sublevel consists of 5 cells f - sublevel consists of 7 cells s p d f

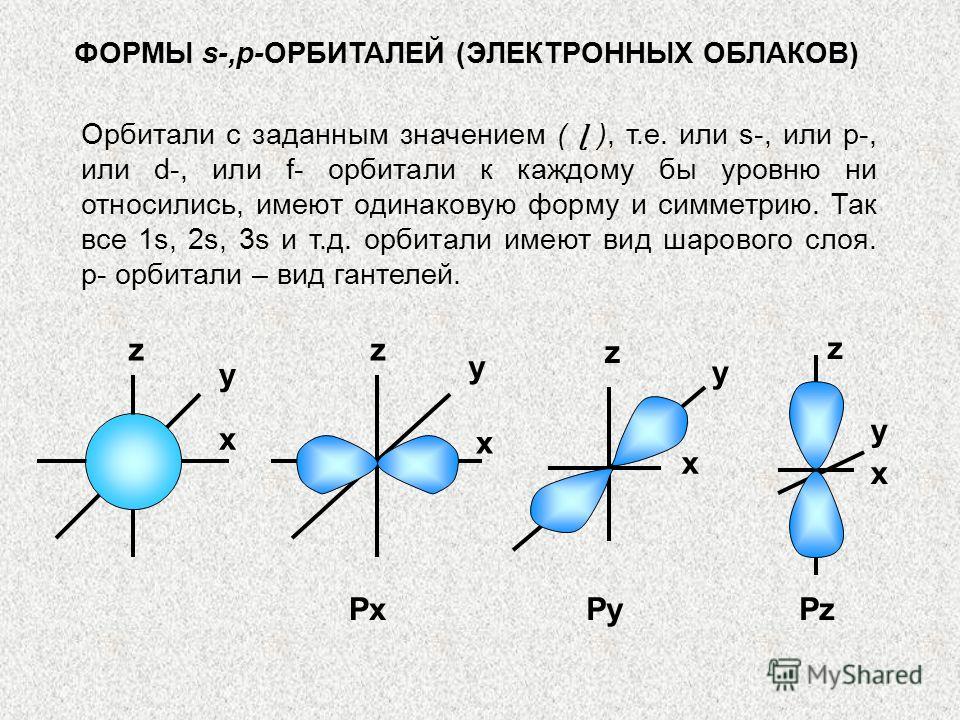
SHAPES of s-,p-ORBITALS (ELECTRON CLOUDS) Orbitals with a given value (ɭ), i.e. or s-, or p-, or d-, or f-orbitals to each level, they have the same shape and symmetry. So everything is 1s, 2s, 3s, etc. orbitals are spherical. p-orbitals are a type of dumbbell. x x x x y z PxPyPz y y y z z z
SPIN QUANTUM NUMBER (S) For a given value of m, the number s can have only two meanings: The hypothesis that an electron has a so-called spin was put forward in 1925 (at first - for clarity - it was believed that this phenomenon is similar to the rotation of the earth around its axis as it moves in orbit around the Sun). + ½ and – ½ In fact, spin is a purely quantum property of an electron that has no classical analogues. Strictly speaking, spin is the proper angular momentum of an electron, not related to motion in space. For all electrons, the absolute value of the spin is always s = 1/2. The projection of the spin onto the Z axis (magnetic spin number) can only have two values: m S = +1/2 or m S = -1/2.

"There cannot be two electrons in an atom with the same values of all four quantum numbers." Since the AO is characterized by three quantum numbers n, l, m, then it can contain no more than two electrons with opposite spins: PAULI PRINCIPLE X e = 2 (2l + 1); s–2; p–6; d - 10; f – 14 The maximum number of electrons is: At the sublevel: At the level: N = 2n2

“When filling levels and sublevels with electrons, the sequence of placement of electrons in an atom should correspond to their greatest connection with the nucleus, i.e. the electron must have the lowest energy." PRINCIPLE OF LEAST ENERGY This principle expresses the general thermodynamic requirements for the stability of systems: maximum stability corresponds to minimum energy. In practice, the "principle of least energy" is applied in the form of Klechkovsky's rules:

Let's compare the energy reserve at the sublevels: 4s 
At sublevels 3d, 4p and 5s the sum (n+l) is equal to 5: SUBLEVEL (n + l) 3+2=5 4+1=5 5+0=5 3d 4p 5s 1s2s2p3s4s3d4p5s4d5p6s4f5d Klechkovsky's rules. Example 2: In this case, the sublevel with the lower value of the main quantum number n is filled first, i.e. in the following sequence: 3d 3p 5s In general, the filling of levels and sublevels goes in the following sequence: 6p7s5f6d6p7s5f6d


In electronic formulas, the letters s, p, d, f denote energy electrons. The numbers in front of the letters indicate the energy level in which the given electron is located, and the index at the top right is the number of electrons in this sublevel Recording 5p 3 means that there are three electrons in the p-sublevel of the fifth energy level. ELECTRONIC FORMULA OF ATOMS

When compiling the electronic formula of an atom of any element, one must be guided by the following sequence: 1. Determine the ordinal number of the element (and, consequently, the number of electrons in the atom); 2. Determine the number of energy levels on which electrons will be located /by period number/; 3. Distribute electrons into sublevels and levels, guided by the requirements of the main provisions. ELECTRONIC FORMULA OF ATOMS

4. Distribute electrons over energy levels and sublevels, guided by the requirements of Pauli's rule, Klechkovsky's rules and Hund's rules, as well as the following table: ELECTRONIC FORMULA OF ATOMS Level number Number of sublevels Types of sublevels Number of orbitals Max. number of electrons per sublevel 11 1s s 2p s 3p 3d s 4p 4d 4f
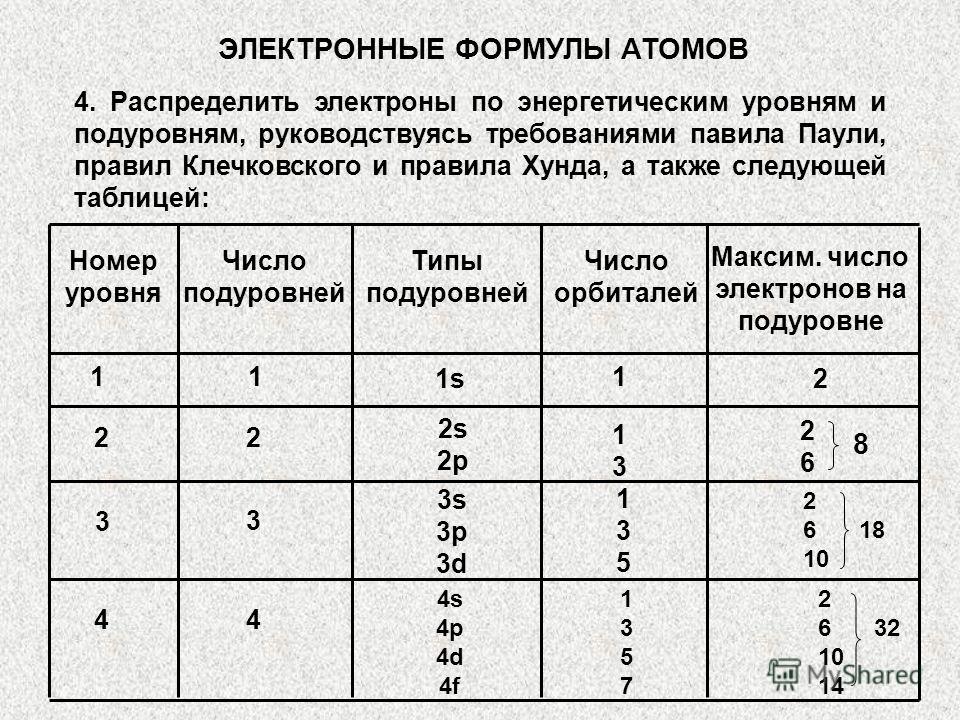
1. Compose the electronic formula of the sulfur atom: 1. Sulfur has a serial number of 16: there are only 16 electrons in the atom 2. Sulfur is in the third period: 16 electrons are located on three energy levels: 1s 2s2p 3s3p3d 3. Let's distribute 16 electrons over energy sublevels in accordance with the principle of least energy and the Pauli principle: 16 S - 1s 2 2s 2 2p 6 3s 2 3p 4 - the formula of the sulfur atom. COMPILATION OF ELECTRONIC FORMULA OF ATOMS

2. Compose the formula of the atom (Ca) of calcium: 1. Serial number Ca \u003d 20: there are 20 electrons in the atom 2. Ca is in the fourth period: 20 electrons are located at four levels: 1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 3. Distribute 20 electrons: 20 Ca - 1s 2 2s 2 2p 6 3s 2 3p 6 3d 0 4s 2 or 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2

3. Compose the formula of the titanium atom / Ti /: 1. Serial number Ti = 22: there are 22 electrons in the atom 2. Ti is in the 4th period: electrons are located at 4 levels: 1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 3. Distribute 22 electrons into sublevels, fulfilling the requirements of the Pauli principle and the principle of least energy: 22 Ti - 1s 2 2s 2 2p 6 3s 2 3p 6 4s 2 3d 2 or 22 Ti - 1s 2 2s 2 2p 6 3s 2 3p 6 3d 2 4s 2 COMPILATION OF ELECTRONIC FORMULA OF ATOMS

4. Compose the formula of the cerium atom (Ce): 1. Serial number Ce \u003d 58: there are 58 electrons in the atom 2. Ce is in the sixth period: 58 electrons are located in six levels: 1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 5s 5p 5d 5f 6s 6p … 3. Distribute 58 electrons among the sublevels 58 Ce – 1s 2 2s 2 2p 6 3s 2 3p 6 3d 10 4s 2 4p 6 4d 10 5s 2 5p 6 6s 2 4f 2 4f (n + l = = 7) 5p (n + l == 6) 5s (n + l == 5) 6s (n + l == 6) 5s 5p 6s 4f

Depending on which sublevel is filled with electrons, all elements are divided into four types (families): 1) S-elements: the S-sublevel of the outer level is filled. Their general formula is: … nS 2 n – period number The s-elements include the first two elements of each period. 2) P-elements: the P-sublevel of the external level is filled. Their general formula is: … nS 2 n P 1–6 The p-elements include the last six elements of each period /except for the 1st and 7th/. FOUR TYPES OF ELEMENTS

3) d - elements: they fill the d-sublevel of the second level from the outside. Their general formula is: ... (n-1) d 1-10 nS 2 At the outer level they have 2 sometimes 1 electron (s 1-2). The d-elements include 10 elements of large periods located between the s- and p-elements. FOUR TYPES OF ELEMENTS or (n-2) f 1-14 (n-1) d 1 nS 2 4) f - elements: they fill the d-sublevel of the second level from the outside. Their general formula is: ... (n-2) f 1-14 nS 2 The f-elements include lanthanides and actinides

Drawing up electronic configurations of atoms without the help of the periodic table To do this, you need to know: 1. How many elements are contained in a period: period Number of elements in a period = 18 3 = 36 4 = 54 5 = 86 6 not finished

2. That the first two elements in a period are S-elements. 3. The last six elements of each period (except the 1st and 7th) are p-elements of elements (starting from the 3rd) of large periods - these are d-elements. 5. Lanthanum (57 La) is followed by 4f elements. 6. After actinium (89 Ac), 5f elements follow Compilation of electronic configurations of atoms without the help of the periodic table

3. Solution 4. Each AO is characterized by three values of quantum numbers: n, l, m l. Level L (n = 2) has two sublevels: l = 0 and l = 1. For l = 0, there is only one" title="(!LANG: Solution 3. No, because for the d-sublevel l = 2, which is possible only for values n > 3. Solution 4. Each AO is characterized by three values of quantum numbers: n, l, m l Level L (n = 2) has two sublevels: l = 0 and l = 1. For l = 0 there is only one" class="link_thumb"> 34 !} Solution 3. No, because for the d-sublevel l = 2, which is possible only for values n > 3. Solution 4. Each AO is characterized by three values of quantum numbers: n, l, m l. Level L (n = 2) has two sublevels: l = 0 and l = 1. At l = 0 there is a single value m l = 0 (one AO), and at l = 1 there are three values m l = 1, 0, + 1 (three AOs in total), therefore, the total number of AOs at the L-level is four. EXAMPLES and CHALLENGES 3. Solution 4. Each AO is characterized by three values of quantum numbers: n, l, m l. Level L (n = 2) has two sublevels: l = 0 and l = 1. For l = 0 there is only one "> 3. Solution 4. Each AO is characterized by three values of quantum numbers: n, l, m l. Level L ( n = 2) has two sublevels: l = 0 and l = 1. At l = 0 there is a single value m l = 0 (one AO), and at l = 1 there are three values m l = 1, 0, + 1 (total three AO), therefore, the total number of AO at the L-level is four. EXAMPLES and PROBLEMS "> 3. Solution 4. Each AO is characterized by three values of quantum numbers: n, l, m l. Level L (n = 2) has two sublevels: l = 0 and l = 1. For l = 0, there is only one" title="(!LANG: Solution 3. No, because for the d-sublevel l = 2, which is possible only for values n > 3. Solution 4. Each AO is characterized by three values of quantum numbers: n, l, m l Level L (n = 2) has two sublevels: l = 0 and l = 1. For l = 0 there is only one"> title="Solution 3. No, because for the d-sublevel l = 2, which is possible only for values n > 3. Solution 4. Each AO is characterized by three values of quantum numbers: n, l, m l. Level L (n = 2) has two sublevels: l = 0 and l = 1. For l = 0 there is only one"> !}
The considered electron shell of an atom is filled with electrons in accordance with three principles: the principle of least energy, the Pauli principle / rule / Hund.
The principle of least states that an electron in an atom occupies the free sublevel at which it will have the minimum energy value. In another way, the electron remains at the sublevel at which the strongest bond with the nucleus is provided.
The sequence of filling the sublevels corresponds to the above actual arrangement of sublevels in the structure of the electron shell of the atom:
1sà2sà2pà3sà3pà4sà3d –… etc. /cm. above/.
The Pauli principle /Pauli prohibition/ says that an atom cannot even have two electrons with the same values of four quantum numbers.
Consequence. An orbital can contain two electrons with different spins (that is, with different values of the spin quantum number: ms = +1/2 and ms = –1/2).
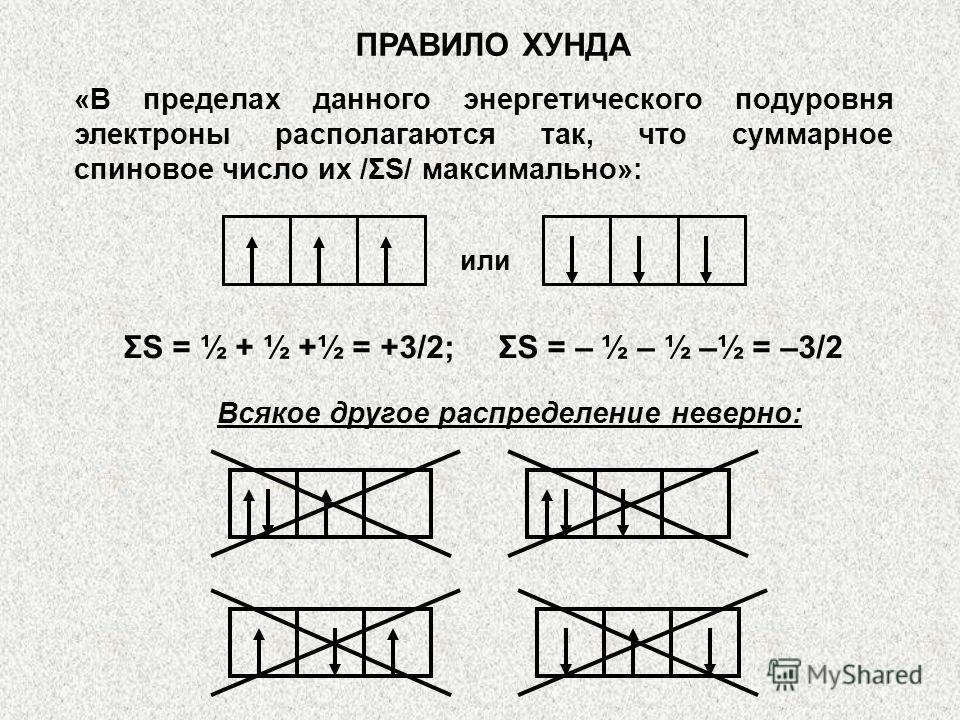
The third principle is the principle or rule of Gunda /Hunda/. It explains the order in which electrons fill the quantum sublevel. Within the sublevel, electrons are distributed in such a way that their total quantum number has a maximum value /first one electron per orbital, and then pairing/. The correct distribution will be, for example, three p-electrons in this way:
Depending on which sublevel is filled with the last electrons, s-, p-, d-, f-elements are distinguished.
s-elements are those elements in whose atoms the last electrons occupy the s-sublevel of the outer quantum level. /For example, sodium, magnesium, potassium, calcium, etc./.
p-elements are those elements in whose atoms the last electrons occupy the p-sublevel of the outer quantum level. /For example, carbon, oxygen, chlorine, etc./.
The d-sublevel, filled with the last electrons, classifies the elements as d-elements. /For example, d-elements are titanium, chromium, iron, copper, because in these elements, the last electrons occupy the d-sublevel of the penultimate level/.
f-elements are those elements in whose atoms the last electrons occupy the f-sublevel of the second from outside the quantum level. /For example, praseodymium, europium, erbium, etc./.
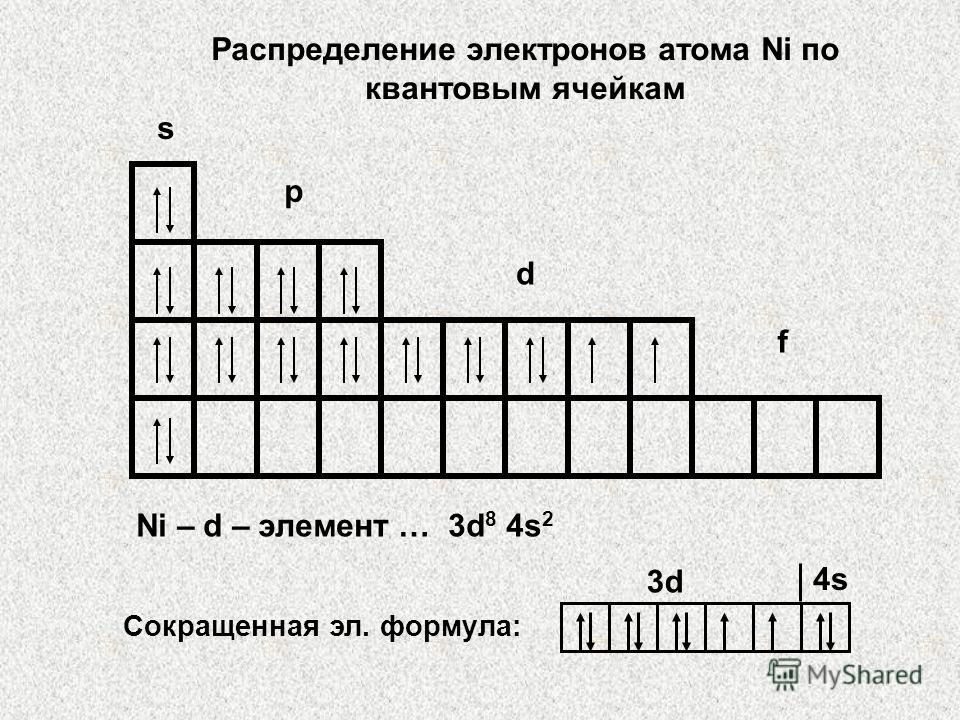
2.1.7. Image of the electronic structure of atoms using electronic formulas and quantum cells.
The electronic structure of any atom is represented by electronic formulas. In electronic formulas, the quantum electronic level is denoted by the numerical value of the main quantum number n, the sublevel is written by the letter designation of the corresponding sublevel, and the number of electrons in the sublevel is indicated by the degree of the sublevel designation. For example, 3d5 means that there are five electrons in the d-sublevel of the 3rd quantum level. The electronic formula of any element consists of a complete set of such fragments, as indicated in the example. Thus, the electronic formula of the titanium atom /№22/ is: 1s22s22p63s23p64s23d2. The sum of all powers is 22, which means that the titanium atom, having a nuclear charge of +22, contains 22 electrons on the electron shell, which, with their total negative charge (–22), compensate for the positive charge of the atomic nucleus, making the atom a complex electrically neutral system.
It is more convenient to compose electronic formulas after considering the structure of the periodic system of elements of D.I. Mendeleev. Looking ahead and based on the knowledge gained in high school, we present the periodic system of elements in the form of electronic formulas. (Fig. 2.10.) We will return later on writing the electronic formulas of a specific element in the periodic system and consider an algorithm by which it is easy to learn how to write the electronic formula of any element. Secondly, the structure of the electron shell of an atom is depicted using quantum cells.

 I 1s2
I 1s2
II 2s2 2p6
VI 6s2 5d1 4f14 5d9 6p6
VII 7s2 6d1 5f14 6d9 7p6
We have already used quantum cells, although we did not introduce the concept of “quantum cell”. A quantum cell is nothing more than a graphic representation of an orbital. It is shown by a cell, and the electrons in the orbital are depicted by an arrow standing in a cell. One cell is assigned for the s-sublevel, since the s-sublevel has only one orbital. Three cells are allocated for the p-sublevel because the p-sublevel contains three p-orbitals. The d-sublevel is represented by five cells, and the f-sublevel by seven cells.
The electronic structure of the titanium atom, for which we have already written the electronic formula, depicted using quantum cells, looks like this:
Ministry of Agriculture of the Russian Federation
FGOU VPO "Ulyanovsk State Agricultural Academy"
Tasks for tests and examination questions in the discipline
Ulyanovsk - 2010
A.L. Ignatov. Tasks for tests and examination questions in the discipline "Chemistry" / Ed. prof. IN AND. Kostina. - Ulyanovsk State Agricultural Academy, 2009, 58s.
Reviewer: Kafiyatullina A.G., Ph.D., Senior Lecturer, Department of Chemistry, Ulyanovsk State Pedagogical University I.N. Ulyanova»
This manual contains control tasks for the main sections of the chemistry course, examples of solving typical problems and a list of exam questions.
For students of the Faculty of Engineering of correspondence courses in the specialty: 110301 "Mechanization of agriculture", 110304 "Technology of maintenance and repair of machines in the agro-industrial complex", 190601 "Automobiles and automotive industry".
© A.L. Ignatov, 2010.
© FGOU VPO "Ulyanovsk State Agricultural Academy", 2010.
CONTROL TASKS
STRUCTURE OF THE SUBSTANCE
Examples of solving typical problems
Task 1. Which energy sublevel of an atom is filled with electrons earlier: a) 4s or 3d; b) 5p or
4d; c) 6p or 4f?
Solution. The order of filling the energy sublevels with electrons is determined by the Klechkovsky rule, according to which the sublevels are filled with electrons in the order of the successive increase in the sum of the main and orbital quantum numbers (n + l), and for the same values of this sum, in the order of increasing of the main quantum number n. Let us find the sum (n+l) for the energy sublevels listed in the condition of the problem.
Sum n+l 4+0=4 |
Consequently, in case (a), the 4s sublevel is first filled with electrons, and then the 3d sublevel; in case (b), first 4d, then 5p; in case (c), first 4f, then 6p.
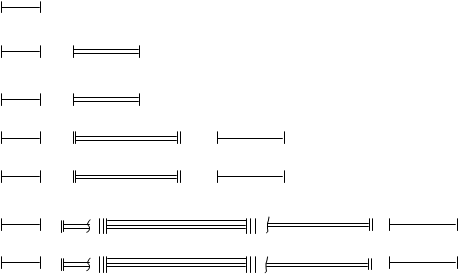
Task 2 . Distribute the electrons by levels, write the electronic formula of the Fe atom in the ground and excited state, indicate the quantum states of its valence electrons and distribute them among the quantum cells.
Solution. The solution of this problem must begin with determining the number of levels that will be occupied by electrons in an unexcited iron atom. Their number is determined by the number of the period in which the element is located. For iron, it is equal to 4. At the first two levels, the maximum number of electrons is 2 and 8, respectively (determined by the doubled square of the main quantum number 2n2). The maximum number of valence electrons is determined by the number of the group in which the element (VIII) is located. Since iron is located in a side subgroup, its valence electrons are distributed between s - a sublevel of the external energy level and d - a sublevel of the preexternal level. So, there are 2 electrons in the 4s state, and 6 in the 3d state (group number minus 2). The total number of electrons in the penultimate energy level of an iron atom is 14.
So, the electrons in an unexcited iron atom are distributed among the levels as follows:
Each nth level is split into n sublevels. When writing the electronic formula of an atom, the sublevels are arranged in ascending order of the sum of the principal and orbital quantum numbers:
Valence electrons - 3d 6 4s2.
The order of filling the quantum cells of the sublevel with electrons is determined by the Hund rule according to the principle of the largest absolute value of the total spin:
In an excited iron atom, one s - electron goes to the 4p - sublevel. In an excited state, electrons are distributed over quantum cells as follows:
Task 3. Write the electronic formulas of the Mn2+, S2-, Br- ions.
Solution. At the Mn atom (d-element), electrons are distributed
energy levels as follows: 1s2 2s2 2p6 3s2 3p6 3d 5 4s 2
When positive ions are formed in d - elements, the s-electrons of the outer layer are always removed first, that is, for Mn + 2, the electronic formula is valid:
1s2 2s2 2p6 3s2 3p6 3d 5 4s 0
then for the S2– ion, the “completion” of the 3p sublevel will occur
S2– :1s2 2s2 2p6 3s 2 3p 6
A similar “completion” of the sublevel occurs during the formation of the Br- ion:
Br:1s2 2s2 2p6 3s2 3p6 3d10 4s 2 4p 5
Br– :1s2 2s2 2p6 3s2 3p6 3d10 4s 2 4p 6 |
|||||||
Task 4. Indicate the position of the element in the periodic system (period, group, subgroup), if the last electron in its atom fell into the state: a) 3d6; b) 4p2 .
Justify the answer.
Solution. a) If the last electron hit the atom in the d-state, then this is an element of the side subgroup. In the atoms of the elements of the secondary subgroups, the last valence electron falls on d - the sublevel of the penultimate energy level. It follows from this that n-1=3 and n=4. The value of the main quantum number - 4 - determines the number of the period - 4. Since the 4s state is filled with electrons earlier than 3d, the total number of electrons that can be valence is 4: 3d2 4s2. This means that this is an element of the 4th period of the IV group of the side subgroup - titanium (Ti).
b) If the last electron entered the atom in the p-state, then this is an element of the main subgroup.
In the atoms of the elements of the main subgroups, valence electrons are located at the outer energy level. Hence the value of the main quantum number - 4 - determines the number of the period. Since the p-state of the outer level is filled with electrons after the s-state, the total number of valence electrons, equal to 4, determines the group number. Therefore, this is an element of the 4th period of the IV group and the main subgroup - germanium.
Task 5. Determine which electron clouds overlap in the BCl3 molecule, what bond angle the molecule has, whether the BCl3 molecule is polar or not. Justify your answer, consider the structure of the BCl3 molecule from the standpoint of the VS method (valence bonds).
Solution. According to the position of the element in the periodic system, indicate the quantum states of valence electrons in atoms that form bonds, and distribute them according to
quantum cells: В…2s 2 2p1 , but since the boron atom forms three chemical bonds, it is in an excited state and hybridization of sp2 electronic orbitals occurs; three hybrid electron clouds are formed.
22p1 | ||||||||
B* ….2s1 2p2 | ||||||||
23p5 | ||||||||
The p-electron is involved in the formation of a bond in chlorine.
The B–Cl bonds are formed by the overlap of the hybrid electron clouds of the В atom and the p-electron cloud of the Cl atom.
The direction of the hybrid electron clouds of the trivalent atom B determines the direction of the bonds and the shape of the BCl3 molecule. The B–Cl bonds are directed at an angle of 1200 , and the BCl3 molecule has the shape of a flat triangle. The scheme of bond formation in a molecule is shown in Fig.1.
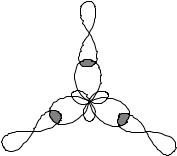
The bond dipole moment vectors µb >0 are directed towards the atom with higher electronegativity. The total dipole moment of the PM molecule is 0, i.e. the molecule is nonpolar, although all B–Cl bonds are polar.
Task 6. What is the relationship between particles in crystals of the following substances: CH4, Ne, Rb, RbF, Si, ZnSe? What type of crystal lattice according to the nature of the particles and the types of bonds between them do these substances have in
condensed state?
Solution. Methane and neon crystals are characterized by a molecular lattice. The sites of the first crystal lattice contain nonpolar CH4 molecules, between which the dispersion component of van der Waals forces acts. Dispersion interaction also manifests itself in crystals between monatomic neon molecules.
Rubidium is a metal; crystalline rubidium is characterized by a metallic lattice; the bond between the rubidium cations located at the lattice sites is metallic.
In the RbF compound, a typical ionic bond operates, since the difference in the electronegativity of the atoms
more than two units: ΔX RbF \u003d XF - XRb \u003d 4.0 - 0.8 \u003d 3.2 (Appendix I), RbF crystals are characterized by an ionic lattice, at the nodes of which there are positive and negative ions Rb + and F -, between which the ionic bond.
Crystalline silicon (silicon is a non-metal) has a covalent crystal lattice like diamond, in which each silicon atom is connected to four neighboring atoms by a non-polar covalent bond. Zinc selenide crystals have a covalent lattice.
A polar covalent bond acts between zinc and selenium atoms located at the nodes of the crystal lattice, since ∆XZnSe = 2.4 - 1.6 = 0.8
Exercise 1
Tasks are given in table 1. The number of the variant corresponds to the row, the task number corresponds to the column.
1. Distribute electrons over energy levels, write the electronic formula of the atom proposed in the task, indicate the quantum states of valence electrons, distribute them among quantum cells in the unexcited and excited states, indicate which electronic family this element belongs to?
2. Write the electronic formulas of the proposed ions, indicate the quantum states of the valence electrons and distribute them among the quantum cells.
3. In what sequence will the sublevels proposed in the task be filled with electrons? Give an explanation.
4. According to the quantum state of the last electron, indicate the position of the element in the periodic system (period, group, subgroup).
5. Consider the structure of the molecules proposed in the task from the standpoint of the method of valence bonds, indicate






