2. KINEMATIČKA ANALIZA MEHANIZAMA

2.1. Ciljevi i zadaci kinematičke analize

Mechanism Synthesis- dizajn - ima značajne poteškoće teorijske prirode, pa je pri izvođenju primijenjenih inženjerskih zadataka rjeđi od analize.

Analiza mehanizama- proučavanje njegovih glavnih parametara u cilju proučavanja zakonitosti promjene i na osnovu toga izbor najboljeg mehanizma iz niza poznatih. U poređenju sa sintezom, analiza mehanizama se široko koristi u praksi.

Ciljevi:

Određivanje kinematičkih karakteristika karika: pomak; brzina; ubrzanje; putanja kretanja; funkcija položaja sa poznatim zakonima kretanja ulaznih (vodećih) karika.

Procjena kinematičkih uslova rada radne (izlazne) veze.

Određivanje potrebnih numeričkih podataka za izvođenje energetskih, dinamičkih, energetskih i drugih proračuna mehanizma.

Zadaci:

o pozicijama karika mehanizma. Određivanje putanja kretanja tačaka;

o brzinama veza ili pojedinačnih tačaka mehanizma;

o ubrzanjima karika ili pojedinačnih tačaka mehanizma.

Metode:

grafički (ili metoda grafikona i dijagrama);

grafičko-analitički (ili metoda planova brzina i ubrzanja);

analitički;

eksperimentalni.

Kinematička analiza mehanizma se vrši sledećim redosledom: prvo se istražuje kretanje početnih karika, a zatim se vrši analiza pojedinih strukturnih grupa po redosledu njihovog pričvršćivanja tokom formiranja mehanizma. U tom slučaju će u svakoj strukturnoj grupi biti poznati položaji, brzine i ubrzanja onih elemenata za koje je ova grupa vezana. Kinematska analiza svake grupe Assur mora započeti određivanjem kinematičkih parametara unutrašnjih parova grupe. Zatim se određuju parametri preostalih tačaka grupe i ugaone brzine i ubrzanja njenih karika.

Svaka klasa grupa Assur odgovara specifičnoj metodi kinematičke analize.

Shodno tome, kinematičke analize mehanizma treba započeti tek nakon strukturna analiza, na osnovu čega se utvrđuje procedura pristupanja grupama Assur.

Također, prije izvođenja kinematičke analize potrebno je obratiti pažnju na poštovanje uslova ručice za pokretanje u kinematičkim parovima. Za neke omjere dimenzija karika njihova rotacija je nemoguća iz geometrijskih razloga. Faktori sile takođe mogu uticati na okretanje karika.

Mogućnost pokretanja karika je glavni faktor koji određuje performanse mehanizma

2.2. Metoda grafičke kinematičke analize

Prednost ove metode je njena jasnoća i jednostavnost. Dobar je za kinematičku analizu karika koje vrše povratno kretanje. Nedostatak metode je niska tačnost, koja zavisi od tačnosti grafičkih konstrukcija.

Problem sa pozicijom rješava se konstruisanjem više kombinovanih planova mehanizma u odabranoj skali dužine sa različitim uzastopnim pozicijama vodeće karike.

Problemi sa brzinama i ubrzanja rješavaju se konstruiranjem grafikona (dijagrama) pomaka, brzina i ubrzanja tačke koja se proučava.

Slijed kinematske analize:

Prvo, nekoliko (najčešće 12 ili više) kombinovanih planova mehanizma se gradi u proizvoljno odabranoj skali dužine.

Zatim se gradi graf putanje (pomeranja) tačke ili karike koja se proučava, za šta se koriste kombinovani planovi mehanizma i sukcesivnih pozicija tačke ili karike koja se proučava.

Grafičkom diferencijacijom grafa pomaka gradi se graf brzine posmatrane tačke.

Grafička diferencijacija grafa brzine gradi graf ubrzanja.

Grafička diferencijacija se može izvesti metodom tetiva i metodom tangenta. Kako bi se poboljšala tačnost, zgodno je koristiti obje metode istovremeno.

Ako se kretanje početne karike mehanizma vrši konstantnom kutnom brzinom, tada se kutno ubrzanje jednako nuli.

Kretanje početnog mehanizma sa ugaonom brzinom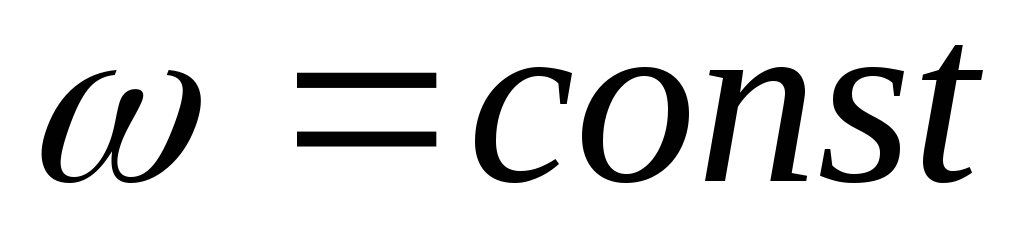

i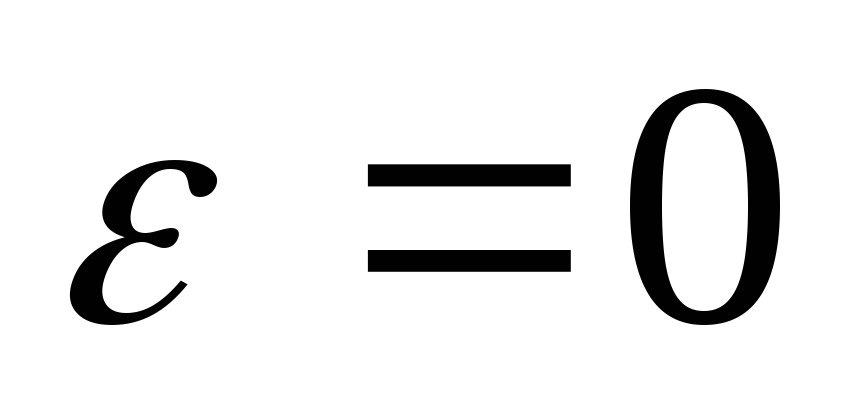

naziva se stalnim ili glavnim kretanjem mehanizma .

Kinematička shema mehanizma izgrađena je strogo prema mjerilu.

Faktor skale u TMM-u je omjer prirodne vrijednosti mjerene u SI jedinicama, tj. u m (metrima) do dužine segmenta koji ga prikazuje, mjereno u mm.

Faktor skale plana mehanizma je označen sa:

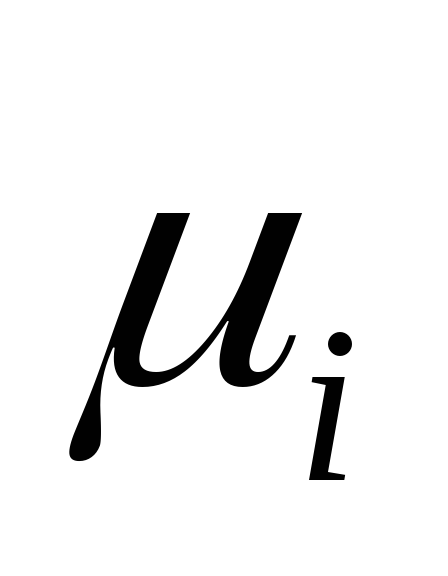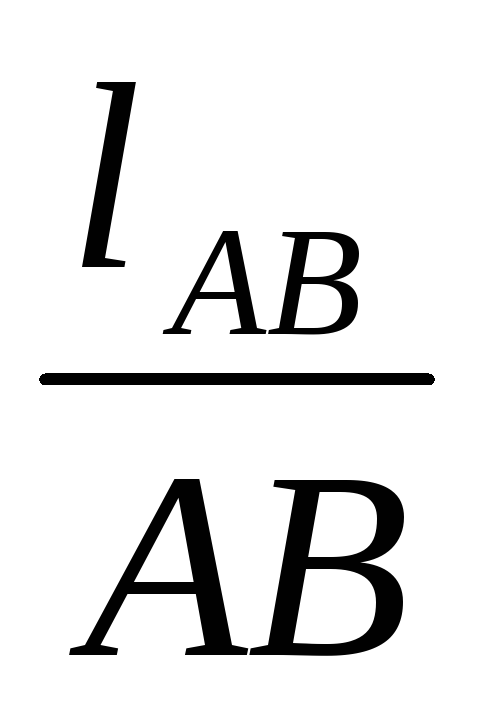
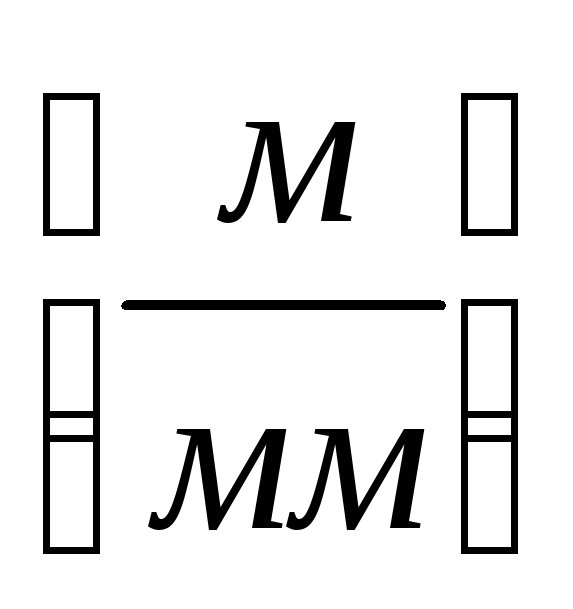= - faktor skale.

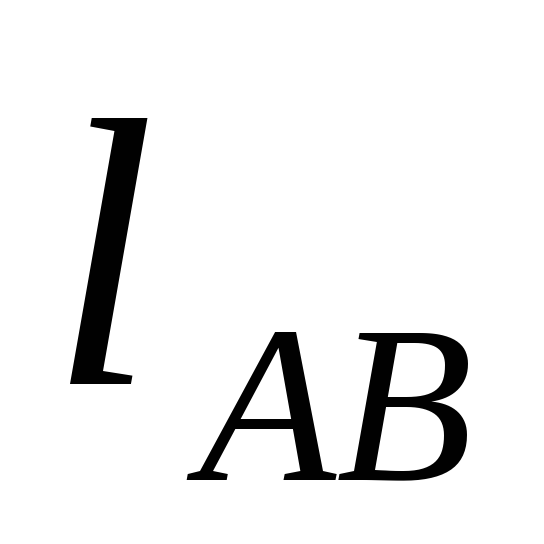_ stvarna dužina veze mjerena u metrima

AB - dužina veze na crtežu u milimetrima

Slika kinematičkog dijagrama mehanizma, koja odgovara određenom položaju početne karike ili početnih karika za mehanizme s nekoliko stupnjeva slobode, naziva se plan mehanizma.

PRIMJER. Izvršite kinematičku analizu mehanizma radilice

Kinematska analiza mehanizma će se izvršiti grafičkom metodom.

Da biste to učinili, ako je početna veza uključena u rotacijski par, ona se rotira za uglove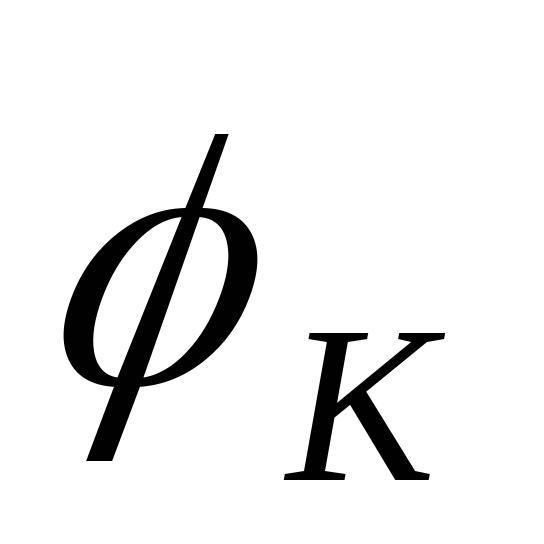

odrediti pomake svih ostalih karika.

Izrada planova položaja veza izvodi se na sljedeći način.

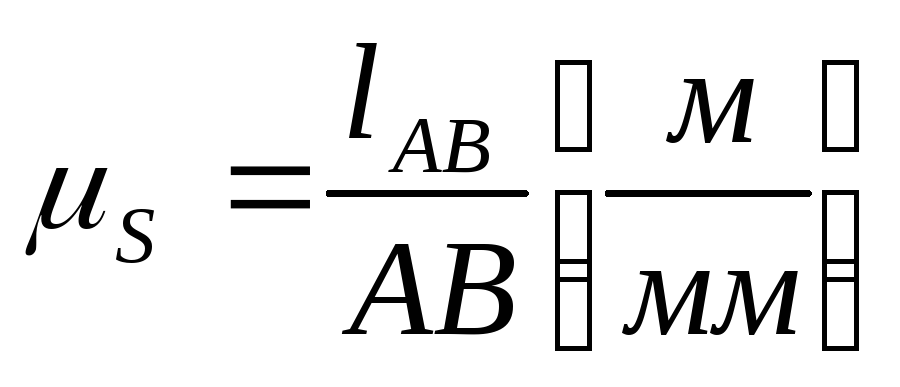
Ako se određivanje kretanja karika ili njihovih brzina može izvršiti bez sudjelovanja jedne ili više karika mehanizma, onda te veze uvode ili pasivna ograničenja ili dodatne stupnjeve slobode.

Konstrukcija kinematičkih dijagrama

U kinematičkom proučavanju mehanizama potrebno ga je izvesti za puni ciklus kretanja mehanizma koji se proučava. Da bi se to postiglo, provodi se analitička ili grafička studija kretanja brzina, ubrzanja za niz položaja mehanizma, koji su prilično blizu jedan drugom. U praktičnim TMM zadacima, svaki kinematički dijagram je obično grafički prikaz promjene jednog od kinematičkih parametara veze: pomaka, ubrzanja, brzine spojne tačke mehanizma koji se proučava u funkciji vremena ili pomaka početna karika mehanizma, tj. u funkciji generalizovane koordinate.

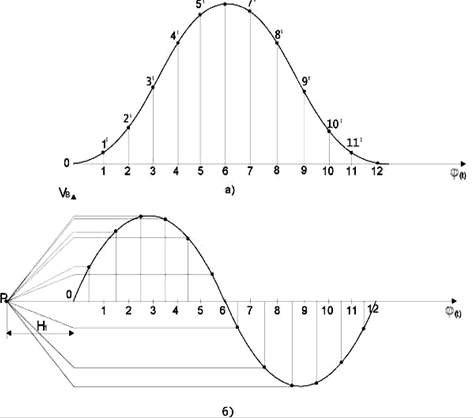
Kao primjer, razmotrite konstrukciju kinematičkih dijagrama S C \u003d S C (t) za trajno kretanje tačke "C" mehanizma klizača radilice ABC, tj. kada se radilica rotira konstantnom kutnom brzinom .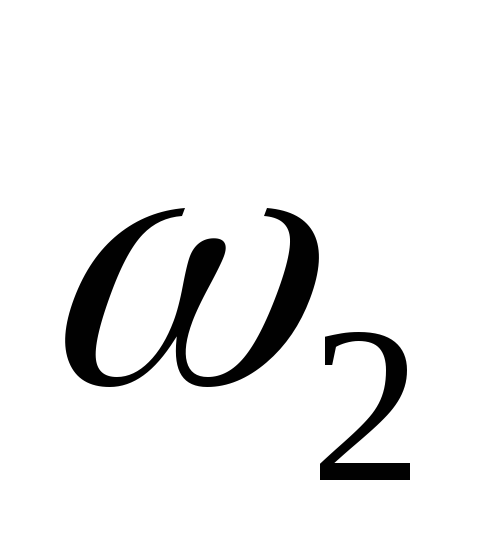

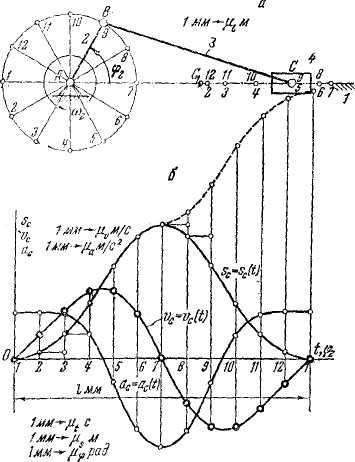
Sl.3.1 Pokretni klizač

mehanizam:

a) kinematička šema;

c) grafikoni koji prikazuju zavisnosti

S C =S C (t); - grafikon pomaka

V c = V c (t); - grafikon brzine

a c = a c (t); - grafikon ubrzanja

Da bismo to uradili, označićemo putanje tačaka B i C. Zgodno je izvesti pomake tačke C sa krajnje leve pozicije klizača. Nacrtamo koordinatne osi i ucrtamo segment l MM na x-osu, što je skala 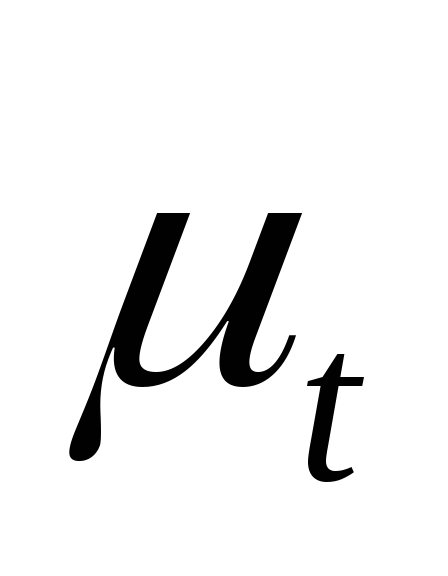vrijeme T jedan puni okret radilica, tj. T=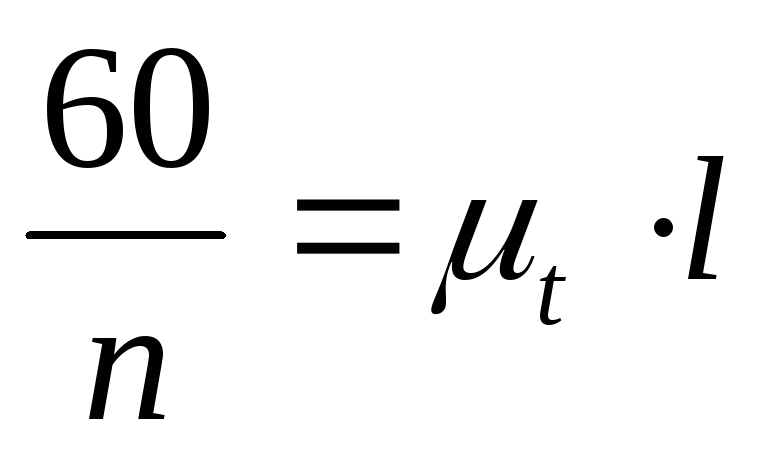

gdje je: n brzina okretaja u minuti,

onda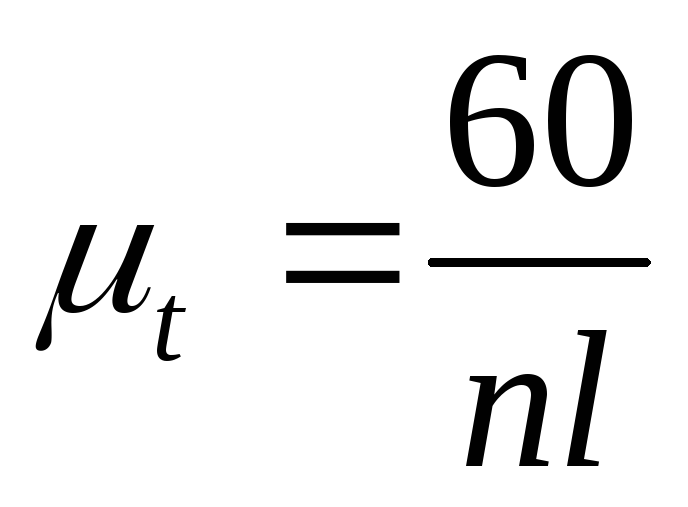

Izrada dijagrama pomaka

Segment l je podijeljen na 12 jednakih dijelova i na odgovarajućim tačkama 1,2,3, itd., odvajamo put koji je prešla tačka “C” od krajnje lijeve pozicije C 1 klizača. Dakle, u tački 2 odvajamo u pravcu paralelnom sa y-osi, segment C 1 C 2; tačka 3-segment C 1 C 3 itd.

Ako se segmenti C 1, C 2, C 1 C 3 odvoje direktno sa dijagrama (slika a), tada

skala dijagrama S C =S C (t) duž y-ose će biti jednaka μ i , tj. skala

konstrukcija sheme. Sa pozicije C 7, kada tačka C skrene desno

položaju, udaljenosti C7C8, C7C9 se oduzimaju od ordinate C1C7 ucrtane na poziciji C7, pa će kriva S C =SC (t) u poziciji kada poluga 2 dođe u početni položaj imati ordinatu jednaku nuli.

Rezultirajuća kriva je kriva udaljenosti tačke C od ekstrema

klizač na lijevoj poziciji. Ako trebate izgraditi krivulju prijeđenih staza

tačke C, a zatim sa pozicije C 7, rastojanja C 7 C 8, C 7 C 9 se moraju dodati prethodno deponovanom segmentu C 1 C 7, na sl. b) - dio krivulje putanje je prikazan crticama. Jer radilica se rotira konstantnom ugaonom brzinom 2, onda možemo pretpostaviti da apscisa nije vrijeme t, a uglovi rotacije φ 2 link 2 , tj. dijagrami S C =S C (t) će istovremeno biti dijagrami S C =S C (φ 2). Skala μ φ \u003d 2π / l, pri čemu se segment l mora uzeti sa crteža u mm.

Konstrukcija dijagrama brzina i ubrzanja metodom

grafička diferencijacija

Imajući kinematički dijagram pomaka karika, moguće je dobiti dijagram brzina pomoću grafičke diferencijacije. Razmotrimo redoslijed konstruiranja dijagrama brzina metoda akorda.

Na dijagramu pomaka crtamo akorde: oh, au, itd.

2. Gradimo koordinatne ose za dijagram brzina i na nastavku ose

apscisa (ot) lijevo, odvojite unutarnju udaljenost polova (OP V).

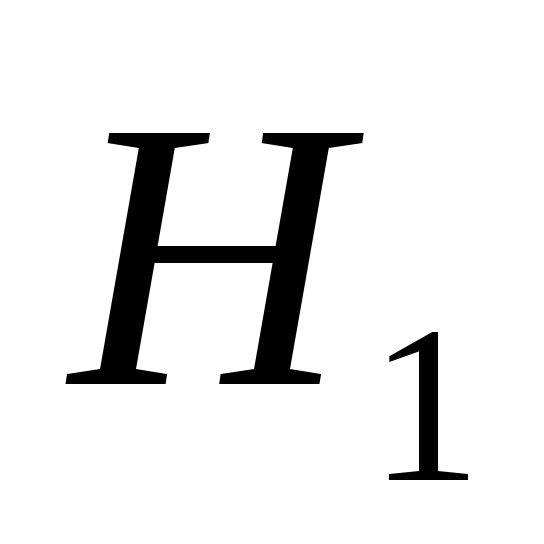= 30 - 60 mm.

3. Iz pola P V povlačimo zrake: 1, 2, 3, ..., itd. paralelno sa tetivama

oh, au, itd. do preseka sa y-osom u tačkama: 1 ’ , 2 ’ , 3 ’ , ….

4. Od tačaka 1 ', 2 ', 3 ' povucite horizontalne linije do sredine

odgovarajući vremenski intervali (1 '' , 2 '' , 3 '' , ...).

5. Dobijene tačke povezujemo glatkom krivom.

6. Izračunajte skalu brzina.

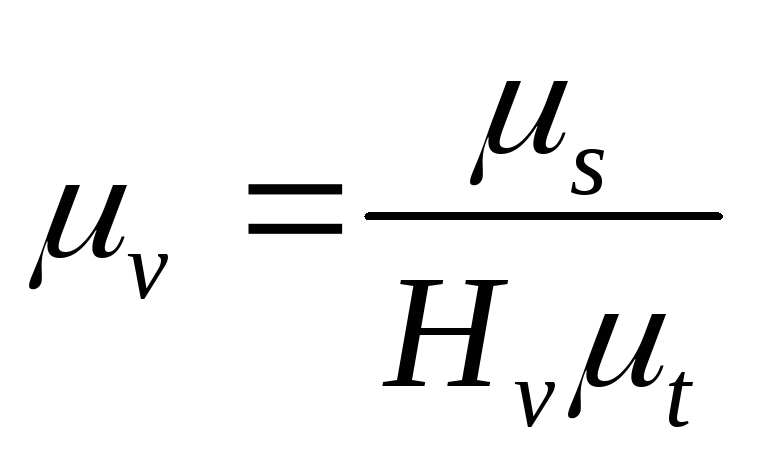
Kada razlikujemo dijagram ugaonih pomaka, dobijamo, odnosno, dijagram ugaonih brzina na skali:

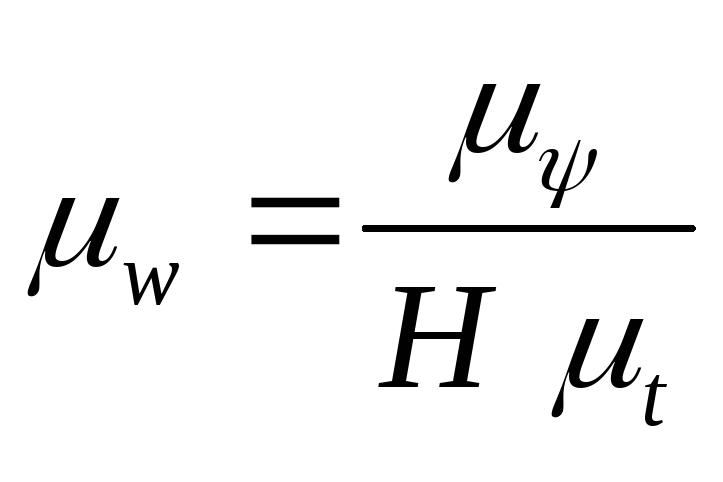
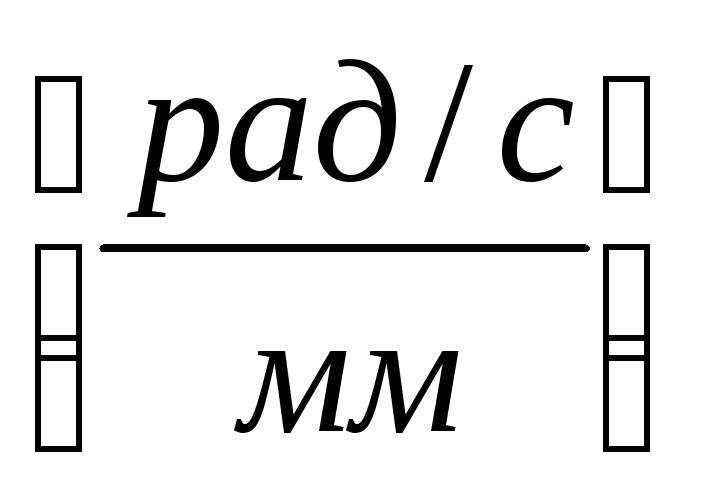
Da bismo dobili graf ubrzanja, vršimo grafičko diferenciranje grafa brzina. pri čemu:

;

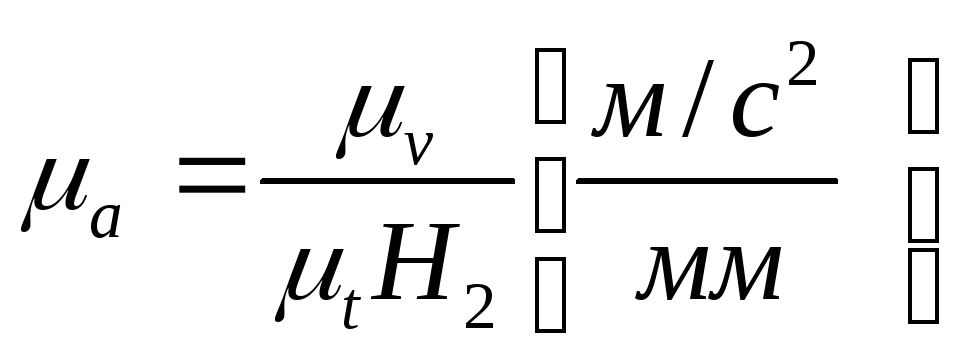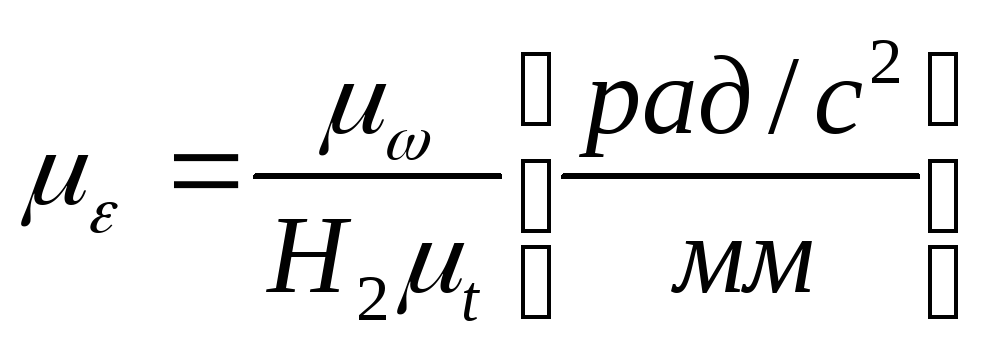
Prilikom diferenciranja grafika brzina potrebno je obratiti pažnju na određivanje vrijednosti ubrzanja u nultom (12) položaju.

Da biste to učinili, koristite tetivu (12 - 1), nastavljajući graf brzine u sljedeći ciklus.

vremenska skala može se izračunati pomoću formule

,

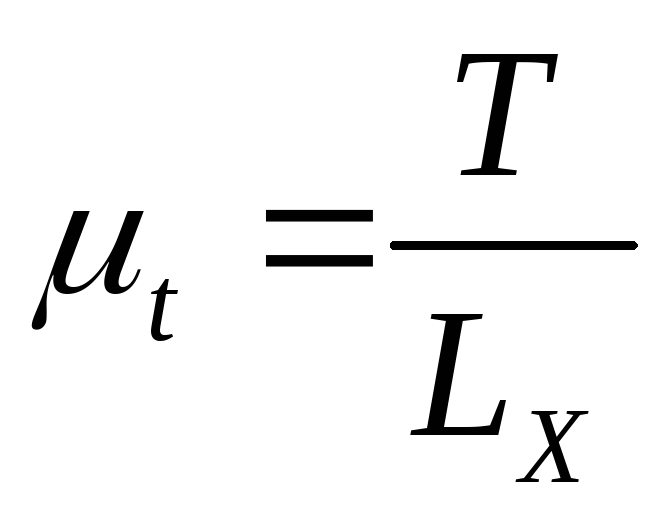gdje T- period jednog obrtaja ručice, s; L X- dužina segmenta između tačaka 1 i 1 na grafikonu (dijagramu) pomaka, mm.

Od perioda T može se izračunati pomoću formula

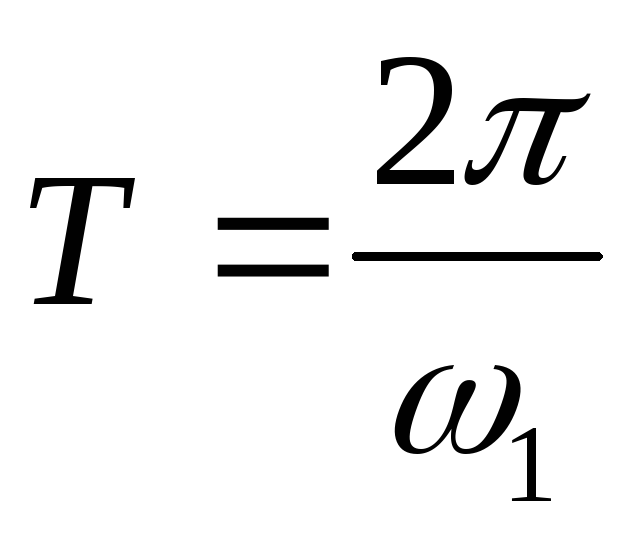, ili

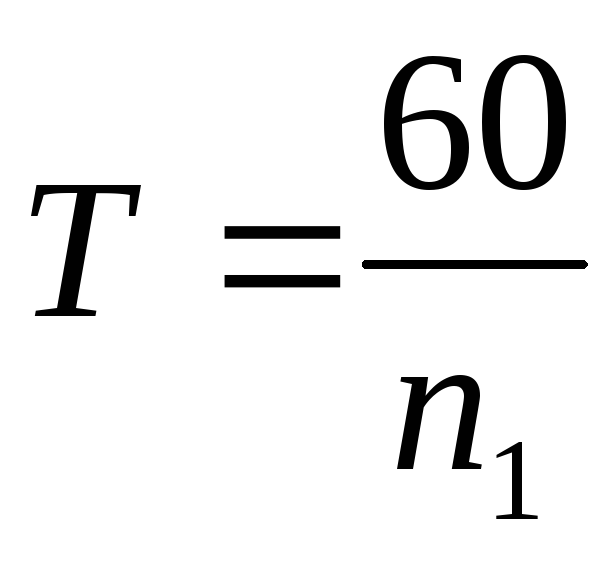, sa,

gdje ω 1 je ugaona brzina radilice, 1/s; n 1 je frekvencija rotacije poluge, o/min, zatim vremenska skala

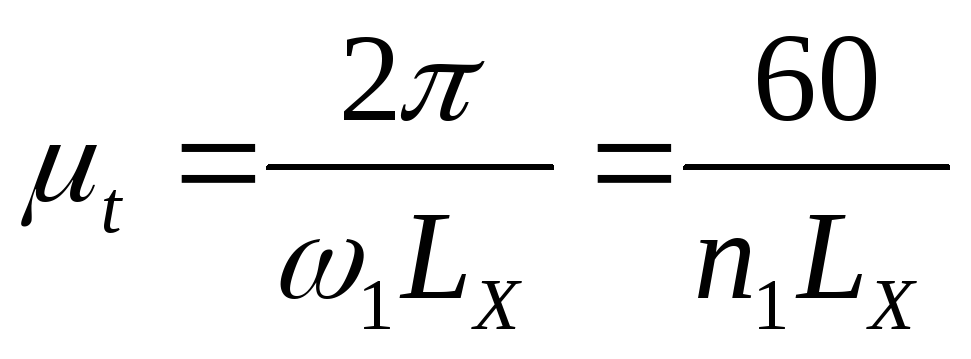, s/mm.

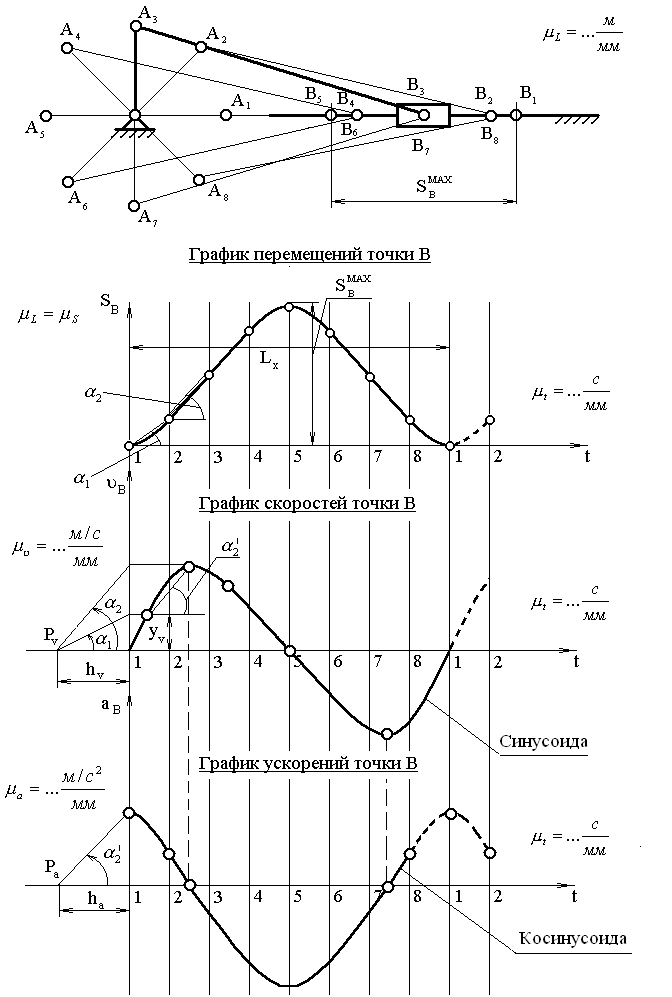Rice. 3.2. Kombinovani planovi mehanizma,

grafovi pomaka, brzina i ubrzanja

3. Primjeri kinematičke analize

3.1. Pravila za formiranje geometrijski nepromenljivih sistema

Svaki geometrijski nepromenljivi deo sistema nazivamo disk.

pravilo 1: čvor je vezan za disk pomoću dve karike koje ne leže na istoj pravoj liniji (slika 3.1).

Pravilo 2: disk je povezan sa drugim diskom pomoću tri karike koje se ne seku u jednoj tački i nisu paralelne jedna s drugom (slika 3.2).

Tačka presjeka dvije veze može se smatrati šarkom - stvarnom ili fiktivnom. Stoga se pravilo 2 može protumačiti kao veza dva diska sa šarkom i jedne veze koja ne prolazi kroz šarku. Na primjer, dva diska prikazana na sl. 3.3 povezani su stvarnom šarkom A i karikom 3. Takođe se može smatrati da su diskovi povezani fiktivnom šarkom B i karikom 1.

Sl.3.1. Priključivanje čvora na disk

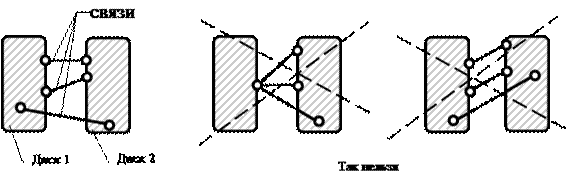
Sl.3.2. Povezivanje dva diska sa tri veze

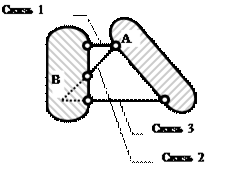
Sl.3.3. Spajanje dva diska sa šarkom i šipkom:

A je prava šarka; B - fiktivna šarka

Pravilo 3: tri diska su međusobno povezana sa tri šarke koje ne leže na jednoj pravoj liniji (slika 3.4). Šarke mogu biti prave ili lažne.

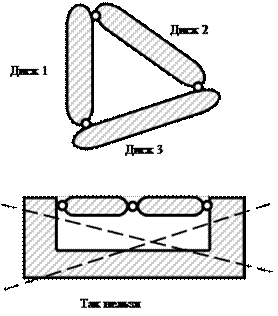
Sl.3.4. Spajanje tri diska sa tri šarke

Ako se bilo koje od ovih pravila prekrši, sistem se ispostavlja geometrijski promjenjivim ili trenutno promjenjivim.

Ako se sistem formira po navedenim pravilima, on će nužno biti geometrijski nepromjenjiv.

Ako na kinematička analiza u geometrijski nepromenljivom sistemu se nalazin redundantne veze, onda se ispostavlja da je sistemn puta statički neodređeno. U nedostatku redundantnih veza, sistem je statički određen.

Sistemi čije obrazovanje poštuje ova pravila nazivaju se sistemi jednostavnog obrazovanja. Postoje sistemi čiji se redoslijed formiranja ne može odrediti gore navedenim pravilima. Za kinematičku analizu takvih sistema koriste se i druge metode, na primjer, metoda zamjene veza, koje se u ovom priručniku ne razmatraju.

3.2. Stepen slobode sistema

Stepen slobode sistema W je broj nezavisnih parametara koji određuju položaj sistema u prostoru.

označiti:

D je broj diskova od kojih je sistem formiran;

W je broj jednostavnih šarki koje međusobno povezuju diskove;

OD je broj veza koje međusobno povezuju diskove;

OD O je broj potpornih karika koji povezuju diskove sa zemljom.

Jednostavno šarka nazvana šarka koja povezuje dva diska, takva šarka je ekvivalentna dvije karike. Ako se šarka spoji d diskovi, to se zove višestruka šarka i njegov višestrukost To =d–1 pokazuje koliko je jednostavnih šarki ekvivalentno (slika 3.5).

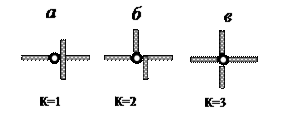
Sl.3.5. jednostavno ( a) i višestruki ( b, c) šarke

Za proizvoljan ravan sistem

Š = 3D - 2Sh - S - S Oh, (1)

štaviše, diskovi ne bi trebali sadržavati suvišne veze.

Za rešetke sa šarkama, stupanj slobode može se odrediti jednostavnijom formulom

W \u003d 2U - C - C Oh (2)

gdje At– broj čvorova farme; OD- broj rešetkastih šipki; OD O je broj veza za podršku.

Ako a W >

Ako a W

Ako a W< 0, то система геометрически неизменяемая и статически неопределимая.

Važno je znati da su uslovi geometrijske nepromjenjivosti W= 0 iW<0 являются необходимыми, но недостаточными. Для окончательного вывода о виде системы следует анализировать порядок образования системы (см. примеры ниже).

Primjer 1 Kinematička analiza grede (slika 3.6, a).

Greda se sastavlja u sljedećem redoslijedu:

1. faza. Disk 1 (štap ABC) je pričvršćen za zemlju, poput diska, uz pomoć tri karike (pravilo 2, sl. 3.6, b).

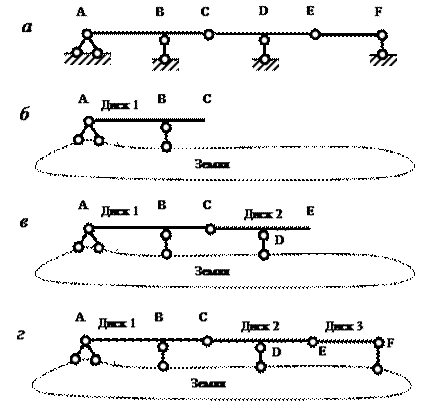
Sl.3.6. Redoslijed sklapanja grede

2. faza. Disk 2 (šipCDE ) koristeći šarku C i potpornu vezu na jednoj tačkiD (opcija pravila 2, slika 3.6, in).

3. faza. Disk 3 (šipEF ) sa šarkomE i referentna veza u tačkiF (opcija pravila 2, sl. 3.6, G). Ovim je završena montaža grede.

Od formiranja grede (slika 3.6, a) poštuje utvrđena pravila i nema dodatnih (redundantnih) veza, tada je dati sistem geometrijski nepromjenjiv i statički određen (GN SS ).

Primjer 2 Kinematička analiza farme (slika 3.7, a).

Farma se sastavlja u sljedećem redoslijedu:

1. faza. Tri šipke (1-2, 2-4, 1-4), kao i tri diska, povezane su sa tri šarke (1, 2, 4) prema pravilu 3.

2. faza. Čvor 3 je pričvršćen na formirani disk 1 (1-2-4) uz pomoć šipki 1-3 i 4-3 prema pravilu 1.

3. faza. Čvor 6 pričvršćen je na rezultirajući disk 2 (1-2-4-3) uz pomoć šipki 4-6 i 3-6 prema pravilu 1.

4. faza. Čvor 5 pričvršćen je na rezultirajući disk 3 uz pomoć šipki 3-5 i 6-5 prema pravilu 1.

5. faza. Rezultirajuća rešetka je pričvršćena za tlo s tri potporne spone prema pravilu 2.

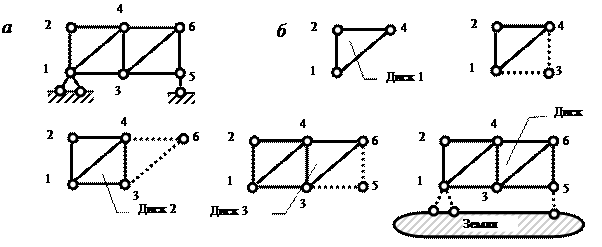
Sl.3.7. Redoslijed montaže farme: a- farma; b- koraci montaže

Od formiranja farme (slika 3.7, a) poštuje utvrđena pravila i nisu identifikovani dodatni (suvišni) štapovi, tada je dati sistem geometrijski nepromenljiv i statički određen (GN SS ).

Farma se može sastaviti drugačijim redoslijedom, ali u svakom slučaju rezultat će biti isti.

Primjer 3 Kinematička analiza okvira (sl. 3.8, a).

Okvir se sastavlja u sljedećem redoslijedu:

1. faza. Štap AB je pričvršćen za tlo (Disk 1 na slici 3.8, b) pomoću krutog stezanja, što je ekvivalentno trima vezama (pravilo 2).

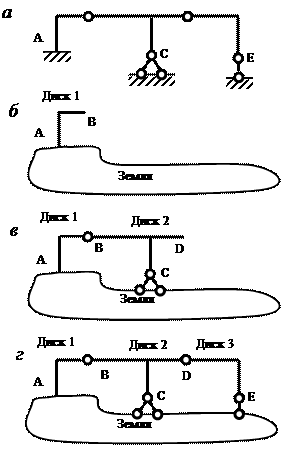
Sl.3.8. Redoslijed sklapanja okvira

2. faza. Disk 2 (šip BCD) je pričvršćen za formirani sistem „Zemlja + Disk 1“ uz pomoć šarke B i dve karike u tački C (slika 3.8, in).

Prema pravilu 2, dovoljno je imati jednu vezu u tački C, pa je druga veza suvišna.

3. faza. Disk 3 je pričvršćen za rezultujući sistem „Zemlja + Disk 1 + Disk 2” (štap DE na slici 2.8, G) sa šarkom D i potporna šipka u tački E (pravilo 2).

Od formiranja okvira (slika 3.8, a) poštuje utvrđena pravila i otkriva se jedna redundantna veza, tada je dati sistem geometrijski nepromjenjiv i jednom statički neodređen (GN SN).

Primjer 4 Kinematička analiza farme (slika 3.9, a).

Farma se sastavlja ovim redoslijedom.

1. faza. Od tri štapa (1-2, 2-4, 1-4) formira se disk - trokut 1-2-4 (pravilo 3), na koji je čvor 3 (pravilo 1) pričvršćen šipkama 1-3 i 4 -3. Rezultirajući disk 1-2-4-3 povezan je sa zemljom pomoću tri potporne karike (pravilo 2), formirajući disk 1 (slika 3.9, b).

2. faza. Tri štapa (5-6, 6-7, 5-7) formiraju disk 2 prema pravilu 3 (sl. 3.9, in).

3. faza. Disk 2 je povezan sa Diskom 1 sa tri veze (4-6, 3-5, 7-8), ali pošto se sve ove veze seku u jednoj tački 7, pravilo 2 je prekršeno. Moguća je međusobna rotacija diska 1 i diska 2 u odnosu na čvor 7 za beskonačno mali ugao.

Sl.3.9. Redoslijed sklapanja farme

Zbog kršenja pravila 2, dati sistem je trenutno promjenjiv i ne može poslužiti kao projektna šema za konstrukciju.

Primjer 5 Pronađite stepen slobode grede (vidi sliku 3.6, a).

Greda se sastoji od tri diska (šipova)AC,CE,EF , međusobno povezani sa dvije jednostavne šarke C i E i pričvršćeni za tlo sa pet potpornih karika. Zbog toga D = 3,W = 2, OD = 0, OD O = 5 i po formuli (1) dobijamoW = 3 3 - 2 2 - 0 - 5 = 9 - 9 = 0, što je neophodna karakteristika geometrijski nepromenljivog i statički određenog sistema. Ovaj zaključak je potvrđen u primjeru 1.

Primjer 6 Pronađite stepen slobode farme (vidi sliku 3.7, a).

Koristit ćemo formulu (1) i svaku šipku rešetke smatrati diskom, tj. D= 9. Šarke 2 i 5 spajaju po dvije rešetkaste šipke, tako da su jednostavne. Šarke 1 i 6 spajaju po tri rešetkaste šipke, tako da su duple. Šarke 3 i 4 su trostruke. Ukupan broj jednostavnih šarki W = 2 1 + 2 2 + 2 3 =12. Postoje tri veze za podršku.

Dobijamo W= 3 9 - 2 12 - 3 = 27 - 27 = 0.

OD = 9, At= 6, OD O = 3.

Dobijamo W\u003d 2 6 - 9 - 3 \u003d 12 - 12 \u003d 0.

Ovaj primjer pokazuje prednost formule (2) u odnosu na formulu (1). Predznak GN CO sistema je potvrđen u primjeru 2.

Primjer 7 Pronađite stepen slobode okvira (vidi sliku 3.8, a).

Okvir se sastoji od tri diskaAB,BCD iDE su međusobno povezani pomoću dvije jednostavne šarkeB iD. Okvir je pričvršćen za podlogu pomoću šest potpornih nosača (tri u krutom spoju A, dva u nosaču C, jedan u nosaču E). Zbog toga D= 3, W = 2, OD= 0, OD O = 6 i po formuli (1) dobijamo

W= 3 3 – 2 2 – 0 – 6 = –1, što je neophodan znak GN SN sistema. Ovaj zaključak je potvrđen u primjeru 3.

Primjer 8. Pronađite stepen slobode farme (vidi sliku 3.9, a).

Kada koristimo formulu (2), imamo OD = 10, At = 7, OD O = 4.

Dobijamo W= 2 7 – 10 – 4 = 14 – 14 =0, što ukazuje na GN CO sistem. Međutim, analiza formiranja farme (vidi primjer 4) dovodi do zaključka o trenutnoj varijabilnosti sistema. Ovaj primjer pokazuje nedovoljnost izračunavanja stepena slobode sistema po formuli za konačni zaključak o tipu sistema.

Primjer 9. Kinematička analiza sistema (slika 3.10, a).

Sistem se sastoji od tri diska D1, D2 i D3, koji su međusobno povezani sa pet karika 1…5. Diskovi D1 i D3 su pričvršćeni za tlo zglobnim osloncima A i B, od kojih je svaki ekvivalentan sa dvije potporne karike. Zbog toga D = 3, W = 0, OD = 5, OD O = 4 i po formuli (1) dobijamo

W= 3 3 - 2 0 - 5 - 4 = 9 - 9 = 0.

Sistem se sklapa u sledećem redosledu:

1. faza. Diskovi D2 i D3 su povezani vezama 3, 4, 5 prema pravilu 2 i formiraju novi disk D (slika 3.10, b);

2. faza. Tri diska (D1, D i zemlja) prema pravilu 3 povezana su sa tri šarke: pravi A, B i fiktivni C, koji ne leže na jednoj pravoj liniji.

Dakle, sistem je GN CO.

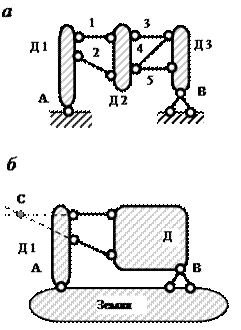
Sl.3.10. Šeme na primjer 9

Primjer 10 Kinematička analiza sistema (slika 3.11).

Da bismo izračunali stepen slobode sistema koristeći formulu (1), razmatramo dve opcije. U prvoj varijanti smatramo da se sistem sastoji od pet diskova - slomljenih šipkiABC,ADC i ravni štapoviB.E.CE,D.E.

Zatim šarke A ,b,D su jednostavne, a šarke C i E su dvostruke.

At D = 5, W = 7, OD = 0, OD O = 3 dobijamo

W= 3 5 - 2 7 - 0 - 3 = 15 - 17 = -2.

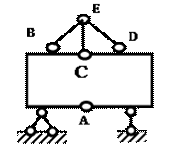
Sl.3.11. Shema na primjer 10

U drugoj varijanti smatramo da se sistem sastoji od tri diska -ABC,ADC iEC, koji su povezani jednostavnom šarkom A, dvostrukom šarkom C i dvije karikeBE andD.E.

At D = 3, W = 3, OD = 2, OD O = 3 dobijamo

W= 3 3 - 2 3 - 2 - 3 = 9 - 11 = -2.

Napomena: Ne možete uzeti u obzir sistem koji se sastoji od samo dva diska (slomljene šipke ABC i ADC ), budući da su u ovom slučaju štapovi B.E. CE, DE ne povezuju diskove jedni s drugima.

Sistem se sklapa u sledećem redosledu:

1. faza Diskovi ABC iADC-ovi su povezani u jedan disk pomoću dvije šarke A i C, odnosno četiri karike, od kojih će jedna biti redundantna (pravilo 2).

Faza 2. Čvor E je vezan za rezultujući disk sa tri veze, od kojih će jedna biti redundantna (pravilo 1).

Faza 3. Sastavljeni disk sa dvije redundantne karike pričvršćen je za tlo sa tri potporne karike (pravilo 3).

Dakle, dati sistem je GN SN (dva puta).

Primjer 11. Izvršite kinematičku analizu sistema (slika 3.12).

Određujemo stepen slobode sistema prema formuli P. L. Čebiševa:

W \u003d 3D - 2Sh - C 0,

gdje D- broj diskova, W je broj jednostavnih šarki, Od 0- broj štapova.

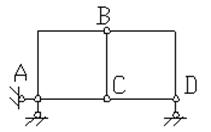
Sl.3.12. Shema na primjer 11

Odbacujući sve šarke i potporne šipke, nalazimo da se sistem sastoji od pet diskova ( D=5). Odbacivanjem potpornih šipki određujemo broj šarki svedenih na jednostavne ( W=6: dva boda AT i OD, jedan po jedan - na tačkama ALI i D). Broj potpornih šipki - Od 0 =3.

Odavde W= 3 ∙ 5 – 2 ∙ 6 – 3 = 0, odnosno sistem može biti geometrijski invarijantan i statički neodređen. Da bismo potvrdili da je to slučaj, analizirajmo strukturu sistema. Od diskova AB, Ned i AC povezani sa tri šarke ALI , AT i OD ne leže na jednoj pravoj liniji, tada formiraju disk za koji je disk čvrsto pričvršćen VD sa šarkom AT i štap SD, čija osa ne prolazi kroz centar šarke. Ova nepromjenjiva figura je čvrsto pričvršćena za tlo pomoću tri šipke koje se ne seku u jednoj tački. Dakle, sistem (slika 1.14) je geometrijski nepromenljiv i nije trenutno promenljiv.

Primjer 12. Izvršite kinematičku analizu sistema (slika 3.13).

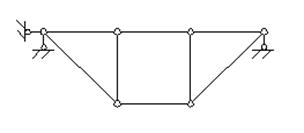
Sl.3.13. Shema na primjer 12

Pošto je sistem šarka, koristimo formulu (2) da odredimo njegov stepen slobode:

W \u003d 2U - C - C 0,

gdje At– broj čvorova farme; OD je broj unutrašnjih šipki; Od 0- broj potpornih šipki.

Evo At =6, OD=8, Od 0=3, dakle, W= 2∙6 – 8 – 3 = 1.

Dakle, sistem ima jedan stepen slobode i ne može se koristiti kao građevinska struktura.

Primjer 13 Istražite farmu (slika 3.14).

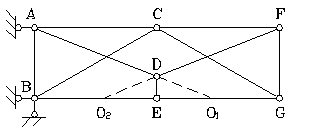
Sl.3.14. Shema na primjer 13

Prema formuli (2) određujemo stepen slobode farme: W= 2 ∙ 7 – 11 – 3 = 0, dakle, sistem može biti geometrijski promjenjiv i statički određen.

Hajde da analiziramo sistem. Sastoji se od tri diska - trougla ABC, CFG i štap DE povezane šipkama BE, AD, EG, D.F., koji se može zamijeniti fiktivnim šarkama Oko 1, oko 2 i šarke OD. Stoga možemo zaključiti: svi štapovi su međusobno kruto povezani i također su čvrsto pričvršćeni za tlo uz pomoć tri šipke koje se ne sijeku u jednoj tački.

Da biste provjerili sistem za trenutnu varijabilnost, prijavite se bez opterećenja- odredit ćemo reakcije i sile potpore u svim štapovima, pod uvjetom da nema vanjskog opterećenja. Iz uslova ravnoteže čitavog sistema (Σ M A= 0; Σ M V= 0; Σ At=0) nalazimo da su reakcije potpore jednake nuli. Rezanje čvora E i projektujući sve sile na vertikalu, nalazimo da je sila u vertikalnom štapu N DE= 0. Zatim, zapisivanje jednadžbi projekcija dviju sila koje konvergiraju u čvoru D(treća sila - N DE= 0), na pravcima normala na ove štapove, nalazimo da su sile u štapovima DA i D.F. takođe su jednake nuli. Konačno, s obzirom na ravnotežu čvorova A, Ž, B, G, nalazimo da su sile u svim štapovima sistema u odsustvu opterećenja jednake nuli, dakle, sistem je nepromjenjiv.

Primjer 14 Izvršite kinematičku analizu sistema (slika 3.15, a).

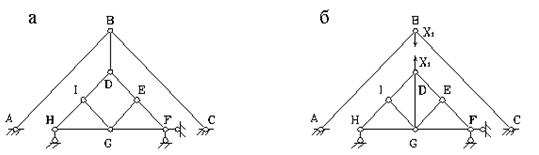
Sl.3.15. Shema na primjer 14

Formulom (2) određujemo stepen slobode: W= 2 ∙ 9 - 11 - 7 = 0, odnosno sistem ima potreban minimum veza da bi bio geometrijski nepromenljiv. Da bismo provjerili je li sistem zaista nepromjenjiv, koristimo se metoda zamjene šipke. Odaberimo sistem za zamjenu (slika 3.15, b). Ovdje je štap ispušten BD, a njegovo djelovanje zamjenjuju sile X 1, i dodana je zamjenska šipka DG. Odabrani sistem zamjene je nepromjenjiv: šipke AB, ned i zemlja su čvrsto povezani sa tri šarke koje ne leže na jednoj pravoj liniji. A donji dio sistema je nepromijenjen, jer se sastoji od trokuta (npr. GHI), na koji su svi ostali čvorovi čvrsto pričvršćeni uz pomoć dijada, a sve je to pričvršćeno za tlo sa tri potporne šipke.

Sada odredimo silu u zamjenskoj šipki iz sila X 1= 1. Uzastopno izrezivanje čvorova E, I, G i uzimajući u obzir njihovu ravnotežu, dobijamo da je sila u zamjenskom štapu nula, dakle, originalni sistem je trenutno promjenjiv.

Primjer 15 Analizirajte formiranje sistema prikazanog na slici 3.16 .

Sl.3.16. Shema na primjer 15

Prvo određujemo stepen slobode sistema. Pošto je sistem šarka, koristimo formulu (2) W \u003d 2U - C - C 0. Broj sistemskih čvorova At=6, broj štapova sistema OD=8, broj potpornih šipki OD 0 =3, dakle,W= 2 ∙ 6 - 8 - 3 = 12 - 1 = +1 Sistem ima jedan stepen slobode i ne može se koristiti kao građevinska konstrukcija.

Primjer 16 Analizirajte formiranje sistema prikazanog na slici 3.17, a.

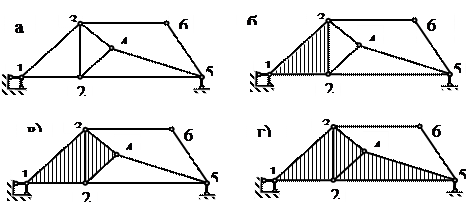
Sl.3.17. Shema na primjer 16

1. Upotreba formule (2) W \u003d 2U - C - C 0 za sisteme šarke određujemo broj stupnjeva slobode. Pošto je broj sistemskih čvorova At=6, broj štapova sistema OD=9, broj potpornih šipki OD 0 =3, dakle,W= 2 ∙ 6 – 9 – 3 = 0, dakle, sistem ima potreban broj veza da bude nepromjenjiv i statički određen.

2. Analiziramo strukturu sistema. Uzmimo u obzir trougao 123, koji je, prema trećoj osobini, nepromjenjiv sistem. Smatrajući to tvrdim diskom (osenčen na slici 3.17, b), na njega ćemo pričvrstiti čvor 4 sa dva štapa (3-4 i 2-4).Ovi štapovi ne leže na jednoj pravoj liniji, stoga je na osnovu prvog principa čvor 4 čvrsto vezan za disk 123. Rezultirajući sistem je takođe čvrsti disk (osenčen na slici 3.17, in). Pričvršćivanjem čvora 5 na njega sa dva štapa (4-5 i 2-5), ponovo dobijamo čvrsti disk, zasenčen na slici 3.17, G). Na ovaj disk ćemo pričvrstiti posljednji čvor 6 sa dvije šipke (3-6 i 5-6) koje ne leže na jednoj pravoj liniji.

Pošto je sistem formiran u skladu sa principima formiranja strukturno nepromenljivih sistema, on je nepromenljiv i nije trenutno promenljiv. Sistem je takođe čvrsto pričvršćen za tlo, uz pomoć tri potporne šipke koje se ne seku u jednoj tački.

Primjer 17. na primjer 17

1. Korištenje formule W \u003d 2U - C - C 0 za sisteme šarke određujemo broj stupnjeva slobode. Pošto je broj sistemskih čvorova At=9, broj štapova sistema OD=15, broj potpornih šipki OD 0 =3, dakle,W= 2 ∙9 - 15 - 3 = 0, dakle, sistem ima potreban broj veza da bi bio geometrijski nepromjenjiv.

2. Analiziramo strukturu sistema. Prvo, hajde da pronađemo očigledno nepromenljive delove sistema - dva diska formirana od trouglova (osenčena na slici 3.18, b). Povezani su sa tri šipke. Međutim, ovi štapovi se sijeku u jednoj tački (tj.k na pirinač. 3.18, b). Stoga je sistem trenutno promjenjiv.

Primjer 18 . Analizirajte sistem prikazan na sl. 3.19.

Sistem se sastoji od četiri diska (A C, C E , EF iFH) tj. D= 4. Broj šarki W = 3 (sve šarke su jednostavne). Broj reference štapovi OD 0 =2+1 ∙ 4=6. Stepen slobode sistema prema formuli W \u003d 3D - 2Sh - C 0 = 3 ∙ 4-2 ∙ 3-6=0.

Sl.3.19. Shema na primjer 18

Neophodan uslov nepromenljivosti sistema je zadovoljen. Analiziramo strukturu. Disk AC povezana sa zemljom sa tri potporne šipke koje se ne seku u jednoj tački. Ovaj dodatak osigurava nepokretnost diska AC. Vezano za njega OD i na tlo sa potpornom šipkom u tačkiD disk priključen SE. U ovom slučaju, osovina štapaD ne prolazi kroz šarku OD. Do rezultirajućeg nepromjenjivog sistema pomoću osovineEF i dvije potporne šipke na tačkamaG i H priključen pogonFH. Ova tri štapa se ne seku u jednoj tački.

Dakle, sistem koji se razmatra je nepromjenjiv i ne može se odmah promijeniti. Prema formuli W \u003d 3D - 2Sh - C 0 = 3 ∙2 -2 ∙1 -4=0.

Shodno tome, sistem ima potreban broj veza da bude nepromjenjiv. Analizirajmo njegovu strukturu.

Zajedno sa zemljom, sistem se sastoji od tri diska međusobno povezana šarkom Sh 1–2 i četiri šipke ekvivalentne uslovnim šarkama Sh 1–3 i Sh 2–3.

Pošto tri šarke koje povezuju tri diska leže na istoj pravoj liniji, sistem je trenutno promenljiv.

Primjer 20. Izvršite kinematičku analizu sistema zglobnih šipki (slika 3.21, a, b).

a) 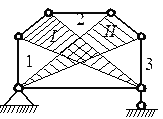b)

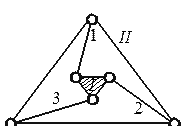
Sl.3.21. Shema na primjer 20

a) nevezana farma, gdje OD = 9, At = 6, 9 = 2 ∙ 6 - 3, geometrijski je nepromijenjen, budući da su unutrašnji - I i vanjski - II diskovi povezani sa tri šipke.

b) priključena farma, gdje OD = 9, At = 6, OD 0 = 3, 9 + 3 = 2 ∙ 6 je geometrijski nepromenljiv, pošto su diskovi I i II povezani sa tri šipke.

Primjer 21. Izvršite kinematičku analizu štapnih sistema (slika 3.22, a B C).

a) nevezani sistem šarke, gdje OD = 11, At = 7, 11 = 2 ∙ 7 - 3, je geometrijski nepromjenjiv. Formiran metodom luka sa tri zgloba, odnosno tri diska I, II, III, povezana jednom stvarnom (1, 2) i dvije fiktivne (2, 3; 1, 3) šarkama koje ne leže na jednoj duž.

b) pričvršćeni sistem šarke, gdje OD = 6, At = 5, OD 0 = 4, 6 + 4 = 2 ∙ 5 je trenutno geometrijski varijabilna. Pošto tri šarke (1, 3; 1, 2; 2, 3) koje povezuju tri diska I, II, III leže na jednoj pravoj liniji.

c) priključeni kombinovani sistem, gde D= 2, W = 1, OD 0 = 4, W = 3 ∙ 2 - 2 ∙ 1 – 4 = 0, trenutno je geometrijski promjenjiv, jer jedna stvarna (1, 2) i dvije fiktivne šarke (1, 3; 2, 3) koje spajaju tri diska I, II, III leže na jednoj pravoj liniji.

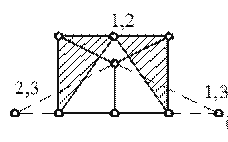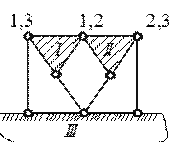a) b) u)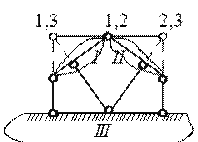

Sl.3.22. Šema na primjer 21

3.3. Stepen varijabilnosti sistema

Sistemi bez zemlje

Za sistem koji nije uzemljen, umjesto stepena slobode W uvodi se karakterističan stepen varijabilnosti V, koji se izračunava po formulama:

V \u003d 3D - 2Sh - C - 3,(3)

V \u003d 2U - C - 3,(4)

pri čemu je značenje notacije isto kao u formulama (1) i (2).

Ako a V> 0, onda je sistem geometrijski varijabilan.

Ako a V= 0, onda je sistem geometrijski nepromjenjiv i statički određen.

Ako a V < 0, то система геометрически неизменяемая и статически неопределимая.

Uslovi za geometrijsku nepromjenjivostV=0 iV<0 являются необходимыми, но недостаточными. Для окончательного вывода о виде системы необходимо анализировать порядок образования системы (см.примеры ниже).

Primjer 22. Kinematička analiza sistema (slika 3.23).

C čitamo da se sistem sastoji od dvije slomljene šipkeABC,CDE i četiri ravna štapaAB, BC, CD,D.E.

šarke A i E - jednostavni, sa šarkamaB iD - dvostruki, šarka C - trostruka.

At D= 6, W = 9, OD= 0 dobiti

V= 3 6 - 2 9 - 0 - 3 = 18 - 21 = -3.

Sl.3.23. Šema na primjer 22

Analiziramo redosled formiranja sistema. Dvije veze AB i BC su postavljene na slomljenu šipku ABC, koje su suvišne. Slično tome, veze su suvišneCD iDE za slomljenu šipkuC.D.E. Dva diska ABC iCDE-ovi su povezani samo šarkom C i jedna karika nedostaje za korištenje pravila 2.

Shodno tome, sistem je geometrijski promjenjiv, iako sadrži tri redundantne karike u svojim zasebnim dijelovima. Sistem se može učiniti geometrijski nepromjenjivim promjenom lokacije nekih karika, na primjer, zamjenom šipkeBC na štapuB.D.

Primjer 23. Kinematička analiza sistema (slika 3.24).

Okvir ima dvije zatvorene konture, a formula (3) ne dozvoljava postojanje zatvorenih kontura. Stoga okvir dijelimo sa četiri dijela na tri dijela (disk), međusobno povezane po tri karike u svakoj od sekcija.

Sl.3.24. Shema na primjer 23

Onda dobijamo D= 3, W = 0,

OD= 3∙4 =12i stepen varijabilnosti

V = 3∙3 –0 – 12 – 3 = –6.

Analiziramo redosled formiranja sistema. Lijevi disk je vezan za srednji disk pomoću šest karika, od kojih su tri redundantne. Zatim se desni disk pričvršćuje na formirani disk uz pomoć šest veza, od kojih su tri također suvišne.

Shodno tome, analizirani sistem je geometrijski nepromenljiv i sadrži šest redundantnih veza.

Kinematička analiza mehanizama

Uvod

5. Kinematički dijagrami

Književnost

Uvod

Tema testnog rada je "Kinematska analiza mehanizama" iz discipline "Teorija mehanizama i mašina".

Svrha rada: formiranje znanja o kinematičkoj analizi mehanizama.

Ciljevi rada: upoznavanje sa metodama kinematičke analize mehanizama.

Glavna pitanja teme:

1. Glavni zadaci i metode kinematičke analize;

2. Konstrukcija pozicija karika mehanizma;

3. Funkcija položaja mehanizma;

4. Osnovne jednačine za određivanje brzina i ubrzanja;

5. Kinematički dijagrami.

1. Glavni zadaci i metode kinematičke analize

Glavni zadatak kinematike mehanizama je proučavanje kretanja karika mehanizama, bez obzira na sile koje djeluju na te karike.

U kinematičkom proučavanju mehanizama razmatraju se sljedeća glavna pitanja:

1) izrada planova brzine;

2) konstrukciju putanje bilo koje tačke mehanizma;

3) određivanje brzina i ubrzanja bilo koje tačke mehanizma, određivanje ugaonih brzina i ubrzanja bilo koje karike mehanizma, određivanje poluprečnika zakrivljenosti u bilo kojoj tački putanje itd.

Kinematsko istraživanje se može izvesti grafičkim metodama i analitički. Metode grafičkog istraživanja, iako pružaju dovoljnu tačnost za inženjersku praksu, obično se ispostavljaju jednostavnijim i jasnijim od analitičkih. Međutim, kada se određeni tip mehanizma sistematski istražuje u dubini, analitička metoda je pogodnija.

U grafičkim konstrukcijama na crtežu potrebno je prikazati ne samo dužine karika, već i brzine i ubrzanja pojedinih tačaka, kao i druge veličine. Pod ovim uslovima, zgodno je koristiti faktor skale, koji je omjer stvarne vrijednosti i slike:

Faktor skale;

Faktor skale;

Faktor skale

2. Konstrukcija pozicija karika mehanizma

Međusobni raspored karika pokretnog mehanizma se stalno mijenja, ali je u svakom trenutku raspored karika sasvim određen. Grafički prikaz relativne pozicije veza koja odgovara odabranoj tački u vremenu naziva se plan mehanizma. Niz uzastopnih planova mehanizma, izgrađenih za trenutke vremena koji slijede jedan za drugim, naziva se planom pozicija i omogućava vam da vizualno pratite kretanje mehanizma.

Konstrukcija plana položaja mehanizma počinje slikom te karike, čija je pozicija postavljena za dati trenutak vremena.

Mehanizam klizača radilice

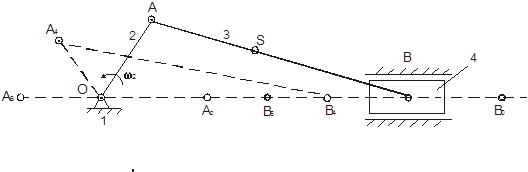
Od centra O - osi rotacije radilice OA sa radijusima i na osi X - X kretanja klizača, označavamo B 0 - desni B 6 - lijevi krajnji klizač B. Direktni OA 0 B 0 i OA 6 B 6 - položaji mehanizma koji odgovaraju krajnjim položajima klizača B 0 i B 6. Podijelimo putanju prsta A radilice iz tačke A 0 na 12 jednakih dijelova i iz dobijenih tačaka A 1, A 2, A 3 ... A 11 poluprečnika AB == ... označavamo pozicije B 1, B 2, B 3 ... B 11 klizača na liniji B 0 V 6 . Povezivanjem tačaka A 1 , A 2 , A 3 ... A 11 sa centrom O i odgovarajućim tačkama B 1 , B 2 , B 3 ... B 11 dobijamo planove mehanizma. Kriva koja serijski povezuje centre S 0 , S 1 , S 2 ... S 11 klipnjače u različitim položajima bit će kriva klipnjače.

3. Funkcija položaja stroja

Funkcija položaja mehanizma je ovisnost koordinate izlazne veze o generaliziranim koordinatama mehanizma.

Pomaci, brzine i ubrzanja karika i tačaka mehanizma funkcije su pomaka, brzina i ubrzanja karika mehanizma uzetih kao vodeće. Broj vodećih karika mehanizma treba da bude jednak broju stepeni slobode mehanizma ili, što je isto, broju generalizovanih koordinata mehanizma.

Hajde da razmotrimo u kom obliku se mogu dati zakoni vodećih veza. Ovi zakoni se nazivaju funkcijama pomaka, brzina i ubrzanja.

Funkcija pomaka se u analitičkom obliku može specificirati kao odgovarajuća funkcija koja povezuje pomak vodeće karike s vremenom (slika 2).

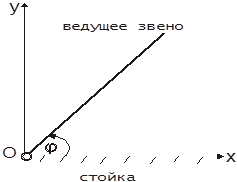
Ako je vodeća karika uključena u rotacijski par sa stalkom, tada se postavlja funkcija φ=φ (t), gdje je: φ ugao rotacije vodeće karike u odnosu na fiksni XOY koordinatni sistem povezan sa stalkom, a t je vrijeme.

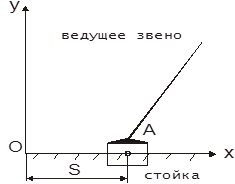
Ako je vodeća karika uključena u translacijski par, tada se postavlja funkcija s=s (t), gdje je s pomak proizvoljno odabrane tačke A vodeće veze u odnosu na fiksni koordinatni sistem povezan sa stalkom, i vrijeme je.

Funkcije φ=φ (t) i s=s (t) mogu se postaviti i grafički u obliku krivulja, gdje se duž ordinatnih osa u nekim odabranim skalama i , a duž ordinatnih osa ucrtavaju uglovi rotacije φ ili pomaka s. apscisa ose vremena t u odabranoj skali (slika 3).

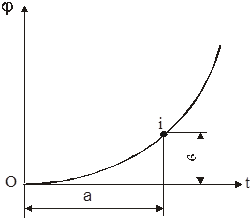
φ 0 = 0; φ i - φ 0 = · in;

U skladu s tim, vrijeme t i , za koje se vodeća karika okrenula kroz ugao φ i je jednako:

t i - t 0 = · a ;

Ako je zakon gibanja vodeće karike zadan u obliku funkcija brzine ω=ω (t) ili v=v (t), tada se prijelaz sa funkcije brzine na funkcije pomaka može izvršiti izračunavanjem integrala:

ubrzanje mehanizma kinematičke analize

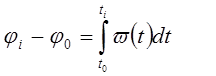i ;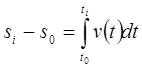

gdje je: φ 0 , s 0 , t 0 - ugao, pomak i vrijeme koje odgovaraju početnoj poziciji vodeće karike.

Ako je zakon gibanja vodeće karike zadan u obliku funkcija ubrzanja ε=ε (t) i ω=ω (t), tada se prijelaz na funkcije brzine vrši izračunavanjem integrala:

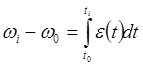i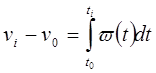

gdje je: ω 0 , v 0 , t 0 - ugaona brzina, linearna brzina i vrijeme koje odgovara početnoj poziciji vodeće veze.

4. Osnovne jednadžbe za određivanje brzina i ubrzanja

Veza između brzina i ubrzanja zajedničkih tačaka karika kinematičkog para zavisi od para.

Razmotrimo dva slučaja sastavljanja vektorskih jednačina za brzine i ubrzanja:

a) dvije tačke pripadaju istoj vezi i međusobno su udaljene rastojanjem l ( sl.4).

Iz teorijske mehanike je poznato da se brzina bilo koje tačke apsolutno krutog tijela može predstaviti kao geometrijski zbir brzina translacijskog i relativnog kretanja.

Translacijsko gibanje za vezu koja se razmatra je translacijsko gibanje brzinom tačke A, a relativno gibanje je rotacijsko kretanje veze oko tačke A. Vektorska jednadžba za brzinu tačke B:

;

Kada se veza rotira oko tačke A, tačka B se kreće u krug ββ opisano iz tačke A. Dakle, brzina V BA je tangencijalna na luk ββ , tj. okomito na pravu AB.

Vrijednost brzine V BA =ω·AB ili V BA =ω·.

Towards V BA možete pronaći smjer ω i obrnuto.

Jer prijenosno kretanje se bira kao translatorno, tada se ubrzanje tačke B može sastojati od 2 ubrzanja: ubrzanja tačke A i ubrzanja tačke B tokom rotacije veze oko tačke A.

Kada se tačka B kreće duž kružnice ββ ubrzanje W BA sastoji se od 2 ubrzanja: normalnog, usmjerenog prema centru rotacije, i tangencijalnog, usmjerenog tangencijalno na luk ββ , tj. okomito na pravu AB. Vektorska jednadžba za ubrzanje tačke B:

;

Vrijednosti ubrzanja i određene su formulama:

= ω 2 = ;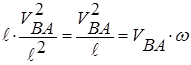

gdje je: ε - kutno ubrzanje;

b) dvije tačke pripadaju dvije karike koje čine translacijski par i u datom trenutku se poklapaju (slika 5).

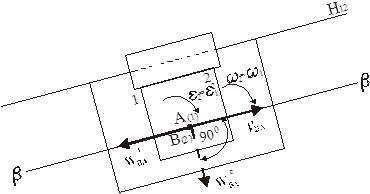
Tačka A pripada vezi 1, tačka B pripada vezi 2. U ovom trenutku, tačke A i B se poklapaju (tačka B leži iznad tačke A). Veze 1 i 2 čine translacijski par sa vodičem H 12 .

Brzinu tačke B čine 2 brzine - prenosiva i relativna. Prijenosno kretanje ovdje je kretanje veze 1, pa je brzina tačke A V A će biti prenosiv. Relativna brzina tačke B jednaka je brzini kretanja veze 2 u odnosu na vezu 1. Kada se veza 2 kreće u odnosu na vezu 1, tačka B se kreće pravolinijski ββ , paralelno sa vodilicom H 12 . Dakle relativna brzina V VA je paralelna sa H 12 .

Ubrzanje tačke B, kada translaciono kretanje nije translaciono, je zbir 3 ubrzanja: prenosivog, tj. ubrzanje tačke A, relativno i rotaciono, ili Coriolis. U relativnom kretanju, tačka B se kreće duž prave ββ , dakle, u ovom kretanju tačka B ima samo tangencijalno ubrzanje usmjereno duž ove linije, tj. paralelno sa vodilicom H 12. Označimo ovo ubrzanje kao . Rotacijsko (Coriolisovo) ubrzanje će biti označeno sa .

Vektorske jednadžbe za brzinu i ubrzanje tačke B će izgledati ovako:

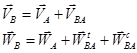
Pošto veze 1 i 2 čine translacijski par, one nemaju relativnu rotaciju. Dakle, ove karike imaju iste ugaone brzine i ugaona ubrzanja, odnosno: ω 2 =ω 1 i ε 2 =ε 1, gde je ω 1 ugaona brzina translacionog kretanja (rotacija karike 1).

Vektor je usmjeren u smjeru u kojem će vektor biti usmjeren ako se zarotira za 90 0 u smjeru kutne brzine ω 1 . Njegova vrijednost je određena formulom:

Odredimo brzinu i ubrzanje klizača mehanizma radilice.

Dat je plan mehanizma, dimenzije su ℓ OA, ℓ AB, ω 2 , ε 2 .

Odredite brzinu i ubrzanje karike 4 (tačke B) i ugaonu brzinu i ubrzanje karike 3 (ojna šipka).

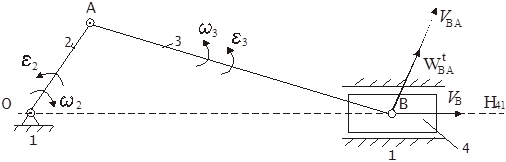
Znajući ω 2 , nalazimo V A = ℓ OA · ω 2 . Brzina VA prikazati na planu brzina u obliku segmenta „P a", okomito na OA (slika 7). Klip (link 4) se kreće naprijed, pa sve njegove tačke imaju istu brzinu i isto ubrzanje kao tačka B.

Sl.7 Sl.8

Međutim, tačka B ne pripada samo karici 4, već i karici 3. Na isti način, tačka A je zajednička tačka za veze 2 i 3. Dakle, na linku 3 postoje dve tačke A i B, odvojene od svake drugi za udaljenost ℓ AB. Dakle, brzina tačke B:

gdje: ║ ;

U skladu sa ovom jednačinom gradimo plan brzine. Prolazak kroz tačku a prava okomita na AB, a kroz tačku P - prava okomita na H 41. Na tački raskrsnice put in. Segment P in predstavlja brzinu tačke B i segmenta av- brzina tačke B u odnosu na A ( V VA). Ugaona brzina veze 3 nalazi se po formuli:

Pomjerajući vektor u tačku B, nalazimo smjer ω 3 (u smjeru suprotnom od kazaljke na satu).

Tačka ubrzanja A:

Odgađajući od pola (sl. 8) ubrzanje i u obliku segmenata i , nalazimo ukupno ubrzanje tačke A (segment ).

Ubrzanje u tački B:

gdje: ; ║ i AB;

Ubrzanje je usmjereno od tačke B do tačke A. Ostavljanje tačke a ' ( na planu ubrzanja) segment a ′ do ′′, odgovarajući , povući kroz tačku u '' prava okomita na AB. Kroz R pol ′ nacrtaj liniju paralelnu sa H 41. Ove prave se seku u tački u ', segment P 'u' predstavlja željeno ubrzanje tačke B (W B), i segmenta u ′′ u ′- ubrzanje. Iz poređenja pravaca W B i V B zaključujemo da se veza 4 trenutno sporo kreće.

Kutno ubrzanje karike 3 se nalazi po formuli: .

Prenošenje vektora u tačku B pokazuje da je ε 3, kao i ω 3 , usmjeren suprotno od kazaljke na satu.

U jednadžbama je vektor poznat po veličini i smjeru podvučen s dvije linije, a vektor poznat samo po smjeru je podvučen jednom linijom.

5. Kinematički dijagrami

Kinematički dijagram je grafički prikaz jednog od kinematičkih parametara (pomaka, brzina i ubrzanja) tačke ili karike mehanizma koji se proučava u funkciji vremena, ugla rotacije ili pomaka vodeće karike ovog mehanizma, tj. u funkciji generalizovane koordinate. Kinematički dijagrami daju potpunu kinematičku karakteristiku mehanizma.

Konstruišemo kinematičke dijagrame kliznog mehanizma radilice.

Za pomake S B , brzine V B i ubrzanja W B tačke B, kako se kreću pravolinijski, zgodno je graditi kinematičke dijagrame u obliku zavisnosti ovih veličina od vremena t ili generalizovana koordinataφ 2 , tj. izgraditi grafički prikaz zavisnosti:

S B =S B (t), V B =V B (t), W B =W B (t) ili:

S B = S B (φ 2), V B = V B (φ 2), W B = W B (φ 2)

ako je kut φ 2 rotacijski link 2 odabran kao generalizirana koordinata.

Ako su ugaoni pomaci φ 3, ugaone brzine ω 3 i ugaona ubrzanja ε 3 klipnjače 3 predmet istraživanja, onda se može izgraditi grafički prikaz zavisnosti:

φ 3 = φ 3 (t), ω 3 = ω 3 (t), ε 3 = ε 3 (t)

φ 3 = φ 3 (φ 2), ω 3 = ω 3 (φ 2), ε 3 = ε 3 (φ 2)

Radilica OA rotira konstantnom ugaonom brzinom ω 2 .

5.1 Izrada dijagrama pomaka

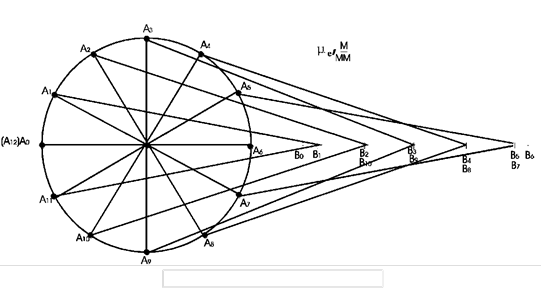
1) Nacrtamo dijagram mehanizma u skali od μ e u nekoliko, na primjer, dvanaest pozicija, koje odgovaraju uzastopnim okretima radilice OA za 30 0 (slika 9). Za početni položaj poluge uzimamo OA 0, u kojem klizač B zauzima krajnji desni položaj B 0;

2) gradimo koordinatne ose S B -t (slika 10a) i nanosimo segment ℓ u mm na osu apscise, prikazujući vrijeme jednog punog okreta kurlice na skali: ; gdje je: rad/mm, ;

Odsječak ℓ podijelimo na 12 jednakih dijelova i u odgovarajućim tačkama 1, 2, 3… duž y-ose iscrtavamo udaljenosti S B 1 , S B 2 … koje prolazi tačka B od njene krajnje desne pozicije B 0 .

Do krajnje lijeve pozicije B 6 rastojanja se povećavaju, a počevši od pozicije B 6 će se smanjivati; kada radilica dođe u početni položaj A 0, ordinata krive (S B -t) će biti jednaka nuli.

3) dobijene tačke 0, 1 ΄, 2 ΄, 3 ΄, … povezujemo serijski glatkom linijom. Dobivena kriva će biti dijagram udaljenosti tačke B.

Ako se, međutim, uglovi rotacije poluge φ nacrtaju duž ose apscise, tada će ova kriva predstavljati funkcionalnu zavisnost:

Dijagrami brzine i ubrzanja mogu se konstruirati korištenjem planova brzine i ubrzanja i metoda grafičke diferencijacije:

.

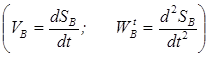Metoda grafičke diferencijacije:

1) ispod dijagrama (S B -t) gradimo koordinatne ose O 1 V B, O 1 t (sl. 2.10b) i na nastavku ose O 1 t lijevo odvajamo segment O 1 P \ u003d H 1 mm (proizvoljno, tako da se diferencijalna kriva nalazi na predviđenom mjestu za njeno crtanje);

2) iz tačke "P" povlačimo zrake P 1, P 2, P 3 ... paralelno sa tetivama krive (S B -t) u presecima 01΄; 12; 2΄3΄….

Ove zrake će se preseći na osi O 1 B segmenti 0 1 1; 0 1 2; 0 1 3…, proporcionalno srednjoj brzini V c u odgovarajućem dijelu dijagrama;

3) stavi ove segmente na prosečne ordinate odgovarajućih preseka;

4) povežite više dobijenih tačaka I, II, III ... glatkom krivom; ova kriva će biti dijagram brzine (V 0 -t).

Imajući dijagram brzina, na sličan način konstruiramo dijagram ubrzanja.

Prilikom konstruisanja dijagrama (V 0 -t) i (W B -t) ovom metodom, nemoguće je dobiti one preseke ovih dijagrama koji odgovaraju polovini ekstremnih preseka x-ose. Da biste dovršili grafikon, morate dodatno izgraditi prosjeke V V i za jedan ili dva dijela sljedećeg ciklusa.

Sl.9 Plan pozicija brzina

Sl.10 Kinematički dijagrami

Skala grafikona ostaje ista kao i ranije.

Razmjere duž ordinatne osi određene su formulama:

za grafikon brzine: ;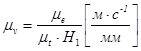

za dijagram ubrzanja: ,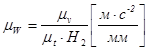

Metoda dijagramiranja je jednostavna i jasna, ali ima sljedeće nedostatke:

1) nepreciznost, posebno pri diferenciranju krivih sa velikom krivinom;

2) nemogućnost potpunog istraživanja krivolinijskog kretanja, jer diferenciranjem krivulje brzine dobijamo dijagrame promjena samo tangencijalnih ubrzanja;

3) dijagrami daju samo numeričke vrijednosti vektora čiji se smjer može utvrditi tek nakon nekih dodatnih konstrukcija.

Metoda planova brzina i ubrzanja nema pomenute nedostatke, pa se široko koristi u proučavanju različitih mehanizama.

Književnost

1. Artobolevsky I.I. Teorija mehanizama i mašina. M, 1975, str. 103-182.

2. Korenyako A.S. i dr. Dizajn kursa iz teorije mehanizama i mašina. Kijev, 1970, str. 82-102.

Kinematička analiza mehanizama. Ciljevi i zadaci kinematičke analize

Analiza kinematskog mehanizma- proučavanje njegovih glavnih parametara u cilju proučavanja zakonitosti promjene i na osnovu toga izbor najboljeg mehanizma iz niza poznatih. U poređenju sa sintezom, analiza mehanizama se široko koristi u praksi.

Kinematička analiza mehanizma se vrši ili za dati trenutak vremena ili za datu poziciju ulazne veze; ponekad se za analiziranu poziciju mehanizma specificira relativni položaj bilo koje njegove karike.

Ciljevi:

1. Određivanje kinematičkih karakteristika karika: pomak; brzina; ubrzanje; putanja kretanja; funkcija položaja sa poznatim zakonima kretanja ulaznih (vodećih) karika.

2. Procjena kinematičkih uslova rada radne (izlazne) veze.

3. Određivanje potrebnih numeričkih podataka za izvođenje energetskih, dinamičkih, energetskih i drugih proračuna mehanizma.

Početni podaci:

1. Kinematički dijagram mehanizma.

2. Dimenzije i drugi geometrijski parametri karika (ali samo oni koji se ne menjaju kada se mehanizam pomera).

3. Zakoni kretanja ulaznih karika (ili parametri kretanja, na primjer, ugaona brzina i ugaono ubrzanje ulazne veze u poziciji mehanizma odabranog za analizu).

Za mehanizme koji podliježu klasifikaciji L. V. Assur, redoslijed kinematičke analize određen je strukturnom formulom: prvo se pronađu parametri kretanja početnih mehanizama, a zatim strukturne grupe redoslijedom kojim se pojavljuju u formuli strukture. Ovdje se treba voditi jednostavnim pravilom: kinematika bilo kojeg elementa strukturne formule može se proučavati tek nakon što je proučena za sve elemente koji joj prethode u ovoj formuli.

Zadaci:

O pozicijama karika mehanizma. Određivanje putanja kretanja tačaka;

O brzinama veza ili pojedinačnih tačaka mehanizma;

O ubrzanju karika ili pojedinačnih tačaka mehanizma.

Metode:

Grafički (ili metoda grafikona i grafikona);

Grafičko-analitički (ili metoda planova brzina i ubrzanja);

Analytical;

Eksperimentalno.

Metoda grafičke kinematičke analize

Prednost ove metode je njena jasnoća i jednostavnost. Dobar je za kinematičku analizu karika koje vrše povratno kretanje. Nedostatak metode je niska tačnost, koja zavisi od tačnosti grafičkih konstrukcija.

Problem sa pozicijom rješava se konstruisanjem više kombinovanih planova mehanizma u odabranoj skali dužine sa različitim uzastopnim pozicijama vodeće karike.

Oni se rješavaju konstruiranjem grafikona (dijagrama) pomaka, brzina i ubrzanja tačke koja se proučava.

Slijed kinematske analize:

1. Prvo se gradi nekoliko (najčešće 12 ili više) kombinovanih planova mehanizma u proizvoljno odabranoj skali dužine.

2. Zatim se gradi graf putanje (kretanja) tačke ili karike koja se proučava, za šta se koriste kombinovani planovi mehanizma i sukcesivnih pozicija tačke ili karike koja se proučava.

3. Grafičkom diferencijacijom grafa pomaka gradi se graf brzine promatrane točke.

4. Grafička diferencijacija grafa brzine gradi graf ubrzanja.

Grafička diferencijacija se može izvesti metodom tetiva i metodom tangenta. Kako bi se poboljšala tačnost, zgodno je koristiti obje metode istovremeno.

Primjer 1

Dat je mehanizam klizača radilice čije su dužine karika - radilica i klipnjača - L OA i L AB, respektivno, i ugaona brzina radilice.

Odredite brzinu i ubrzanje klizača na različitim položajima poluge.

Rješenje.

Biramo skale dužine , m/mm, gde je AO dužina segmenta, mm, koja prikazuje polugu dužine L OA na planu mehanizma u izgradnji; ova dužina se bira proizvoljno, uzimajući u obzir činjenicu da bi kombinovani planovi mehanizma trebali biti postavljeni na dodijeljeno mjesto crteža, a sama ljestvica dužine bila bi prikladna za daljnje proračune.

Izračunavamo dužinu segmenta, mm, koji prikazuje klipnjaču na planu mehanizma. Prilikom izrade kombiniranih planova mehanizma koriste se serif metoda(Sl. 3.1).

Za izradu grafikona brzina i ubrzanja (Sl. 3.1), biraju se razdaljine polova h u i h a, gdje je h u udaljenost polova pri crtanju brzina, koja se bira proizvoljne dužine; preporučljivo je izabrati njegovu vrijednost unutar h u =30…40 mm; h a - rastojanje polova pri crtanju ubrzanja; preporuča se uzeti u roku od h a \u003d 30 ... 40 mm.

Skala vremena, brzine i ubrzanja izračunava se po formulama, čije je izvođenje dato u nastavku.

vremenska skala može se izračunati pomoću formule

gdje je T period jednog okretaja poluge, s; L X je dužina segmenta između tačaka 1 i 1 na grafikonu (dijagramu) pomaka, mm.

Pošto se period T može izračunati po formulama

gdje je ugaona brzina radilice, 1/s; n 1 - brzina ručice, o/min, zatim vremenska skala

, s/mm.

Skala brzine se može izvesti iz uslova da je brzina tačke koja se proučava derivacija pomaka S u odnosu na vrijeme:

.

Ovdje se pretpostavlja da su skala pomaka i vremenska skala konstante.

Od tada , dakle Problem sa pozicijom rješava se grafičkom metodom, odnosno izgradnjom više kombinovanih planova mehanizma u odabranoj skali dužine.

Problemi sa brzinama i ubrzanjima rješavaju se izradom planova za brzine i ubrzanja karika mehanizma na određenim (datim) pozicijama vodeće karike na osnovu unaprijed sastavljenih vektorskih jednačina za brzine i ubrzanja karika mehanizma.

Prednost ove metode u odnosu na grafičku po tome što je manje dugotrajna, jer vam omogućava da odredite brzine i ubrzanja (njihovu veličinu i smjer) na jednom planu brzine ili planu ubrzanja za više tačaka mehanizma.

nedostatak Metoda je da je potrebno izgraditi planove brzine i ubrzanja za više pozicija mehanizma (ako je potrebno odrediti brzinu i ubrzanje na različitim pozicijama mehanizma i njegovih karika).

Treba imati na umu da su zakoni ravnoparalelnog kretanja osnova za izradu planova za brzine i ubrzanja. Prema ovim zakonima:

1. Plan brzine (kao i plan ubrzanja) dobija se kao rezultat grafičkog rješenja vektorskih jednačina za određivanje brzina (ubrzanja) tačaka u ravnoparalelnom kretanju;

2. Vektori apsolutnih brzina tačaka (kada se uzme u obzir njihovo kretanje u odnosu na fiksnu vezu) prikazani su kao da izlaze iz pola plana, a pravac se poklapa sa tangentama na putanju kretanja. Vektori relativnih brzina tačaka (kada se kreću u odnosu na pokretne tačke) su predstavljeni segmentima koji povezuju krajeve odgovarajućih vektora apsolutnih brzina;

3. Dužina vektora relativnih brzina proporcionalna je dužini onih dijelova karika koji predstavljaju polumjere rotacije tačaka u njihovom relativnom kretanju. Ova odredba, poznata kao teorema sličnosti, olakšava određivanje brzina mnogih tačaka koje leže na vezama ravno-paralelnog i rotacionog kretanja.

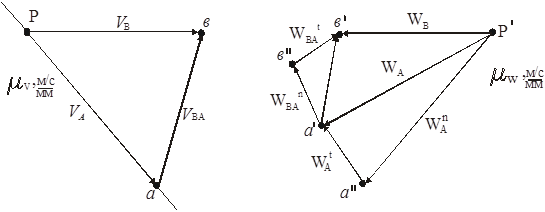
To je plan brzine trougla.

Plan brzine krute veze- lokus tačaka krajeva vektora apsolutnih brzina bilo koje tačke veze, ako su izgrađene iz jedne zajedničke tačke, naziva se pol plana brzine.

Plan brzine je uvijek nacrtan u mjerilu. U disciplini "Teorija mašina i mehanizama" skala ima dimenziju, pa se obično naziva faktor skale: , .

Plan brzine je sličan samom linku i rotira se za devedeset stepeni u pravcu trenutne rotacije.

Ako je plan brzine krute karike sličan njenoj karici, onda plan brzine mehanizma nije sličan samom mehanizmu, jer je, za razliku od krute karike, mehanizam promjenjiv pokretni sistem.

Plan brzine- skup planova brzine pojedinačnih veza, izgrađenih iz jedne zajedničke tačke, koja se naziva stub plana brzine.