1. Oddiy uchburchakni olaylik.
2. Biz undan uchburchakni kesib tashladik, uning uchlari asl tomonlarining o'rtalarida joylashgan. Natijada, biz tekislikda uchta uchburchakni olamiz, ularning har birining maydoni asl maydonidan to'rt baravar kam.
3. Olingan uchburchaklar bilan oldingi manipulyatsiyalarni bajaramiz.

Jarayon quyidagicha ko'rinadi:

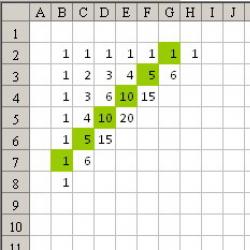
1. Qizig'i shundaki, agar Paskal uchburchagida barcha toq raqamlar bir rangga, juft raqamlar boshqa rangga bo'yalgan bo'lsa, u holda Sierpinski uchburchagi hosil bo'ladi.

Keling, ushbu faktdan foydalanaylik. Faqat Excelda Paskal uchburchagining klassik (satr-qator) shaklini emas, balki undan foydalanish qulayroqdir:

Bu erda binomial koeffitsientlar diagonal ravishda, birinchi to'ldirilgan qatorda va birlikning birinchi to'ldirilgan ustunida, qolganlarida esa yuqori va chap elementlarning yig'indisi yoziladi.

Keling, qurilishga o'tamiz. Biz uchun koeffitsientlarni emas, balki faqat ularning paritetini yozish kifoya.

Birinchidan, Excelda katakchalarning o'lchamini, masalan, 7 dan 7 pikselgacha qilib ko'rsatamiz.

Keling, B2 katakchada turamiz, keyin B2:DY129 maydonini tanlang - buning uchun Ctrl + G tugmalarini bosing va havola maydoniga B2: DY129 yozing.

Endi formulalar qatorida biz yozamiz =AGAR(YOKI(QAT()=2,COLUMN()=2),1,REM(A2+B1,2))
va barcha tanlangan maydonni shunga o'xshash formula bilan to'ldirish uchun Ctrl + Enter tugmalarini bosing.

Qani ketdik Menyu - Shartli formatlash va 1 qiymat uchun biz hujayraning rangini ko'rsatamiz.

Natijada biz quyidagilarni olamiz:

Shuni ta'kidlash kerakki, Sierpinski uchburchagi samolyotda qandaydir tasodifiy yurish orqali olinadi. Aynan:

1. Uchburchakning 3 ta uchini tekislikka mahkamlaymiz va yana bir nuqtani olamiz.
2. Birinchi nuqtani segmentning o'rta nuqtasi sifatida olamiz tasodifan tanlangan cho'qqi va 1-bosqichdan nuqta.
3. Biz ikkinchi nuqtani segmentning o'rta nuqtasi sifatida olamiz tasodifan tanlangan cho'qqi va birinchi nuqta.
4. Jarayonni ko'p marta takrorlaymiz.

Ushbu makrodan foydalanishingiz mumkin:

Umumiy pastki makro()

Dim arRange(1 dan 3 gacha) diapazon sifatida
Dim tekRow Integer
Xira tekustunni butun son sifatida
Dim i Integer
ITni butun son sifatida xiralashtiring

tekRow = Int (1000 * Rnd) + 1
tekColumn = Int (200 * Rnd) + 1

arRange(1) = Hujayralar(1, 1) ni o‘rnating
ArRange(2) = Hujayralar (50, 250) ni o‘rnating
arRange(3) = Hujayralar (200, 20) ni o‘rnating

Hujayralar. Tozalash

i uchun = 1 dan 20000 gacha
iT = (Int(1000 * Rnd) Mod 3) + 1
tekRow = Int((tekRow + arRange(iT).Row) / 2)
tekColumn = Int((tekColumn + arRange(iT).Column) / 2)
Hujayralar(tekRow, tekColumn).Interior.ColorIndex = 5
Keyingisi

End Sub

Sierpinski uchburchagi- fraktal, Kantor to'plamining ikki o'lchovli analoglaridan biri, 1915 yilda polshalik matematik Vaclav Sierpinski tomonidan taklif qilingan. Sierpinskining "salfetkasi" sifatida ham tanilgan.

Sierpinski uchburchagi

Qurilish

Iterativ usul

Sierpinski uchburchagining qurilishi

Teng tomonli uchburchak tomonlarining o'rta nuqtalari segmentlar bilan bog'langan. Siz 4 ta yangi uchburchak olasiz. O'rta uchburchakning ichki qismi asl uchburchakdan chiqariladi. Bu juda ko'p chiqadi T 1 (\displaystyle T_(1)), qolgan 3 ta "birinchi darajali" uchburchakdan iborat. Birinchi darajali uchburchaklarning har biri bilan xuddi shunday qilib, biz to'plamni olamiz T 2 (\displaystyle T_(2)), ikkinchi darajali 9 ta teng qirrali uchburchakdan iborat. Bu jarayonni cheksiz davom ettirsak, biz cheksiz ketma-ketlikni olamiz T 0 ⊃ T 1 ⊃ ⋯ ⊃ T n ⊃ … (\displaystyle T_(0)\supset T_(1)\supset \nuqtalar \supset T_(n)\supset \dots ), a'zolarining kesishishi Sierpinski uchburchagi.

Xaos usuli

1. Attraktorlarning koordinatalari ko'rsatilgan - dastlabki uchburchakning uchlari T 0 (\displaystyle T_(0)). 2. Ehtimollar maydoni (0 ; 1) (\displaystyle (0;1)) 3 ta teng qismga bo'linadi, ularning har biri bitta attraktorga mos keladi. 3. Muayyan boshlang'ich nuqtasi ko'rsatilgan P 0 (\displaystyle P_(0)), uchburchak ichida yotgan T 0 (\displaystyle T_(0)). 4. Sierpinski uchburchagi to'plamiga kiruvchi nuqtalarni qurish siklining boshlanishi. 1. Tasodifiy son hosil bo'ladi n ∈ (0 ; 1) (\displaystyle n\in (0;1)). 2. Faol attraktor hosil bo'lgan son ehtimollik pastki fazosiga tushgan cho'qqiga aylanadi. 3. Nuqta qurilmoqda P i (\displaystyle P_(i)) yangi koordinatalar bilan: x i = x i - 1 + x A 2; y i = y i − 1 + y A 2 (\displaystyle x_(i)=(\frac (x_(i-1)+x_(A))(2));y_(i)=(\frac (y_(i)) -1)+y_(A))(2))), Qayerda: x i - 1 , y i - 1 (\displaystyle x_(i-1),y_(i-1))- oldingi nuqtaning koordinatalari P i - 1 (\displaystyle P_(i-1)); x A , y A (\displaystyle x_(A),y_(A))- faol jalb qiluvchi nuqtaning koordinatalari. 5. Tsiklning boshiga qayting.

Xususiyatlari

Iterativ usulda qurish

Xaos usuli yordamida qurilish

Eslatmalar

Havolalar

L-tizim

L-tizim yoki Lindenmayer tizimi parallel qayta yozish tizimi va rasmiy grammatikaning bir turi. L-tizim satrlarni yaratish uchun ishlatilishi mumkin bo'lgan belgilar alifbosi, har bir belgini almashtirish qoidalarini belgilovchi generatsiya qoidalari to'plami, qurilish boshlanadigan boshlang'ich satr ("aksioma") va mexanizmdan iborat. hosil qilingan ipni geometrik tuzilmalarga aylantirish. L-tizimlari 1968 yilda Utrext universitetida vengriyalik biolog va botanik Aristide Lindenmayer tomonidan taklif qilingan va ishlab chiqilgan. Lindenmayer o'simlik hujayralarining xatti-harakatlarini tasvirlash va o'simliklarning rivojlanish jarayonini modellashtirish uchun L-tizimlaridan foydalangan. L-tizimlari turli organizmlarning morfologiyasini modellashtirish uchun ham ishlatilgan va takrorlanadigan funksiya tizimlari kabi o'ziga o'xshash fraktallarni yaratish uchun ishlatilishi mumkin.

Raket (dasturlash tili)

Racket (ilgari PLTScheme) Lisp/Scheme oilasiga mansub ko'p paradigmali umumiy maqsadli dasturlash tilidir. Tilga yo'naltirilgan dasturlash uchun muhitni ta'minlaydi - reketning maqsadlaridan biri dasturlash tillarini yaratish, ishlab chiqish va amalga oshirishdir. Til turli kontekstlarda qo'llaniladi: skript tili sifatida, umumiy maqsadli til sifatida, informatika o'qitishda, ilmiy tadqiqotlarda.

Platforma foydalanuvchiga Racket tilini, jumladan ishlab chiqilgan ish vaqti tizimi, turli kutubxonalar, JIT kompilyatori va boshqalarni, shuningdek, Racket-da yozilgan DrRacket ishlab chiqish muhitini (ilgari DrScheme nomi bilan tanilgan) taqdim etadi. Ushbu dasturiy ta'minot tizimi MITning ProgramByDesign kursida qo'llaniladi. Asosiy Racket tili kuchli so'l tizimga ega bo'lib, u sizga o'rnatilgan va domenga xos dasturlash tillarini, til konstruksiyalarini (masalan, sinflar va modullar) va turli semantikaga ega Racket dialektlarini yaratishga imkon beradi.

Tizim bepul va ochiq kodli dasturiy ta'minot bo'lib, LGPL shartlari asosida tarqatiladi. Hamjamiyat tomonidan yozilgan kengaytmalar va paketlar tizimning veb-distributivi PLaneT da mavjud.

Fraktal siqish algoritmi

Fraktal tasvirni siqish - tasvirlarga takrorlangan funksiyalar (odatda affin o'zgarishlar) tizimlarini qo'llashga asoslangan yo'qolgan tasvirni siqish algoritmi. Ushbu algoritm ba'zi hollarda tabiiy ob'ektlarning haqiqiy fotosuratlari uchun maqbul vizual sifat bilan juda yuqori siqish nisbatlarini olish imkonini berishi bilan mashhur. Patentlash bilan bog'liq qiyin vaziyat tufayli algoritm keng qo'llanilmadi.

Ajratuvchi plitka

Rep-tile - bu mozaik geometriya tushunchasi bo'lib, uni shaklning o'zidan kichikroq nusxalarga kesib olish mumkin. 2012 yilda Mathematics jurnalida ingliz matematigi Li Salous tomonidan o'z-o'zidan plitkalar to'plami deb ataladigan bo'linadigan plitkalarning umumlashtirilishi taklif qilingan.

Yakuniy bo'linish qoidasi

Matematikada boʻlinishning yakuniy qoidasi koʻpburchak va boshqa ikki oʻlchovli shakllarni kichikroq va kichikroq boʻlaklarga boʻlishning rekursiv usuli hisoblanadi. Bu ma'noda bo'linish qoidalari fraktallarni umumlashtirishdir. Xuddi shu naqshni qayta-qayta takrorlashning o'rniga, har bir qadamda nozik o'zgarishlar mavjud bo'lib, nafis fraktal uslubni saqlab qolgan holda yanada boy tuzilmalarni yaratishga imkon beradi. Bo'linish qoidalari arxitektura, biologiya va informatikada, shuningdek, giperbolik manifoldlarni o'rganishda qo'llaniladi. Plitkalarni almashtirish - bu bo'linish qoidalarining yaxshi o'rganilgan turi.

Peano egri chizig'i

Peano egri chizig'i - tasvirida kvadrat (yoki umuman olganda, fazoning ochiq hududlari) bo'lgan parametrik egri chiziqlarning umumiy nomi. Boshqa nom - bo'shliqni to'ldirish egri chizig'i.

Ushbu turdagi egri chiziqni kashf etgan Juzeppe Peano (1858-1932) sharafiga Peano egri chizig'i Peano topgan maxsus egri chiziqqa berilgan nomdir.

Sierpinskiy egri chizig'i

Sierpinski egri chiziqlari Vaclaw Sierpinski tomonidan kashf etilgan uzluksiz yopiq planar fraktal egri chiziqlarning rekursiv aniqlangan ketma-ketligidir. Limitdagi egri chiziq birlik kvadratini to'liq to'ldiradi, shuning uchun chegara egri chizig'i ham deyiladi Sierpinskiy egri chizig'i, bo'shliqni to'ldiradigan egri chiziqlarga misoldir.

Sierpinski egri chizig'i bo'shliqni to'ldirganligi sababli, uning Hausdorff o'lchami (chegarada n → ∞ (\displaystyle n\o‘ng ko‘rsatkich \infty )) ga teng 2 (\displaystyle 2).
Evklid egri chizig'ining uzunligi

ga teng l n = 2 3 (1 + 2) 2 n - 1 3 (2 - 2) 1 2 n (\displaystyle l_(n)=(2 \3 dan ortiq)(1+(\sqrt (2)))2^( n)-(1 \3 dan ortiq)(2-(\sqrt (2))(1 \2 dan ortiq ^(n))),

ya'ni o'sib bormoqda eksponent sifatida tomonidan n (\displaystyle n), va chegarasi n → ∞ (\displaystyle n\o‘ng ko‘rsatkich \infty ) egri chiziq bilan o'ralgan hududning maydoni S n (\displaystyle S_(n)), hisoblanadi 5/12 (\displaystyle 5/12) kvadrat (Evklid metrikasida).

Logarifm

Raqamning logarifmi b (\displaystyle b) asoslangan a (\displaystyle a) (qadimgi yunon tilidan. λόγος "so'z; munosabat" + ἀριθμός "raqam") bazani ko'tarish kerak bo'lgan quvvatning ko'rsatkichi sifatida aniqlanadi a (\displaystyle a) raqamni olish uchun b (\displaystyle b). Belgilash: log a ⁡ b (\displaystyle \log _(a)b), talaffuz qilinadi: " logarifm b (\displaystyle b) asoslangan a (\displaystyle a) ».

Ta'rifdan shunday xulosa kelib chiqadi x = log a ⁡ b (\displaystyle x=\log _(a)b) tenglamani yechishga teng a x = b (\displaystyle a^(x)=b). Masalan, log 2 ⁡ 8 = 3 (\displaystyle \log _(2)8=3), chunki 2 3 = 8 (\displaystyle 2^(3)=8).

Logarifmni hisoblash deyiladi logarifm bo'yicha. Raqamlar a , b (\displaystyle a,b) ko'pincha haqiqiy, lekin murakkab logarifmlar nazariyasi ham mavjud.

Logarifmlar mehnat talab qiladigan hisob-kitoblarni sezilarli darajada soddalashtirish uchun ularning keng qo'llanilishini aniqlagan noyob xususiyatlarga ega. "Logarifmlar olamiga" o'tishda ko'paytirish ancha soddaroq qo'shish bilan almashtiriladi, bo'linish ayirish bilan almashtiriladi va daraja va ildiz chiqarish mos ravishda darajaga ko'paytirish va bo'linishga aylanadi. Laplasning ta'kidlashicha, logarifmlar ixtirosi "astronomning ishini qisqartirib, uning hayotini ikki barobarga oshirdi".

Logarifmlarning ta'rifi va ularning qiymatlari jadvali (trigonometrik funktsiyalar uchun) birinchi marta 1614 yilda Shotlandiya matematigi Jon Nepier tomonidan nashr etilgan. Boshqa matematiklar tomonidan kengaytirilgan va takomillashtirilgan logarifmik jadvallar uch asrdan ko'proq vaqt davomida, elektron kalkulyator va kompyuterlar paydo bo'lgunga qadar ilmiy va muhandislik hisob-kitoblari uchun keng qo'llanilgan.

Vaqt o'tishi bilan logarifmik funktsiya aniq bo'ldi y = log a ⁡ x (\displaystyle y=\log _(a)x) inson faoliyatining boshqa ko'plab sohalarida o'rnini bosa olmaydi: differensial tenglamalarni echish, miqdorlar qiymatlarini tasniflash (masalan, tovush chastotasi va intensivligi), turli bog'liqliklarni yaqinlashtirish, axborot nazariyasi, ehtimollar nazariyasi va boshqalar. Bu funktsiya quyidagilardan biridir. elementar bo'lsa, u ko'rsatkichli funktsiyaga teskari hisoblanadi. Eng ko'p ishlatiladigan asosli haqiqiy logarifmlardir 2 (\displaystyle 2)(ikkilik), e (\displaystyle e) (tabiiy logarifm) va 10 (\displaystyle 10)(o'nlik).

DNKga asoslangan nanotexnologiya

DNK nanotexnologiyasi - texnologik foydalanish uchun nuklein kislotalardan sun'iy tuzilmalarni ishlab chiqish va ishlab chiqarish. Ushbu ilmiy sohada nuklein kislotalar tirik hujayralardagi genetik ma'lumotni tashuvchisi sifatida emas, balki nanomateriallarning biologik bo'lmagan muhandisligi ehtiyojlari uchun material sifatida ishlatiladi.

Texnologiya nuklein kislotalarning asosli juftlashuvi uchun qat'iy qoidalardan foydalanadi, bu faqat bir-birini to'ldiruvchi asosli ketma-ketlikka ega bo'lgan iplarning qismlarini kuchli, qattiq ikki tomonlama spiral strukturasini yaratish uchun bir-biriga bog'lash imkonini beradi. Ushbu qoidalardan aniq sozlangan nano o'lchamli shakllar va xususiyatlarga ega murakkab maqsadli tuzilmalarni shakllantirish uchun tanlab yig'iladigan asoslar ketma-ketligini yaratish mumkin bo'ladi. Aksariyat materiallar DNK yordamida ishlab chiqariladi, lekin RNK va peptid nuklein kislotalari (PNA) kabi boshqa nuklein kislotalarni o'z ichiga olgan tuzilmalar ham qurilgan, bu texnologiya sohasini "nukleotid asosli nanotexnologiya" deb atashga imkon beradi.

DNKga asoslangan nanotexnologiyaning asosiy kontseptsiyasi birinchi marta 1980-yillarning boshida Nadrian Seaman tomonidan taklif qilingan va bu tadqiqot sohasi 2000-yillarning o'rtalarida keng qiziqish uyg'ota boshlagan. Ushbu rivojlanayotgan texnologiya sohasida ishlaydigan tadqiqotchilar ikki va uch o'lchovli kristall panjaralar, nanotubalar, ko'p yuzli va boshqa erkin shakllar kabi statik tuzilmalarni, shuningdek molekulyar mashinalar va DNK kompyuterlari kabi funktsional tuzilmalarni yaratdilar.

Ushbu tuzilmalarni yig'ish uchun turli xil usullar qo'llaniladi, jumladan plitkalar tuzilishi, bu erda plitkalar kichikroq tuzilmalardan yig'iladi, DNK origami texnikasi yordamida yaratilgan katlama tuzilmalari va iplarni almashtirish texnikasi yordamida yaratilgan dinamik ravishda qayta tashkil etilgan tuzilmalar. Tadqiqot sohasi strukturaviy biologiya va biofizika sohalaridagi asosiy fan muammolarini, shu jumladan kristallografiya va oqsil strukturasini aniqlash uchun spektroskopiyaning amaliy muammolarini hal qilish uchun vosita sifatida qo'llanila boshlandi. Shuningdek, kengaytiriladigan molekulyar elektronika va nanotibbiyotda potentsial ilovalar bo'yicha tadqiqotlar olib borilmoqda.

Tabiiy logarifm

Tabiiy logarifm asosning logarifmidir e, Qayerda e (\displaystyle e)- taxminan 2,72 ga teng irratsional doimiy. sifatida belgilanadi ln ⁡ x (\displaystyle \ln x), log e ⁡ x (\displaystyle \log _(e)x) yoki ba'zan shunchaki log ⁡ x (\displaystyle \log x), agar asos bo'lsa e (\displaystyle e) nazarda tutilgan. Odatda raqam x (\displaystyle x) logarifm belgisi ostida haqiqiy, lekin bu tushunchani murakkab sonlargacha kengaytirish mumkin.

Ta'rifdan kelib chiqadiki, logarifmik bog'liqlik eksponensial uchun teskari funktsiyadir y = e x (\displaystyle y=e^(x)), shuning uchun ularning grafiklari birinchi va uchinchi kvadrantlarning bissektrisalariga nisbatan simmetrikdir (o'ngdagi rasmga qarang). Ko'rsatkichli funktsiya singari, logarifmik funktsiya ham transsendental funktsiyalar toifasiga kiradi.

Tabiiy logarifmlar noma'lum ko'rsatkich sifatida mavjud bo'lgan algebraik tenglamalarni echish uchun foydalidir va ular matematik tahlilda ajralmas hisoblanadi. Masalan, logarifmlar ma'lum yarim yemirilish davri uchun parchalanish konstantasini topish yoki radioaktivlik masalalarini yechishda parchalanish vaqtini topish uchun ishlatiladi. Ular matematika va amaliy fanlarning ko'plab sohalarida muhim rol o'ynaydi va moliyada ko'plab muammolarni, shu jumladan murakkab foizlarni topish uchun ishlatiladi.

Lebeg o'lchami

Lebeg o'lchami yoki topologik o'lchov- qoplamalar bilan aniqlangan o'lcham, topologik makonning eng muhim o'zgarmasligi. Kosmosning Lebeg o'lchami X (\displaystyle X) odatda belgilanadi xira ⁡ X (\displaystyle \dim X).

Rekursiya

Rekursiya - bu ob'ekt yoki jarayonning ushbu ob'ekt yoki jarayonning o'zi ichidagi ta'rifi, tavsifi, tasviri, ya'ni ob'ekt o'zining bir qismi bo'lgan holat. "Rekursiya" atamasi turli xil ixtisoslashgan bilim sohalarida - tilshunoslikdan mantiqgacha qo'llaniladi, lekin eng ko'p matematika va informatikada qo'llaniladi.

Sierpinskiy, Vaclav

Vacław Franciszek Sierpiński, boshqa transkripsiyada - Sierpinski (polyakcha: Wacław Franciszek Sierpiński; 1882 yil 14 mart, Varshava - 1969 yil 21 oktyabr, o'sha yerda) - polshalik matematik va o'qituvchi, uning tanlovi bo'yicha o'z asarlarini tanlagan. kontinuum gipotezasi, sonlar nazariyasi, funksiyalar nazariyasi va topologiya. 724 ta maqola va 50 ta kitob muallifi.

Tetraedr (Bottrop)

Tetraedr (nem. Tetraeder) — Bottrop shahrida (Shimoliy Reyn-Vestfaliya) kuzatuv maydonchasi sifatida foydalaniladigan, chetining uzunligi 60 m boʻlgan, toʻrtta 9 metrli beton tayanchlar bilan mustahkamlangan tetraedr koʻrinishidagi poʻlat konstruksiya. . Tetraedr dengiz sathidan 105 m balandlikda Prosper-Haniel (de: Bergwerk Prosper-Haniel) konining Beckstraße chiqindi uyasi (nem. Beckstraße) tepasida joylashgan. Yuqori kuzatuv maydonchasidan Bottrop, Essen, Oberxauzen, Gladbek shaharlarining ko'rinishini ko'rishingiz mumkin. Yaxshi ko'rish bilan ko'rish diapazoni 40 km ga etadi va hatto Dyusseldorfdagi Rheinturm teleminorasini ajratib ko'rsatishga imkon beradi.

Bottrop tetraedri - Ruhr viloyatining "Sanoat madaniyati yo'li" mintaqaviy loyihasining tematik nuqtasi.

Paskal uchburchagi

Paskal uchburchagi - bu uchburchak shakliga ega binomial koeffitsientlarning cheksiz jadvali. Ushbu uchburchakda tepada va yon tomonda joylashganlar mavjud. Har bir raqam uning ustidagi ikkita sonning yig'indisiga teng. Uchburchakning chiziqlari vertikal o'qga nisbatan simmetrikdir. Blez Paskal nomi bilan atalgan. Paskal uchburchagini tashkil etuvchi raqamlar tabiiy ravishda algebra, kombinatorika, ehtimollar nazariyasi, matematik tahlil va sonlar nazariyasida paydo bo'ladi.

Fraktal

Fraktal (lot. fractus — maydalangan, singan, singan) — oʻziga oʻxshashlik xususiyatiga ega boʻlgan toʻplam (toʻliq yoki taxminan oʻzining bir qismiga toʻgʻri keladigan, yaʼni butun bir yoki bir nechta shaklga ega boʻlgan narsa. qismlar). Matematikada fraktallar Evklid fazosidagi kasr metrik o'lchamiga (Minkovskiy yoki Hausdorff ma'nosida) yoki topologik o'lchovdan farqli metrik o'lchamga ega bo'lgan nuqtalar to'plami sifatida tushuniladi, shuning uchun ularni boshqa geometrik figuralardan ajratib olish kerak. cheklangan miqdordagi havolalar. Cheklangan marta takrorlanadigan o'ziga o'xshash raqamlar prefraktallar deb ataladi.

G'ayrioddiy xususiyatlarga ega o'ziga o'xshash to'plamlarning birinchi namunalari 19-asrda uzluksiz differensiallanmaydigan funktsiyalarni o'rganish natijasida paydo bo'lgan (masalan, Bolzano funktsiyasi, Veyershtrass funktsiyasi, Kantor to'plami). "Fraktal" atamasi 1975 yilda Benoit Mandelbrot tomonidan kiritilgan va 1977 yilda "Tabiatning fraktal geometriyasi" kitobining nashr etilishi bilan keng tarqalgan. Fraktallar kompyuter texnologiyalarining rivojlanishi bilan alohida mashhurlikka erishdi, bu esa ushbu tuzilmalarni samarali tasavvur qilish imkonini berdi.

"Fraktal" so'zi nafaqat matematik atama sifatida ishlatiladi. Fraktalni quyidagi xususiyatlardan kamida bittasiga ega bo'lgan ob'ekt deb atash mumkin:

U barcha miqyosda ahamiyatsiz bo'lmagan tuzilishga ega. Bu oddiy figuralardan (aylana, ellips, silliq funksiya grafigi kabi) farqli o'laroq: agar siz oddiy figuraning kichik bo'lagini juda katta masshtabda ko'rib chiqsangiz, u to'g'ri chiziq bo'lagiga o'xshaydi. Fraktal uchun masshtabni oshirish strukturani soddalashtirishga olib kelmaydi, ya'ni barcha masshtablarda siz bir xil darajada murakkab rasmni ko'rishingiz mumkin.

O'ziga o'xshash yoki taxminan o'ziga o'xshash.

U kasrli metrik o'lchamga yoki topologik o'lchamdan oshib ketadigan metrik o'lchamga ega.Tabiatdagi ko'plab ob'ektlar fraktal xususiyatlarga ega, masalan: qirg'oqlar, bulutlar, daraxt tojlari, qor parchalari, qon aylanish tizimi, alveolalar.

Fraktal o'lcham

Fraktal o'lcham(ingliz fraktal o'lchami) - metrik fazoda to'plamning o'lchamini aniqlash usullaridan biri. Fraktal o'lcham n-o'lchovli to'plamni quyidagi formula yordamida aniqlash mumkin:

D = − lim e → 0 ln ⁡ (N e) ln ⁡ (e) (\displaystyle D=-\lim \limits _(\varepsilon \to 0)(\frac (\ln(N_(\varepsilon ))) (\ln(\varepsilon)))), Qayerda N e (\displaystyle N_(\varepsilon ))- minimal raqam n-radiusning o'lchovli "to'plari" e (\displaystyle \varepsilon), to'plamni qoplash uchun zarur.

Fraktal o'lcham butun son bo'lmagan raqamli qiymatni qabul qilishi mumkin.

Singan o'lchamning asosiy g'oyasi matematika sohasida uzoq tarixga ega, ammo bu atamaning o'zi 1967 yilda Benoit Mandelbrot tomonidan o'zining o'xshashlik haqidagi maqolasida kasr o'lchamini tasvirlab bergan. Ushbu maqolada Mandelbrot Lyuis Fry Richardsonning oldingi ishiga ishora qilib, qirg'oq chizig'ining o'lchangan uzunligi o'lchov tayoqchasining uzunligiga bog'liq degan zid fikrni tasvirlab berdi (1-rasmga qarang). Ushbu g'oyadan so'ng, qirg'oq chizig'ining fraktal o'lchami qirg'oq chizig'ining uzunligini o'lchash uchun zarur bo'lgan qutblar sonining (ma'lum bir miqyosda) qutbning tanlangan shkalasiga nisbatiga mos keladi. Fraktal o'lchamning bir nechta rasmiy matematik ta'riflari [⇨] mavjud bo'lib, ular masshtabning o'zgarishi bilan elementning o'zgarishi haqidagi ushbu asosiy tushunchaga asoslanadi.

Oddiy misollardan biri Koch qor parchasining fraktal o'lchamidir. Uning topologik o'lchami 1 ga teng, lekin u hech qanday tarzda to'g'rilanmaydigan egri chiziq emas, chunki Koch qor parchasining istalgan ikkita nuqtasi orasidagi egri chiziqning uzunligi cheksizdir. Egri chiziqning hech bir qismi, qanchalik kichik bo'lmasin, to'g'ri chiziq segmenti emas. Aksincha, Kochning qor parchasi turli burchaklarda bog'langan cheksiz sonli segmentlardan iborat. Egri chiziqning fraktal o'lchamini intuitiv ravishda tushuntirish mumkin, bu fraktal chiziq bir o'lchovli bo'lish uchun juda batafsil (batafsil), lekin ikki o'lchovli bo'lish uchun etarlicha murakkab emas. Shuning uchun uning o'lchami odatdagi topologik o'lchov 1 bilan emas, balki fraktal o'lchami bilan yaxshiroq tavsiflanadi, bu holda 1 va 2 oralig'ida joylashgan raqamga teng.

Fraktal san'at

Fraktal san'at - bu fraktal ob'ektlarni hisoblash va hisob-kitoblar natijalarini harakatsiz tasvirlar, animatsiyalar va avtomatik ravishda yaratilgan media fayllar sifatida taqdim etish orqali yaratilgan algoritmik san'at shakli. Fraktal san'at 1980-yillarning o'rtalarida boshlangan. Bu yangi media san'atining bir qismi bo'lgan kompyuter san'ati va raqamli san'at janri. Shu bilan birga, fraktal san'at "ilmiy san'at" deb ataladigan sohalardan biridir.

Fraktal san'at kamdan-kam hollarda qo'lda yaratilgan. Odatda uch bosqich orqali fraktallarni yaratuvchi dasturiy ta'minot tomonidan bilvosita yaratiladi: mos keladigan fraktal dasturiy ta'minot parametrlarini o'rnatish; ehtimol uzoq hisob-kitoblarni amalga oshirish; va mahsulotni baholash. Ba'zi hollarda yaratilgan tasvirlarni qayta ishlash uchun boshqa grafik dasturlardan foydalaniladi. Fraktal bo'lmagan tasvirlarni ham badiiy asarga kiritish mumkin. Julia Set va Mandelbrot to'plami fraktal san'atning piktogrammasi hisoblanadi.

Xususiyatlari
Eng oddiy fraktallar

Uni olish uchun siz ichki qismga ega (teng qirrali) uchburchakni olishingiz kerak, unda o'rta chiziqlarni chizishingiz va hosil bo'lgan to'rtta kichik uchburchakning markaziy qismini tashlashingiz kerak. Keyin qolgan uchta uchburchakning har biri bilan bir xil qadamlarni takrorlashingiz kerak va hokazo. Rasmda dastlabki uchta qadam ko'rsatilgan va flesh-namoyishda siz mashq qilishingiz va o'ninchi bosqichgacha bo'lgan qadamlarni olishingiz mumkin.

Markaziy uchburchaklarni tashlash Sierpinski uchburchagi bilan yakunlanishning yagona yo'li emas. Siz "teskari yo'nalishda" harakat qilishingiz mumkin: dastlab "bo'sh" uchburchakni oling, so'ngra undagi o'rta chiziqlardan hosil bo'lgan uchburchakni to'ldiring, so'ngra uchta burchakli uchburchakning har birida xuddi shunday qiling va hokazo. Avvaliga raqamlar bo'ladi. juda farq qiladi, lekin iteratsiya soni ortib borishi bilan ular bir-biriga tobora o'xshash bo'ladi va chegarada ular mos keladi.

Sierpinski uchburchagini olishning keyingi usuli, keyingi iteratsiya qismlarini masshtabli fragment bilan almashtirish orqali geometrik fraktallarni qurishning odatiy sxemasiga ko'proq o'xshaydi. Bu erda, har bir bosqichda, singan chiziqni tashkil etuvchi segmentlar uchta bo'g'inning singan chizig'i bilan almashtiriladi (uning o'zi birinchi iteratsiyada olinadi). Bu singan chiziqni navbatma-navbat o'ngga, keyin esa chapga yotqizishingiz kerak. Ko'rinib turibdiki, sakkizinchi iteratsiya fraktalga juda yaqin va u qanchalik uzoqlashsa, chiziq unga yaqinlashadi.

Lekin bu hammasi emas. Ma'lum bo'lishicha, Sierpinski uchburchagi nuqtaning tekislikdagi tasodifiy yurishi turlaridan biri natijasida olingan. Bu usul "Xaos o'yini" deb ataladi. Uning yordami bilan siz boshqa fraktallarni qurishingiz mumkin.

"O'yin" ning mohiyati shundan iborat. Muntazam uchburchak tekislikda o'rnatiladi A 1 A 2 A 3. Har qanday boshlang'ich nuqtasini belgilang B 0 . Keyin uchburchakning uchta uchidan birini tasodifiy tanlang va nuqtani belgilang B 1 - uchlari shu cho'qqida va da joylashgan segmentning o'rtasi B 0 (o'ngdagi rasmda cho'qqi tasodifiy tanlangan A 1). Xuddi shu narsa nuqta bilan takrorlanadi B 1 olish B 2. Keyin ular ochko oladilar B 3 , B 4 va hokazo. Nuqtaning tasodifiy "sakrashi", ya'ni har safar uchburchakning cho'qqisi oldingi bosqichlarda nima tanlanganidan qat'i nazar, tasodifiy tanlanishi muhim ahamiyatga ega. Agar ketma-ketlikdan nuqtalarni belgilasangiz, ajoyib B i, keyin Sierpinski uchburchagi tez orada paydo bo'la boshlaydi. Quyida 100, 500 va 2500 ball belgilanganda nima sodir bo'ladi.

Ba'zi xususiyatlar

Variantlar

Sierpinski tomonidan gilam (kvadrat, peçete). Kvadrat shakli 1916 yilda Vaclaw Sierpinski tomonidan tasvirlangan. U o'z-o'zidan kesishmasdan tekislikda chizilishi mumkin bo'lgan har qanday egri chiziq bu teshik kvadratining ba'zi bir kichik to'plamiga gomeomorf ekanligini isbotlashga muvaffaq bo'ldi. Uchburchak kabi, kvadrat turli dizaynlardan tayyorlanishi mumkin. O'ngda klassik usul: kvadratni 9 qismga bo'lish va markaziy qismni tashlash. Keyin qolgan 8 kvadrat uchun ham xuddi shunday takrorlanadi va hokazo.

Uchburchak kabi, kvadrat nol maydonga ega. Sierpinski gilamining fraktal o'lchami uchburchakning o'lchamiga o'xshash hisoblangan log 3 8 ga teng.

Sierpinskiy piramidasi. Sierpinski uchburchagining uch o'lchovli analoglaridan biri. U xuddi shunday tarzda, sodir bo'layotgan narsaning uch o'lchovliligini hisobga olgan holda tuzilgan: dastlabki piramidaning 5 nusxasi, ikki marta siqilgan, birinchi iteratsiyani tashkil qiladi, uning 5 nusxasi ikkinchi iteratsiyani tashkil qiladi va hokazo. Fraktal. o'lcham log 2 ga teng 5. Shakl nol hajmga ega (har bir qadamda hajmning yarmi tashqariga tashlanadi), lekin shu bilan birga sirt maydoni iteratsiyadan iteratsiyagacha saqlanib qoladi va fraktal uchun u bir xil bo'ladi. boshlang'ich piramida.

Menger shimgichi. Sierpinski gilamini uch o'lchovli fazoga umumlashtirish. Shimgichni qurish uchun sizga protsedurani cheksiz takrorlash kerak bo'ladi: iteratsiyani tashkil etuvchi kublarning har biri 27 ta uch baravar kichik kublarga bo'linadi, ulardan markaziy va uning 6 ta qo'shnisi tashlanadi. Ya'ni, har bir kub uch barobar kichikroq 20 ta yangi hosil qiladi. Shuning uchun fraktal o'lcham log 3 20. Bu fraktal universal egri chiziqdir: uch o'lchovli fazodagi har qanday egri shimgichning ba'zi bir kichik to'plamiga gomeomorfdir. Shimgich nol hajmga ega (chunki har bir qadamda u 20/27 ga ko'paytiriladi), lekin u cheksiz katta maydonga ega.

L
Ummon liniyasi:

N - segmentlar soni, o'lchami A.

D - "egilish darajasi"

N=(1/a)D; S=N*a; S=(1/a)D-1

TO
Riva Koch

2) N=4L=1/3S(4)=4/3

N=16 L=1/9S(16)=16/9

Fraktal o'lcham:

D=lg4 /lg3=1,26…

To'plamning fraktal o'lchami

Undagi fraktal hajmi joylashtirish maydoni har doim nolga teng. Biroq, u pastroq o'lchamdagi bo'shliqda nolga teng bo'lishi mumkin. Ushbu bo'shliqning o'lchamini aniqlash uchun D, keling, hamma narsani buzamiz n-qirra uzunligi bo'lgan kichik kublarga o'lchovli fazo ε va hajm ε n- 1-rasm. Mayli N(ε ) - fraktal to'plamni to'liq qoplaydigan kublarning minimal soni, keyin ta'rifi bo'yicha

Ushbu chegaraning mavjudligi fraktal hajmning chekli ekanligini anglatadi D-o'lchovli bo'shliq: kichik bilan ε

va odatdagi o'lchamdan farqli o'laroq D kasr qiymati bo'lishi mumkin, bu ko'pincha fraktal to'plamlar uchun bo'ladi.

Shubhasiz, oddiy to'plamlar uchun bu ta'rif taniqli natijalarga olib keladi. Shunday qilib, ko'pchilik uchun N bizda alohida nuqtalar mavjud N(ε ) =N va shuning uchun

Segment uchun uzunlikdagi silliq chiziq etarli L:N(ε ) =L/ε va shuning uchun D= 1. Sayt uchun S Ikki o'lchovli sirt: N(ε ) =S/ε 2 va D= 2 va boshqalar.

Konstruktiv fraktallarni qurishning rekursiv algoritmi.

1. Sierpinski uchburchagi

Sierpinski uchburchagi

Sierpinski uchburchagi- fraktal, 1915 yilda polshalik matematik Sierpinski tomonidan taklif qilingan Cantor to'plamining ikki o'lchovli analoglaridan biri. Sierpinski "panjara" yoki "salfetka" sifatida ham tanilgan.

Qurilish

Qattiq teng qirrali uchburchak olinadi va birinchi bosqichda o'rta uchburchakning ichki qismi markazdan chiqariladi. Ikkinchi bosqichda uchta o'rta uchburchak qolgan uchta uchburchakdan chiqariladi va hokazo. Ushbu protsedura cheksiz takrorlangandan so'ng, qattiq uchburchakning kichik to'plami qoladi - Sierpinski uchburchagi.

Sierpinski uchburchagining qurilishi

Sierpinski uchburchagini quyidagi algoritm yordamida ham olish mumkin:

Samolyotda uchta nuqtani oling va uchburchak chizing.

Tasodifiy ravishda uchburchak ichidagi istalgan nuqtani tanlang va bu nuqtadan masofaning yarmini uchburchakning uchta uchidan istalganiga o'tkazing.

Joriy pozitsiyani belgilang.

2-bosqichdan boshlab takrorlang.

70-yillarning oxirida paydo bo'lgan fraktal va fraktal geometriya tushunchalari 80-yillarning o'rtalaridan boshlab matematiklar va dasturchilar orasida mustahkam o'rin egalladi. Fraktal so'zi lotincha fractusdan olingan bo'lib, bo'laklardan iborat degan ma'noni bildiradi. 1975 yilda Benoit Mandelbrot tomonidan o'zi qiziqqan tartibsiz, ammo o'ziga o'xshash tuzilmalarga murojaat qilishni taklif qilgan. Fraktal geometriyaning tug'ilishi odatda 1977 yilda Mandelbrotning "Tabiatning fraktal geometriyasi" kitobining nashr etilishi bilan bog'liq. Uning asarlarida 1875-1925 yillarda xuddi shu sohada ishlagan boshqa olimlarning ilmiy natijalaridan foydalanilgan (Puankare, Fatu, Julia, Cantor, Hausdorff Lekin faqat bizning davrimizda ularning ishlarini yagona tizimga birlashtirish mumkin edi.
Hozirgi kunda kompyuter grafikasida fraktallarning roli ancha katta. Ular, masalan, kerak bo'lganda, bir nechta koeffitsientlardan foydalanib, juda murakkab shakllarning chiziqlari va sirtlarini aniqlash uchun yordamga kelishadi. Kompyuter grafikasi nuqtai nazaridan fraktal geometriya sun'iy bulutlar, tog'lar va dengiz sathlarini yaratishda ajralmas hisoblanadi. Darhaqiqat, tasvirlari tabiiy ob'ektlarga juda o'xshash bo'lgan Evklid bo'lmagan murakkab ob'ektlarni osongina tasvirlash usuli topildi.
Fraktallarning asosiy xususiyatlaridan biri o'ziga o'xshashlikdir. Eng oddiy holatda, fraktalning kichik bir qismi butun fraktal haqida ma'lumotni o'z ichiga oladi. Mandelbrotning fraktalga ta'rifi quyidagicha: "Fraktal - bu qaysidir ma'noda butunga o'xshash qismlardan tashkil topgan tuzilishdir".

Fraktallar deb ataladigan juda ko'p matematik ob'ektlar mavjud (Sierpinski uchburchagi, Kox qor parchasi, Peano egri chizig'i, Mandelbrot to'plami va Lorentz attraktorlari). Fraktallar haqiqiy dunyoning ko'plab jismoniy hodisalari va shakllanishlarini katta aniqlik bilan tasvirlaydi: tog'lar, bulutlar, turbulent (girdob) oqimlari, daraxtlarning ildizlari, shoxlari va barglari, oddiy geometrik raqamlarga mos kelmaydigan qon tomirlari. Birinchi marta Benua Mandelbrot o'zining "Tabiatning fraktal geometriyasi" asarida dunyomizning fraktal tabiati haqida gapirdi.
Fraktal atamasi 1977 yilda Benoit Mandelbrot tomonidan o'zining "Fraktallar, shakllar, xaos va o'lchovlar" fundamental asarida kiritilgan. Mandelbrotning so'zlariga ko'ra, fraktal so'zi lotincha fractus - fraksiya va frangere - sindirish so'zidan kelib chiqqan bo'lib, fraktalning mohiyatini "buzilgan", tartibsiz to'plam sifatida aks ettiradi.

Fraktallarning tasnifi.

Buning uchun Fraktallarning butun xilma-xilligini taqdim etish uchun ularning umumiy qabul qilingan tasnifiga murojaat qilish qulay. Fraktallarning uchta klassi mavjud.

1. Geometrik fraktallar.

Ushbu sinfning fraktallari eng ingl. Ikki o'lchovli holatda ular generator deb ataladigan singan chiziq (yoki uch o'lchovli holatda sirt) yordamida olinadi. Algoritmning bir bosqichida singan chiziqni tashkil etuvchi segmentlarning har biri bilan almashtiriladi poliline-generator tegishli miqyosda. Ushbu protsedurani cheksiz takrorlash natijasida geometrik fraktal olinadi.

Keling, ushbu fraktal ob'ektlardan birining misolini ko'rib chiqaylik - triadik Koch egri chizig'i.

Triadik Kox egri chizig'ini qurish.

Uzunligi 1 bo'lgan to'g'ri segmentni olaylik urug'. Keling, urug'ni 1/3 uzunlikdagi uchta teng qismga ajratamiz, o'rta qismini tashlab, uning o'rniga 1/3 uzunlikdagi ikkita bo'g'inli singan chiziq bilan almashtiramiz.

Biz umumiy uzunligi 4/3 bo'lgan 4 ta havoladan iborat singan chiziqni olamiz, shuning uchun biz qo'ng'iroq qilamiz birinchi avlod.

Koch egri chizig'ining keyingi avlodiga o'tish uchun har bir bo'g'inning o'rta qismini tashlash va almashtirish kerak. Shunga ko'ra, ikkinchi avlodning uzunligi 16/9, uchinchisi - 64/27 bo'ladi. agar bu jarayonni cheksiz davom ettirsak, natijada triadik Koch egri chizig'i hosil bo'ladi.

Keling, triadik Koch egri chizig'ining xususiyatlarini ko'rib chiqaylik va fraktallar nima uchun "yirtqich hayvonlar" deb atalganini bilib olaylik.

Birinchidan, bu egri chiziqning uzunligi yo'q - biz ko'rganimizdek, avlodlar soni bilan uning uzunligi cheksizlikka intiladi.

Ikkinchidan, bu egri chiziqqa tangens qurish mumkin emas - uning har bir nuqtasi hosila mavjud bo'lmagan burilish nuqtasidir - bu egri chiziq silliq emas.

Uzunlik va silliqlik egri chiziqlarning asosiy xususiyatlari bo'lib, ularni Evklid geometriyasi ham, Lobachevskiy va Riman geometriyasi ham o'rganadi. Geometrik tahlilning an'anaviy usullari triadik Koch egri chizig'ida qo'llanilmaydigan bo'lib chiqdi, shuning uchun Koch egri yirtqich hayvonga aylandi - an'anaviy geometriyalarning silliq aholisi orasida "yirtqich hayvon".

Harter-Haithway "ajdaho" ning qurilishi.

Boshqa fraktal ob'ektni olish uchun siz qurilish qoidalarini o'zgartirishingiz kerak. Shakllantiruvchi element to'g'ri burchak ostida ulangan ikkita teng segment bo'lsin. Nolinchi avlodda birlik segmentini bilan almashtiring burchak tepada bo'lishi uchun bu shakllantirish elementi. Aytishimiz mumkinki, bunday almashtirish bilan bo'g'inning o'rtasining siljishi mavjud. Keyingi avlodlarni qurishda qoidaga amal qilinadi: chapdagi birinchi bo'g'in shakllantiruvchi element bilan almashtiriladi, shunda bo'g'inning o'rtasi harakat yo'nalishining chap tomoniga siljiydi va keyingi bo'g'inlarni almashtirganda, yo'nalishlar. segmentlar o'rtalarining siljishi muqobil bo'lishi kerak. Rasmda yuqorida tavsiflangan printsipga muvofiq qurilgan egri chiziqning birinchi avlodlari va 11-avlodlari ko'rsatilgan. n cheksizlikka intiluvchi egri chiziq Xarter-Xeytauey ajdahosi deyiladi.
Kompyuter grafikasida daraxtlar va butalar tasvirini olishda geometrik fraktallardan foydalanish zarur. Ikki o'lchovli geometrik fraktallar uch o'lchovli teksturalarni (ob'ekt yuzasida naqshlar) yaratish uchun ishlatiladi.

2.Algebraik fraktallar

Bu fraktallarning eng katta guruhidir. Ular n o'lchovli fazolarda chiziqli bo'lmagan jarayonlar yordamida olinadi. Ikki o'lchovli jarayonlar eng ko'p o'rganilgan. Chiziqli bo'lmagan iterativ jarayonni diskret dinamik tizim sifatida izohlashda ushbu tizimlar nazariyasi terminologiyasidan foydalanish mumkin: fazali portret, barqaror holat jarayoni, attraktor va boshqalar.
Ma'lumki, chiziqli bo'lmagan dinamik tizimlar bir nechta barqaror holatlarga ega. Dinamik tizimning ma'lum miqdordagi iteratsiyadan so'ng o'zini topadigan holati uning dastlabki holatiga bog'liq. Shuning uchun har bir barqaror holat (yoki ular aytganidek, jalb qiluvchi) boshlang'ich holatlarning ma'lum bir mintaqasiga ega bo'lib, undan tizim ko'rib chiqilayotgan yakuniy holatlarga tushadi. Shunday qilib, tizimning fazaviy maydoni attraktorlarni jalb qilish joylariga bo'linadi. Agar fazali fazo ikki o'lchovli bo'shliq bo'lsa, unda diqqatga sazovor joylarni turli ranglar bilan bo'yash orqali ushbu tizimning rangli fazali portretini olish mumkin (iterativ jarayon). Rang tanlash algoritmini o'zgartirib, siz g'alati ko'p rangli naqshlar bilan murakkab fraktal naqshlarni olishingiz mumkin. Matematiklar uchun hayratlanarli narsa ibtidoiy algoritmlar yordamida juda murakkab notrivial tuzilmalarni yaratish qobiliyati edi.

Mandelbrot to'plami.

Misol sifatida, Mandelbrot to'plamini ko'rib chiqing. Uni qurish algoritmi juda oddiy va oddiy iterativ ifodaga asoslangan: Z = Z * Z + C, Qayerda Zi Va C- murakkab o'zgaruvchilar. Takrorlash har bir boshlang'ich nuqtasi uchun to'rtburchaklar yoki kvadrat mintaqadan - murakkab tekislikning kichik to'plamidan amalga oshiriladi. Iterativ jarayongacha davom etadi Z markazi (0,0) nuqtada joylashgan 2 radiusli doiradan tashqariga chiqmaydi (bu dinamik tizimning attraktori cheksizlikda ekanligini anglatadi) yoki etarlicha ko'p takrorlashdan keyin (masalan, , 200-500) Z aylananing qaysidir nuqtasiga yaqinlashadi. Qaysi davomida takrorlashlar soniga qarab Z doira ichida qolsa, nuqta rangini o'rnatishingiz mumkin C(Agar Z etarlicha katta miqdordagi takrorlash uchun doira ichida qoladi, takrorlash jarayoni to'xtaydi va bu rastr nuqtasi qora rangga bo'yalgan).

3. Stokastik fraktallar

Fraktallarning yana bir mashhur sinfi stokastik fraktallar bo‘lib, ular iterativ jarayonda uning ayrim parametrlari tasodifiy o‘zgartirilsa olinadi. Bunday holda, hosil bo'lgan ob'ektlar tabiiy narsalarga juda o'xshash - assimetrik daraxtlar, qirg'oqning qattiq qirg'oqlari va boshqalar. Ikki o'lchovli stokastik fraktallar er va dengiz yuzasini modellashtirishda qo'llaniladi.
Fraktallarning boshqa tasniflari ham mavjud, masalan, fraktallarni deterministik (algebraik va geometrik) va deterministik bo'lmagan (stokastik) ga bo'lish.

Fraktallardan foydalanish haqida

Birinchidan, fraktallar eng oddiy formulalar va algoritmlar yordamida g'ayrioddiy go'zallik va murakkablik rasmlari olinadigan ajoyib matematik san'at sohasidir! Barglar, daraxtlar va gullar ko'pincha tuzilgan tasvirlarning konturlarida ko'rinadi.

Fraktallarning eng kuchli ilovalari kompyuter grafikasida yotadi. Birinchidan, bu tasvirlarni fraktal siqish, ikkinchidan, landshaftlar, daraxtlar, o'simliklar qurish va fraktal to'qimalarni yaratish. Zamonaviy fizika va mexanika fraktal ob'ektlarning xatti-harakatlarini o'rganishni endigina boshlaydi. Va, albatta, fraktallar to'g'ridan-to'g'ri matematikaning o'zida qo'llaniladi.
Fraktal tasvirni siqish algoritmlarining afzalliklari qadoqlangan faylning juda kichik hajmi va tasvirni tiklash vaqtining qisqaligidir. Fraktal qadoqlangan tasvirlarni piksellanishga olib kelmasdan masshtablash mumkin. Ammo siqish jarayoni uzoq davom etadi va ba'zan soatlab davom etadi. Fraktal yo'qotilgan qadoqlash algoritmi jpeg formatiga o'xshash siqishni nisbatini o'rnatishga imkon beradi. Algoritm ba'zi kichik qismlarga o'xshash tasvirning katta qismlarini qidirishga asoslangan. Va faqat qaysi qismga o'xshash bo'lsa, chiqish fayliga yoziladi. Siqishda odatda kvadrat panjara ishlatiladi (qismlar kvadratchalar), bu tasvirni tiklashda engil burchakka olib keladi; olti burchakli panjarada bunday kamchilik yo'q.
Iterated yangi "Sting" tasvir formatini ishlab chiqdi, u fraktal va "to'lqin" (masalan, jpeg) yo'qotishsiz siqishni birlashtiradi. Yangi format keyinchalik yuqori sifatli masshtablash imkoniyati bilan tasvirlarni yaratish imkonini beradi va grafik fayllar hajmi siqilmagan tasvirlar hajmining 15-20% ni tashkil qiladi.
Fraktallarning tog'larga, gullarga va daraxtlarga o'xshash tendentsiyasidan ba'zi grafik muharrirlar foydalanadi, masalan, MAX 3D studio fraktal bulutlari, World Builder'dagi fraktal tog'lar. Fraktal daraxtlar, tog'lar va butun landshaftlar oddiy formulalar bilan belgilanadi, ularni dasturlash oson va yaqinlashganda alohida uchburchak va kublarga bo'linmaydi.
Matematikaning o'zida fraktallardan foydalanishni e'tiborsiz qoldirib bo'lmaydi. To'plamlar nazariyasida Cantor to'plami mukammal hech qanday joyda zich to'plamlar mavjudligini isbotlaydi; o'lchovlar nazariyasida "Kantorning narvonlari" o'z-o'ziga affin funktsiyasi yagona o'lchovni taqsimlash funktsiyasining yaxshi namunasidir.
Mexanika va fizikada fraktallar ko'plab tabiiy ob'ektlarning konturlarini takrorlashning o'ziga xos xususiyati tufayli qo'llaniladi. Fraktallar segmentlar yoki ko'pburchaklar to'plamlari (bir xil miqdordagi saqlangan ma'lumotlar bilan) yordamida daraxtlar, tog'lar va yoriqlar to'plamini taxmin qilishdan ko'ra yuqori aniqlik bilan taxmin qilish imkonini beradi. Fraktal modellar, tabiiy ob'ektlar kabi, "qo'pollik" ga ega va bu xususiyat modelning kattalashishi qanchalik katta bo'lishidan qat'i nazar, saqlanib qoladi. Fraktallar bo'yicha yagona o'lchovning mavjudligi integratsiyani, potentsial nazariyani qo'llash va ularni allaqachon o'rganilgan tenglamalarda standart ob'ektlar o'rniga ishlatish imkonini beradi.
Fraktal yondashuv bilan xaos ko'k tartibsizlik bo'lishni to'xtatadi va nozik tuzilishga ega bo'ladi. Fraktal fani hali juda yosh va uni buyuk kelajak kutmoqda. Fraktallarning go'zalligi tugamaydi va bizga hali ham ko'plab durdonalarni beradi - ko'zni quvontiradigan va ongga haqiqiy zavq keltiradigan.

Fraktallarni qurish haqida

Ketma-ket yaqinlashish usuli

Ushbu rasmga qarab, o'zingizga o'xshash fraktalni qanday qurishingiz mumkinligini tushunish qiyin emas (bu holda, Sierpinski piramidasi). Biz muntazam piramidani (tetraedr) olishimiz kerak, so'ngra uning o'rtasini (oktaedr) kesib tashlashimiz kerak, natijada to'rtta kichik piramida hosil bo'ladi. Ularning har biri bilan biz bir xil operatsiyani bajaramiz va hokazo. Bu biroz sodda, ammo aniq tushuntirish.

Keling, usulning mohiyatini qat'iyroq ko'rib chiqaylik. Ba'zi IFS tizimi bo'lsin, ya'ni. siqishni xaritalash tizimi S=(S 1 ,...,S m ) S i:R n ->R n (masalan, bizning piramidamiz uchun xaritalashlar S i (x )=1/2*x+o i ga o'xshaydi, bu erda o i tetraedrning uchlari, i=1,..,4). Keyin biz R n ichida qandaydir ixcham A 1 to'plamini tanlaymiz (bizning holatimizda biz tetraedrni tanlaymiz). Va A k:A k+1 =S 1 (A k ) U...U S m (A k ) to‘plamlar ketma-ketligini induksiya orqali aniqlaymiz. Ma'lumki, k ortib borayotgan A k to'plamlari tizimning kerakli attraktoriga yaxshiroq va yaxshiroq yaqinlashadi S.

E'tibor bering, bu iteratsiyalarning har biri o'ziga jalb qiladi takrorlanuvchi funksiyalarning takrorlanuvchi tizimi(inglizcha atama Digraf IFS, RIFS va shuningdek Grafikga yo'naltirilgan IFS) va shuning uchun ularni bizning dasturimiz yordamida qurish oson.

Nuqtama-nuqta yoki ehtimollik usuli

Bu kompyuterda amalga oshirishning eng oson usuli. Oddiylik uchun biz tekis o'z-o'zidan affin to'plam holatini ko'rib chiqamiz. Demak, (S 1,..,S m) qandaydir afinik kelishiklar sistemasi bo‘lsin. S i xaritalashlari quyidagi ko‘rinishda ifodalanadi: S i (x)=A i (x-o i)+o i, bu yerda A i 2x2 o‘lchamdagi qo‘zg‘almas matritsa va o i ikki o‘lchovli ustun vektori.

· Keling, dastlabki S 1 xaritalashning belgilangan nuqtasini boshlang'ich nuqtasi sifatida olaylik:
x : = o1;
Bu erda biz S 1 ,..,S m siqilishning barcha sobit nuqtalari fraktalga tegishli ekanligidan foydalanamiz. Siz ixtiyoriy nuqtani boshlang'ich nuqtasi sifatida tanlashingiz mumkin va u tomonidan yaratilgan nuqtalar ketma-ketligi fraktalga tortiladi, ammo keyin ekranda bir nechta qo'shimcha nuqtalar paydo bo'ladi.

· Joriy nuqtani ekranda x= (x 1 ,x 2) belgilaymiz:
putpixel(x 1 ,x 2 ,15);

· 1 dan m gacha j sonni tasodifiy tanlaymiz va x nuqtaning koordinatalarini qayta hisoblaymiz:
j:=Tasodifiy (m )+1;
x:=S j (x);

· Biz 2-bosqichga o'tamiz yoki agar biz juda ko'p takrorlashlarni amalga oshirgan bo'lsak, to'xtatamiz.
Eslatma. Agar S i xaritalarining siqish nisbatlari har xil bo'lsa, fraktal notekis nuqtalar bilan to'ldiriladi. Agar S i xaritalari o'xshash bo'lsa, algoritmni biroz murakkablashtirish orqali buni oldini olish mumkin. Buning uchun algoritmning 3-bosqichida 1 dan m gacha j soni p 1 =r 1 s,..,p m =r m s ehtimolliklar bilan tanlanishi kerak, bu erda r i Si xaritalashlarning siqilish koeffitsientlarini bildiradi va s soni (o‘xshashlik o‘lchami deb ataladi) r 1 s +...+r m s =1 tenglamasidan topiladi. Bu tenglamaning yechimini, masalan, Nyuton usulida topish mumkin.

Fraktallar va ularning algoritmlari haqida

Fraktal lotincha "fractus" sifatdoshidan kelib chiqqan bo'lib, tarjimada bo'laklardan tashkil topgan degan ma'noni bildiradi va tegishli lotincha "frangere" fe'li sindirish, ya'ni tartibsiz bo'laklar hosil qilish degan ma'noni anglatadi. 70-yillarning oxirida paydo bo'lgan fraktal va fraktal geometriya tushunchalari 80-yillarning o'rtalaridan boshlab matematiklar va dasturchilar orasida mustahkam o'rin egalladi. Bu atama 1975 yilda Benoit Mandelbrot tomonidan o'zi qiziqqan tartibsiz, ammo o'ziga o'xshash tuzilmalarga ishora qilish uchun kiritilgan. Fraktal geometriyaning tug'ilishi odatda 1977 yilda Mandelbrotning "Tabiatning fraktal geometriyasi" kitobining nashr etilishi bilan bog'liq. Uning asarlarida 1875-1925 yillarda shu sohada ishlagan boshqa olimlarning (Puankare, Fatu, Yuliya, Kantor, Xausdorf) ilmiy natijalaridan foydalanilgan.

Tuzatishlar

H.-O kitobida taklif qilingan algoritmlarga ba'zi tuzatishlar kiritishga ruxsat bering. Peitgen va P.H.Rixter "Fraktallarning go'zalligi" M. 1993 yil faqat matn terish xatolarini yo'q qilish va jarayonlarni tushunishni osonlashtirish uchun, chunki ularni o'rganganimdan keyin men uchun ko'p narsa sir bo'lib qoldi. Afsuski, bu "tushunarli" va "oddiy" algoritmlar chayqaladigan turmush tarziga olib keladi.

Fraktallarni qurish z = > z 2 +c teskari aloqa bilan murakkab jarayonning ma'lum bir chiziqli bo'lmagan funktsiyasiga asoslanadi, chunki z va c -k kompleks sonlar bo'lsa, u holda z = x + iy , c = p + iq bo'lishi kerak. Oddiy odam uchun aniqroq tekislikka o'tish uchun uni x va y ga ajrating:

x(k+1)=x(k) 2 -y(k) 2 + p,
y(k+1)=2*x(k)*y(k) + q.

Barcha juftliklardan (x,y ) tashkil topgan tekislikni qat'iy belgilangan qiymatlar deb hisoblash mumkin R va q, va dinamiklari bilan. Birinchi holda, barcha nuqtalardan o'tish orqali (x ,y) tekisliklar va ularni takrorlash jarayonidan chiqish uchun zarur bo'lgan funktsiyalarni takrorlash soniga qarab rang berish yoki ruxsat etilgan maksimal takrorlashlar oshib ketganda ularni rang bermaslik (qora rang), biz Julia to'plamining xaritasini olamiz. Aksincha, biz (x,y) qiymatlarning dastlabki juftligini aniqlasak va uning rang-barang taqdirini p va q parametrlarining dinamik o'zgaruvchan qiymatlari bilan kuzatsak, u holda biz Mandelbrot to'plamlari deb ataladigan tasvirlarni olamiz.

Fraktallarni bo'yash algoritmlari masalasi bo'yicha.

Odatda to'plamning tanasi qora maydon sifatida ifodalanadi, garchi qora rangni boshqasi bilan almashtirish mumkinligi aniq, ammo bu ham biroz qiziqarli natija. Barcha ranglarda bo'yalgan to'plamning tasvirini olish tsiklik operatsiyalar yordamida hal etilmaydigan vazifadir, chunki jismni tashkil etuvchi to'plamlarning takrorlanish soni maksimal mumkin bo'lgan miqdorga teng va har doim bir xil bo'ladi. Loopdan chiqish sharti (z_magnitude) yoki unga oʻxshash, lekin boshqa matematik amallar yordamida tekshirish natijasini rang raqami sifatida ishlatib, toʻplamni turli ranglarda boʻyash mumkin.

"Fraktal mikroskop" ni qo'llash

chegaraviy hodisalarni ko'rsatish.

Attraktorlar samolyotda hukmronlik uchun kurash olib boradigan markazlardir. Attraktorlar o'rtasida gulli naqshni ifodalovchi chegara paydo bo'ladi. To'plam chegaralarida ko'rib chiqish ko'lamini oshirish orqali tabiat olamidagi keng tarqalgan hodisa - deterministik xaos holatini aks ettiruvchi noaniq naqshlarni olish mumkin.

Geograflar tomonidan o'rganilayotgan ob'ektlar juda murakkab tashkil etilgan chegaralarga ega tizimni tashkil qiladi va shuning uchun ularni aniqlash oddiy amaliy vazifaga aylanib qolmaydi. Tabiiy komplekslar o'ziga xoslik yadrolariga ega bo'lib, ular o'z hududiga o'z ta'sirini yo'qotadigan jalb qiluvchi rol o'ynaydi.

Mandelbrot va Julia to'plamlari uchun fraktal mikroskopdan foydalanib, ko'rib chiqish miqyosidan qat'i nazar, bir xil darajada murakkab bo'lgan chegara jarayonlari va hodisalari haqida tasavvur hosil qilish mumkin va shu bilan mutaxassisning idrokini dinamik va xaotik ko'rinadigan tabiiy ob'ekt bilan uchrashishga tayyorlash mumkin. fazo va vaqtda, fraktal geometriya tabiatini tushunish uchun. Rang-barang ranglar va fraktal musiqa talabalar ongida chuqur iz qoldirishi aniq.

Minglab nashrlar va keng Internet-resurslar fraktallarga bag'ishlangan, ammo kompyuter fanidan uzoq bo'lgan ko'plab mutaxassislar uchun bu atama mutlaqo yangi ko'rinadi. Fraktallar turli bilim sohalaridagi mutaxassislarni qiziqtiradigan ob'ektlar sifatida informatika kurslarida munosib o'rin egallashlari kerak.

Misollar

SIEPINSKI GRID

Bu Mandelbrot fraktal o'lchamlar va iteratsiya tushunchalarini ishlab chiqishda tajriba o'tkazgan fraktallardan biridir. Kattaroq uchburchakning o'rta nuqtalarini bog'lash orqali hosil qilingan uchburchaklar kesiladi asosiy uchburchakdan ko'proq teshiklari bo'lgan uchburchak hosil qiladi. Bunday holda, tashabbuskor katta uchburchakdir va shablon kattaroqqa o'xshash uchburchaklarni kesish operatsiyasidir. Bundan tashqari, oddiy tetraedr yordamida va kichik tetraedrlarni kesib, uchburchakning uch o'lchovli versiyasini olishingiz mumkin. Bunday fraktalning o'lchami ln3/ln2 = 1,584962501. Olish uchun Sierpinski gilami, kvadratni oling, uni to'qqizta kvadratga bo'ling va o'rtasini kesib oling. Qolganlari, kichikroq kvadratchalar bilan ham xuddi shunday qilamiz. Oxir-oqibat, tekis fraktal panjara hosil bo'ladi, uning maydoni yo'q, lekin cheksiz ulanishlarga ega. O'zining fazoviy shaklida Sierpinski shimgichi oxirigacha shakllar tizimiga aylantiriladi, unda har bir uchi uchi element doimiy ravishda o'z turi bilan almashtiriladi. Ushbu tuzilish suyak to'qimalarining bir qismiga juda o'xshaydi. Bir kun kelib bunday takrorlanuvchi tuzilmalar qurilish tuzilmalarining elementiga aylanadi. Ularning statikasi va dinamikasi, Mandelbrotning fikricha, yaqindan o'rganishga loyiqdir.

SIERPINSKI FRAKTALI

Ushbu fraktalni Sierpinski panjarasi bilan aralashtirib yubormang. Bu ikkita butunlay boshqa ob'ektlar. Bu fraktalda inisiator va generator bir xil. Har bir iteratsiyada generatorning har bir burchagiga tashabbuskorning kichikroq nusxasi qo'shiladi va hokazo. Agar ushbu fraktalni yaratishda cheksiz ko'p takrorlashlar bajarilsa, u bitta teshik qoldirmasdan butun tekislikni egallaydi. Shuning uchun uning fraktal o'lchami ln9/ln3 = 2,0 ga teng.

KOCH CURVE

Koch egri chizig'i eng tipik deterministik fraktallardan biridir. U o'n to'qqizinchi asrda Xelge fon Kox ismli nemis matematigi tomonidan ixtiro qilingan bo'lib, u Georg Kontor va Karl Weierstrasse ishini o'rganayotganda, g'ayrioddiy xatti-harakatlarga ega bo'lgan g'alati egri chiziqlarning tavsiflariga duch keldi. Boshlovchi to'g'ri chiziqdir. Generator teng qirrali uchburchak bo'lib, uning tomonlari kattaroq segment uzunligining uchdan biriga teng. Ushbu uchburchaklar har bir segmentning o'rtasiga qayta-qayta qo'shiladi. O'z tadqiqotida Mandelbrot Kox egri chiziqlari bilan keng tajriba o'tkazdi va tetraedrdan foydalangan holda va uning har bir yuziga kichikroq tetraedrlarni qo'shish orqali Kox orollari, Kox xochlari, Koch qor parchalari va hatto Koch egri chizig'ining uch o'lchovli tasvirlarini yaratdi. Koch egri chizig'i ln4/ln3 = 1,261859507 o'lchamga ega.

MANDELBROT FRAKTALI

Bu siz tez-tez ko'radigan Mandelbrot to'plami emas. Mandelbrot to'plami chiziqli bo'lmagan tenglamalarga asoslangan va murakkab fraktaldir. Bu ham Koch egri chizig'ining bir variantidir, garchi bu ob'ekt unga o'xshamasa ham. Boshlovchi va generator, shuningdek, Koch egri printsipiga asoslangan fraktallarni yaratish uchun ishlatiladiganlardan farq qiladi, ammo g'oya bir xil bo'lib qoladi. Teng tomonli uchburchaklarni egri segmentga birlashtirish o'rniga kvadratlar kvadratga birlashtiriladi. Ushbu fraktal har bir iteratsiyada ajratilgan maydonning to'liq yarmini egallaganligi sababli, u 3/2 = 1,5 oddiy fraktal o'lchamga ega.

FRAKTALLAR YULDUZ VA QOR FLAKE

Bu ikkala ob'ekt klassik fraktallar emas va ular Mandelbrot yoki boshqa mashhur matematik tomonidan ixtiro qilinmagan. Men bu fraktallarni shunchaki qiziqish va dasturlash bilan tajriba qilish uchun yaratdim. Bu yerda inisiator ham, generator ham tomonlarning oʻrta nuqtalarini qarama-qarshi tomonlarning oʻrta nuqtalari bilan muntazam olti burchakli bogʻlashdan hosil boʻlgan figuradir. Bundan tashqari, men faqat bu fraktallarning o'lchamidan shubha qilishim mumkin.

DAROQ PENTAGON

Fraktal bir-biriga siqilgan beshburchaklar to'plamiga o'xshaydi. Aslida, u generator sifatida katta tomonning kichik tomoniga nisbati oltin nisbat deb ataladigan (1,618033989 yoki 1/(2cos72)) ga teng bo'lgan beshburchakni tashabbuskor va teng yonli uchburchaklardan foydalangan holda hosil bo'ladi. . Ushbu uchburchaklar har bir beshburchakning o'rtasidan kesiladi, natijada bitta kattaga yopishtirilgan 5 ta kichik beshburchakga o'xshash shakl hosil bo'ladi. Ushbu fraktalning variantini olti burchakli inisiator sifatida ishlatish mumkin. Bu fraktal Dovud yulduzi deb ataladi va u Koch qor parchasining olti burchakli versiyasiga juda o'xshaydi. Darer beshburchakning fraktal o'lchami ln6/ln (1+g), bu erda g - uchburchakning katta tomoni uzunligining kichikroq tomoni uzunligiga nisbati. Bunday holda, g - Oltin nisbat, shuning uchun fraktal o'lcham taxminan 1,86171596 ga teng. Dovud yulduzining fraktal o'lchami ln6/ln3 yoki 1,630929754.

HILBERT EĞRISI

Bu fraktal labirint fraktaliga juda o'xshaydi, faqat generator bo'lgan U harfining kengligi har bir iteratsiyada o'zgarmasligidan tashqari. Biroq, labirint fraktalidan farqli o'laroq, Hilbert egri chizig'i, shuningdek, Hilbert mehmonxonasi deb ham ataladi, bitta fraktal o'lchamga ega, bu aniq 2,0 ga teng, chunki cheksiz ko'p takrorlash bilan u butun tekislikni egallaydi. fraktal va keyin bu maydonning kichik maydoni bilan xuddi shunday qiling, ikkita kattalashtirish bir-biridan sezilarli darajada farq qiladi. Ikkita rasm batafsil jihatdan juda o'xshash bo'ladi, lekin ular butunlay bir xil bo'lmaydi. Shakl 1. Mandelbrot to'plamining yaqinlashuvi Masalan, bu erda ko'rsatilgan Mandelbrot to'plamining rasmlarini solishtiring, ulardan biri ikkinchisining ma'lum bir maydonini kattalashtirish orqali olingan. Ko'rib turganingizdek, ular mutlaqo bir xil emas, garchi ikkalasida ham biz qora doirani ko'ramiz, undan alangali chodirlar turli yo'nalishlarda cho'zilgan. Bu elementlar kamayib borayotgan nisbatlarda Mandelbrot to'plamida cheksiz takrorlanadi. Deterministik fraktallar chiziqli, murakkab fraktallar esa chiziqli emas. Nochiziqli bo'lgani uchun, bu fraktallar Mandelbrot chiziqli bo'lmagan algebraik tenglamalar tomonidan yaratilgan. Bunga yaxshi misol Zn+1=ZnI+C jarayoni bo‘lib, u ikkinchi darajali Mandelbrot va Julia to‘plamini qurishda qo‘llaniladigan tenglama hisoblanadi. Ushbu matematik tenglamalarni yechish murakkab va xayoliy sonlarni o'z ichiga oladi. Tenglama murakkab tekislikda grafik tarzda talqin qilinganda, natijada g'alati figura paydo bo'ladi, unda to'g'ri chiziqlar egri chiziqlarga aylanadi va deformatsiyalarsiz bo'lsa-da, har xil masshtab darajalarida o'ziga o'xshashlik effektlari paydo bo'ladi. Shu bilan birga, butun rasm umuman oldindan aytib bo'lmaydigan va juda xaotik. Rasmlarni ko'rib turganingizdek, murakkab fraktallar haqiqatan ham juda murakkab va ularni kompyuter yordamisiz yaratib bo'lmaydi. Rangli natijalarga erishish uchun ushbu kompyuter kuchli matematik protsessor va yuqori aniqlikdagi monitorga ega bo'lishi kerak. Deterministik fraktallardan farqli o'laroq, murakkab fraktallar 5-10 iteratsiyada hisoblanmaydi. Kompyuter ekranidagi deyarli har bir nuqta alohida fraktalga o'xshaydi. Matematik ishlov berish jarayonida har bir nuqta alohida chizma sifatida qaraladi. Har bir nuqta ma'lum bir qiymatga mos keladi. Tenglama har bir nuqta uchun tuziladi va bajariladi, masalan, 1000 iteratsiya. Uy kompyuterlari uchun maqbul vaqt oralig'ida nisbatan buzilmagan tasvirni olish uchun bir nuqta uchun 250 ta takrorlashni amalga oshirish mumkin. Bugungi kunda biz ko'rayotgan fraktallarning aksariyati chiroyli rangga ega. Ehtimol, fraktal tasvirlar rang sxemalari tufayli juda katta estetik ahamiyatga ega. Tenglama hisoblangandan so'ng, kompyuter natijalarni tahlil qiladi. Agar natijalar barqaror bo'lib qolsa yoki ma'lum bir qiymat atrofida o'zgarib tursa, nuqta odatda qora rangga aylanadi. Agar u yoki bu qadamdagi qiymat cheksizlikka intilsa, nuqta boshqa rangga, ehtimol ko'k yoki qizil rangga bo'yalgan. Ushbu jarayon davomida kompyuter barcha harakat tezligiga ranglarni belgilaydi. Odatda, tez harakatlanuvchi nuqtalar qizil rangga, sekinroqlari esa sariq rangga va hokazo. Qorong'u dog'lar, ehtimol, eng barqarordir. Murakkab fraktallar bir-biridan farq qiladi deterministik ular cheksiz murakkab, lekin ayni paytda juda oddiy formula bilan hosil bo'lishi mumkin degan ma'noda. Deterministik fraktallar formulalar yoki tenglamalarni talab qilmaydi. Bir oz chizilgan qog'ozni oling va siz hech qanday qiyinchiliksiz 3 yoki 4 marta takrorlanadigan Sierpinski elakini qurishingiz mumkin. Buni ko'plab Julia bilan sinab ko'ring! Angliya qirg'oq chizig'ining uzunligini o'lchash osonroq! MANDELBROT to'plami 2-rasm. Mandelbrot to'plami Mandelbrot va Julia to'plamlari, ehtimol, murakkab fraktallar orasida eng keng tarqalgan ikkitadir. Ularni ko'plab ilmiy jurnallarda, kitob muqovalarida, otkritkalarda va kompyuter ekran saqlovchilarida topish mumkin. Benoit Mandelbrot tomonidan qurilgan Mandelbrot to'plami, ehtimol, fraktal so'zini eshitganda odamlar paydo bo'ladigan birinchi assotsiatsiyadir. Olovli daraxtga o'xshash va dumaloq joylar biriktirilgan tarash mashinasiga o'xshash bu fraktal oddiy Zn+1=Zna+C formulasi bilan hosil bo'ladi, bunda Z va C kompleks sonlar, a esa musbat sondir. Ko'pincha ko'rish mumkin bo'lgan Mandelbrot to'plami 2-darajali Mandelbrot to'plamidir, ya'ni a = 2. Mandelbrot to'plamining nafaqat Zn+1=ZnI+C, balki fraktal bo'lib, formulasidagi indikator har qanday musbat son bo'lishi mumkinligi ko'pchilikni chalg'itdi. Ushbu sahifada siz a ko'rsatkichining turli qiymatlari uchun Mandelbrot to'plamining namunasini ko'rasiz. 3-rasm. a=3,5 da pufakchalarning ko'rinishi Z=Z*tg (Z+C) jarayoni ham mashhur. Tangens funksiyasini qo'shish orqali natija olmaga o'xshash maydon bilan o'ralgan Mandelbrot to'plamidir. Kosinus funktsiyasidan foydalanganda havo pufakchalari effektlari olinadi. Muxtasar qilib aytganda, Mandelbrot to'plamini turli xil chiroyli rasmlarni yaratish uchun sozlashning cheksiz ko'p usullari mavjud. KO'P JULIA Ajablanarlisi shundaki, Julia to'plamlari Mandelbrot to'plami bilan bir xil formuladan foydalangan holda tuzilgan. Julia to'plamini frantsuz matematigi Gaston Julia ixtiro qilgan, to'plam uning nomi bilan atalgan. Mandelbrot va Julia to'plamlari bilan vizual tanishuvdan so'ng paydo bo'ladigan birinchi savol: "agar ikkala fraktal bir xil formula bo'yicha yaratilgan bo'lsa, nega ular bir-biridan juda farq qiladi?" Avval Julia to'plamining rasmlariga qarang. Ajabo, Julia to'plamlarining har xil turlari mavjud. Fraktalni turli boshlang'ich nuqtalardan foydalangan holda chizishda (iteratsiya jarayonini boshlash uchun) turli xil tasvirlar hosil bo'ladi. Bu faqat Julia to'plamiga tegishli. Shakl 4. Julia to'plami Rasmda ko'rinmasa ham, Mandelbrot fraktallari aslida bir-biriga bog'langan ko'plab Julia fraktallaridir. Mandelbrot to'plamining har bir nuqtasi (yoki koordinatasi) Julia fraktaliga to'g'ri keladi. Yuliya to'plamlari ushbu nuqtalardan Z=ZI+C tenglamasida boshlang'ich qiymatlar sifatida yaratilishi mumkin. Ammo bu, agar siz Mandelbrot fraktalidagi nuqtani tanlab, uni kattalashtirsangiz, Julia fraktalini olishingiz mumkin degani emas. Bu ikki nuqta bir xil, lekin faqat matematik ma'noda. Agar siz ushbu nuqtani qabul qilsangiz va uni ushbu formuladan foydalanib hisoblasangiz, Mandelbrot fraktalining ma'lum bir nuqtasiga mos keladigan Julia fraktalini olishingiz mumkin.