3.1. Doğrunun kanonik denklemleri.

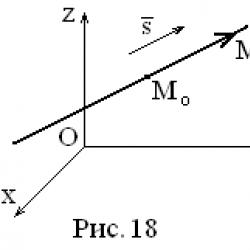
Oxyz koordinat sisteminde noktadan geçen düz bir çizgi verilsin

(bkz. Şekil 18).
belirli bir çizgiye paralel bir vektör. Vektör isminde Bir doğrunun yönlendirici vektörü. Düz bir çizgi üzerinde bir nokta alalım
ve vektör vektörlerini düşünün
eşdoğrusaldır, dolayısıyla karşılık gelen koordinatları orantılıdır:

(3.3.1 )

Bu denklemlere denir kanonik denklemler dümdüz.

Örnek: M(1, 2, –1) noktasından vektöre paralel geçen doğrunun denklemlerini yazınız.

Çözüm: Vektör istenilen çizginin yön vektörüdür. (3.1.1) formüllerini uygulayarak şunu elde ederiz:

Bunlar doğrunun kanonik denklemleridir.

Yorum: Paydalardan birinin sıfıra çevrilmesi karşılık gelen payın sıfıra çevrilmesi anlamına gelir, yani y – 2 = 0; y = 2. Bu doğru y = 2 düzleminde, Oxz düzlemine paraleldir.

3.2. Düz bir çizginin parametrik denklemleri.

Düz çizginin kanonik denklemlerle verilebilmesine izin verin

Haydi belirtelim
Daha sonra
t değerine parametre denir ve herhangi bir değeri alabilir:
.

x, y ve z'yi t cinsinden ifade edelim:

(3.2.1 )

Ortaya çıkan denklemlere denir Düz bir çizginin parametrik denklemleri.

Örnek 1: Vektöre paralel M (1, 2, –1) noktasından geçen düz bir çizginin parametrik denklemlerini oluşturun

Çözüm: Bu çizginin kanonik denklemleri paragraf 3.1 örneğinde elde edilmiştir:

Düz bir çizginin parametrik denklemlerini bulmak için formüllerin (3.2.1) türetilmesini uygularız:

Bu yüzden,
- belirli bir hattın parametrik denklemleri.

Cevap:

Örnek 2. Vektöre paralel M (–1, 0, 1) noktasından geçen bir çizginin parametrik denklemlerini yazın
burada A (2, 1, –1), B (–1, 3, 2).

Çözüm: Vektör
istenilen çizginin yön vektörüdür.

Vektörü bulalım
.

= (–3; 2; 3). Formülleri (3.2.1) kullanarak düz çizginin denklemlerini yazıyoruz:

doğrunun gerekli parametrik denklemleridir.

3.3. Verilen iki noktadan geçen doğrunun denklemleri.

Uzayda verilen iki noktadan tek bir düz çizgi geçer (bkz. Şekil 20). Puan verilsin.
bu doğrunun yön vektörü olarak alınabilir. Daha sonra denklemler doğrudan bulunabilir. formüllere (3.1.1) göre:
).

(3.3.1)

Örnek 1. Noktalardan geçen bir doğrunun kanonik ve parametrik denklemlerini oluşturun

Çözüm: (3.3.1) formülünü uyguluyoruz

Doğrunun kanonik denklemlerini elde ettik. Parametrik denklemler elde etmek için formüllerin (3.2.1) türetilmesini uygularız. Aldık

bir doğrunun parametrik denklemleridir.

Örnek 2. Noktalardan geçen bir doğrunun kanonik ve parametrik denklemlerini oluşturun

Çözüm: Formül (3.3.1)'i kullanarak şunu elde ederiz:

Bunlar kanonik denklemlerdir.

Parametrik denklemlere geçelim:

- parametrik denklemler.

Ortaya çıkan düz çizgi oz eksenine paraleldir (bkz. Şekil 21).

Uzayda iki uçak verilsin

Bu düzlemler çakışmıyorsa ve paralel değilse, düz bir çizgide kesişirler:

Bu iki doğrusal denklem sistemi, düz bir çizgiyi iki düzlemin kesişme çizgisi olarak tanımlar. Denklemlerden (3.4.1) kanonik denklemlere (3.1.1) veya parametrik denklemlere (3.2.1) gidilebilir. Bunu yapmak için bir nokta bulmanız gerekir
düz bir çizgi üzerinde uzanıyor ve yön vektörü Nokta koordinatları
koordinatlardan birine isteğe bağlı bir değer vererek (örneğin, z = 0) sistemden (3.4.1) elde ederiz. Kılavuz vektörünün arkasında vektörlerin vektör çarpımını alabilirsiniz, yani

Örnek 1. Doğrunun kanonik denklemlerini oluşturun

Çözüm: z = 0 olsun. Sistemi çözelim.

Bu denklemleri topladığımızda şunu elde ederiz: 3x + 6 = 0
x = –2. Bulunan x = –2 değerini sistemin ilk denkleminde yerine koyun ve şunu elde edin: –2 + y + 1 = 0
y = 1.

Yani, dönem
istenilen çizgide yer alır.

Düz bir çizginin yön vektörünü bulmak için düzlemlerin normal vektörlerini yazıp bunların vektör çarpımını buluruz:

Düz çizginin denklemlerini formülleri (3.1.1) kullanarak buluyoruz:

Cevap:
.

Diğer yol: Doğrunun (3.4.1) kanonik ve parametrik denklemleri, sistemden (3.4.1) doğru üzerindeki iki farklı noktanın bulunması ve ardından formüllerin (3.3.1) uygulanması ve formüllerin (3.2) türetilmesiyle kolaylıkla elde edilebilir. .1).

Örnek 2. Doğrunun kanonik ve parametrik denklemlerini oluşturun

Çözüm: y = 0 olsun. O zaman sistem şu formu alacaktır:

Denklemleri topladığımızda şunu elde ederiz: 2x + 4 = 0; x = –2. Sistemin ikinci denkleminde x = –2'yi yerine koyarsak şunu elde ederiz: –2 –z +1 = 0
z = –1. Yani asıl noktayı bulduk

İkinci noktayı bulmak için x = 0'ı kabul edelim. Şunu elde ederiz:

Yani

Doğrunun kanonik denklemlerini elde ettik.

Düz çizginin parametrik denklemlerini oluşturalım:

Cevap:
;
.

3.5. İki çizginin uzaydaki göreceli konumu.

Düz bırak
denklemlerle verilmektedir:

:
;
:

.

Bu çizgiler arasındaki açı, yön vektörleri arasındaki açı olarak anlaşılmaktadır (bkz. Şekil 22). Bu açı vektör cebirinden bir formül kullanarak buluyoruz:
veya

(3.5.1)

Düz ise
dikey (
),O
Buradan,

Bu, uzayda iki doğrunun birbirine dik olması durumudur.

Düz ise
paralel (
), bu durumda yön vektörleri eşdoğrusaldır (
), yani

(3.5.3 )

Bu, uzayda iki doğrunun paralelliği durumudur.

Örnek 1. Düz çizgiler arasındaki açıyı bulun:

A).
Ve

B).
Ve

Çözüm: A). Düz çizginin yön vektörünü yazalım
Yön vektörünü bulalım
Sisteme dahil olan uçakların vektör çarpımını buluyoruz:

(bkz. madde 3.4, örnek 1).

Formül (3.5.1)'i kullanarak şunu elde ederiz:

Buradan,

B). Bu düz çizgilerin yön vektörlerini yazalım: Vektörler
eşdoğrusaldır çünkü karşılık gelen koordinatları orantılıdır:

Yani düz
paralel (
), yani

Cevap: A).
B).

Örnek 2.Çizgilerin dikliğini kanıtlayın:

Ve

Çözüm:İlk düz çizginin yön vektörünü yazalım

Yön vektörünü bulalım ikinci düz çizgi. Bunu yapmak için normal vektörleri buluyoruz
Sisteme dahil olan uçakların vektörel çarpımını hesaplayalım:

(Paragraf 3.4'teki örnek 1'e bakınız).

Çizgilerin diklik koşulunu (3.5.2) uygulayalım:

Koşul karşılandı; bu nedenle çizgiler diktir (
).

Uzayda düz bir çizginin denklemleri nasıl yazılır?

Uzayda düz bir çizginin denklemleri

"Düz" bir çizgiye benzer şekilde, uzayda bir çizgiyi tanımlamanın birkaç yolu vardır. Kanonlarla başlayalım - çizginin noktası ve yönlendirici vektörü:

Uzayda bir doğruya ait belirli bir nokta ve bu doğrunun yön vektörü biliniyorsa, bu doğrunun kanonik denklemleri aşağıdaki formüllerle ifade edilir:

Yukarıdaki gösterimde yön vektörünün koordinatlarının olduğu varsayılmaktadır. sıfıra eşit değil. Bir veya iki koordinatın sıfır olması durumunda ne yapacağımıza biraz sonra bakacağız.

Makaledekinin aynısı Düzlem denklemi Basitlik açısından dersin tüm problemlerinde eylemlerin ortonormal uzay bazında gerçekleştirildiğini varsayacağız.

örnek 1

Noktası ve yön vektörü verilen bir doğrunun kanonik denklemlerini oluşturun

Çözüm: Doğrunun kanonik denklemlerini aşağıdaki formülü kullanarak oluşturuyoruz:

Cevap:

Ve bu hiç de akıllıca değil… gerçi, hayır, hiç de akıllıca değil.

Bu çok basit örnekte nelere dikkat etmelisiniz? İlk olarak, ortaya çıkan denklemlerin bir birim azaltılmasına gerek YOKTUR: . Daha doğrusu kısaltmak mümkün ama alışılmadık derecede göze zarar veriyor ve problem çözerken rahatsızlık yaratıyor.

İkincisi, analitik geometride iki şey kaçınılmazdır; doğrulama ve test etme:

Her ihtimale karşı, denklemlerin paydalarına bakarız ve kontrol ederiz - doğru mu yön vektörünün koordinatları orada yazılır. Hayır, düşünmeyin, Brake anaokulunda ders yapmıyoruz. Bu tavsiye çok önemlidir çünkü yanlışlıkla yapılan hataları tamamen ortadan kaldırmanıza olanak tanır. Kimse sigortalı değil, ya yanlış kopyaladılarsa? Darwin Geometri Ödülü'ne layık görülecek.

Doğru eşitlikler elde edilir, bu da noktanın koordinatlarının denklemlerimizi karşıladığı ve noktanın kendisinin gerçekten bu doğruya ait olduğu anlamına gelir.

Testin sözlü olarak yapılması çok kolaydır (ve hızlıdır!).

Bazı problemlerde belirli bir doğruya ait başka bir noktanın bulunması gerekir. Nasıl yapılır?

Ortaya çıkan denklemleri alıyoruz ve zihinsel olarak "sıkıştırma", örneğin sol parça: . Şimdi bu parçayı eşitleyelim herhangi bir numaraya(zaten bir sıfır olduğunu unutmayın), örneğin bire: . O zamandan beri diğer iki "parça" da bire eşit olmalıdır. Temel olarak sistemi çözmeniz gerekir:

Bulunan noktanın denklemleri karşılayıp karşılamadığını kontrol edelim :

Doğru eşitlikler elde edilir, bu da noktanın gerçekten verilen çizgi üzerinde olduğu anlamına gelir.

Çizimi dikdörtgen koordinat sisteminde yapalım. Aynı zamanda uzaydaki noktaların nasıl doğru şekilde işaretleneceğini de hatırlayalım:

Bir noktaya değinelim:
– eksenin negatif yönündeki koordinatların başlangıç ​​noktasından itibaren ilk koordinatın bir parçasını çizeriz (yeşil noktalı çizgi);
– ikinci koordinat sıfırdır, bu nedenle eksenden sola veya sağa “sarsmayız”;
– üçüncü koordinata uygun olarak üç birim yukarı doğru ölçün (mor noktalı çizgi).

Bir nokta oluşturun: “kendinize doğru” iki birim (sarı noktalı çizgi), bir birim sağa (mavi noktalı çizgi) ve iki birim aşağıya (kahverengi noktalı çizgi) ölçün. Kahverengi noktalı çizgi ve noktanın kendisi koordinat ekseninin üzerine bindirilmiştir; bunların alt yarı alanda ve eksenin ÖNÜNDE olduklarını unutmayın.

Düz çizginin kendisi eksenin üzerinden geçiyor ve eğer gözüm yanılmıyorsa eksenin üzerinden geçiyor. Başarısız olmadığına analitik olarak ikna oldum. Düz çizgi eksenin ARKASINDAN geçerse, o zaman kesişme noktasının üstündeki ve altındaki çizginin bir kısmını bir silgiyle silmeniz gerekir.

Düz bir çizginin sonsuz sayıda yön vektörü vardır, örneğin:
(kırmızı ok)

Sonuç tam olarak orijinal vektördü ama bu tamamen bir kazaydı, ben noktayı bu şekilde seçtim. Düz bir çizginin tüm yön vektörleri eşdoğrusaldır ve karşılık gelen koordinatları orantılıdır (daha fazla ayrıntı için bkz. Vektörlerin doğrusal (bağımsız) bağımlılığı. Vektörlerin temeli). Yani vektörler aynı zamanda bu doğrunun yön vektörleri olacaktır.

Kareli kağıt üzerinde üç boyutlu çizimler oluşturmaya ilişkin ek bilgileri kılavuzun başında bulabilirsiniz. Fonksiyonların grafikleri ve özellikleri. Bir defterde, noktalara giden çok renkli noktalı yollar (çizime bakınız) genellikle aynı noktalı çizgi kullanılarak basit bir kalemle ince bir şekilde çizilir.

Yön vektörünün bir veya iki koordinatının sıfır olduğu özel durumları ele alalım. Aynı zamanda dersin başında başlayan mekansal görme eğitimine de devam ediyoruz. Düzlem denklemi. Ve yine size çıplak kralın hikayesini anlatacağım - boş bir koordinat sistemi çizeceğim ve sizi orada uzaysal çizgiler olduğuna ikna edeceğim =)

Altı durumun tamamını listelemek daha kolaydır:

1) Bir nokta ve yön vektörü için doğrunun kanonik denklemleri üçe ayrılır: bireysel denklemler: .

Veya kısaca:

Örnek 2: Bir nokta ve yön vektörü kullanarak düz bir çizginin denklemlerini oluşturalım:

Bu nasıl bir çizgi? Düz çizginin yön vektörü birim vektörle eşdoğrusaldır, bu da bu düz çizginin eksene paralel olacağı anlamına gelir. Kanonik denklemler şu şekilde anlaşılmalıdır:
a) – “y” ve “z” kalıcı, eşittir belirli sayılar;
b) “x” değişkeni herhangi bir değeri alabilir: (pratikte bu denklem genellikle yazılmaz).

Özellikle denklemler eksenin kendisini tanımlar. Aslında "x" her değeri alır ve "y" ile "z" her zaman sıfıra eşittir.

Söz konusu denklemler başka bir şekilde yorumlanabilir: örneğin apsis ekseninin analitik gösterimine bakalım: . Sonuçta bunlar iki düzlemin denklemleri! Denklem koordinat düzlemini belirtir ve denklem koordinat düzlemini belirtir. Doğru düşünüyorsunuz - bu koordinat düzlemleri eksen boyunca kesişiyor. Dersin en sonunda uzayda bir doğrunun iki düzlemin kesişimiyle tanımlandığı yöntemi ele alacağız.

İki benzer durum:

2) Vektöre paralel bir noktadan geçen bir doğrunun kanonik denklemleri formüllerle ifade edilir.

Bu tür düz çizgiler koordinat eksenine paralel olacaktır. Özellikle denklemler koordinat ekseninin kendisini belirtir.

3) Vektöre paralel bir noktadan geçen bir doğrunun kanonik denklemleri formüllerle ifade edilir.

Bu düz çizgiler koordinat eksenine paraleldir ve denklemler uygulanan eksenin kendisini tanımlar.

İkinci üçünü tezgaha koyalım:

4) Bir nokta ve yön vektörü için doğrunun kanonik denklemleri oran ve oranlara ayrılır. düzlem denklemi .

Örnek 3: Bir nokta ve yön vektörü kullanarak düz bir çizginin denklemlerini oluşturalım.

İzin vermek ben- düz bir uzay çizgisi. Planimetride olduğu gibi herhangi bir vektör

A =/= 0, eşdoğrusal çizgi ben, isminde kılavuz vektör bu düz çizgi.

Doğrunun uzaydaki konumu tamamen yön vektörü ve doğruya ait nokta belirtilerek belirlenir.

Düz olmasına izin ver ben kılavuz vektörü ile A M 0 noktasından geçer ve M uzayda keyfi bir noktadır. Açıkçası, M noktası (Şekil 197) çizgiye aittir. ben ancak ve ancak \(\overrightarrow(M_0 M)\) vektörü vektörle eşdoğrusal ise A yani

\(\overrightarrow(M_0 M)\) = T A , T\(\içinde\) R. (1)

M ve M 0 noktaları yarıçap vektörleriyle belirtilmişse R Ve R 0 (Şekil 198) uzaydaki bir O noktasına göre, bu durumda \(\overrightarrow(M_0 M)\) = R - R 0 ve denklem (1) şu şekli alır:

R = R 0 + T A , T\(\içinde\) R. (2)

Denklemler (1) ve (2) denir düz bir çizginin vektör-parametrik denklemleri. Değişken T vektör-parametrik denklemlerde düz çizgiye denir parametre.

M 0 noktası düz bir çizgi olsun ben ve yön vektörü a koordinatlarıyla verilir:

M 0 ( X 0 ; en 0 , z 0), A = (A 1 ; A 2 ; A 3).

O zaman eğer ( X; y; z) - düz bir çizginin keyfi bir M noktasının koordinatları ben, O

\(\overrightarrow(M_0 M) \) = ( x - x 0 ; y - y 0 ; z - z 0)

ve vektör denklemi (1) aşağıdaki üç denkleme eşdeğerdir:

x - x 0 = ta 1 , y - y 0 = ta 2 , z - z 0 = ta 3

$$ \begin(cases) x = x_0 + ta_1 \\ y = y_0 + ta_2 \\ z = z_0 + ta_3, \;\;t\in R\end(cases) (3)$$

Denklemler (3) çağrılır doğrunun parametrik denklemleri boşlukta.

Görev 1. Bir noktadan geçen bir çizgi için parametrik denklemler yazın

M 0 (-3; 2; 4) ve yön vektörüne sahip A = (2; -5; 3).

Bu durumda X 0 = -3, en 0 = 2, z 0 = 4; A 1 = 2; A 2 = -5; A 3 = 3. Bu değerleri formül (3)'te yerine koyarak bu doğrunun parametrik denklemlerini elde ederiz.

$$ \begin(case) x = -3 - 2t \\ y = 2 - 5t \\ z = 4 + 3t, ​​\;\;t\in R\end(case) $$

Parametreyi hariç tutalım T denklemlerden (3). Bu yapılabilir çünkü A =/= 0 ve dolayısıyla vektör koordinatlarından biri A sıfırdan farklı olduğu açıktır.

Öncelikle tüm koordinatların sıfırdan farklı olmasına izin verin. Daha sonra

$$ t=\frac(x-x_0)(a_1),\;\;t=\frac(y-y_0)(a_2),\;\;t=\frac(z-z_0)(a_3) $$

ve bu nedenle

$$ \frac(x-x_0)(a_1)=\frac(y-y_0)(a_2)=\frac(z-z_0)(a_3) \;\; (4)$$

Bu denklemlere denir doğrunun kanonik denklemleri .

Denklemlerin (4) üç değişkenli iki denklemden oluşan bir sistem oluşturduğuna dikkat edin. x, y Ve z.

Denklemlerde (3) vektör koordinatlarından biri varsa A , Örneğin A 1 sıfıra eşittir, ardından parametreyi ortadan kaldırarak T yine üç değişkenli iki denklemden oluşan bir sistem elde ederiz x, y Ve z:

\(x=x_0, \;\; \frac(y-y_0)(a_2)=\frac(z-z_0)(a_3)\)

Bu denklemlere kanonik doğru denklemleri de denir. Tekdüzelik için geleneksel olarak şu şekilde de yazılırlar: (4)

\(\frac(x-x_0)(0)=\frac(y-y_0)(a_2)=\frac(z-z_0)(a_3)\)

eğer payda sıfırsa karşılık gelen payın da sıfır olduğunu varsayalım. Bu denklemler M 0 ( X 0 ; en 0 , z 0) koordinat düzlemine paralel yOz, yön vektörü (0; A 2 ; A 3).

Son olarak, eğer denklem (3)'te iki vektör koordinatı varsa A , Örneğin A 1 ve A 2 sıfıra eşitse bu denklemler şu şekli alır:

X = X 0 , sen = en 0 , z = z 0 + T A 3 , T\(\içinde\) R.

Bunlar M 0 noktasından geçen bir çizginin denklemleridir ( X 0 ; en 0 ; z 0) eksene paralel Oz. Böyle düz bir çizgi için X = X 0 , sen = en 0 , bir z- herhangi bir numara. Ve bu durumda, tekdüzelik için, düz çizginin denklemi (aynı çekinceyle) (4) biçiminde yazılabilir.

\(\frac(x-x_0)(0)=\frac(y-y_0)(0)=\frac(z-z_0)(a_3)\)

Böylece, uzaydaki herhangi bir çizgi için kanonik denklemler (4) ve bunun tersine, katsayılardan en az birinin sağlanması koşuluyla (4) biçimindeki herhangi bir denklem yazılabilir. A 1 , A 2 , A 3 sıfıra eşit değildir, uzayda bir düz çizgiyi tanımlar.

Görev 2. M 0 (- 1; 1, 7) noktasından vektöre paralel geçen bir doğrunun kanonik denklemlerini yazın A = (1; 2; 3).

Bu durumda denklemler (4) aşağıdaki gibi yazılır:

\(\frac(x+1)(1)=\frac(y-1)(2)=\frac(z-7)(3)\)

Verilen iki M 1 noktasından geçen bir doğrunun denklemlerini türetelim ( X 1 ; en 1 ; z 1) ve

M2( X 2 ; en 2 ; z 2). Açıkçası, vektörü alabiliriz A = (X 2 - X 1 ; en 2 - en 1 ; z 2 - z 1) ve düz bir çizginin geçtiği M 0 noktasının ötesinde, örneğin M 1 noktası. Daha sonra denklemler (4) aşağıdaki gibi yazılacaktır:

\(\frac(x-x_1)(x_2 - x_1)=\frac(y-y_1)(y_2 - y_1)=\frac(z-z_1)(z_2 - z_1)\) (5)

Bunlar iki M 1 noktasından geçen bir çizginin denklemleridir ( X 1 ; en 1 ; z 1) ve

M2( X 2 ; en 2 ;z 2).

Görev 3. M 1 (-4; 1; -3) ve M 2 (-5; 0; 3) noktalarından geçen düz bir çizginin denklemlerini yazın.

Bu durumda X 1 = -4, en 1 = 1, z 1 = -3, X 2 = -5, en 2 = 0, z 2 = 3. Bu değerleri formül (5)'te yerine koyarak şunu elde ederiz:

\(\frac(x+4)(-1)=\frac(y-1)(-1)=\frac(z+3)(6)\)

Görev 4. M 1 (3; -2; 1) ve M 1 (3; -2; 1) noktalarından geçen doğrunun denklemlerini yazınız.

M2 (5; -2; 1/2).

M 1 ve M 2 noktalarının koordinatlarını denklemlerde (5) değiştirdikten sonra şunu elde ederiz:

\(\frac(x-3)(2)=\frac(y+2)(0)=\frac(z-1)(-\frac(1)(2))\)

Doğrunun kanonik denklemleri

Sorunun formülasyonu. İki düzlemin kesişim çizgisi olarak verilen bir doğrunun kanonik denklemlerini bulun (genel denklemler)

Çözüm planı. Yön vektörlü düz bir çizginin kanonik denklemleri Belirli bir noktadan geçerken , forma sahip ol

. (1)

Bu nedenle bir doğrunun kanonik denklemlerini yazabilmek için onun yön vektörünü ve doğru üzerinde bir noktayı bulmak gerekir.

1. Düz çizgi aynı anda her iki düzleme de ait olduğundan, yön vektörü her iki düzlemin normal vektörlerine diktir; bir vektör çarpımının tanımına göre elimizde

. (2)

2. Doğru üzerinde bir nokta seçin. Düz çizginin yön vektörü koordinat düzlemlerinden en az birine paralel olmadığından, düz çizgi bu koordinat düzlemini keser. Sonuç olarak, bu koordinat düzlemiyle kesiştiği nokta, bir çizgi üzerinde bir nokta olarak alınabilir.

3. Kılavuz vektörünün bulunan koordinatlarını yerine koyun ve düz çizginin (1) kanonik denklemlerini işaretleyin.

Yorum. Vektör çarpımı (2) sıfıra eşitse düzlemler kesişmez (paralel) olmaz ve doğrunun kanonik denklemlerini yazmak mümkün olmaz.

Sorun 12. Doğrunun kanonik denklemlerini yazınız.

Doğrunun kanonik denklemleri:

,

Nerede – bir çizgi üzerindeki herhangi bir noktanın koordinatları, onun yön vektörüdür.

Doğru üzerinde bir nokta bulalım. Olsun o zaman

Buradan, – bir doğruya ait bir noktanın koordinatları.

Örnek çözüme bakalım.

Örnek.

Kesişen iki düzlemin denklemleriyle uzayda tanımlanan bir çizgi üzerindeki herhangi bir noktanın koordinatlarını bulun .

Çözüm.

Denklem sistemini aşağıdaki biçimde yeniden yazalım.

Sistemin ana matrisinin temel minörü olarak ikinci dereceden sıfır olmayan bir minör alıyoruz yani z serbest bilinmeyen bir değişkendir. Z içeren terimleri denklemlerin sağ taraflarına taşıyalım: .

O halde keyfi bir gerçek sayının nerede olduğunu kabul edelim.

Ortaya çıkan denklem sistemini çözelim:

Böylece denklem sisteminin genel çözümü formu var, nerede.

Parametrenin belirli bir değerini alırsak, denklem sistemine özel bir çözüm elde ederiz, bu da bize belirli bir çizgi üzerinde bulunan bir noktanın istenen koordinatlarını verir. alalım o zaman dolayısıyla doğrunun istenen noktasıdır.

Bir noktanın bulunan koordinatlarını, bunları kesişen iki düzlemin orijinal denklemleriyle değiştirerek kontrol edebilirsiniz:

Cevap:

İki düzlemin kesiştiği çizginin yön vektörü.

Dikdörtgen bir koordinat sisteminde, düz çizginin yönlendirici vektörü düz bir çizgiden ayrılamaz. Üç boyutlu uzayda dikdörtgen bir koordinat sistemindeki düz çizgi a, kesişen iki düzlemin denklemleri ile verildiğinde ve , o zaman düz çizginin yönlendirici vektörünün koordinatları görünmez. Şimdi bunları nasıl belirleyeceğimizi göstereceğiz.

Bir doğrunun o düzlemde bulunan herhangi bir doğruya dik olması durumunda o düzleme dik olduğunu biliyoruz. O halde bir düzlemin normal vektörü, bu düzlemde bulunan sıfırdan farklı herhangi bir vektöre diktir. Doğrunun yön vektörünü bulmak için bu gerçekleri kullanacağız.

Düz çizgi a hem düzlemde hem de düzlemde bulunur. Bu nedenle a çizgisinin yön vektörü normal vektöre diktir düzlem ve normal vektör uçak Böylece, a düz çizgisinin yön vektörü Ve :

Bir doğrunun tüm yön vektörlerinin kümesidir ve bunu şu şekilde tanımlayabiliriz: sıfır dışında herhangi bir gerçek değeri alabilen bir parametredir.

Örnek.

Üç boyutlu uzayda Oxyz dikdörtgen koordinat sisteminde belirtilen bir düz çizginin herhangi bir yön vektörünün koordinatlarını kesişen iki düzlemin denklemleriyle bulun .

Çözüm.

Düzlemlerin normal vektörleri vektörlerdir Ve sırasıyla. Belirli iki düzlemin kesişimi olan düz bir çizginin yönlendirici vektörü, normal vektörlerin vektör çarpımıdır:

Cevap:

Uzayda bir doğrunun parametrik ve kanonik denklemlerine geçiş.

Düz bir çizgiyi tanımlamak için kesişen iki düzlemin denklemlerini kullanmanın tamamen uygun olmadığı durumlar vardır. Uzaydaki düz bir çizginin kanonik denklemleri biliniyorsa bazı problemleri çözmek daha kolaydır: veya formun uzayındaki bir çizginin parametrik denklemleri burada x 1 , y 1 , z 1 çizgi üzerindeki belirli bir noktanın koordinatlarıdır, a x , a y , a z ise çizgiyi yönlendiren vektörün koordinatlarıdır ve keyfi gerçek değerler alan bir parametredir. Formun doğrusal denklemlerinden geçiş sürecini tanımlayalım Uzayda bir doğrunun kanonik ve parametrik denklemleri.

Önceki paragraflarda, bir doğru üzerindeki belirli bir noktanın koordinatlarını bulmanın yanı sıra, kesişen iki düzlemin denklemleriyle verilen bir doğrunun belirli bir yön vektörünün koordinatlarını bulmayı öğrendik. Bu veri, uzaydaki dikdörtgen koordinat sisteminde bu doğrunun hem kanonik hem de parametrik denklemlerini yazmak için yeterlidir.

Örneğin çözümünü düşünelim ve ardından uzaydaki bir doğrunun kanonik ve parametrik denklemlerini bulmanın başka bir yolunu göstereceğiz.

Örnek.

Çözüm.

Önce düz çizginin yönlendirici vektörünün koordinatlarını hesaplayalım. Bunu yapmak için normal vektörlerin vektör çarpımını buluyoruz Ve yüzeyleri Ve :

Yani, .

Şimdi belirli bir doğru üzerindeki belirli bir noktanın koordinatlarını belirleyelim. Bunu yapmak için denklem sisteminin çözümlerinden birini bulacağız. .

Belirleyici sıfırdan farklıysa onu sistemin ana matrisinin temel minörü olarak alalım. Daha sonra z değişkeni serbesttir, onunla birlikte terimleri denklemlerin sağ taraflarına aktarırız ve z değişkenine isteğe bağlı bir değer veririz:

Ortaya çıkan denklem sistemini Cramer yöntemini kullanarak çözüyoruz:

Buradan,

kabul ediyoruz ve doğru üzerindeki noktanın koordinatlarını elde ediyoruz: .

Artık uzaydaki orijinal doğrunun gerekli kanonik ve parametrik denklemlerini yazabiliriz:

Cevap:

Ve

İşte bu sorunu çözmenin ikinci yolu.

Bir doğru üzerinde belirli bir noktanın koordinatlarını bulurken denklem sistemini çözeriz . Genel olarak çözümleri şeklinde yazılabilir. .

Ve bunlar tam olarak uzaydaki düz bir çizginin gerekli parametrik denklemleridir. Ortaya çıkan denklemlerin her biri bir parametreye göre çözülürse ve ardından eşitliklerin sağ tarafları eşitlenirse, uzaydaki düz bir çizginin kanonik denklemlerini elde ederiz.

Bu yöntemi kullanarak önceki problemin çözümünü gösterelim.

Örnek.

Üç boyutlu uzayda düz bir çizgi, kesişen iki düzlemin denklemleriyle tanımlanır . Bu doğrunun kanonik ve parametrik denklemlerini yazınız.

Çözüm.

Üç bilinmeyenli bu iki denklem sistemini çözüyoruz (çözüm önceki örnekte verilmiştir, tekrarlamayacağız). Bu durumda elde ederiz . Bunlar uzaydaki düz bir çizginin istenen parametrik denklemleridir.

Geriye uzaydaki düz bir çizginin kanonik denklemlerini elde etmek kalıyor:

Ortaya çıkan düz çizgi denklemleri, önceki örnekte elde edilen denklemlerden dışsal olarak farklıdır, ancak eşdeğerdirler çünkü üç boyutlu uzayda aynı nokta kümesini (ve dolayısıyla aynı düz çizgiyi) tanımlarlar.

Cevap:

Ve

Kaynakça.

• Bugrov Ya.S., Nikolsky S.M. Yüksek Matematik. Birinci cilt: doğrusal cebir ve analitik geometrinin unsurları.
• Ilyin V.A., Poznyak E.G. Analitik Geometri.