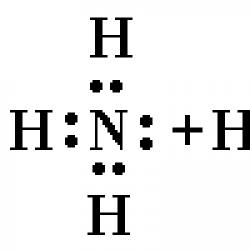Proprietățile de bază ale unui cicloid. Proprietățile unui cicloid în analiza matematică a subiectului
Vă amintiți reflectoarele portocalii din plastic care se atașează la spițele unei roți de bicicletă? Să atașăm reflectorul de janta în sine și să urmăm traiectoria acestuia. Curbele rezultate aparțin familiei cicloidelor. Roata se numește cercul generator (sau cerc) al cicloidului. Dar să ne întoarcem la secolul nostru și să trecem la o tehnologie mai modernă. Pe drumul bicicletei era o pietricică care s-a blocat în banda de rulare a anvelopei.
După ce învârti roata de câteva ori, unde va zbura piatra când iese din banda de rulare? Împotriva direcției motocicletei sau spre ea? După cum se știe, mișcarea liberă a unui corp începe tangențial la traiectoria pe care s-a deplasat. Tangenta la cicloidă este întotdeauna îndreptată în direcția mișcării și trece prin punctul de sus al cercului generator. Pietrișul nostru va zbura în direcția mișcării. Îți amintești cum ai călărit prin bălți pe o bicicletă fără aripa din spate când erai copil? O dungă umedă pe spate este confirmarea zilnică a rezultatului pe care tocmai l-ați obținut.
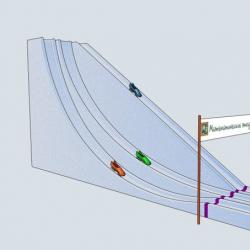
Secolul al XVII-lea este secolul cicloidului. Cei mai buni oameni de știință au studiat proprietățile sale uimitoare. Ce traiectorie va conduce un corp care se deplasează sub influența gravitației dintr-un punct în altul în cel mai scurt timp? Aceasta a fost una dintre primele probleme ale științei care se numește acum calculul variațiilor. Puteți minimiza (sau maximiza) diferite lucruri - lungimea traseului, viteza, timpul. În problema brahistocronului, timpul este minimizat (care este subliniat de numele însuși: grecește βράχιστος - cel mai mic, χρόνος - timp). Primul lucru care îmi vine în minte este o traiectorie dreaptă. Să luăm în considerare, de asemenea, un cicloid inversat cu un cuspid în partea de sus a punctelor date. Și, după Galileo Galilei, un sfert de cerc care leagă punctele noastre. Să facem piste de bob cu profilele luate în considerare și să vedem care bob vine primul. Istoria bobului își are originea în Elveția. În 1924 au avut loc primele Jocuri Olimpice de iarnă în orașul francez Chamonix. Ei găzduiesc deja competiții de bob pentru echipe de doi și patru.
Singurul an în care un echipaj de bob era format din cinci persoane la Jocurile Olimpice a fost 1928. De atunci, echipele masculine de doi și patru au concurat întotdeauna la bob. Există o mulțime de lucruri interesante în regulile de bob. Desigur, există restricții în ceea ce privește greutatea bob-ului și a echipei, dar există chiar și restricții cu privire la materialele care pot fi folosite în patinele bob (perechea din față este mobilă și conectată la ghidon, perechea din spate este fixată rigid) . De exemplu, radiul nu poate fi folosit la fabricarea patinelor.

Haideți să dăm un început. Care bob va fi primul care va ajunge la linia de sosire? Green Bob, care joacă pentru echipa de Studii Matematice și se rostogolește pe toboganul cicloidal, este primul! De ce a considerat Galileo Galilei un sfert de cerc și a considerat că aceasta a fost cea mai bună traiectorie de coborâre din punct de vedere al timpului? El a introdus linii întrerupte în el și a observat că pe măsură ce numărul de legături creștea, timpul de coborâre a scăzut. De aici Galileo sa mutat în mod natural într-un cerc, dar a ajuns la concluzia incorectă că această traiectorie era cea mai bună dintre toate posibilele. După cum am văzut, cea mai bună traiectorie este o cicloidă. Prin aceste două puncte poate fi desenat un cicloid unic cu condiția ca cuspidul cicloidului să fie în punctul de sus. Și chiar și atunci când cicloidul trebuie să se ridice pentru a trece prin al doilea punct, tot va fi curba de coborâre cea mai abruptă! O altă problemă frumoasă legată de cicloidă este problema tautocronei. Tradus din greacă, ταύτίς înseamnă „același”, χρόνος, așa cum știm deja - „timp”. Să facem trei diapozitive identice cu un profil sub formă de cicloid, astfel încât capetele diapozitivelor să coincidă și să fie situate în vârful cicloidului. Să punem trei fasole la înălțimi diferite și să dăm voie.
Cel mai uimitor fapt este că toate boabele vor coborî în același timp! Iarna, puteți construi un tobogan de gheață în curtea dvs. și puteți testa această proprietate în persoană. Problema tautocronei constă în găsirea unei curbe astfel încât, pornind de la orice poziție inițială, timpul de coborâre într-un punct dat să fie același. Christiaan Huygens a demonstrat că singurul tautocron este cicloidul. Desigur, Huygens nu era interesat să coboare pe toboganele de gheață. La acea vreme, oamenii de știință nu aveau luxul de a urma știința din dragoste pentru artă. Problemele care au fost studiate s-au bazat pe viața și cerințele tehnologiei din acea vreme. În secolul al XVII-lea, deja aveau loc călătorii mari pe mare. Marinarii erau deja capabili să determine latitudinea destul de precis, dar, în mod surprinzător, nu au putut determina deloc longitudinea. Iar una dintre metodele propuse pentru măsurarea latitudinii s-a bazat pe prezența unor cronometre precise. Prima persoană care s-a gândit să facă ceasuri cu pendul care să fie precise a fost Galileo Galilei. Cu toate acestea, în momentul în care începe să le implementeze, este deja bătrân, este orb, iar în anul rămas din viață, omul de știință nu are timp să facă un ceas. Îi lasă moștenire fiului său, dar el ezită și începe să lucreze la pendul abia înainte de moartea sa și nu are timp să realizeze planul.
Următoarea figură iconică a fost Christiaan Huygens. El a observat că perioada de oscilație a unui pendul obișnuit, considerată de Galileo, depinde de poziția inițială, adică. din amplitudine. Gândindu-se la care ar trebui să fie traiectoria încărcăturii, astfel încât timpul de rulare de-a lungul acesteia să nu depindă de amplitudine, el rezolvă problema tautocronei. Dar cum să faci o sarcină să se miște de-a lungul unui cicloid? Transpunând cercetările teoretice într-un plan practic, Huygens face „obraji” pe care se înfășoară funia pendulului și rezolvă mai multe probleme matematice. El demonstrează că „obrajii” trebuie să aibă profilul aceluiași cicloid, arătând astfel că evoluția unui cicloid este un cicloid cu aceiași parametri. În plus, proiectarea unui pendul cicloidal propus de Huygens face posibilă calcularea lungimii cicloidului. Dacă un fir albastru, a cărui lungime este egală cu patru raze ale cercului generator, este deviat cât mai mult posibil, atunci capătul său se va afla în punctul de intersecție al „obrazului” și al traiectoriei cicloidale, adică. la vârful cicloidului - „obraji”. Deoarece aceasta este jumătate din lungimea arcului cicloid, lungimea totală este egală cu opt raze ale cercului generator. Christiaan Huygens a realizat un pendul cicloidal, iar ceasurile cu acesta au fost testate în călătorii pe mare, dar nu au prins rădăcini. Cu toate acestea, la fel ca un ceas cu un pendul obișnuit în aceste scopuri. De ce, totuși, există încă mecanisme de ceas cu un pendul obișnuit? Dacă te uiți atent, cu mici abateri, precum pendulul roșu, „obrajii” pendulului cicloidal aproape că nu au niciun efect. În consecință, mișcarea de-a lungul cicloidului și de-a lungul cercului pentru abateri mici aproape coincide.
Literatură:
G. N. Berman. Cicloid. M.: Nauka, 1980.
S. G. Gindikin. Povești despre fizicieni și matematicieni. M.: MTsNMO, 2006.
| Comentarii: 1 |
Vladimir Zaharov
Prelegere susținută de un academician al Academiei Ruse de Științe, doctor în științe fizice și matematice, președinte al Consiliului Științific al Academiei Ruse de Științe privind dinamica neliniară, șef. Departamentul de Fizică Matematică la Institutul de Fizică al Academiei Ruse de Științe. Lebedev, profesor la Universitatea din Arizona (SUA), de două ori câștigător al Premiului de Stat, câștigător al medaliei Dirac de Vladimir Evgenievich Zakharov, susținută pe 27 mai 2010 la Muzeul Politehnic în cadrul proiectului „Prelegeri publice către Polit. ru”.
Serghei Kuksin
Conferința științifică internațională „Zilele mecanicii clasice” Moscova, Institutul de Matematică Steklov, st. Gubkina, 8 26 ianuarie 2015
 Chaos este un film matematic format din nouă capitole, fiecare de treisprezece minute. Acesta este un film pentru publicul larg, dedicat sistemelor dinamice, efectului fluture și teoriei haosului.
Chaos este un film matematic format din nouă capitole, fiecare de treisprezece minute. Acesta este un film pentru publicul larg, dedicat sistemelor dinamice, efectului fluture și teoriei haosului.
Alexandra Skripcenko
Matematicianul Alexandra Skripchenko despre biliard ca sistem dinamic, unghiuri raționale și teorema lui Poincaré.
Iuli Ilyașenko
Teoria Kolmogorov–Arnold–Moser răspunde la întrebări precum „Pot planetele să cadă în Soare? Dacă da, atunci cu ce probabilitate? Și după cât timp?” Formularea matematică a problemei: să presupunem că masele sunt atât de mici încât atracția lor una față de cealaltă poate fi neglijată. Apoi se pot calcula traiectoriile planetelor; Newton a făcut asta. Dacă trecem la cazul real, când atracția reciprocă a planetelor le afectează orbitele, obținem o mică perturbare a integrabilului, adică. sistem exact rezolvabil. Poincaré a considerat că studiul micilor perturbații ale sistemelor integrabile ale mecanicii clasice este sarcina principală a teoriei ecuațiilor diferențiale. Prelegerile vor vorbi, la un nivel accesibil școlarilor mai mari, despre ideile principale ale teoriei KAM. Nu vom trece la problema n-corpilor și mecanica clasică, ci vom discuta despre difeomorfisme ale cercului și pasul de bază al procesului de inducție propus de Kolmogorov pentru problemele de mecanică cerească.
Olga Romaskevici
Dacă acționezi foarte crud și îi iei creionul și hârtia unui matematician, el va privi spre cer în căutarea unor noi probleme. Problema mișcării planetare (în lumea matematică numită în cod „problema n-corpilor”) este extrem de complexă - atât de complexă încât chiar și pentru subcazuri speciale ale cazului n=3, un număr mare de lucrări sunt publicate în fiecare an. Este imposibil să analizezi toate aspectele acestei probleme chiar și într-un curs semestrial. Nouă, însă, nu ne vom teme și vom încerca să ne jucăm cu matematica care apare aici. Principala motivație pentru noi va fi problema celor două corpuri: problema mișcării unei planete în jurul Soarelui, în ipoteza că nu par să existe alte planete în apropiere.
Dmitri Anosov
Cartea vorbește despre ecuații diferențiale. În unele cazuri, autorul explică modul în care sunt rezolvate ecuațiile diferențiale, iar în altele, modul în care considerațiile geometrice ajută la înțelegerea proprietăților soluțiilor lor. (Cuvintele „rezolvăm, apoi desenăm” din titlul cărții sunt legate de aceasta.) Sunt luate în considerare mai multe exemple fizice. La cel mai simplificat nivel, sunt descrise unele realizări ale secolului al XX-lea, inclusiv o înțelegere a mecanismului apariției „haosului” în comportamentul obiectelor deterministe. Cartea este destinată elevilor de liceu interesați de matematică. Tot ce trebuie să facă este să înțeleagă sensul derivatei ca viteză instantanee.
Alexei Belov
Există o problemă binecunoscută la olimpiade: pe o masă plată sunt monede (cifre convexe). Apoi unul dintre ei poate fi scos de pe masă fără a-i afecta pe ceilalți. Multă vreme, matematicienii au încercat să demonstreze analogul spațial al acestei afirmații, până când s-a construit un contraexemplu! A apărut o idee: în boabele mici, adesea nu există crăpătură, fisura nu crește dincolo de limita granulelor, iar crăpăturile se țin între ele. Această idee face teoretic posibilă crearea de compozite în care fisurile nu cresc, în special armuri ceramice.
Alexei Sosinsky
Unul dintre cele mai importante concepte de mecanică și fizică teoretică - conceptul de spațiu de configurare al unui sistem mecanic - din anumite motive rămâne necunoscut nu numai școlarilor, ci și majorității studenților la matematică. Prelegerea discută o clasă foarte simplă, dar foarte semnificativă de sisteme mecanice - mecanisme plate cu balamale cu două grade de libertate. Vom descoperi că în „cazul general” spațiile lor de configurare sunt suprafețe bidimensionale și vom încerca să înțelegem care sunt acestea. (Iată rezultatele finale de acum zece ani de către Dima Zvonkin.) În continuare, sunt discutate problemele matematice nerezolvate asociate cu mecanismele balamale. (Inclusiv două ipoteze, sau mai degrabă teoreme nedovedite, ale matematicianului american Bill Thurston.)
Vladimir Protasov
Calculul variațiilor este știința de a găsi minimumul unei funcții într-un spațiu infinit-dimensional. Spre deosebire de problemele minime cu care suntem obișnuiți, atunci când trebuie să alegem în mod optim un număr (parametru) sau, să zicem, un punct pe un plan, în problemele variaționale trebuie să găsim funcția optimă. În același timp, probleme de origini foarte diferite sunt rezolvate folosind același set de instrumente: de la mecanică clasică, geometrie, economie matematică etc. Vom începe cu probleme vechi, cunoscute încă din secolul al XVII-lea, și, construind punți de la o problemă la alta, vom ajunge rapid la rezultate moderne și la probleme nerezolvate.
(tradus din greacă. circular) – o curbă transcendentală plată, care este descrisă de un punct pe un cerc de rază r rularea de-a lungul unei linii drepte fără alunecare (o curbă transcendentală este o curbă care nu poate fi descrisă printr-o ecuație algebrică în coordonate dreptunghiulare). Ecuația sa parametrică
X = rt – r sin t,
y= r – r cos t
Punctele de intersecție ale cicloidei cu linia dreaptă de-a lungul căreia se rostogolește cercul (acest cerc se numește cerc generator, iar linia dreaptă de-a lungul căreia se rostogolește se numește directivă) se numesc puncte cusp, iar cele mai înalte puncte de pe cicloidă. , situate la mijloc între punctele cuspide adiacente, se numesc vârfurile cicloidei.
Galileo Galilei a fost primul care a studiat cicloidul. Lungimea unui arc cicloid a fost determinată în 1658 de arhitectul și matematicianul englez Christopher Wren, autorul proiectării și constructorului cupolei Catedralei Sf. Paul din Londra. S-a dovedit că lungimea cicloidei este egală cu 8 raze ale cercului generator.
Una dintre proprietățile remarcabile ale cicloidului, care i-a dat numele - brachistochrone (din cuvintele grecești „cel mai scurt” și „timp”) este asociată cu rezolvarea problemei celei mai abrupte coborâri. A apărut întrebarea ce formă ar trebui să fie dată unei caneluri bine lustruite (pentru a elimina practic frecarea) care conectează două puncte, astfel încât mingea să se rostogolească în jos dintr-un punct în altul în cel mai scurt timp posibil. Frații Bernoulli au demonstrat că șanțul ar trebui să aibă forma unui cicloid descendent.
Curbele legate de cicloidă pot fi obținute luând în considerare traiectoriile punctelor care nu sunt situate pe cercul generator.
Lasă punctul De la 0 este în interiorul cercului. Dacă se realizează De la 0 cerc auxiliar cu același centru ca și cercul generator, apoi când cercul generator se rostogolește de-a lungul unei linii drepte AB un cerc mic se va rostogoli în linie dreaptă A´ ÎN´, dar rularea lui va fi însoțită de alunecare, și punct De la 0 descrie o curbă numită cicloidă scurtată.
Un cicloid alungit este definit într-un mod similar - aceasta este traiectoria unui punct situat pe o prelungire a razei cercului generator, în timp ce rularea este însoțită de alunecare în direcția opusă.
Curbele cicloidale sunt folosite în multe calcule tehnice și proprietățile lor sunt folosite, de exemplu, în construirea profilelor dinților dintate, în pendulele cicloidale, în optică și, astfel, studiul acestor curbe este important din punct de vedere aplicativ. Este la fel de important ca, studiind aceste curbe și proprietățile lor, oamenii de știință din secolul al XVII-lea. au dezvoltat tehnici care au condus la crearea calculului diferenţial şi integral, iar problema brahistocronei a fost un pas către inventarea calculului variaţiilor.
Elena Malishevskaya
LEMNICATE
Ecuația în coordonate polare:
r 2 = a 2 cos2θ
(x 2 + y 2) 2 = a 2 (x 2 - y 2)
Unghiul dintre AB" sau A"B și axa x = 45 o
Aria unei bucle = a 2/2
CICLOID
Aria unui arc = 3πa 2
Lungimea arcului unui arc = 8a
Aceasta este o curbă descrisă de un punct P pe un cerc cu raza a, care se rostogolește de-a lungul axei x. 
HIPOCICLODII CU PATRU SPARE
Ecuația în coordonate dreptunghiulare:
x 2/3 + y 2/3 = a 2/3
Ecuații în formă parametrică: 
Aria cuprinsă de curbă = 3πa 2 /8
Lungimea arcului întregii curbe = 6a
Aceasta este o curbă descrisă de un punct P pe un cerc cu raza a/4, care se rostogolește în interiorul unui cerc cu raza a. 
CARDIOID
Ecuația: r = a(1 + cosθ)
Aria cuprinsă de curbă = 3πa 2 /2
Lungimea arcului curbei = 8a
Este o curbă descrisă de un punct P pe un cerc cu raza a, care se rostogolește în afara cercului cu raza a. Această curbă este și un caz special al melcului lui Pascal. 
LINIA LANTULUI
Ecuația:
y = a(e x/a + e -x/a)/2 = acosh(x/a)
Aceasta este curba de-a lungul căreia ar atârna un lanț atunci când este suspendat vertical de la punctul A la B. 
Trandafir cu trei petale
Ecuația: r = acos3θ
Ecuația r = acos3θ este similară cu curba obținută prin rotirea în sens invers acelor de ceasornic de-a lungul unei curbe de 30 o sau π/6 radiani.
În general, r = acosnθ sau r = asinnθ are n lobi dacă n este impar. 
Trandafirul cu patru petale
Ecuația: r = acos2θ
Ecuația r = asin2θ este similară cu curba obținută prin rotirea în sens invers acelor de ceasornic de-a lungul unei curbe de 45 o sau π/4 radian.
În general, r = acosnθ sau r = asinnθ are 2n petale dacă n este par. 
EPICYCLOID
Ecuații parametrice: 
Este curba descrisă de punctul P pe un cerc cu raza b în timp ce se rostogolește de-a lungul exteriorului cercului cu raza a. Cardioid este un caz special de epicicloid. 
HIPOCYCLOID GENERAL
Ecuații parametrice: 
Este curba descrisă de punctul P pe un cerc cu raza b în timp ce se rostogolește de-a lungul exteriorului cercului cu raza a.
Dacă b = a/4, curba este o hipocicloidă cu patru puncte. 
TROHOID
Ecuații parametrice: 
Aceasta este curba descrisă de punctul P la o distanță b de centrul unui cerc cu raza a în timp ce acesta se rostogolește de-a lungul axei x.
Dacă b este un cicloid scurtat.
Dacă b > a, curba are forma prezentată în Fig. 11-11 și este numit cadru de mers.
Dacă b = a, curba este o cicloidă. 
TRAKTRICE
Ecuații parametrice: 
Este curba descrisă de punctul final P al unui șir întins de lungime PQ atunci când celălalt capăt Q este deplasat de-a lungul axei x. 
VERZIERA (VERZIERA) AGNEZI (CATEAORI CURL AGNEZI)
Ecuație în coordonate dreptunghiulare: y = 8a 3 /(x 2 + 4a 2)
Ecuații parametrice: 
B. În figură, dreapta variabilă OA intersectează y = 2a și un cerc cu raza a cu centrul (0,a) în A și, respectiv, B. Orice punct P de pe „ondulă” este determinat prin construirea de linii paralele cu axele x și y, prin B și, respectiv, A și definirea punctului de intersecție al lui P. 
FRUNZĂ DESCARTES
Ecuația în coordonate dreptunghiulare:
x 3 + y 3 = 3axi
Ecuații parametrice: 
Zona buclei 3a 2 /2
Ecuația asimptotă: x + y + a = 0. 
CERCUL IMPLICAT
Ecuații parametrice: 
Aceasta este curba descrisă de punctul final P al șirului pe măsură ce se desfășoară dintr-un cerc cu raza a. 
ELIPSĂ IMPLICATĂ
Ecuația în coordonate dreptunghiulare:
(ax) 2/3 + (prin) 2/3 = (a 2 - b 2) 2/3
Ecuații parametrice: 
Această curbă este anvelopa normală la elipsa x 2 /a 2 + y 2 /b 2 = 1. 
CASSINI OVALE
Ecuația polară: r 4 + a 4 - 2a 2 r 2 cos2θ = b 4.
Este o curbă descrisă de un punct P astfel încât produsul distanței sale de la două puncte fixe [distanța 2a la latură] este o constantă b 2 .
Curba ca în figurile de mai jos când b a respectiv.
Dacă b = a, curba este lemniscate
MOLCUL LUI PASCAL
Ecuația polară: r = b + acosθ
Fie OQ linia care leagă centrul lui O cu orice punct Q pe un cerc cu diametrul a care trece prin O. Atunci curba este focarul tuturor punctelor P astfel încât PQ = b.
Curba prezentată în figurile de mai jos când b > a sau b 
CISSOIDUL DIOCLELOR
Ecuația în coordonate dreptunghiulare: y 2 = x 3 /(2a - x)
Ecuații parametrice: 
Aceasta este o curbă descrisă de un punct P astfel încât distanța OP = distanța RS. Folosit în sarcină dublarea cubului, adică găsirea laturii unui cub care are de două ori volumul unui cub dat 
SPIRALA LUI ARHIMEDE
Ecuația polară: r = aθ 
5. Ecuația cicloidă parametrică și ecuația în coordonate carteziene
Să presupunem că ni se dă un cicloid format dintr-un cerc de rază a cu centru în punctul A.
Daca alegem ca parametru determinant pozitiei punctului unghiul t=∟NDM prin care raza, care avea pozitie verticala AO la inceputul laminarii, a reusit sa se roteasca, atunci coordonatele x si y ale punctului M vor se exprimă după cum urmează:
x= OF = ON - NF = NM - MG = at-a sin t,
y= FM = NG = ND – GD = a – a cos t
Deci ecuațiile parametrice ale cicloidei au forma:

Când t se schimbă de la -∞ la +∞, se va obține o curbă, constând dintr-un număr infinit de ramuri precum cele prezentate în această figură.
De asemenea, pe lângă ecuația parametrică a cicloidei, există și ecuația sa în coordonate carteziene:
Unde r este raza cercului care formează cicloida.
6. Probleme privind găsirea părților unui cicloid și a figurilor formate dintr-un cicloid
Sarcina nr. 1. Găsiți aria unei figuri delimitate de un arc al unui cicloid a cărui ecuație este dată parametric
![]()
iar axa Bou.

Soluţie. Pentru a rezolva această problemă, vom folosi faptele pe care le cunoaștem din teoria integralelor și anume:
Zona unui sector curbat.
Considerăm o funcție r = r(ϕ) definită pe [α, β].
ϕ 0 ∈ [α, β] corespunde lui r 0 = r(ϕ 0) și, prin urmare, punctului M 0 (ϕ 0 , r 0), unde ϕ 0,
r 0 - coordonatele polare ale punctului. Dacă ϕ se modifică, „parcurgând” întregul [α, β], atunci punctul variabil M va descrie o curbă AB, dată fiind
ecuația r = r(ϕ).
Definiție 7.4. Un sector curbiliniu este o figură delimitată de două raze ϕ = α, ϕ = β și o curbă AB definită în polar
coordonate prin ecuația r = r(ϕ), α ≤ ϕ ≤ β.
Următoarele sunt adevărate
Teorema. Dacă funcția r(ϕ) > 0 și este continuă pe [α, β], atunci aria
sectorul curbiliniu se calculează prin formula:

Această teoremă a fost demonstrată mai devreme în subiectul integrală definită.
Pe baza teoremei de mai sus, problema noastră de a găsi aria unei figuri limitate de un arc de cicloid, a cărei ecuație este dată de parametrii parametrici x= a (t – sin t), y= a (1). – cos t), iar axa Ox, se reduce la următoarea soluție .
Soluţie. Din ecuația curbei dx = a(1−cos t) dt. Primul arc al cicloidului corespunde unei modificări a parametrului t de la 0 la 2π. Prin urmare,

Sarcina nr. 2. Aflați lungimea unui arc al cicloidei
![]()
Următoarea teoremă și corolarul ei au fost, de asemenea, studiate în calcul integral.
Teorema. Dacă curba AB este dată de ecuația y = f(x), unde f(x) și f ’ (x) sunt continue pe , atunci AB este rectificabilă și
Consecinţă. Fie dat AB parametric
L AB = ![]() (1)
(1)
Fie funcțiile x(t), y(t) diferențiabile continuu pe [α, β]. Apoi
formula (1) poate fi scrisă după cum urmează

Să facem o schimbare de variabile în această integrală x = x(t), apoi y’(x)= ;
dx= x’(t)dt și deci:

Acum să revenim la rezolvarea problemei noastre.
Soluţie. Avem, și prin urmare
Sarcina nr. 3. Trebuie să găsim aria suprafeței S formată din rotația unui arc al cicloidei
L=((x,y): x=a(t – sin t), y=a(1 – cost), 0≤ t ≤ 2π)
În calculul integral, există următoarea formulă pentru găsirea suprafeței unui corp de revoluție în jurul axei x a unei curbe definite parametric pe un segment: x=φ(t), y=ψ(t) (t 0 ≤t ≤t 1)
Aplicând această formulă la ecuația noastră cicloidă obținem:

Sarcina nr. 4. Aflați volumul corpului obținut prin rotirea arcului cicloid
![]()
De-a lungul axei Ox.
În calculul integral, la studierea volumelor, există următoarea remarcă:
Dacă curba care mărginește un trapez curbiliniu este dată de ecuații parametrice și funcțiile din aceste ecuații îndeplinesc condițiile teoremei privind modificarea variabilei într-o anumită integrală, atunci volumul corpului de revoluție al trapezului în jurul axei Ox va se calculează prin formula

Să folosim această formulă pentru a găsi volumul de care avem nevoie.
Problema este rezolvată.
Concluzie
Deci, în cursul acestei lucrări, au fost clarificate proprietățile de bază ale cicloidului. De asemenea, am învățat cum să construim un cicloid și am aflat semnificația geometrică a unui cicloid. După cum sa dovedit, cicloidul are aplicații practice enorme nu numai în matematică, ci și în calcule tehnologice și fizică. Dar cicloidul are alte merite. A fost folosit de oamenii de știință din secolul al XVII-lea atunci când au dezvoltat tehnici pentru studierea liniilor curbe - acele tehnici care au dus în cele din urmă la inventarea calculului diferențial și integral. A fost, de asemenea, una dintre „pietrele de atingere” pe care Newton, Leibniz și primii lor cercetători au testat puterea unor noi metode matematice puternice. În cele din urmă, problema brahistocronei a dus la inventarea calculului variațiilor, care este atât de necesar pentru fizicienii de astăzi. Astfel, cicloidul s-a dovedit a fi indisolubil legat de una dintre cele mai interesante perioade din istoria matematicii.
Literatură
1. Berman G.N. Cicloid. – M., 1980
2. Verov S.G. Brachistochrone, sau alt secret al cicloidului // Quantum. – 1975. - Nr. 5
3. Verov S.G. Secretele cicloidului // Quantum. – 1975. - Nr. 8.
4. Gavrilova R.M., Govorukhina A.A., Kartasheva L.V., Kostetskaya G.S., Radchenko T.N. Aplicații ale unei integrale definite. Instrucțiuni metodologice și sarcini individuale pentru studenții din anul I ai Facultății de Fizică. - Rostov n/a: UPL RSU, 1994.
5. Gindikin S.G. Epoca stelară a cicloidulului // Quantum. – 1985. - Nr. 6.
6. Fikhtengolts G.M. Curs de calcul diferențial și integral. T.1. – M., 1969
Această linie se numește „plic”. Fiecare linie curbă este un plic al tangentelor sale.
Materia și mișcarea, precum și metoda pe care o constituie, permit tuturor să-și realizeze potențialul în cunoașterea adevărului. Elaborarea unei metodologii pentru dezvoltarea unei forme dialectico-materialiste de gândire și stăpânirea unei metode similare de cunoaștere este al doilea pas către rezolvarea problemei dezvoltării și realizării capacităților umane. Fragmentul XX Oportunități...
În această situație, oamenii pot dezvolta nevrastenie - o nevroză, pe baza tabloului clinic al cărei stare este astenia. Atât în cazul neurasteniei, cât și în cazul decompensării psihopatiei neurastenice, esența apărării mentale (psihologice) se reflectă în retragerea din dificultăți în slăbiciune iritabilă cu disfuncții vegetative: fie persoana inconștient „combate” mai mult atacul. ..





Diverse tipuri de activități; dezvoltarea imaginației spațiale și a conceptelor spațiale, gândirea figurativă, spațială, logică, abstractă a școlarilor; dezvoltarea capacității de a aplica cunoștințe și abilități geometrice și grafice pentru a rezolva diverse probleme aplicate; familiarizarea cu conținutul și succesiunea etapelor activităților proiectului în domeniul tehnic și...
Arcuri. Spiralele sunt și evolvente ale curbelor închise, de exemplu evolvena unui cerc. Denumirile unor spirale sunt date de asemănarea ecuaţiilor lor polare cu ecuaţiile curbelor în coordonate carteziene, de exemplu: · spirală parabolică (a - r)2 = bj, · spirală hiperbolică: r = a/j. · Tijă: r2 = a/j · si-ci-spirală, ale căror ecuații parametrice au forma: , )