Lecția video „Inegalități cu două variabile” este destinată predării algebrei pe această temă în clasa a IX-a a unei școli gimnaziale. Lecția video conține o descriere a fundamentelor teoretice ale rezolvării inegalităților, descrie în detaliu procesul de rezolvare a inegalităților într-un mod grafic, caracteristicile acestuia și demonstrează exemple de rezolvare a sarcinilor pe această temă. Scopul acestei lecții video este de a facilita înțelegerea materialului folosind o prezentare vizuală a informațiilor, de a promova formarea deprinderilor în rezolvarea problemelor folosind metodele matematice studiate.

Principalele instrumente ale lecției video sunt utilizarea animației în prezentarea graficelor și a informațiilor teoretice, evidențierea conceptelor și caracteristicilor importante pentru înțelegerea și memorarea materialului în culori și alte moduri grafice, explicații vocale în scopul memorării mai ușoare a informațiilor și formarea capacităţii de a folosi limbajul matematic.

Lecția video începe prin introducerea subiectului și a unui exemplu care demonstrează conceptul de rezolvare a unei inegalități. Pentru a înțelege semnificația conceptului de soluție, este prezentată inegalitatea 3x 2 -y<10, в которое подставляется пара значений х=2 и у=6. Демонстрируется, как после подстановки данных значений неравенство становится верным. Понятие решения данного неравенства как пары значений (2;6) выведено на экран, подчеркивая его важность. Затем представляется определение рассмотренного понятия для запоминания его учениками или записи в тетрадь.

O parte importantă a capacității de a rezolva inegalitățile este capacitatea de a reprezenta setul soluțiilor sale pe un plan de coordonate. Formarea unei astfel de abilități în această lecție începe cu o demonstrație a găsirii unui set de soluții la inegalitățile liniare ax+by c. Se notează particularitățile definirii inegalității - x și y sunt variabile, a, b, c sunt unele numere, dintre care a și b nu sunt egale cu zero.

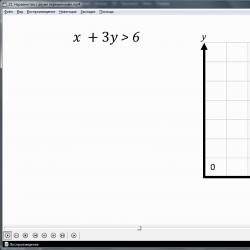
Un exemplu de astfel de inegalitate este x+3y>6. Pentru a transforma inegalitatea într-o inegalitate echivalentă care reflectă dependența valorilor lui y de valorile lui x, ambele părți ale inegalității sunt împărțite la 3, y rămâne pe o parte a ecuației și x este mutat în celălalt. Valoarea x=3 este selectată în mod arbitrar pentru înlocuirea în inegalitate. Se observă că dacă înlocuiți această valoare x în inegalitate și înlocuiți semnul inegalității cu un semn egal, puteți găsi valoarea corespunzătoare y=1. Perechea (3;1) va fi o soluție a ecuației y=-(1/3)x+2. Dacă înlocuim orice valoare a lui y mai mare decât 1, atunci inegalitatea cu o valoare dată a lui x va fi adevărată: (3;2), (3;8), etc. Similar cu acest proces de găsire a unei soluții, este considerat cazul general pentru găsirea unui set de soluții la o inegalitate dată. Căutarea unui set de soluții la inegalitatea începe cu înlocuirea unei anumite valori x 0. În partea dreaptă a inegalității obținem expresia -(1/3)x 0 +2. O anumită pereche de numere (x 0;y 0) este o soluție a ecuației y=-(1/3)x+2. În consecință, soluțiile inegalității y>-(1/3)x 0 +2 vor fi perechile corespunzătoare de valori cu x 0, unde y este mai mare decât valorile lui y 0. Adică, soluțiile acestei inegalități vor fi perechi de valori (x 0 ; y).

Pentru a găsi mulțimea soluțiilor inegalității x+3y>6 pe planul de coordonate, se demonstrează pe ea construcția unei drepte corespunzătoare ecuației y=-(1/3)x+2. Pe această linie, punctul M este marcat cu coordonatele (x 0; y 0). Se observă că toate punctele K(x 0 ;y) cu ordonate y>y 0, adică situate deasupra acestei drepte, vor îndeplini condițiile de inegalitate y>-(1/3)x+2. Din analiză se concluzionează că această inegalitate este dată de o mulțime de puncte care sunt situate deasupra dreptei y=-(1/3)x+2. Acest set de puncte constituie un semiplan peste o dreaptă dată. Deoarece inegalitatea este strictă, linia dreaptă în sine nu se află printre soluții. În figură, acest fapt este marcat cu o desemnare punctată.

Rezumând datele obținute în urma descrierii soluției inegalității x+3y>6, putem spune că dreapta x+3y=6 împarte planul în două semiplane, în timp ce semiplanul situat mai sus reflectă set de valori care satisface inegalitatea x+3y>6 și situate sub linie - soluție la inegalitatea x+3y<6. Данный вывод является важным для понимания, каким образом решаются неравенства, поэтому выведен на экран отдельно в рамке.

În continuare, luăm în considerare un exemplu de rezolvare a unei inegalități nestricte de gradul doi y>=(x-3) 2. Pentru a determina setul de soluții, în apropiere în figură se construiește o parabolă y = (x-3) 2. Punctul M(x 0 ; y 0) este marcat pe parabolă, ale cărui valori vor fi soluții ale ecuației y = (x-3) 2. În acest punct, se construiește o perpendiculară, pe care se marchează un punct K(x 0 ;y) deasupra parabolei, care va fi soluția inegalității y>(x-3) 2. Putem concluziona că inegalitatea inițială este satisfăcută de coordonatele punctelor situate pe o parabolă dată y=(x-3) 2 și deasupra acesteia. În figură, această zonă de soluție este marcată prin umbrire.

Următorul exemplu care demonstrează poziția pe planul punctelor care sunt o soluție a unei inegalități de gradul doi este o descriere a soluției inegalității x 2 + y 2<=9. На координатной плоскости строится окружность радиусом 3 с центром в начале координат. Отмечается, что решениями уравнения будут точки, сумма квадратов координат которых не превышает квадрата радиуса. Также отмечается, что окружность х 2 +у 2 =9 разбивает плоскость на области внутри окружности и вне круга. Очевидно, что множество точек внутренней части круга удовлетворяют неравенству х 2 +у 2 <9, а внешняя часть - неравенству х 2 +у 2 >9. În consecință, soluția inegalității inițiale va fi mulțimea de puncte de pe cerc și regiunea din interiorul acestuia.

În continuare, luăm în considerare soluția ecuației xy>8. Pe planul de coordonate de lângă sarcină, se construiește o hiperbolă care satisface ecuația xy=8. Marcați punctul M(x 0;y 0) aparținând hiperbolei și K(x 0;y) deasupra acestuia paralel cu axa y. Este evident că coordonatele punctului K corespund inegalității xy>8, întrucât produsul coordonatelor acestui punct depășește 8. Se indică faptul că în același mod se poate demonstra corespondența punctelor aparținând zonei B cu inegalitatea xy<8. Следовательно, решением неравенства ху>8 va exista un set de puncte situate în zonele A și C.

Lecția video „Inegalități cu două variabile” poate servi drept ajutor vizual pentru profesor în clasă. Materialul va ajuta, de asemenea, elevii care învață materialul pe cont propriu. Este util să folosiți o lecție video în timpul învățământului la distanță.

Inegalitatea cu două variabilex și y numită inegalitate de forma:

(sau semn)

unde este o expresie cu aceste variabile.

Prin decizie inegalitățile din două variabile se numesc o pereche ordonată de numere sub care această inegalitate se transformă într-o adevărată inegalitate numerică.

Rezolvați inegalitatea- înseamnă găsirea ansamblului tuturor soluțiilor sale. Soluția unei inegalități cu două variabile este un anumit set de puncte pe planul de coordonate.

Principala metodă de rezolvare a acestor inegalități este grafic metodă. Constă în trasarea unor linii de delimitare (dacă inegalitatea este strictă, linia este trasată cu linie punctată). Obținem ecuația la graniță dacă într-o inegalitate dată înlocuim semnul inegalității cu un semn egal. Toate liniile împreună împart planul de coordonate în părți. Setul necesar de puncte care corespunde unei anumite inegalități sau unui sistem de inegalități poate fi determinat prin luarea unui punct de control în interiorul fiecărei regiuni a regiunii.

Mulțimea inegalităților cu două variabile are forma

Soluția pentru populație este unirea tuturor soluțiilor la inegalități.

Exemplul 1. Rezolvați sistemul

Soluţie. Să construim în sistem Ohoo linii corespunzătoare (Fig. 19):

Ecuația definește un cerc centrat pe DESPRE¢(0; 1) și R = 2.

Ecuația definește o parabolă cu vârful la DESPRE(0; 0).

Să găsim soluții la fiecare dintre inegalitățile incluse în sistem. Prima inegalitate corespunde ariei din interiorul cercului și cercului însuși (suntem convinși de validitatea acesteia dacă substituim coordonatele oricărui punct din această zonă în inegalitate). A doua inegalitate corespunde zonei situate sub parabolă.

Soluția sistemului este intersecția celor două zone indicate (prezentată în Fig. 19 prin suprapunerea a două hașuri).

Sarcini

nivelez

1.1. Rezolvați grafic:

3) ; 4) ;

5) ; 6) ;

7) ;

Nivelul II

2.1. Rezolvați grafic:

1) 2)

2.2. Aflați numărul de soluții întregi ale sistemului:

1) 2) 3)

2.3. Găsiți toate soluțiile întregi ale sistemului:

1) 2)

3)

2.4. Rezolvați inegalitatea. În răspunsul dvs., indicați numărul de soluții cu două coordonate întregi

Dacă într-un curs școlar de matematică și algebră scoatem în evidență tema „inegalității” separat, atunci de cele mai multe ori vom învăța elementele de bază ale lucrului cu inegalitățile care conțin o variabilă în notația lor. În acest articol ne vom uita la ce sunt inegalitățile cu variabile, vom spune cum se numește soluția lor și, de asemenea, ne vom da seama cum sunt scrise soluțiile inegalităților. Pentru clarificare, vom oferi exemple și comentarii necesare.

Navigare în pagină.

Ce sunt inegalitățile cu variabile?

De exemplu, dacă o inegalitate nu are soluții, atunci ei scriu „fără soluții” sau folosesc semnul set gol ∅.

Când soluția generală a unei inegalități este un număr, atunci se scrie așa, de exemplu, 0, −7,2 sau 7/9, și uneori, de asemenea, cuprins între paranteze.

Dacă soluția unei inegalități este reprezentată de mai multe numere și numărul lor este mic, atunci ele sunt pur și simplu enumerate separate prin virgule (sau separate prin punct și virgulă), sau scrise separate prin virgule în paranteze. De exemplu, dacă soluția generală a unei inegalități cu o variabilă este trei numere −5, 1,5 și 47, atunci scrieți −5, 1,5, 47 sau (−5, 1,5, 47).

Și pentru a scrie soluții la inegalitățile care au un număr infinit de soluții, ei folosesc atât denumirile acceptate pentru mulțimi de numere naturale, întregi, raționale, reale de forma N, Z, Q și R, desemnări pentru intervale numerice și seturi de numere individuale. numere, cele mai simple inegalități și o descriere a unei mulțimi printr-o proprietate caracteristică și toate metodele nenumite. Dar, în practică, cele mai simple inegalități și intervale numerice sunt cele mai des folosite. De exemplu, dacă soluția inegalității este numărul 1, semiintervalul (3, 7] și raza, ∪; editat de S. A. Telyakovsky. - Ed. a XVI-a - M.: Educație, 2008. - 271 p. : ill. - ISBN 978-5-09-019243-9.

https://accounts.google.com

Subtitrările diapozitivelor:

Inegalitățile cu două variabile și sistemele lor Lecția 1

Inegalități cu două variabile Inegalități 3x – 4y  0; și sunt inegalități cu două variabile x și y. Soluția unei inegalități în două variabile este o pereche de valori ale variabilelor care o transformă într-o adevărată inegalitate numerică. Pentru x = 5 și y = 3, inegalitatea 3x - 4y  0 se transformă în inegalitatea numerică corectă 3  0. Perechea de numere (5;3) este o soluție a acestei inegalități. Perechea de numere (3;5) nu este soluția ei.

Este perechea de numere (-2; 3) o soluție a inegalității: nr. 482 (b, c) Nu este Este

Soluția unei inegalități este o pereche ordonată de numere reale care transformă inegalitatea într-o inegalitate numerică adevărată. Grafic, aceasta corespunde cu specificarea unui punct pe planul de coordonate. Rezolvarea unei inegalități înseamnă găsirea multor soluții la aceasta.

Inegalitățile cu două variabile au forma: Mulțimea soluțiilor unei inegalități este mulțimea tuturor punctelor planului de coordonate care satisfac o inegalitate dată.

Mulțimi de soluții pentru inegalitatea F(x,y) ≥ 0 x y F(x,y)≤0 x y

F(x, y)>0 F(x, y)

Regula punctului de probă Construiți F(x ; y)=0 Luând un punct de probă din orice zonă, stabiliți dacă coordonatele lui sunt o soluție a inegalității Trageți o concluzie despre soluția inegalității x y 1 1 2 A(1;2) F (x; y) =0

Inegalități liniare cu două variabile O inegalitate lineară cu două variabile se numește inegalități de forma ax + bx +c  0 sau ax + bx +c

Găsiți eroarea! nr. 484 (b) -4 2 x 2 -6 y 6 -2 0 4 -2 - 4

Rezolvați grafic inegalitatea: -1 -1 0 x 1 -2 y -2 2 2 1 Desenăm grafice cu linii continue:

Să determinăm semnul de inegalitate în fiecare dintre zonele -1 -1 0 x 1 -2 y -2 2 2 1 3 4 - + 1 + 2 - 7 + 6 - 5 +

Soluția inegalității este o mulțime de puncte din ariile care conțin semnul plus și soluții ale ecuației -1 -1 0 x 1 -2 y -2 2 2 1 3 4 - + 1 + 2 - 7 + 6 - 5 +

Să rezolvăm împreună Nr. 485 (b) Nr. 486 (b, d) Nr. 1. Stabiliți inegalitatea și trasați pe planul de coordonate mulțimea punctelor pentru care: a) abscisa este mai mare decât ordonata; b) suma absciselor și ordonatei este mai mare decât dubla diferență a acestora.

Să rezolvăm împreună Nr. 2. Definiți prin inegalitate un semiplan deschis situat deasupra dreptei AB care trece prin punctele A(1;4) și B(3;5). Răspuns: y  0,5x +3,5 Nr. 3. Pentru ce valori ale lui b mulțimea soluțiilor inegalității 3x – b y + 7  0 reprezintă un semiplan deschis situat deasupra dreptei 3x – b y + 7 = 0. Răspuns: b  0.

Tema P. 21, Nr. 483; Nr. 484(c,d); nr. 485(a); Nr. 486(c).

Previzualizare:

Pentru a utiliza previzualizările prezentării, creați un cont Google și conectați-vă la el: https://accounts.google.com

Subtitrările diapozitivelor:

Inegalități cu două variabile și sistemele lor Lecția 2

Sisteme de inegalități cu două variabile

Soluția unui sistem de inegalități cu două variabile este o pereche de valori ale variabilelor care transformă fiecare dintre inegalitățile sistemului într-o adevărată inegalitate numerică. Nr. 1. Desenați setul de soluții ale sistemelor de inegalități. nr. 496 (oral)

a) x y 2 2 x y 2 2 b)

Să rezolvăm împreună numărul 1. La ce valori ale lui k definește sistemul de inegalități un triunghi pe planul de coordonate? Raspuns: 0

Rezolvăm împreună x y 2 2 2 2 Nr. 2. În figura este prezentat un triunghi cu vârfurile A(0;5), B(4;0), C(1;-2), D(-4;2). Definiți acest patrulater cu un sistem de inegalități. A B C D

Să rezolvăm împreună Nr. 3. Pentru ce k și b este mulțimea punctelor planului de coordonate definit de sistemul de inegalități: a) bandă; b) unghi; c) set gol. Răspuns: a) k= 2,b  3; b) k ≠ 2, b – orice număr; c) k = 2; b

Să rezolvăm împreună numărul 4. Ce cifră este dată de ecuație? (oral) 1) 2) 3) Nr. 5. Desenați pe planul de coordonate mulțimea soluțiilor punctelor specificate de inegalitate.

Să rezolvăm împreună nr 497 (c, d), 498 (c)

Tema P.22 Nr. 496, Nr. 497 (a, b), Nr. 498 (a, b), Nr. 504.

Previzualizare:

Pentru a utiliza previzualizările prezentării, creați un cont Google și conectați-vă la el: https://accounts.google.com

Subtitrările diapozitivelor:

Inegalitățile cu două variabile și sistemele lor Lecția 3

Găsiți eroarea! -4 2 x 2 -6 y 6 -2 0 4 -2 - 4

Găsiți eroarea! | | | | | | | | | | | | | | | | | | 1 x y 2

Determinați inegalitatea 0 - 6 - 1 5 3 1 2 y x - 3 - 2 1 -3 4

0 - 6 - 1 5 3 1 2 y x - 3 - 2 1 -3 4 Determinați inegalitatea

0 - 3 - 1 5 3 1 2 y x - 3 - 2 1 Determinați semnul inegalității ≤

Rezolvați grafic sistemul de inegalități -1 -1 0 x 1 -2 y -2 2 2 1

Inegalități și sisteme de inegalități de grade superioare cu două variabile Nr. 1. Desenați pe planul de coordonate mulțimea de puncte specificată de sistemul de inegalități

Inegalități și sisteme de inegalități de grade superioare cu două variabile Nr. 2. Desenați pe planul de coordonate mulțimea de puncte specificată de sistemul de inegalități

Inegalități și sisteme de inegalități de grade superioare cu două variabile Nr 3. Desenați pe planul de coordonate mulțimea punctelor specificate de sistemul de inegalități.Să transformăm prima inegalitate a sistemului:

Inegalităţi şi sisteme de inegalităţi de grade superioare cu două variabile Se obţine un sistem echivalent

Inegalități și sisteme de inegalități de grade superioare cu două variabile Nr. 4. Desenați pe planul de coordonate mulțimea de puncte specificată de sistemul de inegalități

Să decidem împreună Nr. 502 Colecția lui Galitsky. Nr. 9.66 b) y ≤ |3x -2| 0 - 6 - 1 5 3 1 2 y x - 3 - 2 1 -3 4

. Nr. 9.66(c) Rezolvați împreună 0 - 6 - 1 5 3 1 2 y x - 3 - 2 1 -3 4 |y| ≥ 3x - 2

Rezolvăm împreună Nr. 9.66(g) 0 - 6 - 1 5 3 1 2 y x - 3 - 2 1 -3 4 |y|

Rezolvați inegalitatea: x y -1 -1 0 1 -2 -2 2 2 1

0 - 6 - 1 5 3 1 2 y x - 3 - 2 1 -3 4 Scrieți sistemul de inegalități

11:11 3) Ce cifră este determinată de setul de soluții ale sistemului de inegalități? Găsiți aria fiecărei figuri. 6) Câte perechi de numere naturale sunt soluții ale sistemului de inegalități? Calculați suma tuturor acestor numere. Rezolvarea exercițiilor de antrenament 2) Scrieți un sistem de inegalități cu două variabile, a cărui mulțime de soluții este prezentată în Figura 0 2 x y 2 1) Desenați mulțimea soluțiilor sistemului pe planul de coordonate: 4) Definiți inelul prezentat în figură ca un sistem de inegalități. 5) Rezolvați sistemul de inegalități y x 0 5 10 5 10

Rezolvarea exercițiilor de antrenament 7) Calculați aria figurii dată de mulțimea soluțiilor sistemului de inegalități și găsiți cea mai mare distanță dintre punctele acestei figuri 8) La ce valoare a lui m are sistemul de inegalități doar o solutie? 9) Indicați câteva valori ale lui k și b la care sistemul de inegalități definește pe planul de coordonate: a) o bandă; b) unghi.

Acest lucru este interesant.Matematicianul englez Thomas Harriot (Harriot T., 1560-1621) a introdus cunoscutul semn al inegalității, argumentând-o astfel: „Dacă două segmente paralele servesc ca simbol al egalității, atunci segmentele care se intersectează trebuie să fie un simbol al inegalității. .” În 1585, tânărul Harriot a fost trimis de regina Angliei într-o expediție de explorare în America de Nord. Acolo a văzut un tatuaj popular în rândul indienilor sub formă. Acesta este probabil motivul pentru care Harriot a propus semnul inegalității în două dintre formele sale: „>” este mai mare decât... și „

Acest lucru este interesant.Simbolurile ≤ și ≥ pentru comparație nestrictă au fost propuse de Wallis în 1670. Inițial, linia era deasupra semnului de comparație și nu sub acesta, așa cum este acum. Aceste simboluri au devenit răspândite după sprijinul matematicianului francez Pierre Bouguer (1734), de la care și-au căpătat forma modernă.

Tema lecției: Inegalități cu două variabile.

Scopul lecției:Învățați elevii cum să rezolve inegalitățile din două variabile.

Obiectivele lecției:

1. Introduceți conceptul de inegalitate cu două variabile. Învățați elevii cum să rezolve inegalitățile. Pentru a dezvolta abilități de utilizare a metodei grafice la rezolvarea inegalităților, capacitatea de a arăta soluția pe un plan de coordonate.

2. Dezvoltați gândirea elevilor, dezvoltați abilitățile practice ale elevilor.

3. Să insufle studenților munca asiduă, independența, o atitudine responsabilă față de afaceri, inițiativa și luarea independentă a deciziilor.

Manual/literatură: Algebra 9, materiale didactice.

În timpul orelor:

1. Conceptul de inegalitate cu două variabile și soluția acestuia.

2. Inegalitatea liniară cu două variabile.

Să considerăm inegalitățile: 0.5x 2 -2y+l 20 - inegalitatea cu două variabile.

Se consideră inegalitatea 0,5x 2 -2y+l

Când x=1, y=2. Obținem inegalitatea corectă 0,5 1 - 2 2 + 1

O pereche de numere (1; 2), în care valoarea x este pe primul loc, iar valoarea y pe locul doi, se numește soluția inegalității 0,5x 2 -2y+l

Definiție. O soluție la o inegalitate în două variabile este o pereche de valori ale acestor variabile care transformă inegalitatea într-o inegalitate numerică adevărată.

Dacă fiecare soluție a unei inegalități cu două variabile este reprezentată de un punct în planul de coordonate, atunci se va obține un grafic al acestei inegalități. El este un fel de figură. Se spune că această cifră este dată sau descrisă de o inegalitate.

Să considerăm inegalitățile liniare cu două variabile.

Definiție. O inegalitate liniară cu două variabile este o inegalitate de forma ax + prin c, unde x și y sunt variabile, a, b și c sunt niște numere.

Într-o inegalitate liniară cu două variabile, dacă înlocuiți semnul inegalității cu un semn egal, obțineți o ecuație liniară. Graficul unei ecuații liniare ax + by = c, în care a sau b nu este egal cu zero, este o dreaptă. Împarte setul de puncte ale planului de coordonate care nu îi aparțin în două regiuni reprezentând semiplanuri deschise.

Folosind exemple, vom lua în considerare modul în care mulțimea soluțiilor unei inegalități cu două variabile este reprezentată pe planul de coordonate.

Exemplul 1. Să descriem pe planul de coordonate mulțimea soluțiilor inegalității 2y+3x≤6.

Construim o linie dreaptă 2y+3x=6, y=3-1.5x

O linie dreaptă împarte setul tuturor punctelor planului de coordonate în puncte situate sub el și puncte situate deasupra acestuia. Să luăm un punct de control din fiecare zonă: A(1;1), B(1;3).

Coordonatele punctului A satisfac această inegalitate 2y+3x≤6, 2·1+3·1≤6, 5≤6

Coordonatele punctului B nu satisfac această inegalitate: 2y+3x≤6, 2·3+3·1≤6.

Această inegalitate este satisfăcută de mulțimea de puncte din regiunea în care se află punctul A. Să umbrim această regiune. Am prezentat setul de soluții la inegalitatea 2y+3x≤6.

Pentru a reprezenta un set de soluții ale inegalităților pe planul de coordonate, procedați după cum urmează:

1. Construim un grafic al funcției y = f(x), care împarte planul în două regiuni.

2. Selectați oricare dintre zonele rezultate și luați în considerare un punct arbitrar din ea. Verificăm fezabilitatea inegalității originale pentru acest punct. Dacă testul are ca rezultat o inegalitate numerică corectă, atunci concluzionăm că inegalitatea inițială este satisfăcută în întreaga regiune căreia îi aparține punctul selectat. Astfel, setul de soluții ale inegalității este regiunea căreia îi aparține punctul selectat. Dacă rezultatul verificării este o inegalitate numerică incorectă, atunci setul de soluții ale inegalității va fi a doua regiune căreia nu îi aparține punctul selectat.

3. Dacă inegalitatea este strictă, atunci limitele regiunii, adică punctele graficului funcției y = f(x), nu sunt incluse în mulțimea de soluții, iar granița este reprezentată cu o linie punctată . Dacă inegalitatea nu este strictă, limitele regiunii, adică punctele graficului funcției y = f(x), sunt incluse în setul de soluții ale acestei inegalități și granița în acest caz este reprezentată ca o linie continuă.

Concluzie: - soluția inegalității f(x,y)˃0, )