Zadatak B9 daje graf funkcije ili derivacije iz kojeg trebate odrediti jednu od sljedećih veličina:

1. Vrijednost derivacije u nekoj točki x 0,
2. Maksimalni ili minimalni bodovi (ekstremni bodovi),
3. Intervali rastućih i padajućih funkcija (intervali monotonosti).

Funkcije i derivacije predstavljene u ovom problemu uvijek su kontinuirane, što rješenje čini puno lakšim. Unatoč činjenici da zadatak pripada odjeljku matematičke analize, mogu ga napraviti i najslabiji učenici, jer ovdje nije potrebno duboko teorijsko znanje.

Za pronalaženje vrijednosti derivacije, točaka ekstrema i intervala monotonosti postoje jednostavni i univerzalni algoritmi - o svima će biti riječi u nastavku.

Pažljivo pročitajte uvjete zadatka B9 kako ne biste napravili glupe pogreške: ponekad naiđete na dosta dugačke tekstove, ali postoji nekoliko važnih uvjeta koji utječu na tijek rješavanja.

Izračun vrijednosti derivata. Metoda dvije točke

Ako je problemu dan graf funkcije f(x), tangenta na taj graf u nekoj točki x 0, i potrebno je pronaći vrijednost derivacije u toj točki, primjenjuje se sljedeći algoritam:

1. Pronađite dvije “odgovarajuće” točke na grafu tangente: njihove koordinate moraju biti cijeli brojevi. Označimo te točke kao A (x 1 ; y 1) i B (x 2 ; y 2). Točno zapišite koordinate - ovo je ključna točka u rješenju, a svaka pogreška ovdje dovest će do netočnog odgovora.
2. Poznavajući koordinate, lako je izračunati priraštaj argumenta Δx = x 2 − x 1 i priraštaj funkcije Δy = y 2 − y 1 .
3. Konačno, nalazimo vrijednost derivacije D = Δy/Δx. Drugim riječima, trebate podijeliti prirast funkcije s prirastom argumenta - i to će biti odgovor.

Napomenimo još jednom: točke A i B potrebno je tražiti upravo na tangenti, a ne na grafu funkcije f(x), kako se često događa. Tangenta će nužno sadržavati najmanje dvije takve točke - inače problem neće biti ispravno formuliran.

Promotrimo točke A (−3; 2) i B (−1; 6) i pronađi priraštaje:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.

Nađimo vrijednost derivacije: D = Δy/Δx = 4/2 = 2.

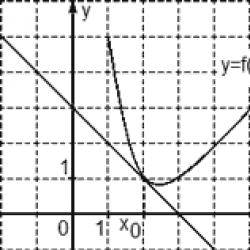
Zadatak. Na slici je prikazan graf funkcije y = f(x) i tangenta na nju u točki s apscisom x 0. Odredite vrijednost derivacije funkcije f(x) u točki x 0 .

Razmotrite točke A (0; 3) i B (3; 0), pronađite priraštaje:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.

Sada nalazimo vrijednost derivacije: D = Δy/Δx = −3/3 = −1.

Zadatak. Na slici je prikazan graf funkcije y = f(x) i tangenta na nju u točki s apscisom x 0. Odredite vrijednost derivacije funkcije f(x) u točki x 0 .

Razmotrite točke A (0; 2) i B (5; 2) i pronađite priraštaje:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.

Ostaje pronaći vrijednost derivacije: D = Δy/Δx = 0/5 = 0.

Iz posljednjeg primjera možemo formulirati pravilo: ako je tangenta paralelna s osi OX, derivacija funkcije u točki dodirivanja je nula. U ovom slučaju ne morate ništa ni brojati - samo pogledajte grafikon.

Izračunavanje maksimalnih i minimalnih bodova

Ponekad, umjesto grafa funkcije, zadatak B9 daje graf derivacije i zahtijeva pronalaženje maksimalne ili minimalne točke funkcije. U ovoj situaciji metoda dvije točke je beskorisna, ali postoji još jedan, još jednostavniji algoritam. Prvo, definirajmo terminologiju:

1. Točku x 0 nazivamo točkom maksimuma funkcije f(x) ako u nekoj okolini te točke vrijedi nejednakost: f(x 0) ≥ f(x).
2. Točku x 0 nazivamo točkom minimuma funkcije f(x) ako u nekoj okolini te točke vrijedi nejednakost: f(x 0) ≤ f(x).

Kako biste pronašli maksimalne i minimalne točke iz grafa izvedenica, samo slijedite ove korake:

1. Ponovno nacrtajte graf izvedenica, uklanjajući sve nepotrebne podatke. Kao što praksa pokazuje, nepotrebni podaci samo ometaju odluku. Stoga označavamo nule derivacije na koordinatnoj osi - i to je to.
2. Utvrdite predznake izvoda na intervalima između nula. Ako je za neku točku x 0 poznato da je f'(x 0) ≠ 0, tada su moguće samo dvije opcije: f'(x 0) ≥ 0 ili f'(x 0) ≤ 0. Predznak derivacije je lako odrediti iz izvornog crteža: ako derivacijski graf leži iznad OX osi, tada je f'(x) ≥ 0. I obrnuto, ako derivacijski graf leži ispod OX osi, tada je f'(x) ≤ 0.
3. Ponovno provjeravamo nule i predznake izvoda. Tamo gdje se predznak mijenja iz minusa u plus je minimalna točka. Obrnuto, ako se predznak derivacije mijenja s plusa na minus, to je najveća točka. Brojanje se uvijek vrši s lijeva na desno.

Ova shema radi samo za kontinuirane funkcije - nema drugih u zadatku B9.

Zadatak. Na slici je prikazan graf derivacije funkcije f(x) definirane na intervalu [−5; 5]. Pronađite točku minimuma funkcije f(x) na tom segmentu.

Oslobodimo se nepotrebnih informacija i ostavimo samo granice [−5; 5] i nulte derivacije x = −3 i x = 2,5. Također bilježimo znakove:

Očito se u točki x = −3 predznak derivacije mijenja s minusa na plus. Ovo je minimalna točka.

Zadatak. Na slici je prikazan graf derivacije funkcije f(x) definirane na intervalu [−3; 7]. Pronađite točku maksimuma funkcije f(x) na tom segmentu.

Ponovno nacrtajmo graf, ostavljajući samo granice [−3; 7] i nule derivacije x = −1.7 i x = 5. Zabilježimo predznake derivacije na dobivenom grafu. Imamo:

Očito, u točki x = 5 znak derivacije se mijenja iz plusa u minus - to je maksimalna točka.

Zadatak. Na slici je prikazan graf derivacije funkcije f(x), definirane na intervalu [−6; 4]. Odredite broj maksimalnih točaka funkcije f(x) koje pripadaju segmentu [−4; 3].

Iz uvjeta zadatka proizlazi da je dovoljno razmotriti samo dio grafa ograničen segmentom [−4; 3]. Stoga gradimo novi graf na kojem označavamo samo granice [−4; 3] i nule derivacije unutar njega. Naime, točke x = −3,5 i x = 2. Dobivamo:

Na ovom grafu postoji samo jedna maksimalna točka x = 2. U toj točki se predznak derivacije mijenja iz plusa u minus.

Mala napomena o točkama s necijelobrojnim koordinatama. Na primjer, u prošlom zadatku razmatrana je točka x = −3,5, ali s istim uspjehom možemo uzeti x = −3,4. Ako je problem ispravno sastavljen, takve promjene ne bi trebale utjecati na odgovor, budući da bodovi "bez stalnog mjesta stanovanja" ne sudjeluju izravno u rješavanju problema. Naravno, ovaj trik neće raditi s cjelobrojnim točkama.

Određivanje intervala rastućih i padajućih funkcija

U takvom problemu, poput točaka maksimuma i minimuma, predlaže se korištenje grafa derivacije za pronalaženje područja u kojima sama funkcija raste ili opada. Prvo, definirajmo što su povećanje i opadanje:

1. Kaže se da je funkcija f(x) rastuća na segmentu ako za bilo koje dvije točke x 1 i x 2 iz tog segmenta vrijedi sljedeća izjava: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . Drugim riječima, što je veća vrijednost argumenta, to je veća vrijednost funkcije.
2. Funkcija f(x) se naziva padajućom na segmentu ako za bilo koje dvije točke x 1 i x 2 iz tog segmenta vrijedi sljedeća tvrdnja: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Oni. Veća vrijednost argumenta odgovara manjoj vrijednosti funkcije.

Formulirajmo dovoljne uvjete za povećanje i smanjenje:

1. Da bi kontinuirana funkcija f(x) rasla na segmentu dovoljno je da njezina derivacija unutar segmenta bude pozitivna, tj. f’(x) ≥ 0.
2. Da bi kontinuirana funkcija f(x) opadala na segmentu dovoljno je da njezina derivacija unutar segmenta bude negativna, tj. f’(x) ≤ 0.

Prihvatimo ove izjave bez dokaza. Dakle, dobivamo shemu za pronalaženje intervala povećanja i opadanja, koja je na mnogo načina slična algoritmu za izračunavanje ekstremnih točaka:

1. Uklonite sve nepotrebne podatke. U izvornom grafu derivacije nas prvenstveno zanimaju nule funkcije pa ćemo ostaviti samo njih.
2. Označite predznake izvoda na razmacima između nula. Gdje je f’(x) ≥ 0, funkcija raste, a gdje je f’(x) ≤ 0, opada. Ako problem postavlja ograničenja na varijablu x, dodatno ih označavamo na novom grafu.
3. Sada kada znamo ponašanje funkcije i ograničenja, ostaje izračunati količinu potrebnu u problemu.

Zadatak. Na slici je prikazan graf derivacije funkcije f(x) definirane na intervalu [−3; 7.5]. Odredite intervale opadanja funkcije f(x). U svom odgovoru naznačite zbroj cijelih brojeva uključenih u ove intervale.

Kao i obično, ponovno nacrtajmo graf i označimo granice [−3; 7.5], kao i nulte derivacije x = −1.5 i x = 5.3. Zatim bilježimo predznake izvedenice. Imamo:

Budući da je derivacija negativna na intervalu (− 1,5), to je interval opadajuće funkcije. Ostaje zbrojiti sve cijele brojeve koji se nalaze unutar ovog intervala:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Zadatak. Na slici je prikazan graf derivacije funkcije f(x), definirane na intervalu [−10; 4]. Odredite intervale porasta funkcije f(x). U odgovoru navedite duljinu najvećeg od njih.

Oslobodimo se nepotrebnih informacija. Ostavimo samo granice [−10; 4] i nulte derivacije kojih je ovoga puta bilo četiri: x = −8, x = −6, x = −3 i x = 2. Označimo predznake derivacije i dobijemo sljedeću sliku:

Zanimaju nas intervali rastuće funkcije, tj. tako da je f’(x) ≥ 0. Dva su takva intervala na grafu: (−8; −6) i (−3; 2). Izračunajmo njihove duljine:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Budući da trebamo pronaći duljinu najvećeg od intervala, zapisujemo vrijednost l 2 = 5 kao odgovor.

Prikaz veze između predznaka izvoda i prirode monotonosti funkcije.

Budite izuzetno oprezni u vezi sa sljedećim. Pogledajte, raspored ŠTO vam je dano! Funkcija ili njezina derivacija

Ako je dan graf derivacije, tada će nas zanimati samo funkcijski predznaci i nule. Nikakva “brda” i “udubine” nas u principu ne zanimaju!

Zadatak 1.

Na slici je prikazan graf funkcije definirane na intervalu. Odredite broj cjelobrojnih točaka u kojima je derivacija funkcije negativna.

Riješenje:

Na slici su područja opadajuće funkcije označena bojom:

Ova padajuća područja funkcije sadrže 4 cjelobrojne vrijednosti.

Zadatak 2.

Na slici je prikazan graf funkcije definirane na intervalu. Odredite broj točaka u kojima je tangenta na graf funkcije paralelna s pravcem ili se s njim poklapa.

Riješenje:

Jednom kada je tangenta na graf funkcije paralelna (ili se podudara) s ravnom linijom (ili, što je isto), imajući nagib, jednak nuli, tada tangenta ima kutni koeficijent .

To opet znači da je tangenta paralelna s osi, jer je nagib tangens kuta nagiba tangente na os.

Stoga na grafu nalazimo točke ekstrema (točke maksimuma i minimuma) - u tim će točkama funkcije tangente na graf biti paralelne s osi.

Postoje 4 takve točke.

Zadatak 3.

Na slici je prikazan graf derivacije funkcije definirane na intervalu. Odredite broj točaka u kojima je tangenta na graf funkcije paralelna s pravcem ili se s njim poklapa.

Riješenje:

Budući da je tangenta na graf funkcije paralelna (ili se poklapa) s pravcem koji ima nagib, tada i tangenta ima nagib.

To pak znači da na dodirnim točkama.

Stoga gledamo koliko točaka na grafu ima ordinatu jednaku .

Kao što vidite, postoje četiri takve točke.

Zadatak 4.

Na slici je prikazan graf funkcije definirane na intervalu. Odredite broj točaka u kojima je derivacija funkcije 0.

Riješenje:

Derivacija je jednaka nuli u točkama ekstrema. Imamo ih 4:

Zadatak 5.

Slika prikazuje graf funkcije i jedanaest točaka na x-osi:. U koliko je od ovih točaka derivacija funkcije negativna?

Riješenje:

Na intervalima opadajuće funkcije njezina derivacija poprima negativne vrijednosti. I funkcija opada u točkama. Postoje 4 takve točke.

Zadatak 6.

Na slici je prikazan graf funkcije definirane na intervalu. Odredi zbroj točaka ekstrema funkcije.

Riješenje:

Ekstremne točke– to su maksimalni bodovi (-3, -1, 1) i minimalni bodovi (-2, 0, 3).

Zbroj točaka ekstrema: -3-1+1-2+0+3=-2.

Zadatak 7.

Na slici je prikazan graf derivacije funkcije definirane na intervalu. Odredite intervale porasta funkcije. U odgovoru navedite zbroj cjelobrojnih točaka uključenih u te intervale.

Riješenje:

Na slici su istaknuti intervali u kojima je derivacija funkcije nenegativna.

Na malom rastućem intervalu nema cjelobrojnih točaka, na rastućem intervalu postoje četiri cjelobrojne vrijednosti: , , i .

Njihov zbroj:

Zadatak 8.

Na slici je prikazan graf derivacije funkcije definirane na intervalu. Odredite intervale porasta funkcije. U odgovoru navedite duljinu najvećeg od njih.

Riješenje:

Na slici su bojom označeni svi intervali na kojima je derivacija pozitivna, što znači da sama funkcija raste na tim intervalima.

Duljina najvećeg od njih je 6.

Zadatak 9.

Na slici je prikazan graf derivacije funkcije definirane na intervalu. U kojoj točki segmenta poprima najveću vrijednost?

Riješenje:

Pogledajmo kako se graf ponaša na segmentu koji nas zanima samo znak izvedenice .

Predznak derivacije na je minus, jer je graf na ovom segmentu ispod osi.

U međuvremenu ( A,b), A x- je nasumično odabrana točka u zadanom intervalu. Dajmo argument x prirastΔx (pozitivan ili negativan).

Funkcija y =f(x) dobit će prirast Δu jednak:

Δy = f(x + Δx)-f(x).

Na infinitezimalnom Δh prirastΔy je također beskonačno malen.

Na primjer:

Razmotrimo rješavanje derivacije funkcije na primjeru tijela koje slobodno pada.

Kako je t 2 = t l + Δt, tada

.

Izračunavanjem granice nalazimo:

Oznaka t 1 uvedena je kako bi se naglasila konstantnost t pri računanju limita funkcije. Budući da je t 1 proizvoljna vremenska vrijednost, indeks 1 se može odbaciti; tada dobivamo:

Vidi se da je brzina v, poput načina s, Tamo je funkcija vrijeme. Vrsta funkcije v u potpunosti ovisi o vrsti funkcije s, dakle funkcija s kao da "proizvodi" funkciju v. Otuda naziv " izvodna funkcija».

Razmislite o drugom primjer.

Nađi vrijednost derivacije funkcije:

y = x 2 na x = 7.

Riješenje. Na x = 7 imamo y=7 2 = 49. Dajmo argument x prirast Δ x. Argument će postati jednak 7 + Δ x, a funkcija će primiti vrijednost (7 + Δ x) 2.