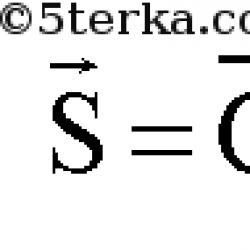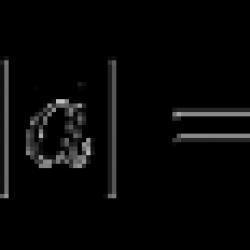Samolyotning boshlang'ich nuqtasidan masofasini hisoblang. Nuqtadan tekislikgacha bo'lgan masofa: ta'rif va topishga misollar. Nuqtadan tekislikgacha bo'lgan masofani topishga misollar
Shunday qilib, men ushbu sahifada biror narsa o'qidim (http://gamedeveloperjourney.blogspot.com/2009/04/point-plane-collision-detection.html)
D = - D3DXVec3Dot(&vP1, &vNormal);
bu erda vP1 - tekislikdagi nuqta va vNormal - tekislik uchun normal. Bu sizga dunyoning boshlanishidan masofani qanday berishiga qiziqaman, chunki natija har doim 0 bo'ladi. Bundan tashqari, tushunarli bo'lishim kerak (chunki men hali ham 2D tenglamaning D qismida biroz noaniqman), d 2D tenglamada tekislikning boshlanishigacha bo'lgan chiziqdan dunyoning boshigacha bo'lgan masofa?
matematika3 ta javob
6
Umuman olganda, p nuqta va tekislik orasidagi masofani formula yordamida hisoblash mumkin
Qayerda
va bu erda p0 - tekislikdagi nuqta.
Agar n birlik uzunligiga ega bo'lsa, u holda vektor va u o'rtasidagi nuqta mahsuloti vektorning Normalga proyeksiyasining (belgilangan) uzunligidir.
Siz xabar bergan formula p nuqtasi boshlang'ich bo'lgan maxsus holatdir. Ushbu holatda
Masofa = Bu tenglik texnik jihatdan noto'g'ri, chunki nuqta mahsuloti nuqtalar haqida emas, balki vektorlar haqida ... lekin hali ham son jihatdan o'zini tutadi. Aniq formulani yozish orqali siz buni olasiz (0 - p0.x)*n.x + (0 - p0.y)*n.y + (0 - p0.z)*n.z xuddi shunday - (p0.x*n.x + p0.y*n.y + p0.z*n.z)
Natija har doim ham nolga teng emas. Agar tekislik koordinatali nuqtadan o'tsa, natija nolga teng bo'ladi. (Mana, samolyot boshlang'ich nuqtadan o'tmaydi deb faraz qilaylik.) Asosan, sizga boshlang'ich nuqtadan tekislikning biron bir nuqtasiga chiziq beriladi. (Ya'ni sizda boshlang'ichdan vP1gacha vektor mavjud). Ushbu vektor bilan bog'liq muammo shundaki, u katta ehtimol bilan qiyshayib, samolyotning eng yaqin nuqtasiga emas, balki samolyotning uzoq joyiga yo'l oladi. Shunday qilib, agar siz faqat vP1 uzunligini olgan bo'lsangiz, siz juda ko'p masofaga erishasiz. Siz nima qilishingiz kerak bo'lsa, vP1 proyeksiyasini tekislikka perpendikulyar deb bilgan vektorga olishdir. Bu, albatta, vNormal. Shunday qilib, vP1 va vNormalning nuqta mahsulotini oling va uni vNormal uzunligiga bo'ling va javobingiz bor. (Agar ular sizga allaqachon katta bo'lgan vNormalni berish uchun etarlicha mehribon bo'lsa, unda ajratishning hojati yo'q.)
Ushbu muammoni Lagrange multiplikatorlari yordamida hal qilishingiz mumkin: Bilasizmi, samolyotdagi eng yaqin nuqta quyidagicha ko'rinishi kerak: C=p+v Bu erda c - eng yaqin nuqta va v - tekislik bo'ylab vektor (shuning uchun u n ga normalga ortogonal). Siz eng kichik norma (yoki kvadrat me'yor) bilan c ni topishga harakat qilyapsiz. Shunday qilib, v n ga ortogonal bo'lsa, nuqta (c, c) ni minimallashtirishga harakat qilyapsiz (shuning uchun nuqta (v, n) = 0). Shunday qilib, Lagrangianni o'rnating: L = nuqta(c,c) + lambda * (nuqta(v,n)) L = nuqta(p+v,p+v) + lambda * (nuqta(v,n)) L = nuqta(p,p) + 2*nuqta(p,v) + nuqta(v,v) * lambda * (nuqta(v,n)) Va hosil qilish uchun v ga nisbatan hosila oling (va 0 ga qo'ying): 2 * p + 2 * v + lambda * n = 0 Yuqoridagi tenglamadagi lambdani nuqta bilan echishingiz mumkin, buning uchun ikkala tomonni n ga chiqaring. 2 * nuqta(p,n) + 2 * nuqta(v,n) + lambda * nuqta(n,n) = 0 2 * nuqta(p,n) + lambda = 0 lambda = - 2 * nuqta(p,n) )) Yana e'tibor bering, nuqta(n,n) = 1 va nuqta(v,n) = 0 (chunki v tekislikda va n unga ortogonaldir). Substitute lambda keyin quyidagini olish uchun qaytib keladi: 2 * p + 2 * v - 2 * nuqta (p, n) * n = 0 va olish uchun v uchun hal qiling: V = nuqta (p, n) * n - p Keyin uni c = p + v ga qayta ulang: C = nuqta (p, n) * n Bu vektorning uzunligi |dot(p,n)| , va ishora nuqta koordinata boshidan normal vektor yo‘nalishida yoki koordinata boshidan teskari yo‘nalishda ekanligini bildiradi. Menda ax+by+cz=d tekislik tenglamasi bor deylik, tekislikdan boshlanish nuqtasigacha bo'lgan eng qisqa masofani qanday topish mumkin? Men bu postdan orqaga ketyapman. Ushbu postda ular ... Aytaylik, Kinect (0,0,0) da o'tirib, +Z yo'nalishiga qaraydi. Faraz qilaylik, (1, 1, 1) da ob'ekt bor va Kinect chuqurligi tasviridagi piksellardan biri bu ob'ektni ifodalaydi.... Men nuqtalardan ikkita koordinatali dataframe tomonidan berilgan barcha nuqtalargacha bo'lgan masofani tenglashtirmoqchiman. Menda barcha fikrlar bor: x y 1 0,0 0,0 2 -4,0 -2,8 3 -7,0 -6,5 4 -9,0 -11,1... Asosiy ma'lumot Bu erda ko'rsatilgandek sferik koordinatalar tizimini ko'rib chiqing: Koordinatalar tizimi http://www.shokhirev.com/nikolai/projects/global/image013.gif Muayyan nuqta uchun biz... Menda 3D sahna va gluPerspective bilan belgilangan kamera bor. Menda qat'iy FOV bor va men har qanday geometriyaning kameradan minimal masofasini bilaman (bu birinchi shaxs ko'rinishi, shuning uchun ... Menda A, B, C nuqtalari va kosmosdagi nuqta (P) bo'lgan uchburchak bor. Bir nuqtadan tekislikgacha bo'lgan masofani qanday aniqlash mumkin? Men P dan samolyotgacha bo'lgan masofani hisoblashim kerak, garchi mening ... Men CGPoint (qizil to'rtburchak) ni boshqa CGPoint (ko'k to'rtburchak) atrofida aylantirmoqchiman, lekin u boshlang'ichdan (ko'k to'rtburchak) masofani o'zgartiradi ... burchakda 270 ni berganimda, u yaratadi ... Men X, Y, Z tekislik markazini, Kartezian koordinatalarini olishim kerak. Menda tekislikning Normali va uning markaz nuqtasidan boshlanish nuqtasigacha bo'lgan masofa bor. Men nuqta(lar)ni istalgan joyga joylashtirishim mumkin va... Berilgan: nuqta (x1, y1, z1) yo'nalish vektori (a1, b1, c1) tekislik ax + by + cz + d = 0 Ushbu vektor bo'ylab D nuqtadan tekislikgacha bo'lgan masofani qanday topish mumkin? rahmat Menda aylanish matritsasi R va jahon koordinata tizimiga nisbatan T tarjimasi bilan belgilangan kamera koordinatalari tizimi mavjud. Tekislik kamera koordinatalarida oddiy N va undagi P nuqta bilan aniqlanadi.... Ushbu maqolada biz nuqtadan tekislikgacha bo'lgan masofani aniqlaymiz va uch o'lchovli fazoda berilgan nuqtadan berilgan tekislikgacha bo'lgan masofani topishga imkon beruvchi koordinata usulini tahlil qilamiz. Nazariya taqdimotidan so'ng biz bir nechta tipik misollar va muammolarning echimlarini batafsil tahlil qilamiz. Sahifani navigatsiya qilish. Nuqtadan tekislikgacha bo'lgan masofa orqali aniqlanadi, ulardan biri berilgan nuqta, ikkinchisi esa berilgan nuqtaning berilgan tekislikka proyeksiyasi. Uch o'lchamli fazoda M 1 nuqta va tekislik berilgan bo'lsin. M 1 nuqta orqali tekislikka perpendikulyar a to'g'ri chiziq o'tkazamiz. a to g ri chiziq va tekislikning kesishish nuqtasini H 1 deb belgilaymiz. M 1 H 1 segmenti deyiladi perpendikulyar, M 1 nuqtasidan tekislikka tushirildi va H 1 nuqtasi - perpendikulyarning asosi. Ta'rif. berilgan nuqtadan berilgan tekislikka chizilgan perpendikulyarning asosigacha bo'lgan masofa. Nuqtadan tekislikgacha bo'lgan masofani aniqlash quyidagi shaklda ko'proq uchraydi. Ta'rif.
Nuqtadan tekislikgacha bo'lgan masofa- berilgan nuqtadan berilgan tekislikka tushirilgan perpendikulyar uzunligi. Shuni ta'kidlash kerakki, M 1 nuqtadan tekislikgacha bo'lgan masofa, shu tarzda aniqlangan, berilgan M 1 nuqtadan tekislikning istalgan nuqtasigacha bo'lgan masofalarning eng kichiki hisoblanadi. Haqiqatan ham, H 2 nuqtasi tekislikda yotsin va H 1 nuqtasidan farqli bo'lsin. Shubhasiz, M 2 H 1 H 2 uchburchak to'rtburchaklar, unda M 1 H 1 oyoq, M 1 H 2 esa gipotenuzadir, shuning uchun Yechishning qaysidir bosqichidagi ba'zi geometrik masalalar nuqtadan tekislikgacha bo'lgan masofani topishni talab qiladi. Buning uchun usul manba ma'lumotlariga qarab tanlanadi. Odatda, natijada Pifagor teoremasi yoki uchburchaklarning tenglik va o'xshashlik belgilaridan foydalanish olinadi. Agar siz uch o'lchamli fazoda berilgan nuqtadan tekislikgacha bo'lgan masofani topishingiz kerak bo'lsa, u holda koordinata usuli yordamga keladi. Maqolaning ushbu bandida biz uni faqat tahlil qilamiz. Birinchidan, biz muammoning shartini shakllantiramiz. To'rtburchaklar koordinatalar tizimida Oxyz uch o'lchovli fazoda nuqta berilgan Keling, ushbu muammoni hal qilishning ikkita usulini ko'rib chiqaylik. Nuqtadan tekislikgacha bo'lgan masofani hisoblash imkonini beruvchi birinchi usul H 1 nuqtaning koordinatalarini - M 1 nuqtadan tekislikka tushirilgan perpendikulyar asosini topishga, keyin esa masofani hisoblashga asoslangan. M 1 va H 1 nuqtalari o'rtasida. Berilgan nuqtadan berilgan tekislikgacha bo'lgan masofani topishning ikkinchi usuli berilgan tekislik uchun normal tenglamadan foydalanishni o'z ichiga oladi. M 1 nuqtadan tekislikka chizilgan perpendikulyarning asosi H 1 bo'lsin. Agar biz H 1 nuqtasining koordinatalarini aniqlasak, u holda M 1 nuqtadan tekislikka kerakli masofani nuqtalar orasidagi masofa sifatida hisoblash mumkin. Shunday qilib, nuqtadan masofani topish algoritmi Bizga Oxyz to'rtburchaklar koordinatalar sistemasida tekislik berilganligi sababli tekislikning normal tenglamasini ko'rinishda olishimiz mumkin. Keyin nuqtadan masofa Teorema. Oxyz to'rtburchak koordinatalar tizimi uch o'lchamli fazoda, nuqtada o'rnatilgan bo'lsin Isbot. Bu teoremaning isboti "Nuqtadan chiziqgacha bo'lgan masofani topish" bo'limida berilgan shunga o'xshash teoremaning isbotiga mutlaqo o'xshaydi. M 1 nuqtadan tekislikgacha bo'lgan masofa M 1 sonli proyeksiya va koordinata boshidan tekislikgacha bo'lgan masofa orasidagi farq moduliga teng ekanligini ko'rsatish oson, ya'ni.
Shunday qilib, nuqtadan masofa Misol. Nuqtadan masofani toping Yechim. Birinchi yo'l. Masalaning shartida bizga ko'rinish tekisligining umumiy tenglamasi berilgan, undan ko'rinib turibdiki. Keling, chiziqning kesishish nuqtasining koordinatalarini topishni boshlaylik Endi tenglamalar sistemasini yechamiz Shunday qilib, . Berilgan nuqtadan berilgan tekislikka kerakli masofani nuqtalar orasidagi masofa sifatida hisoblash qoladi Ikkinchi yechim. Berilgan tekislikning normal tenglamasini olaylik. Buning uchun tekislikning umumiy tenglamasini normal holatga keltirishimiz kerak. Normallashtiruvchi omilni aniqlagandan so'ng Ushbu maqola nuqtadan tekislikgacha bo'lgan masofani aniqlash haqida gapiradi. uch o‘lchamli fazoda berilgan nuqtadan masofani topish imkonini beradigan koordinata usulini tahlil qilaylik. Birlashtirish uchun bir nechta topshiriqlarning misollarini ko'rib chiqing. Nuqtadan tekislikgacha bo'lgan masofa nuqtadan nuqtagacha bo'lgan ma'lum masofa yordamida topiladi, bu erda ulardan biri berilgan, ikkinchisi esa berilgan tekislikka proyeksiyadir. Fazoda ch tekislikli M 1 nuqta berilganda, nuqta orqali tekislikka perpendikulyar to'g'ri chiziq o'tkazish mumkin. H 1 - ularning kesishishining umumiy nuqtasi. Bu yerdan biz M 1 H 1 segmenti perpendikulyar ekanligini tushunamiz, u M 1 nuqtadan ch tekislikka o'tkazilgan, bu erda H 1 nuqta perpendikulyar asosdir. Ta'rif 1 Ular berilgan nuqtadan berilgan tekislikka o'tkazilgan perpendikulyar asosgacha bo'lgan masofani chaqiradilar. Ta'rif turli formulalarda yozilishi mumkin. Ta'rif 2 Nuqtadan tekislikgacha bo'lgan masofa berilgan nuqtadan berilgan tekislikka chizilgan perpendikulyar uzunligi deyiladi. M 1 nuqtadan ch tekislikgacha bo'lgan masofa quyidagicha aniqlanadi: M 1 nuqtadan ch tekislikgacha bo'lgan masofa berilgan nuqtadan tekislikning istalgan nuqtasigacha bo'lgan eng kichik bo'ladi. Agar H 2 nuqta ch tekisligida joylashgan bo'lsa va H 2 nuqtaga teng bo'lmasa, biz M 2 H 1 H 2 ko'rinishdagi to'g'ri burchakli uchburchakni olamiz.
, bu to'rtburchaklar, bu erda M 2 H 1, M 2 H 2 oyog'i mavjud
- gipotenuza. Demak, bu M 1 H 1 ekanligini bildiradi< M 1 H 2 . Тогда отрезок М 2 H 1
qiya deb hisoblanadi, u M 1 nuqtadan ch tekislikka tortiladi. Bizda ma'lum nuqtadan tekislikka o'tkazilgan perpendikulyar nuqtadan berilgan tekislikka o'tkazilgan qiyalikdan kichikroq ekanligi bor. Quyidagi rasmda ushbu holatni ko'rib chiqing. Bir qator geometrik masalalar mavjud, ularning yechimlari nuqtadan tekislikgacha bo'lgan masofani o'z ichiga olishi kerak. Buni aniqlash usullari boshqacha bo'lishi mumkin. Yechish uchun Pifagor teoremasi yoki uchburchaklarning o'xshashligidan foydalaning. Shartga ko'ra, uch o'lchovli fazoning to'rtburchaklar koordinata tizimida berilgan nuqtadan tekislikgacha bo'lgan masofani hisoblash kerak bo'lganda, ular koordinata usuli yordamida hal qilishadi. Ushbu paragraf ushbu usul bilan bog'liq. Masalaning shartiga ko‘ra, uch o‘lchamli fazoda ch tekislik bilan koordinatalari M 1 (x 1, y 1, z 1) bo‘lgan nuqta berilgan bo‘lsa, M 1 dan masofani aniqlash kerak. samolyot ch. Yechish uchun bir nechta echimlar qo'llaniladi. Birinchi yo'l
Bu usul M 1 nuqtadan ch tekislikka perpendikulyar asos bo'lgan H 1 nuqtaning koordinatalari yordamida nuqtadan tekislikgacha bo'lgan masofani topishga asoslangan. Keyinchalik, M 1 va H 1 orasidagi masofani hisoblashingiz kerak. Masalani ikkinchi usulda yechish uchun berilgan tekislikning normal tenglamasidan foydalaniladi. Ikkinchi yo'l
Shartga ko'ra, H 1 perpendikulyar asos bo'lib, u M 1 nuqtadan ch tekisligiga tushirildi. Keyin H 1 nuqtaning koordinatalarini (x 2, y 2, z 2) aniqlaymiz. M 1 dan ch tekisligiga kerakli masofa M 1 H 1 \u003d (x 2 - x 1) 2 + (y 2 - y 1) 2 + (z 2 - z 1) 2 formulasi bo'yicha topiladi, bu erda M 1 (x 1, y 1, z 1) va H 1 (x 2, y 2, z 2) . Yechish uchun siz H 1 nuqtasining koordinatalarini bilishingiz kerak. Bizda H 1 ch tekislikning ch tekislikka perpendikulyar joylashgan M 1 nuqtasidan o‘tuvchi a to‘g‘ri chiziq bilan kesishish nuqtasi ekanligiga egamiz. Bundan kelib chiqadiki, berilgan tekislikka perpendikulyar berilgan nuqtadan o'tuvchi to'g'ri chiziq tenglamasini shakllantirish kerak. Shunda biz H 1 nuqtaning koordinatalarini aniqlashimiz mumkin. Chiziq va tekislikning kesishish nuqtasining koordinatalarini hisoblash kerak. Koordinatalari M 1 (x 1, y 1, z 1) nuqtadan ch tekislikgacha bo‘lgan masofani topish algoritmi: Ta'rif 3 Uchinchi yo'l
Berilgan O x y z to rtburchak koordinatalar sistemasida ch tekislik mavjud bo lsa, u holda cos a · x + cos b · y + cos g · z - p = 0 ko rinishdagi tekislikning normal tenglamasini olamiz. Bu yerdan M 1 (x 1 , y 1 , z 1) nuqta bilan M 1 H 1 masofa ch tekislikka tortilganligini M 1 H 1 = cos a x + cos b y + cos formulasi bilan hisoblab chiqamiz. g z-p. Bu formula to'g'ri, chunki u teorema tufayli o'rnatiladi. Teorema Agar M 1 (x 1, y 1, z 1) nuqta uch o‘lchamli fazoda berilgan bo‘lsa, cos a x + cos b y + cos g z - p = 0 ko‘rinishdagi ch tekisligining normal tenglamasiga ega bo‘lsa, u holda nuqtadan M 1 H 1 tekislikgacha bo'lgan masofani hisoblash M 1 H 1 = cos a · x + cos b · y + cos g · z - p formulasidan kelib chiqadi, chunki x = x 1 , y = y 1 , z = z 1. Isbot Teoremaning isboti nuqtadan chiziqgacha bo'lgan masofani topishga qisqartiriladi. Bu erdan biz M 1 dan ch tekislikgacha bo'lgan masofa M 1 radius vektorining son proyeksiyasining koordinata boshidan ch tekislikgacha bo'lgan masofasi orasidagi farqning moduli ekanligini tushunamiz. Keyin M 1 H 1 = n p n → O M → - p ifodasini olamiz. ch tekislikning normal vektori n → = cos a, cos b, cos g ko‘rinishga ega bo‘lib, uzunligi bir ga teng, n p n → O M → O M → = (x 1, y 1) vektorning sonli proyeksiyasi. , z 1) n → vektor bilan aniqlangan yo'nalishda. Skayar vektorlarni hisoblash formulasini qo'llaymiz. Keyin n →, O M → = n → n p n → O M → = 1 n p n → O M → = n p n → O M → ko‘rinishdagi vektorni topish ifodasini olamiz, chunki n → = cos a, cos b, cos g z va O M → = (x 1 , y 1 , z 1) . Belgilanishning koordinata shakli n →, O M → = cos a x 1 + cos b y 1 + cos g z 1, keyin M 1 H 1 = n p n → O M → - p = cos a x 1 + cos ko‘rinishini oladi. b · y 1 + cos g · z 1 - p. Teorema isbotlangan. Bu yerdan M 1 (x 1, y 1, z 1) nuqtadan ch tekislikgacha bo‘lgan masofani tekislikning normal tenglamasining chap tomoniga cos a x + cos b y + cos qo‘yish yo‘li bilan hisoblanadi. g z - p = 0 o'rniga x, y, z koordinatalari x 1 , y 1 va z1 olingan qiymatning mutlaq qiymatini olib, M 1 nuqtasiga tegishli. Koordinatalari bo'lgan nuqtadan berilgan tekislikgacha bo'lgan masofani topish misollarini ko'rib chiqing. 1-misol Koordinatalari M 1 (5 , - 3 , 10) nuqtadan 2 x - y + 5 z - 3 = 0 tekislikgacha bo'lgan masofani hisoblang. Yechim
Keling, muammoni ikki yo'l bilan hal qilaylik. Birinchi usul a chiziqning yo'nalish vektorini hisoblashdan boshlanadi. Shartga ko'ra, berilgan 2 x - y + 5 z - 3 = 0 tenglama umumiy tekislik tenglamasi, n → = (2 , - 1 , 5) esa berilgan tekislikning normal vektori ekanligini bilib olamiz. Berilgan tekislikka perpendikulyar bo'lgan a to'g'ri chiziq uchun yo'naltiruvchi vektor sifatida ishlatiladi. M 1 (5, - 3, 10) dan o'tuvchi fazodagi to'g'ri chiziqning kanonik tenglamasini koordinatalari 2, - 1, 5 bo'lgan yo'nalish vektori bilan yozish kerak. Tenglama x - 5 2 = y - (- 3) - 1 = z - 10 5 ⇔ x - 5 2 = y + 3 - 1 = z - 10 5 ko'rinishida bo'ladi. Kesishish nuqtalari aniqlanishi kerak. Buning uchun tenglamalarni kanonikdan ikkita kesishuvchi chiziq tenglamalariga o'tish uchun tizimga yumshoq tarzda birlashtiring. Bu nuqtani H 1 deb olaylik. Biz buni tushunamiz x - 5 2 = y + 3 - 1 = z - 10 5 ⇔ - 1 (x - 5) = 2 (y + 3) 5 (x - 5) = 2 (z - 10) 5 ( y + 3) = - 1 (z - 10) ⇔ ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 Keyin tizimni yoqishingiz kerak x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 2 x - y + 5 z - 3 = 0 ⇔ x + 2 y = 1 5 x - 2 z = 5 2 x - y + 5 z = 3 Keling, Gauss bo'yicha tizimni yechish qoidasiga murojaat qilaylik: 1 2 0 - 1 5 0 - 2 5 2 - 1 5 3 ~ 1 2 0 - 1 0 - 10 - 2 10 0 - 5 5 5 ~ 1 2 0 - 1 0 - 10 - 2 10 0 0 6 0 ⇒ ⇒ z = 0 6 = 0, y = - 1 10 10 + 2 z = - 1, x = - 1 - 2 y = 1 Biz H 1 (1, - 1, 0) ni olamiz. Berilgan nuqtadan tekislikgacha bo'lgan masofani hisoblaymiz. M 1 (5, - 3, 10) va H 1 (1, - 1, 0) nuqtalarini olamiz va olamiz. M 1 H 1 \u003d (1 - 5) 2 + (- 1 - (- 3)) 2 + (0 - 10) 2 \u003d 2 30 Ikkinchi yechim avval berilgan 2 x - y + 5 z - 3 = 0 tenglamani normal ko'rinishga keltirishdir. Biz normallashtiruvchi omilni aniqlaymiz va 1 2 2 + (- 1) 2 + 5 2 = 1 30 ni olamiz. Bu yerdan 2 30 · x - 1 30 · y + 5 30 · z - 3 30 = 0 tekislikning tenglamasini olamiz. Tenglamaning chap tomoni x \u003d 5, y \u003d - 3, z \u003d 10 ni almashtirish orqali hisoblanadi va siz M 1 (5, - 3, 10) dan 2 x - y + gacha bo'lgan masofani olishingiz kerak. 5 z - 3 = 0 modul. Biz ifodani olamiz: M 1 H 1 \u003d 2 30 5 - 1 30 - 3 + 5 30 10 - 3 30 \u003d 60 30 \u003d 2 30 Javob: 2 30 . ch tekisligi tekislikni ko'rsatish uchun kesma usullarining usullaridan biri bilan ko'rsatilganda, siz birinchi navbatda ch tekisligining tenglamasini olishingiz va istalgan usul yordamida kerakli masofani hisoblashingiz kerak. 2-misol Koordinatalari M 1 (5 , - 3 , 10) , A (0 , 2 , 1) , B (2 , 6 , 1) , C (4 , 0 , - 1) boʻlgan nuqtalar uch oʻlchamli fazoda oʻrnatiladi. M 1 dan A B C tekislikgacha bo'lgan masofani hisoblang. Yechim
Avval M 1 (5, - 3, 10) , A (0, 2, 1) , B (2 , 6 , 1) , C ( koordinatalari bilan berilgan uch nuqtadan oʻtuvchi tekislik tenglamasini yozishingiz kerak. 4 , 0 , - 1) . x - 0 y - 2 z - 1 2 - 0 6 - 2 1 - 1 4 - 0 0 - 2 - 1 - 1 = 0 ⇔ x y - 2 z - 1 2 4 0 4 - 2 - 2 = 0 ⇔ ⇔ - 8x + 4y - 20z + 12 = 0 ⇔ 2x - y + 5z - 3 = 0 Bundan kelib chiqadiki, muammo avvalgisiga o'xshash echimga ega. Demak, M 1 nuqtadan A B C tekislikgacha bo'lgan masofa 2 30 ga teng. Javob: 2 30 . Tekislikning berilgan nuqtasidan yoki ular parallel boʻlgan tekislikgacha boʻlgan masofani topish M 1 H 1 = cos a · x 1 + cos b · y 1 + cos g · z 1 - p formulasini qoʻllash orqali qulayroqdir. . Bu yerdan biz tekisliklarning normal tenglamalari bir necha bosqichda olinadi. 3-misol M 1 (- 3 , 2 , - 7) koordinatali berilgan nuqtadan O x y z koordinata tekisligiga va 2 y - 5 = 0 tenglama bilan berilgan tekislikka masofani toping. Yechim
O y z koordinata tekisligi x = 0 ko‘rinishdagi tenglamaga mos keladi. O y z tekisligi uchun bu normal holat. Shuning uchun ifodaning chap tomoniga x \u003d - 3 qiymatlarini qo'yish va M 1 (- 3, 2, - 7) koordinatali nuqtadan tekislikgacha bo'lgan masofaning mutlaq qiymatini olish kerak. . Biz - 3 = 3 ga teng qiymatni olamiz. Transformatsiyadan so'ng 2 y - 5 = 0 tekislikning normal tenglamasi y - 5 2 = 0 ko'rinishini oladi. Keyin koordinatalari M 1 (- 3 , 2 , - 7) nuqtadan 2 y - 5 = 0 tekislikkacha kerakli masofani topishingiz mumkin. O'rniga qo'yish va hisoblash, biz 2 - 5 2 = 5 2 - 2 ni olamiz. Javob: M 1 (- 3, 2, - 7) dan O y z gacha bo'lgan kerakli masofa 3 ga, 2 y - 5 = 0 gacha esa 5 2 - 2 qiymatiga ega. Agar siz matnda xatolikni sezsangiz, uni belgilab, Ctrl+Enter tugmalarini bosing
2
1
tekislik tenglamasidan foydalanib, tekislikdan boshlanish nuqtasigacha bo'lgan eng qisqa masofa
Kinect chuqurligi tasviri boshlang'ichgacha bo'lgan masofani yoki XY tekisligigacha bo'lgan masofani ifodalaydimi?
Koordinatalar kelib chiqishidan fazodagi nuqtagacha bo'lgan masofa
sferik koordinatalar - tekislikgacha bo'lgan masofa
Perspektiv proyeksiya uchun yaqin klip tekislik masofasini metodik ravishda qanday tanlash mumkin?
3D da nuqtadan tekislikgacha bo'lgan masofani qanday olish mumkin?
CG nuqtasini aylantirish boshlang'ichdan masofani o'zgartiradi
Samolyot markazi X, Y, Z, Dekart koordinatalarini oling
nuqtadan ma'lum bir yo'nalishdagi tekislikgacha bo'lgan masofa
Tekislikni boshqa koordinatalar tizimiga aylantirish Nuqtadan tekislikgacha bo'lgan masofa ta'rifdir.
. Aytgancha, M 1 H 2 segmenti deyiladi qiyshiq M 1 nuqtadan tekislikka tortilgan. Demak, berilgan nuqtadan berilgan tekislikka tushirilgan perpendikulyar har doim bir xil nuqtadan berilgan tekislikka tortilgan qiyalikdan kichikdir.
Nuqtadan tekislikgacha bo'lgan masofa - nazariya, misollar, echimlar.
, tekislik va M 1 nuqtadan tekislikgacha bo'lgan masofani topish talab qilinadi.Nuqtadan masofani hisoblashning birinchi usuli
samolyotga.Va 
formula bo'yicha. Shunday qilib, H 1 nuqtasining koordinatalarini topish qoladi.samolyotgacha Keyingisi:Ikkinchi usul, nuqtadan masofani topish uchun mos keladi
samolyotga.tekislikka formula bilan hisoblanadi. Nuqtadan tekislikgacha bo'lgan masofani topish uchun ushbu formulaning haqiqiyligi quyidagi teorema bilan belgilanadi.va shakl tekisligining normal tenglamasi. M 1 nuqtadan tekislikgacha bo'lgan masofa tekislikning normal tenglamasining chap tomonidagi ifoda qiymatining mutlaq qiymatiga teng bo'lib, da hisoblangan, ya'ni.
, Qayerda 
- tekislikning normal vektori birga teng, - 
vektor tomonidan aniqlangan yo'nalishga.Va ta'rifi bo'yicha, lekin koordinatali shaklda. Shuning uchun va isbotlash uchun talab qilinganidek.tekislikka M 1 nuqtaning x, y va z o'rniga x 1, y 1 va z 1 koordinatalarini tekislikning normal tenglamasining chap tomoniga qo'yish va olingan qiymatning mutlaq qiymatini olish orqali hisoblash mumkin. .Nuqtadan masofani topishga misollar
samolyotga.
samolyotga.
bu tekislikning normal vektori. Bu vektorni berilgan tekislikka perpendikulyar a to'g'ri chiziqning yo'naltiruvchi vektori sifatida olish mumkin. Keyin nuqtadan o'tuvchi to'g'ri chiziqning kanonik tenglamalarini fazoda yozishimiz mumkin va koordinatalari bo'lgan yo'nalish vektoriga ega, ular o'xshaydi.
va samolyotlar. Uni H 1 deb belgilaymiz. Buning uchun birinchi navbatda to'g'ri chiziqning kanonik tenglamalaridan ikkita kesishuvchi tekislik tenglamalariga o'tishni amalga oshiramiz: 
(agar kerak bo'lsa, maqolaga qarang). Biz foydalanamiz: 
Va:
.
, tekislikning normal tenglamasini olamiz 
. Olingan tenglamaning chap tomonining qiymatini hisoblash qoladi 
va olingan qiymat modulini oling - bu nuqtadan kerakli masofani beradi samolyotga: 
Nuqtadan tekislikgacha bo'lgan masofa - nazariya, misollar, echimlar
