Trigonometrik funksiyalarning integrallari.
Yechim misollari

Bu darsda trigonometrik funksiyalarning integrallarini ko'rib chiqamiz, ya'ni integrallarning to'ldirilishi har xil birikmalarda sinuslar, kosinuslar, tangenslar va kotangentlar bo'ladi. Barcha misollar batafsil tahlil qilinadi, hatto choynak uchun ham tushunarli va tushunarli bo'ladi.

Trigonometrik funktsiyalarning integrallarini muvaffaqiyatli o'rganish uchun siz eng oddiy integrallarni yaxshi bilishingiz, shuningdek, ba'zi integratsiya usullarini o'zlashtirishingiz kerak. Ushbu materiallar bilan ma'ruzalarda tanishishingiz mumkin. Noaniq integral. Yechim misollari Va .

Va endi bizga kerak: Integrallar jadvali, Hosiliy jadval Va Trigonometrik formulalar bo'yicha ma'lumotnoma. Barcha qo'llanmalarni sahifada topish mumkin Matematik formulalar va jadvallar. Men hamma narsani chop etishni tavsiya qilaman. Men ayniqsa trigonometrik formulalarga e'tibor qarataman, ular sizning ko'zingiz oldida bo'lishi kerak- busiz ish samaradorligi sezilarli darajada pasayadi.

Lekin birinchi navbatda, ushbu maqolada qaysi integrallar haqida Yo'q. Bu erda shaklning integrallari yo'q, - kosinus, sinus ba'zi bir polinomga ko'paytiriladi (kamroq, tangens yoki kotangensli narsa). Bunday integrallar qismlar bo'yicha integrallanadi va usulni o'rganish uchun qismlar bo'yicha integratsiya darsiga tashrif buyuring. Yechimlarga misollar.Shuningdek, "arklar" bilan integrallar yo'q - yoy tangensi, yoy sinusi va boshqalar, ular ham ko'pincha qismlar bilan integrallanadi.

Trigonometrik funktsiyalarning integrallarini topishda bir qator usullar qo'llaniladi:

(4) Jadval formulasidan foydalaning , yagona farq shundaki, "x" o'rniga biz murakkab ifodaga egamiz.

2-misol

3-misol

Noaniq integralni toping.

Turnir jadvalida g'arq bo'lganlar uchun janr klassikasi. Siz sezgan bo'lsangiz kerak, integrallar jadvalida tangens va kotangensning integrali yo'q, ammo shunga qaramay, bunday integrallarni topish mumkin.

(1) Biz trigonometrik formuladan foydalanamiz

(2) Funksiyani differentsial belgisi ostida keltiramiz.

(3) Jadvalli integraldan foydalaning .

4-misol

Noaniq integralni toping.

Bu o'z-o'zidan hal qilish uchun misol, to'liq yechim va javob dars oxirida.

5-misol

Noaniq integralni toping.

Bizning darajalarimiz asta-sekin oshadi =).
Birinchi yechim:

(1) Biz formuladan foydalanamiz

(2) Biz asosiy trigonometrik identifikatsiyadan foydalanamiz , shundan kelib chiqadiki .

(3) Numeratorni maxraj a'zosiga bo'ling.

(4) Noaniq integralning chiziqlilik xossasidan foydalanamiz.

(5) Biz jadval yordamida integratsiya qilamiz.

6-misol

Noaniq integralni toping.

Bu o'z-o'zidan hal qilish uchun misol, to'liq yechim va javob dars oxirida.

Bundan tashqari, yuqori darajalarda bo'lgan tangens va kotangentlarning integrallari mavjud. Darsda kubdagi tangensning integrali ko'rib chiqiladi Samolyot figurasining maydonini qanday hisoblash mumkin? To'rtinchi va beshinchi darajalardagi tangens (kotangens) integrallarini sahifada olish mumkin. Kompleks integrallar.

Integrand darajasini pasaytirish

Ushbu usul integrallar sinuslar va kosinuslar bilan to'ldirilganda ishlaydi hatto daraja. Darajani kamaytirish uchun trigonometrik formulalar qo'llaniladi , va , va oxirgi formula ko'proq qarama-qarshi yo'nalishda ishlatiladi: .

7-misol

Noaniq integralni toping.

Yechim:

Aslida, bu erda hech qanday yangilik yo'q, faqat biz formulani qo'llaganmiz (integrand darajasini pasaytirish). E'tibor bering, men yechimni qisqartirdim. Tajriba orttirilganligi sababli integralini og'zaki topish mumkin, bu vaqtni tejaydi va topshiriqlarni bajarishda juda maqbuldir. Bunday holda, qoidani yozmaslik tavsiya etiladi , avval og'zaki 1 ning integralini olamiz, keyin - ning.

8-misol

Noaniq integralni toping.

Bu o'z-o'zidan hal qilish uchun misol, to'liq yechim va javob dars oxirida.

Bu va'da qilingan darajani oshirish:

9-misol

Noaniq integralni toping.

Avval yechim, keyin sharhlar:

(1) Formulani qo'llash uchun integralni tayyorlang .

(2) Biz formulani amalda qo'llaymiz.

(3) Biz maxrajni kvadratga aylantiramiz va doimiyni integral belgisidan chiqaramiz. Buni biroz boshqacha qilish mumkin edi, lekin menimcha, bu qulayroq.

(4) Biz formuladan foydalanamiz

(5) Uchinchi muddatda biz yana darajani pasaytiramiz, lekin formuladan foydalanamiz .

(6) Biz shunga o'xshash shartlarni beramiz (bu erda men atamani atamaga ajratdim va qo'shimcha qildim).

(7) Biz aslida integral, chiziqlilik qoidasini olamiz funksiyani differensial belgisi ostiga keltirish usuli esa og‘zaki bajariladi.

(8) Javobni taraymiz.

! Noaniq integralda javob ko'pincha bir necha usulda yozilishi mumkin.

Ko'rib chiqilgan misolda yakuniy javob boshqacha yozilishi mumkin - qavslarni oching va hatto ifodani birlashtirishdan oldin buni bajaring, ya'ni misolning quyidagi oxiri juda maqbuldir:

Ehtimol, bu variant yanada qulayroqdir, men buni o'zim qaror qilganimdek tushuntirdim). Mustaqil yechim uchun yana bir tipik misol:

10-misol

Noaniq integralni toping.

Ushbu misol ikki yo'l bilan hal qilinadi va siz olishingiz mumkin ikkita butunlay boshqacha javoblar.(aniqrog'i, ular butunlay boshqacha ko'rinadi, lekin matematik nuqtai nazardan ular ekvivalent bo'ladi). Ehtimol, siz eng oqilona yo'lni ko'rmaysiz va boshqa trigonometrik formulalardan foydalangan holda qavslarni ochish bilan azoblanasiz. Eng samarali yechim dars oxirida beriladi.

Paragrafni umumlashtirib, biz shaklning har qanday integrali degan xulosaga kelamiz , qaerda va - hatto soni, integral darajasini pasaytirish yo'li bilan yechiladi.
Amalda men 8 va 10 darajali integrallarni uchratdim, men ularning dahshatli gemorroylarini darajani bir necha marta pasaytirish orqali hal qilishim kerak edi, natijada uzoq, uzoq javoblar paydo bo'ldi.

O'zgaruvchan almashtirish usuli

Maqolada aytib o'tilganidek Noaniq integralda o'zgaruvchilarni o'zgartirish usuli, almashtirish usulini qo'llashning asosiy sharti - bu integralda ba'zi funksiya va uning hosilasi mavjud:
(funktsiyalar mahsulotda bo'lishi shart emas)

11-misol

Noaniq integralni toping.

Biz hosilalar jadvaliga qaraymiz va formulalarga e'tibor beramiz, , ya'ni integramizda funktsiya va uning hosilasi mavjud. Biroq, biz farqlashda kosinus va sinus o'zaro bir-biriga aylanishini ko'ramiz va savol tug'iladi: o'zgaruvchini qanday o'zgartirish kerak va nimani belgilash kerak - sinus yoki kosinus ?! Savolni ilmiy poke usuli bilan hal qilish mumkin: agar biz almashtirishni noto'g'ri bajarsak, unda hech qanday yaxshi narsa bo'lmaydi.

Umumiy ko'rsatma: shunga o'xshash holatlarda siz maxrajdagi funktsiyani belgilashingiz kerak.

Biz yechimni to'xtatamiz va almashtirishni amalga oshiramiz

Denominatorda bizda hamma narsa yaxshi, hamma narsa faqat ga bog'liq, endi u nimaga aylanishini bilish qoladi.
Buning uchun biz differentsialni topamiz:

Yoki qisqasi:
Olingan tenglikdan, mutanosiblik qoidasiga ko'ra, bizga kerak bo'lgan ifodani ifodalaymiz:

Shunday qilib:

Endi butun integral faqat unga bog'liq va biz yechimni davom ettirishimiz mumkin

Tayyor. Sizga shuni eslatib o'tamanki, almashtirishning maqsadi integralni soddalashtirishdir, bu holda hammasi stol ustidagi quvvat funktsiyasini birlashtirishga to'g'ri keladi.

Men bu misolni bu qadar batafsil chizganim tasodif emas, bu dars materiallarini takrorlash va mustahkamlash uchun qilingan. Noaniq integralda o'zgaruvchilarni o'zgartirish usuli.

Va endi mustaqil yechim uchun ikkita misol:

12-misol

Noaniq integralni toping.

13-misol

Noaniq integralni toping.

Dars oxirida to'liq echimlar va javoblar.

14-misol

Noaniq integralni toping.

Bu erda yana, integrandda kosinusli sinus (hosilasi bilan funktsiya), lekin mahsulotda allaqachon mavjud va dilemma paydo bo'ladi - sinus yoki kosinus nimani belgilash kerak?

Siz ilmiy poke usuli yordamida almashtirishga harakat qilishingiz mumkin va agar hech narsa ishlamasa, uni boshqa funktsiya sifatida belgilang, ammo mavjud:

Umumiy ko'rsatma: siz majoziy ma'noda "noqulay holatda" bo'lgan funktsiyani belgilashingiz kerak..

Bu misolda talaba kosinus darajadan “azob chekadi”, sinus esa shunday erkin, o‘z-o‘zidan o‘tirishini ko‘ramiz.

Shunday qilib, keling, almashtirishni amalga oshiramiz:

Agar kimdir o'zgaruvchilarni o'zgartirish algoritmi va differentsialni topishda hali ham qiyinchiliklarga duch kelsa, siz darsga qaytishingiz kerak. Noaniq integralda o'zgaruvchilarni o'zgartirish usuli.

15-misol

Noaniq integralni toping.

Biz integrandni tahlil qilamiz, nima bilan belgilanishi kerak?
Keling, ko'rsatmalarimizni ko'rib chiqaylik:
1) Funksiya katta ehtimol bilan maxrajda;
2) Funktsiya "noqulay holatda".

Aytgancha, bu ko'rsatmalar nafaqat trigonometrik funktsiyalar uchun amal qiladi.

Ikkala mezon bo'yicha (ayniqsa, ikkinchisi ostida) sinus mos keladi, shuning uchun almashtirish o'zini taklif qiladi. Aslida, almashtirish allaqachon amalga oshirilishi mumkin, lekin avval nima qilish kerakligini aniqlab olish yaxshi bo'lar edi? Birinchidan, biz bitta kosinusni "chiqib" olamiz:

Biz "kelajak" differensialligimiz uchun zaxiraga olamiz

Va biz asosiy trigonometrik identifikatsiyadan foydalanib, sinus orqali ifodalaymiz:

Endi almashtirish:

Umumiy qoida: Agar integralda trigonometrik funksiyalardan biri (sinus yoki kosinus) bo'lsa g'alati daraja, keyin siz bir funktsiyani g'alati darajadan "tishlab" olishingiz va orqasida boshqa funktsiyani belgilashingiz kerak. Biz faqat kosinuslar va sinuslar mavjud bo'lgan integrallar haqida gapiramiz.

Ko'rib chiqilgan misolda bizda g'alati darajadagi kosinus bor edi, shuning uchun biz bir kosinusni darajadan chimchilab oldik va sinusni belgiladik.

16-misol

Noaniq integralni toping.

Darajalar ko'tarilmoqda =).
Bu o'z-o'zidan bajariladigan misol. To'liq yechim va javob dars oxirida.

Universal trigonometrik almashtirish

Umumjahon trigonometrik almashtirish - o'zgaruvchilar usulini o'zgartirishning keng tarqalgan holati. Siz "nima qilishni bilmasangiz" uni qo'llashga harakat qilishingiz mumkin. Lekin, aslida, uni qo'llash uchun ba'zi ko'rsatmalar mavjud. Umumjahon trigonometrik almashtirish qo'llanilishi kerak bo'lgan tipik integrallar quyidagi integrallardir: , , , va hokazo.

17-misol

Noaniq integralni toping.

Bu holda universal trigonometrik almashtirish quyidagi tarzda amalga oshiriladi. Keling, almashtiramiz: . Men maktubni ishlatmayman, lekin harfni ishlatmayman, bu qandaydir qoida emas, men yana qaror qabul qilishga o'rganib qolganman.

Bu erda farqni topish qulayroq, buning uchun tenglikdan men ifodalayman:
Men yoy tangensining ikkala qismiga osilganman:

Arktangens va tangens bir-birini bekor qiladi:

Shunday qilib:

Amalda, siz bunday tafsilotlarni bo'yashingiz mumkin emas, shunchaki tayyor natijadan foydalaning:

! Ifoda faqat sinuslar va kosinuslar ostida integral uchun "xes" bo'lsagina amal qiladi. (bu haqda keyinroq gaplashamiz) hamma narsa biroz boshqacha bo'ladi!

Sinuslar va kosinuslarni almashtirganda, biz quyidagi kasrlarga aylanamiz:
, , bu tengliklar mashhur trigonometrik formulalarga asoslanadi: ,

Shunday qilib, tozalash quyidagicha ko'rinishi mumkin:

Keling, universal trigonometrik almashtirishni amalga oshiramiz:

Mustaqil hal qilish uchun vazifalar ham bo'ladi, siz javoblarni ko'rishingiz mumkin.

Integratsiyani trigonometrik funktsiyalarning ko'paytmasidan yig'indiga aylantirish mumkin

X ning birinchi darajali sinuslari va kosinuslarining ko'paytmasi bo'lgan integrallarni, ya'ni ko'rinishdagi integrallarni ko'rib chiqing.

Taniqli trigonometrik formulalardan foydalanish

(2)
(3)
(4)
(31) ko'rinishdagi integrallarning har birini algebraik yig'indiga aylantirish va formulalar bo'yicha integrallash mumkin.

(5)

(6)

1-misol Toping

Yechim. Formulaga muvofiq (2) da

2-misol Toping trigonometrik funktsiyaning integrali

Yechim. Formulaga muvofiq (3) da

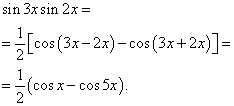
3-misol Toping trigonometrik funktsiyaning integrali

Yechim. Formulaga muvofiq (4) da biz integralning quyidagi o'zgarishini olamiz:

Formulani (6) qo'llash orqali biz olamiz

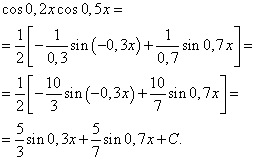
Xuddi shu argumentning sinus va kosinus darajalari hosilasining integrali

Keling, bir xil argumentning sinus va kosinus kuchlarining mahsuloti bo'lgan funktsiyalarning integrallarini ko'rib chiqaylik, ya'ni.

(7)

Xususan, ko'rsatkichlardan biri ( m yoki n) nolga teng bo'lishi mumkin.

Bunday funksiyalarni integrallashda kosinusning teng kuchini sinus bilan ifodalash mumkinligi, sinusning differentsiali esa cos ga teng ekanligidan foydalaniladi. x dx(yoki sinusning teng kuchi kosinus bilan ifodalanishi mumkin va kosinus differensial - sin x dx ) .

Ikkita holatni ajratib ko'rsatish kerak: 1) ko'rsatkichlardan kamida bittasi m Va n g'alati; 2) ikkala ko'rsatkich ham juft.

Birinchi holat, ya'ni ko'rsatkich bo'lsin n = 2k+ 1 - g'alati. Keyin, buni hisobga olgan holda

Integrasiya shunday berilganki, uning bir qismi faqat sinusning funksiyasi, ikkinchisi esa sinusning differensial qismidir. Endi o'zgaruvchining o'zgarishi bilan t= gunoh x yechim ko'phadni ga nisbatan integrallashga keltiriladi t. Agar faqat daraja bo'lsa m g'alati, keyin ham xuddi shunday qiling, omil gunohni ajrating x, integrandning qolgan qismini cos bilan ifodalaydi x va taxmin qilish t= cos x. Bu yondashuv qachon ham foydalanish mumkin sinus va kosinusning qisman kuchlarining integratsiyasi , Qachon ko'rsatkichlardan kamida bittasi toq . Gap shundaki sinus va kosinus kuchlarining nisbati ularning mahsulotining alohida holatidir : trigonometrik funktsiya integralning maxrajida bo'lsa, uning darajasi manfiy bo'ladi. Ammo qisman trigonometrik funktsiyalarning darajalari faqat juft bo'lgan holatlar ham mavjud. Ular haqida - keyingi paragraf.

Ikkala ko'rsatkich bo'lsa m Va n juft bo'lsa, trigonometrik formulalar qo'llaniladi

sinus va kosinusning ko'rsatkichlarini pasaytiring, shundan so'ng yuqoridagi kabi bir xil turdagi integral olinadi. Shuning uchun integratsiyani xuddi shu tarzda davom ettirish kerak. Agar juft ko'rsatkichlardan biri manfiy bo'lsa, ya'ni sinus va kosinusning juft darajalari nisbati hisobga olinsa, bu sxema mos kelmaydi. . Keyin integralni qanday o'zgartirish mumkinligiga qarab, o'zgaruvchining o'zgarishi qo'llaniladi. Bunday holat keyingi bobda ko'rib chiqiladi.

4-misol Toping trigonometrik funktsiyaning integrali

Yechim. Kosinusning ko'rsatkichi toq. Shuning uchun, tasavvur qiling

t= gunoh x(Keyin dt= cos x dx ). Keyin olamiz

Eski o'zgaruvchiga qaytsak, biz nihoyat topamiz

5-misol Toping trigonometrik funktsiyaning integrali

.

Yechim. Kosinusning ko'rsatkichi, oldingi misolda bo'lgani kabi, g'alati, lekin ko'proq. Tasavvur qiling

va o'zgaruvchining o'zgarishini amalga oshiring t= gunoh x(Keyin dt= cos x dx ). Keyin olamiz

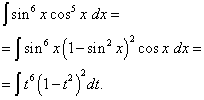
Qavslarni ochamiz

va oling

Eski o'zgaruvchiga qaytsak, biz yechimni olamiz

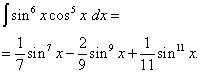
6-misol Toping trigonometrik funktsiyaning integrali

Yechim. Sinus va kosinusning darajalari juftdir. Shunday qilib, biz integralni quyidagicha o'zgartiramiz:

Keyin olamiz

Ikkinchi integralda biz o'zgaruvchini o'zgartiramiz, sozlash t= gunoh2 x. Keyin (1/2)dt= cos2 x dx . Demak,

Nihoyat, olamiz

O'zgaruvchilarni almashtirish usulidan foydalanish

O'zgaruvchan almashtirish usuli trigonometrik funksiyalarni integrallashda u sinus yoki kosinus birinchi darajali, tangens yoki kotangens bo‘lgan sinus va kosinusning ko‘paytmasi bo‘lgan integralda faqat sinus yoki faqat kosinus bo‘lgan hollarda qo‘llanilishi mumkin. bir va bir xil argumentning sinus va kosinusning juft darajalarining nisbati sifatida. Bunday holda, faqat gunoh emas, balki almashtirishni amalga oshirish mumkin x = t va gunoh x = t, balki tg x = t va ctg x = t .

8-misol Toping trigonometrik funktsiyaning integrali

.

Yechim. O'zgaruvchini o'zgartiramiz: , keyin . Olingan integral integrallar jadvali orqali osonlik bilan integrallanadi:

.

9-misol Toping trigonometrik funktsiyaning integrali

Yechim. Tangensni sinus va kosinus nisbatiga aylantiramiz:

O'zgaruvchini o'zgartiramiz: , keyin . Olingan integral jadval integrali minus belgisi bilan:

.

Asl o'zgaruvchiga qaytsak, biz nihoyat quyidagilarni olamiz:

.

10-misol Toping trigonometrik funktsiyaning integrali

Yechim. O'zgaruvchini o'zgartiramiz: , keyin .

Trigonometrik identifikatsiyani qo'llash uchun biz integralni o'zgartiramiz :

Biz o'zgaruvchini o'zgartiramiz, integral oldiga minus belgisini qo'yishni unutmang (yuqoriga qarang, nimaga teng dt). Keyinchalik, biz integralni omillarga ajratamiz va jadvalga muvofiq integrallaymiz:

Asl o'zgaruvchiga qaytsak, biz nihoyat quyidagilarni olamiz:

.

Trigonometrik funktsiyaning integralini o'zingiz toping va keyin yechimni ko'ring

Universal trigonometrik almashtirish

Universal trigonometrik almashtirish integrand oldingi bandlarda ko'rib chiqilgan holatlarga kirmaydigan hollarda qo'llanilishi mumkin. Asosan sinus yoki kosinus (yoki ikkalasi) kasrning maxrajida bo'lganda. Sinus va kosinusni asl burchakning yarmi tangensini o'z ichiga olgan boshqa ifoda bilan quyidagi tarzda almashtirish mumkinligi isbotlangan:

Ammo shuni yodda tutingki, universal trigonometrik almashtirish ko'pincha juda murakkab algebraik o'zgarishlarni talab qiladi, shuning uchun boshqa hech qanday usul ishlamasa, uni ishlatish yaxshiroqdir. Keling, universal trigonometrik almashtirish bilan birgalikda differentsial belgisi ostida almashtirish va noaniq koeffitsientlar usuli qo'llaniladigan misollarni ko'rib chiqaylik.

12-misol. Toping trigonometrik funktsiyaning integrali

.

Yechim. Yechim. Keling, foydalanaylik universal trigonometrik almashtirish. Keyin
.

Numerator va maxrajdagi kasrlarni ga ko'paytiramiz va ikkilikni olib, integral belgisi oldiga qo'yamiz. Keyin

Antiderivativlar jadvali ("integrallar"). Integrallar jadvali. Jadvalli noaniq integrallar. (Parametrli oddiy integrallar va integrallar). Qismlar bo'yicha integratsiya uchun formulalar. Nyuton-Leybnits formulasi.

Qismlar bo'yicha integratsiya uchun formulalar. Integratsiya qoidalari.

Hosiliy jadval. Jadval hosilalari. Mahsulotning hosilasi. Xususiyning hosilasi. Murakkab funktsiyaning hosilasi.

Agar x mustaqil o'zgaruvchi bo'lsa, u holda:

Logarifmlarning xossalari. Logarifmlarning asosiy formulalari. O'nlik (lg) va natural logarifmlar (ln).

Natural logarifm ln (logarifm asosi e = 2,718281828459045…) ln(e)=1; log(1)=0

Teylor seriyasi. Teylor qatoridagi funksiyani kengaytirish.

Ma'lum bo'lishicha, eng ko'p amalda yuzaga keladi matematik funktsiyalar o'zgaruvchining kuchlarini o'sish tartibida o'z ichiga olgan darajalar qatori shaklida ma'lum bir nuqtaga yaqin joyda har qanday aniqlik bilan ifodalanishi mumkin. Masalan, x=1 nuqtaga yaqin joyda:

Chaqirilgan qatorlarni ishlatganda Teylor qatorlari, algebraik, trigonometrik va ko'rsatkichli funktsiyalarni o'z ichiga olgan aralash funktsiyalarni sof algebraik funktsiyalar sifatida ifodalash mumkin. Seriyalar yordamida differentsiatsiya va integratsiya tez-tez tez amalga oshirilishi mumkin.

A nuqtaga yaqin joylashgan Teylor qatori quyidagi shakllarga ega:

1) , bu yerda f(x) funksiya x=a da barcha tartibli hosilalarga ega. R n - Teylor qatoridagi qolgan had ifoda bilan aniqlanadi

2)

qatorning k-koeffitsienti (x k da) formula bilan aniqlanadi

3) Teylor seriyasining alohida holati Maklaurin seriyasidir (=McLaren) (parchalanish a=0 nuqta atrofida sodir bo'ladi)

a=0 uchun

qator a'zolari formula bo'yicha aniqlanadi

Teylor seriyasini qo'llash shartlari.

1. f(x) funksiya Teylor qatorida (-R;R) oraliqda kengayishi uchun buning uchun Teylor formulasidagi qolgan had (Maklaurin (=McLaren)) zarur va yetarli. funktsiya belgilangan intervalda (-R;R) k →∞ da nolga intiladi.

2. Biz Teylor qatorini qurmoqchi bo'lgan yaqin nuqtada bu funktsiyaning hosilalari bo'lishi kerak.

Teylor seriyasining xossalari.

Agar f analitik funktsiya bo'lsa, u holda f sohasining istalgan a nuqtasida uning Teylor qatori a ning qaysidir qo'shnisida f ga yaqinlashadi.

Cheksiz differensiallanuvchi funksiyalar mavjudki, ularning Teylor qatorlari yaqinlashadi, lekin a ning istalgan qo‘shnisidagi funksiyadan farq qiladi. Masalan:

Teylor qatorlari yaqinlashtirish (yaqinlashma - bu ba'zi ob'ektlarni u yoki bu ma'noda asliga yaqinroq, ammo soddaroq bo'lgan boshqa ob'ektlar bilan almashtirishdan iborat bo'lgan ilmiy usul) polinomlar tomonidan qo'llaniladi. Xususan, chiziqlilashtirish ((linearisdan - chiziqli), yopiq chiziqli bo'lmagan tizimlarni taxminiy ko'rsatish usullaridan biri bo'lib, unda chiziqli bo'lmagan tizimni o'rganish chiziqli tizimni tahlil qilish bilan almashtiriladi, ma'lum ma'noda asl tizimga ekvivalent bo'ladi. .) tenglamalar Teylor qatoriga kengayib, birinchi tartibdagi barcha hadlarni kesib tashlash orqali yuzaga keladi.

Shunday qilib, deyarli har qanday funktsiya berilgan aniqlik bilan ko'phad sifatida ifodalanishi mumkin.

Maklaurin seriyalarida (=McLaren, Teylor 0 nuqta yaqinida) va 1 nuqta yaqinida Teylorda quvvat funksiyalarining ba'zi umumiy kengayishlariga misollar. Teylor va Maklaren qatorlarida asosiy funktsiyalarni kengaytirishning birinchi shartlari.

Maklaurin seriyasidagi quvvat funktsiyalarining ba'zi keng tarqalgan kengayishlariga misollar (= MacLaren, Teylor 0 nuqtasi yaqinida)

1-band atrofidagi ba'zi keng tarqalgan Teylor seriyali kengayishlariga misollar

Integrallarni qismlar bo'yicha yechish misollari batafsil ko'rib chiqiladi, ularning integrali ko'phad va ko'rsatkich (e ning x darajasiga) yoki sinus (sin x) yoki kosinus (cos x) ko'paytmasidir.

Shuningdek qarang: Qismlar bo'yicha integratsiya usuli
Noaniq integrallar jadvali
Noaniq integrallarni hisoblash usullari
Asosiy elementar funksiyalar va ularning xossalari

Qismlar formulasi bo'yicha integratsiya

Ushbu bo'limdagi misollarni echishda qismlar bo'yicha integratsiya formulasi qo'llaniladi:
;
.

Ko‘phad va sin x, cos x yoki e x ko‘paytmasi bo‘lgan integrallarga misollar.

Mana shunday integrallarga misollar:
, , .

Bunday integrallarni integrallash uchun ko‘phad u bilan, qolgani esa v dx bilan belgilanadi. Keyinchalik, biz qismlar bo'yicha integratsiya formulasini qo'llaymiz.

Quyida ushbu misollarning batafsil yechimi keltirilgan.

Integrallarni yechishga misollar

X ning kuchiga e ko'rsatkichli misol

Integralni aniqlang:
.

Differensial belgisi ostida ko'rsatkichni kiritamiz:
e - x dx = - e - x d(-x) = - d(e - x).

Biz qismlarga birlashamiz.

Bu yerga
.
Qolgan integral ham qismlarga integrallanadi.
.
.
.
Nihoyat bizda:
.

Integralni sinus bilan belgilashga misol

Integralni hisoblang:
.

Differensial belgisi ostida sinusni kiritamiz:

Biz qismlarga birlashamiz.

bu yerda u = x 2, v = cos(2x+3), du = ( x2 )′ dx

Qolgan integral ham qismlarga integrallanadi. Buning uchun differensial belgisi ostida kosinusni kiritamiz.


bu yerda u = x, v = gunoh (2x+3), du = dx

Nihoyat bizda:

Ko'phad va kosinus ko'paytmasiga misol

Integralni hisoblang:
.

Differensial belgisi ostida kosinusni kiritamiz:

Biz qismlarga birlashamiz.

bu erda u = x 2+3x+5, v = sin2x, du = ( x 2 + 3 x + 5 )′ dx